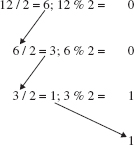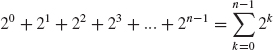CHAPTER 5
Recursion
One of the skills that distinguish a novice programmer from an experienced one is an understanding of recursion. The goal of this chapter is to give you a feel for situations in which a recursive method is appropriate. Along the way you may start to see the power and elegance of recursion, as well as its potential for misuse. Recursion plays a minor role in the Java Collections Framework: two of the sort methods are recursive, and there are several recursive methods in the TreeMap class. But the value of recursion extends far beyond these methods. For example, one of the applications of the stack class in Chapter 8 is the translation of recursive methods into machine code. The sooner you are exposed to recursion, the more likely you will be able to spot situations where it is appropriate—and to use it.
CHAPTER OBJECTIVES
- Recognize the characteristics of those problems for which recursive solutions may be appropriate.
- Compare recursive and iterative methods with respect to time, space, and ease of development.
- Trace the execution of a recursive method with the help of execution frames.
- Understand the backtracking design pattern.
5.1 Introduction
Roughly, a method is recursive if it contains a call to itself.1 From this description, you may initially fear that the execution of a recursive method will lead to an infinite sequence of recursive calls. But under normal circumstances, this calamity does not occur, and the sequence of calls eventually stops. To show you how recursive methods terminate, here is the skeleton of the body of a typical recursive method:
if (simplest case) solve directly else make a recursive call with a simpler case
This outline suggests that recursion should be considered whenever the problem to be solved has these two characteristics;
- The simplest case(s) can be solved directly.
- Complex cases of the problem can be reduced to simpler cases of the same form as the original problem.
Incidentally, if you are familiar with the Principle of Mathematical Induction, you may have observed that these two characteristics correspond to the base case and inductive case, respectively. In case you are not familiar with that principle, Section A2.5 of Appendix 2 is devoted to mathematical induction.
As we work through the following examples, do not be inhibited by old ways of thinking. As each problem is stated, try to frame a solution in terms of a simpler problem of the same form. Think recursively!
5.2 Factorials
Given a positive integer n, the factorial of n, written n!, is the product of all integers between n and 1, inclusive. For example,
4! = 4 * 3 * 2 * 1 = 24
and
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
Another way to calculate 4! is as follows:
4! = 4 * 3!
This formulation is not helpful unless we know what 3! is. But we can continue to calculate factorials in terms of smaller factorials (Aha!):
3! = 3 * 2!
2! = 2 * 1!
Note that 1! Can be calculated directly; its value is 1. Now we work backwards to calculate 4!:
2! = 2 * 1! = 2 * 1 = 2
3! = 3 * 2! = 3 * 2 = 6
Finally, we get
4! = 4 * 3! = 4 * 6 = 24
For n > 1, we reduce the problem of calculating n! to the problem of calculating (n - 1)!. We stop reducing when we get to 1!, which is simply 1. For the sake of completeness2, we define 0! to be 1.
There is a final consideration before we specify, test and define the factorial method: what about exceptions? If n is less than zero, we should throw an exception—illegalArgumentException is appropriate. And because n! is exponential in n, the value of n! will be greater than Long.MAX_VALUE for not-very-large values of n. In fact, 21!> Long.MAX_VALUE, so we should also throw IllegalArgumentException for n > 20.
Here is the method specification:
/** * Calculates the factorial of a non-negative integer, that is, the product of all * integers between 1 and the given integer, inclusive. The worstTime(n) is O(n), * where n is the given integer. * * @param n the integer whose factorial is calculated. * * @return the factorial of n * * @throws IllegalArgumentException if n is less than 0 or greater than 20 (note * that 21! > Long.MAX_VALUE). * */ public static long factorial (int n)
Note that factorial has a static modifier in its heading (see Section 2.1 in Chapter 2). Why? All the information needed by the method is provided by the parameter, and the only effect of a call to the method is the value returned. So a calling object would neither affect nor be affected by an invocation of the method. As noted in Chapter 2, we adhere to the test-first model. So the test class, based on the method specification only, is developed before the method itself is defined. Here is the test class, with special emphasis on boundary conditions, and including the usual stub within the test class itself:
import org.junit.*; import static org.junit.Assert.*; import org.junit.runner.Result; import static org.junit.runner.JUnitCore.runClasses; import java.util.*; public class FactorialTest { public static void main(String[ ] args) { Result result = runClasses (FactorialTest.class); System.out.println ("Tests run = " + result.getRunCount() + " Tests failed = " + result.getFailures()); } // method main import org.junit.*; @Test public void factorialTest1() { assertEquals (24, factorial (4)); } // method factorialTest1 @Test public void factorialTest2() { assertEquals (1, factorial (0)); } // method factorialTest2 @Test public void factorialTest3() { assertEquals (1, factorial (1)); } // method factorialTest3 @Test public void factorialTest4() { assertEquals (2432902008176640000L, factorial (20)); } // method factorialTest4 @Test (expected = IllegalArgumentException.class) public void factorialTest5() { factorial (21); } // method factorialTest5 @Test (expected = IllegalArgumentException.class) public void factorialTest6 () { factorial (-1); } // method factorialTest6 public static long factorial (int n) { throw new UnsupportedOperationException(); } // method factorial } // class FactorialTest
As expected, all tests of the factorial method failed.
We now define the factorial method. For the sake of efficiency, checking for values of n less than 0 or greater than 20 should be done just once, instead of during each recursive call. To accomplish this, we will define a wrapper method that throws an exception for out-of-range values of n, and (otherwise) calls a recursive method to actually calculate n!. Here are the method definitions.
public static long factorial (int n) { final int MAX_INT = 20; // because 21! > Long.MAX_VALUE final String ERROR_MESSAGE = "The value of n must be >= 0 and <= " + Integer.toString (MAX_INT); if (n < 0 || n > MAX_INT) throw new IllegalArgumentException (ERROR_MESSAGE); return fact (n); } // method factorial /** * Calculates n!. * * @param n the integer whose factorial is calculated. * * @return n!. * */ protected static long fact (int n) { if (n <= 1) return 1; return n * fact (n - 1); } // method fact
The testing of the wrapper method, factorial, incorporates the testing of the wrapped method, fact. The book's website has similar test classes for all recursive functions in this chapter.
Within the method fact, there is a call to the method fact, and so fact, unlike factorial, is a recursive method. The parameter n has its value reduced by 1 with each recursive call. But after the final call with n = 1, the previous values of n are needed for the multiplications. For example, when n = 4, the calculation of n * fact (n - 1) is postponed until the call to fact (n - 1) is completed. When this finally happens and the value 6 (that is, fact (3)) is returned, the value of 4 for n must be available to calculate the product.
Somehow, the value of n must be saved when the call to fact (n - 1) is made. That value must be restored after the call to fact (n - 1) is completed so that the value of n * fact (n - 1) can be calculated. The beauty of recursion is that the programmer need not explicitly handle these savings and restorings; the compiler and computer do the work.
5.2.1 Execution Frames
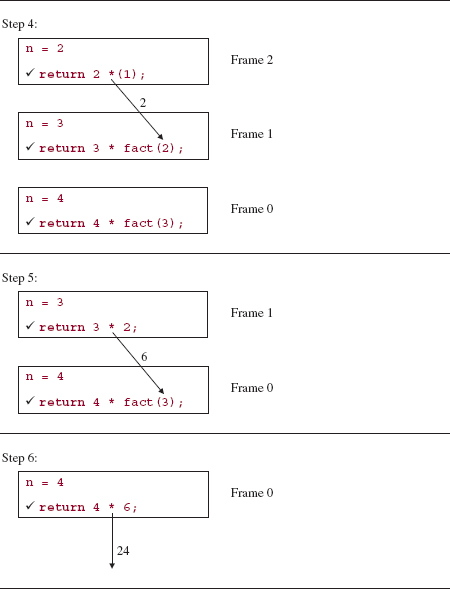
The trace of a recursive method can be illustrated through execution frames: boxes that contain information related to each invocation of the method. Each execution frame includes the values of parameters and other local variables. Each frame also has the relevant part of the recursive method's code—especially the recursive calls, with values for the arguments. When a recursive call is made, a new execution frame will be constructed on top of the current one; this new frame is destroyed when the call that caused its creation has been completed. A check mark indicates either the statement being executed in the current frame or the statement, in a previous frame, whose recursive call created (immediately or eventually) the current frame.
At any time, the top frame contains information relevant to the current execution of the recursive method. For example, here is a step-by-step, execution-frame trace of the fact method after an initial call of fact (4):
The analysis of the fact method is fairly clear-cut. The execution-time requirements correspond to the number of recursive calls. For any argument n, there will be exactly n - 1 recursive calls. During each recursive call, the if statement will be executed in constant time, so worstTime(n) is linear in n. Recursive methods often have an additional cost in terms of memory requirements. For example, when each recursive call to fact is made, the return address and a copy of the argument are saved. So worstSpace (n) is also linear in n.
Recursion can often make it easier for us to solve problems, but any problem that can be solved recursively can also be solved iteratively. An iterative method is one that has a loop instead of a recursive call. For example, here is an iterative method to calculate factorials. No wrapper method is needed because there are no recursive calls.
/** * Calculates the factorial of a non-negative integer, that is, the product of all * integers between 1 and the given integer, inclusive. The worstTime(n) is O(n), * where n is the given integer. * * @param n the non-negative integer whose factorial is calculated. * * @return the factorial of n * * @throws IllegalArgumentException if n is less than 0 or greater than 20 (note * that 21! > Long.MAX_VALUE). * */ public static long factorial (int n) { final int MAX_INT = 20; // because 21! > Long.MAX_VALUE final String ERROR_MESSAGE = "The value of n must be >= 0 and <= " + Integer.toString (MAX_INT); if (n < 0 || n > MAX_INT) throw new IllegalArgumentException (ERROR_MESSAGE); long product = n; if (n == 0) return 1; for (int i = n-1; i > 1; i-) product = product * i; return product; } // method factorial
This version of factorial passed all of the tests in FactorialTest. For this version of factorial, worstTime(n) is linear in n, the same as for the recursive version. But no matter what value n has, only three variables (n, product and i) are allocated in a trace of the iterative version, so worstSpace(n) is constant, versus linear in n for the recursive version. Finally, the iterative version follows directly from the definition of factorials, whereas the recursive version represents your first exposure to a new problem-solving technique, and that takes some extra effort.
So in this example, the iterative version of the factorial method is better than the recursive version. The whole purpose of the example was to provide a simple situation in which recursion was worth considering, even though we ultimately decided that iteration was better. In the next example, an iterative alternative is slightly less appealing.
5.3 Decimal to Binary
Humans count in base ten, possibly because we were born with ten fingers. Computers count in base two because of the binary nature of electronic switches. One of the tasks a computer performs is to convert from decimal (base ten) to binary (base two). Let's develop a method to solve a simplified version of this problem:
Given a nonnegative integer n, determine its binary equivalent.
For example, if n is 25, the binary equivalent is 11001 = 1*24 + 1*23 + 0*22 + 0*21 + 1*20. For a large int value such as one billion, the binary equivalent will have about 30 bits. But 30 digits of zeros and ones are too big for an int or even a long. So we will store the binary equivalent in a String object. The method specification is:
/** * * Determines the binary equivalent of a non-negative integer. The worstTime(n) * is O(log n), where n is the given integer. * * * @param n the non-negative integer, in decimal notation. * * @return a String representation of the binary equivalent of n. * * @throws IllegalArgumentException if n is negative. */ public static String getBinary (int n)
The test class for this method can be found on the book's website, and includes the following test:
@Test (expected = IllegalArgumentException.class)
public void getBinaryTest5()
{
getBinary (-1);
} // method getBinaryTest5
There are several approaches to solving this problem. One of them is based on the following observation:
The rightmost bit has the value of n%2; the other bits are the binary equivalent of n/2. (Aha!)
For example, if n is 12, the rightmost bit in the binary equivalent of n is 12% 2, namely, 0; the remaining bits are the binary equivalent of 12/2, that is, the binary equivalent of 6. So we can obtain all the bits as follows:
When the quotient is 1, the binary equivalent is simply 1. We concatenate (that is, join together) these bits from the bottom up, so that the rightmost bit will be joined last. The result would then be
1100
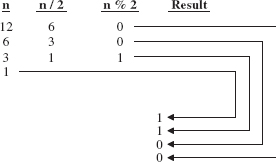
The following table graphically illustrates the effect of calling getBinary (12):
This discussion suggests that we must perform all of the calculations before we return the result. Speaking recursively, we need to calculate the binary equivalent of n/2 before we append the value of n% 2. In other words, we need to append the result of n%2 to the result of the recursive call.
We will stop when n is 1 or 0, and 0 will occur only if n is initially 0. As we did in Section 5.2, we make getBinary a wrapper method for the recursive getBin method. The method definitions are:
public static String getBinary (int n) { if (n < 0) throw new IllegalArgumentException(); return getBin (n); } // method getBinary public static String getBin (int n) { if (n <= 1) return Integer.toString (n); return getBin (n / 2) + Integer.toString (n % 2); } // method getBin
We are assured that the simple case of n <= 1 will eventually be reached because in each execution of the method, the argument to the recursive call is at most half as big as the method parameter's value.
Here is a step-by-step, execution-frame trace of the getBin method after an initial call of getBin (12):
The final value returned is the string:
1100
And that is the binary equivalent of 12.
As we noted earlier, the order of operands in the string expression of the last return statement in getBin enables us to postpone the final return until all of the bit values have been calculated. If the order had been reversed, the bits would have been returned in reverse order. Recursion is such a powerful tool that the effects of slight changes are magnified.
As usually happens with recursive methods, the time and space requirements for getBin are estimated by the number of recursive calls. The number of recursive calls is the number of times that n can be divided by 2 until n equals 1. As we saw in Section 3.1.2 of Chapter 3, this value is floor(log2 n), so worstTime(n) and worstSpace(n) are both logarithmic in n.
A user can call the getBinary method from the following run method (in a BinaryUser class whose main method simply calls new BinaryUser().run() ):
public static void run() { final int SENTINEL=-1; final String INPUT_PROMPT= " n Please enter a non-negative base-10 integer(or"+ SENTINEL+"to quit):"; final String RESULT_MESSAGE="The binary equivalent is "; Scanner sc = new Scanner (System.in); int n; while (true) { try { System.out.print (INPUT_PROMPT); n = sc.nextInt(); if (n == SENTINEL) break; System.out.println (RESULT_MESSAGE + getBinary (n)); } // try catch (Exception e) { System.out.println (e); sc.nextLine(); }// catch Exception }// while } // method run
You are invited to develop an iterative version of the getBinary method. (See Programming Exercise 5.2.) After you have completed the iterative method, you will probably agree that it was somewhat harder to develop than the recursive method. This is typical, and probably obvious: recursive solutions usually flow more easily than iterative solutions to those problems for which recursion is appropriate. Recursion is appropriate when larger instances of the problem can be reduced to smaller instances that have the same form as the larger instances.
You are now prepared to do Lab 7: Fibonacci Numbers
For the next problem, an iterative solution is much harder to develop than a recursive solution.
5.4 Towers of Hanoi
In the Towers of Hanoi game, there are three poles, labeled 'A', 'B' and 'C', and several, different-sized, numbered disks, each with a hole in the center. Initially, all of the disks are on pole 'A', with the largest disk on the bottom, then the next largest, and so on. Figure 5.1 shows the initial configuration if we started with four disks, numbered from smallest to largest.
FIGURE 5.1 The starting position for the Towers of Hanoi game with four disks
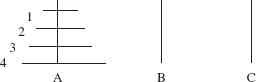
The object of the game is to move all of the disks from pole 'A' to pole 'B'; pole 'C' is used for temporary storage3. The rules of the game are:
- Only one disk may be moved at a time.
- No disk may ever be placed on top of a smaller disk.
- Other than the prohibition of rule 2, the top disk on any pole may be moved to either of the other two poles.
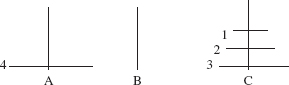
FIGURE 5.2 The game configuration for the Towers of Hanoi just before moving disk 4 from pole 'A' to pole 'B'
We will solve this problem in the following generalization: Show the steps to move n disks from an origin pole to a destination pole, using the third pole as a temporary. Here is the method specification for this generalization:
/** * Determines the steps needed to move n disks from an origin to a destination. * The worstTime(n) is O(2n). * * @param n the number of disks to be moved. * @param orig the pole where the disks are originally. * @param dest the destination pole * @param temp the pole used for temporary storage. * * @return a String representation of the moves needed, where each * move is in the form "Move disk ? from ? to ? ". * * @throws IllegalArgumentException if n is less than or equal to 0. */ public static String moveDisks (int n, char orig, char dest, char temp)
The test class for moveDisks can be found on the book's website, and includes the following test:
@Test
public void moveDisksTest1()
{
assertEquals ("Move disk 1 from A to B
Move disk 2 from A to C n" +
"Move disk 1 from B to C
Move disk 3 from A to B n" +
"Move disk 1 from C to A
Move disk 2 from C to B n" +
"Move disk 1 from A to B
", moveDisks (3, 'A', 'B', 'C'));
} // method moveDisksTest1
Let's try to play the game with the initial configuration given in Figure 5.1. We are immediately faced with a dilemma: Do we move disk 1 to pole 'B' or to pole 'C'? If we make the wrong move, we may end up with the four disks on pole 'C' rather than on pole 'B'.
Instead of trying to figure out where disk 1 should be moved initially, we will focus our attention on disk 4, the bottom disk. Of course, we can't move disk 4 right away, but eventually, disk 4 will have to be moved from pole 'A' to pole 'B'. By the rules of the game, the configuration just before moving disk 4 must be as shown in Figure 5.2.
Does this observation help us to figure out how to move 4 disks from 'A' to 'B'? Well, sort of. We still need to determine how to move three disks (one at a time) from pole 'A' to pole 'C'. We can then move disk 4 from 'A' to 'B'. Finally, we will need to determine how to move three disks (one at a time) from 'C' to 'B'.
The significance of this strategy is that we have reduced the problem from figuring how to move four disks to one of figuring how to move three disks. (Aha!) We still need to determine how to move three disks from one pole to another pole.
But the above strategy can be re-applied. To move three disks from, say, pole 'A' to pole 'C', we first move two disks (one at a time) from 'A' to 'B', then we move disk 3 from 'A' to 'C', and finally, we move two disks from 'B' to 'C'. Continually reducing the problem, we eventually face the trivial task of moving disk 1 from one pole to another.
There is nothing special about the number 4 in the above approach. For any positive integer n we can describe how to move n disks from pole 'A' to pole 'B': if n = 1, we simply move disk 1 from pole 'A' to pole 'B'. For n > 1,
- First, move n — 1 disks from pole 'A' to pole 'C', using pole 'B' as a temporary.
- Then move disk n from pole 'A' to pole 'B'.
- Finally, move n — 1 disks from pole 'C' to pole 'B', using pole 'A' as a temporary.
This does not quite solve the problem because, for example, we have not described how to move n — 1 disks from 'A' to 'C'. But our strategy is easily generalized by replacing the constants 'A', 'B', and 'C' with variables origin, destination, and temporary. For example, we will initially have
origin = 'A' destination = 'B' temporary = 'C'
Then the general strategy for moving n disks from origin to destination is as follows:
If n is 1, move disk 1 from origin to destination.
Otherwise,
- Move n — 1 disks (one at a time) from origin to temporary;
- Move disk n from origin to destination;
- Move n — 1 disks (one at a time) from temporary to destination.
The following recursive method incorporates the above strategy for moving n disks. If n = 1, the String representing the move, namely, "Move disk 1 from"+orig+"to" + dest + " " is simply returned. Otherwise, the String object returned consists of three String objects concatenated together, namely, the strings returned by
move (n - 1, orig, temp, dest) "Move disk " + n + " from " + orig + " to " + dest + " " move (n - 1, temp, dest, orig)
When the final return is made, the return value is the complete sequence of moves. This String object can then be printed to the console window, to a GUI window, or to a file. For the sake of efficiency, the test for n 0 is made—once—in a wrapper method moveDisks that calls the move method. Here is the method specification for moveDisks:
/** * Determines the steps needed to move disks from an origin to a destination. * The worstTime(n) is O(2n). * * @param n the number of disks to be moved. * @param orig the pole where the disks are originally. * @param dest the destination pole * @param temp the pole used for temporary storage. * * @return a String representation of the moves needed. * * @throws IllegalArgumentException if n is less than or equal to 0. */ public static String moveDisks (int n, char orig, char dest, char temp)
The test class for moveDisks can be found on the book's website. The definitions of moveDisks and move are as follows:
public static String moveDisks (int n, char orig, char dest, char temp) { if (n <= 0) throw new IllegalArgumentException(); return move (n, orig, dest, temp); } // method moveDisks /** * Determines the steps needed to move disks from an origin to a destination. * The worstTime(n) is O(2n). * * @param n the number of disks to be moved. * @param orig the pole where the disks are originally. * @param dest the destination pole * @param temp the pole used for temporary storage. * * @return a String representation of the moves needed. * */ public static String move (int n, char orig, char dest, char temp) { final String DIRECT_MOVE = "Move disk " + n + " from " + orig + " to " + dest + " "; if (n == 1) return DIRECT_MOVE; String result = move (n - 1, orig, temp, dest); result += DIRECT_MOVE; result += move (n - 1, temp, dest, orig); return result; } // method move
It is difficult to trace the execution of the move method because the interrelationship of parameter and argument values makes it difficult to keep track of which pole is currently the origin, which is the destination and which is the temporary. In the following execution frames, the parameter values are the argument values from the call, and the argument values for subsequent calls come from the method code and the current parameter values. For example, suppose the initial call is:
move (3, A, B, C );
Then the parameter values at step 0 will be those argument values, so we have:
n = 3 orig = 'A' dest = 'B' temp = 'C'
Because n is not equal to 1, the recursive part is executed:
String result = move (n - 1, orig, temp, dest);
result += DIRECT_MOVE;
result += move (n - 1, temp, dest, orig);
return result;
The values of those arguments are obtained from the parameters' values, so the statements are equivalent to:
String result = move (2, 'A', 'C', 'B' );
result = "Move disk 3 from A to B
";
result = move (2, 'C', 'B', 'A' );
return result;
Make sure you understand how to obtain the parameter values and argument values before you try to follow the trace given below.
Here is a step-by-step, execution-frame trace of the move method when the initial call is:
move (3, 'A', 'B', 'C'),
value of result
Notice the disparity between the relative ease in developing the recursive method and the relative difficulty in tracing its execution. Imagine what it would be like to trace the execution of move (15, 'A', 'B', 'C'). Fortunately, you need not undergo such torture. Computers handle this type of tedious detail very well. You "merely" develop the correct program and the computer handles the execution. For the move method—as well as for the other recursive methods in this chapter—you can actually prove the correctness of the method. See Exercise 5.5.
The significance of ensuring the precondition (see the @throws specification) is illustrated in the move method. For example, let's see what would happen if no exception were thrown and move were called with 0 as the first argument. Since n would have the value 0, the condition of the if statement would be false, and there would be a call to move (-1,…). Within that call, n would still be unequal to 1, so there would be a call to move (-2,…) then to move (-3,….), move (-4,…), move (-5,…), and so on. Eventually, saving all those copies of n would overflow an area of memory called the stack. This phenomenon known is as infinite recursion. A StackOverflowError—not an exception—is generated, and the execution of the project terminates. In general, infinite recursion is avoided if each recursive call makes progress toward a "simplest" case. And, just to be on the safe side, the method should throw an exception if the precondition is violated.
A recursive method does not explicitly describe the considerable detail involved in its execution. For this reason, recursion is sometimes referred to as "the lazy programmer's problem-solving tool." If you want to appreciate the value of recursion, try to develop an iterative version of the move method. Programming Project 5.1 provides some hints.
5.4.1 Analysis of the move Method
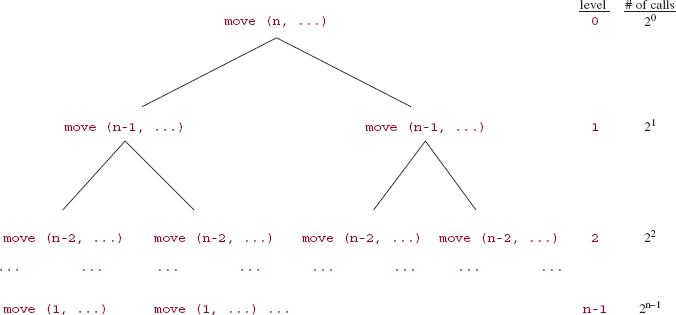
What about worstTime(n)? In determining the time requirements of a recursive method, the number of calls to the method is of paramount importance. To get an idea of the number of calls to the move method, look at the tree in Figure 5.3.
As illustrated in Figure 5.3, the first call to the move method has n as the first argument. During that call, two recursive calls to the move method are made, and each of those two calls has n - 1 as the first argument. From each of those calls, we get two more calls to move, and each of those four calls has n - 2 as the first argument. This process continues until, finally, we get calls with 1 as the first argument.
FIGURE 5.3 A schematic of the number of calls to the move method
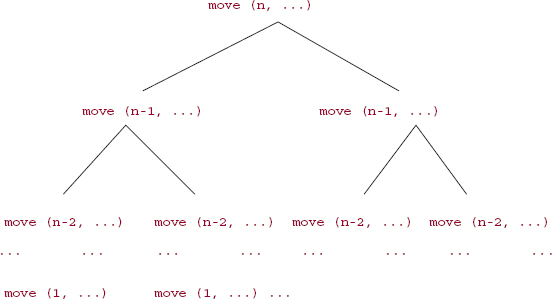
To calculate the total number of calls to the move method, we augment the tree in Figure 5.3 by identifying levels in the tree, starting with level 0 at the top, and include the number of calls at each level. At level 0, the number of calls is 1(= 2°). At level 1, the number of calls is 2 (= 21). In general, at level k there are 2k calls to the move method. Because there are n levels in the tree and the top is level 0, the bottom must be level n — 1, where there are 2n—1 calls to the move method. See Figure 5.4.
From Figure 5.4, we see that the total number of calls to the move method is
By Example A2.6 in Appendix 2, this sum is equal to 2n — 1. That is, the number of calls to the move method is 2n — 1. We conclude that, for the move method, worstTime(n) is exponential in n; specifically, worstTime(n) is Θ(2n). In fact, since any definition of the move method must return a string that has 2n — 1 lines, the Towers of Hanoi problem is intractable. That is, any solution to the Towers of Hanoi problem must take exponential time.
The memory requirements for move are modest because although space is allocated when move is called, that space is deallocated when the call is completed. So the amount of additional memory needed for move depends, not simply on the number of calls to move, but on the maximum number of started-but-not-completed calls. We can determine this number from the execution frames. Each time a recursive call is made, another frame is constructed, and each time a return is made, that frame is destroyed. For example, if n = 3 in the original call to move, then the maximum number of execution frames is 3. In general, the maximum number of execution frames is n. So worstSpace(n) is linear in n.
We now turn our attention to a widely known search technique: binary search. We will develop a recursive method to perform a binary search on an array. Lab 9 deals with the development of an iterative version of a binary search.
FIGURE 5.4 The relationship between level and number of calls to the move method in the tree from Figure 5.3
5.5 Searching an Array
Suppose you want to search an n-element array for an element. We assume that the element class implements the Comparable<T> interface (in java.lang):
public interface Comparable<T> { /** * Returns an int less than, equal to or greater than 0, depending on * whether the calling object is less than, equal to or greater than a * specified object. * * @param obj - the specified object that the calling object is compared to. * * @return an int value less than, equal to, or greater than 0, depending on * whether the calling object is less than, equal to, or greater than * obj, respectively. * * @throws ClassCastException - if the calling object and obj are not in the * same class. * */ public int compareTo(T obj) } // interface Comparable<T>
For example, the String class implements the Comparable<String> interface, so we can write the following:
String s = "elfin";
System.out.println (s.compareTo ("elastic"));
The output will be greater than 0 because "elfin" is lexicographically greater than "elastic"; in other words, "elfin" comes after "elastic" according to the Unicode values of the characters in those two strings. Specifically, the 'f" in "elfin" comes after the 'a' in "elastic".
The simplest way to conduct the search is sequentially: start at the first location, and keep checking successively higher locations until either the element is found or you reach the end of the array. This search strategy, known as a sequential search, is the basis for the following generic algorithm (that is, static method):
/** * Determines whether an array contains an element equal to a given key. * The worstTime(n) is O(n). * * @param a the array to be searched. * @param key the element searched for in the array a. * * @return the index of an element in a that is equal to key, if such an element * exists; otherwise, -1. * * @throws ClassCastException, if the element class does not implement the * Comparable interface. * */ public static int sequentialSearch (Object[ ] a, Object key) { for (int i = 0; i < a.length; i++) if (((Comparable) a [i]).compareTo (key) == 0) return i; return -1; } // sequentialSearch
Because the element type of the array parameter is Object, the element type of the array argument can be any type. But within the sequentialSearch method, the compiler requires that a [i] must be cast to a type that implements the Comparable<Object> interface. For the sake of simplicity, we use the "raw" type Comparable instead of the equivalent Comparable<Object>.
The sequentialSearch method is not explicitly included in the Java Collections Framework. But it is the basis for several of the method definitions in the ArrayList and LinkedList classes, which are in the framework.
For an unsuccessful sequential search of an array, the entire array must be scanned. So both worstTime(n) and averageTime(n) are linear in n for an unsuccessful search. For a successful sequential search, the entire array must be scanned in the worst case. In the average case, assuming each location is equally likely to house the element sought, we probe about n/2 elements. We conclude that for a successful search, both worstTime(n) and averageTime(n) are also linear in n.
Can we improve on these times? Definitely. In this section we will develop an array-based search technique for which worstTime(n) and averageTime(n) are only logarithmic in n. And in Chapter 14, we will encounter a powerful search technique—hashing—for which averageTime(n) is constant, but worstTime(n) is still linear in n.
Given an array to be searched and a value to be searched for, we will develop a binary search, so called because the size of the region searched is divided by two at each stage until the search is completed. Initially, the first index in the region is index 0, and the last index is at the end of the array. One important restriction is this: A binary search requires that the array be sorted.
We assume, as above, that the array's element class implements the Comparable interface.
Here is the method specification, identical to one in the Arrays class in the package java.util:
/** * Searches the specified array for the specified object using the binary * search algorithm. The array must be sorted into ascending order * according to the <i>natural ordering</i> of its elements (as by * <tt>Sort(Object[ ]</tt>), above) prior to making this call. If it is * not sorted, the results are undefined. If the array contains multiple * elements equal to the specified object, there is no guarantee which * one will be found. The worstTime(n) is O(log n). * * @param a the array to be searched. * @param key the value to be searched for. * * @return index of the search key, if it is contained in the array; * otherwise, <tt>(-(<i>insertion point</i>) - 1)</tt>. The * <i>insertion point</i> is defined as the point at which the * key would be inserted into the array: the index of the first * element greater than the key, or <tt>a.length</tt>, if all * elements in the array are less than the specified key. Note * that this guarantees that the return value will be >= 0 if * and only if the key is found. * * @throws ClassCastException if the array contains elements that are not * <i>mutually comparable</i> (for example, strings and integers), * or the search key in not mutually comparable with the elements * of the array. * @see Comparable * @see #sort(Object[ ]) */ public static int binarySearch (Object[ ] a, Object key)
In javadoc, the html tag <tt> signifies code, <i>signifies italics, and Θgt; signifies the greater than symbol, '>'. The symbol '>' by itself would be interpreted as part of an html tag. The "#" in one of the @see lines creates a link to the given sort method in the document generated through javadoc; that line expands to
See Also:
sort(Object[])
The BinarySearchTest class is available from the book's website, and includes the following test (names is the array of String elements from Figure 5.5):
@Test
public void binarySearchTest6()
{
assertEquals (-11, binarySearch (names, "Joseph"));
} // method binarySearchTest6
For the sake of utilizing recursion, we will focus on the first and last indexes in the region being searched. Initially, first = 0 and last = a.length - 1. So the original version of binarySearch will be a wrapper that simply calls
return binarySearch (a, 0, a.length - 1, key);
The corresponding method heading is
public static int binarySearch (Object[ ] a, int first, int last, Object key)
For defining this version of the binarySearch method, the basic strategy is this: We compare the element at the middle index of the current region to the key sought. If the middle element is less than the key, we recursively search the array from the middle index + 1toindex last. If the middle element is greater than the key, we recursively search the array from index first to the middle index — 1. If the middle element is equal to the key, we are done.
Assume, for now, that first <= last. Later on we'll take care of the case where first > last. Following the basic strategy given earlier, we start by finding the middle index:
int mid = (first + last) >> 1;
The right-hand-side expression uses the right-shift bitwise operator, >>, to shift the binary representation of (first + last) to the right by 1. This operation is equivalent to, but executes faster than
int mid = (first + last) / 2;
The middle element is at index mid in the array a. We need to compare (the element referenced by) a [mid] to (the element referenced by) key. The compareTo method is ideal for the comparison, but that method is not defined in the element class, Object. Fortunately, the compareTo method is defined in any class that implements the Comparable interface. So we cast a [mid] to a Comparable object and then call the method compareTo:
Comparable midVal = (Comparable)a [mid];
int comp = midVal.compareTo (key);
If the result of this comparison is < 0, perform a binary search on the region from mid +1 to last and return the result of that search. That is:
if (comp < 0) return binarySearch (a, mid + 1, last, key);
Otherwise, if comp > 0, perform a binary search on the region from first to mid-1 and return the result. That is,
if (comp > 0) return binarySearch (a, first, mid - 1, key);
Otherwise, return mid, because comp == 0 and so a [mid] is equal to key.
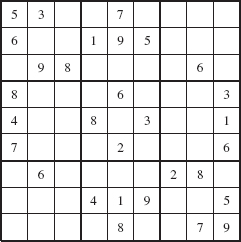
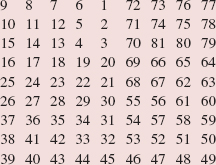
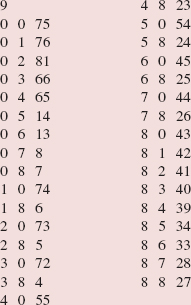
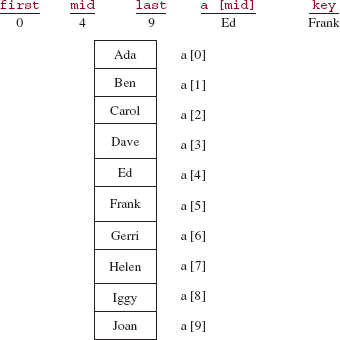
For example, let's follow this strategy in searching for "Frank" in the array names shown in Figure 5.5. That figure shows the state of the program when the binarySearch method is called to find "Frank".
The assignment:
mid = (first + last) >> 1;
gives mid the value (0 + 9)/2, which is 4.
FIGURE 5.5 The state of the program at the beginning of the method called binarySearch (names, 0, 9, "Frank"). The parameter list is Object[ ] a, int first, int last and Object key. (For simplicity, we pretend that names is an array of Strings rather than an array of references to Strings)
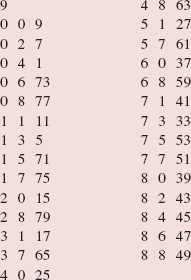
The middle element, "Ed", is less than "Frank", so we perform a binary search of the region from mid + 1 to last. The call is
binarySearch (a, mid + 1, last, key);
The parameter first gets the value of the argument mid + 1. During this execution of binarySearch, the assignment
mid = (first + last) >> 1;
gives mid the value (5 + 9)/2, which is 7, so midVal is "Helen". See Figure 5.6.
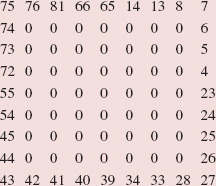
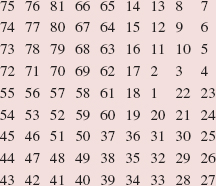
The middle element, "Helen", is greater than "Frank", so a binary search is performed on the region from indexes 5 through 6. The call is
binarySearch (a, first, mid - 1, key);
The parameter last gets the value of the argument mid - 1. During this execution of binarySearch, the assignment
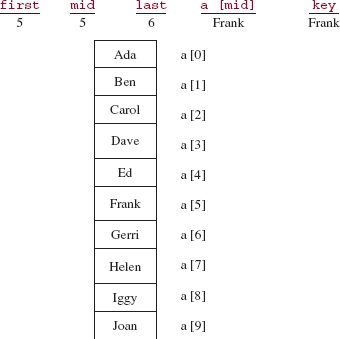
mid = (first + last) >> 1;
gives mid the value (5 + 6)/2, which is 5, so the middle element is "Frank". See Figure 5.7.
Success! The middle element is equal to key, so the value returned is mid, the index of the middle element.
The only unresolved issue is what happens if the array does not have an element equal to key. In that case, we want to return -insertion Point - 1, where insertionPoint is the index where key could be inserted without disordering the array. The reason we don't return -insertionPoint is that we would have an ambiguity if insertionPoint were equal to 0: a return of 0 could be interpreted as the index where key was found.
How can we determine what value to give insertionPoint? If first > last initially, we must have an empty region, with first = 0 and last = −1, so insertionPoint should get the value of first. Otherwise we must have first <= last during the first call to binarySearch. Whenever first <= last at the beginning of a call to binarySearch, we have
FIGURE 5.6 The state of the program at the beginning of the binary search for "Frank" in the region from indexes 5 through 9
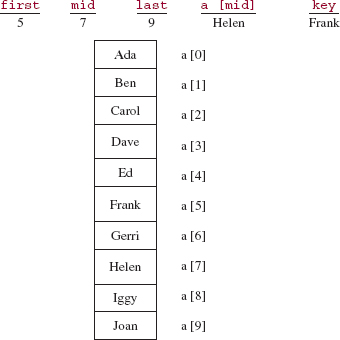
FIGURE 5.7 The state of the program at the beginning of the binary search for "Frank" in the region from indexes 5 through 6
first <= mid <= last
So mid + 1 < = last + 1 and first - 1 < = mid - 1.
If comp < 0, we call
binarySearch (a, mid + 1, last, key);
At the beginning of that call, we have
first <= last + 1
On the other hand, if comp > 0, we call
binarySearch (a, first, mid - 1, key);
At the beginning of that call, we have
first-1<= last
In either case, at the beginning of the call to binarySearch, we have
first <= last + 1
So when we finally get first > last, we must have
first = last + 1
But any element with an index less than first must be less than key, and any element with an index greater than last must be greater than key, so when we finish, first is the smallest index of any element greater than key. That is where key should be inserted.
Here is the complete definition:
public static int binarySearch(Object[ ] a, int first, int last, Object key) { if (first <= last) { int mid = (first + last) >> 1; Comparable midVal = (Comparable)a [mid]; int comp = midVal.compareTo (key); if (comp < 0) return binarySearch (a, mid + 1, last, key); if (comp > 0) return binarySearch (a, first, mid - 1, key); return mid; // key found } // if first <= last return -first - 1; // key not found; belongs at a[first] } // method binarySearch
Here is a BinarySearchUser class that allows an end-user to enter names for which a given array will be searched binarily:
public class BinarySearchUser { public static void main (String[ ] args) { new BinarySearchUser ().run(); } // method main public void run() { final String ARRAY_MESSAGE = "The array on which binary searches will be performed is: n" + "Ada, Ben, Carol, Dave, Ed, Frank, Gerri, Helen, Iggy, Joan"; final String SENTINEL = "***"; final String INPUT_PROMPT = " Please enter a name to be searched for in the array (or " + SENTINEL + " to quit): "; final String[ ] names = {"Ada", "Ben", "Carol", "Dave", "Ed", "Frank", "Gerri", "Helen", "Iggy", "Joan"}; final String FOUND = "That name was found at index "; final String NOT_FOUND = "That name was not found, but could be " + "inserted at index "; String name; Scanner sc = new Scanner (System.in); int index; System.out.println (ARRAY_MESSAGE); while (true) { System.out.print (INPUT_PROMPT); name = sc.next(); if (name.equals(SENTINEL)) break; index = binarySearch (names, 0, names.length - 1, name); if (index >= 0) System.out.println (FOUND + index); else System.out.println (NOT_FOUND + (-index - 1)); } // while } // method run public static int binarySearch(Object[ ] a, int first, int last, Object key) { if (first <= last) { int mid = (first + last) >> 1; Comparable midVal = (Comparable)a [mid]; int comp = midVal.compareTo (key); if (comp < 0) return binarySearch (a, mid + 1, last, key); if (comp > 0) return binarySearch (a, first, mid - 1, key); return mid; // key found } // if first <= last return -first - 1; // key not found; belongs at a[first] } // method binarySearch } // class BinarySearchUser
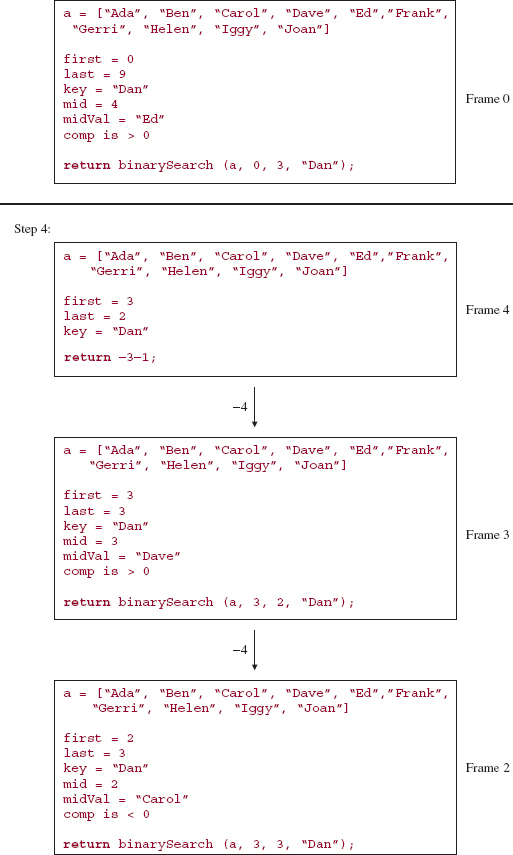
Here is a step-by-step, execution-frame trace of the binarySearch method after an initial call of
binarySearch (names, 0, 9, "Dan");
Note that "Dan" is not in the array names.
How long does the binarySearch method take? We need to make a distinction between an unsuccessful search, in which the element is not found, and a successful search, in which the element is found. We start with an analysis of an unsuccessful search.
During each execution of the binarySearch method in which the middle element is not equal to key, the size of the region searched during the next execution is, approximately, halved. If the element sought is not in the array, we keep dividing by 2 as long as the region has at least one element. Let n represent the size of the region. The number of times n can be divided by 2 until n = 0 is logarithmic in n —this is, basically, the Splitting Rule from Chapter 3. So for a failed search, worstTime(n) is logarithmic in n. Since we are assuming the search is unsuccessful, the same number of searches will be performed in the average case as in the worst case, so averageTime(n) is logarithmic in n for a failed search.
The worst case for a successful search requires one less call to the binarySearch method than the worst case (or average case) for an unsuccessful search. So for a successful search, worstTime(n) is still logarithmic in n. In the average case for a successful search, the analysis—see Concept Exercise 5.15—is more complicated, but the result is the same: averageTime(n) is logarithmic in n.
During each call, a constant amount of information is saved: the entire array is not saved, only a reference to the array. So the space requirements are also logarithmic in n, for both successful and unsuccessful searches and for both the worst case and the average case.
In the Arrays class of the java.util package, there is an iterative version of the binary search algorithm. In Lab 8, you will conduct an experiment to compare the time to recursively search an array of int s, iteratively search an array of int s, and iteratively search an array of Integer s. Which of the three do you think will be slowest?
You are now prepared to do Lab 8: Iterative Binary Search
Lab 9 introduces another recursive method whose development is far easier than its iterative counterpart. The method for generating permutations is from Roberts' delightful book, Thinking Recursively [Roberts, 1986].
You are now prepared to do Lab 9: Generating Permutations
Section 5.6 deals with another design pattern (a general strategy for solving a variety of problems): backtracking. You have employed this strategy whenever you had to re-trace your steps on the way to some goal. The BackTrack class also illustrates the value of using interfaces.
5.6 Backtracking
The basic idea with backtracking is this: From a given starting position, we want to reach a goal position. We repeatedly choose, maybe by guessing, what our next position should be. If a given choice is valid—that is, the new position might be on a path to the goal—we advance to that new position and continue. If a choice leads to a dead end, we back up to the previous position and make another choice. Backtracking is the strategy of trying to reach a goal by a sequence of chosen positions, with a re-tracing in reverse order of positions that cannot lead to the goal.
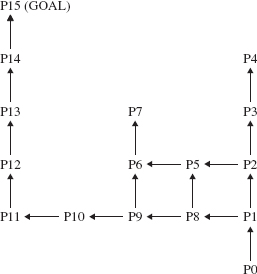
For example, look at the picture in Figure 5.8. We start at position P0 and we want to find a path to the goal state, P14. We are allowed to move in only two directions: north and west. But we cannot "see" any farther than the next position. Here is a strategy: From any position, we first try to go north; if we are unable to go north, we try to go west; if we are unable to go west, we back up to the most recent position where we chose north and try to choose west instead. We never re-visit a position that has been discovered to be a dead end. The positions in Figure 5.8 are numbered in the order they would be tried according to this strategy.
Figure 5.8 casts some light on the phrase "re-tracing in reverse order." When we are unable to go north or west from position P4, we first back up to position P3, where west is not an option. So we back up to P2. Eventually, this leads to a dead end, and we back up to P1, which leads to the goal state.
When a position is visited, it is marked as possibly being on a path to the goal, but this marking must be undone if the position leads only to a dead end. That enables us to avoid re-visiting any dead-end position. For example, in Figure 5.8, P5 is not visited from P8 because by the time we got to P8, P5 had already been recognized as a dead end.
We can now refine our strategy. To try to reach a goal from a given position, enumerate over all positions directly accessible from the given position, and keep looping until either a goal has been reached or we can no longer advance to another position. During each loop iteration, get the next accessible position. If that position may be on a path to a goal, mark that position as possibly leading to a goal and, if it is a goal, the search has been successful; otherwise, attempt to reach a goal from that position, and mark the position as a dead end if the attempt fails.
FIGURE 5.8 Backtracking to obtain a path to a goal. The solution path is P0, P1, P8, P9, P10, P11, P12, P13, P14, P15
Make sure you have a good understanding of the previous paragraph before you proceed. That paragraph contains the essence of backtracking. The rest of this section and Section 5.6.1 are almost superfluous by comparison.
Instead of developing a backtracking method for a particular application, we will utilize a generalized backtracking algorithm from Wirth [1976, p.138]. We then demonstrate that algorithm on a particular application, maze searching. Four other applications are left as programming projects in this chapter. And Chapter 15 has another application of backtracking: a programming project for searching a network. Backtracking is a design pattern because it is a generic programming technique that can be applied in a variety of contexts.
The BackTrack class below is based on one in Noonan [2000]. The details of the application class will be transparent to the BackTrack class, which works through an interface, Application. The Application interface will be implemented by the particular application.
A user (of the BackTrack class) supplies:
- the class implementing the Application interface (note: to access the positions available from a given position, the iterator design-pattern is employed, with a nested iterator class);
- a Position class to define what "position" means for this application;
The Application methods are generalizations of the previous outline of backtracking. Here is the Application interface:
import java.util.*; public interface Application { /** * Determines if a given position is legal and not a dead end. * * @param pos - the given position. * * @return true if pos is a legal position and not a dead end. */ boolean isOK (Position pos); /** * Indicates that a given position is possibly on a path to a goal. * * @param pos the position that has been marked as possibly being on a * path to a goal. */ void markAsPossible (Position pos); /** * Indicates whether a given position is a goal position. * * @param pos the position that may or may not be a goal position. * * @return true if pos is a goal position; false otherwise. */ boolean isGoal (Position pos); /** * Indicates that a given position is not on any path to a goal position. * * @param pos the position that has been marked as not being on any path to * a goal position. */ void markAsDeadEnd (Position pos); /** * Converts this Application object into a String object. * * @return the String representation of this Application object. */ String toString(); /** * Produces an Iterator object that starts at a given position. * * @param pos the position the Iterator object starts at. * * @return an Iterator object that accesses the positions directly * available from pos. */ Iterator<Position> iterator (Position pos); } // interface Application
The BackTrack class has two responsibilities: to initialize a BackTrack object from a given application object, and to try to reach a goal position from a given position. The method specifications are
/** * Initializes this BackTrack object from an application. * @param app the application */ public BackTrack (Application app) /** * Attempts to reach a goal through a given position. * * @param pos the given position. * * @return true if the attempt succeeds; otherwise, false. */ public boolean tryToReachGoal (Position pos)
The only field needed is (a reference to) an Application. The definition of the constructor is straightforward. The definition of the tryToReachGoal method is based on the outline of backtracking given above: To "enumerate over all positions accessible from the given position," we create an iterator. The phrase "attempt to reach a goal from that position" becomes a recursive call to the method tryToReachGoal. The complete BackTrack class, without any application-specific information, is as follows:
import java.util.*; public class BackTrack { protected Application app; /** * Initializes this BackTrack object from an application. * * @param app the application */ public BackTrack (Application app) { this.app = app; } // constructor /** * Attempts to reach a goal through a given position. * * @param pos the given position. * * @return true if the attempt succeeds; otherwise, false. */ public boolean tryToReachGoal (Position pos) { Iterator<Position> itr = app.iterator (pos); while (itr.hasNext()) { pos = itr.next(); if (app.isOK (pos)) { app.markAsPossible (pos); if (app.isGoal (pos) || tryToReachGoal (pos)) return true ; app.markAsDeadEnd (pos); } // pos may be on a path to a goal } // while return false; } // method tryToReachGoal } // class BackTrack
Let's focus on the tryToReachGoal method, the essence of backtracking. We look at the possible choices of moves from the pos parameter. There are three possibilities:
- One of those choices is a goal position. Then true is returned to indicate success.
- One of those choices is valid but not a goal position. Then another call to tryToReachGoal is made, starting at the valid choice.
- None of the choices is valid. Then the while loop terminates and false is returned to indicate failure to reach a goal position from the current position.
The argument to tryToReachGoal represents a position that has been marked as possibly being on a path to a goal position. Whenever a return is made from tryToReachGoal, the pre-call value of pos is restored, to be marked as a dead end if it does not lead to a goal position.
Now that we have developed a framework for backtracking, it is straightforward to utilize this framework to solve a variety of problems.
5.6.1 An A-maze-ing Application
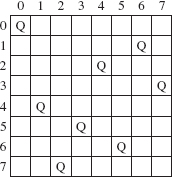
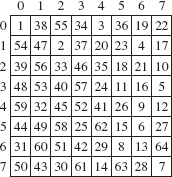
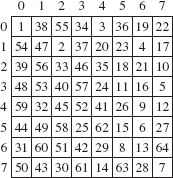
For one application of backtracking, let's develop a program to try to find a path through a maze. For example, Figure 5.9 has a 7-by-13 maze, with a 1 representing a corridor and a 0 representing a wall. The only valid moves are along a corridor, and only horizontal and vertical moves are allowed; diagonal moves are prohibited. The starting position is in the upper left-hand corner and the goal position is in the lower-right-hand corner.
FIGURE 5.9 A maze: 1 represents a corridor and 0 represents a wall. Assume the starting position is in the upper left-hand corner, and the goal position is in the lower right-hand corner

A successful traversal of this maze will show a path leading from the start position to the goal position. We mark each such position with the number 9. Because there are two possible paths through this maze, the actual path chosen will depend on how the iterator class orders the possible choices. For the sake of specificity, assume the order of choices is north, east, south, and west. For example, from the position at coordinates (5, 8), the first choice would be (4, 8), followed by (5, 9), (6, 8), and (5, 7).
From the initial position at (0, 0), the following positions are recorded as possibly being on a solution-path:
(0, 1) // moving east
(0, 2) // moving east
(1, 2) // moving south
(1, 3) // moving east
(1, 4) // moving east
(0, 4) // moving north
(0, 5) // moving east;
This last position is a dead end, so we "undo" (0, 5) and (0, 4), backtrack to (1, 4) and then record the following as possibly leading to the goal:
(2, 4) // moving south
(3, 4) // moving south
(3, 5) // moving east;
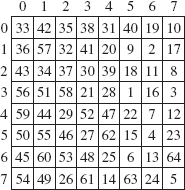
From here we eventually reach a dead end. After we undo (3, 5) and re-trace to (3, 4), we advance—without any further backtracking—to the goal position. Figure 5.10 uses 9' to show the corresponding path through the maze of Figure 5.9, with dead-end positions marked with 2's.
For this application, a position is simply a pair: row, column. The Position class is easily developed:
public class Position { protected int row, column; /** * Initializes this Position object to (0, 0). */ public Position () { row = 0;
FIGURE 5.10 A path through the maze of Figure 5.9. The path positions are marked with 9's and the dead-end positions are marked with 2's

column = 0; } // default constructor /** * Initializes this Position object to (row, column). * * @param row the row this Position object has been initialized to. * @param column the column this Position object has been initialized to. */ public Position (int row, int column) { this.row = row; this.column = column; } // constructor /** * Determines the row of this Position object. * * @return the row of this Position object. */ public int getRow () { return row; } // method getRow /** * Determines the column of this Position object. * * @return the column of this Position object. */ public int getColumn () { return column; } // method getColumn } // class Position
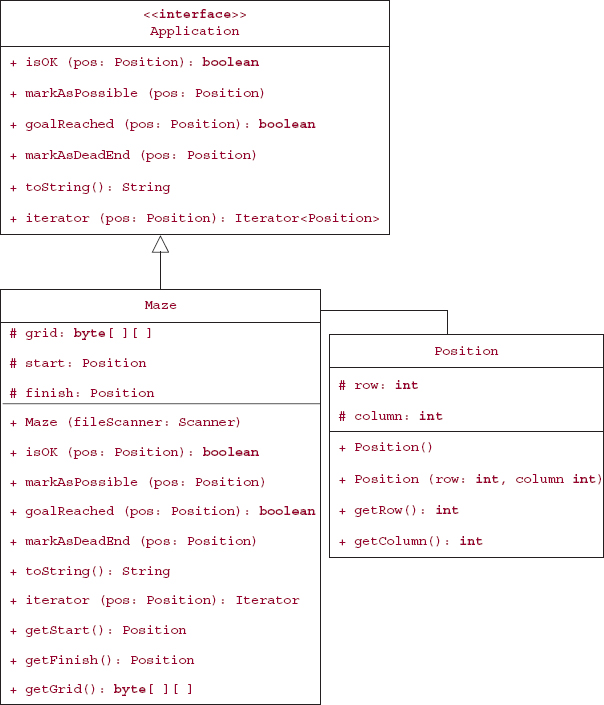
For this application, the Application interface is implemented in a Maze class. The only fields are a grid to hold the maze and start and finish positions. Figure 5.11 has the UML diagrams for the Maze class and Application interface.
Except for the Maze class constructor and the three accessors (getGrid was developed for the sake of testing), the method specifications for the Maze class are identical to those in the Application interfaces given earlier. For the embedded MazeIterator class, the constructor's specification is provided, but the method specifications for the hasNext, next and remove methods are boilerplate, so we need not list them. Here are the specifications for the Maze and MazeIterator constructors:
/** * Initializes this Maze object from a file scanner over a file. * * @param fileScanner - the scanner over the file that holds the * maze information. * * @throws InputMismatchException - if any of the row or column values are non- * integers, or if any of the grid entries are non-integers. * @throws NumberFormatException - if the grid entries are integers but neither * WALL nor CORRIDOR
FIGURE 5.11 The class diagram for the Maze class, which implements the Application interface and has grid, start, and finish fields
*/ public Maze(ScannerfileScanner) /** * InitializesthisMazeIteratorobjectto startatagivenposition. * * @paramposthepositiontheIteratorobjectsstartsat. */ public MazeIterator(Positionpos)
The MazeTest class, available on the book's website, starts by declaring a maze field and then creating a maze (the one shown in Figure 5.9) from a file:
protected Maze maze; @Before public void runBeforeEachTest() throws IOException { fileScanner = new Scanner ( new File (" maze.txt")); maze = new Maze (fileScanner); } // method runBeforeEachTest
Here are four of the boundary-condition tests of the is OK method:
@Test public void is OKTest1() { Position pos = new Position (0, 0); assertEquals ( true, maze.is OK (pos)); } // isOKTest1 @Test public void isOKTest2() { Position pos = new Position (6, 12); assertEquals ( true, maze.isOK (pos)); } // isOKTest2 @Test public void isOKTest3() { Position pos = new Position (7, 0); assertEquals ( false, maze.isOK (pos)); } // isOKTest3 @Test public void isOKTest4() { Position pos = new Position (0, 13); assertEquals ( false, maze.isOK (pos)); } // isOKTest4
Here is the complete Maze class, including the embedded MazeIterator class:
import java.util.*; public class Maze implements Application { public static final byte WALL = 0; public static final byte CORRIDOR = 1; public static final byte PATH = 9; public static final byte DEAD_END = 2; protected Position start, finish; protected byte[ ][ ] grid; /** * Initializes this Maze object from a file scanner over a file. * * @param fileScanner - the scanner over the file that holds the * maze information. * * @throws InputMismatchException - if any of the row or column values are non- * integers, or if any of the grid entries are non-integers. * @throws NumberFormatException - if the grid entries are integers but neither * WALL nor CORRIDOR */ public Maze (Scanner fileScanner) { int rows = fileScanner.nextInt(), columns = fileScanner.nextInt(); grid = new byte [rows][columns]; start = new Position (fileScanner.nextInt(), fileScanner.nextInt()); finish = new Position (fileScanner.nextInt(), fileScanner.nextInt()); for (int i = 0; i < rows; i++) for (int j = 0; j < columns; j++) { grid [i][j] = fileScanner.nextByte(); if (grid [i][j] != WALL "" grid [i][j] != CORRIDOR) throw new NumberFormatException ("At position (" + i + ", " + j + "), " + grid [i][j] + " should be " + WALL + " or " + CORRIDOR + "."); } // for j } // constructor /** * Determines if a given position is legal and not a dead end. * * @param pos - the given position. * * @return true if pos is a legal position and not a dead end. */ public boolean isOK (Position pos) { return pos.getRow() >= 0 "" pos.getRow() < grid.length "" pos.getColumn() >= 0 "" pos.getColumn() < grid [0].length "" grid [pos.getRow()][pos.getColumn()] == CORRIDOR; } // method isOK /** * Indicates that a given position is possibly on a path to a goal. * * @param pos the position that has been marked as possibly being on a path * to a goal. */ public void markAsPossible (Position pos) { grid [pos.getRow ()][pos.getColumn ()] = PATH; } // method markAsPossible /** * Indicates whether a given position is a goal position. * * @param pos the position that may or may not be a goal position. * * @return true if pos is a goal position; false otherwise. */ public boolean isGoal (Position pos) { return pos.getRow() == finish.getRow() "" pos.getColumn() == finish.getColumn(); } // method isGoal /** * Indicates that a given position is not on any path to a goal position. * * @param pos the position that has been marked as not being on any path to a * goal position. */ public void markAsDeadEnd (Position pos) { grid [pos.getRow()][pos.getColumn()] = DEAD_END; } // method markAsDeadEnd /** * Converts this Application object into a String object. * * @return the String representation of this Application object. */ public String toString () { String result = " "; result += start.getRow() + " " + start.getColumn() + " "; result += finish.getRow() + " " + finish.getColumn() + " "; for (int row = 0; row < grid.length; row++) { for (int column = 0; column < grid [0].length; column++) result += String.valueOf (grid [row][column]) + ' '; result += " "; } // for row = 0 return result; } // method toString /** * Produces an Iterator object, over elements of type Position, that starts at a given * position. * * @param pos - the position the Iterator object starts at. * * @return the Iterator object. */ public Iterator<Position> iterator (Position pos) { return new MazeIterator (pos); } // method iterator /** * Returns the start position of this maze. * * @return - the start position of this maze * */ public Position getStart() { return start; } // method getStart /** * Returns the finish position of this maze. * * @return - the finish position of this maze * */ public Position getFinish() { return finish; } // method getFinish /** * Returns a 2-dimensional array that holds a copy of the maze configuration. * * @return - a 2-dimensional array that holds a copy of the maze configuration. * */ public byte[ ][ ] getGrid() { byte[ ][ ] gridCopy = new byte[grid.length][grid[0].length]; for (int i = 0; i < grid.length; i++) for (int j = 0; j < grid[i].length; j++) gridCopy[i][j] = grid[i][j]; return gridCopy; } // method getGrid protected class MazeIterator implements Iterator<Position> { protected static final int MAX_MOVES = 4; protected int row, column, count; /** * Initializes this MazeIterator object to start at a given position. * * @param pos the position the Iterator objects starts at. */ public MazeIterator (Position pos) { row = pos.getRow(); column = pos.getColumn(); count = 0; } // constructor /** * Determines if this MazeIterator object can advance to another * position. * * @return true if this MazeIterator object can advance; false otherwise. */ public boolean hasNext () { return count < MAX_MOVES; } // method hasNext /** * Advances this MazeIterator object to the next position. * * @return the position advanced to. */ public Position next () { Position nextPosition = new Position(); switch (count++) { case 0: nextPosition = new Position (row-1, column); // north break ; case 1: nextPosition = new Position (row, column+1); // east break ; case 2: nextPosition = new Position (row+1, column); // south break ; case 3: nextPosition = new Position (row, column-1); // west } // switch; return nextPosition; } // method next public void remove () { // removal is illegal for a MazeIterator object throw new UnsupportedOperationException(); } // method remove } // class MazeIterator } // class Maze
To show how a user might utilize the Maze class, we develop a MazeUser class. The MazeUser class creates a maze from a file scanner. There is a method to search for a path through the maze. The output is either a solution or a statement that no solution is possible. The method specifications (except for the usual main method) are
/** * Runs the application. */ public void run() /** * Searches for a solution path through the maze from the start position * * * @param maze - the maze to be searched * * @return true - if there is a path through the maze; otherwise, false. * */ public boolean searchMaze (Maze maze)
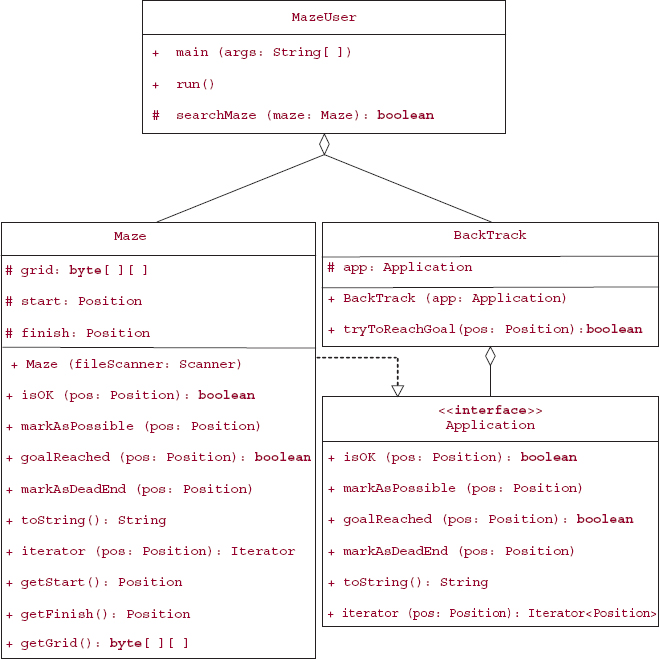
Figure 5.12 has the UML class diagrams that illustrate the overall design. Because the Position class is quite simple and its diagram is in Figure 5.11, its class diagram is omitted.
The implementation of the MazeUser class is as follows:
FIGURE 5.12 The UML class diagrams for the maze-search project
import java.util.*; public class MazeUser { public static void main (String[ ] args) { new MazeUser().run(); } // method main public void run() { final String INPUT_PROMPT = " Please enter the path for the file whose first line contains the " + "number of rows and columns, whose 2nd line the start row and column, " + "whose 3rd line the finish row and column, and then the maze, row-by-row: "; final String INITIAL_STATE = " The initial state is as follows (0 = WALL, 1 = CORRIDOR): "; final String START_INVALID = "The start position is invalid."; final String FINISH_INVALID = "The finish position is invalid."; final String FINAL_STATE = "The final state is as follows (2 = DEAD END, 9 = PATH): "; final String SUCCESS = " A solution has been found:"; final String FAILURE = " There is no solution:"; Maze maze = null; Scanner keyboardScanner = new Scanner (System.in), fileScanner = null; String fileName; while (true) { try { System.out.print (INPUT_PROMPT); fileName = keyboardScanner.next(); fileScanner = new Scanner (new File (fileName)); break; } // try catch (IOException e) { System.out.println (" " + e); } // catch IOException } // while try { maze = new Maze (fileScanner); System.out.println (INITIAL_STATE + maze); Scanner stringScanner = new Scanner (maze.toString()); Position start = new Position (stringScanner.nextInt(), stringScanner.nextInt()), finish = new Position (stringScanner.nextInt(), stringScanner.nextInt()); if (!maze.isOK (start)) System.out.println (START_INVALID); else if (!maze.isOK (finish)) System.out.println (FINISH_INVALID); else { if (searchMaze (maze, start)) System.out.println (SUCCESS); else System.out.println (FAILURE); System.out.println (FINAL_STATE + maze); } // else valid search } // try catch (InputMismatchException e) { System.out.println (" " + e + ": " + fileScanner.nextLine()); } // catch InputMismatchException catch (NumberFormatException e) { System.out.println (" " + e); } // catch NumberFormatException catch (RuntimeException e) { System.out.println (" " + e); System.out.println (FINAL_STATE + maze); } // catch NumberFormatException } // method run /** * Performs the maze search. * * @param maze - the maze to be searched. * * @return true - if there is a path through this maze; otherwise, false * */ public boolean searchMaze (Maze maze) { Position start = maze.getStart(); maze.markAsPossible (start); BackTrack backTrack = new BackTrack (maze); if (maze.isGoal (start) || backTrack.tryToReachGoal (start)) return true; maze.markAsDeadEnd (start); return false; } // method searchMaze } // class MazeUser
In this project, and in general, the run method is not tested because it involves end-user input and output. All of the files, including the Application interface and the BackTrack, Position, Maze, MazeTest, MazeUser, and MazeUserTest (for the searchMaze method) classes, are available from the book's website.
FIGURE 5.13 A worst-case maze: in columns 1, 4, 7,…, every row except the last contains a 0; every other position in the maze contains a 1. The start position is in the upper-left corner, and the finish position is in the lower-right corner

How long does the tryToReachGoal method in the BackTrack class take? Suppose the maze has n positions. In the worst case, such as in Figure 5.13, every position would be considered, so worstTime(n) is linear in n. And with more than half of the positions on a path to the goal position, there would be at least n/2 recursive calls to the tryToReachGoal method, so worstSpace(n) is also linear in n.
Projects 5.2, 5.3, 5.4, and 5.5 have other examples of backtracking. Because the previous project separated the backtracking aspects from the maze traversing aspects, the BackTrack class and Application interface are unchanged. The Position class for Projects 5.2, 5.3, and 5.5 is the same Position class declared earlier, and the Position class for Project 5.4 is only slightly different.
We will re-visit backtracking in Chapter 15 in the context of searching a network. And, of course, the BackTrack class and Application interface are the same as given earlier.
At the beginning of this chapter we informally described a recursive method as a method that called itself. Section 5.7 indicates why that description does not suffice as a definition and then provides a definition.
5.7 Indirect Recursion
Java allows methods to be indirectly recursive. For example, if method A calls method B and method B calls method A, then both A and B are recursive. Indirect recursion can occur in the development of a grammar for a programming language such as Java.
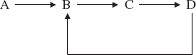
Because indirect recursion is legal, we cannot simply define a method to be recursive if it calls itself. To provide a formal definition of recursive, we first define active. A method is active if it is being executed or has called an active method. For example, consider a chain of method calls
That is, A calls B, B calls C, and C calls D. When D is being executed, the active methods are
D, because it is being executed;
C, because it has called D and D is active;
B, because it has called C and C is active;
A, because it has called B and B is active.
We can now define "recursive." A method is recursive if it can be called while it is active. For example, suppose we had the following sequence of calls:
Then B, C, and D are recursive because each can be called while it is active.
When a recursive method is invoked, a certain amount of information must be saved so that information will not be written over during the execution of the recursive call. This information is restored when the execution of the method has been completed. This saving and restoring, and other work related to the support of recursion, carry some cost in terms of execution time and memory space. Section 5.8 estimates the cost of recursion, and attempts to determine whether that cost is justified.
5.8 The Cost of Recursion
We have seen that a certain amount of information is saved every time a method calls itself. This information is collectively referred to as an activation record because it pertains to the execution state of the method that is active during the call. In fact, an activation record is created whenever any method is called; this relieves the compiler of the burden of determining if a given method is indirectly recursive.
Essentially, an activation record is an execution frame without the statements. Each activation record contains:
- the return address, that is, the address of the statement that will be executed when the call has been completed;
- the value of each argument: a copy of the corresponding argument is made (if the type of the argument is reference-to-object, the reference is copied);
- the values of the local variables declared within the body of the called method.
After the call has been completed, the previous activation record's information is restored and the execution of the calling method is resumed. For methods that return a value, the value is placed on top of the previous activation record's information just prior to the resumption of the calling method's execution. The calling method's first order of business is to get that return value.
There is an execution-time cost of saving and restoring these records, and the records themselves take up space. But these costs are negligible relative to the cost of a programmer's time to develop an iterative method when a recursive method would be more appropriate. Recursive methods, such as move, tryToReachGoal, and permute (from Lab 9) are far simpler and more elegant than their iterative counterparts.
How can you decide whether a recursive method or iterative method is more appropriate? Basically, if you can readily develop an iterative solution, go for it. If not, you need to decide if recursion is appropriate for the problem. That is, if complex cases of the problem can be reduced to simpler cases of the same form as the original and the simplest case(s) can be solved directly, you should try to develop a recursive method.
If an iterative method is not easy to develop, and recursion is appropriate, how does recursion compare with iteration? At worst, the recursive will take about as long (and have similar time/space performance) as the iterative version. At best, developing the recursive method will take far less time than the iterative version, and have similar time/space performance. See, for example, the move, tryToReachGoal, and permute methods. Of course, it is possible to design an inefficient recursive method, such as the original version of fib in Lab 7, just as iterative methods can have poor performance.
In this chapter we have focused on what recursion is. We postpone to Chapter 8 a discussion of the mechanism, called a stack, by which the compiler implements the saving and restoring of activation records. As we saw in Chapter 1, this abstraction—the separation of what is done from how it is done—is critically important in problem solving.
SUMMARY
The purpose of this chapter was to familiarize you with the basic idea of recursion so you will be able to understand the recursive methods in subsequent chapters and to design your own recursive methods when the need arises.
A method is recursive if it can be called while it is active—an active method is one that either is being executed or has called an active method.
If an iterative method to solve a problem can readily be developed, then that should be done. Otherwise, recursion should be considered if the problem has the following characteristics:
- Complex cases of the problem can be reduced to simpler cases of the same form as the original problem.
- The simplest case(s) can be solved directly.
For such problems, it is often straightforward to develop a recursive method. Whenever any method (recursive or not) is called, a new activation record is created to provide a frame of reference for the execution of the method. Each activation record contains
- the return address, that is, the address of the statement that will be executed when the call has been completed;
- the value of each argument: a copy of the corresponding argument is made (if the type of the argument is reference-to-object, the reference is copied);
- the values of the method's other local variables;
Activation records make recursion possible because they hold information that might otherwise be destroyed if the method called itself. When the execution of the current method has been completed, a return is made to the address specified in the current activation record. The previous activation record is then used as the frame of reference for that method's execution.
Any problem that can be solved with recursive methods can also be solved iteratively, that is, with a loop. Typically, iterative methods are slightly more efficient than their recursive counterparts because far fewer activation records are created and maintained. But the elegance and coding simplicity of recursion more than compensates for this slight disadvantage.
A backtracking strategy advances step-by-step toward a goal. At each step, a choice is made, but when a dead end is reached, the steps are re-traced in reverse order; that is, the most recent choice is discarded and a new choice is made. Backtracking was deployed for the maze-search application above, and can be used in Programming Projects 5.2 (eight-queens), 5.3 (knight's tour), 5.4 (Sudoku), and 5.5 (Numbrix).
CROSSWORD PUZZLE
| ACROSS | DOWN |
| 3. The strategy of trying to reach a goal by a sequence of chosen positions, with a re-tracing in reverse order of positions that cannot lead to the goal. | 1. The mechanism by which the compiler implements the saving and restoring of activation records. |
| 6. For the move method, worstSpace(n) is _______ in n. | 2. In the binarySearch method, the index where the key could be inserted without disordering the array. |
| 7. A precondition of the binarySearch method is that the array is _______ . | 4. A method is ______ if it can be called while it is active. |
| 8. What is generated when infinite recursion occurs. | 5. A method is ______ if it is being executed or has called an active method. |
| 9. Boxes that contain information (both variables and code) related to each invocation of the method. | |
| 10. The information that is saved every time a method is called. |
CONCEPT EXERCISES
5.1 What is wrong with the following underlying method for calculating factorials?
/** * Calculates the factorial of a non-negative integer, that is, the product of all * integers between 1 and the given integer, inclusive. The worstTime(n) is O(n), * where n is the given integer. * * @param n the non-negative integer whose factorial is calculated. * * @return the factorial of n * */ public static long fact (int n) { if (n <= 1) return 1; return fact (n+1) / (n+1); } // fact
5.2 Show the first three steps in an execution-frames trace of the move method after an initial call of
move (4, 'A', 'B', 'C'),
5.3 Perform an execution-frames trace to determine the output from the following incorrect version of the recPermute method (from Lab 9) after an initial call to
permute ("ABC");
invokes
recPermute (['A', 'B', 'C'], 0); /** * Finds all permutations of a subarray from a given position to the end of the array. * * @param c an array of characters * @param k the starting position in c of the subarray to be permuted. * * @return a String representation of all the permutations. * */ public static String recPermute (char[ ] c, int k) { if (k == c.length - 1) return String.valueOf (c) + " "; else { String allPermutations = new String(); char temp; for (int i = k; i < c.length; i++) { temp = c [i]; c [i] = c [k + 1]; c [k + 1] = temp; allPermutations += recPermute (String.valueOf (c).toCharArray(), k+1); } // for return allPermutations; } // else } // method recPermute
5.4 Perform an execution-frames trace to determine the output from the following incorrect version of the recPermute method (from Lab 9) after an initial call to
permute ("ABC");
invokes
recPermute (['A', 'B', 'C'], 0); /** * Finds all permutations of a subarray from a given position to the end of the array. * * @param c an array of characters * @param k the starting position in c of the subarray to be permuted. * * @return a String representation of all the permutations. * */ public static String recPermute (char[ ] c, int k) { if (k == c.length - 1) return String.valueOf (c) + " "; else { String allPermutations = new String(); char temp; for (int i = k; i < c.length; i++) { allPermutations += recPermute (String.valueOf (c).toCharArray(), k+1); temp = c [i]; c [i] = c [k]; c [k] = temp; } // for return allPermutations; } // else } // method recPermute
5.5 Use the Principle of Mathematical Induction (Appendix 1) to prove that the move method in the Towers of Hanoi example is correct, that is, for any integer n > = 1, move (n, orig, dest, temp) returns the steps to move n disks from pole orig to pole dest.
Hint: for n = 1, 2, 3,…, let Sn be the statement:
move (n, orig, dest, temp) returns the steps to move n disks from any pole orig to any other pole dest.
- base case. Show that S1 is true.
- inductive case. Let n be any integer greater than 1 and assume Sn—1 is true. Then show that Sn is true. According the code of the move method, what happens when move (n, orig, dest, temp) is called and n is greater than 1?
5.6 In an execution trace of the move method in the Towers of Hanoi application, the number of steps is equal to the number of recursive calls to the move method plus the number of direct moves. Because each call to the move method includes a direct move, the number of recursive calls to the move method is always one less than the number of direct moves. For example, in the execution trace shown in the chapter, n = 3. The total number of calls to move is 2n — 1 = 7. Then the number of recursive calls to move is 6, and the number of direct moves is 7, for a total of 13 steps (recall that we started at Step 0, so the last step is Step 12). How many steps would there be for an execution trace with n = 4?
5.7 Show that, for the recursive binarySearch method, averageTime(n) is logarithmic in n for a successful search.
Hint: Let n represent the size of the array to be searched. Because the average number of calls is a non-decreasing function of n, it is enough to show that the claim is true for values of n that are one less than a power of 2. So assume that
n = 2k — 1, for some positive integer k.
In a successful search,
one call is sufficient if the item sought is half-way through the region to be searched;
two calls are needed if the item sought is one-fourth or three-fourths of the way through that region;
three calls are needed if the item sought is one-eighth, three-eighths, five-eighths or seven-eighths of the way through the region;
and so on.
The total number of calls for all successful searches is
(1 * 1) + (2 * 2) + (3 * 4) + (4 * 8) + (5 * 16) + ... + (k * 2k—1)
The average number of calls, and hence an estimate of averageTime(n), is this sum divided by n. Now use the result from Exercise 2.6 of Appendix 2 and the fact that
k = log2 (n + 1)
5.8 If a call to the binarySearch method is successful, will the index returned always be the smallest index of an item equal to the key sought? Explain.
PROGRAMMING EXERCISES
5.1 Develop an iterative version of the getBinary method in Section 5.3. Test that method with the same BinaryTest class (available on the book's website) used to test the recursive version.
5.2 Develop an iterative version of the permute method (from Lab 9). Here is the method specification:
/**
* Finds all permutations of a specified String.
*
* @param s - the String to be permuted.
*
* @return a String representation of all the permutations, with a line separator
* (that is, "
") after each permutation.
*/
public static String permute (String s)
For example, if the original string is "BADCGEFH", the value returned would be
ABCDEFGH,
ABCDEFHG
ABCDEGFH
ABCDEGHF
ABCDEHFG
and so on. Test your method with the same PermuteTest method developed in Lab 9 to test the recursive version.
Hint: One strategy starts by converting s to a character array c. Then the elements in c can be easily swapped with the help of the index operator, [ ]. To get the first permutation, use the static method sort in the Arrays class of java.util. To give you an idea of how the next permutation can be constructed from the current permutation, suppose, after some permutations have been printed,
c = ['A', 'H', 'E', 'G', 'F', 'D', 'C', 'B']
What is the smallest index whose character will be swapped to obtain the next permutation? It is index 2, because the characters at indexes 3 through 7 are already in reverse alphabetical order: 'G' > 'F' > 'D' > 'C' > 'B'. We swap 'E' with 'F', the smallest character greater than 'E' at an index greater than 2. After swapping, we have
c = ['A', 'H', 'F', 'G', 'E', 'D', 'C', 'B']
We then reverse the characters at indexes 3 through 7 to get those characters into increasing order:
c = ['A', 'H', 'F', 'B', 'C', 'D', 'E', 'G'],
the next higher permutation after 'A', 'H', 'E', 'G', 'F', 'D', 'C', 'B'. Here is an outline:
public static String permute (String s) { int n = s.length(); boolean finished = false; char[ ] c = s.toCharArray(); String perms = ""; Arrays.sort (c); // c is now in ascending order while (!finished) { perms += String.valueOf (c)); // In 0 ... n-1, find the highest index p such that // p = 0 or c [p - 1] < c [p]. ... if (p == 0) finished = true; else { // In p ... n-1, find the largest index i such that c [i] > c [p - 1]. ... // Swap c [i] with c [p - 1]. // Swap c [p] with c [n-1], swap c [p+1] with c[n-2], // swap c [p+2] with c [n-3], ... ... } // else } // while return perms; } // method permute
In the above example, p −1 = 2 and i = 4, so c[p-1], namely, 'E' is swapped with c [i], namely, 'F'.
Explain how strings with duplicate characters are treated differently in this method than in the recursive version.
5.3 Given two positive integers i and j, the greatest common divisor of i and j, written
gcd (i, j)
is the largest integer k such that
(i % k = 0) and (j % k = 0).
For example, gcd (35, 21) = 7 and gcd (8, 15) = 1. Test and develop a wrapper method and a wrapped recursive method that return the greatest common divisor of i and j. Here is the method specification for the wrapper method:
/** * Finds the greatest common divisor of two given positive integers * * @param i - one of the given positive integers. * @param j - the other given positive integer. * * @return the greatest common divisor of iand j. * * @throws IllegalArgumentException - if either i or j is not a positive integer. * */ public static int gcd ( int i, int j)
Big hint: According to Euclid's algorithm, the greatest common divisor of i and j is j if i % j = 0. Otherwise, the greatest common divisor of i and j is the greatest common divisor of j and (i % j).
5.4 A palindrome is a string that is the same from right-to-left as from left-to-right. For example, the following are palindromes:
ABADABA
RADAR
OTTO
MADAMIMADAM
EVE
For this exercise, we restrict each string to upper-case letters only. (You are asked to remove this restriction in the next exercise.)
Test and develop a method that uses recursion to check for palindromes. The only parameter is a string that is to be checked for palindromity. The method specification is
/**
* Determines whether a given string of upper-case letters is a palindrome.
* A palindrome is a string that is the same from right-to-left as from left-to-right.
*
* @param s - (a reference to) the given string
*
* @return true - if the string s is a palindrome; otherwise, false.
*
* @throws NullPointerException - if s is null.
* @throws IllegalArgumentException - if s is the empty string.
*
*/
public static boolean isPalindrome (String s)
5.5 Expand the recursive method (and test class) developed in Programming Exercise 5.4 so that, in testing to see whether s is a palindrome, non-letters are ignored and no distinction is made between upper-case and lower-case letters. Throw IllegalArgumentException if s has no letters. For example, the following are palindromes:
Madam, I'm Adam.
Able was I 'ere I saw Elba.
A man. A plan. A canal. Panama!
Hint: The toUpperCase() method in the String class returns the upper-case String corresponding to the calling object.
a. Test and develop a wrapper method power and an underlying recursive method that return the result of integer exponentiation. The method specification of the wrapper method is
/** * Calculates the value of a given integer raised to the power of a second integer. * The worstTime(n) is O(n), where n is the second integer. * * @param i - the base integer (to be raised to a power). * @param n - the exponent (the power i is to be raised to). * * @return the value of i to the nth power. * * @throws IllegalArgumentException - if n is a negative integer or if i raised to * to the n is greater than Long.MAX_VALUE. * */ public static long power (long i, int n)
Hint: We define 00 = 1, so for any integer i, i0 = 1. For any integers i > O and n > 0,
in = i* in-1
b. Develop an iterative version of the power method.
c. Develop an underlying recursive version called by the power method for which worstTime(n) is logarithmic in n.
Hint: If n is even, power (i, n) = power (i * i, n/2); if n is odd, power (i, n)=i* in-1 = i * power (i * i, n/2).
For testing parts b and c, use the same test suite you developed for part a.
5.7 Test and develop a recursive method to determine the number of distinct ways in which a given amount of money in cents can be changed into quarters, dimes, nickels, and pennies. For example, if the amount is 17 cents, then there are six ways to make change:
1 dime, 1 nickel and 2 pennies;
1 dime and 7 pennies;
3 nickels and 2 pennies;
2 nickels and 7 pennies;
1 nickel and 12 pennies;
17 pennies.
Here are some amount/ways pairs. The first number in each pair is the amount, and the second number is the number of ways in which that amount can be changed into quarters, dimes, nickels and pennies:
| 17 | 6 |
| 5 | 2 |
| 10 | 4 |
| 25 | 13 |
| 42 | 31 |
| 61 | 73 |
| 99 | 213 |
Here is the method specification:
/** * Calculates the number of ways that a given amount can be changed * into coins whose values are no larger than a given denomination. * * @param amount - the given amount. * @param denomination - the given denomination (1 = penny, * 2 = nickel, 3 = dime, 4 = quarter). * * @return 0 - if amount is less than 0; otherwise, the number of ways * that amount can be changed into coins whose values are no * larger than denomination. * */ public static int ways (int amount, int denomination)
For the sake of simplifying the ways method, either develop an enumerated type Coin or develop a coins method that returns the value of each denomination. Thus, coins (1) returns 1, coins (2) returns 5, coins (3) returns 10, and coins (4) returns 25.
Hint: The number of ways that one can make change for an amount using coins no larger than a quarter is equal to the number of ways that one can make change for amount—25 using coins no larger than a quarter plus the number of ways one can make change for amount using coins no larger than a dime.
5.8 Modify the maze-search application to allow an end user to enter the maze information directly, instead of in a file. Throw exceptions for incorrect row or column numbers in the start and finish positions.
5.9 Modify the maze-search application so that diagonal moves would be valid. Hint: only the MazeIterator class needs to be modified.
Programming Project 5.1: Iterative Version of the Towers of Hanoi
Develop an iterative version of the moveDisks method in the Towers of Hanoi game. Test your version with the same test suite, on the book's website, developed for the recursive version.
Hint: We can determine the proper move at each stage provided we can answer the following three questions:
- Which disk is to be moved?
To answer this question, we set up an n-bit counter, wheren is the number of disks, and initialize that counter to all zeros. The counter can be implemented as an n-element array of zeros and ones, or as an n-element array of boolean values. That is the only array you should use for this project. For example, if n = 5, we would start with
00000
Each bit position corresponds to a disk: the rightmost bit corresponds to disk 1, the next rightmost bit to disk 2, and so on.
At each stage, the rightmost zero bit corresponds to the disk to be moved, so the first disk to be moved is, as you would expect, disk 1.
After a disk has been moved, we increment the counter as follows: starting at the rightmost bit and working to the left, keep flipping bits (0 to 1, 1 to 0) until a zero gets flipped. For example, the first few increments and moves are as follows:
00000 // move disk 1
00001 // move disk 2
00010 // move disk 1
00011 // move disk 3
00100 // move disk 1
00101 // move disk 2
After 31 moves, the counter will contain all ones, so no further moves will be needed or possible. In general, 2n — 1 moves and 2n — 1 increments will be made.
- In which direction should that disk be moved?
If n is odd, then odd-numbered disks move clockwise:
and even-numbered disks move counter clockwise:
If n is even, even-numbered disks move clockwise and odd-numbered disks move counter clockwise.
If we number the poles 0, 1, and 2 instead of 'A', 'B', and 'C', then movements can be accomplished simply with modular arithmetic. Namely, if we are currently at pole k, then
k = (k +1) % 3;
achieves a clockwise move, and
k = (k +2) % 3;
achieves a counter-clockwise move. For the pole on which the just moved disk resides, we cast back to a character:
char(k + 'A') - Where is that disk now?
Keep track of where disk 1 is. If the counter indicates that disk 1 is to be moved, use the answer to question 2 to move that disk. If the counter indicates that the disk to be moved is not disk 1, then the answer to question 2 tells you where that disk is now. Why? Because that disk cannot be moved on top of disk 1 and cannot be moved from the pole where disk 1 is now.
Programming Project 5.2: Eight Queens
(This problem can be straightforwardly solved by using the BackTrack class and implementing the Application interface.) Test and develop an EightQueens class to place eight queens on a chess board in such a way that no queen is under attack from any other queen. Also, test and develop an EightQueensUser classsimilar to the MazeUser class in Section 5.6.1.
Analysis A chess board has eight rows and eight columns. In the game of chess, the queen is the most powerful piece: she can attack any piece in her row, any piece in her column, and any piece in either of her diagonals. See Figure 5.14.
FIGURE 5.14 Positions vulnerable to a queen in chess. The arrows indicate the positions that can be attacked by the queen 'Q' in the center of the figure
The output should show the chess board after the placement of the eight queens. For example:
Hint: There must be exactly one queen in each row and exactly one queen in each column. There is no input: start with a queen at (0, 0), and place a queen in each column. A valid position is one that is not in the same row, column or diagonal as any queen placed in a previous column. The QueensIterator constructor should advance to row 0 of the next column. The next method should advance to the next row in the same column. So the first time the tryToReachGoal method in the BackTrack class (which cannot be modified by you) is called, the choices are:
(0, 1) // invalid: in the same row as the queen at (0, 0)
(1, 1) // invalid: in the same diagonal as the queen at (0, 0)
(2, 1) // valid
When the tryToReachGoal method is called again, the choices are:
(0, 2) // invalid: in the same row as the queen at (0, 0)
(1, 2) // invalid: in the same diagonal as the queen at (1, 2)
(2, 2) // invalid: in the same row as the queen at (1, 2)
(3, 2) // invalid: in the same diagonal as the queen at (1, 2)
(4, 2) // valid
Programming Project 5.3: A Knight's Tour
(This problem can be straightforwardly solved by using the BackTrack class and implementing the Application interface.) Test and develop a KnightsTour class to show the moves of a knight in traversing a chess board. Also, test and develop a KnightsTourUser class—similar to the MazeUser class in Section 5.6.1. The Backtrack class and Application interface are not to be modified by you.
Analysis A chess board has eight rows and eight columns. From its current position, a knight's next position will be either two rows and one column or one row and two columns from the current position. For example, Figure 5.15 shows the legal moves of a knight at position (5, 3), that is, row 5 and column 3.
FIGURE 5.15 For a knight (K) at coordinates (5, 3), the legal moves are to the grid entries labeled K0 through K7
For simplicity, the knight starts at position (0, 0). Assume the moves are tried in the order given in Figure 5.15. That is, from position (row, column), the order tried is:
(row - 1, column + 2)
(row + 1, column + 2)
(row + 2, column +1)
(row + 2, column −1)
(row +1, column - 2)
(row - 1, column - 2)
(row - 2, column −1)
Figure 5.16 shows the first few moves.
FIGURE 5.16 The first few valid moves by a knight that starts at position (0, 0) and iterates according to the order shown in Figure 5.15. The integer at each filled entry indicates the order in which the moves were made
For the nine moves, starting at (0, 0), in Figure 5.16, no backtracking occurs. In fact, the first 36 moves are never backtracked over. But the total number of backtracks is substantial: over 3 million. The solution obtained by the above order of iteration is:
Notice that the 37th move, from position (1, 3), does not take the first available choice—to position (3, 2) —nor the second available choice—to position (2, 1). Both of those choices led to dead ends, and backtracking occurred. The third available choice, to (0, 1), eventually led to a solution.
System Test 1 (the input is in boldface)
Enter the starting row and column: 0 0
Starting at row 0 and column 0, the solution is
Note: The lines are not part of the output; they are included for readability.
System Test 2
Enter the starting row and column: 35
Starting at row 3 and column 5, the solution is
This solution requires 11 million backtracks. Some starting positions, for example (0, 1), require over 600 million backtracks. But for every possible starting position, there is a solution.
Programming Project 5.4: Sudoku
(This problem can be solved by using the BackTrack class and implementing the Application interface.) Sudoku (from the Japanese "single number") is a puzzle game in which the board is a 9-by-9 grid, further subdivided into nine 3-by-3 minigrids. Initially, each cell in the grid has either a single digit or a blank. For example, here (from http://en.wikipedia.org/wiki/Sudoku) is a sample initial configuration:
The rules of the game are simple: Replace each blank cell with a single digit so that each row, each column, and each minigrid contain the digits 1 through 9. For example, in the above grid, what digit must be stored in the cell at row 6 and column 5? (The row numbers and column numbers start at 0, so the cell at (6, 5) is in the upper right-hand corner of the bottom center minigrid.) The value cannot be
1, because there is already a 1 in that minigrid
2, because there is already a 2 in row 6
3, because there is already a 3 in column 5
4, because there is already a 4 in that minigrid
5, because there is already a 5 in column 5
6, because there is already a 6 in row 6
8, because there is already an 8 in that minigrid (and in row 6)
9, because there is already a 9 in that minigrid
By a process of elimination, we conclude that the digit 7 should be placed in the cell at (6, 5). Using logic only, you can determine the complete solution to the puzzle. If you click on the link above, you will see the solution.
Instead of solving Sudoku puzzles by logic, you can solve them with backtracking. You would not want to do this by hand, because for some Sudoku puzzles, over 100,000 backtracks would be needed. But you can solve any Sudoku puzzle with the help of the BackTrack class (which you are not allowed to modify). You will need to supply a Sudoku class that implements the Application interface, and a SudokuUser class (similar to the MazeUser class in Section 5.6.1). You may want to modify the Position class from Section 5.6.1 to include a digit field. Then the iteration will be over the digit values that a position can take on, and the SudokuIterator constructor will advance to the next position in the grid whose digit value is 0.
The initial configuration will be supplied from a file in which each line has a row, column, and digit-value. For example,
For the SudokuTest class, include a test to make sure the iterator method starts at the appropriate row and column, and the next method advances the position's digit. For one test of the isOK method, the initial configuration should have 2 in (0, 0) and 1 in (0, 1); after several calls to the next() method, the isOK method should return true. To test the isGoal method, the initial configuration should be a complete solution except for a blank in (8, 8); isGoal should eventually return true. Also include tests for the following:
InputMismatchException, if the row or column is not an int, or if the value is not a byte.
ArrayIndexOutOfBoundsException, if the row or column is not in the range 0 … 8, inclusive.
IllegalArgumentException, if the value is not a single digit or duplicates the value in the same row, same column, or same minigrid.
IllegalStateException, if there is no solution to the puzzle.
Include tests in which the solution is found.
Programming Project 5.5: Numbrix
(This problem can be straightforwardly solved by using the BackTrack class and implementing the Application interface.) Numbrix, invented by Marilyn vos Savant, is a number-positioning puzzle. You start with a square grid—we will use a 9 × 9 grid for example. Initially, some of the grid has been filled in with integers in the range from 1 through 81. The goal is to complete the grid so that each number (except 81) is connected to the next higher number either horizontally or vertically. Here is an initial state:
Here is the final state:
Design, test and write and program to solve any Numbrix puzzle. The first line of the input file will contain the grid's side length, and each subsequent line will contain the row, column and value of some initial entry in the grid.
System Test 1 (input in boldface)
Please enter the path for the file that contains, on the first line, the grid length, and then, on each other line, the row, column, and value of each non-zero entry in the initial state: numbrix.in1
The initial state is as follows:
A solution has been found.
The final state is as follows:
Note: The file numbrix.in1 consists of the following:
System Test 2 (input in boldface)
Please enter the path for the file that contains on the first line, the grid length, and then, on each other line, the row, column, and value of each non-zero entry in the initial state: numbrix.in2
The initial state is as follows:
A solution has been found:
The final state is as follows:
Note: The file numbrix.in2 consists of the following:
Also include tests for the following:
InputMismatchException, if the row or column is not an int, or if the value is not an int.
ArrayIndexOutOfBoundsException, if the row or column is not in the range 0 … grid length, inclusive.
IllegalArgumentException, if the value is greater than grid length squared or duplicates a value already in the grid.
IllegalStateException, if there is no solution to the puzzle.
Hint: The implementation is simplified if you assume that one of the original values in the grid is 1, as in System Tests 1 and 2. After you have tested your implementation with that assumption, remove the assumption. Here are two system tests in which 1 is not one of the original values in the grid:
System Test 3 (input in boldface)
Please enter the path for the file that contains, on the first line, the grid length, and then, on each other line, the row, column, and value of each non-zero entry in the initial state: numbrix.in3
The initial state is as follows:
A solution has been found:
The final state is as follows:
Note: The file numbrix.in3 consists of the following:
System Test 4 (input in boldface)
Please enter the path for the file that contains, on the first line, the grid length, and then, on each other line, the row, column, and value of each non-zero entry in the initial state: numbrix.in4 The initial state is as follows:
A solution has been found:
The final state is as follows:
Note: The file numbrix.in4 consists of the following:
1 A formal definition of "recursive" is given later in this chapter.
2 The calculation of 0! occurs in the study of probability: The number of combinations of n things taken k at a time is calculated as n!/(k !(n — k)!). When n = k, we get n !/(n!) (0!), which has the value 1 because 0! = 1. And note that 1 is the number of combinations of n things taken n at a time.
3 In some versions, the goal is to move the disks from pole 'A' to pole 'C', with pole 'B' used for temporary storage.