CHAPTER 3
Analysis of Algorithms
As notedinSection2.2, a correct method is one that satisfies its specification. In defining a method, the first goal is to make sure the method is correct, and unit testing allows us to increase our confidence in a method's correctness. But if the method's execution time or memory requirements are excessive, the method may be of little value to the application. This chapter introduces two tools for measuring a method's efficiency. The first tool provides an estimate, based on studying the method, of the number of statements executed and number of variables allocated in a trace of the method. The second tool entails a run-time analysis of the method. Both tools are useful for comparing the efficiency of methods, and the tools can complement each other.
CHAPTER OBJECTIVES
- Be able to use Big-O (and Big-Theta) notation to estimate the time and space requirements of methods.
- Be able to conduct run-time analyses of methods.
3.1 Estimating the Efficiency of Methods
The correctness of a method depends only on whether the method does what it is supposed to do. But the efficiency of a method depends to a great extent on how that method is defined. How can efficiency be measured? We could test the method repeatedly, with different arguments. But then the analysis would depend on the thoroughness of the testing regimen, and also on the compiler, operating system and computer used. As we will see in Section 3.2, run-time analysis can have blaring weaknesses, mainly due to the "noise" of other processes that are executing at the same time as the method being tested.
At this stage, we prefer a more abstract analysis that can be performed by directly investigating the method's definition. We will ignore all memory restrictions, and so, for example, we will allow an int variable to take on any integer value and an array to be arbitrarily large. Because we will study the method without regard to a specific computer environment, we can refer to the method as an algorithm, that is, a finite sequence of explicit instructions to solve a problem in a finite amount of time.
The question then is, how can we estimate the execution-time requirements of a method from the method's definition? We take the number of statements executed in a trace of a method as a measure of the execution-time requirements of that method. This measure will be represented as a function of the "size" of the problem. Given a method for a problem of size n, let worstTime(n) be the maximum—over all possible parameter/input values—number of statements executed in a trace of the method.
For example, let's determine worstTime(n) for the following method, which returns the number of elements greater than the mean of an array of non-negative double values. Here n refers to the length of the array.
/** * Returns the number of elements in a non-empty array that are greater than * the mean of that array. * * @param a - an array of double values * @param mean - the sum of the elements in a, divided by a.length. * * @return the number of elements in a that are greater than mean * */ public static int aboveMeanCount (double[ ] a, double mean) { int n = a.length, count = 0; for (int i = 0; i < n; i++) if (a [i] > mean) count++; return count; } // method aboveMeanCount
There are six statements that will be executed only once: the assignment of the arguments to the parameters a and mean; the initialization of n, count and i; and the return of count. Within the for statement, i will be compared to n a total of n + 1 times, i will be incremented n times and the comparison of a [i] to mean will be made n times. If n - 1 elements have the value 1.0 and the other element has the value 0.0, then a [i] will be greater than mean a total of n - 1 times, so count will be incremented n - 1 times. The total number of statements executed in the worst case, that is, worstTime(n), is
6 + (n + 1) + n + n + (n - 1) = 4n + 6
Sometimes we will also be interested in the average-case performance of a method. We define average-Time(n) to be the average number of statements executed in a trace of the method. This average is taken over all invocations of the method, and we assume that each set of n parameter/input values for a call is equally likely. For some applications, that assumption is unrealistic, so averageTime(n) may not be relevant.
In the for loop of the just completed example, a [i] will be greater than mean, on average, half of the time, so count will be incremented only n/2 times. Then averageTime(n) is 3.5n + 7.
Occasionally, especially in Chapters 5 and 11, we will also be interested in estimating the space requirements of a method. To that end, we define worstSpace(n) to be the maximum number of variables allocated in a trace of the method, and averageSpace(n) to be the average number of variables allocated in a trace of the method. For an array, we treat each element—that is, indexed variable—to be a separate variable. So an array of length n would contribute n variables. The aboveMeanCount method does not create an array; worstSpace(n) = averageSpace(n) = 5.
3.1.1 Big-O Notation
We need not calculate worstTime(n) and averageTime(n)—or worstSpace(n) and averageSpace(n)— exactly since they are only crude approximations of the time requirements of the corresponding method. Instead, we approximate those functions by means of "Big-O" notation, defined in the next paragraph. Because we are looking at the method by itself, this "approximation of an approximation" is quite satisfactory for giving us an idea of how fast the method will be.
The basic idea behind Big-O notation is that we often want to determine an upper bound for the behavior of a function, that is, to determine how bad the performance of the function can get. For example, suppose we are given a function f. If some function g is, loosely speaking, an upper bound for f, then we say that f is Big-O of g. When we replace "loosely speaking" with specifics, we get the following definition:
Let g be a function that has non-negative integer arguments and returns a non-negative value for all arguments. A function f is said to be O(g) if for some positive constant C and some non-negative constant K,
f(n) ≤ Cg(n) for all n ≥ K.
If f is O(g), pronounced "big-oh of g", we can also say "f is of order g".
The idea behind Big-O notation is that if f is O(g) then eventually f is bounded above by some constant times g, so we can use g as a crude upper-bound estimate of the function f.
By a standard abuse of notation, we often associate a function with the value it calculates. For example, let g be the function defined by
g (n) = n 3, for n = 0,1,2,…
Instead of writing O(g) we write O(n3).
The following three examples will help you to understand the details of Big-O notation. Then, in Section 3.1.2, we will describe how to arrive at Big-O estimates without going through the details.
Example 3.1
Let f be the function worstTime defined for the aboveMeanCount method in Section 3.1 and repeated here:
public static int aboveMeanCount (double[ ] a, double mean) { int n = a.length, count = 0; for (int i = 0; i < n; i++) if (a [i] > mean) count++; return count; } // method aboveMeanCount
Then
f(n) = 4n + 6, for n = 0,1,2,
Show that f is O(n).
We need to find non-negative constants C and K such that f(n) < C*n for all n > K. We will show that each term in the definition of f is less than or equal to some constant times n for n greater than or equal to some non-negative integer. Right away, we get:
4n ≤ 4n for n ≥ 0, and.
6 ≤ 6n for n ≥ 1.
So for any n ≥ 1,
f(n) ≤ 4n + 6n = 10n.
That is, for C = 10 and K = 1, f(n) ≥ C*n for all n ≤ K. This shows that f is O(n).
In general, if f is a polynomial of the form
aini + ai-1ni-1 +...+ a1n + a0
then we can establish that f is O(ni) by choosing K = 1, C = |ai | + |ai-1| + ... + |a1| + |a0| and proceeding as in Example 3.1.
The next example shows that we can ignore the base of a logarithm when determining the order of a function.
Example 3.2
Let a and b be positive constants. Show that if f is O(loga n)then f is also O(logb n).
SOLUTION
Assume that f is O(loga n). Then there are non-negative constants C and K such that for all n > K,
f(n) < C * loga n
By a fundamental property of logarithms (see Section A2.4 of Appendix 2),
loga n = (loga b) * (logb n) for any n > 0.
Let C1 = C * loga b.
Then for all n > K, we have
f(n) < C * loga n = C * loga b * logb n = C1 * logb n,
and so f is O(logb n).
Because the base of the logarithm is irrelevant in Big-O estimates, the base is usually omitted. For example, you will often see O(log n) instead of O(log2 n) or O(log10 n).
The final example in this introduction to Big-O notation illustrates the significance of nested loops in estimating worstTime(n).
Example 3.3
Show that worstTime(n) is O(n2) for the following nested loop:
for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) System.out.println (i + j);
SOLUTION
For this nested loop, every trace will entail the execution of the same number of statements. So worstTime(n) and averageTime(n) will be equal. And that is frequently the case.
In the outer loop, the initialization of i is executed once, the continuation condition, i < n, is executed n + 1times, and i is incremented n times. So far, we have
1 + (n + 1) + n
statements executed. For each of the n iterations of the outer loop, the initialization of j is executed once, the continuation condition, j < n, is executed n + 1times, j is incremented n times, and the call to println is executed n times. That increases the number of statements executed by
n(1 + (n + 1) + n)
The total number of statements executed is
1 + (n + 1) + n + n(1 + (n + 1) + n) = 2n2 + 4n + 2
Since the same number of statements will be executed in every trace, we have
worstTime(n) = 2n2 + 4n + 2
By the same technique used in Example 3.1,
worstTime(n) ≤ 8n2 for all n ≥ 1.
We conclude that worstTime(n) is O(n2).
In Example 3.3, the number of statements executed in the outer loop is only 2n + 2, while 2n2 + 2n statements are executed in the inner loop. In general, most of the execution time of a method with nested loops is consumed in the execution of the inner(most) loop. So that is where you should devote your efforts to improving efficiency.
Note that Big-O notation merely gives an upper bound for a function. For example, if f is O(n2), then f is also O(n2 + 5n + 2), O(n3) and O(n10 + 3). Whenever possible, we choose the smallest element from a hierarchy of orders, of which the most commonly used are shown in Figure 3.1. For example, if f (n) = n + 7 for n = 0,1,2,…, it is most informative to say that f is O(n)—even though f is also O(n log n)and O(n3). Similarly, we write O(n) instead of O(2n + 4) or O(n - log n), even though O(n) = O(2n + 4) = O(n - log n); see Exercise 3.9.
Figure 3.2 shows some more examples of functions and where they fit in the order hierarchy.
FIGURE 3.1 Some elements in the Big-O hierarchy. The symbol "![]() " means "is contained in". For example, every function that is in O(1) is also in O(log n)
" means "is contained in". For example, every function that is in O(1) is also in O(log n)

FIGURE 3.2 Some sample functions in the order hierarchy

One danger with Big-O notation is that it can be misleading when the values of n are small. For example, consider the following two functions for n = 0, 1, 2, ….
f (n) = 1000 n is O(n)
and
g (n) = n2/10 is O(n2)
But f (n) is larger than g (n) for all values of n less than 10,000.
The next section illustrates how easy it can be to approximate worstTime(n)—or averageTime(n)— with the help of Big-O notation.
3.1.2 Getting Big-O Estimates Quickly
By estimating the number of loop iterations in a method, we can often determine at a glance an upper bound for worstTime(n). Let S represent any sequence of statements whose execution does not include a loop statement for which the number of iterations depends on n. The following method skeletons provide paradigms for determining an upper bound for worstTime(n).
Skeleton 1. worstTime(n) is O(1):
S
For example, for the following constructor from Chapter 1, worstTime(n) is O(1):
public HourlyEmployee (String name, int hoursWorked, double payRate) { this.name = name; this.hoursWorked = hoursWorked; this.payRate = payRate; if (hoursWorked <= MAX_REGULAR_HOURS) { regularPay = hoursWorked * payRate; overtimePay = 0.00; }// if else { regularPay = MAX_REGULAR_HOURS * payRate; overtimePay = (hoursWorked - MAX_REGULAR_HOURS) * (payRate * 1.5); } // else grossPay = regularPay + overtimePay; } // 3-parameter constructor
Because n is not specified or implied, the number of statements executed is constant—no matter what n is—so worstTime(n) is O(1). It follows that for the following method in the HourlyCompany class, worstTime(n) is also O(1):
protected FullTimeEmployee getNextEmployee (Scanner sc) { String name = sc.next(); int hoursWorked = sc.nextInt(); double payRate = sc.nextDouble(); return new HourlyEmployee (name, hoursWorked, payRate); } // method getNextEmployee
Note that the execution of S may entail the execution of millions of statements. For example:
double sum=0; for (int i = 0; i < 10000000; i++) sum += Math.sqrt (i);
The reason that worstTime(n) is O(1 ) is that the number of loop iterations is constant and therefore independent of n. In fact, n does not even appear in the code. In any subsequent analysis of a method, n will be given explicitly or will be clear from the context, so you needn't worry about "What is n?"
Skeleton 2. worstTime(n) is O(log n):
while (n > 1)
{
n = n /2;
S
} // while
Let t(n) be the number of times that S is executed during the execution of the while statement. Then t(n) is equal to the number of times that n can be divided by 2 until n equals 1. By Example A2.2 in Section A2.5 of Appendix 2, t(n) is the largest integer ≤ log2 n. That is, t (n) = floor (log2 n ).1 Since floor (log2 n) ≤ log2 (n) for any positive integer n, we conclude that t(n) is O(log n) and so worstTime(n) is also O(logn).
The phenomenon of repeatedly splitting a collection in two will re-appear time and again in the remaining chapters. Be on the lookout for the splitting: it signals that worstTime(n) will be O(log n).
The Splitting Rule
In general, if during each loop iteration, n is divided by some constant greater than 1, worstTime(n) will be O(log n) for that loop.
As an example of the Splitting Rule, here—from the Arrays class in the package java.util—is the most widely known algorithm in computer science: the Binary Search Algorithm. Don't get hung up in the details; we will study a binary search algorithm carefully in Chapter 5. Here, n refers to the size of the array being searched.
/** * Searches the specified array of ints for the specified value using the * binary search algorithm. The array must be sorted (as * by the sort method, above) prior to making this call. If it * is not sorted, the results are undefined. If the array contains * multiple elements with the specified value, there is no guarantee which * one will be found. * * @param a the array to be searched. * @param key the value to be searched for. * @return index of the search key, if it is contained in the list; * otherwise, (-(insertion point) - 1). The * insertion point is defined as the point at which the * key would be inserted into the array a: the index of the first * element greater than the key, or a.length, if all * elements in the array are less than the specified key. Note * that this guarantees that the return value will be greater than * or equal to 0 if and only if the key is found. * @see #sort(int[ ]) */ public static int binarySearch(int[ ] a, int key) { int low = 0; int high = a.length−1; while (low <= high) { int mid = (low + high) > > 1; // same effect as (low + high) / 2, // but see Programming Exercise 3.5 int midVal = a[mid]; if (midVal < key) low = mid + 1; else if (midVal > key) high = mid − 1; else return mid; // key found } // while return -(low + 1); // key not found. } // method binarySearch
At the start of each loop iteration, the area searched is from index low through index high, and the action of the loop reduces the area searched by half. In the worst case, the key is not in the array, and the loop continues until low > high. In other words, we keep dividing n by 2 until n = 0. (Incidentally, this repeated dividing by 2 is where the "binary" comes from in Binary Search Algorithm.) Then, by the Splitting Rule, worstTime(n) is O(log n) for the loop. And with just a constant number of statements outside of the loop, it is clear that worstTime(n) is O(log n) for the entire method.
Skeleton 3. worstTime(n) is O(n):
for (int i = 0; i < n; i++) { S } //for
The reason that worstTime(n) is O(n) is simply that the for loop is executed n times. It does not matter how many statements are executed during each iteration of the for loop: suppose the maximum is k statements, for some positive integer k. Then the total number of statements executed is ≤ kn. Note that k must be positive because during each iteration, i is incremented and tested against n.
As we saw in Section 3.1, worstTime(n) is O(n) for the aboveMeanCount method. But now we can obtain that estimate simply by noting that the loop is executed n times.
public static int aboveMeanCount (double[ ] a, double mean) { int n = a.length, count = 0; for (int i = 0; i < n; i++) if (a [i] > mean) count++; return count; } // method aboveMeanCount
For another example of a method whose worstTime(n) is O(n), here is another method from the Arrays class of the package java.util. This method performs a sequential search of two arrays for equality; that is, the search starts at index 0 of each array, and compares the elements at each index until either two unequal elements are found or the end of the arrays is reached.
/** * Returns true if the two specified arrays of longs are * equal to one another. Two arrays are considered equal if both * arrays contain the same number of elements, and all corresponding pairs * of elements in the two arrays are equal. In other words, two arrays * are equal if they contain the same elements in the same order. Also, * two array references are considered equal if both are null. * * @param a one array to be tested for equality. * @param a2 the other array to be tested for equality. * @return true if the two arrays are equal. */ public static boolean equals (long[] a, long[] a2) { if (a==a2) return true ; if (a==null || a2==null) return false ; int length = a.length; if (a2.length != length) return false ; for (int i=0; i<length; i++) if (a[i] != a2[i]) return false; return true; } // method equals
Skeleton 4. worstTime(n) is O(n log n):
int m; for (int i = 0; i < n; i++) { m = n; while (m>1) { m = m / 2; S } // while } // for
The for loop is executed n times. For each iteration of the for loop, the while loop is executed floor (log2 n) times—see Example 2 above—which is ≤ log2 n. Therefore worstTime(n) is O(n log n). We needed to include the variable m because if the inner loop started with while (n > 1), the outer loop would have terminated after just one iteration.
In Chapter 11, we will encounter several sorting algorithms whose worstTime(n) is O(n log n), where n is the number of items to be sorted.
Skeleton 5. worstTime(n) is O(n2):
a. for int i = 0; i < n; for (int j = 0; j < n; { S } // forj
The number of times that s is executed is n2. That is all we need to know to conclude that worstTime(n) is O(n2). In Example 3.3, we painstakingly counted the exact number of statements executed and came up with the same result.
b. for (int i = 0; i < n; for (int k = i; k < n; k++) { S } // for k
The number of times that S is executed is
As shown in Example A2.1 of Appendix 2, the above sum is equal to
n (n + 1)12,
which is O(n2). That is, worstTime(n) is O(n2).
The selectionSort method, developed in Chapter 11, uses the above skeleton. Here, n refers to the size of the array to be sorted.
/** * Sorts a specified array of int values into ascending order. * The worstTime(n) is O(n * n). * * @param x - the array to be sorted. * */ public static void selectionSort (int [ ] x) { // Make x [0 . . . i] sorted and <= x [i + 1] . . .x [x.length -1]: for (int i = 0; i < x.length -1; i++) { int pos = i; for (int j = i + 1; j < x.length; j++) if (x [j] < x [pos]) pos = j; int temp = x [i]; x [i] = x [pos]; x [pos] = temp; } // for i } // method selectionSort
There are n - 1 iterations of the outer loop; when the smallest values are at indexes x [0], x [1], … x [n - 2], the largest value will automatically be at index x [n - 1]. So the total number of inner-loop iterations is
We conclude that worstTime(n) is O(n2).
C. for (int i = 0; i < n; i++) { S } // for i for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) { S } // for j
For the first segment, worstTime(n) is O(n), and for the second segment, worstTime(n) is O(n2), so for both segments together, worstTime(n) is O(n + n2), which is equal to O(n2). In general, for the sequence
A
B
if worstTime(n) is O(t) for A and worstTime(n) is O(g) for B, then worstTime(n) is O(f+ g) for the sequence A, B.
3.1.3 Big-Omega, Big-Theta and Plain English
In addition to Big-O notation, there are two other notations that you should know about: Big-Omega and Big-Theta. Whereas Big-O provides a crude upper bound for a function, Big-Omega supplies a crude lower bound. Here is the definition:
Let g be a function that has non-negative integer arguments and returns a non-negative value for all arguments. We define Ω(g) to be the set of functions f such that for some positive constant C and some non-negative constant K,
f(n) ≥ Cg(n) for all n ≥ K.
If f is in Ω(g) we say that f is "Big-Omega of g". Notice that the definition of Big-Omega differs from the definition of Big-O only in that the last line has f (n) ≥ Cg (n) instead of f (n) ≤ Cg (n), as we had for Big-O.
All of the Big-O examples from Section 3.1.1 are also Big-Omega examples. Specifically, in Example 3.1, the function f defined by
f (n) = 2n2 + 4n + 2, for n = 0,1,2,...
is Ω(n2): for C = 2and K = 0, f (n) ≥ Cn2 for all n > K. Also, for all of the code skeletons and methods in Section 3.1.2, we can replace O with Ω as a bound on worstTime(n).
Big-Omega notation is used less frequently than Big-O notation because we are usually more interested in providing an upper bound than a lower bound for worstTime(n) or averageTime(n). That is, "can't be any worse than" is often more relevant than "can't be any better than." Occasionally, knowledge of a theoretical lower bound can guide those trying to come up with an optimal algorithm. And in Chapter 11, we establish the important result that for any comparison-based sort method, averageTime(n)—and therefore, worstTime(n)—is Q(n log n).
A somewhat artificial example shows that Big-O and Big-Omega are distinct. Let f be the function defined by
f (n) = n, for n = 0,1,2,…
Clearly, f is O(n), and therefore, f is also O(n2). But f is not Ω(n2). And that same function f is clearly Ω(n), and therefore Ω(1). But f is not O(1). In fact, the Big-Omega hierarchy is just the reverse of the Big-O hierarchy in Figure 3.1. For example,
Ω(n2) ![]() Ω(n log n)
Ω(n log n) ![]() Ω(n)
Ω(n) ![]() Ω(1)
Ω(1)
In most cases the same function will serve as both a lower bound and an upper bound, and this leads us to the definition of Big-Theta:
Let g be a function that has non-negative integer arguments and returns a non-negative value for all arguments. We define Θ(g) to be the set of functions f such that for some positive constants C1 and C2, and some non-negative constant K,
C1 g(n) ≤ f(n) ≤ C2 g(n)for all n ≥ K.
The idea is that if f is Θ(g), then eventually (that is, for all n ≥ K), f (n) is bounded below by some constant times g(n) and also bounded above by some constant times g(n). In other words, to say that a function f is Θ(g) is exactly the same as saying that f is both O(g) and Ω(g). When we establish that a function f is Θ(g), we have "nailed down" the function f in the sense that f is, roughly, bounded above by g and also bounded below by g.
As an example of Big-Theta, consider the function f defined by
f (n) = 2n2 + 4n + 2, for n = 0,1,2,…
We showed in Example 3.3 that f is O(n2), and earlier in this section we showed that f is Ω(n2). We conclude that f is Θ(n2).
For ease of reading, we adopt plain-English terms instead of Big-Theta notation for several families of functions in the Big-Theta hierarchy. For example, if f is Θ(n), we say that f is "linear in n". Table 3.1 shows some English-language replacements for Big-Theta notation.
We prefer to use plain English (such as "constant," "linear," and "quadratic") whenever possible. But as we will see in Section 3.1.5, there will still be many occasions when all we specify is an upper bound—namely, Big O—estimate.
3.1.4 Growth Rates
In this section, we look at the growth rate of functions. Specifically, we are interested in how rapidly a function increases based on its Big-Theta classification. Suppose we have a method whose worstTime(n) is linear in n. Then we can write:
worstTime(n) ![]() C n, for some constant C (and for sufficiently large values of n).
C n, for some constant C (and for sufficiently large values of n).
What will be the effect of doubling the size of the problem, that is, of doubling n?
worstTime(2n) ![]() C 2 n
C 2 n
= 2 C n
![]() 2 worstTime(n)
2 worstTime(n)
In other words, if we double n, we double the estimate of worst time.
Table 3.1 Some English-language equivalents to Big-Theta notation
| Big-Theta | English |
| Θ(c), for some constant c ≥ 0 | constant |
| Θ(log n) | logarithmic in n |
| Θ(n) | linear in n |
| Θ(n log n) | linear-logarithmic in n |
| Θ(n2) | quadratic in n |
Similarly, if a method has worstTime(n) that is quadratic in n, we can write:
worstTime(n) ![]() Cn for some constant C (and for sufficiently large values of n).
Cn for some constant C (and for sufficiently large values of n).
Then
worstTime(2n) ![]() C (2n)2
C (2n)2
= C 4 n 2
= 4 C n 2
![]() 4 worstTime(n)
4 worstTime(n)
In other words, if we double n, we quadruple the estimate of worst time. Other examples of this kind of relationship are explored in Concept Exercise 3.7, Concept Exercise 11.5 and in later labs.
Figure 3.3 shows the relative growth rates of worstTime(n) for several families of functions.
FIGURE 3.3 The graphs of worstTime(n) for several families of functions
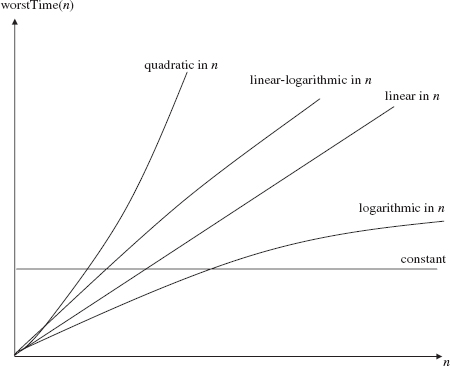
Figure 3.4 indicates why Big-Theta differences eventually dominate constant factors in estimating the behavior of a function. For example, if n is sufficiently large, t1(n) = n2/100 is much greater than t2(n) = 100 n log2 n. But the phrase "if n is sufficiently large" should be viewed as a warning. Note that t1 is smaller than t2 for arguments less than 100,000. So whether Big-Theta (or Big-O or Big-Omega) is relevant may depend on how large the size of your problem might get.
Figure 3.4 has a concrete example of the differences between several families in the Big-Theta hierarchy. For a representative member of the family—expressed as a function of n—the time to execute that many statements is estimated when n equals one billion.
Some of the differences shown in Figure 3.4 are worth exploring. For example, there is a huge difference between the values of log2 n and n. In Chapter 10, we will study a data structure—the binary search tree—for which averageTime(n) is logarithmic in n for inserting, removing, and searching, but worstTime(n) is linear in n for those methods.
FIGURE 3.4 Estimated time to execute a given number of statements for various functions of n when n = 1,000,000,000 and 1,000,000 statements are executed per second. For example, to execute n log2 n statements takes approximately 7 hours

Another notable comparison in Figure 3.4 is between n log2 n and n2. In Chapter 11, on sort methods, we will see tangible evidence of this difference. Roughly speaking, there are two categories of sort methods: fast sorts, whose averageTime(n) is linear-logarithmic in n, and simple sorts, whose averageTime(n) is quadratic in n.
All of the methods we have seen so far are polynomial-time methods. A polynomial-time method is one for which worstTime(n) is O(ni) for some positive integer i. For example, a method whose worstTime(n) is (O n2) is a polynomial-time method. Similarly, a method whose worstTime(n) is(Olog n) is polynomial-time because (Olog n) ![]() O (n).
O (n).
When we try to develop a method to solve a given problem, we prefer polynomial-time methods whenever possible. For some methods, their run time is so long it is infeasible to run the methods for large values of n. Such methods are in the category of exponential-time methods. An exponential-time method is one whose worstTime(n) is Ω(xn) for some real number x > 0. Then we say worstTime(n) is exponential in n. For example, a method whose worstTime(n ) is Ω(2n) is an exponential-time method. Chapter 5 has an example of an exponential-time method, and Labs 7 and 9 have two more exponential-time methods. As you might expect, a polynomial-time method cannot also be exponential-time (Concept Exercise 3.10).
The existence of exponential-time methods gives rise to an interesting question: For a given exponential-time method, might there be a polynomial-time method to solve the same problem? In some cases, the answer is no. An intractable problem is one for which any method to solve the problem is an exponential-time method. For example, a problem that requires 2n values to be printed is intractable because any method to solve that problem must execute at least Ω(2n) statements. The problem in Chapter 5 for which an exponential-time method is supplied is an intractable problem. The problem in Lab 9 is also intractable, but the problem in Lab 7 has a polynomial-time solution.
Lab 23 investigates the Traveling Salesperson Problem, for which the only known methods to solve the problem are exponential-time methods. The most famous open question in computer science is whether the Traveling Salesperson Problem is intractable. There may be a polynomial-time method to solve that problem, but no one has found one, and most experts believe that no such method is possible.
If we are working on a single method only, it may be feasible to optimize that method's averageTime(n) and worstTime(n), with the intent of optimizing execution time. But for the management of an entire project, it is usually necessary to strike a balance. The next section explores the relevance of other factors, such as memory utilization and project deadlines.
3.1.5 Trade-Offs
In the previous section we saw how to estimate a method's execution-time requirements. The same Big-O (or Big-Omega or Big-Theta) notation can be used to estimate the memory requirements of a method. Ideally, we will be able to develop methods that are both fast enough and small enough. But in the real world, we seldom attain the ideal. More likely, we will encounter one or more of the following obstacles during programming:
- The program's estimated execution time may be longer than acceptable according to the performance requirements. Performance requirements, when given, state the time and space upper-bounds for all or part of a program.
- The program's estimated memory requirements may be larger than acceptable according to the performance requirements. This situation frequently arises for hand-held devices.
- The program may require understanding a technique about which the programmer is only vaguely familiar. This may create an unacceptable delay of the entire project.
Often, a trade-off must be made: a program that reduces one of the three obstacles may intensify the other two. For example, if you had to develop a project by tomorrow, you would probably ignore time and space constraints and focus on understanding the problem well enough to create a project. The point is that real-life programming involves hard decisions. It is not nearly enough that you can develop programs that run. Adapting to constraints such as those mentioned above will make you a better programmer by increasing your flexibility.
We can incorporate efficiency concerns into the correctness of a method by including performance requirements in the method's specification (but see Programming Exercise 3.5). For example, part of the specification for the Quick Sort method in Chapter 11 is:
The worstTime (n) is O(n2).
Then for a definition of that method to be correct, worstTime(n) would have to be O(n2). Recall that the Big-O estimates provide upper bounds only. But the class developer is free to improve on the upper bounds for average time or worst time. For example, there is a way to define that sort method so that worstTime(n) is linear-logarithmic in n.
We want to allow developers of methods the flexibility to improve the efficiency of those methods without violating the contract between users and developers. So any performance requirements in method specifications will be given in terms of upper-bounds (that is, Big-O) only. Here are three conventions regarding the Big-O estimates in method specifications:
0. If a class stores a collection of elements, then unless otherwise noted, the variable n refers to the number of elements in the collection.
1. For many methods, worstTime(n) is O(1). If no estimate of worstTime(n) is given, you may assume that worstTime(n) is O(1).
2. Often, averageTime(n) has the same Big-O estimate as worstTime(n), and then we will specify the worstTime(n) estimate only. When they are different, we will specify both.
When we analyze the time (or space) efficiency of a specific method definition, we will determine lower as well as upper bounds, so we will use Big-Theta notation—or the English-language equivalent: constant, linear-in-n, and so on.
Up until now, we have separated concerns about correctness from concerns about efficiency. According to the Principle of Data Abstraction, the correctness of code that uses a class should be independent of that class's implementation details. But the efficiency of that code may well depend on those details. In other words, the developer of a class is free—for the sake of efficiency—to choose any combination of fields and method definitions, provided the correctness of the class's methods do not rely on those choices. For example, suppose a class developer can create three different versions of a class:
A: correct, inefficient, does not allow users to access fields;
B: correct, somewhat efficient, does not allow users to access fields;
C: correct, highly efficient, allows users to access fields.
In most cases, the appropriate choice is B. Choosing C would violate the Principle of Data Abstraction because the correctness of a program that uses C could depend on C's fields.
Big-O analysis provides a cross-platform estimate of the efficiency of a method. The following section explores an execution-time tool for measuring efficiency.
3.2 Run-Time Analysis
We have seen that Big-O notation allows us to estimate the efficiency of methods independently of any particular computing environment. For practical reasons, we may also want to estimate efficiency within some fixed environment. Why settle for estimates? For one thing,
In multi-programming environments such as Windows, it is very difficult to determine how long a single task takes.
Why? Because there is so much going on behind the scenes, such as the maintaining the desktop clock, executing a wait-loop until a mouse click occurs, and updating information from your mailer and browser. At any given time, there might be dozens of such processes under control of the Windows Manager. And each process will get a time slice of several milliseconds. The bottom line is that the elapsed time for a task is seldom an accurate measure of how long the task took.
Another problem with seeking an exact measure of efficiency is that it might take a very long time—O(forever). For example, suppose we are comparing two sorting methods, and we want to determine the average time each one takes to sort some collection of elements. The time may depend heavily on the particular arrangement of the elements chosen. Because the number of different arrangements of n distinct elements is n!, it is not feasible to generate every possible arrangement, run the method for each arrangement, and calculate the average time.
Instead, we will generate a sample ordering that is in "no particular order." The statistical concept corresponding to "no particular order" is randomness. We will use the time to sort a random sample as an estimate of the average sorting time. We start with a discussion of timing because, as we will see later, one aspect of randomness depends on the result of a timing method.
3.2.1 Timing
To assist in the timing of methods, Java supplies nanoTime(), a static method in the System class of java.lang. This method returns a long whose value is the number of nanoseconds—that is, billionths of a second—elapsed since some fixed but arbitrary time. To estimate how much execution time a task consumes, we calculate the time immediately before and immediately after the code for the task. The difference in the two times represents the elapsed time. As noted previously, elapsed time is a very, very crude estimate of the time the task consumed. The following code serves as a skeleton for estimating the time expended by a method:
final String ANSWER_1 = "The elapsed time was "; final double NANO_FACTOR = 1000000000.0; // nanoseconds per second final String ANSWER_2 = " seconds."; long startTime, finishTime, elapsedTime; startTime = System.nanoTime(); // Perform the task: ... // Calculate the elapsed time: finishTime = System. nanoTime(); elapsedTime = finishTime - startTime; System.out.println (ANSWER_1 + (elapsedTime / NANO_FACTOR) + ANSWER_2);
This skeleton determines the elapsed time for the task in seconds, with fractional digits. For example, if startTime has the value 885161724000 and finishTime has the value 889961724000, then elapsedTime has the value 4800000000, that is, four billion and eight hundred million. Then elapsedTime/NANO_FACTOR has the value 4.8 (seconds).
We will use the time to process a random sample of values as an estimate of the average processing time. Section 3.2.2 contains an introduction to—or review of—the Random class, part of the package java.util.
3.2.2 Overview of the Random Class
If each number in a sequence of numbers has the same chance of being selected, the sequence is said to be uniformly distributed. A number so selected from a uniformly-distributed sequence is called a random number. And a method that, when repeatedly called, returns a sequence of random numbers is called a random-number generator.
The Random class in java.util supplies several random-number generators. We will look at three of those methods. Strictly speaking, the sequence of numbers returned by repeated calls to any one of those methods is a pseudo-random-number sequence because the numbers calculated are not random at all—they are determined by the code in the method. The numbers appear to be random if we do not see how they are calculated. If you look at the definition of this method in the Random class, the mystery and appearance of randomness will disappear.
Here is the method specification for one of the random-number generators:
/** * Returns a pseudo-random int in the range from 0 (inclusive) to a specified int * (exclusive). * * @param n - the specified int, one more than the largest possible value * returned. * * @return a random int in the range from 0 to n -1, inclusive. * * @throws IllegalArgumentException - if n is less than or equal to zero. * */ public int nextInt (int n)
For example, a call to nextint (100) will return a random integer in the range from 0 to 99, inclusive.
For another example, suppose we want to simulate the roll of a die. The value from one roll of a die will be an integer in the range 1… 6, inclusive. The call to nextint (6) returns an int value in the range from 0 to 5, inclusive, so we need to add 1 to that returned value. Here is the code to print out that pseudo-random die roll:
Random die = new Random(); int oneRoll = die.nextint (6) + 1; System.out.println (oneRoll);
The value calculated by the nextint (int n) method depends on the seed it is given. The variable seed is a private long field in the Random class. The initial value of seed depends on the constructor called. If, as above, the Random object is created with the default constructor, then seed is initialized to System.nanoTime(). The other form of the constructor has a long parameter, and seed is initialized to the argument corresponding to that parameter. Each time the method nextint (int n) is called, the current value of the seed is used to determine the next value of the seed, which determines the int returned by the method.
For example, suppose that two programs have
Random die = new Random (800); for (int i = 0; i < 5; System.out.println (die.nextint (6) + 1);
The output from both programs would be exactly the same:
3 5 3 6 2
This repeatability can be helpful when we want to compare the behavior of programs, as we will in Chapters 5—15. In general, repeatability is an essential feature of the scientific method.
If we do not want repeatability, we use the default constructor. Recall that the default constructor initializes the seed to System.nanoTime().
Here are two other random-number generators in the Random class:
/** * Returns a pseudo-random int in the range from Integer.MIN_VALUE to * Integer.MAX_VALUE. * * * @return a pseudo-random int in the range from Integer.MIN_VALUE to * Integer.MAX_VALUE. * */ public int nextInt () /** * Returns a pseudo-random double in the range from 0.0 (inclusive) to * 1.0 (exclusive). * */ public double nextDouble ()
The following program combines randomness and timing with repeated calls to the selectionSort method of Section 3.1.2. The higher levels of the program—input, output, and exception handling—are handled in the run( ) method. The randomTimer method generates an array of random integers, calls the selectionSort method, and calculates the elapsed time. The randomTimer method is not unit-tested because timing results will vary widely from computer to computer. The unit tests for selectionSort and other sort methods are in the Chapter 11 directory of the website's source code section.
import java.util.*; public class TimingRandom { public static void main (String[ ] args) { new TimingRandom().run(); } // method main public void run() { final int SENTINEL = -1; final String INPUT_PROMPT = " Please enter the number of"+ " integers to be sorted (or " + SENTINEL + " to quit): "; final String ANSWER_1 = "The elapsed time was "; final double NANO_FACTOR = 1000000000.0; // nanoseconds per second final String ANSWER_2 = " seconds."; Scanner sc = new Scanner (System.in); long elapsedTime; while (true) { try { System.out.print (INPUT_PROMPT); int n = sc.nextInt(); if (n == SENTINEL) break ; elapsedTime = randomTimer (n); System.out.println (ANSWER_1 + (elapsedTime / NANO_FACTOR) + ANSWER_2); } // try catch (Exception e) { System.out.println (e); sc.nextLine(); } // catch } // while } // method run /** * Determines the elapsed time to sort a randomly generated array of ints. * * @param n - the size of the array to be generated and sorted. * * @return the elapsed time to sort the randomly generated array. * * @throws NegativeArraySizeException - if n is less than 0. * */ public long randomTimer (int n) { Random r = new Random(); long startTime, finishTime, elapsedTime; int[ ] x = new int [n]; for (int i = 0; i < n; i++) x [i] = r.nextInt(); startTime = System.nanoTime(); // Sort x into ascending order: selectionSort (x); // Calculate the elapsed time: finishTime = System.nanoTime(); elapsedTime = finishTime - startTime; return elapsedTime; } // method randomTimer /** * Sorts a specified array of int values into ascending order. * The worstTime(n) is O(n * n). * * @param x - the array to be sorted. * */ public static void selectionSort (int [ ] x) { // Make x [0 ... i] sorted and <= x [i + 1] ... x [x.length -1]: for (int i = 0; i < x.length - 1; i++) { int pos = i; for (int j = i + 1; j < x.length; j++) if (x [j] < x [pos]) pos = j; int temp = x [i]; x [i] = x [pos]; x [pos] = temp; } // for i } // method selectionSort } // class TimingRandom
The number of iterations of the while loop is independent of n, so for the run() method, worstTime(n) is determined by the estimate of worstTime(n )for randomTimer. The randomTimer method has a loop to generate the array, and worstTime(n) for this generation is O(n). Then randomTimer calls selectionSort. In Section 3.1.2, we showed that worstTime(n)for selectionSort is O(n2). Since the number of iterations is the same for any arrangement of the n elements, averageTime(n) is O(n2). In fact, n2 provides a crude lower bound as well as a crude upper bound, so averageTime(n) is quadratic in n. Then we expect the average run time—over all possible arrangements of n doubles—to be quadratic in n. As suggested in Section 3.2, we use the elapsed time to sort n pseudo-random doubles as an approximation of the average run time for all arrangements of n doubles.
The elapsed time gives further credence to that estimate: for n = 50000, the elapsed time is 19.985 seconds, and for n = 100000, the elapsed time is 80.766 seconds. The actual times are irrelevant since they depend on the computer used, but the relative times are significant: when n doubles, the elapsed time quadruples (approximately). According to Section 3.1.4 on growth rates, that ratio is symptomatic of quadratic time.
Randomness and timing are also combined in the experiment in Lab 4: You are given the unreadable (but runnable) bytecode versions of the classes instead of source code.
You are now prepared to do Lab 4:
Randomness and Timing of Four Mystery Classes
SUMMARY
Big-O notation allows us to quickly estimate an upper bound on the time/space efficiency of methods. Because Big-O estimates allow function arguments to be arbitrarily large integers, we treat methods as algorithms by ignoring the space requirements imposed by Java and a particular computing environment. In addition to Big-O notation, we also looked at Big-Ω notation (for lower bounds) and Big-Θ notation (when the upper-bound and lower-bound are roughly the same).
Run-time analysis allows methods to be tested on a specific computer. But the estimates produced are often very crude, especially in a multiprogramming environment. Run-time tools include the nanoTime() method and several methods from the Random class.
CROSSWORD PUZZLE
| ACROSS | DOWN |
| 7. The private long field in the Random class whose initial value depends on the constructor called. | 1. The rule that states "In general, if during each loop iteration, n is divided by some constant greater than 1, worstTime(n) will be O(log n) for that loop." |
| 9. A finite sequence of explicit instructions to solve a problem in a finite amount of time. | 2. A problem for which for which any method to solve the problem is an exponential-time method is said to be_____________. |
| 10. A function of g that is both Big O of g and Big Omega of g is said to be __________ of g. | 3. A method whose worstTime(n) is bounded below by x to the n for some real number x > 1.0 is said to be an _________ time method. |
| 4. A function of n, the problem size, that returns the maximum (over all possible parameter/input values) number of statements executed in a trace of the method. | |
| 5. A hallmark of the Scientific Method, and the reason we do not always want a random seed for the random number generator in the Random class. | |
| 6. A function of n that is Big Theta of n-squared is said to be _______ in n. | |
| 8. A static method in the System class that returns a long whose value is the number of billionths of a second elapsed since some fixed but arbitrary time. |
CONCEPT EXERCISES
3.1 Create a method, sample (int n), for which worstTime(n) is O(n) but worstTime(n) is not linear in n. Hint: O(n) indicates that n may be (crudely) viewed as an upper bound, but linear-in-n indicates that n may be (crudely) viewed as both an upper bound and a lower bound.
3.2 Study the following algorithm:
i = 0;
while (!a [i].equals (element))
i++;
Assume that a is an array of n elements and that there is at least one index k in 0...n-1 such that a [k].equals element).
Use Big-O notation to estimate worstTime(n). Use Big-Ω and Big-Θ notation to estimate worstTime(n). In plain English, estimate worstTime(n).
3.3 Study the following method:
/** * Sorts a specified array of int values into ascending order. * The worstTime(n) is O(n * n). * * @param x - the array to be sorted. * */ public static void selectionSort (int [ ] x) { // Make x [0 ... i] sorted and <= x [i + 1] ... x [x.length -1]: for (int i = 0; i < x.length - 1; i++) { int pos = i; for (int j = i + 1; j < x.length; j++) if (x [j] < x [pos]) pos = j; int temp = x [i]; x [i] = x [pos]; x [pos] = temp; } // for i } // method selectionSort
- For the inner for statement, when i = 0, j takes on values from 1 to n - 1, and so there are n - 1 iterations of the inner for statement when i = 0. How many iterations are there when i = 1? When i = 2?
- Determine, as a function of n, the total number of iterations of the inner for statement as i takes on values from 0 to n- 2.
- Use Big-O notation to estimate worstTime(n). In plain English, estimate worstTime(n)—the choices are constant, logarithmic in n, linear in n, linear-logarithmic in n, quadratic in n and exponential in n.
3.4 For each of the following functions f, where n = 0, 1, 2, 3,…, estimate f using Big-O notation and plain English:
- f(n) = (2 + n)*(3 + log(n))
- f(n) = 11 * log(n) + n/2 - 3452
- f(n) = 1 + 2 + 3 +... + n
- f(n) = n *(3 + n) − 7* n
- f(n) = 7* n + (n − 1) * log (n − 4)
- f(n) = log (n2)+ n
- f(n) =
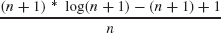
- f(n) = n + n/2 + n/4 + n/8 + n/16 + ...
3.5 In the Order Hierarchy in Figure 3.1, we have…, O(log n), O(n1/2),…. Show that, for integers n > 16, log2 n < n1/2. Hint from calculus: Show that for all real numbers x > 16, the slope of the function log2 x is less than the slope of the function x1/2. Since log2(16) == 161/2, we conclude that for all real numbers x > 16, log2 x < x1/2.
3.6 For each of the following code segments, estimate worstTime(n)using Big Ω notation or plain English. In each segment, S represents a sequence of statements in which there are no n-dependent loops.
a. for (int i = 0; i * i < n; i + S b. for (int i = 0; Math.sqrt (i) < n; S c. int k= 1; for (int i = 0; i < n; i++) k*=2; for (int i = 0; i < k; i++) S
Hint: In each case, 2 is part of the answer.
3.7.
- Suppose we have a method whose worstTime(n) is linear in n. Estimate the effect of tripling n on run time—the actual time to execute the method in a particular computing environment. That is, estimate runTime(3n) in terms of runTime(n).
- Suppose we have a method whose worstTime(n) is quadratic in n. Estimate the effect of tripling n on run time—the actual time to execute the method in a particular computing environment. That is, estimate runTime(3n) in terms of runTime(n).
- Suppose we have a method whose worstTime(n) is constant. Estimate the effect of tripling n on run time—the actual time to execute the method in a particular computing environment. That is, estimate runTime(3n) in terms of runTime(n).
3.8 This exercise proves that the Big-O families do not constitute a strict hierarchy. Consider the function f, defined for all non-negative integers as follows:
n, if n is even;
f(n) =
0, if n is odd
Define a function g on all non-negative integers such that f is not O(g) and g is not Of).
3.9 Show that O(n) = O(n + 7). Hint: use the definition of Big-O.
3.10 Show that if f (n) is polynomial in n, f (n) cannot be exponential in n.
3.11 Suppose, for some method, worstTime(n) = nn. Show that the method is an exponential-time method (that is, worstTime(n) is Ω(xn) for some real number x > 1.0). But show that worstTime(n) is not Θ(xn)—that is, Big Theta of xn —for any real number x > 1.0.
3.12 This exercise illustrates some anomalies of Θ(1).
- Define f (n) to be 0 for all n > 0. Show that f is not Θ(1), but f is Θ(0).
- Define f (n) to be (n + 2)/(n + 1) for all n ≥ 0. Show that f is Θ(1)—and so can be said to be "constant"—even though f is not a constant function.
3.13
- Assume that worstTime(n) = C (statements) for some constant C and for all values of n ≥ 0. Determine worstTime(2n) in terms of worstTime(n).
- Assume that worstTime(n) = log2 n (statements) for all values of n ≥ 0. Determine worstTime(2n)in terms of worstTime(n).
- Assume that worstTime(n) = n (statements) for all values of n ≥ 0. Determine worstTime(2n) in terms of worstTime(n).
- Assume that worstTime(n) = n log2 n (statements) for all values of n ≥ 0. Determine worstTime(2n)in terms of worstTime(n).
- Assume that worstTime(n) = n2 (statements) for all values of n ≥ 0. Determine worstTime(2n) in terms of worstTime(n).
- Assume that worstTime(n) = 2n (statements) for all values of n ≥ 0. Determine worstTime(n + 1) in terms of worstTime(n). Determine worstTime(2n) in terms of worstTime(n).
3.14 If worstTime(n) is exponential in n for some method sample, which of the following must be true about that method?
- worstTime(n) is O(2n).
- worstTime(n) is Ω(2n).
- worstTime(n) is Θ(2n).
- worstTime(n) is O(nn).
- none of the above.
PROGRAMMING EXERCISES
3.1 In mathematics, the absolute value function returns a non-negative integer for any integer argument. Develop a run method to show that the Java method Math.abs (int a) does not always return a non-negative integer.
Hint: See Programming Exercise 0.1.
3.2 Assume that r is (a reference to) an object in the Random class. Show that the value of the following expression is not necessarily in the range 0 … 99:
Math.abs (r.nextInt()) % 100
Hint: See Programming Exercise 3.1.
3.3 Develop a run method that initializes a Random object with the default constructor and then determines the elapsed time for the nextInt() method to generate 123456789.
3.4 Suppose a method specification includes a Big-O estimate for worstTime(n). Explain why it would be impossible to create a unit test to support the Big-O estimate.
3.5 In the binarySearch method in Section 3.1.2, the average of low and high was calculated by the following expression
(low + high) >> 1
Compare that expression to
low + ((high - low) >> 1)
The two expressions are mathematically equivalent, and the first expression is slightly more efficient, but will return an incorrect result for some values of low and high. Find values of low and high for which the first expression returns an incorrect value for the average of low and high. Hint: The largest possible int value is Integer.MAX_VALUE, approximately 2 billion.
Programming Project 3.1: Let's Make a Deal!
This project is based on the following modification—proposed by Marilyn Vos Savant—to the game show "Let's Make a Deal." A contestant is given a choice of three doors. Behind one door there is an expensive car; behind each of the other doors there is a goat.
After the contestant makes an initial guess, the announcer peeks behind the other two doors and eliminates one of them that does not have the car behind it. For example, if the initial guess is door 2 and the car is behind door 3, then the announcer will show that there is a goat behind door 1.
If the initial guess is correct, the announcer will randomly decide which of the other two doors to eliminate. For example, if the initial guess is door 2 and the car is behind door 2, the announcer will randomly decide whether to show a goat behind door 1 or a goat behind door 3. After the initial guess has been made and the announcer has eliminated one of the other doors, the contestant must then make the final choice.
Develop and test a program to determine the answer to the following questions:
- Should the contestant stay with the initial guess, or switch?
- How much more likely is it that an always-switching contestant will win instead of a never-switching contestant? For the sake of repeatability, the following system tests used a seed of 100 for the random-number generator.
Please enter the number of times the game will be played: 10000
Please enter 0 for a never-switching contestant or 1 for always-switching: 0
The number of wins was 3330
System Test 2:
Please enter the number of times the game will be played: 10000
Please enter 0 for a never-switching contestant or 1 for always-switching: 1
The number of wins was 6628
Based on the output, what are your answers to the two questions given above?
Suppose, instead of working with three doors, the number of doors is input, along with the number of times the game will be played. Hypothesize how likely it is that the always-switching contestant will win. Modify and then run your project to confirm or reject your hypothesis. (Keep hypothesizing, and modifying and running your project until your hypothesis is confirmed.)
Hint for Hypothesis: Suppose the number of doors is n, where n can be any positive integer greater than 2. For an always-switching contestant to win, the initial guess must be incorrect, and then the final guess must be correct. What is the probability, with n doors, that the initial guess will be incorrect? Given that the initial guess is incorrect, how many doors will the always-switching contestant have to choose from for the final guess (remember that the announcer will eliminate one of those doors)? The probability that the always-switching contestant will win is the probability that the initial guess is incorrect times the probability that the final guess is then correct.
1. floor(x) returns the largest integer that is less than or equal to x.