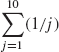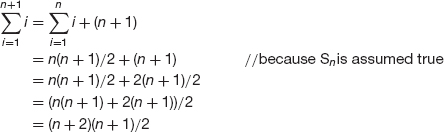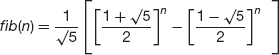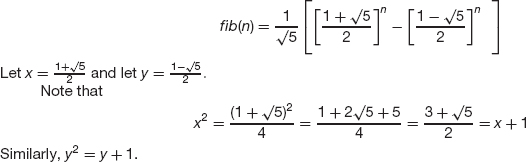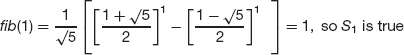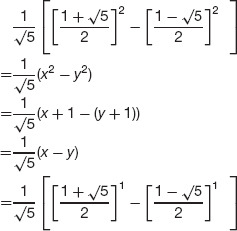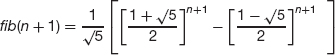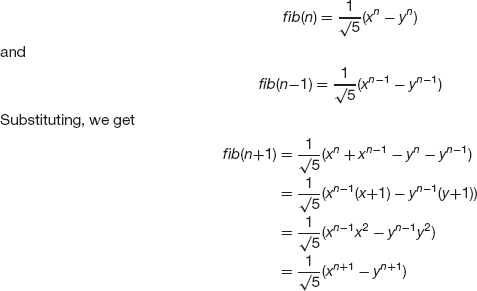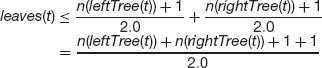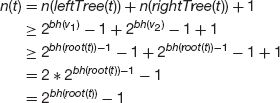APPENDIX 2
Mathematical Background
A2.1 Introduction
Mathematics is one of the outstanding accomplishments of the human mind. Its abstract models of real-life phenomena have fostered advances in every field of science and engineering. Most of computer science is based on mathematics, and this book is no exception. This appendix provides an introduction to those mathematical concepts referred to in the chapters. Some exercises are given at the end of the appendix, so that you can practice the skills while you are learning them.
A2.2 Functions and Sequences
An amazing aspect of mathematics, first revealed by Whitehead and Russell [1910], is that only two basic concepts are required. Every other mathematical term can be built up from the primitives set and element. For example, an ordered pair < a, b > can be defined as a set with two elements:
< a, b > = {a, {a, b}}
The element a is called the first component of the ordered pair, and b is called the second component. Given two sets A and B, we can define a function f from A to B, written
f : A → B
as a set of ordered pairs < a, b >, where a is an element of A, b is an element of B, and each element in A is the first component of exactly one ordered pair in f. Thus no two ordered pairs in a function have the same first element. The sets A and B are called the domain and co-domain, respectively.
For example,
f = {< −2,4 >, < −1,1 >, < 0,0 >, < 1,1 >, < 2,4 >}
defines the "square" function with domain { −2, −1, 0, 1, 2 } and co-domain { 0, 1, 2, 4 }. No two ordered pairs in the function have the same first component, but it is legal for two ordered pairs to have the same second component. For example, the pairs
<-1, 1> and <1, 1>
have the same second component, namely, 1.
If< a, b> is an element of f, we write f(a) = b. This gives us a more familiar description of the above function: the function f is defined by
f(i) = i2, for i in −2…2.
Another name for a function is a map. This is the term used in Chapters 12, 14, and 15 to describe a collection of elements in which each element has a unique key part and a value part. There is, in effect, a function from the keys to the values, and that is why the keys must be unique.
A finite sequence t is a function such that for some positive integer k, called the length of the sequence, the domain of t is the set { 0, 1, 2, …, k-1 }. For example, the following defines a finite sequence of length 4:
t(0) = "Karen"
t(1) = "Don"
t(2) = "Mark"
t(3) = "Courtney"
Because the domain of each finite sequence starts at 0, the domain is often left implicit, and we write
t = "Karen", "Don", "Mark", "Courtney"
A2.3 Sums and Products
Mathematics entails quite a bit of symbol manipulation. For this reason, brevity is an important consideration. An example of abbreviated notation can be found in the way that sums are represented. Instead of writing
Xo + Xi + X2 + ... + Xn-1
we can write
This expression is read as "the sum, as i goes from 0 to n −1, of xsub i." We say that i is the count index. A count index corresponds to a loop-control variable in a for statement. For example, the following code will store in sum the sum of components 0 through n-1 in the array x:
double sum = 0.0; for (i = 0; i < n; sum += x [i];
Of course, there is nothing special about the letter "i." We can write, for example,
as shorthand for
1 + 1/2 + 1/3 + ... + 1/10
Similarly, if n > = m,
is shorthand for
m 2-m + (m+1)2-(m+1) + ... + n 2-n
Another abbreviation, less frequently seen than summation notation, is product notation. For example,
is shorthand for
a [0] * a [1] * a [2] * a [3] * a [4]
A2.4 Logarithms
John Napier, a Scottish baron and part-time mathematician, first described logarithms in a paper he published in 1614. From that time until the invention of computers, the principal value of logarithms was in number-crunching: logarithms enabled multiplication (and division) of large numbers to be accomplished through mere addition (and subtraction).
Nowadays, logarithms have only a few computational applications—for example, the Richter scale for measuring earthquakes. But logarithms provide a useful tool for analyzing algorithms, as you saw (or will see) in Chapter 3 through 15.
We define logarithms in terms of exponents, just as subtraction can be defined in terms of addition, and division can be defined in terms of multiplication.
Given a real number b > 1, we refer to b as the base. The logarithm, base b, of any real number x > 0, written
logbx
is defined to be that real number y such that
by = x
For example, log216 = 4 because 24 = 16. Similarly, log10100 = 2 because 102 = 100. What is log2 64? What is log8 64? Estimate log10 64.
The following relations can be proved from the above definition and the corresponding properties of exponents. For any real value b > 1 and for any positive real numbers x and y,
Properties of Logarithms
- logfa 1 = 0
- logfa b = 1
- logfa (xy) = logfa x + logfa y
- logfa (x/y) = logfa x-logfa y
- logfa b* = x
- fa, ogfax =x logfa = ylogfa x
From these equations, we can obtain the formula for converting logarithms from one base to another. For any bases a and b> 1 and for any X> 0,
logb x = logb alog a x {by property 5}
= (loga x)(logb a){by property 7}
The base e e are called natural logarithms and are written in the shorthand ln instead of loge.
To convert from a natural logarithm to a base 2 logarithm, we apply the base-conversion formula just derived. For any x > 0,
ln x = (log2 x )(ln2)
Dividing both sides of this equation by ln 2, we get
log2 x = ln x / ln2
We assume the function ln is predefined, so this equation can be used to approximate log2x. Similarly, using base-10 logarithms,
log2 x = log10 x / >log102
The function ln and its inverse exp provide one way to perform exponentiation. For example, suppose we want to calculate xy where x and y are of type double and x > 0. We first rewrite xy:
xy = eln(x)y {by Property 6, above}
= ey ln x {by Property 7}
This last expression can be written in Java as
Math.exp (y * Math.ln (x))
or, equivalently, and without any derivation,
Math.pow (x, y)
A2.5 Mathematical Induction
Many of the claims in the analysis of algorithms can be stated as properties of integers. For example, for any positive integer n,
In such situations, the claims can be proved by the Principle of Mathematical Induction.
Principle of Mathematical Induction
Let S1, S2, … be a sequence of statements. If both of the following cases hold:
- S1 is true
- For any positive integer n, whenever Sn is true, Sn+1 is true then the statement Sn is true for any positive integer n.
To help you to understand why this principle makes sense, suppose that S1, S2, … is a sequence of statements for which cases 1 and 2 are true. By case 1, S1 must be true. By case 2, since S1 is true, S2 must be true. Applying case 2 again, since S2 is true, S3 must be true. Continually applying case 2 from this point, we conclude that S4 is true, and then that S5 is true, and so on. This indicates that the conclusion in the principle is reasonable.
To prove a claim by mathematical induction, we first state the claim in terms of a sequence of statements S1, S2, …. We then show that S1 is true—this is called the base case. Finally, we need to prove case 2, the inductive case.
Here is an outline of the strategy for a proof of the inductive case: let n be any positive integer and assume that Sn is true. To show that Sn+1 is true, relate Sn+1 back to Sn, which is assumed to be true. The remainder of the proof often utilizes arithmetic or algebra.
Example A2.1 Sum of Initial Sequence of Positive Integers
We will use the Principle of Mathematical Induction to prove the following:
Claim For any positive integer n,
Proof We start by stating the claim in terms of a sequence of statements. For n = 1,2, ..., let Sn be the statement
- Base case.
Therefore S1 is true.
- Inductive case. Let n be any positive integer and assume that Sn is true. That is,
We need to show that Sn+1 is true, namely,
We relate Sn+1 back to Sn by making the following observation: The sum of the first n+1 integers is the sum of the first n integers plus n+1. That is,
We conclude that Sn+1 is true (whenever Sn is true). So, by the Principle of Mathematical Induction, the statement Sn is true for any positive integer n.
An important variant of the Principle of Mathematical Induction is the following:
Principle of Mathematical Induction—Strong Form
Let S1, S2, … be a sequence of statements. If both of the following cases hold:
- S1 is true
- For any positive integer n, whenever S1, S2, ..., Sn are true, Sn+1 is true then the statement Sn is true for any positive integer n.
The difference between this version and the previous version is in the inductive case. Here, when we want to establish that Sn+1 is true, we can assume that S1, S2, …, Sn are true.
Before you go any further, try to convince (or at least, persuade) yourself that this version of the principle is reasonable. At first glance, you might think that the strong form is more powerful than the original version. But in fact, they are equivalent.
We now apply the strong form of the Principle of Mathematical Induction to obtain a simple but important result.
Example A2.2 Number of Iterations of "Halving" Loop
Show that for any positive integer n, the number of iterations of the following loop statement is floor(log2n):
while (n > 1)
n = n / 2;
Proof For n = 1,2 let f(n) be the number of loop iterations. For n = 1,2 let Sn be the statement:
f(n) = floor(log2 n)
- Base case. When n = 1, the loop is not executed at all, and so f(n) = 0 = floor (log2n). That is S1 is true.
- Inducfive case. Let n be any positive integer and assume that S1, S2, ..., Sn are all true. We need to show that Sn+1 is true. There are two cases to consider:
Therefore, by the strong form of the Principle of Mathematical Induction, Sn is true for any positive integer n.
Before we leave this example, we note that an almost identical proof shows that in the worst case for an unsuccessful binary search, the number of iterations is
floor(log2 n) +1
In the original and "strong" forms of the Principle of Mathematical Induction, the base case consists of a proof that S1 is true. In some situations we may need to start at some integer other than 1. For example, suppose we want to show that
n! > 2n
for any n> = 4. (Notice that this statement is false for n = 1, 2, and 3.) Then the sequence of statements is S4, S5, … For the base case we need to show that S4 is true.
In still other situations, there may be several base cases. For example, suppose we want to show that
fib(n)< 2n
for any positive integer n. (The method fib, defined in Lab 7, calculates Fibonacci numbers.) The base cases are:
fib (1)< 21
and
fib (2)< 22
These observations lead us to the following:
Principle of Mathematical Induction —General Form
Let K and L be any integers such that K <= L and let SK, SK+1, … be a sequence of statements. If both of the following cases hold:
- SK, SK+1,…, SL are true
- For any integer n>= L, ifSK, SK+1, …, Sn are true, then Sn+1 is true. then the statement Sn is true for any integer n>= K.
The general form extends the strong form by allowing the sequence of statements to start at any integer (K) and to have any number of base cases (SK, SK+1v.., SL). If K = L = 1, the general form reduces to the strong form.
The next two examples use the general form of the Principle of Mathematical Induction to prove claims about Fibonacci numbers.
Example A2.3 Upper Bound on nth Fibonacci Number
Show that
fib(n) < 2n
for any positive integer n.
Proof For n = 1, 2, …, letSn be the statement
fib(n) < 2n
In the terminology of the general form of the Principle of Mathematical Induction, K = 1 because the sequence starts at 1; L = 2 because there are two base cases.
- fib(1) = 1 < 2 = 21, and so S1 is true.
fib(2) = 1 < 4 = 22, and so S2 is true.
- Let n be any integer > 2 and assume that S1, S2 Sn are true. We need to show that Sn+1 is true (that is, we need to show that fib(n+1)<2n+1).
By the definition of Fibonacci numbers,
fib(n+1) = fib(n) + fib(n-1), forn > 2.
Since S1, S2 Sn are true, we know that Sn-1 and Sn are true. Thus
fib(n-1) < 2n-1
and
fib(n) < 2n
We then get
fib(n+1) = fib(n) + fib(n-1)
< 2n + 2n-1
< 2n + 2n
= 2n+1
And so fib (n+1) is true.
We conclude, by the general form of the Principle of Mathematical Induction, that
fib(n) < 2n
for any positive integer n.
You could now proceed, in a similar fashion, to develop the following lower bound for Fibonacci numbers:
fib(n )>(6/5)n
for all integers n ≥ 3.
Hint: Use the general form of the Principle of Mathematical Induction, with K = 3and L = 4.
Now that lower and upper bounds for Fibonacci numbers have been established, you might wonder if we can improve on those bounds. We will do even better. In the next example we verify an exact, closed formula for the nth Fibonacci number. A closed formula is one that is neither recursive nor iterative.
Example A2.4 Closed-Form Formula for nth Fibonacci Number
Show that for any positive integer n,
Before you look at the proof below, calculate a few values to convince yourself that the formula actually does provide the correct values.
Proof For n = 1,2, . . ., let Sn be the statement
- We now proceed with the proof.
To show that S2 is true, we proceed as follows:
- Let n be any positive integer greater than 1 and assume that S1, S2, ..., Sn are true. We need to show
By the definition of Fibonacci numbers,
fib(n+1) = fib(n) + fib(n-1)
Since Sn and Sn-1 are true by the induction hypothesis, we have (using x and y)
Therefore Sn+1 is true.
We conclude, by the general form of the Principle of Mathematical Induction, that Sn is true for any positive integer n.
The next example establishes part 1 of the Binary Tree Theorem in Chapter 9: the number of leaves is at most the number of elements in the tree plus one, all divided by 2.0. The induction is on the height of the tree and so the base case is for single-item tree, that is, a tree of height 0.
Example A2.5 Upper Bound on Number of Leaves in a Non-Empty Binary Tree
Let f be a non-empty binary tree, with leaves(t) leaves and n(t) elements. We claim that
Proof For k = 0, 1, 2 let Sk be the statement: For any nonempty binary tree f of height k,
- If f has height 0, then leaves(t) = n(t) = 1, and so
Therefore S0 is true.
- Let k be any integer > 0, and assume that S0, S1 Sk are true. We need to show that Sk+1 is true. Let t be a non-empty binary tree of height k+1. Both leftTree(t) and rightTree(t) have height < k, soboth satisfy the induction hypothesis. That is,
But each leaf in t is either in leftTree(t) or in rightTree(t). That is,
leaves(t) = leaves(leftTree(t)) + leaves(rightTree(t))
Then we have
Except for the root element of t, each element in t is either in leftTree(t) or in rightTree(t), and so
n(t) = n(leftTree(t)) + n(rightTree(t)) + 1
Substituting this equation's left-hand side for its right-hand side in the previous inequality, we get
That is, Sk+1 is true.
Therefore, by the general form of the Principle of Mathematical Induction, Sk is true for any nonnegative integer k. This completes the proof of the claim.
The next example, relevant to Chapter 12, shows that the height of any red-black tree is logarithmic in n.
Example A2.6 The Height of a Red-Black Tree
As noted in Chapter 12, the TreeMap and TreeSet classes require only logarithmic time — even in the worst case-to insert, remove, or search. The reason for this speed is that those classes are based on red-black trees, whose height is always logarithmic in the number of elements in the tree. The proof that red-black trees are balanced utilizes the General Form of the Principle of Mathematical Induction.
Theorem The height of any red-black tree is logarithmic in n, the number of elements in the tree.
In order to prove this theorem, we first need a couple of preliminary results.
Claim 1. Let y be the root of a subtree of a red-black tree. The number of black elements is the same in a path from y to any one of its descendants with no children or one child.
Suppose x is the root of a red-black tree, and y is the root of a subtree. Let fa0 be the number of black elements from x (inclusive) to y (exclusive). For example, in Figure A2.1, if x is 50 and y is 131, fa0 = 1, the number of black elements in the path from 50 through 90; 131 is not counted in fa0.
FIGURE A2.1 A red-black tree of 14 elements with maximum height, 5
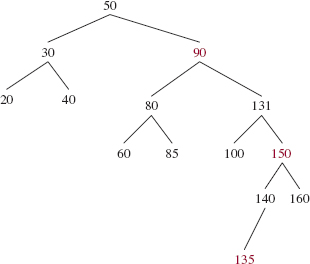
Let b1 be the number of black elements from y (inclusive) to any one of its descendants with no children or one child (inclusive), and let b2 be the number of black elements from y (inclusive) to any other one of its descendants with no children or one child (inclusive). Figure A2.2 depicts this situation.
For example, in Figure A2.1, suppose that y is 131 and the two descendants of y are 100 and 135. Then b0 = 1 because 50 is black; b1 = 2 because 131 and 100 are black; b2 = 2 because 131 and 140 are black.
In general, by the Path Rule for the whole tree, we must have b0 + b1 = b0 + b2. This implies that b1 = b2. In other words, the number of black elements is the same in any path from y to any of its descendants that have no children or one child. We have established Claim 1.
Now that Claim 1 has been verified, we can make the following definition. Let y be an element in a red-black tree; we define the black-height of y, written bh(y), as follows:
bh(y) = the number of black elements in any path from y to any descendant of y that has no children or one child.
FIGURE A2.2 Part of a red-black tree rooted at x;y is a descendant of x, and and Z2 are two arbitrarily chosen descendants of y that have no children or one child. Then b0 represents the number of black descendants in the path from x up to but not including y; b1 and b2 represent the number of black elements in the path from y to Z1 and Z2, respectively

FIGURE A2.3 A red-black tree whose root has a black height of 3
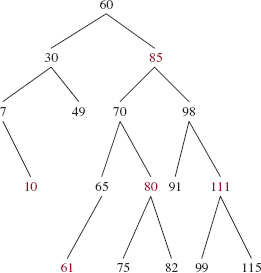
By Claim 1, the number of black elements must be the same in any path from an element to any of its descendants with no children or one child. So black-height is well defined. For an example of black height, in Figure 12.3 from Chapter 12, the black-height of 50 is 2, the black height of 20, 30, 40, or 90 is 1, and the black-height of 10 is 0. Figure A2.3 shows a red-black tree in which 60 has a black height of 3 and 85 has a black height of 2
Claim 2. For any non-empty subtree f of a red-black tree,
n(t) ≤ 2bh(roof(t)) - 1
(In the claim, n(t) is the number of elements in f, and root(t) is the root element of f.) The proof of this claim is, as usual, by induction on the height of t.
Base case: Assume that height(t) = 0. Then n(t) = 1, and bh(root(t)) = 1 if the root is black and 0 if the root is red. In either case, 1 ≥ bh(roof(t)). We have
n(t) = 1 = 21 - 1 ≥ 2bh(room - 1
This proves Claim 2 for the base case.
Inductive case: Let k be any non-negative integer, and assume Claim 2 is true for any subtree whose height is ≤ k. Let f be a subtree of height k + 1.
If the root of f has one child, then the root must be black and the child must be red, and so bh(roof(t)) = 1. Therefore,
n(t) ≥ 1 = 21 - 1 = 2bh(room - 1
This completes the proof of the inductive case if the root of f has only one child.
Otherwise, the root of f must have a left child, v1, and a right child, v2. If the root of f is red, bh(root(t)) = bh(v1) = bh(v2). If the root of f is black, bh(root(t)) = bh(v1) + 1 = bh(v2) + 1. In either case,
bh(v1) ≥ bh(root(t)) — 1
and
bh(v2) ≥ bh(root(t)) — 1
The left and right subtrees of f have height ≤ k, and so the induction hypothesis applies and we have
n(leffTree(t)) ≥ 2bh(v1) - 1
and
n(righfTree(t)) ≥ 2bh(v2) - 1
The number of elements in f is one more than the number of elements in leftTree(t) plus the number of elements in rightTree(t).
Putting all of the above together, we get:
This complete the proof of the inductive case when the root of f has two children.
Therefore, by the Principle of Mathematical Induction, Claim 2 is true for all non-empty subtrees of red-black trees.
Finally, we get to show the important result that the height of any non-empty red-black tree is logarithmic in n, wheren represents the number of elements in the tree.
Theorem For any non-empty red-black tree f with n elements, height(t) is logarithmic in n.
Proof Let f be a non-empty red-black tree. By the Red Rule, at most half of the elements in the path from the root to the farthest leaf can be red, so at least half of those elements must be black. That is,
bh(root(t)) ≥ height(f)/2
From Claim 2,
n(t) ≥ 2bh(root(t))− 1
≥ 2height(t)/2 1
From this we obtain
heighf(t) ≤ 2log2(n(t) + 1)
This inequality implies that height(f) isO(logn). By the Binary Tree Theorem in Chapter 9,
heighf(t) ≥ log2≥n(t) + 1)/2.0)
Combining these two inequalities, we conclude that height(t) is logarithmic in n.
This theorem states that red-black trees never get far out of balance. For an arbitrary binary search tree on the other hand, the height can be linear in n—for example, if the tree is a chain.
A2.6 Induction and Recursion
Induction is similar to recursion. Each has a number of base cases. Also, each has a general case that reduces to one or more simpler cases, which, eventually, reduce to the base case(s). But the direction is different. With recursion, we start with the general case and, eventually, reduce it to the base case. With induction, we start with the base case and use it to develop the general case.
CONCEPT EXERCISES
A2.1 Use mathematical induction to show that, in the Towers of Hanoi game from Chapter 5, moving n disks from pole a to pole b requires a total of 2n - 1 moves for any positive integer n.
A2.2 Use mathematical induction to show that for any positive integer n,
where A is a constant and f is a function.
A2.3 Use mathematical induction to show that for any positive integer n,
A2.4 Let n0 be the smallest positive integer such that
fib(n0)>n20
- Find n0.
- Use mathematical induction to show that, for all integers n ≥ n0,
fib (n) > n2
A2.5 Show that fib(n) is exponential in n, specifically, ![]()
Hint: See the formula in Example A1.4 above. Note that the absolute value of
becomes insignificant for sufficiently large n.
A2.6 Show that
for any nonnegative integer n.
A2.7 Find the flaw in the following proof.
Claim All dogs have the same hair color.
Proof For n = 1,2 let Sn be the statement:
In any set of n dogs, all dogs in the set have the same hair color.
Base Case: If n = 1, there is only one dog in the set, so all dogs in that set have the same hair color. Thus, S1 is true.
Inductive Case: Let n be any positive integer and assume that Sn is true; that is, in any set of n dogs, all the dogs in the group have the same hair color. We need to show that Sn+1 is true. Suppose we have a set of n + 1 dogs:
d1, d2, d3....dn, dn+1
The set d1, d2, d3, …, dn has size n, so by the Induction hypothesis, all the dogs in that set have the same hair color.
The set d2, d3 dn, dn+1 also has size n, so by the Induction hypothesis, all the dogs in that set have the same hair color.
But the two sets have at least one dog, dn, in common. So whatever color that dog's hair is must be the color of all dogs in both sets, that is, of all n + 1dogs. In other words, Sn+1 is true.
Therefore, by the Principle of Mathematical Induction, Sn is true for any non-negative integer n.