2
Discrete-Event Simulation: A Primer
Stewart Robinson
School of Business and Economics, Loughborough University, UK
2.1 Introduction
Discrete-event simulation (DES) grew largely out of a desire to model manufacturing systems. Based upon the foundation of Monte Carlo methods, DES models were developed to improve the design and operation of manufacturing plants. Among the earliest examples is the work of K.D. Tocher who developed the General Simulation Program in the late 1950s at the United Steels Companies in the United Kingdom; see Hollocks (2008) for an excellent summary of these early developments.
Over the years DES has been applied to a much broader set of applications including health, service industries, transportation, warehousing, supply chains, defence, computer systems and business process management. Much of this work has focused on improving the design and operation of the systems under investigation, but there have also been examples of DES for aiding strategic decision making.
DES is seen as a, if not the, mainstream simulation approach in the field of operational research (OR). Indeed, many OR specialists simply refer to it as ‘simulation’, seemingly ignoring the potential to simulate using other approaches, including system dynamics. DES does imply a very specific approach to simulation from both a technical and a philosophical perspective. In this chapter we will explore both of these perspectives. To set a context, we first present an example of a DES model. We then discuss how DES works (the technical perspective) followed by the worldview adopted by DES modellers (the philosophical perspective).
2.2 An Example of a Discrete-Event Simulation: Modelling a Hospital Theatres Process
Figure 2.1 shows an example of a DES model, in this case of a hospital theatres process (Burgess et al., 2011). This model can be accessed from www.simlean.org (accessed May 2012) as either a model file (for which the proprietary software is required) or as video files. The model simulates the flow of patients through an outpatients theatre over the period of a day. Patients arrive at a reception area and having registered they are prepared for their operation. Following the operation in one of the four theatres, they are moved to a recovery area. From here they are generally discharged, but in some cases the patient needs to be admitted to a ward.

Figure 2.1 A simple DES model of a hospital theatres process (Source: Burgess et al., 2011; Robinson et al., 2012). Reproduced by permission of Elsevier.
Figure 2.1 shows the state of the model at around 11:35 in the morning, after an 8 a.m. start. At this time the theatres and preparation area are both fully utilised, resulting in a queue of patients waiting post-reception. There is also a queue for discharge since there is insufficient resource available for discharging patients at this point in the day.
While the model runs it records data on the performance of the system. These performance data typically summarise the experience of the individuals in the system, in this case patients, or the experience of the activities (e.g. preparation, theatres) and resources (e.g. receptionist, nurses, doctors). We are specifically interested in the amount of time the individuals spend waiting versus being worked on, which must be balanced with the utilisation of the activities and resources. By nature, high utilisation tends to lead to more waiting as the system becomes overloaded, while low waiting times tend to result from underutilised resources. The aim is to find an appropriate balance between these two measures of performance.
Figure 2.2 shows an example of some results from the hospital theatres process model. This splits the patient experience into value (receiving attention or treatment), waiting and blocked (an activity is complete, but the patient cannot move on because there is no space downstream, e.g. unable to leave the theatre because recovery is full). The pattern that emerges is, because patients arrive in batches, patients at the tail of a batch have to wait much longer to be seen.

Figure 2.2 Results generated from the DES model of a hospital theatres process (Source: Burgess et al., 2011). Reproduced with permission from SimLean Publishing.
There is clearly a problem with waiting and blocking in the theatres process as it stands. The simulation can be used to investigate alternative process designs, different ways of scheduling and allocating resources, and changes to the management of the process.
2.3 The Technical Perspective: How DES Works
In simple terms, DES models queuing systems as they progress through time. In doing so it represents the world as entities that flow through a network of queues and activities. Where resources are shared between activities, these are also represented in a DES model. As such, the fundamental building blocks of a DES model are as follows:
- Entities: individual items that flow through the system, for example widgets in a manufacturing plant, people in a service system or hospital, packets of information in a computer network, vehicles in a transport system, orders in a supply chain.
- Queues: areas where entities wait to be worked on, for example buffers and stores, inventory, waiting areas, waiting lists, phone call queuing.
- Activities: perform work on entities, for example machines, travelling, moving, serving, printing.
- Resources: required to be present to operate activities, for example operators, equipment, doctors.
This structure is very flexible and it can be used to model a wide variety of systems. It is for this reason that DES has been widely used in OR for the types of application listed in the introduction to this chapter.
Figure 2.3 shows an example of a queuing system. Entities arrive at queue 1 and are then directed to either activity 1a or 1b; this could be based on the individual requirements of the entity or at random. Resource 1 is required to be present while activity 1 is taking place, hence it is shared between activities 1a and 1b. Following activity 1, all entities go to queue 2 to await activity 2, after which they leave the system. This system could represent many forms of two-stage queuing process, for instance a doctor's surgery with a reception area (with two distinct checking-in processes) followed by a consultation with the doctor.
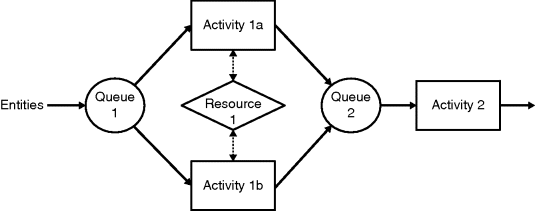
Figure 2.3 An example of a queuing system.
An important feature of entities in DES models is that they have attributes that describe specific features of an entity. These can describe features such as entity type, dimensions, weight, priority, order number and time in system. The values of these attributes can vary from entity to entity. As such, the attributes can be used to determine the logic of the model, for instance the time an individual entity will spend in an activity, its priority in a queue, or its route through the system. This ability to model the detail of individual entities is a particularly powerful feature of DES models.
Beyond these fundamental building blocks, there are two other key elements of DES models: the time-handling mechanism and methods for random sampling. We will now explore both of these in turn.
2.3.1 Time Handling in DES
A simple way of modelling the progression of time in simulation models is to use a constant time step. This approach works well for modelling systems that change continuously; a fixed time step is used to update the state of a system that is continuously changing. Of course, this only approximates continuous change, but digital computers are not able to truly model continuous time. If the time step is sufficiently small, the approximation enables the system to be modelled with sufficient accuracy. There is a trade-off, however, between run-time and accuracy, both of which increase with smaller time steps.
Such ‘continuous’ simulation is used widely in, for instance, the physical sciences and engineering for modelling continuous processes such as wave motion or the aerodynamics of a vehicle. It is also used in a business context to model processes that are subject to continuous change, for instance chemical plants or oil pipelines. Inventory systems, including supply chains, can be modelled using this approach if we are satisfied with updating the state of the system at fixed intervals, say daily. System dynamics is itself a form of continuous simulation.
Given that DES focuses on modelling individual entities that flow through a set of queues and activities, the exact timing of a change in the state of the system is difficult to predict. While an entity is being worked on in an activity, the state of the system remains unchanged. It is only when the activity is finished that the system state changes; the entity moves to the next stage of the process and the activity can start work on another entity. To model this accurately might require that time is modelled in very fine-grained units. To achieve this using a continuous simulation approach would require a very small time step. Because the system state only changes relatively rarely in comparison with the scale of the time step, the simulation would be extremely inefficient and slow since the majority of time steps would model points at which there is no change in system state.
To overcome this problem, DES focuses only on time points where there is a change in the state of the system. We define events as discrete points in time at which the system state changes. Typical events are an entity arrives, an activity starts and an activity ends. Since these events occur at irregular intervals, the time in a DES model does not move forward in a regular fashion, but jumps forward irregularly between the times at which events occur. It is this focus on events that leads to the name discrete-event simulation; that is, the name of the approach is describing the manner in which time is handled.
Table 2.1 shows an example of a DES of the queuing system in Figure 2.3. The table describes the sequence of events (in italics) and the consequences of those events. For instance, the first entity (Entity 1) arrives at the start of the simulation (time = 0). Because Activity 1a is idle, the entity can pass straight through Queue 1 into the activity which can then start work. For simplicity, Resource 1 is not included in this simulation. The first column of the table shows how time moves forward in an irregular fashion. Entities 1 to 4 arrive at times 0, 2, 7 and 23 respectively. We will show how to model these irregular arrival times in the next subsection. Meanwhile, Activity 1a takes 11 minutes, Activity 1b takes 25 minutes and Activity 2 takes 19 minutes. There is no reason, of course, that the times have to be integer numbers. We would normally model time using real numbers to the level of precision that the data, and computer technology, will allow.
Table 2.1 Example of a DES of the queuing system in Figure 2.3.
| Time (min) | Event |
| 0 | Entity 1 arrives, passes through Queue 1 to Activity 1a, Activity 1a starts |
| 2 | Entity 2 arrives, passes through Queue 1 to Activity 1b, Activity 1b starts |
| 7 | Entity 3 arrives and waits in Queue 1 |
| 11 | Activity 1a finishes, Entity 1 passes through Queue 2 to Activity 2, Activity 2 starts, Entity 3 moves to Activity 1a, Activity 1a starts |
| 22 | Activity 1a finishes, Entity 3 waits in Queue 2 |
| 23 | Entity 4 arrives, passes through Queue 1 to Activity 1a, Activity 1a starts |
| 27 | Activity 1b finishes, Entity 2 waits in Queue 2 |
| 30 | Activity 2 finishes, Entity 1 leaves the system, Entity 3 moves to Activity 2, Activity 2 starts |
There is a range of ways that are used for managing the progression of time in DES. This requires determining the time at which events are due to occur, maintaining a record of those events and then, at the appropriate time, executing the events along with any consequent changes to the system state. We will not discuss the time-handling mechanisms for DES in detail here. For those that are interested, there is a very good description of these in Pidd (2004). For our purposes, it suffices to understand the key principle of moving time forward based on the instants at which discrete changes in system state (events) occur, which leads to an irregular time step.
2.3.2 Random Sampling in DES
A key element of almost all DES models is the need to represent randomness in the system under study, in recognition of the fact that many systems are by nature stochastic. Randomness occurs in the length of time an activity takes, for instance the time to serve a customer, the time to repair a piece of equipment and the time to process an order. It is also common for the arrival of entities to be subject to randomness, for example the arrival time of customers at a service system. Other factors are also random in nature, such as the size of an order, the weight of an item and the route an entity will choose to take through the system. In all these cases we might know how the data vary, in other words we know the distribution of the data, but we do not know what the exact value of the data will be in the next instance. So, for example, we might know that service time varies between 10 and 20 minutes, we might even know the exact shape of the distribution for service time, but we cannot predict what the exact service time for the next customer will be. To simulate systems that are subject to such randomness we need a mechanism for modelling this variability, for which Monte Carlo methods are employed. We now discuss how this is achieved in DES.
Say that we wish to simulate a ticketing web site and as part of that we want to model the number of tickets a customer will buy for a sports event. We may have looked at historic data for similar events and observed the distribution shown in Figure 2.4.
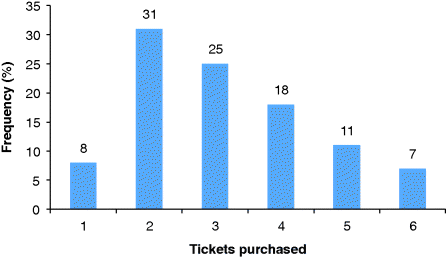
Figure 2.4 Distribution of tickets purchased by customers for sports events.
Given that there are six possible outcomes, an obvious way to model this might be to role a six-sided die. This would give us variability in the right range (1–6), but it would not model the differing probabilities of the six outcomes; it would assume all outcomes had a probability of one-sixth. It is also not very practical to ask a computer to role a die! So we need an approach that allows us to represent the differing probabilities and that can be implemented on a computer for our simulations. To achieve this we need to use random numbers.
2.3.2.1 Random Numbers and Generating Random Numbers
Random numbers are a sequence of numbers that appear in a random order. Typically these numbers are on the scale [0,1), the square bracket signifying that 0 is included in the range and the bracket signifying that the highest possible random number is just less than 1. Table 2.2 shows an example of random numbers in this range.
Table 2.2 Example of 100 random numbers on the scale [0,1) to two decimal places.
| 0.74 | 0.45 | 0.21 | 0.18 | 0.71 | 0.12 | 0.19 | 0.33 | 0.63 | 0.46 |
| 0.40 | 0.54 | 0.13 | 0.86 | 0.29 | 0.14 | 0.21 | 0.98 | 0.30 | 0.47 |
| 0.84 | 0.48 | 0.08 | 0.04 | 0.70 | 0.89 | 0.07 | 0.18 | 0.76 | 0.36 |
| 0.22 | 0.98 | 0.61 | 0.18 | 0.64 | 0.85 | 0.89 | 0.81 | 0.21 | 0.03 |
| 0.07 | 0.80 | 0.71 | 0.47 | 0.82 | 0.46 | 0.80 | 0.34 | 0.99 | 0.99 |
| 0.12 | 0.88 | 0.52 | 0.02 | 0.75 | 0.89 | 0.60 | 0.14 | 0.36 | 0.58 |
| 0.91 | 0.41 | 0.18 | 0.78 | 0.61 | 0.05 | 0.30 | 0.34 | 0.32 | 0.91 |
| 0.25 | 0.55 | 0.64 | 0.55 | 0.87 | 0.99 | 0.20 | 0.40 | 0.61 | 0.68 |
| 0.44 | 0.15 | 0.03 | 0.80 | 0.02 | 0.57 | 0.41 | 0.17 | 0.46 | 0.28 |
| 0.74 | 0.30 | 0.33 | 0.25 | 0.58 | 0.07 | 0.27 | 0.93 | 0.70 | 0.39 |
Random numbers have two important properties:
- Uniform: there is the same probability of any number occurring at any point in the sequence.
- Independent: once a number has been chosen, this does not affect the probability of its being chosen again or of another number being chosen.
This can be understood in terms of drawing numbers from a hat. Say we have 100 tickets with the numbers 0 to 99 written on them; we simply divide these numbers by 100 to get the random numbers in Table 2.2. We fold the tickets up so we cannot see the numbers and place them in a hat. We then draw one ticket at random. There is, of course, a 1 in 100 probability of any one of the tickets being selected, hence the probability is said to be uniform. In the case of the numbers in Table 2.2, the first ticket chosen is the number 74 (or 0.74). Having chosen this ticket we then fold it up and place it in the hat again. We then pick another ticket at random (number 45 if we write the numbers down across the row in Table 2.2). The importance of placing ticket 74 back into the hat is that the probability of any ticket being chosen second remains as 1 in 100. Otherwise, we would have had a 1 in 99 chance of any ticket being chosen with the exception of 74 which would have a zero probability. So by placing the tickets back in the hat after we have selected them, the probabilities remain unchanged and the selection of the next ticket is in no way affected by the ticket that went before it. In other words, the numbers chosen are independent of one another. The procedure then continues and we can, as in Table 2.2, create a sequence of random numbers.
Because of the procedure followed, Table 2.2 will not contain every number in the range [0,1) to two decimal places, despite there being 100 numbers in the table. It is difficult to spot a missing number, but it is quite straightforward to identify numbers that appear more than once: for example, 0.21 appears in the first and second rows. Notice that 0.99 appears twice together at the end of the fifth row. This seems unlikely to occur and indeed it is, with only a 1 in 10 000 (100 × 100) chance of this happening. That said, there is only a 1 in 10 000 chance of any predefined sequence of two numbers occurring, such as 0.74 and 0.45 at the start of the table. Although not every number appears in Table 2.2, if we continued the procedure and selected thousands or even millions of random numbers, eventually every number would be selected and the percentage of times each number appeared would be close to 1% each.
Random numbers such as these have a third important property and that is that we can generate these numbers using a computer. Strictly speaking, computers cannot generate random numbers, since they are perfectly logical. However, we can fool a computer into generating numbers that to all intents and purposes appear to be random, that is they appear to be uniform and independent. This is achieved through the use of special algorithms. For a description of some of these algorithms see Pidd (2004), Law (2007) and Banks et al. (2005). There has been much research into the creation of effective and efficient random number generators. Good examples are L'Ecuyer (1999) and the Mersenne Twister (Matsumoto and Nishimura, 1998).
2.3.2.2 Random Sampling with Random Numbers
Once we have random numbers available to us, it is relatively straightforward to use these to sample from a distribution such as that in Figure 2.4. To achieve this we simply relate the right proportion of random numbers to each outcome in order to ensure that outcome has the correct probability of happening. So, if we wish to have 8% of customers purchasing one ticket, then we associate 8% of the random numbers with that outcome. We can do this by saying that if the random number is less than 0.08 then the customer will purchase one ticket.
Table 2.3 shows the allocation of random numbers required to sample from the distribution in Figure 2.4. Notice how the numbers in the brackets are the cumulative values from the second column. The ranges are interpreted as 0 ≤ random number < 0.08, 0.08 ≤ random number < 0.39, and so on. As such, the random number 0.08 would give a sample value of two tickets. This is correct, since 8% of the random numbers (0.00, 0.01. 0.02,…, 0.07) would give a sample value of one ticket.
Table 2.3 Allocation of random numbers for distribution of tickets purchased by customers for sports events (Figure 2.4).
| Tickets purchased | Frequency (%) | Random numbers |
| 1 | 8 | [0.00,0.08) |
| 2 | 31 | [0.08,0.39) |
| 3 | 25 | [0.39,0.64) |
| 4 | 18 | [0.64,0.82) |
| 5 | 11 | [0.82,0.93) |
| 6 | 7 | [0.93,1.00) |
We can use the random numbers in Table 2.2 to simulate the number of tickets each customer purchases. If we read across the rows in Table 2.2, then we would use 0.74 to determine the number of tickets the first customer purchases and then 0.45 to determine the tickets purchased by the second customer, and so on. The result of this process for the first 10 customers is shown in Table 2.4. Notice how no one purchases one, five or six tickets in this very small sample size. However, if this process was continued for thousands or even millions of random samples, the percentage of customers buying the different numbers of tickets would become increasingly close to the values in the distribution in Figure 2.4.
Table 2.4 Sample values for the number of tickets purchased by customers.
| Customer | Random number | Tickets purchased |
| 1 | 0.74 | 4 |
| 2 | 0.45 | 3 |
| 3 | 0.21 | 2 |
| 4 | 0.18 | 2 |
| 5 | 0.71 | 4 |
| 6 | 0.12 | 2 |
| 7 | 0.19 | 2 |
| 8 | 0.33 | 2 |
| 9 | 0.63 | 3 |
| 10 | 0.46 | 3 |
2.3.2.3 Sampling from Continuous Distributions
The distribution in Figure 2.4 contains discrete (integer) data. The sampling task is to determine which discrete value to select. What happens if we wish to model continuous data such as those shown in Figure 2.5? This shows a negative exponential distribution with a mean of 1. This distribution is typically used to model the time between entity arrivals when they occur on a random basis, such as telephone enquiries into a call centre. The only parameter required for this distribution is the mean, which in Figure 2.5 is 1. The graph shows the probability density function (PDF) for the sample value x. The probability of a specific sample value increases with the height of the line. So in Figure 2.5, values of x close to 0 (although not exactly 0) are much more likely than higher values of x. When used for simulating the arrival of entities, this means that there are generally quite short gaps between entities, but then occasionally there will be quite long periods between entity arrivals.
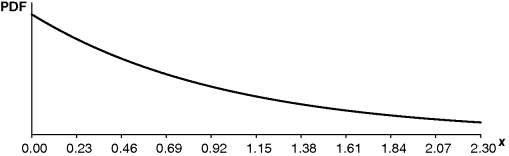
Figure 2.5 An example of a continuous distribution: a negative exponential distribution (mean = 1).
To sample from a continuous distribution we need to be able to relate a random number to the proportion of the area under the curve. For instance, if our random number is 0.05, then we would find the value of x at which 5% of the area under the curve is to the left of x, giving a small value for x. If the random number is 0.95, then we would find the value of x at which 95% of the area under the curve is to the left of x, giving a large value for x. In the case of the negative exponential distribution this can be achieved by integrating the distribution's PDF to obtain its cumulative distribution function. This gives the formula
where:
- x = random sample
- μ = mean of the distribution
- u = random number,
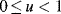
Using the first row of random numbers in Table 2.2, 10 samples from the negative exponential distribution are shown in Table 2.5.
Table 2.5 Samples from a negative exponential distribution.
| Entity | Random number | Inter-arrival time (IAT) | Actual arrival time (cumulative IAT) |
| 1 | 0.74 | 1.35 | 1.35 |
| 2 | 0.45 | 0.60 | 1.94 |
| 3 | 0.21 | 0.24 | 2.18 |
| 4 | 0.18 | 0.20 | 2.38 |
| 5 | 0.71 | 1.24 | 3.62 |
| 6 | 0.12 | 0.13 | 3.74 |
| 7 | 0.19 | 0.21 | 3.96 |
| 8 | 0.33 | 0.40 | 4.36 |
| 9 | 0.63 | 0.99 | 5.35 |
| 10 | 0.46 | 0.62 | 5.97 |
The negative exponential distribution is just one example of a standard continuous distribution that is used for sampling in DES. It is also possible to sample from continuous distributions based on empirical data. There is not space here to go into a detailed discussion of the distribution types, their uses and sampling methods. For the interested reader see Robinson (2004), Pidd (2004) and Law (2007) for a more detailed discussion on distributions and random sampling. The key point here is to understand that in DES modelling random numbers are used as the basis of sampling from discrete and continuous distributions in order to model the random nature of the system under study.
2.4 The Philosophical Perspective: The DES Worldview
Section 2.3 focuses on the technical perspective, in other words how a DES model works. This is important for understanding the method and for being able to compare it with other possible modelling approaches, including system dynamics. At least as important, if not more so, is to gain an understanding of how DES modellers approach a problem situation with their modelling technique. The contention is that the worldview of the modeller will have an impact on how he or she models the world. We might describe this as his or her modelling philosophy.
Although there does not appear to have been a specific debate about the worldview that DES modellers adopt, we can draw some inferences from the nature of the method and what we know about the way problems are modelled in DES. Our own research lends support to the discussion that follows (Tako and Robinson, 2010; Tako, 2009); the former reference is reproduced as a chapter in this book (Chapter 8).
The driving philosophy of a DES modeller is that the world can be understood as a set of interconnected activities and queues that are subject to random (stochastic) variation. As such, when faced with a modelling problem, the DES modeller is immediately aiming to define the system in terms of its queuing structure and the variability that the system is subject to. If the problem does not fit this structure, then DES will not be seen as useful for addressing the problem at hand. Since a wide range of problems do fit this structure, DES is widely applicable, although in some cases its use may not be ideal – there are cases of people fitting the problem to the modelling approach.
The DES worldview is not without a good foundation. Frequently complexity can arise from systems of interconnected randomness that is not evident if the random variability is not taken into account. As an illustration of this let us consider the simplest form of a system that is subject to interconnected randomness, namely a single server queue (Figure 2.6). Here entities arrive into a queue and are then served by a single activity. If the activity is available when the entity arrives then no queuing time is incurred, otherwise the entity must wait in the queue.
Figure 2.6 A single server queue.
We start with the assumption that there is no stochastic variation in the system. If the service time is one time unit and the rate at which entities arrive is 0.9 per time unit (an inter-arrival time of 1/0.9), then we would say the traffic intensity of the system is 0.9 (arrival rate/service rate). The traffic intensity describes the loading of the system. In this example we would expect the activity to be busy 0.9, or 90%, of the time. If we were to ask what the average time is that an entity spends in this system, our expectation would be exactly one time unit. In fact, we would not expect any queuing as the service rate is greater than the arrival rate (traffic intensity < 1) and we would expect every entity to spend exactly one time unit in the system, all of which involves receiving service – perfection!
Now if we add stochastic variation to this system we get a very different result. Under the assumption that the inter-arrival time of entities and the service time of the activity both vary according to a negative exponential distribution, and the mean inter-arrival time is 1/0.9 and mean service time is 1, the average time an entity spends in the system is 10 time units. This is a result of the interaction of random arrivals with random service times, which lead to the build-up of a queue. On average entities spend nine time units in the queue and one time unit receiving service – much less than perfection!
For a simple system such as this, with the assumption that the variability is negative exponentially distributed, we are able to calculate the time in the system for any traffic intensity using the queuing formula (Winston, 1994). Figure 2.7 shows the relationship between mean time in the system and traffic intensity for a system with a mean service time of one time unit. What is immediately obvious is that once the traffic intensity is above about 0.8, the mean time in the system starts to increase to what is likely to be an unacceptable level.
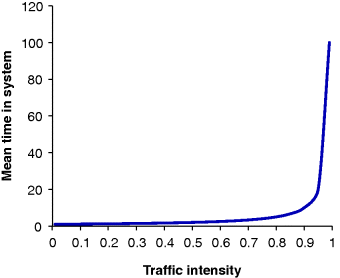
Figure 2.7 Mean time in system for a single server queue with mean service time of 1 time unit.
From a DES perspective this is an important result. Typical DES models can include tens, hundreds or even thousands of activities and queues, which are subject to many sources of stochastic variability that can follow any distribution. This implies a multiplication of the complexity in the single server queue problem which cannot be solved analytically, but only through DES. The fact that interconnected randomness can lead to very different results than would be expected from simple calculations based on averages is a key reason for using DES. For an example of this see Robinson and Higton (1995), where three designs of a brick factory were shown not to be able to meet the company's production requirements through a DES model, despite the design calculations suggesting all three would suffice.
This need to model the random variation in a system has significant implications for the management of data in DES studies. First, the modeller requires data on the input distributions for all the sources of stochastic variation. Such data can be difficult to obtain and can be difficult to analyse, especially if there are correlations between the sources of variation. Second, the analysis of the simulation output requires careful consideration. A single run of a DES model provides just one sample of the possible range of system performances. This is because it is the result of the random samples taken from the input distributions during a run. By changing the stream of random numbers that are being used during a simulation run, different samples will be taken, leading to a different result for system performance. As such, experimentation with a DES model is a sampling process which aims to estimate the output distribution for the result of interest (e.g. time in system or throughput). The more runs that can be performed with the simulation model, the greater the sample size, and the better the understanding of the output distribution. This adds a layer of complexity to estimating system performance and comparing alternative systems. For an introduction to the issues involved in input modelling and output analysis see Law (2007) and Banks et al. (2005).
2.5 Software for DES
We complete this chapter with a brief discussion on the software available for DES. In simple terms there are three options for developing DES models: spreadsheets, specialist simulation software and programming languages. Spreadsheets do have some basic facilities that help with DES modelling (e.g. random number generators and random sampling), but time handling in a spreadsheet is not so simple. For all but the simplest of models, programming constructs (e.g. Visual Basic for Applications) will be required to enhance the capabilities of the spreadsheet.
Programming languages are typically used when specialist simulation software is not available to the modeller or the model's complexity is so great that it is beyond the capabilities of a specialist package. Both cases have become less frequent over the years as a result of the reducing price of simulation software and the increasing capabilities of these packages.
The majority of DES work is carried out using specialist DES packages. Most of these provide facilities for building the model through a menu-based system and an animated visual display of the model as it runs. Programming constructs are normally available for enhancing the logic of the model. Table 2.6 provides a list of some of the packages that are available at the time of writing. This list is not exhaustive and it is recommended that the reader makes a more detailed search of the options before purchasing a package. A useful source of information is the biennial INFORMS simulation software survey that is provided in the society's magazine ORMS Today (www.orms-today.org, accessed May 2012). The latest version can be found in Swain (2011). DES packages can cost from around $1000 to $20 000.
Table 2.6 Examples of specialist DES software packages (listed alphabetically).
| Arena | ProModel |
| Extend | Simio |
| Flexsim | SIMUL8 |
| MicroSaint | Witness |
2.6 Conclusion
This chapter provides a brief introduction to DES. Our focus has been on the technical perspective, how DES works, and the philosophical perspective, the worldview of DES modellers. We have also seen an example of a DES model and discussed the software that is available for DES.
At the centre of DES modelling is the view that it is interconnected randomness that leads to system performance. The term discrete-event simulation describes the time-handling method that the modelling approach employs. Perhaps it would be better to name DES after the worldview that the modelling approach encapsulates – stochastic dynamics.
References
- Banks, J., Carson, J.S., Nelson, B.L. and Nicol, D.M. (2005) Discrete-Event System Simulation, 4th edn, Prentice Hall, Upper Saddle River, NJ.
- Burgess, N., Worthington, C., Davis, N. et al. (2011) SimLean Healthcare: Handbook, SimLean Publishing, www.simlean.org (accessed May 2012).
- Hollocks, B.W. (2008) Intelligence, innovation and integrity – KD Tocher and the dawn of simulation. Journal of Simulation, 2 (3), 128–137.
- Law, A.M. (2007) Simulation Modeling and Analysis, 4th edn, McGraw-Hill, New York.
- L'Ecuyer, P. (1999) Good parameters and implementations for combined multiple recursive random number generators. Operations Research, 47 (1), 159–164.
- Matsumoto, M. and Nishimura, T. (1998) Mersenne Twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Transactions on Modeling and Computer Simulation, 8 (1), 3–30.
- Pidd, M. (2004) Computer Simulation in Management Science, 5th edn, John Wiley & Sons, Ltd, Chichester.
- Robinson, S. (2004) Simulation: The Practice of Model Development and Use, John Wiley & Sons, Ltd, Chichester.
- Robinson, S. and Higton, N. (1995) Computer simulation for quality and reliability engineering. Quality and Reliability Engineering International, 11, 371–377.
- Robinson, S., Radnor, Z.J., Burgess, N. and Worthington, C. (2012) SimLean: utilising simulation in the implementation of lean in healthcare. European Journal of Operational Research, 219, 188–197.
- Swain, J.J. (2011) Software survey: simulation – back to the future. ORMS Today, 38 (5), 56–69.
- Tako, A.A. (2009) Development and Use of Simulation Models in Operational Research: A Comparison of Discrete-Event Simulation and System Dynamics. PhD thesis. Warwick Business School, University of Warwick.
- Tako, A.A. and Robinson, S. (2010) Model development in discrete-event simulation and system dynamics: an empirical study of expert modellers. European Journal of Operational Research, 207, 784–794.
- Winston, W.L. (1994) Operations Research: Applications and Algorithms, 3rd edn, Duxbury Press, Belmont, CA.
