9
Explaining Puzzling Dynamics: A Comparison of System Dynamics and Discrete-Event Simulation
John Morecroft1 and Stewart Robinson2
1London Business School, London, UK
2School of Business and Economics, Loughborough University, UK
9.1 Introduction
Everyday situations present many examples of puzzling dynamics – performance over time that defies intuition and common sense. You drive for miles at a fast and steady speed on a busy motorway yet sometimes encounter unexpected tailbacks with no apparent cause. You occasionally visit your hairdresser. These visits are on the same day of the week at the same time but you never know in advance whether you will wait one minute or half an hour for a haircut.
One way to investigate such puzzling dynamics is to build a computer simulation model that represents the various interrelated factors and pressures at work in the situation, and then run the model to see whether or not it is capable of generating similar puzzling performance. If a model can, in some meaningful way, mimic observed performance then modellers claim they have an explanation for the phenomenon. In developing a simulation model to investigate puzzling dynamics, the analyst can select from a number of approaches, among which two of the most common are discrete-event simulation (DES) (Banks et al., 2001; Pidd, 2004; Robinson, 2004; Law, 2007) and system dynamics (SD) (Forrester, 1961; Richardson and Pugh, 1981; Coyle, 1996; Sterman, 2000; Morecroft, 2007). Both are widely used to examine the performance over time of interconnected systems. The analyst is left to select the appropriate method. It is apparent that most analysts opt for the method with which they are most familiar. Perhaps this tendency is unsurprising given that, in the past, there appear to be very few studies that compare SD and DES, let alone give guidance on which approach might be most appropriate in different circumstances.
Our intention in this chapter is to address the question of which method to use and why, by exploring how SD and DES models help us make sense of puzzling dynamics. We begin with a brief review of existing comparisons of SD and DES in the literature that pre-date this edited volume. Collectively they highlight several important technical and conceptual differences between the approaches. Following this the focus of our research is explained and the case study of erratic fisheries, around which our investigation revolves, is described. A series of SD and DES models are then developed and compared, from which differences in both the representation and interpretation of the fisheries problem are identified. Limitations of the study are discussed before returning to the question of which approach to use and when.
9.2 Existing Comparisons of SD and DES
Coyle (1985) discusses how discrete events might be modelled in an SD simulator. In doing so he notes two key differences between the SD and DES approaches. First, there is the tendency for DES models to include randomness. He argues that in SD models stochastic noise can be subsumed into an appropriate delay. The second difference he identifies is that in DES modelling an open-process structure is adopted, while in SD a closed-loop structure is used in which feedback is explicitly identified.
Writing from the perspective of healthcare modellers, Brailsford and Hilton (2000) briefly describe health-related DES and SD studies including an SD model of NHS waiting lists for cardiac surgery and a discrete-event model of AIDS transmission in a localized population. Table 9.1 summarizes the main technical distinctions the authors identify from their experience of modelling in general and from these healthcare studies in particular.
Table 9.1 Technical differences between DES and SD identified by Brailsford and Hilton (2000).
| Discrete-event simulation | System dynamics |
| Systems (such as healthcare) can be viewed as networks of queues and activities | Systems (such as healthcare) can be viewed as a series of stocks and flows |
| Objects in a system are distinct individuals (such as patients in a hospital), each possessing characteristics that determine what happens to that individual | Entities (such as patients) are treated as a continuous quantity, rather like a fluid, flowing through reservoirs or tanks connected by pipes |
| Activity durations are sampled for each individual from probability distributions and the modeller has almost unlimited flexibility in the choice of these functions and can easily specify non-exponential dwelling times | The time spent in each reservoir is modelled as a delay with limited flexibility to specify a dwelling time other than exponential |
| State changes occur at discrete points of time | State changes are continuous |
| Models are by definition stochastic in nature | Models are deterministic |
| Models are simulated in unequal time steps, when ‘something happens’ | Models are simulated in finely sliced time steps of equal duration |
Writing from the perspective of an experienced SD modeller, Lane (2000) identifies conceptual differences between DES and SD in terms of the eight categories shown in Table 9.2. Consider for example the modeller's perspective on problem situations. A DES modeller captures detail complexity in the network of activities and queues conceived at a functional operating level. An SD modeller captures dynamic complexity in closed feedback loops linking stocks and flows normally conceived at a cross-functional strategic level. Related to the perspective on complexity there is the degree of resolution of models: a close-up resolution in DES that picks out individual entities, attributes, decisions and events versus a distant resolution in SD that captures homogenized entities and continuous policy pressures. There is the type of problem studied, usually operational for DES and more strategic for SD. There is the portrayal of human agents viewed as decision makers in DES (choosing between well-defined options) and as boundedly rational policy implementers in SD (responding to organizational pressures). There are model outputs that in DES take the form of point predictions and detailed performance measures and in SD take the form of simulations that enhance understanding of the structural source of behaviour modes. It should be noted that Robinson (2001) does not agree with this last point in regard to DES, where he argues that DES can be used for developing an understanding of a system's behaviour and does not necessarily have to focus on point prediction.
Table 9.2 Conceptual differences between DES and SD identified by Lane (2000).
| Discrete-event simulation | System dynamics | |
| Perspective | Analytic; emphasis on detail complexity | Holistic; emphasis on dynamic complexity |
| Resolution of models | Individual entities, attributes, decision and events | Homogenized entities, continuous policy pressures and emergent behaviour |
| Data sources | Primarily numerical with some judgemental elements | Broadly drawn |
| Problems studied | Operational | Strategic |
| Model elements | Physical, tangible and some informational | Physical, tangible, judgemental and information links |
| Human agents represented in models as | Decision makers | Boundedly rational policy implementers |
| Clients find the model | Opaque/dark grey box, nevertheless convincing | Transparent/fuzzy glass box, nevertheless compelling |
| Model outputs | Point predictions and detailed performance measures across a range of parameters, decision rules and scenarios | Understanding of structural source of behaviour modes, location of key performance indicators and effective policy levers |
Further comparisons are found in DES textbooks (though not in SD textbooks until recently). For example, Pidd (2004) comments on the relative level of detail in DES and SD models noting that while discrete-event models concentrate on the state changes and interactions of individual entities, it is normal in SD to operate at a much more aggregate level by concentrating on the rates of change of populations of entities. Moreover, he succinctly observes that: ‘In order to model feedback systems for simulation it is important to concentrate on their structure rather than their content. The structure defines how the variables interact, the content is the meaning of those variables for the organization’. Robinson (2004) observes that DES is generally more appropriate when the details of a system need to be modelled, especially when individual items need to be tracked.
Finally, in her doctoral thesis, Mak (1992) investigates how activity cycle diagrams for DES models can be converted into stock and flow representations (used for representing SD models), developing guidelines and software to automate the process. In doing so she identifies a number of differences between the DES and SD approaches. Many of the differences are similar to those already described above. In addition, she notes that SD models explicitly show information feedback while DES models do not, albeit that this information is normally held within the logic of DES models. It is also noted that SD models tend to study the interaction of control policies, exogenous events and feedback structure. DES models tend to be used for ‘what-if’ experimentation, in which the effects of various options are investigated.
A shortcoming of all these comparisons is that they are written from the perspective of either a specialist in SD or a DES specialist. Until recently a comparison that took a more balanced view did not seem to exist. Tako and Robinson have attempted to address this through three separate studies. The first engaged MBA students with an SD and a DES model of the same problem situation and sought to discover how the two models compared through the eyes of a manager (Tako and Robinson, 2009). They found that there was very little difference from the user's perspective. In a follow-up study, they asked expert SD and DES modellers to build simulations of the same problem (Tako and Robinson, 2010, presented as Chapter 8 of this book). This demonstrated that the modellers followed quite different patterns in the tasks they performed while building the model. The third study is a literature review which compares the use of SD and DES in the supply chain context (Tako and Robinson, 2012). This study demonstrates that there are some different patterns of use with respect to the problems being tackled, but also that there is a significant amount of overlap in the use of SD and DES.
Finally we note that comparisons based on a literature search are confounded by the lack of articles on the underlying philosophy of DES modelling. Whereas SD modellers have a well-formed modelling philosophy (Forrester, 1968; Lane, 1999; Morecroft, 2004; Richardson, 1991; Sterman, 1989), such writings seem to be limited within the DES community, though the situation is changing. Recent interest in conceptual modelling for DES focuses on the process of abstracting a model from a real-world situation, where practice meets philosophy (Robinson et al., 2011). The introduction to DES which forms Chapter 2 of this book also attempts to define the modelling philosophy of a DES modeller.
9.3 Research Focus
Rather than focus on technical and conceptual differences, we compare the nature of explanations and insights these two approaches have to offer about puzzling dynamics. Our premise is that the modelling style you choose affects the way you represent and interpret phenomena from the real world. Broadly speaking, SD primarily investigates the performance over time of an interconnected system arising from its internal feedback structure. DES primarily investigates the performance over time of an interconnected system subject to internal (e.g. process failure) and external (e.g. environmental conditions) random variability. Either approach can portray realistic situations such as those mentioned above: the movement of traffic on a motorway, the build-up of queues in retail outlets. But what do they tell us? What, if anything, is different about the understanding, explanation and communication of dynamics that arises from such alternative styles of modelling?
These questions stem from our complementary professional backgrounds. Both of us are experienced modellers, one specialising in SD and the other in DES. We share an interest in how people learn from models and simulation, and the relationship between hard and soft OR. We therefore address the shortcoming of previous comparisons by combining expertise from the quite separate SD and DES worlds.
9.4 Erratic Fisheries – Chance, Destiny and Limited Foresight
For our comparison we developed two models of similar size and detail to represent the dynamics of fisheries. There are several reasons for choosing fisheries. The application is novel (at least among SD–DES comparisons), yet appropriate and important. The problems of overexploitation facing international fisheries are well known, widely reported in the press, and a subject of government policy in many nations. Moreover, fisheries management has been studied by economists (Arnason, 2007; Hardin, 1968), scientists (Roughgarden and Smith, 1996) and operational researchers/modellers (Dudley, 2003; Farber, 1991; Moxnes, 1998; Otto and Struben, 2004). The performance of international fisheries is indeed puzzling. Fish naturally regenerate. They are a renewable resource, in apparently endless supply, providing valuable and healthy food for billions of consumers and a livelihood for millions of fishing communities worldwide. The fishing industry has been in existence since the dawn of civilization and should last for ever. Yet fish stocks around the world are volatile and some are even collapsing. Once-rich fishing grounds such as Canada's Grand Banks now yield no catch at all. Stocks in other areas, such as the English Channel, the North Sea and the Baltic, are in terminal decline.
Figure 9.1 shows typical volatile time series data from real fisheries. The top chart shows the Pacific sardine catch in thousands of tonnes per year over the period 1916 to 1996. The annual catch grew remarkably between 1920 and 1940, starting around 50 000 tonnes and peaking at 700 000 tonnes – a 14-fold increase. Over the next four years to 1944 the catch fell to 500 000 tonnes, stabilized for a few years and then collapsed dramatically to almost zero in 1952. Since then it has never properly recovered. The bottom chart shows a similar story for the North Sea herring catch in the period 1950 to 1998. However, in this case, following a collapse between 1974 and 1979, the fishery did recover in the 1980s and early 1990s with an average annual catch around 600 000 tonnes, similar to the catch in the 1950s and 1960s.
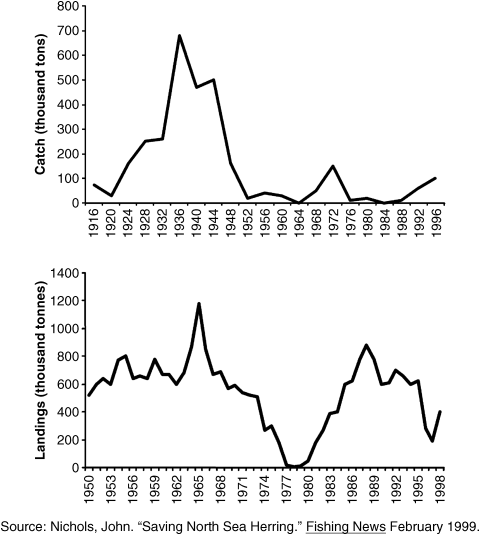
Figure 9.1 Pacific sardine catch (top) and North Sea herring catch (bottom) except from Fish Banks debriefing materials, Meadows et al. (2001). This particular figure was re-printed in Morecroft (2007) and is reproduced by permission of Wiley.
This visible and contemporary problem is amenable to small and transparent models that (despite being small) nevertheless portray dynamic complexity typical of SD and DES. Since neither of us are experts on fisheries we have based our models loosely on a popular fisheries gaming simulator called Fish Banks Ltd (Meadows, Fiddaman and Shannon, 2001) used to teach principles of sustainable development to a wide variety of audiences ranging from politicians, business leaders and government policy advisers to fishing communities and high school students.
In Fish Banks there is a finite offshore region of ocean containing fish. Fish regenerate as a function of the existing population. The local fishing community buys ships from the shipyard and takes them to sea to harvest fish. The total catch depends on the number of ships, the fish population and other factors such as the weather. In the game, as in real life, the fish population is not known accurately, although it can be estimated. Also, in the game, as in real life, the process of fish regeneration is not fully understood by those in the system (players or fishermen). Regeneration is related to the (unknown) fish population, but the relationship is complex and may involve other external factors.
We have taken this situation as a common starting point and then separately developed SD and DES models using the conceptualization, visualization, formulation and interpretation guidelines of our respective modelling disciplines. From the very outset we were aware of philosophical differences in the way we approached the problem. A system dynamicist takes the view that puzzling dynamics arise from endogenous, deterministic and structural properties of the system – the natural laws governing fish regeneration, the policies guiding investment in ships, the productivity of ships for harvesting and processes of stock accumulation that accurately account for and conserve the number of ships and fish introduced or removed from the system. All these relationships form the feedback structure of the fishery that can be visualized as a network of interlocking feedback loops. The destiny of the fishery (whether it is sustainable and whether future harvest rates will grow, remain stable or collapse) is assumed to be predetermined by the feedback structure, although this future is not known with certainty by fishermen. They, like any other stakeholders in business and society, have limited foresight relative to the dynamically complex system they operate. It only takes two or three nonlinear feedback loops (in a system comprising as few as two stock accumulations) to generate puzzling, counterintuitive dynamics. A simple SD fisheries model comfortably meets this complexity criterion.
In contrast a discrete-event modeller takes the view that puzzling dynamics arise from the interaction of random processes coupled together by endogenous structure (Robinson, 2004). So, again, the natural laws governing fish regeneration and the rules for investment in ships and harvesting are important, but are now assumed to be overlaid by random processes. For example, fish regeneration, though related endogenously to the size of the fish stock, is also affected by a variety of external factors (e.g. the climate and environmental changes), beyond the control of stakeholders, factors that manifest themselves as random variation. Similarly the harvest rate or fish catch is influenced endogenously by the size of the fishing fleet (with more ships you can expect a bigger total catch, other things being equal), but is also affected by random operational factors such as the position of ships at sea, the mood of the crew and the weather. The destiny of the fishery is assumed to be partly and significantly a matter of chance. This future is not known with certainty because it involves random variation. Moreover, the effect of randomness is counterintuitive to fishermen, (as it would be to other stakeholders with limited but normal human foresight), because it involves another kind of dynamic complexity, this time arising from multiple interacting random processes. It takes only two or three interacting random processes, even in a linear system, to generate puzzling dynamics. A simple DES fisheries model comfortably meets this complexity criterion.
It is an empirical matter whether a source of variability in a model is shaped by factors other than those endogenously specified. For example, the fish regeneration rate in an SD fisheries model is expressed as a nonlinear function of the fish population – an endogenous feedback relationship linking the accumulated stock of fish to its rate of increase. A DES model will include a similar relationship, because it fits the facts, though the nonlinearity would not normally receive great attention. Instead attention shifts to the random process that is presumed to overlay population-dependent regeneration. These differences in formulation will be explored more carefully later. But for now consider the philosophical difference. There is scientific evidence for an endogenous formulation controlling regeneration (see for example Townsend, Begon and Harper, 2003, an introductory ecology textbook), which can be described as a ‘humped relationship between the net recruitment into a population (births minus deaths) and the size of that population resulting from the effects of intraspecific competition’. There is also evidence of profound external environmental fluctuations, for example an El Niño event ‘when warm tropical water from the north reduces the upwelling, and hence the productivity, of the nutrient-rich cold Peruvian current coming from the south’. Either or both deterministic–endogenous and random–external formulations may be appropriate. In a practical fisheries modelling project the facts would obviously be pertinent and modellers, SD or DES, could (with varying degrees of ease) adapt their model and formulations accordingly. However, our point here is to observe that the type of representation and explanation for puzzling dynamics that a modeller seeks depends on the approach adopted. It is natural for an SD modeller to look for an endogenous structural representation that fits the available facts. It is natural for a discrete-event modeller to look for a structural and random process representation that also fits the facts. These unavoidable methodological biases affect what modellers choose to include and how they go about constructing and communicating a model-based argument (see also Meadows (1980) for a related discussion of methodological biases in SD and econometrics). Does this matter? Our in-depth comparison of models and simulations in the next and later sections sheds more light on this question.
9.5 Structure and Behaviour in Fisheries: A Comparison of SD and DES Models
The title of this section, ‘Structure and behaviour …’, is instantly recognizable to a system dynamicist. The reason is that in SD an explanation of puzzling dynamics is deemed to exist when one can show, justify and interpret the interlocking feedback loops (structure) that cause the dynamic phenomenon (or behaviour over time) of interest. Growth is caused by reinforcing (positive) feedback. Fluctuations stem from goal-seeking or balancing (negative) feedback involving delayed adjustment. Growth and collapse arise from nonlinear reinforcing and balancing feedback combined. Although discrete-event modellers do not normally think in terms of feedback structure (they rarely if ever visualize feedback loops, even when such loops exist), they are nevertheless aware that a combination of structural relationships and random processes lies behind simulated dynamics. To illustrate this difference in approach to the meaning and use of model structure we now present and compare, step by step, our fisheries models, the corresponding equation formulations, and the simulated behaviour (dynamics) that the structures produce.
Our stepwise analysis begins with a natural fishery in which there are no fishermen, no ships and no harvesting – just a self-regulating fish population governed by biological laws and natural limits to growth. Simulations of both SD and DES models show population growth and saturation, with superimposed random variation in the DES model. We then present a harvested fishery in a series of equilibria, with a fixed number of ships and without randomness or bias in any process. Simulations show the SD and DES models can achieve identical equilibria in terms of fish population and fleet size. We then relax the equilibrium assumptions of our ideal harvested fishery to arrive at more realistic disequilibrium models with potentially volatile population dynamics. But the assumptions we relax are different and conditioned by our contrasting approaches. In the SD model we incorporate pressure for growth in fleet size (a bias of human nature – ‘more is better’), presumed to exist in many investment policies. In the DES model we introduce random variation in fish regeneration and the catch. Again we compare simulations. This time the simulations are quite different, although in both cases the fish population is volatile and departs a long way from the ideal equilibrium. Moreover, the style of explanation for these outcomes (how the structure, processes and behaviour are interpreted and presented, and the use made of diagrams, equations and simulations) is distinctive and unique to each approach.
9.5.1 Alternative Models of a Natural Fishery
9.5.1.1 SD Model
Figure 9.2 shows the diagram and equations for an SD model of a natural fishery in the format of the popular iThink language (Richmond et al., 2004 and isee systems). This format is pretty much a standard format used for all SD models.

Figure 9.2 Diagram and equations for SD model of a natural fishery.
The fish stock is represented as a level that accumulates the inflow of new fish per year (here the inflow is defined as a net flow of births minus deaths). Initially there are 200 fish in the sea and the maximum fishery size is assumed to be 4000 fish. Incidentally, the initial value and maximum size can be rescaled to be more realistic without changing the resulting dynamics. For example, a fishery starting with a biomass of 20 000 tonnes of a given species and an assumed maximum fishery size of 400 000 tonnes would generate equivalent results.
The structurally important relationships are those that define the endogenous feedback effect of fish stock on net regeneration, which in this model is identically equal to new fish per year. Net regeneration is a nonlinear function of fish density as shown in Figure 9.3. Note that the function is hump-shaped. Normal practice in SD modelling is to avoid the use of functions involving a reversal of gradient because they can sometimes lead to feedback loops with ambiguous polarity (Sterman, 2000, pp. 577–578). In this case we have chosen to retain the function because it is widely used in fisheries models (Townsend, Begon and Harper, 2003) and is identical to the function used in the popular Fish Banks gaming simulator (Meadows, Fiddaman and Shannon, 2001). For those who are interested, it is possible to eliminate the hump-shaped function and to replace it with two monotonic functions by separately modelling fish regeneration and fish deaths (rather than net regeneration). A good example can be found in Dudley (2003).
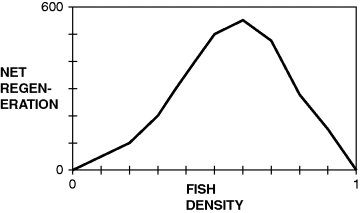
Figure 9.3 Net regeneration as a nonlinear function of fish density.
9.5.1.2 DES Model
Figure 9.4 shows the diagram and equations for a DES model of the same fishery. Unlike SD, there is no agreed standard diagramming method for representing DES models. Various approaches are available including activity cycle diagrams (Hills, 1971), process mapping/process flow diagrams (Davis, 2001), Petri nets (Torn, 1981), event graphs (Som and Sargent, 1989) and the Unified Modeling Language (UML) (Richter and März, 2000). Pooley (1991) gives a useful summary of diagramming techniques for DES. For the purposes of this work, process flow diagrams have been used.
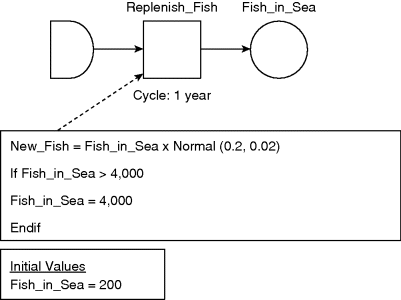
Figure 9.4 Diagram and equations for DES model of a natural fishery.
In Figure 9.4 the fish stock is represented as a queue that is fed by the annual process (activity with a cycle of one year) of fish replenishment. New fish are sourced from outside the model by the ‘source’ on the left of the diagram. As for the SD model, there are assumed to be initially 200 fish in the sea and a maximum of 4000 fish can be sustained.
Fish regeneration is seen as a linear, but random, relation to the number of fish in the sea. Fish grow at an average rate of 20% per year, varying according to a normal distribution with a standard deviation of 2%. This figure is selected as it represents a roughly similar average growth rate as in the SD model. The limit to growth of 4000 is represented as a discrete cut-off which does not allow Fish_in_Sea to exceed this limit.
The simulation was developed using the Witness simulation software (Lanner, 2007). This is one of a number of leading DES software packages.
9.5.1.3 Comparison of SD and DES Representations
There are some clear differences in the representations presented by the DES and SD models. The SD model uses stocks and flows while the DES model uses queues and activities. However, the sharpness of this distinction blurs when one recognizes the essential equivalence of stocks and queues, and of flows and activities. Nevertheless, in SD models the contents of a stock accumulation are normally assumed to be perfectly mixed at all times so that all items in the stock have the same probability of exit, independent of their arrival time (Sterman, 2000, pp. 416–417). This perfect mixing is markedly different from the individual entities represented in a discrete-event queue and is consistent with the drive for aggregation in SD in order to portray cross-functional and inter-sector feedback loops.
The feedback structure is explicit within the SD model, but hidden in the equations of the DES representation (the relationship between fish replenishment and the number of fish in the sea). The relationship between fish stocks and fish regeneration in the SD model is nonlinear, but linear in the DES model. As expected, the DES model includes the randomness, which is not present in the SD version. However, it should be noted that SD models are not entirely devoid of random processes, or need not be. For example, it is common in factory and supply chain models to add randomness to demand in order to invoke cyclical dynamics. But system dynamicists do not normally set out to explore surprising bottlenecks and queues (stock accumulations) that stem from interlocking streams of random events. As Forrester (1961) explains in Industrial Dynamics (Appendix F on Noise), ‘we have chosen to formulate models around the continuous noise-free flows of information, decisions and action. After the noise-free dynamic character of the system is observed, noise is then added to see what randomness contributes to system operation.’ An overwhelming number of SD studies in practice are restricted to examination of the noise-free dynamic character of systems, consistent with the philosophical view in system dynamics that enduring feedback structure gives rise to dynamic behaviour.
9.5.1.4 Simulated Dynamics of a Natural Fishery
Our first simulations show the dynamics of a ‘natural’ fishery starting with an initial population of 200 fish. There are no ships and no investment. Fishermen are not yet part of the system. The SD model (Figure 9.5) shows smooth S-shaped growth due to its nonlinear, deterministic formulations for fish regeneration. Until year 18 the fish stock follows a typical pattern of compounding growth associated with a reinforcing feedback loop. The population grows from 200 to 2500 fish. Fish regeneration (new fish per year) also increases until year 18 as rising fish density enables fish to reproduce more successfully. Thereafter crowding becomes a significant factor according to the nonlinear net regeneration curve in Figure 9.3. The number of new fish per year falls as the population density rises, eventually bringing population growth to a halt as the fish stock approaches its maximum sustainable value of 4000 fish.

Figure 9.5 Simulation of SD model of a natural fishery with an initial population of 200 fish and maximum fishery size of 4000. From Morecroft (2007). Reproduced by permission of Wiley.
The results from the DES model are shown in Figure 9.6. This is the output from a single replication (a run driven with a specific stream of random numbers). If the random number seeds were changed to perform further replications, the exact pattern of growth and fish regeneration would alter. Figure 9.6 shows an increasing growth rate with a discrete cut-off. This is unlike the SD representation in two ways. First, the growth is not as smooth due to the randomness within the regeneration process. This is clearly evidenced by the graph showing new fish. Second, the SD representation shows an asymptotic growth towards the limit of 4000, while the DES model reaches the limit in a discrete step. Both of these differences are a result of the model formulations.

Figure 9.6 Simulation of DES model of a natural fishery with initial population of 200 fish and maximum fishery size of 4000.
9.5.2 Alternative Models of a Simple Harvested Fishery
Imagine that a fleet of ships arrives in the region and sets about harvesting fish. The total catch depends on both the number of ships and their productivity (how many fish each ship catches in a typical year). SD and DES both shed light on the problem of coordinating the size of a fishing fleet (and the catch) with a regenerating fish population. What we know from real fisheries is that satisfactory coordination is difficult to achieve. But why?
9.5.2.1 SD Model
In SD we can make a start on this question by investigating the relationship between catch and fish population under a scenario of varying fleet size. A simple harvested fishery is shown in Figure 9.7. All the original relationships of the natural fishery (Figure 9.2) remain intact but now the fish stock is depleted by a harvest rate, equal to the catch and proportional to the number of ships at sea.
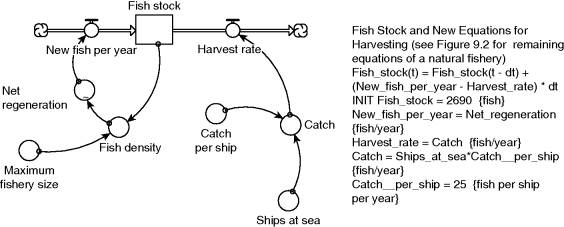
Figure 9.7 Diagram and new equations for SD model of a simple harvested fishery.
9.5.2.2 DES Model
Figure 9.8 shows a DES representation of a harvested fishery. The first part of the process flow diagram is the same as for the natural fishery (Figure 9.4). A second activity, ‘Catch_Fish’, is now added, which represents the catching of fish which are then sent to the sink on the right side of the diagram. The formula for the number of fish caught consists of two parts. The first sees the catch as an increasing proportion of the fish in the sea, a proportion that increases with the number of ships. The formula is nonlinear, giving a reduced catch per ship with increasing numbers of ships. It is envisaged that as more ships are fishing in the same area their productivity will fall. The second part of the formula adds a random element to the catch. Many factors, such as climate and environmental factors, may affect the catch on any given day and in any year. The variation in annual catch is represented by a normal distribution with a standard deviation of 10% of the mean.
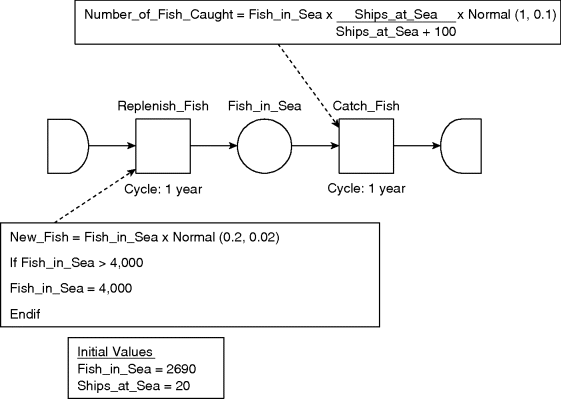
Figure 9.8 Diagram and equations for DES model of a simple harvested fishery.
At first sight it may seem that the average fish regeneration rate (20%) is greater than the average catch rate with 20 ships (20/120 = 16.67%). The model is, however, in equilibrium since it first determines the catch and reduces the fish population, before determining the number of fish regenerated.
9.5.2.3 Comparison of SD and DES Representations
The differences between the SD and DES models identified for the natural fishery apply equally to this case: the method of representation, the explicitness of the feedback structure and the inclusion of randomness. Interestingly, the DES model represents the catch per ship as a nonlinear function of the number of ships, while for now the SD model represents this as a linear relation.
9.5.2.4 Simulated Dynamics of a Simple Harvested Fishery: Equilibrium Models
Simulation of the models shows that both are in equilibrium. Each year in the SD model there is a catch of 500 fish by 20 ships from a population of 2690 fish. Similarly, if the randomness is removed from the DES model, the fish population remains at 2690 year on year, since fish regeneration matches the catch exactly.
9.5.2.5 Simulated Dynamics of a Simple Harvested Fishery: Non-Equilibrium Models
To move from an equilibrium to a non-equilibrium model, two different approaches are taken in the SD model and the DES model. In the SD model, non-equilibrium conditions are created by changing the size of the fishing fleet. In the DES model, randomness is added to the model to create a non-equilibrium state. These reflect typical analyses that might be carried out with SD and DES models. The former explores the effects of nonlinearities (by changing the number of ships) and the latter explores the effects of randomness.
Consider a scenario in which the fleet size grows in steps of 10 from 0 to 30 ships. The productivity of these ships is identical. They can each catch 25 fish per year. (Do not dwell on the numerical value – remember that this is an imaginary but scalable world). In typical SD fashion we assume there is no stochastic variation in productivity. Figure 9.9 is a simulation of this stepwise scenario. At the start the fishery is at its maximum size of 4000 fish and the population is in a deterministic equilibrium where births exactly equal deaths. Ten ships arrive in year 4 and for the next 12 years they harvest the fishery. The catch rises to 250 fish per year (10 × 25). As a result the fish stock begins to fall. Then something dynamically interesting happens. Because the fishery is less heavily populated, fish regenerate faster. The lower the fish stock, the lower the fish density and the higher the number of new fish per year, as determined by the values on the right of the nonlinear net regeneration function described earlier. As the years pass the number of new fish added to the population each year approaches ever closer to the harvest rate (and the catch) and so, by the end of year 15, the fish population settles into a sustainable equilibrium.
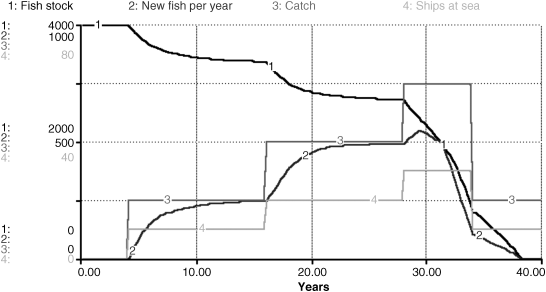
Figure 9.9 Simulation of SD model of a harvested fishery with stepwise changes in fleet size and an initial population of 4000 fish. From Morecroft (2007). Reproduced by permission of Wiley.
In year 16 another 10 ships arrive, bringing the fleet size to 20, and they fish for a further 12 years. A similar process unfolds. A doubling of the fleet leads to a doubling of the harvest rate, a fall in the fish population and eventually a compensating rise in the net regeneration of fish.
In year 28 yet another 10 ships arrive, bringing the total to 30. For almost two years it looks as though the fishery will continue its bountiful supply. The catch rises to 750 fish per year (30 × 25). The population falls below its previous equilibrium (of about 2700 fish) and the number of new fish per year begins to rise. However, by year 30 it is clear something new is happening. While the catch remains at 750, the number of new fish per year begins to fall (for the first time in the entire simulation). As a result the rate of decline of the fish stock begins to accelerate (rather than to moderate). The fishery has passed the peak of the net regeneration curve. It is now operating on the left-hand side of the curve, beyond a critical ‘tipping point’. The fish density is now so low that any further reductions cause the regeneration rate to decline rather than rise. There are simply too few fish in the sea to breed at the rate previously achieved. The fish population continues to fall precipitously and is now being over-harvested. At the end of year 33 the population is down to 1000 and still falling.
The model provides one further insight into the dynamics of fish stocks. Imagine, at the start of year 34, the fleet is reduced to only 10 ships, the size it was between years 4 and 16. Back then the fishery had achieved a sustainable equilibrium. Now it is unable to do so. Not surprisingly the catch falls dramatically back to 250 fish per year (10 × 25) as ships are removed or idled. But net new fish per year is even lower at around 100 fish per year. The fish population and fish density therefore decline and by year 38 the population has collapsed to zero. The message from this compact SD model is that a harvested fishery is dynamically complex, even without randomness, due to stock accumulation, feedback and nonlinearity.
Figure 9.10 shows the results from a simulation of the harvested fishery with the DES model, now with randomness included for the catch and regeneration of fish. Because there is randomness in the model, the simulation has been replicated 10 times, using different random number streams, the results showing the mean of the replications. The use of multiple replications is standard practice in DES modelling for determining the range of outcomes and the mean performance of a system (Law, 2007; Robinson, 2004). The results show the catch and the number of fish in the sea over a 40-year period.
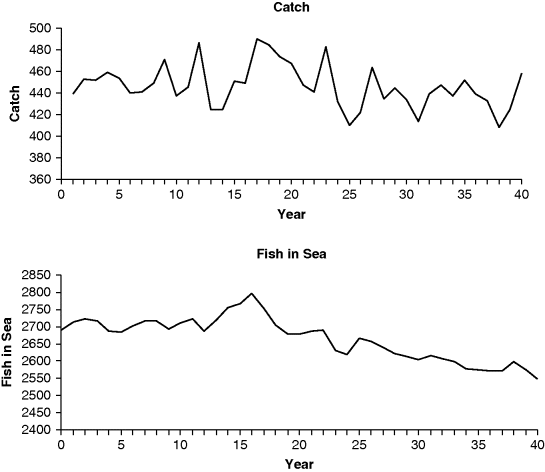
Figure 9.10 Simulation of DES model of a simple harvested fishery: non-equilibrium model.
The graphs show the variation in the annual catch with the mean shifting between just above 400 to just below 500. Similarly there is some variation in the fish stock, peaking at about 2800 and falling to about 2600. Such variation is not surprising given the randomness in the model. It would be difficult to predict the interconnected effect of variations in fish regeneration and fish catch without a simulation.
Inspecting the graph for the fish in the sea, there appears to be a downward trend. This is surprising as the system is in perfect equilibrium (the catch and regeneration rates are the same) as demonstrated by the results from the equilibrium model; remember that the number of ships is fixed at 20 (Figure 9.9). As such, it would be assumed that the steady-state mean of the model including randomness would remain constant, albeit that there are annual variations. A longer run of the simulation (not shown), however, confirms that there is a downward trend in the fish stock. Over 10 000 years the fish stock falls from 2690 to 300, and after 20 000 years the fish stock disappears altogether. Experiments showed that the greater the randomness in the system, as defined by the standard deviation of the normal distributions, the faster the collapse in fish stocks.
How can these puzzling dynamics occur in a system that is apparently in equilibrium? The reason is most simply explained with reference to an example. Starting with, say, a fish stock of 1000 in any particular year, the probability of there being 10% more or 10% less fish in the next year is the same. This can be concluded because the distributions used in the simulation are symmetrical. However, the probability of returning to the equilibrium of 1000 fish from 1100 or 900 fish is not the same. To decrease from 1100 to 1000 fish requires only a 9.1% fall in the fish population. To increase from 900 to 1000 fish requires an 11.1% increase. Because the distributions are symmetrical, the probability of increasing the fish population of 900 back to the equilibrium is lower than the probability of reducing it from 1100 to 1000. As a result, there is a constant downward pressure on the fish population, with ‘bad’ years in which the fish population falls being hard to recover from. Ultimately this leads to the complete collapse of the fish population. Although this outcome is purely a numerical effect, it does demonstrate how the inclusion of interconnected random events can lead to a puzzling, and very different, dynamic.
The SD and DES non-equilibrium models are based on quite different assumptions. The SD model investigates the effect of changing the number of ships over time, while the DES model represents the effect of random variation in the regeneration of fish and the catch. The practical, commercial results of the two models are similar. Both lead to a collapse in the fish stock, although the timescales are quite different. Both demonstrate a dynamic that could not easily have been predicted without the simulation.
9.5.3 Alternative Models of a Harvested Fishery with Endogenous Ship Purchasing
Both the SD and DES models show that a fishery can operate for long periods in equilibrium providing there are an appropriate number of ships at sea – not too few and not too many. Here a long period may be hundreds of years, spanning the lifetime of a stable fishing community. The remaining piece of the dynamical puzzle is investment in new ships. Why would fishermen purchase too many ships if, as we have seen, a large fleet can lead to overfishing? And why would they not reduce the fleet size to re-establish a sustainable equilibrium? A comparison of the investment process in SD and DES provides distinctive answers to these questions.
9.5.3.1 SD Model
An SD modeller thinks of investment as a collective decision-making process (or policy) representing, in aggregate, the judgements of those people most closely involved (fishermen in this case) and the information sources on which their decisions are based. Such decision-making processes are behavioural in the sense that they capture the broad intention of investment without necessarily assuming decision makers have perfect information or perfect foresight. A typical investment policy has three main parts. There is a goal, a specific condition to be achieved, in this case the desired number of ships in the fleet. There is monitoring of the current state of the system, how many ships are currently in operation. And finally there is corrective action, the purchase or sale of ships, to bring the current state of the system in line with the goal. This overall three-part process is known as ‘asset stock adjustment’ and is absolutely central to an information feedback representation of business and social systems (Sterman, 2000). It is a process generalizable across a wide range of investment situations covering inventories, tangible capital goods, human resources and intangible assets. At the heart of the decision making is subtle, purposive (and often judgemental) information processing in which people with responsibility for investment form a view of the appropriate incremental adjustment of important assets.
Figure 9.11 shows asset stock adjustment in the fisheries model. Notice that connections between variables are shown as dashed lines denoting flows of information. The connections are not ‘hardwired’ as they were for the natural fishery. They are discretionary and reflect the information available and deemed most relevant to investment. The desired fleet size (the goal) depends on the number of ships at sea and the propensity for growth. Specifically the desired fleet size is equal to ships at sea multiplied by a factor (1 + propensity for growth). Here is an important behavioural assumption. Since fishermen do not have the information to decide an optimal fleet size they form their goal more simply with reference to the existing fleet size. We assume that the normal propensity for growth is 0.1, so the desired fleet size is 10% larger than the current fleet size. In other words, fishermen normally and collectively want a bigger fleet than they now have, an attribute of human nature – bigger is better, growth is inherently attractive. As we will see later, the propensity for growth also depends on conditions in the fishery; a poor catch will dampen enthusiasm for a larger fleet, despite an underlying bias towards growth.

Figure 9.11 Asset stock adjustment – the decision-making process for the purchase or sale of ships in the fishery.
Once the desired fleet size is established then the rest of the asset stock adjustment formulation is easy to understand. The gap in fleet size is the difference between the desired fleet size and ships at sea. If there is a large positive gap then conditions for investment are favourable. The purchase or sale of ships closes the gap over an assumed time span of one year, which is the time taken to adjust the fleet (including ordering, construction and delivery).
Perhaps the most crucial formulation in the SD model is the propensity for growth and the factors that determine it. As mentioned above, fishermen do not know the optimal fleet size and so they prefer, more simply and pragmatically, to grow the fleet until there is compelling evidence to stop. The question is what evidence is persuasive enough to curb investment and will this result in a sustainable balance between the fish population and ships at sea? In SD evidence takes the form of information. Persuasive information is both credible and readily available to decision makers. In a real fishery, fishermen know the catch per ship – they themselves bring in the catch and it is vitally important to their livelihood. They may also know, at least roughly, the total catch of all ships in the fishery. Significantly they do not know the fish population or the fish regeneration rate. That is all happening under water. Moreover, they do not believe scientific estimates of low fish stocks unless confirmed by the catch. Such practical considerations suggest that propensity for growth is curbed by low catch rather than by objective evidence of fish stocks. As a result, investment is boundedly rational, sensing only indirectly the true state of the fish population on which the long-term sustainability of the fishery depends.
Figure 9.12 shows one possible SD formulation that captures the essential limited information characteristic of fishermen's boundedly rational decision making. Propensity for growth depends on the normal propensity for growth (set at 0.1 or 10%, to reflect a prevalent view that growth is a good thing) multiplied by the curbing effect of catch per ship. This curbing effect is nonlinear and captures another typical human tendency, which is to ignore bad news until it is really bad. If catch per ship falls from 25 fish per year to 15 per year (a 40% decline) propensity for growth falls from 0.1 to 0.09 (a decline of only 10%). Thereafter the effect becomes much stronger. If the catch per ship falls to 10 fish per year, then propensity for growth falls to zero and fishermen stop purchasing ships. If the catch falls still further then the propensity for growth becomes negative and fishermen sell ships because collectively they sense it is futile to retain a large and unproductive fleet.
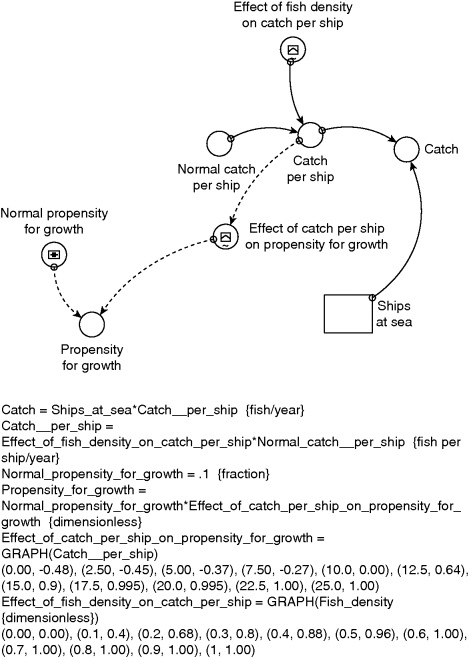
Figure 9.12 Propensity for growth and catch per ship.
Catch per ship measures ships' productivity and is modelled here as a deterministic function of fish density. The scarcer are the fish, then the lower the productivity. But the relationship is nonlinear. For moderate to high fish density (between 0.5 and 1) catch per ship remains close to normal. The assumption is that fishermen do not really notice a difference in the catch if the sea is teeming with fish or only half-teeming with fish, because fish tend to school or cluster. Catch per ship is still 68% of normal when the fish density is only 0.2, or in other words when the fish population is 20% of the maximum sustainable. But thereafter catch per ship falls quickly to zero as schools of fish become increasingly difficult to find and are hotly contested by rival ships.
9.5.3.2 DES Model
In DES modelling there is no equivalent to the ‘asset stock adjustment’ process in SD modelling. Policies for purchasing and releasing ships would be determined by discussion with relevant stakeholders, as in SD, but without the guiding framework of stock adjustment. In this case a simple policy for adjusting the number of ships is added to the model, using the formula
In other words, for every 22 fish caught in any year, one ship will be allowed to fish in the following year. This is just one of many formulations that might be used, depending on the findings from discussions with stakeholders. The formula above represents an information feedback process between the catch and the number of ships, which can be thought of as a reinforcing loop. This facet, however, is not made explicit in the DES model formulation.
9.5.3.3 Comparison of SD and DES Representations
In addition to the differences identified for earlier versions of the models, there is now the way that decision-making processes are perceived. It is apparent that in SD the modeller is guided not only by discussion with decision makers, but also by principles for modelling decision making. These principles include five formulation fundamentals, described in Sterman (2000, Chapter 13), based on ideas from information feedback theory and bounded rationality (Morecroft, 2007, Chapter 7). In DES such principles do not appear to be in common use. Instead, decision-making processes are derived from direct discussion with and observation of decision makers (Robinson et al., 2005). Uncertainties in making decisions are primarily derived from future unknown stochastic events, which in themselves engender a particular and different form of bounded rationality.
9.5.3.4 Simulated Dynamics of a Harvested Fishery with Endogenous Investment
The simulations in this section start with both SD and DES models in a sustainable equilibrium. The SD model starts with 10 ships and 3370 fish, resulting in a catch of 250 fish per year (below the maximum sustainable yield to allow room for growth and to investigate boundedly rational misinvestment). The DES model starts with 20 ships and 2690 fish, resulting in an average catch equal to the regeneration of fish (at a theoretical equilibrium of 500 fish per year), to investigate stochastic misinvestment (described later). The equilibrium is then disturbed in contrasting ways typical of each approach.
In the SD model the normal propensity for growth is artificially held at zero at the start of the simulation. A small-is-beautiful mindset has temporarily taken hold. Then in year 10 the normal propensity for growth returns to a value of 0.1, or 10% of the current fleet size. Figure 9.13 shows the results. Equilibrium prevails until year 10. Then the number of ships at sea increases steadily under the influence of an investment policy biased towards growth. For more than 10 years the catch rises. Meanwhile the catch per ship remains steady, suggesting that continued investment is both feasible and desirable. Below the waves conditions are changing, but remember that these conditions cannot be directly observed by fishermen. The regeneration rate of fish (new fish per year) rises healthily as one would expect in a well-harvested fishery. The fish population falls, but that too is expected in a harvested fishery.

Figure 9.13 Simulation of SD model of a fishery that starts in equilibrium, grows with investment and then unexpectedly collapses. From Morecroft (2007). Reproduced by permission of Wiley.
Signs of trouble appear under water in year 21 when, for the first time, regeneration (new fish per year) falls. This reversal of replenishment is a signal that the fishery has passed the tipping point of the nonlinear regeneration curve. The decline in the fish stock begins to accelerate. But interestingly the catch continues to rise for fully three more years, until year 24, and the catch per ship remains close to normal. From the viewpoint of growth-orientated fishermen floating on the surface of the sea, it is business as usual. The fleet continues to grow until year 26 when it reaches a size of 46 ships. By then the catch per ship has fallen to less than one-third of normal (only 8 fish per ship per year instead of 25), sufficient to curb further investment.
By now the hidden fish stock has fallen to a precariously low level of only 300, less than one-tenth of its initial value. With so few fish in the sea the regeneration rate is very low at only 30 new fish per year, well below the catch of around 300 fish per year. Fishermen are now well aware of the underwater crisis and respond accordingly by selling ships. The fleet size falls from a peak of 47 ships in year 26 to 39 ships in year 30. But it is too little action, too late. The boundedly rational investment policy is unable to reduce the fleet quickly enough to halt the decline of the fish stock. By year 30 there are only four fish left in the sea and regeneration has fallen to zero. The fishery has collapsed with a huge excess of relatively new ships owned by fishermen reluctant to sell and still dependent on the fishery for their livelihood. The dismal dynamics of the Pacific sardine catch in Figure 9.1 have been played out in a purely deterministic nonlinear simulation model.
Figure 9.14 shows the output from the DES model with investment in ships. As before, the results shown are the mean of 10 replications. Over the 40-year period it is apparent that the output is moving into an oscillation that is characteristic of a delayed negative feedback loop. This is confirmed by a longer simulation run (Figure 9.15). The amplitude and frequency of the oscillation vary due to the random nature of the fish catch and fish regeneration.
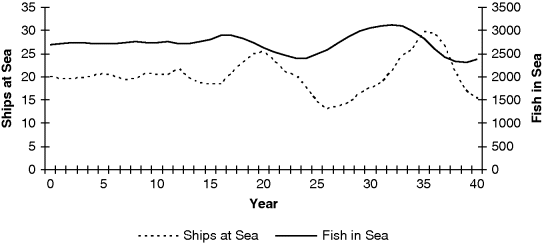
Figure 9.14 Simulation of DES model with investment showing start of oscillation.

Figure 9.15 Simulation of DES model with investment showing oscillation over 500 years.
The oscillation represents a puzzling dynamic. The system is theoretically in equilibrium with the fish catch and regeneration rates set as equal. So what is the cause of the oscillation? Figures 9.14 and 9.15 show, unsurprisingly, that the catch oscillates in line with the number of ships at sea. There is a lag, however, between an increase or decrease in the fish stock and a corresponding increase or decrease in the number of ships. This is to be expected as the purchase and sale of ships is dependent on the previous year's catch.
At the beginning of the simulation the number of ships, the catch and the fish in the sea remain relatively stable, as would be expected in an equilibrium state. In year 17 there is an increase in the number of fish caught. This is presumed to be a combination of two random events, a good year for fishing and a previous good year for regeneration, as evidenced by the catch and fish stock graphs (only the fish stock graph, fish in sea, is shown here). As a result of an increased catch more ships are purchased. As more ships are purchased the catch initially grows, but eventually this affects fish stocks and the catch then falls leading to disinvestment in ships. Once started, the oscillation perpetuates as in any typical delayed negative feedback loop. The oscillation is a result of an initial random variation, to which the ship investment policy reacts, causing the fishery to move into a permanent oscillation of fish stocks, catch and ships. Had there been no random variations, then the oscillation would not have started. Note that from an SD perspective a one-time-step change in either the catch or ships at sea would trigger a similar cyclical behaviour.
What the model demonstrates is a ship investment policy that is too sensitive to random variations (stochastic misinvestment). The decision to grow the shipping fleet is based on the only measurable data concerning likely fish stocks, that is the catch. However, due to random variations in the catch an increased catch does not necessarily indicate a growth in fish stocks. Indeed, it is possible for fish stocks to fall and the catch to rise. In this example there should not have been any investment in ships, as there was no underlying trend suggesting an increase in fish stocks. The fishermen have simply reacted to a random variation in the catch.
Here it is useful to think of the problem in terms of the two types of variation identified in statistical process control theory (Montgomery and Runger, 1994). ‘Common’ causes of variation are simply random variations that do not indicate any underlying change in the system. ‘Special’ causes of variation are shifts that do indicate an underlying change, or trend. In quality control the aim is to devise policies that only react to special causes of variation. In the fisheries example we see a typical case of an over-sensitive policy in which a change is made as a result of common causes of variation. Such a reaction can lead to an unexpected outcome; in this case the result is the oscillation evidenced in Figures 9.14 and 9.15.
The SD and DES models represent different policies for investment in the fishing fleet. Both policies are shown to be defective. In the SD model the policy leads to a complete collapse in fish stocks whose deterministic regeneration rate is highly nonlinear. In the DES model the investment policy combined with random variations leads to a boom and bust business cycle in fish stocks whose stochastic regeneration rate is essentially linear, but capped. Interestingly these behaviours closely represent the behaviours of the real fisheries shown in Figure 9.1. The Pacific sardine data showed a collapse in the sardine catch and presumably the sardine stock. This is similar to the output of the SD model. Meanwhile, the North Sea herring data seems to show the beginnings of an oscillation in the catch similar to that predicted by the DES model.
9.6 Summary of Findings
The processes of developing SD and DES models of the same problem situation are described above. The models have been developed separately by an expert in each field with a view to understanding the nature of the modelling process and insights gained from the two types of modelling approach. Our premise was that the use of SD or DES affects the representation and interpretation of phenomena from the real world. This premise is borne out in the work described.
Table 9.3 summarizes the key differences in the SD and DES approaches that have emerged as a result of this investigation into the fisheries problem. Although the list of differences is not exhaustive, and not all differences would apply to every modelling situation, nevertheless it is obvious that many of the representational differences are similar to those identified in previous studies comparing SD with DES described at the start of this chapter. But there are new insights too about differences in the interpretation of puzzling dynamics.
Table 9.3 Key differences between SD and DES approaches emerging from fisheries models.
| SD ‘deterministic complexity’ | DES ‘interconnected randomness’ |
| Representation | |
| System represented as stocks and flows | System represented as queues and activities |
| Feedback explicit | Feedback implicit |
| Many relationships are nonlinear | Many relationships are linear |
| Randomness is generally not modelled, or is added later after noise-free simulations | Randomness explicitly modelled |
| Growth/decay modelled as exponential or S-shaped | Growth/decay represented as random often with discrete steps, for example a cut-off point |
| Standard recurring modelling structures exist, for example asset stock adjustment process | Standard modelling structures generally do not exist |
| Standard diagramming format | No agreed standard diagramming format |
| Interpretation | |
| Feedback, stock accumulation, delays and nonlinearities are vital to system performance | Feedback, delays and nonlinearities are not emphasized |
| Randomness is not normally important to system performance | Randomness is a vital element of system performance |
| Structure leads to system behaviour over time | Randomness leads to system behaviour over time |
In general SD is primarily involved with understanding the performance over time of an interconnected system arising from its internal feedback structure. This feedback structure is made explicit in the representation of an SD model and expressed through a series of differential equations that are frequently nonlinear. Randomness is rarely considered and, when included, is simplified and often added later in a study after noise-free simulations have been conducted. Growth and decay processes are normally considered to be exponential or S-shaped in form. A number of standard recurring modelling structures exist (often stemming from assumptions about bounded rationality and managerial decision making) that guide model conceptualization and equation formulation in SD models. The diagramming format for representing SD simulation models (stock and flow diagrams) is seen as a standard, though causal loop diagrams are also widely used qualitatively to depict feedback structure.
DES primarily focuses on the performance over time of an interconnected system subject to internal and external random variation. Feedback structures are included in these models, but they are not made explicit. This use of feedback contradicts the view of Coyle (1985) that DES models are always open-process structures. DES modellers tend to adopt relationships that are linear in form, although not exclusively. Meanwhile, randomness is seen as a vital part of system behaviour and it is explicitly modelled whenever and wherever in the system it is believed to occur. Growth and decay processes are therefore seen as random but limits are often represented as discrete cut-off points. DES modellers do not have standard modelling structures to guide equation formulation, nor is there an agreed diagramming format for representing DES models.
Building on these representational distinctions, SD modellers see feedback, delays and nonlinearities as vital to the performance of a system, while randomness is normally of little or no importance (or is viewed as something that evokes the latent dynamics of feedback structure). DES modellers place the emphasis on randomness with little direct concern for the effects of feedback. As a result SD modellers see feedback structure as the prime source of system behaviour, while DES modellers consider randomness to be the main cause.
What is clear is that SD and DES adopt quite different modelling philosophies. The similarities between the two approaches seem to end at the fact that both are simulation methods aimed at modelling the progress of a system through time. Further to this, and based on our experiences with the fisheries model, we might argue that both adopt an evolutionary approach to model development.
9.7 Limitations of the Study
There are some limitations of this study and two specifically need to be highlighted. First, there is a variety of both SD and DES models that could be developed for this problem. We have only developed one example of each. Alternative models may have led to different findings. That said, the fact that these models have been developed by experts of long standing in both fields suggests that they are representative of the typical SD and DES modelling approach. The research strategy adopted here is certainly an improvement on an individual developing both models, where that individual is bound to be more steeped in one modelling approach over the other. This is a drawback of previous comparative research, as identified in Section 9.2.
The second key limitation is that the DES model does not use the full set of DES modelling facilities. In particular, the model does not represent individual fish (instead an entity represents the population of fish) and the time step is fixed (at one year) and does not vary. Modelling individuals and a varying (random) time step are both features of many DES models. It would not be true to say, however, that DES modellers do not adopt the approach taken here. Robinson (2004) describes ‘grouping entities’ as a standard model simplification method in DES and there are examples of DES models with a constant time step (Bowman et al., 1998). Indeed, DES modellers are keen to stress the importance of building an appropriate model, not one that necessarily uses every feature of the approach (Pidd, 2003). The important feature of this work is that the two models were built for the same problem using the modelling philosophy of both an SD and a DES modeller.
Given these limitations, we believe that it would be beneficial if there were more comparisons of SD and DES that followed a similar approach to that taken here. In this way, through a series of studies, a more complete understanding of the similarities and differences between SD and DES could be derived. Since we first worked on this problem a few such studies have been undertaken and some are reported in this edited volume.
9.8 SD or DES?
Having identified a series of differences between SD and DES modelling, we return to the original question of this chapter: which method to use and why? In the case of fisheries both models seem to offer plausible explanations for the behaviours seen in Figure 9.1. This outcome would suggest that neither method is necessarily superior to the other, but that either may be useful in different circumstances. While each approach represents certain facets of the real world, both approaches also simplify or downplay other facets. Given that both SD and DES modellers would agree that all useful models are simplifications of reality (Meadows, 1980; Pidd, 2003), this selective attention of the two approaches is not in itself a shortcoming. It is, however, important that modellers first recognize what simplifications a modelling approach entails and, second, that they select a modelling approach based on the facets of the problem situation and the attributes of the modelling approach. Table 9.3 should help in determining which attributes each modelling approach includes and which it excludes. Interpreting the important facets of the real world is dependent on the specific problem situation.
Where the facets of the real world and their implications for the problem situation are not clearly understood (which is likely to be the main motivation for modelling) then the advice might be to build both types of models, since both give important and possibly differing insights. Indeed, Renshaw, in writing about the modelling of biological populations, states:
The tragedy is that too few researchers realize that both deterministic [SD] and stochastic [DES] models have important roles to play in the analysis of any particular system. Slavish obedience to one specific approach can lead to disaster … So pursuing both approaches simultaneously ensures that we do not become trapped either by deterministic fantasy or unnecessary mathematical detail.
(Renshaw, 1991, p. 2)
Similarly, Koopman (2002) discusses the modelling of a smallpox outbreak with the aim of determining how best to respond. Discrete and continuous simulation models give quite different insights into the benefits of mass vaccination over targeted vaccination.
Perhaps it is time that more SD and DES modellers crossed the divide and considered applying both approaches, or at least considered more carefully situations in which the application of both approaches might yield complementary insights. In fact modellers do sometimes combine both deterministic feedback structure and stochastic inputs. For example, Dudley (2003), a policy adviser to the fishing industry and an expert in fisheries modelling, adds random variation to the recruitment of juvenile fish (i.e. regeneration) in an SD model of a fishery. His model includes not only harvesting but also fishery management. Noise-free simulations show cyclicality in fish stocks and catch. He notes that ‘with random variation added to recruitment the system shows significant variability but the overall cyclical pattern of the fishery remains’. This overlaying of randomness in a single rate equation formulation is representative of SD practice (as mentioned earlier). But the practice is quite rare. Moreover, such bolt-on noise tests, applied to individual rate equations, do not necessarily recognize the dynamic significance of multiple interacting random processes typical of DES studies.
This step of applying both approaches requires more than simply learning about the modelling techniques and tools involved in either approach. The modeller also needs to adopt, or acknowledge, a completely different modelling philosophy and temporarily to suspend deeply held beliefs about reasons for system behaviour over time. Our experiences with the simple fisheries models have made us more aware, and more accepting, of alternative plausible interpretations for puzzling dynamics. We have moved forward in what Lane (2000) has described as ‘mode 3 discourse’ between DES and SD, building on a growing appreciation of differences and similarities between the two approaches. Probably each of us will remain anchored in our core disciplines, but we can now see enough of the ‘other’ discipline to sense where future collaboration might be beneficial.
A sample of ideas for future collaboration is a fitting end to the chapter. We have discovered paradigm differences between DES and SD. One loose yet concise way to communicate these differences is to say that DES illuminates ‘interconnected randomness’ whereas SD illuminates ‘deterministic complexity’. The real world contains both. Maybe interconnected randomness is most evident in functional/operational problems of the kind frequently tackled by DES modellers, whereas deterministic complexity shows up in cross-functional/strategic problems most often addressed in SD. More likely both SD and DES are capable of addressing operational and strategic issues and it is just a matter of which components you choose for your simulated enterprise and whether or not you believe randomness or feedback structure plays the dominant role in the unfolding future. To take a practical example, the oil producers' microworld (Morecroft, 2007, Chapter 8; Langley, 1995) is an industry-level deterministic SD simulator linking rival aggregate producers of oil to world demand for oil products. Its purpose is to understand global oil market dynamics and long-term oil price. There are five main sectors in the model. There is no reason why these same sectors could not be reconceptualized in a DES model that emphasizes the randomness and turmoil that undoubtedly pervade the oil industry. On the other hand, in the manufacturing heartland of DES exemplified by, for instance, the brick factory model reported by Robinson and Higton (1995), there is surely potential for an SD model of the same factory. However, instead of investigating the stochastic interaction of individual factory machines and manufacturing processes it would emphasize deterministic nonlinear feedback processes in manufacturing control and shed new and complementary light on factory management and brick production. Food for thought …
Acknowledgements
This chapter is based on the paper Morecroft, J. and Robinson, S. (2005). Explaining Puzzling Dynamics: Comparing the Use of System Dynamics and Discrete-Event Simulation. The 23rd International Conference of the System Dynamics Society, July 17–21, 2005, Boston.
References
- Arnason, R. (2007) Fisheries management, in Handbook on Operations Research in Natural Resources, vol. 99 (eds A. Weintraub et al.), International Series in Operations Research & Management Science, Springer, New York.
- Banks, J., Carson, J.S., Nelson, B.L. and Nicol, D.M. (2001) Discrete-Event System Simulation, 3rd edn, Prentice Hall, Upper Saddle River, NJ.
- Bowman, R.A., Haimowitz, I.J., Mattheyses, R.M., Özge, A.Y. and Phillips, M.C. (1998) Discrete time simulation of an equipment rental business, in Proceedings of the 1998 Winter Simulation Conference (eds D.J. Medeiros et al.). IEEE Press, Piscataway, NJ, pp. 1505–1512.
- Brailsford, S. and Hilton, N. (2001) A comparison of discrete event simulation and system dynamics for modelling healthcare systems. Proceedings of the 26th Meeting of the ORAHS Working Group 2000, Glasgow Caledonian University, Glasgow, Scotland, pp. 18–39.
- Coyle, R.G. (1985) Representing discrete events in system dynamics models: a theoretical application to modelling coal production. Journal of the Operational Research Society, 36 (4), 307–318.
- Coyle, R.G. (1996) System Dynamics Modelling, Chapman & Hall, London.
- Davis, R. (2001) Business Process Modelling with ARIS: A Practical Guide, Springer, Berlin.
- Dudley, R.G. (2003) A basis for understanding fisheries management complexities. Proceedings of the International System Dynamics Conference, New York City 2003, manuscript 118, http://www.systemdynamics.org/conferences.
- Farber, M.I. (1991) A methodology for simulating the US recreational fishery for billfish. Proceedings of the 1991 Winter Simulation Conference, pp. 832–840.
- Forrester, J.W. (1961) Industrial Dynamics, MIT Press, Cambridge, MA (reprinted by Pegasus Communications, Waltham, MA).
- Forrester, J.W. (1968) Industrial dynamics – after the first decade. Management Science, 14 (7), 398–415.
- Hardin, G. (1968) The tragedy of the commons. Science, 162, 1243–1248.
- Hills, P.R. (1971) HOCUS, P-E Group, Egham.
- Koopman, J. (2002) Controlling smallpox. Science, 298 (5597), 1342–1344.
- Lane, D.C. (1999) Social theory and system dynamics practice. European Journal of Operational Research, 113, 501–527.
- Lane, D.C. (2000) You just don't understand me: modes of failure and success in the discourse between system dynamics and discrete event simulation. LSE OR Department, Working Paper LSEOR 00-34.
- Langley, P. (1995) An experimental study of the impact of online cognitive feedback on performance and learning in an oil producers' microworld. PhD thesis, London Business School.
- Lanner (2007) Witness Simulation Software. www.lanner.com (accessed June 2007).
- Law, A.M. (2007) Simulation Modeling and Analysis, 4th edn, McGraw-Hill, New York.
- Mak, H.-Y. (1992) System dynamics and discrete event simulation modelling. PhD thesis. London School of Economics and Political Science.
- Meadows, D.H. (1980) The unavoidable a priori, in Elements of the System Dynamics Method (ed. J. Randers), MIT Press, Cambridge, MA, pp. 23–57.
- Meadows, D.L., Fiddaman, T. and Shannon, D. (2001). FishBanks, Ltd. A Micro-computer Assisted Group Simulation That Teaches Principles of Sustainable Management of Renewable Natural Resources, 5th ed., The FishBanks Ltd. game was developed by Professor Dennis Meadows, co-author of “Limits to Growth.” The board game kits which include the game software, PowerPoint slide sets for introducing and debriefing the game, instructions for playing the game, the role description, game board, and pieces are sold through the System Dynamics Society http://www.systemdynamics.org/.
- Montgomery, D.C. and Runger, G.C. (1994) Applied Statistics and Probability for Engineers, John Wiley & Sons, Inc., New York.
- Morecroft, J. (2004) Mental models and learning in system dynamics practice, in Systems Modelling: Theory and Practice (ed. M. Pidd), John Wiley & Sons, Ltd, Chichester, pp. 101–126.
- Morecroft, J. (2007) Strategic Modelling and Business Dynamics, John Wiley & Sons, Ltd, Chichester.
- Moxnes, E. (1998) Not only the tragedy of the commons: misperceptions of bioeconomics. Management Science, 44 (9), 1234–1248.
- Otto, P. and Struben, J. (2004) Gloucester fishery: insights from a group modeling intervention. System Dynamics Review, 20 (4), 287–312.
- Pidd, M. (2003) Tools for Thinking: Modelling in Management Science, 2nd edn, John Wiley & Sons, Ltd, Chichester.
- Pidd, M. (2004) Computer Simulation in Management Science, 5th edn, John Wiley & Sons, Ltd, Chichester.
- Pooley, R.J. (1991) Towards a standard for hierarchical process oriented discrete event diagrams. Transactions of the Society for Computer Simulation, 8 (1), 1–41.
- Renshaw, E. (1991) Modelling Biological Populations in Space and Time, Cambridge University Press, Cambridge.
- Richardson, G.P. (1991) Feedback Thought in Social Science and Systems Theory, University of Pennsylvania Press, Philadelphia.
- Richardson, G.P. and Pugh, A.L. (1981) Introduction to System Dynamics Modeling with DYNAMO, MIT Press, Cambridge, MA.
- Richmond, B., Peterson, S., Chichakly, K., Liu, W. and Wallis, J. (2004) iThink Software, Isee Systems Inc., Lebanon, NH.
- Richter, H. and März, L. (2000) Toward a standard process: the use of UML for designing simulation models, in Proceedings of the 2000 Winter Simulation Conference (eds J.A. Joineset al.), IEEE Press, Piscataway, NJ, pp. 394–398.
- Robinson, S. (2001) Soft with a hard centre: discrete-event simulation in facilitation. Journal of the Operational Research Society, 52 (8), 905–915.
- Robinson, S. (2004) Simulation: The Practice of Model Development and Use, John Wiley & Sons, Ltd, Chichester.
- Robinson, S., Alifantis, T., Edwards, J.S., Ladbrook, J. and Waller, T. (2005) Knowledge based improvement: simulation and artificial intelligence for identifying and improving human decision-making in an operations system. Journal of the Operational Research Society, 56 (8), 912–921.
- Robinson, S., Brooks, R., Kotiadis, K. and van der Zee, D.-J. (eds) (2011) Conceptual Modeling for Discrete-Event Simulation, CRC Press, Boca Raton, FL.
- Robinson, S. and Higton, N. (1995) Computer simulation for quality and reliability engineering. Quality and Reliability Engineering International, 11, 371–377.
- Roughgarden, J. and Smith, F. (1996) Why fisheries collapse and what to do about it. Proceedings of the National Academy of Science, 93 (10), 5078–5083.
- Som, T.K. and Sargent, R.G. (1989) A formal development of event graphs as an aid to structured and efficient simulation programs. ORSA Journal on Computing, 1 (2), 107–125.
- Sterman, J.D. (1989) Modeling managerial behavior: misperceptions of feedback in a dynamic decision making experiment. Management Science, 35 (3), 321–339.
- Sterman, J.D. (2000) Business Dynamics: Systems Thinking and Modeling for a Complex World, Irwin/McGraw-Hill, Boston, MA.
- Tako, A.A. and Robinson, S. (2009) Comparing discrete-event simulation and system dynamics: users' perceptions. Journal of the Operational Research Society, 60 (3), 296–312.
- Tako, A.A. and Robinson, S. (2010) Model development in discrete-event simulation and system dynamics: an empirical study of expert modellers. European Journal of Operational Research, 207, 784–794.
- Tako, A.A. and Robinson, S. (2012) The application of discrete event simulation and system dynamics in the supply chain context. Decision Support Systems, 52 (4), 802–815.
- Torn, A.A. (1981) Simulation graphs: a general tool for modeling simulation designs. Simulation, 37 (6), 187–194.
- Townsend, C.R., Begon, M. and Harper, J.L. (2003) Essentials of Ecology, 2nd edn, Blackwell, Oxford.
