chapter 14
Time-Independent Perturbation Theory
Perturbation theory is a technique used to solve problems involving Hamiltonians that may be too difficult to solve directly but where the Hamiltonian is only slightly different from one for a system with a known solution. That is, the new Hamiltonian is a slight “perturbation” of the one that we know well. A few examples include
• A square well with a Dirac delta function in the center
• A charged oscillator in a weak electric field
• The hydrogen atom in a weak electric field (the “Stark” effect)
• The Zeeman effect
When considering the application of perturbation theory, we start with the simpler case of a time-independent Hamiltonian and the stationary states of the system. The more complicated situation involving time dependence is more advanced and will be considered later.
CHAPTER OBJECTIVES
In this chapter you will
• Learn about perturbations to the hamiltonian
• Learn how to compute corrections to energy levels
• Learn about the stark effect
When Is Perturbation Theory Needed?
So when is the application of perturbation theory appropriate? We are looking for situations that can be described in the following way. Suppose that we have a Hamiltonian that could be broken into a sum as
Here,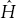 
0 is some Hamiltonian where we know the exact solution for the system. The other piece, 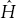′, is a perturbation that is very small compared to the Hamiltonian 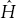0. In particular, the perturbation can be written in terms of a small real constant λ in the following way:
0 is some Hamiltonian where we know the exact solution for the system. The other piece, ′, is a perturbation that is very small compared to the Hamiltonian 0. In particular, the perturbation can be written in terms of a small real constant λ in the following way:
where
In a nutshell, time-independent perturbation theory can be thought of as looking at a power series solution for a given system. If the states of the system are
then imagine expanding these states in a series:
The system will have eigenvalues that can similarly be expanded as a power series:
Here, the eigenstates and eigenvalues of the unperturbed system are
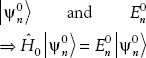
Since
and the eigenvalue problem being studied is
then
Hence to “lowest order” we get the old system that we’re familiar with; e.g., maybe it’s the infinite square well. As with any problem involving power series, taking more and more terms will increase the accuracy of our solution, but often we only need the first-order or second-order correction to a given problem.
The solution we already know is also referred to as the zero-order term. Another example could be the hydrogen atom in a weak electric field. The zero-order term would be the solution for the hydrogen atom without any electric field present. To get the first- and second-order corrections, we simply do some brute-force algebra and collect terms in powers of λ:
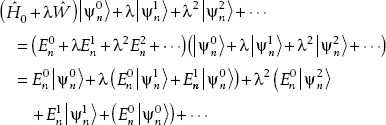
To get the first-order correction, then, we consider only those terms multiplied on both sides by the first power of λ. We end up with
Now use the following. Since the eigenstates of the unperturbed system are orthonormal, we have
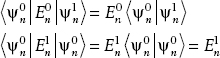
Moreover,
So we can act from the left with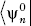 
on
on
and we obtain
Canceling the common term from both sides gives the first-order correction to the energy in the perturbed system:
Or put another way, the first-order change (or correction) in the energy of a state is found by adding the expectation value of the perturbation Hamiltonian in that state.
EXAMPLE 14-1 
Find the first-order correction to the energy of the nth excited state for a spin-less particle of mass m trapped in a square well of width 2a where the potential has been raised to
SOLUTION We already know the solution to the basic square well problem, where we have
In that case the wavefunctions are given by
and the energies are given by
En =Kn2
where K is a constant involving the mass of the particle, Planck’s constant, and the width of the well. Using first-order perturbation theory, the energy of the nth state is going to be written as
We find the correction term by using
In this case the perturbation is just the constant, so we take
and we’ve got
Using the relation
we get
Therefore to first order, the energy of the perturbed system is given by
Still StrugglingThere is really nothing new here. We are simply doing more calculations with inner products that add to what we already know.
EXAMPLE 14-2 Consider once again the infinite square well, this time with
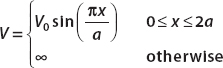
SOLUTION The wavefunctions and energies for the unperturbed system are exactly the same as given in Example 14-1. The procedure outline is also the same. This time we need to find
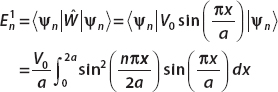
This integral can be calculated using
together with
When the calculation is carried out, we find
Hence, to first order, the energies of the perturbed system are
En =Kn2
EXAMPLE 14-3 Once again consider the infinite square well of width 2a, this time with the perturbation
SOLUTION The energies and eigenstates in the unperturbed system are given by
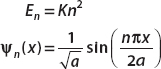
To first order, the energies of the perturbed system are
In this case we calculate the expectation value
Using the sampling property of the Dirac delta function, this is just
Therefore, if n is even, the energies are unchanged:
If n is odd, we get
EXAMPLE 14-4 Suppose that
Write the Hamiltonian as a given Hamiltonian plus a perturbed piece, and find the unperturbed energies and eigenstates. Then find the corrected energies, using first-order perturbation theory.
SOLUTION Simply break the matrix apart to separate out the small perturbation, i.e.,
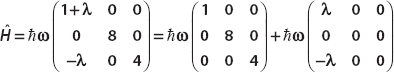
The first matrix is the unperturbed Hamiltonian, and it’s diagonal, so we can just read off the energy eigenvalues:
The energy eigenstates are just the normalized eigenvectors of the matrix:
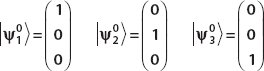
To find the correction for the first energy, we calculate
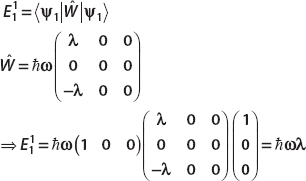
For the second energy, we find the correction as
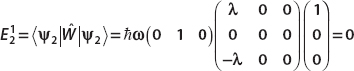
Similarly, for the third energy we obtain
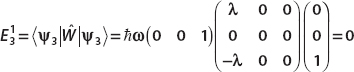
Therefore, to first order, the corrected energies are
Still StrugglingWhen doing a perturbation problem involving the hamiltonian expressed in matrix form, break up the matrix in a way that gives you a hamiltonian you already know plus something else. that something else is the perturbation.
EXAMPLE 14-5 Suppose that the Hamiltonian for a particle of mass m is given by
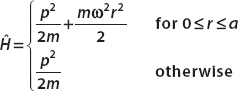
Find the correction to the ground state energy of the particle to first order.
SOLUTION We take
and define
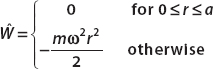
Then the unperturbed case should be familiar from Chap. 12. The wavefunction for the ground state is given by
The ground state energy is
Defining
the first-order correction to the energy is
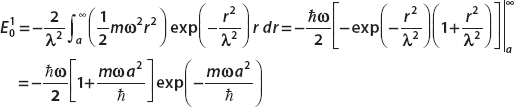
Hence to first order, the ground state energy is
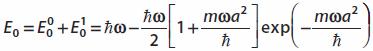
The Stark Effect
Consider a hydrogen atom placed in an external electric field directed along the z axis
Here the electric field is a weak field. The effect of the field is to shift the energy levels of the atom, which results in a shift of the spectral lines. We can figure out what that shift is by using perturbation theory. First recall that without any electric field, the Hamiltonian is given by
with eigenstates (see Chap. 12)
With an applied electric field along the z axis, the perturbation part of the Hamiltonian will be
To apply perturbation theory, the requirement to be met is
We can apply nondegenerate perturbation theory to the ground state of the hydrogen atom. The correction to the energy is given by
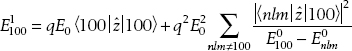
where the unperturbed energies of the hydrogen atom are
and 100 = nlm is the ground state energy. Now, under parity
and
That is, z is odd under parity while the wavefunction is even. Hence the integral will vanish:
The energy shift for a hydrogen atom in a weak, uniform electric field is then given by the left over quadratic term
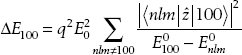
This is called the quadratic Stark effect. To do the calculation, we can insert a complete set of states:
This gives
Explicit calculation gives
And so the amount of energy shift or “quadratic Stark effect” is
It’s also instructive to look at the effect of an external electric field on the energy levels of the n = 2 states of the hydrogen atom. In this case, the perturbation part of the Hamiltonian will have nonzero matrix elements between states of opposite parity. In this case
l = 0 and l = 1
And we can construct the matrix elements of the perturbation Hamiltonian as
It can be shown by explicit calculation that
And so the eigenvalues and hence the energy shifts are
It is also easy to show that the normalized eigenvectors of the system are superpositions of the 2p and 2s states:
In the case where there is no applied electric field, the two states have the same energy. When an electric field is applied as described here, the energy of the first state shifts up by
while the energy of the second state shifts down by
Summary
In this chapter we learned how to handle perturbations.
• Break up the Hamiltonian into two parts, one that you know and a second piece that is the perturbation.
• Calculate corrections to the energy levels that arise from inner products calculated with this new piece (the perturbation Hamiltonian).
QUIZ
1. Consider an infinite square well. In the unperturbed state, the potential is given by
Suppose that a potential of magnitude A is applied for
0 ≤ x ≤ a
Find the first-order correction to the energy levels.
2. Consider a particle in a two-dimensional infinite potential well with length a in each direction. Show that if the particle is subject to a perturbing Hamiltonian of the form
where A is a constant, the first-order correction to the energy is given by
3. Again a particle is in a two-dimensional square box with sides of length a. If the potential inside the box is
show that the first-order correction to the ground state energy is
Assume that
λ << 1
4. In first-order perturbation theory, which of the following best describes the means used to calculate corrections to the energy levels?
A. Find the expectation value of the perturbation Hamiltonian with respect to the perturbed states.
B. Find the expectation value of the perturbation Hamiltonian with respect to the unperturbed states.
C. Find the eigenvalues and eigenstates of the unperturbed Hamiltonian.
D. Add correction terms to the unperturbed eigenstates of the Hamiltonian.
5. The Hamiltonian of a given system is given by the matrix
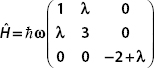
Show that the unperturbed energies of this system are given by
Then show that to second order, the energies of the perturbed system are
6. A particle is trapped in an infinite three-dimensional square well with potential
A Dirac delta perturbation is now added to the well:
Show that to first order, the ground state energy of the perturbed system is
7. Consider a two-dimensional harmonic oscillator with unperturbed Hamiltonian
Suppose that the following perturbation is added to the system:
Show that the first-order energy shift is given by
8. The reason that the Stark shift shows up for the n = 2 states of the hydrogen atom but that there is no correction to the linear term for the n = 1 or ground state is
A. The ground state of the hydrogen atom has a nonvanishing electric dipole moment.
B. The superposition states for n = 2 in the presence of an external electric field are eigenstates of the parity operator, but the ground state is not, and hence it has a nonvanishing dipole moment.
C. The ground state of the hydrogen atom has no permanent electric dipole moment. The superposition eigenstates constructed for the n = 2 case are not eigenstates of the parity operator and have nonvanishing electric dipole moment.
9. The condition under which perturbation theory can be applied is best described as
A. The perturbation that is applied is large with respect to the Hamiltonian.
B. The eigenvalues of the unperturbed Hamiltonian are unknown.
C. The perturbation that is applied is small with respect to a Hamiltonian whose solution we know.
D. Perturbation theory can at best give approximate solutions, so can only be applied when the perturbation is approximately known.
10. To find the solution to a perturbed system
A. Expand the Hamiltonian as a power series
B. Expand the energies and eigenstates in a power series and keep order to desired accuracy
C. Expand the Hamiltonian but only to second order
D. Expand only the energy levels in a power series
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.