chapter 4
An Introduction to Hilbert Space
Hilbert space is the mathematical foundation used for quantum mechanics. This formalism uses the basic ideas of vector analysis, with functions taking the role of vectors. In this chapter we will highlight a few of the key ideas used in quantum mechanics.
CHAPTER OBJECTIVES
In this chapter you will
• Understand the underlying mathematical structure of quantum mechanics
• Learn to connect vectors to representations of particle states in quantum mechanics
Basic Definitions
Let us quickly review elementary vector analysis and the concepts that will be carried over to define the notion of Hilbert space. A vector A in three-dimensional euclidean space (using cartesian coordinates) is defined as
The numbers (Ax, Ay, Az) are the components of the vector with respect to the basis 
. We could, if desired, represent the vector in another coordinate system (such as spherical coordinates). This would entail representing the vector with respect to a different basis 
. In that case the vector would have different components (Ar, Aφ, AΦ). Let’s think about some of the basic operations that can be carried out with vectors.
. We could, if desired, represent the vector in another coordinate system (such as spherical coordinates). This would entail representing the vector with respect to a different basis . In that case the vector would have different components (Ar, Aφ, AΦ). Let’s think about some of the basic operations that can be carried out with vectors.Given a second vector, 
, we can add or subtract the two vectors, producing a new vector 
:
, we can add or subtract the two vectors, producing a new vector :
We can multiply a vector by a scalar to produce a new vector:
There exists an inner product between two vectors, which is a number:
This allows us to define the length of a vector, which is given by
Any vector can be “expanded” in terms of the basis vectors . A fancy way of saying this is that the basis vectors “span” the space. Furthermore, the basis vectors are orthnormal, meaning
. A fancy way of saying this is that the basis vectors “span” the space. Furthermore, the basis vectors are orthnormal, meaning
In a Hilbert space, we take notions like these and generalize them to a space in which either the “vectors” can have an arbitrary number of n components (which can be complex numbers) or the vectors are functions, making the number of “dimensions” infinite.
Hilbert Space Definitions
In a Hilbert space, we abstract all the basic definitions we are familiar with from vector analysis, such as vector addition, a basis, an inner product, and generalize this to a space where the elements of the space are functions instead of vectors. In quantum mechanics we will have occasion to work with discrete vectors in finite dimensions v = (v1, v2, …, vn), as well as infinite dimensional vectors (functions) φ(x) (note that the elements of a Hilbert space can be complex).
In analogy with the properties of vectors defined earlier, we define some basic operations and properties of a Hilbert space.
1. Let φ(x) belong to a given Hilbert space, and let a be a complex number. The element αϕ(x), formed by multiplication by α, also belongs to the space. In the discrete case this is also true and is indicated by saying that if v = (v 1, v2, …, vn) belongs to the space, so does (αv1, αv2, …, αvn).
2. Let φ(x) and ψ(x) be two elements of the Hilbert space. Then φ(x) ± ψ(x) also belongs to the space. In the discrete case, if v = (v1, v2, …, vn) and w = (w1, w2, …, wn) belong to the space, then so does v ± w = (v1 ± w1, v2 ± w2, …, vn ± wn). This property along with property 1 characterizes a Hilbert space as linear.
3. There exists an inner product on the space which is a complex number. In the infinite dimensional or continuous case, we define this as
In the event that the interval of definition is restricted to a ≤ x ≤ b, this becomes
In the discrete case of a dimensional space, the inner product is defined to be
The inner product, being a complex number, is not an element of the Hilbert space. We define the length or norm of a vector by computing the inner product of the vector with itself. Specifically, in the continuous case, we define norm ||φ|| as
where the integral is taken over the range of definition for the space. For a discrete vector with n components, the square of the norm ||v|| is given by
Since elements of Hilbert space can be complex, we take the complex conjugate in the computation of the inner product so that the norm will be a real number. We take the positive square root so that ||ϕ|| ≥ 0 and ||v|| ≥ 0.
For a given space, there exist a set of basis vectors that span the space. Any function on that space can be expanded as a linear combination of the basis vectors. This also applies in the discrete case. If we label the basis by ei, we can write
Last, there exists a zero vector and identity such that if f belongs to the Hilbert space (continuous or discrete), then
Let’s consider two examples of a Hilbert space in the continuous case. L2 is the set of functions ψ(x) defined over all space with finite norm, that is,
Still StrugglingParticle states in quantum mechanics can be thought of mathematically as vectors. use what you know about ordinary vectors, but applied to different numbers of dimensions.
EXAMPLE 4-1 
Show that
where φ is the Heaviside or unit step function, and belongs to space L2.
SOLUTION The unit step function is defined to be 1 for x ≥ 0 and 0 otherwise. Figure 4-1 is a plot.
FIGURE 4-1
Now φ(x – 10) shifts the discontinuity to x =10. Therefore this function is 1 for x ≥ 10 and is 0 otherwise (see Fig. 4-2).
FIGURE 4-2
Subtracting this from φ(x) to get φ(x) – φ(x – 10), we obtain a function that is 1 for 0 ≤ x ≤ 10 and is 0 otherwise (see Fig. 4-3).
FIGURE 4-3
Therefore we see that the function f (x) – xe−x [φ(x)−φ(x − 10)] is going to be nonzero only for 0 ≤ x ≤ 10. Figure 4-4 is a plot of the function, to get an idea of its behavior.
FIGURE 4-4
Since this function is nonzero over a finite interval, we expect it to have a finite integral and to belong to L2. We compute ∫ f2(x)dx:
(This integral can be computed by using integration by parts.) Evaluating it at the limits x = 10 and x = 0, we find that
(Since e−20 is very small, we can take it to be zero.) The norm of the function is finite, and so this integral belongs to the Hilbert space L2.
EXAMPLE 4-2 Let a Hilbert space consist of functions defined over the range 0 < x < 3. Does the function
satisfy the requirement that 
SOLUTION A plot of the function (Fig. 4-5) follows.
FIGURE 4-5
In Fig. 4-6 we plot the square of the function.
FIGURE 4-6
From the plots, it is apparent that the function does belong to the Hilbert space. But let’s compute the integral explicitly.
We use a familiar trig identity to rewrite the integrand:
The result of the first integral is immediately apparent:
For the second integral, ignoring the ½ out in front, we obtain
So the integral is finite:
and this function satisfies the requirement that 
The task of expanding a function in terms of a given basis is encountered frequently in quantum mechanics. We have already seen this in previous chapters. Let’s examine how to find the components of an arbitrary function expanded in some basis.
EXAMPLE 4-3 Suppose that we have an infinite square well of width a. The wavefunctions that are the solutions to the Schrödinger equation are the basis functions for a Hilbert space defined over 0 ≤ x ≤ a. We recall that these basis functions are given by
We can expand any function in terms of these basis functions, using φ(x) = 
, where the expansion coefficients are found from
, where the expansion coefficients are found from
Let φ(x)= cosh(x) where cosh is the hyperbolic cosine function. Find the expansion coefficients necessary to express φ in terms of the basis functions of the square well.
SOLUTION A plot of φ(x) over a finite range 0 ≤ x ≤ a is shown in Fig. 4-7.
FIGURE 4-7
Does this wavefunction have a finite norm, as the plot indicates?
Since cosh(0) = 1 and sinh(0) = 0, the integral vanishes at the lower limit and
So the wavefunction has a finite norm. The integral required to determine the coefficients of expansion is given by
To compute this integral, we can expand both functions in the integrand in terms of exponentials. First, to simplify the notation we let
then
Substituting these relations into the integral, we obtain
This integral can be done term by term, using the u substitution technique. We illustrate this with the first term only. Let u = (iβ + 1)x, then du = (iβ + 1) dx, and the integral becomes
Carrying out a similar procedure for the remaining terms and rewriting the exponentials in terms of sine and cosh functions, we obtain
The Dirac Delta Function
In this section we briefly touch on a tool from mathematics that we will have occasion to use called the Dirac delta function. The Dirac delta function is an infinite “spike” located at the origin denoted by δ(x). If we define
then we can think of δ(x) in terms of the limits δε(x). We can see what some of the properties of δ(x) are by examining how δ(x) behaves. For example,
It is also true that
One important property of the Dirac delta function is the sampling property:
We can also shift δ(x) to another point along the real line to δ(x – a). Then the sampling property becomes
In this way δ(x – a) can be viewed as representing the presence of a particle at x = a. The Dirac delta function can be extended to three dimensions by using
Some of the basic properties of the Dirac delta function follow:
1. 
2. 
3. 
4. 
We can use the sampling property to obtain the Fourier transform of the Dirac delta function:
Still StrugglingNote that the Dirac delta function only makes sense inside an integral. It picks out the value of the function it is multiplied by, at the point indicated by the argument to the Dirac delta function.
EXAMPLE 4-4 Find the Fourier transform of δ(ax).
SOLUTION The Fourier transform is
Let u = ax; then du = adx and the integral becomes
If we denote the Fourier transform of f(x) by F[f (x)], this is the same as saying that
since F[δ(ax)] is given by
Summary
In this chapter we introduced the mathematical arena where quantum mechanics takes place, which is called Hilbert space. Concepts of norm and inner product, which are important for making physical predictions in quantum theory, were explored in this context.
QUIZ
1. Two vectors in 5 dimensions are given by
A = (2, 4i, 0, 1, −7i) B = (1, 0, 1, 9i, 2)
Show that (A, B) = 2 + 23i and (B, A) = 2 − 23i.
2. Determine which of the following functions belong to L2.
A. f (x) = sech(x)
B. f (x) = e−x cosh(x) for x ≥ 0, zero otherwise
C. f (x) = e−x sin(π x) for x ≥ 0, zero otherwise
3. Verify the properties of the Dirac delta function listed here by considering integrals.
A. 
B. 
4. Compute 
.
.5. Compute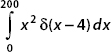 
.
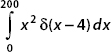...................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.