
chapter 8
The Foundations of Quantum Mechanics
The postulates of quantum mechanics are mathematical prescriptions for using the theory to predict the results of experiments. These postulates can be presented in terms of the state vector or by using the density operator. We discuss both topics and cover material related to the representation of composite quantum states and the Heisenberg picture. We also introduce a useful tool for two-level systems called the Bloch vector.
CHAPTER OBJECTIVES
In this chapter you will
• Learn how physical systems are represented in quantum theory
• Learn how to represent operators in Dirac notation
• understand spectral decomposition of an operator
• Learn about projective measurements
• illustrate these ideas with two-level systems
The Postulates of Quantum Mechanics
In this section the postulates of quantum mechanics are described in terms of the state vector. This formalism works for an isolated physical system.
POSTULATE 1: States of physical systems are represented by vectors.
The state of a physical system is described by a state vector  that belongs to a complex Hilbert space. The superposition principle holds, meaning that if
that belongs to a complex Hilbert space. The superposition principle holds, meaning that if  are kets belonging to the Hilbert space, the linear combination
are kets belonging to the Hilbert space, the linear combination
is also a valid state that belongs to the Hilbert space. States are normalized to conform to the Born probability interpretation, meaning
If a state is formed from a superposition of other states, normalization implies that the squares of the expansion coefficients must add to 1:
Two-Level System Example: State Vectors
A quantum-bit or qubit is a quantum state that is the basic unit of information in a quantum computer. The state space is two-dimensional with orthonormal basis vectors  :
:
An arbitrary state  that belongs to this vector space can be written as a superposition of the basis states
that belongs to this vector space can be written as a superposition of the basis states
where α and β are generally complex numbers. Normalization of the state implies that
The Born rule tells us that the coefficients in the expansion are related to the probability of obtaining a given measurement as follows:
The probability that measurement finds the system in state  is
is
The probability that measurement finds the system in state  is
is
POSTULATE 2: Physical observables are represented by operators.
Physically measureable quantities like energy and momentum are known as observables. Mathematically, an observable is a Hermitian operator that acts on state vectors in the Hilbert space. The eigenvectors of Hermitian operators form an orthonormal basis of the state space for the system.
Two-Level System Example: The Pauli Operators
The Pauli operators X, Y, and Z correspond to the measurement of spin (intrinsic angular momentum of a particle) along the x, y, and z axes, respectively. They act on the basis states  as follows:
as follows:

We see that the basis states are eigenvectors of Z. Let’s remind ourselves how to construct the matrix representation of an operator.
REMINDER: The Matrix Representation of an Operator
In a discrete basis  , an operator is represented by a set of numbers
, an operator is represented by a set of numbers
These numbers are arranged into a square matrix such that Aij is the element at the ith row and jth column.
The matrix representation of the Pauli operators can be derived using the  basis (remember, we could equally well choose a different basis, giving a different matrix representation). In this basis we form the matrix representation of an operator A by calculating
basis (remember, we could equally well choose a different basis, giving a different matrix representation). In this basis we form the matrix representation of an operator A by calculating
The basis is orthonormal, and so

Using the action of the X operator described earlier, we find
A similar procedure applied to the other operators shows that
Writing an Operator in Terms of Outer Products
Consider two kets  and
and  . The quantity formed by their outer product
. The quantity formed by their outer product
is an operator. Any operator can be written in this fashion. In terms of some basis  , an operator A can be written as
, an operator A can be written as
Looking at the matrix representation of the Pauli X operator
we see that, with respect to the  basis, the operator can be written as
basis, the operator can be written as
A useful operator in quantum information theory is known as the Hadamard gate. This operator can be used to construct superposition states from {|0_, |1_}. In this basis the Hadamard gate has the representation
In outer product notation, the operator is written as

We can use this representation to quickly find the action of H on a state. For example,

We also have
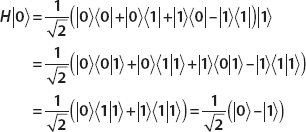
Using these results, we find that for an arbitrary state

An operator can be written in terms of projection operators formed by its own eigenvectors. This is called the spectral decomposition.
Spectral Decomposition
Suppose that an operator A has eigenvalues λi and eigenvectors  :
:
The spectral decomposition of operator A is a representation of the operator in terms of its eigenvalues and the projector
given by
Two-Level System Example: Spectral Decomposition of Z
A quick exercise shows that the eigenvectors of Z are  with eigenvalues ±1
with eigenvalues ±1
The spectral decomposition of Z is given by
POSTULATE 3: The possible results of a measurement are the eigenvalues of an operator.
The possible results of a measurement of a physical quantity are the eigenvalues of its corresponding operator.
Elementary particles such as electrons carry an intrinsic angular momentum called spin. Measurement of spin 1/2 along the x axis is represented by the Pauli operator
If spin is measured along the x axis, what are the possible results of measurement?
The possible results of measurement are found from the eigenvalues of the matrix. The characteristic polynomial is found from

This equation is satisfied by
Therefore the possible results of measurement of spin along the x axis are
According to the measurement postulate, these are the only values of measurement that will ever be found.
Projective Measurements
Projective measurements—the type encountered in standard quantum mechanics—deal with mutually exclusive measurement results. For example, we can ask if a particle is located at position x1 or position x2. Another example might be asking if a trapped electron has ground state energy E1 or excited state energy E2. Mutually exclusive measurement outcomes such as these are represented by orthogonal projection operators
The statement that two projection operators are orthogonal means that if i ≠ j, then
We can see this by using the spectral decomposition of some operator A:
The eigenvectors of a Hermitian operator are orthogonal, and in fact the practice is to normalize them. Assuming the eigenvectors are orthonormal, we have
Therefore if i ≠ j, we obtain PiPj = 0. However, if i = j, then
Two-Level System Example: Projection Operators
In the standard basis, there are two projection operators that correspond to measurements of +1 and −1:
The operator P0 projects any state onto  while P1 projects any state onto
while P1 projects any state onto 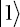 .
.
For some arbitrary state  , we have
, we have
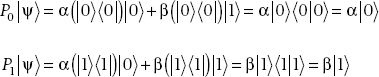
since  . Now we consider the sum of a set of projection operators.
. Now we consider the sum of a set of projection operators.
The Completeness Relation
The sum of the projection operators gives the identity
For the two-level system we have been studying, this means that
We can show this by calculating the matrix representations of the outer products

Suppose that an operator A has eigenvalues λi and eigenvectors  :
:
We can expand a state  in terms of the eigenvectors of A:
in terms of the eigenvectors of A:
The probability of obtaining measurement result λi, which is associated with eigenvector  , is given by the Born rule:
, is given by the Born rule:
Probability of finding 
Remember, the inner product is a complex number:
Since these are numbers, we can change their order and write the probability in terms of a projection operator:
A quantum system is in the state
where the 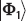 constitute an orthonormal basis. These states are eigenvectors of the Hamiltonian operator such that
constitute an orthonormal basis. These states are eigenvectors of the Hamiltonian operator such that
(a) Is  normalized?
normalized?
(b) If the energy is measured, what are the probabilities of obtaining E, 2E, and 3E ?
(a) The bra that corresponds to the state is given by
Therefore the norm of the state is found to be

Notice that we have used the fact that the basis is orthonormal, and so
Since 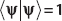 we conclude the state is normalized.
we conclude the state is normalized.
(b) To find the probability of obtaining each measurement, we use the Born rule. We have
The Born rule tells us that the probability of obtaining measurement result E is

For the next eigenvector, we find
The Born rule tells us that the probability of obtaining measurement result 2E is

Finally, we have
The Born rule tells us that the probability of finding 3E upon measurement is
Although we have already verified that the state is normalized, it is always a good idea to sum the probabilities and verify that they sum to 1, as they do in this case:
An orthonormal basis of a Hamiltonian operator in four dimensions is defined as follows:
A system is in the state
(a) If a measurement of the energy is made, what results can be found and with what probabilities?
(b) Find the average energy of the system.
First we check to see if the state is normalized. We have
Therefore it is necessary to normalize the state. The normalized state is found by dividing by  . Calling the normalized state
. Calling the normalized state  , we obtain
, we obtain
Since the state is expanded in the eigenbasis of the Hamiltonian, the only possible values of measurement are the eigenvalues of the Hamiltonian, which have been given to us as (E, 2E, 3E, 4E). The probabilities of obtaining each measurement are found by application of the Born rule, squaring the coefficients for the normalized state.
(a) The probability of obtaining E is
The probability of obtaining 2E is
The probability of obtaining 3E is
The probability of finding 4E is
A quick check shows these probabilities add to 1:
(b) We can find the average energy from
where p(Ei) is the probability of obtaining measurement result Ei. We find that the average energy is
Aside on Degeneracy
Suppose that an operator A has degenerate eigenvalues corresponding to eigenvectors
Where each of these eigenvectors corresponds to the same eigenvector

This set of eigenvectors constitutes a subspace of the vector space ε. In the case of degeneracy, the probability of obtaining measurement result λm is found by summing over the inner products of all the eigenvectors that belong to this subspace:
Probability of finding 

POSTULATE 4: The state of a system after measurement.
The reader who studies quantum theory more extensively will find that not all measurements can be described as projective measurements, as we have done here. Nonetheless, in a first exposure to quantum theory it is good to restrict our attention to measurements of this type. We consider the nondegenerate case first. Immediately after a measurement, the state of the system is given by the eigenvector corresponding to the eigenvalue that has been measured. If the state of the system is given by
then suppose a measurement is made and the result λi is obtained. The state of the system immediately after measurement is
In terms of projection operators, the state of the system after measurement is
Two-Level System Example: State of the System after Measurement
Recalling the projection operators for the two-state system
and the action on a state  that we found to be
that we found to be

the state after measurement is found by dividing these quantities by  . We have
. We have
and
Therefore, if measurement result +1 is obtained, the state of the system after measurement is
and if −1 is obtained, it is
Suppose a Hamiltonian operator has a basis 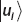 such that
such that

The system is in the state
(a) Write the Hamiltonian operator in outer product notation.
(b) Write the projection operator P that projects a state onto the subspace spanned by  .
.
(c) The energy is measured. What values can be found, and with what probabilities?
(d) Suppose the energy is measured and found to be E. What is the state of the system after measurement?
(a) Using the spectral decomposition of H, we find
(b) The projection operator for the subspace spanned by  is found by summing over the individual projection operators for each state:
is found by summing over the individual projection operators for each state:
(c) The reader should verify that the state is normalized. The possible results of measurement are E, 2E, and 4E, corresponding to eigenvectors  , and
, and  , respectively. To calculate the probability of obtaining the measurement result E, which is degenerate, we use
, respectively. To calculate the probability of obtaining the measurement result E, which is degenerate, we use
The other probabilities are for nondegenerate eigenvalues and can be calculated immediately by using the Born rule:

(d) If the energy is measured and is found to be E, the state after measurement is
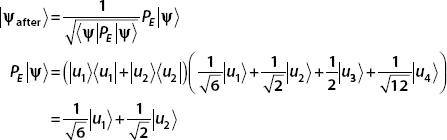
It is easy to show that
and so we have

Therefore, the state after measurement is

Note: The state of the system cannot be further distinguished; with the information given there is nothing we can do to distinguish 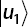 from
from  .
.
POSTULATE 5: The time evolution of a quantum system is governed by the Schrödinger equation.
The Schrödinger equation determines how a quantum system changes with time according to
where H is the Hamiltonian and t0 is some initial time. For an isolated system the Hamiltonian is independent of time. The equation can be integrated in that case, giving
The exponential term defines a time evolution operator, which we denote by U because this operator is unitary:
The infinitesimal operator is found by expanding I in a Taylor series and keeping the first two terms:
Completely Specifying a State with a CSCO
In a previous example, we found that when two energy eigenstates had the same eigenvalue E, and a measurement result turned out to be E, then the state of the system after measurement was
There was no way to distinguish between the states  . There are many situations like this that can arise. However, many eigenfunctions of one operator with degenerate eigenvalues turn out to be eigenfunctions of another operator with eigenvalues that can be used to distinguish the states. For example, free particle energy states have degenerate energy eigenvalues, but can be distinguished by momentum ±p. So, to completely distinguish the state, the energy E is not enough; we must also specify a momentum of +p or −p. This notion is formalized by the idea of a CSCO. A CSCO is a complete set of commuting observables and is the minimum set of operators required to completely specify a state. Two or more operators that commute can be simultaneously measured. Suppose that
. There are many situations like this that can arise. However, many eigenfunctions of one operator with degenerate eigenvalues turn out to be eigenfunctions of another operator with eigenvalues that can be used to distinguish the states. For example, free particle energy states have degenerate energy eigenvalues, but can be distinguished by momentum ±p. So, to completely distinguish the state, the energy E is not enough; we must also specify a momentum of +p or −p. This notion is formalized by the idea of a CSCO. A CSCO is a complete set of commuting observables and is the minimum set of operators required to completely specify a state. Two or more operators that commute can be simultaneously measured. Suppose that
Now notice what happens when we apply the product AB to the state
and the application of BA gives
and so
Since the state  , we must have
, we must have
Now suppose that a state 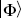 is also an eigenstate of A with the same eigenvalue a, so that this eigenvalue is degenerate. Then a measurement of A cannot distinguish the states. However, if
is also an eigenstate of A with the same eigenvalue a, so that this eigenvalue is degenerate. Then a measurement of A cannot distinguish the states. However, if 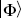 is also an eigenvector of B such that
is also an eigenvector of B such that
then we can distinguish the states by measuring B. In this example, A and B form a CSCO. What if the eigenvalues of B are also degenerate? Then we must find an operator C that commutes with both A and B, but has eigenvalues such that the states can be distinguished. If it turns out that no such set of operators can be found, then the states are physically indistinguishable.
The Heisenberg versus Schrödinger Pictures
In the Schrödinger picture, the time evolution of the system is contained in the state. However, since the physical predictions of quantum mechanics are determined by inner products, the time evolution can be moved from states to operators:
We can then describe time evolution in terms of evolving the operator forward in time according to
The governing equation for time evolution is given by
where H is the system’s Hamiltonian.
Describing Composite Systems in Quantum Mechanics
Sometimes it is necessary to describe a system that is composed of multiple particles, each particle being a system in its own right described by a vector space. A mathematical technique called the tensor product allows us to bring vector spaces that describe individual systems together into a larger vector space. The tensor product between vector spaces V and W is denoted by writing  .
.
Dimension of a Vector Space Formed by a Tensor Product
If V is a vector space of dimension p and W is a vector space of dimension q, then the vector space
has dimension pq.
Let  be two vectors. Then the vector
be two vectors. Then the vector  . Alternative shorthand notations for the vector
. Alternative shorthand notations for the vector  include
include 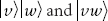 .
.
If A is an operator that acts on the vector space V and B is an operator that acts on the vector space W, then the operator formed by the tensor product given by
acts on vectors  in the following way:
in the following way:
We now consider the norm of a state that belongs to  . Suppose that
. Suppose that
Then the norm is
The Matrix Representation of a Tensor Product
Let A be an m × n matrix and B be a p × q matrix. The tensor product  is a matrix with mp rows and nq columns. The elements of this matrix are constructed by the submatrices
is a matrix with mp rows and nq columns. The elements of this matrix are constructed by the submatrices
that is, multiply B by each component of A and then arrange these submatrices into a larger matrix. The entire matrix representing the tensor product is

A column vector in two dimensions has two rows and one column. Since the tensor product between an m × n matrix and a p × q matrix has mp rows and nq columns, the tensor product between two 2 × 1 column vectors has 2 × 2 = 4 rows and 1 × 1 = 1 column. The way to compute this is
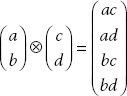
Now consider the tensor product of two 2 × 2 matrices. This tensor product will be a matrix with 2 × 2 = 4 rows and 2 × 2 = 4 columns. If we let
then the tensor product of these two matrices is

Consider the two Pauli matrices Y and Z. Compute the tensor product  .
.
Recalling that
we have

The Tensor Product of State Vectors
We can use the tensor product to compute the tensor product of a state with itself n times. This is represented by the notation
Let
where  . Find
. Find  .
.
It is helpful to write the state as a column vector:

So we obtain

The tensor product

Consider a composite system of qubits. The first qubit is denoted by A and the second by B. The spin-singlet state is formed from a linear superposition:
The operator XA applies the X operator only to states belonging to subsystem A. Suppose that the operator XA acts on the state. What is the resulting state of the system?
The operator X is
and it acts as follows:
Therefore, when XA acts on the composite state, we find

Suppose that a two-qubit system is in the state
Find 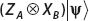 .
.
Recalling that 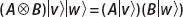 , we have
, we have

and so

The Density Operator
So far our studies of quantum systems have involved the examination of a single state. This state can be expanded in terms of basis kets:
Such an expansion is referred to as a coherent superposition of the  states. The task has been to find out what the possible measurement results are on the system and to calculate the probability of obtaining each possible result.
states. The task has been to find out what the possible measurement results are on the system and to calculate the probability of obtaining each possible result.
Now consider an ensemble of quantum states that is prepared as a classical statistical mixture. The members of the ensemble are the states  , and the probability of finding each state is given by p1, p2, . . . , pn. We can describe this type of mixture of states with a density operator, which is usually represented by the symbol ρ.
, and the probability of finding each state is given by p1, p2, . . . , pn. We can describe this type of mixture of states with a density operator, which is usually represented by the symbol ρ.
The density operator representing a collection of states  is
is
If the state of a system is known exactly, we say it is a pure state. This is a state where a single pi = 1 and all others are zero. This means that the density operator for a pure state  can be written as
can be written as
This is a projection operator, so in the case of a pure state, the density operator satisfies ρ2 = ρ. A mixed state is a collection of different pure states, each occurring with a given probability.
Properties of the Density Operator
• The density operator is Hermitian, ρ = ρ†.
• The trace of any density matrix is equal to 1: Tr(ρ) = 1.
• For a pure state, since ρ2 = ρ, Tr(ρ2) = 1.
• For a mixed state Tr(ρ2) < 1.
• The eigenvalues of a density operator satisfy 0 ≤ λi ≤ 1.
• The expectation value of an operator A can be calculated using  .
.
We can use a density operator to make all the physical predictions of quantum mechanics. Let a measurement result m be represented by a projection operator 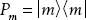 . The probability of obtaining measurement result m is
. The probability of obtaining measurement result m is
Density operators can be represented by matrices. The off-diagonal elements of a density matrix represent the ability of the system to exhibit quantum interference. Consider, once again, a state formed by a superposition:
This type of state is a pure state. In this case the density operator is found from the outer product
It is not too hard to show that this is
We see that the density operator for this pure state can be split into two parts. The terms in the first part tell us
which is the probability of finding the system in state 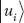 .
.
To determine the meaning of the second part of the density operator, given by the sum
first recall that the expansion coefficients are complex numbers. We can write any complex number in polar form, that is, z = reiΦ;. In this case we have
So, with respect to the second summation, we have
The phase difference in the exponential expresses the coherence or capability of terms in the state to interfere with one another. This is a characteristic of a pure quantum state, and these terms are represented by off-diagonal elements in the density matrix. Mixed states are classical statistical mixtures and therefore have no terms of this form.
The off-diagonal elements of a mixed state will be zero, while those of a pure state—a state with coherences—will be nonzero. Note, however, that the presence of the off-diagonal terms is basis-dependent. Always check purity by computing the trace Tr(ρ2).
A completely mixed state is one for which the probability of each state is equal to all others. For example,
is a completely mixed state with a 50% probability of finding the system in state  .
.
The Density Operator for a Completely Mixed State
In an n-dimensional Hilbert space, the density operator can be expressed in terms of the identity matrix, and
A completely mixed state represents one extreme possibility—a statistical mixture with no interference terms. A pure state represents the other extreme—a quantum state in a coherent superposition. A measure of purity can be expressed by computing the trace of ρ2 and setting it in between these bounds:
A state that falls in this range without being pure Tr(ρ2) = 1 or completely mixed for which
is called partially coherent. Testing purity by checking the trace of the square of the density matrix is a basis-independent concept, unlike the values of the off-diagonal elements of the matrix, which depend on the basis you choose to express the density operator.
In this example we compare pure versus mixed states for a three-dimensional quantum system. We consider two orthonormal bases
The second basis can be expressed in terms of the first, using the relations

Now consider the pure state
The state  is a coherent superposition of states
is a coherent superposition of states  . Notice that in this state the probabilities of finding states
. Notice that in this state the probabilities of finding states  are
are
The state  is pure because if we make a measurement in the
is pure because if we make a measurement in the 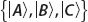 basis, the probabilities of obtaining each measurement result are
basis, the probabilities of obtaining each measurement result are
Now, using the expansion of  in the {
in the { } basis, we can write the density operator
} basis, we can write the density operator  as
as

Now we consider another state, a state that is a statistical mixture of the  states. Let
states. Let
Recalling that a density operator is a summation of the form
where pi is the probability of finding state  , we see that in the state qm the probabilities of finding each of the states are
, we see that in the state qm the probabilities of finding each of the states are

These are the same probabilities we found for the state  , and so this seems to describe the same state. However, what are the probabilities of finding the system in the states
, and so this seems to describe the same state. However, what are the probabilities of finding the system in the states 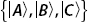 when the system is in the state described by ρm? We can answer this question by considering the projection operators
when the system is in the state described by ρm? We can answer this question by considering the projection operators  ,
, 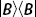 , and
, and  and using
and using  . The probability of finding
. The probability of finding  when the system is described by ρm is
when the system is described by ρm is
Now

and so
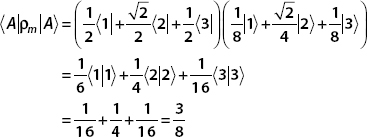
This is quite different from the pure state where we found prob 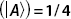 . A similar procedure using the expansion of the state
. A similar procedure using the expansion of the state  in the
in the  basis shows that the probability of finding
basis shows that the probability of finding  in the state ρm is
in the state ρm is
This is certainly different from what we found for ρA, where the probability was zero. In conclusion, the predictions of ρm are identical to those of ρA for measurements in the  , basis, but they are quite different for the
, basis, but they are quite different for the  basis.
basis.
Now let’s consider the matrix representations of these density operators in the  basis. We have
basis. We have

Notice that
as it should for a density matrix.
An exercise shows that the density operator representing ρA in this basis is

Notice that the mixed state has zero off-diagonal elements and the pure state has nonzero off-diagonal elements. While this is a characteristic property, it depends on the basis chosen to represent the density operator (try writing the matrix for ρA in the  basis). We also have
basis). We also have
Now consider the square of this matrix. A calculation shows

telling us that this is a pure state. Now consider

Therefore, this density operator represents a mixed state (as we knew already). Recalling that the dimension n = 3 of this Hilbert space, the completely mixed state would be represented by the density operator
The matrix representation in this basis is

We see that
and so
This is the completely mixed state for three dimensions. And so we have the bounds
where ρA is a pure state. The state ρm is a partially coherent state.
We work in a two-dimensional vector space with basis  . Consider an ensemble of systems prepared in the following way. We have two quantum states
. Consider an ensemble of systems prepared in the following way. We have two quantum states
In the preparation of the ensemble, three-fourths of the states are prepared in state  and one-fourth of the states are prepared in state
and one-fourth of the states are prepared in state  .
.
(a) Write down the density operator for each individual pure state  and
and  .
.
(b) Write down the density operator for the ensemble.
(c) Express the density operator as a matrix with respect to the  basis.
basis.
(d) Compute the trace.
(e) If a particle is drawn from the ensemble and a measurement is performed, what is the probability it is found in state 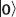 ? What is the probability it is found in state
? What is the probability it is found in state  ?
?
(f) Suppose there is another measurement with basis states  . A particle is drawn from the ensemble, and a measurement is made in this basis. What is the probability of finding
. A particle is drawn from the ensemble, and a measurement is made in this basis. What is the probability of finding  and what is the probability of finding
and what is the probability of finding  ?
?
(a) The density operators for each pure state are

(b) The density operator for the ensemble can be found from the formula
We are told that three-fourths of the systems are prepared in state  and one-fourth of the systems are prepared in state
and one-fourth of the systems are prepared in state  . Therefore in this case we have
. Therefore in this case we have
Now

Adding these terms gives

(c) The matrix that represents this density operator in the  basis is
basis is

(d) We find the trace by summing the diagonal elements
as it should be for a density matrix.
(e) The probabilities that a particle drawn is found in the state 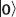 or the state
or the state  are found from the elements along the diagonal of the matrix. The probability the particle is found to be in state
are found from the elements along the diagonal of the matrix. The probability the particle is found to be in state 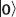 is 63/80 = 0.79. The probability the particle is found to be in state
is 63/80 = 0.79. The probability the particle is found to be in state  is 17/80 = 0.21.
is 17/80 = 0.21.
(f) We can find the probability that a particle is found in the state  by calculating
by calculating  . The column vector representation of
. The column vector representation of  is
is
We can calculate the probability using matrix multiplication:
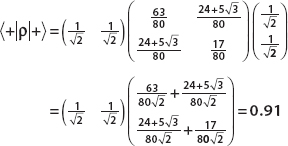
The probability that the particle is found in the state 
 is
is

A density matrix is given by
In quantum information theory, a measurement of information content is given by the entropy. The entropy is given by
where the λi, are the eigenvalues of the density matrix and the log is to base 2. Higher entropy means greater disorder (and less information) in a system. Find the entropy for the system described by this density matrix.
The eigenvalues of this matrix are {0.933, 0.067}. The entropy is
S = −0.933log(0.933) − 0.067log(0.067) = 0.25
The maximum entropy for the basic unit of quantum information theory, a qubit, is S = 1.
Suppose the density matrix for some system is
(a) Show that this is a mixed state.
(b) Find  for this state.
for this state.
(a) We calculate the square of the matrix
The trace is
Therefore this is a mixed state.
(b) We calculate the matrix product
The expectation value can be found from
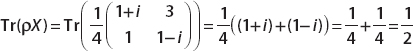
For Z we have
and the expectation value is given by
A Brief Introduction to the Bloch Vector
For a two-level system, we can write the density operator in the following form:
The vector  is called the Bloch vector. We can use the Bloch vector to determine if a state is a pure state or a mixed state.
is called the Bloch vector. We can use the Bloch vector to determine if a state is a pure state or a mixed state.
The magnitude of the Bloch vector is less than or equal to 1 (with equality only for a pure state):
The components of the Bloch vector are calculated from
where X, Y, Z are the Pauli operators.
A density operator for some system is given by
(a) Find the components of the Bloch vector.
(b) Is this state mixed or pure?
(c) A measurement of spin is made in the z direction. What is the probability that the measurement result is spin-down? What is the probability that the measurement is spin-up?
(a) The components of the Bloch vector are

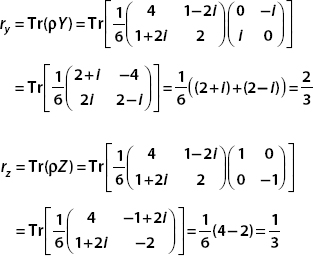
(b) The magnitude of the Bloch vector is
Since the magnitude is less than 1, this density operator represents a mixed state.
(c) The probability of obtaining a given result is given by Tr(ρP), where P is a projection operator corresponding to the given measurement. The projection operator for spin-down is

The probability is found from the trace, which is
For spin-up, the projection operator is
The product of the matrices is
and so the probability of finding spin-up for this state is
Summary
In this chapter we learned the fundamental postulates of quantum mechanics and how to apply them using a two-state system. We also learned the modern concepts of the density operator which is important in many applications such as quantum computing.
QUIZ
1. Using matrix representation, show that the Hadamard matrix
produces superposition states out of
2. For the system described by the density matrix

show that  .
.
3. These basis states are given:
A. Verify that the new basis is orthonormal. Write down the density operator for each state, and then derive the density matrices.
B. Suppose that an ensemble of systems is prepared with 50% of the systems in state  and 50% of the systems in state
and 50% of the systems in state  . Write down the density operator that describes this state.
. Write down the density operator that describes this state.
C. For each density matrix in this problem, is the state pure or mixed? In each state, what is the probability of finding  ?
?
4. The density matrix for a given state is
A. Is this a pure state?
B. Show that the components of the Bloch vector are  . What can you learn about the purity of the state from the Bloch vector?
. What can you learn about the purity of the state from the Bloch vector?
C. If the Z operator is measured, show that the probability of finding  is
is  .
.
5. Consider an orthonormal basis  . The Hamiltonian acts on this basis as
. The Hamiltonian acts on this basis as
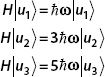
A system is in the state  .
.
A. Write down the bra that corresponds to the state  .
.
B. Find A so that the state is normalized.
C. Write down the outer product and matrix representations of the Hamiltonian.
D. Write  as a column vector.
as a column vector.
E. Using the Born rule, find the probabilities of obtaining each of the possible measurement results when the energy is measured.
F. Find the average energy for this system.
G. How does this state evolve in time?
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
