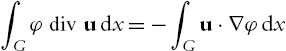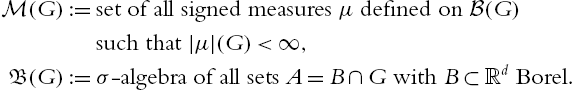Function spaces
A.1 Function spaces involving the divergence
Given a Young function A, denote by HA(G)![]() the Banach space of those vector-valued functions u:G→Rn
the Banach space of those vector-valued functions u:G→Rn![]() such that the norm
such that the norm
‖u‖HA(G)=‖u‖LA(G,Rn)+‖divu‖LA(G)
is finite. We also denote by HA0(G)![]() its subspace of those functions u∈HA(G)
its subspace of those functions u∈HA(G)![]() whose normal component on ∂G vanishes, in the sense that
whose normal component on ∂G vanishes, in the sense that
∫Gφdivudx=−∫Gu⋅∇φdx
for every φ∈C∞(‾G)![]() . It is easy to see that both HA(G)
. It is easy to see that both HA(G)![]() and HA0(G)
and HA0(G)![]() are Banach spaces. We are interested in some smooth approximation theorems.
are Banach spaces. We are interested in some smooth approximation theorems.
A.2 Function spaces involving symmetric gradients
We start with a survey about the space BD(G)![]() containing all functions of bounded deformation introduced by Suquet [136] and by Matthies, Strang, Christiansen [110]. The class BD(G)
containing all functions of bounded deformation introduced by Suquet [136] and by Matthies, Strang, Christiansen [110]. The class BD(G)![]() has been widely considered in the literature in connection with problems from plasticity, we refer to the works of Anzellotti and Giaquinta [11], Teman and Strang [135] and Teman [138]. The space BD(G)
has been widely considered in the literature in connection with problems from plasticity, we refer to the works of Anzellotti and Giaquinta [11], Teman and Strang [135] and Teman [138]. The space BD(G)![]() is defined as the set of L1
is defined as the set of L1![]() -functions u with
-functions u with
supη∈C10(G,Rd×dsym),‖η‖∞=1∫Gu⋅divηdx<∞.
By Riesz' representation Theorem it can be shown u∈L1(G)![]() belongs to BD(G)
belongs to BD(G)![]() if and only if ε(u)
if and only if ε(u)![]() generates a bounded Radon measure on G. This means every component of ε(u)
generates a bounded Radon measure on G. This means every component of ε(u)![]() belongs to the class
belongs to the class
M(G):=set of all signed measures μ defined on B(G)such that |μ|(G)<∞,B(G):=σ-algebra of all sets A=B∩G with B⊂Rd Borel.
If u∈BD(G)![]() then there is μ=(μij)di,j=1
then there is μ=(μij)di,j=1![]() with μij∈M(G)
with μij∈M(G)![]() for i,j=1,...,d
for i,j=1,...,d![]() such that the distributions
such that the distributions
C∞0(G)∋φ↦〈εij(u),φ〉=−12∫G(ui∂jφ+uj∂iφ)dx
can be represented as
〈εij(u),φ〉=∫Gφdμij
and we have
|μij|(A)=|εij(u)|(A)=supφ∈C∞0(A),‖φ‖∞=1〈εij(u),φ〉,|μ|(A)=|ε(u)|(A)=(d∑i,j=1|εij(u)|2(A))12,
for all A∈B(G)![]() . The space BD(G)
. The space BD(G)![]() is a Banach space equipped with the norm
is a Banach space equipped with the norm
‖u‖BD(G):=‖u‖L1(G)+|ε(u)|(G),
where |ε(u)|(G)![]() is the total variation of the matrix valued measure ε(u)
is the total variation of the matrix valued measure ε(u)![]() . From the above references we deduce the following basic properties of BD(G)
. From the above references we deduce the following basic properties of BD(G)![]() .
.
Having in mind the results about the space BD(G)![]() we introduce the space (this part presents results from [33])
we introduce the space (this part presents results from [33])
Eh(G):={u∈L1(G):∫Gh(|ε(u)|)dx<∞},h(t)=tln(1+t),‖u‖Eh(G):=‖u‖L1(G)+‖ε(u)‖Lh(G).
Note that we can similarly introduce spaces EA(G)![]() with an arbitrary N-function A. We will use the notation Ep(G)
with an arbitrary N-function A. We will use the notation Ep(G)![]() for the space of functions with symmetric gradients in Lp(G)
for the space of functions with symmetric gradients in Lp(G)![]() , 1⩽p⩽∞
, 1⩽p⩽∞![]() . From (A.2.5) it follows that on the subspace BD(Ω)∩{u:u|∂Ω=0}
. From (A.2.5) it follows that on the subspace BD(Ω)∩{u:u|∂Ω=0}![]() the BD-norm defined in (A.2.4) can be replaced by the equivalent norm |ε(⋅)|(G)
the BD-norm defined in (A.2.4) can be replaced by the equivalent norm |ε(⋅)|(G)![]() . We observe that (cf. [77], Lemma 4.1.6)
. We observe that (cf. [77], Lemma 4.1.6)
Eh0(G):=‾C∞0(G)Eh(G)={u∈Eh(G):u|∂G=0},Eh0(G):=‾C∞0,div(G)Eh(G)={u∈Eh0(G):divu=0},
where u|∂Ω![]() has to be understood in the BD-trace sense. We therefore have inequality (A.2.5) for functions u∈Eh0(Ω)
has to be understood in the BD-trace sense. We therefore have inequality (A.2.5) for functions u∈Eh0(Ω)![]() , which means that
, which means that
‖u‖Eh0(G):=‖ε(u)‖Lh(G)
is a norm equivalent to ‖⋅‖E1,h(G)![]() on the class Eh0(G)
on the class Eh0(G)![]() .
.
From Korn's inequality (see Theorem 2.3.11) it follows that Eh0(G)↪W1,10(G)![]() .
.
Another consequence of Korn's inequality is:
Now we can prove the main result of this section:
In the setting of Prandtl–Eyring fluids we have to work in the space Eh0,div(G)![]() which according to Lemma 4.1.6 in [77] is the closure of C∞0,div(G)
which according to Lemma 4.1.6 in [77] is the closure of C∞0,div(G)![]() in the class Eh(G)
in the class Eh(G)![]() w.r.t. the norm ‖⋅‖Eh(G)
w.r.t. the norm ‖⋅‖Eh(G)![]() . From Theorem A.2.47 it follows
. From Theorem A.2.47 it follows