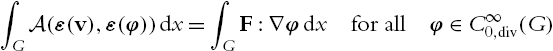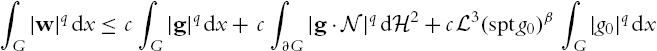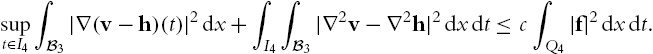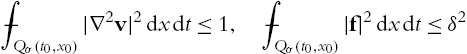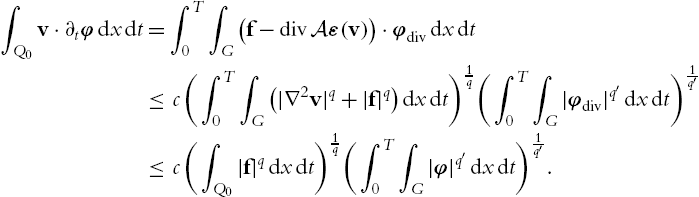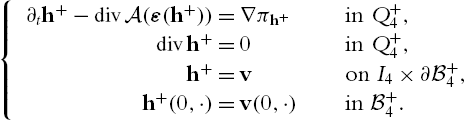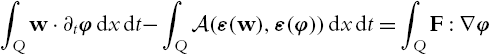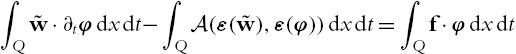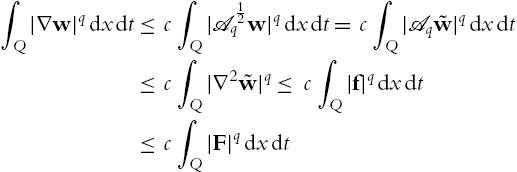Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Appendix B

The $A$ -Stokes system

The aim of this section is to present regularity results for the (non-stationary) $A$ -Stokes system depending on the right hand side (in divergence form). Let us fix for this section a bounded domain $G \subset R^{3}$ with $C^{2}$ -boundary and a time interval $(0, T)$ . Moreover, let $A : R^{3 \times 3} \to R^{3 \times 3}$ be an elliptic tensor.

B.1 The stationary problem

The $A$ -Stokes problem (in the pressure-free formulation) with right hand side $f \in L^{1} (G)$ reads as: find $v \in {LD}_{0, div} (G)$ such that

$\int_{G} A (ε (v), ε (φ)) d x = \int_{G} f \cdot φ d x for all φ \in C_{0, div}^{\infty} (G) .$

(B.1.1)

The right hand side can also be given in divergence form, i.e.

$\int_{G} A (ε (v), ε (φ)) d x = \int_{G} F : \nabla φ d x for all φ \in C_{0, div}^{\infty} (G)$

(B.1.2)

for $F \in L^{1} (G)$ . For certain purposes it is convenient to discuss the problem with a fixed divergence. To be precise for $g \in L_{⊥}^{1} (G)$ we are seeking for a function $v \in {LD}_{0} (G)$ with $div v = g$ satisfying (B.1.1) or (B.1.2). We have the following $L^{q}$ -estimates.

Lemma B.1.1

Let $G \subset R^{3}$ be a bounded $C^{2}$ -domain and $1 < q < \infty$ .

a) Let $f \in L^{q} (G)$ and $g \in W^{1, q} (G)$ with $\int_{G} g d x = 0$ . Then there is a unique solution $w \in W^{2, q} \cap W_{0}^{1, q} (G)$ to (B.1.1) such that $div v = g$ and

$\underset{B}{⨍} | \nabla^{2} w |^{q} d x ⩽ c \underset{G}{⨍} | f |^{q} d x + c \underset{G}{⨍} | \nabla g |^{q} d x,$

where c only depends on $A$ and q.

b) Let $F \in L^{q} (G)$ and $g \in L_{0}^{q} (G)$ . Then there is a unique solution $w \in W_{0}^{1, q} (G)$ to (B.1.2) such that $div v = g$ and

$\underset{G}{⨍} | \nabla w |^{q} d x ⩽ c \underset{G}{⨍} | F |^{q} d x + c \underset{G}{⨍} | g |^{q} d x,$

where c only depends on $A$ and q.

In case $A = I$ both parts follow from [10], Thm. 4.1. However, the main tool in [10] is the theory from [6,7] where very general linear systems are investigated. Hence it is clear that the results also hold in case of an arbitrary elliptic tensor $A$ .

Corollary B.1.1

Let the assumptions of Lemma B.1.1 be satisfied. Assume further that $f = 0$ and

$g = div g + g_{0}$

(B.1.3)

with $g \in W^{1, q} (G)$ and $g_{0} \in L_{0}^{q} (G)$ with $spt g_{0} ⋐ G$ . Then we have

$\int_{G} | w |^{q} d x ⩽ c \int_{G} | g |^{q} d x + c \int_{\partial G} | g \cdot N |^{q} d H^{2} + c L^{3} {(spt g_{0})}^{β} \int_{G} | g_{0} |^{q} d x$

for some $β > 0$ .

Proof

We follow the lines of [133, Thm. 2.4]. Let $ψ \in L^{q^{'}} (G)$ be arbitrary. In accordance to Lemma B.1.1 a) there is a unique solution $u \in W^{2, q^{'}} \cap W_{0, div}^{1, q^{'}} (G)$ to the $A$ -Stokes problem with right-hand-side ψ such that

$\int_{G} | \nabla^{2} u |^{q^{'}} d x ⩽ c \int_{G} | ψ |^{q^{'}} d x .$

By De Rahm's theorem there is a unique $ϑ \in L_{⊥}^{q^{'}} (G)$ such that

$\int_{G} A (ε (u), ε (φ)) d x = \int_{G} ϑ div φ + \int_{G} ψ \cdot φ d x for all φ \in W_{0}^{1, q} (G) .$

We can conclude that $ϑ \in W^{1, q^{'}} (G)$ with

$\underset{G}{⨍} | \nabla ϑ |^{q^{'}} d x ⩽ c (\underset{G}{⨍} | \nabla^{2} u |^{q^{'}} d x + \underset{G}{⨍} | ψ |^{q^{'}} d x) ⩽ c \underset{G}{⨍} | ψ |^{q^{'}} d x .$

(B.1.4)

We proceed by

$\begin{matrix} \int_{G} w \cdot ψ d x & = \int_{G} A (ε (u), ε (w)) d x - \int_{G} ϑ div w d x = - \int_{G} ϑ div w d x \\ = - \int_{G} ϑ div g d x - \int_{G} g_{0} ϑ d x \\ = \int_{G} \nabla ϑ \cdot g d x - \int_{\partial G} g \cdot N ϑ d H^{2} - \int_{G} g_{0} ϑ d x . \end{matrix}$

We finish the proof by estimating this integrals separately using (B.1.4). For the first one we obtain

$\begin{matrix} | \int_{G} \nabla ϑ \cdot g d x | & ⩽ {(\int_{G} | \nabla ϑ |^{q^{'}} d x)}^{\frac{1}{q^{'}}} {(\int_{G} | g |^{q} d x)}^{\frac{1}{q}} \\ ⩽ {(\int_{G} | ψ |^{q^{'}} d x)}^{\frac{1}{q^{'}}} {(\int_{G} | g |^{q} d x)}^{\frac{1}{q}} . \end{matrix}$

Similarly, we estimate using the trace theorem

$\begin{matrix} | \int_{\partial G} ϑ g \cdot N d H^{2} | & ⩽ {(\int_{\partial G} | ϑ |^{q^{'}} d H^{2})}^{\frac{1}{q^{'}}} {(\int_{\partial G} | g \cdot N |^{q} d H^{2})}^{\frac{1}{q}} \\ ⩽ {(\int_{G} | \nabla ϑ |^{q^{'}} d x)}^{\frac{1}{q^{'}}} {(\int_{\partial G} | g \cdot N |^{q} d H^{2})}^{\frac{1}{q}} \\ ⩽ {(\int_{G} | ψ |^{q^{'}} d x)}^{\frac{1}{q^{'}}} {(\int_{\partial G} | g \cdot N |^{q} d H^{2})}^{\frac{1}{q}} . \end{matrix}$

In case $q^{'} < 3$ we obtain for the third integral

$\begin{matrix} | \int_{G} g_{0} ϑ d x | & ⩽ {(\int_{G} | ϑ |^{\frac{3 q^{'}}{3 - q^{'}}} d x)}^{\frac{3 - q^{'}}{d q^{'}}} {(\int_{G} | g_{0} |^{\frac{3 q^{'}}{4 q^{'} - 3}} d x)}^{\frac{4 q^{'} - 3}{3 q^{'}}} \\ ⩽ {(\int_{G} | \nabla ϑ |^{q^{'}} d x)}^{q^{'}} L^{3} {(spt g_{0})}^{β} {(\int_{G} | g_{0} |^{q} d x)}^{\frac{1}{q}} \\ ⩽ {(\int_{G} | ψ |^{q^{'}} d x)}^{\frac{1}{q^{'}}} L^{3} {(spt g_{0})}^{β} {(\int_{G} | g_{0} |^{q} d x)}^{\frac{1}{q}}, \end{matrix}$

where $β = \frac{1}{3}$ . If $q^{'} ⩾ 3$ we can modify the proof by replacing $\frac{3 q^{'}}{3 - q^{'}}$ with an arbitrary number $r > q^{'}$ and choose $β = 3 r^{'}$ . As ψ is arbitrary, the claim follows. □

B.2 The non-stationary problem

Now we turn to the parabolic problem and the first result is a local $L^{q}$ -estimate for weak solutions. In case of the $A$ -heat system this follows from the continuity of the corresponding semigroup (see [132]). It is also known for the non-stationary Stokes-system (see [133] and [88]) but not in our setting.

Theorem B.2.48

Let $f \in L^{q} (Q_{0})$ for some $q > 2$ , where $Q_{0} : = (0, T) \times R^{3}$ and let $v \in L^{2} ((0, T); W_{0, div}^{1, 2} (R^{3}))$ be the unique weak solution to

$\int_{Q_{0}} v \cdot \partial_{t} φ d x d t - \int_{Q_{0}} A (ε (v), ε (φ)) d x = \int_{Q_{0}} f \cdot φ d x d t$

(B.2.5)

for all $φ \in C_{0, div}^{\infty} ([0, T) \times R^{3})$ . Then we have $\nabla^{2} v \in L_{l o c}^{q} (Q_{0})$ and there holds

$\int_{0}^{T} \int_{B} | \nabla^{2} v |^{q} d x d t ⩽ c_{B} \int_{Q_{0}} | f |^{q} d x d t$

for all balls $B \subset R^{3}$ .

Proof

The main ingredient is the proof of the following auxiliary result which has been used in a similar version in [42].

i) We start with interior estimates. Let

$Q_{r} : = Q_{r} (x_{0}, t_{0}) : = (t_{0} - r^{2}, t_{0} + r^{2}) \times B_{r} (x_{0})$

be a parabolic cylinder such that $4 Q_{r} \subset Q_{0}$ . We claim the following: There is a constant $N_{1} > 0$ such that for every $ε > 0$ there is $δ = δ (ε) > 0$ such that (since $f \in L^{2} (0, T; L_{l o c}^{2} (R^{3}))$ the standard interior regularity theory implies $\nabla^{2} v \in L^{2} (0, T; L_{l o c}^{2} (R^{3}))$ and $\partial_{t} v \in L^{2} (0, T; L_{l o c}^{2} (R^{3}))$ )

$\begin{matrix} L^{4} (Q_{r} \cap {M {(| f |)}^{2} > N_{1}^{2}}) ⩾ ε L^{4} (Q_{r}) \\ \Rightarrow & Q_{r} \subset {M (| \nabla^{2} v |^{2}) > 1} \cup {M (| f |^{2}) > δ^{2}} . \end{matrix}$

(B.2.6)

Let us assume for simplicity that $r = 1$ . In fact, we will establish (B.2.6) by showing

$\begin{matrix} Q_{1} \cap {M (| \nabla^{2} v |^{2}) ⩽ 1} \cap {M (| f |^{2}) ⩽ δ^{2}} \neq \emptyset \\ \Rightarrow & L^{4} (Q_{1} \cap {M {(| \nabla v |)}^{2} > N_{1}^{2}}) < ε L^{4} (Q_{1}) \end{matrix}$

(B.2.7)

and applying a simple scaling argument. In order to show (B.2.7) we compare v with a solution to a homogeneous problem on

$Q_{4} = (t_{0}^{4} - 4^{2}, t_{0}^{4} + 4^{2}) \times B_{4} (x_{0}^{4}) \subset Q_{0}$

which is smooth in the interior. So let us define h as the unique solution to

${\begin{matrix} \partial_{t} h - div A (ε (h)) & = \nabla π_{h} & in Q_{4}, \\ div h & = 0 & in Q_{4}, \\ h & = v & on I_{4} \times \partial B_{4}, \\ h (t_{0}^{4}, \cdot) & = v (t_{0}^{4}, \cdot) & in B_{4} . \end{matrix}$

(B.2.8)

We test the difference of both equations with $v - h$ . This yields by the ellipticity of $A$

$\begin{matrix} \sup_{t \in I_{4}} \int_{B_{4}} | v (t) - h (t) |^{2} d x + \int_{Q_{4}} | ε (v) - ε (h) |^{2} d x d t \\ ⩽ c \int_{Q_{4}} | f |^{2} d x d t + c \int_{Q_{4}} | v - h |^{2} d x d t . \end{matrix}$

An application of Korn's inequality and Gronwall's lemma implies

$\sup_{t \in I_{4}} \int_{B_{4}} | v (t) - h (t) |^{2} d x + \int_{Q_{4}} | \nabla v - \nabla h |^{2} d x d t ⩽ c \int_{Q_{4}} | f |^{2} d x d t .$

(B.2.9)

First we insert $\partial_{t} (v - h)$ which yields similarly

$\int_{Q_{4}} | \partial_{t} (v - h) |^{2} d x + \sup_{t \in I_{4}} \int_{B_{4}} | \nabla v - \nabla h |^{2} d x ⩽ c \int_{Q_{4}} | f |^{2} d x d t .$

(B.2.10)

We can introduce the pressure terms $π_{v}, π_{h} \in L^{2} (I_{4}, L_{0}^{2} (B_{4}))$ in the equations for v and h and show

$\int_{Q_{4}} | π_{v} - π_{h} |^{2} d x ⩽ c \int_{Q_{4}} | f |^{2} d x d t .$

(B.2.11)

Estimate (B.2.11) can be shown by using the Bogovskiĭ operator, see Section 2.1. Setting $Bog = {Bog}_{B_{4}}$ we gain due to (B.2.10) for any $φ \in C_{0}^{\infty} (Q_{4})$ that

$\begin{matrix} \int_{Q_{4}} (π_{v} - π_{h}) φ d x d t = \int_{Q_{4}} (π_{v} - π_{h}) div Bog (φ - φ_{B_{4}}) d x d t \\ = \int_{Q_{4}} A (ε (v - h), ε (Bog (φ - φ_{B_{4}}))) d x d t \\ + \int_{Q_{4}} f \cdot Bog (φ - φ_{B_{4}})) d x d t \\ - \int_{Q_{4}} \partial_{t} (v - h) \cdot Bog (φ - φ_{B_{4}}) d x d t \\ ⩽ c ({‖ \nabla (v - h) ‖}_{2} + {‖ f ‖}_{2} + {‖ \partial_{t} (v - h) ‖}_{2}) {‖ \nabla Bog (φ - {(φ)}_{B_{4}}) ‖}_{2} \\ ⩽ c {(\int_{Q_{4}} | f |^{2} d x d t)}^{\frac{1}{2}} {(\int_{Q_{4}} | φ |^{2} d x d t)}^{\frac{1}{2}} . \end{matrix}$

Now we choose a cut off function $η \in C_{0}^{\infty} (B_{4})$ with $0 ⩽ η ⩽ 1$ and $η \equiv 1$ on $B_{3}$ . We insert $\partial_{γ} (η^{2} \partial_{γ} (v - h))$ in the equation for $v - h$ and sum over $γ \in {1, 2, 3}$ . We gain

$\begin{matrix} \sup_{t \in I_{4}} \int_{B_{4}} η^{2} | \nabla (v - h) |^{2} d x + \int_{Q_{4}} η^{2} | \nabla ε (v) - \nabla ε (h) |^{2} d x d t \\ ⩽ c \int_{Q_{4}} f \cdot \partial_{γ} (η^{2} \partial_{γ} (h - h)) d x d t + c (\nabla η) \int_{Q_{4}} | \nabla v - \nabla h |^{2} d x d t \\ + c \int_{Q_{4}} (π - π_{h}) \cdot \partial_{γ} (\nabla η^{2} \cdot \partial_{γ} (h - h)) d x d t . \end{matrix}$

We estimate the term involving f by

$\begin{matrix} \int_{Q_{4}} f \cdot \partial_{γ} (η^{2} \partial_{γ} (v - h)) d x d t \\ ⩽ c (κ) \int_{Q_{4}} | f |^{2} d x d t + κ \int_{Q_{4}} η^{2} | \nabla^{2} v - \nabla^{2} h |^{2} d x d t \\ + c (\nabla η) \int_{Q_{4}} | \nabla v - \nabla h |^{2} d x d t, \end{matrix}$

where $κ > 0$ is arbitrary. The term involving $π - π_{h}$ can be estimated in the same fashion. Choosing $κ > 0$ small enough and using the inequality $| \nabla^{2} u | ⩽ c | \nabla ε (u) |$ as well as (B.2.9)–(B.2.11) shows

$\sup_{t \in I_{4}} \int_{B_{3}} | \nabla (v - h) (t) |^{2} d x + \int_{I_{4}} \int_{B_{3}} | \nabla^{2} v - \nabla^{2} h |^{2} d x d t ⩽ c \int_{Q_{4}} | f |^{2} d x d t .$

(B.2.12)

Now, let us assume that (B.2.7)₁ holds. Then there is a point $(t_{0}, x_{0}) \in Q_{1}$ such that

$\underset{Q_{σ} (t_{0}, x_{0})}{⨍} | \nabla^{2} v |^{2} d x d t ⩽ 1, \underset{Q_{σ} (t_{0}, x_{0})}{⨍} | f |^{2} d x d t ⩽ δ^{2}$

(B.2.13)

for all $σ > 0$ . Since $Q_{4} \subset Q_{6} (t_{0}, x_{0})$ we have

$\int_{Q_{4}} | \nabla^{2} v |^{2} d x d t ⩽ c, \int_{Q_{4}} | f |^{2} d x d t ⩽ c δ^{2} .$

(B.2.14)

As h is smooth we know that

$N_{0}^{2} : = \sup_{Q_{3}} | \nabla^{2} h |^{2} < \infty .$

(B.2.15)

From this we aim to conclude that

$Q_{1} \cap {M (| \nabla^{2} v |^{2}) > N_{1}^{2}} \subset Q_{1} \cap {M (χ_{Q_{3}} | \nabla^{2} v - \nabla^{2} h |^{2}) > N_{0}^{2}}$

(B.2.16)

for $N_{1}^{2} : = \max {4 N_{0}^{2}, 2^{5}}$ . To establish (B.2.16) suppose that

$(t, x) \in Q_{1} \cap {M (χ_{Q_{3}} | \nabla^{2} v - \nabla^{2} h |^{2}) ⩽ N_{0}^{2}} .$

(B.2.17)

If $σ ⩽ 2$ we have $Q_{σ} (t, x) \subset Q_{3}$ and gain by (B.2.15)

$\begin{matrix} \underset{Q_{σ} (t, x)}{⨍} | \nabla^{2} v |^{2} d x d t \\ ⩽ 2 \underset{Q_{σ} (t, x)}{⨍} χ_{Q_{3}} | \nabla^{2} v - \nabla^{2} h |^{2} d x d t + 2 \underset{Q_{σ} (t, x)}{⨍} χ_{Q_{3}} | \nabla^{2} h |^{2} d x d t \\ ⩽ 4 N_{0}^{2} . \end{matrix}$

If $σ ⩾ 2$ we have by (B.2.13)

$\underset{Q_{σ} (t, x)}{⨍} | \nabla^{2} v |^{2} d x d t ⩽ 2^{5} \underset{Q_{2 σ} (t_{0}, x_{0})}{⨍} | \nabla^{2} v |^{2} d x d t ⩽ 2^{5} .$

Combining the both cases yields (B.2.16). This implies together with the continuity of the maximal function on $L^{2}$ , (B.2.12) and (B.2.14)

$\begin{matrix} L^{4} (Q_{1} \cap {M (| \nabla^{2} v |^{2}) > N_{1}^{2}}) \\ ⩽ L^{d + 1} (Q_{1} \cap {M (χ_{Q_{3}} | \nabla^{2} v - \nabla^{2} h |^{2}) > N_{0}^{2}}) \\ ⩽ \frac{c}{N_{0}^{2}} \int_{Q_{3}} | \nabla^{2} v - \nabla^{2} h |^{2} d x d t \\ ⩽ \frac{c}{N_{0}^{2}} \int_{Q_{3}} | f |^{2} d x d t ⩽ \frac{c}{N_{0}^{2}} δ^{2} \\ = ε L^{4} (Q_{1}), \end{matrix}$

choosing $δ : = c^{- 1 / 2} N_{0} \sqrt{ε}$ . So we have shown (B.2.7) which yields (B.2.6) by a scaling argument.

If (B.2.6)₁ holds then we have

$\begin{matrix} L^{4} (Q_{r} \cap {M {(| \nabla^{2} v |)}^{2} > N_{1}^{2}}) \\ ⩽ ε L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > 1} \cup {M (| f |^{2}) > δ^{2}}) \\ ⩽ ε (L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > 1}) + L^{4} (Q_{r} \cap {M (| f |^{2}) > δ^{2}})) . \end{matrix}$

Multiplying the equation for v by some small number $ϱ = ϱ ({‖ f ‖}_{q}, {‖ \nabla^{2} v ‖}_{2})$ we can assume that

$L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > N_{1}^{2}}) < ε .$

(B.2.18)

By induction we can establish that

$\begin{matrix} L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > N_{1}^{2 k}}) \\ ⩽ ε^{k} L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > 1} \\ + c \sum_{i = 1}^{k} ε^{i} L^{4} (Q_{r} \cap {M (| f |^{2}) > δ^{2} N_{1}^{2 (k - i)}}) . \end{matrix}$

In the induction step one has to introduce $v_{1} : = \frac{v}{N_{1}}$ which is a solution to the $A$ -Stokes problem with right hand side $f_{1} : = \frac{f}{N_{1}}$ . Now we will show $\nabla^{2} v \in L^{q} (Q_{r})$ . For this we use the equivalence for $1 ⩽ q_{0} < \infty$

$\sum_{k = 1}^{\infty} L^{q_{0} k} L^{4} (Q_{r} \cap {(t, x) : | u (t, x) | > θ L^{k}}) < \infty \Leftrightarrow u \in L^{q_{0}} (Q_{r}),$

which holds for any measurable function u, see [44]. Here $L > 1$ and $θ > 0$ are arbitrary. So we aim to prove that

$\sum_{k = 1}^{\infty} {(N_{1}^{2})}^{\frac{q}{2} k} L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > N_{1}^{2 k}}) < \infty$

(B.2.19)

to conclude $M (| \nabla^{2} v |^{2}) \in L^{\frac{q}{2}} (Q_{r})$ and hence $\nabla^{2} v \in L^{q} (Q_{r})$ . Since $f \in L^{q} (Q_{r})$ we have $M (| f |^{2}) \in L^{q / 2} (Q_{r})$ (recall (5.2.4)) and we have

$\sum_{k = 1}^{\infty} {(N_{1}^{2})}^{\frac{q}{2} k} L^{4} (Q_{r} \cap {M (| f |^{2}) > δ^{2} N_{1}^{2 k}}) < \infty .$

We obtain

$\begin{matrix} \sum_{k = 1}^{\infty} {(N_{1})}^{q k} L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > N_{1}^{2 k}}) \\ ⩽ c \sum_{k = 1}^{\infty} {(N_{1})}^{q k} ε^{k} L^{4} (Q_{r} \cap {M (| \nabla^{2} v |^{2}) > 1}) \\ + c \sum_{k = 1}^{\infty} {(N_{1})}^{q k} \sum_{i = 1}^{k} ε^{i} L^{4} (Q_{r} \cap {M (| f |^{2}) > δ^{2} N_{1}^{2 (k - i)}}) \\ ⩽ c_{r} \sum_{k = 1}^{\infty} {(ε N_{1})}^{q k} \\ + c \sum_{i = 1}^{\infty} ε^{i} {(N_{1})}^{q i} \sum_{k = i}^{\infty} {(N_{1})}^{q (k - i)} L^{4} (Q_{r} \cap {M (| f |^{2}) > δ^{2} N_{1}^{2 (k - i)}}) \\ ⩽ c_{r} \sum_{k = 1}^{\infty} {(ε N_{1}^{q})}^{k} . \end{matrix}$

If we choose $ε N_{1}^{q} < 1$ the sum in (B.2.19) is converging and we have $\nabla^{2} v \in L^{q} (Q_{r})$ . Since the mapping $f \mapsto \nabla^{2} v$ is linear we gain the desired estimate

$\int_{Q_{r}} | \nabla^{2} v |^{q} d x d t ⩽ c_{r} \int_{Q_{0}} | f |^{q} d x d t .$

(B.2.20)

ii) Now let $Q_{1}$ be a cylinder such that $4 Q_{1} \cap (- \infty, 0] \times R^{3} \neq \emptyset$ . Moreover, assume that $Q_{1} \cap Q_{0} \neq \emptyset$ . We consider the solution $\tilde{h}$ to

${\begin{matrix} \partial_{t} \tilde{h} - div A (ε (\tilde{h})) & = \nabla π_{\tilde{h}} & in {\tilde{Q}}_{4}, \\ div \tilde{h} & = 0 & in {\tilde{Q}}_{4}, \\ \tilde{h} & = v & on {\tilde{I}}_{4} \times \partial B_{4}, \\ \tilde{h} (t_{0}^{4}, \cdot) & = 0 & in B_{4}, \end{matrix}$

(B.2.21)

where ${\tilde{I}}_{m} : = I_{m} \cap (0, T)$ and ${\tilde{Q}}_{m} : = {\tilde{I}}_{m} \times B_{m}$ . We can establish a variant of (B.2.12) on ${\tilde{Q}}_{4}$ . Now we have $\sup_{{\tilde{Q}}_{3}} | \nabla^{2} \tilde{h} |^{2} < \infty$ due to the smooth initial datum of $\tilde{h}$ (recall that $v (0, \cdot) = 0$ a.e.). So we can finish the proof as before and gain $\nabla^{2} v \in L^{q} (Q_{1})$ . This implies again (B.2.20).

iii) The situation $4 Q_{1} \cap [T, \infty) \times R^{3} \neq \emptyset$ is uncritical again and we can assume that ii) and iii) do not occur for the same cylinder (by choosing sufficiently small cubes).

Covering the set $(0, T) \times B$ by smaller cylinders and combing i)–iii) yield the desired estimate. □

Corollary B.2.1

Under the assumptions of Theorem B.2.48 we have for all balls $B \subset R^{3}$ the following estimates for some constant $c_{B}$ which does not depend on T.

a) The following holds

$\int_{0}^{T} \int_{B} (| \frac{v}{T} |^{q} + | \frac{\nabla v}{\sqrt{T}} |^{q} + | \nabla^{2} v |^{q}) d x d t ⩽ c_{B} \int_{Q_{0}} | f |^{q} d x d t .$

b) We have $\partial_{t} v \in L^{q} (0, T; L_{l o c}^{q} (R^{3}))$ together with

$\int_{0}^{T} \int_{B} | \partial_{t} v |^{q} d x d t ⩽ c_{B} \int_{Q_{0}} | f |^{q} d x d t .$

c) There is $π \in L^{q} ((0, T), W_{l o c}^{1, q} (R^{3}))$ such that

$\begin{matrix} \int_{Q_{0}} v \cdot \partial_{t} φ d x d t - \int_{Q_{0}} A (ε (v), ε (φ)) d x \\ = \int_{Q_{0}} π div φ d x d t + \int_{Q_{0}} f \cdot φ d x d t \end{matrix}$

for all $φ \in C_{0}^{\infty} ([0, T) \times R^{3})$ .

d) The following holds

$\int_{0}^{T} \int_{B} (| \frac{π}{\sqrt{T}} |^{q} + | \nabla π |^{q}) d x d t ⩽ c_{B} \int_{Q_{0}} | f |^{q} d x d t .$

Proof

The estimate in a) is a simple scaling argument. Having a solution v defined on $(0, T) \times R^{3}$ we gain a solution $\hat{v}$ on $(0, 1) \times R^{3}$ by setting

$\hat{v} (s, x) : = \frac{1}{T} v (T s, \sqrt{T} x) .$

Now we apply Theorem B.2.48 to $\hat{v}$ . The constant which appears is independent of T. Transforming back to v yields the claimed inequality.

b) For $φ \in C_{0}^{\infty} (Q_{0})$ with $φ (t, x) = τ (t) ψ (x)$ where $φ \in C_{0}^{\infty} (G)$ ( $G \in R^{3}$ a bounded Lipschitz domain) we have

$\begin{matrix} \int_{Q_{0}} v \cdot \partial_{t} φ d x d t & = \int_{0}^{T} \partial_{t} τ \int_{R^{3}} v \cdot (ψ_{div} + \nabla Ψ) d x d t \\ = \int_{0}^{T} \partial_{t} τ \int_{R^{3}} v \cdot ψ_{div} d x d t \\ = \int_{Q_{0}} v \cdot \partial_{t} φ_{div} d x d t \end{matrix}$

where $ψ_{div} : = ψ - \nabla Δ_{G}^{- 1} div ψ$ and $Ψ : = Δ_{G}^{- 1} div ψ$ . (Here $Δ_{G}^{- 1}$ is the solution operator to the Laplace equation with zero boundary datum on ∂G.) Here we took into account $Ψ |_{\partial G} = 0$ as well as $div v = 0$ . Using $\nabla^{2} v \in L^{2} (0, T; L_{l o c}^{2} (R^{3}))$ we proceed by

$\begin{matrix} \int_{Q_{0}} v \cdot \partial_{t} φ d x d t & = \int_{0}^{T} \int_{G} (f - div A ε (v)) \cdot φ_{div} d x d t \\ ⩽ c {(\int_{0}^{T} \int_{G} (| \nabla^{2} v |^{q} + | f |^{q}) d x d t)}^{\frac{1}{q}} {(\int_{0}^{T} \int_{G} | φ_{div} |^{q^{'}} d x d t)}^{\frac{1}{q^{'}}} \\ ⩽ c {(\int_{Q_{0}} | f |^{q} d x d t)}^{\frac{1}{q}} {(\int_{0}^{T} \int_{G} | φ |^{q^{'}} d x d t)}^{\frac{1}{q^{'}}} . \end{matrix}$

In the last step we used the estimate from Theorem B.2.48 and continuity of $\nabla Δ_{G}^{- 1} div$ on $L^{q^{'}} (G)$ . Duality implies $\partial_{t} v \in L^{q} (0, T; L_{l o c}^{q} (R^{3}))$ and we can introduce the pressure function $π \in L^{q} (0, T; L_{l o c}^{q} (R^{3}))$ as claimed in b) by De Rahm's Theorem. Using the equation for v and the estimates in a) and b) we gain

$\int_{Q} | \nabla π |^{q} d x d t ⩽ c \int_{Q_{0}} | f |^{q} d x d t .$

The estimate for π in d) follows again by scaling. □

Corollary B.2.2

Let $f \in L^{q} (Q_{0}^{+})$ for some $q > 2$ where $Q_{0}^{+} : = (0, T) \times R_{+}^{3}$ , $R_{+}^{3} = R^{3} \cap [x_{3} > 0]$ , and let $v \in L^{2} ((0, T); W_{0, div}^{1, 2} (R_{+}^{3}))$ with $v |_{x_{3} = 0} = 0$ be the unique weak solution to

$\int_{Q_{0}^{+}} v \cdot \partial_{t} φ d x d t - \int_{Q_{0}^{+}} A (ε (v), ε (φ)) d x = \int_{Q_{0}^{+}} f \cdot φ d x d t$

(B.2.22)

for all $φ \in C_{0, div}^{\infty} ([0, T) \times R_{+}^{3})$ . Then the results from Theorem B.2.48 and Corollary B.2.1 hold for v for all half balls $B^{+} (z) = B (z) \cap [x_{3} > 0] \subset R^{3}$ with $z_{3} = 0$ .

Proof

We will show a variant of the $L^{q}$ -estimate from Theorem B.2.48 on half balls $B^{+}$ , i.e.

$\int_{0}^{T} \int_{B^{+}} | \nabla^{2} v |^{q} d x d t ⩽ c_{B} \int_{0}^{T} \int_{Q^{+}} | f |^{q} d x d t .$

(B.2.23)

From this we can follow estimates in the fashion of Corollary B.2.1 as done there. In order to establish (B.2.23) we will proceed as in the proof of Theorem B.2.48 replacing all balls with half ball. So let $Q_{1} \subset R^{4}$ such that $4 Q_{1} \subset Q_{0}$ (the other situation can be shown along the modifications indicated at the end of the proof of Theorem B.2.48). Moreover, assume that $Q_{1} = I_{1} \times B_{1} (z)$ where $z_{3} = 0$ . We compare v with the unique solution $h^{+}$ to

${\begin{matrix} \partial_{t} h^{+} - div A (ε (h^{+})) & = \nabla π_{h^{+}} & in Q_{4}^{+}, \\ div h^{+} & = 0 & in Q_{4}^{+}, \\ h^{+} & = v & on I_{4} \times \partial B_{4}^{+}, \\ h^{+} (0, \cdot) & = v (0, \cdot) & in B_{4}^{+} . \end{matrix}$

(B.2.24)

We gain a version of the estimate (B.2.9) and (B.2.10) on half-balls. In fact, there holds

$\sup_{t \in I_{4}} \int_{B_{4}^{+}} | v - h^{+} |^{2} d x + \int_{Q_{4}^{+}} | \nabla v - \nabla h^{+} |^{2} d x d t ⩽ c \int_{Q_{4}^{+}} | f |^{2} d x d t,$

(B.2.25)

$\int_{Q_{4}^{+}} | \partial_{t} (v - h^{+}) |^{2} d x + \sup_{t \in I_{4}} \int_{B_{4}^{+}} | \nabla v - \nabla h^{+} |^{2} d x ⩽ c \int_{Q_{4}^{+}} | f |^{2} d x d t .$

(B.2.26)

We can introduce the pressure terms $π_{v}, π_{h^{+}} \in L^{2} (I_{4}, L_{0}^{2} (B_{4}^{+}))$ in the equations for v and $h^{+}$ and show

$\int_{Q_{4}^{+}} | π_{v} - π_{h^{+}} |^{2} d x ⩽ c \int_{Q_{4}^{+}} | f |^{2} d x d t .$

(B.2.27)

This can be done as in the proof of (B.2.11) using the Bogovskiĭ operator on $B_{4}^{+}$ . Estimate (B.2.27) can be shown by using the Bogovskiĭ operator introduced in [24]. Now we insert $\partial_{γ} (η^{2} \partial_{γ} (v - h))$ for $γ \in {1, 2}$ in the equation for $v - h$ . Here we choose $η \in C_{0}^{\infty} (B_{4})$ with $0 ⩽ η ⩽ 1$ and $η \equiv 1$ on $B_{3}$ . This yields together with (B.2.25)–(B.2.27)

$\int_{Q_{3}^{+}} | \tilde{\nabla} \nabla (v - h) |^{2} d x ⩽ c \int_{Q_{4}^{+}} | f |^{2} d x d t,$

(B.2.28)

where $\tilde{\nabla} : = (\partial_{1}, \partial_{2})$ . Finally, the only term which is missing is $\partial_{3}^{2} (v - h)$ . On account of $div (v - h) = 0$ we have (cf. [21])

$| \partial_{3}^{2} (v - h) | ⩽ c (| \tilde{\nabla} (π_{v} - π_{h^{+}}) | + | \tilde{\nabla} \nabla (v - h) | + | f |) .$

(B.2.29)

So we have to estimate derivatives of the pressure. In fact we have

$\int_{Q_{3}^{+}} | \tilde{\nabla} (π_{v} - π_{h^{+}}) |^{2} d x ⩽ c \int_{Q_{4}^{+}} | f |^{2} d x d t .$

(B.2.30)

We can show this similarly to the proof of (B.2.27) replacing φ by $\partial_{γ} φ$ and using (B.2.28). Combining (B.2.28)–(B.2.30) implies

$\int_{Q_{3}^{+}} | \nabla^{2} v - \nabla^{2} h |^{2} d x ⩽ c \int_{Q_{4}^{+}} | f |^{2} d x d t .$

Moreover, we know $\sup_{Q_{3}^{+}} | \nabla^{2} h^{+} |^{2} < \infty$ . Note that $h^{+} = 0$ on $Q_{3} \cap [x_{3} = 0]$ . This allows to show $\nabla^{2} v \in L^{q} (Q_{1}^{+})$ as in the proof of Theorem B.2.48. □

Corollary B.2.3

Let $f \in L^{q} (Q_{0}^{ν, ξ})$ for some $q > 2$ where $Q_{0}^{ν, ξ} : = (0, T) \times R_{ν, ξ}^{3}$ , $R_{ν, ξ}^{3} = R^{3} \cap [(x - ξ) \cdot ν > 0]$ for some $ν, ξ \in R^{3}$ . Let $v \in L^{2} (0, T; W_{0, div}^{1, 2} (R_{ν, ξ}^{3}))$ with $v |_{(x - ξ) \cdot ν = 0} = 0$ be the unique weak solution to

$\int_{Q_{0}^{ν, ξ}} v \cdot \partial_{t} φ d x d t - \int_{Q_{0}^{ν, ξ}} A (ε (v), ε (φ)) d x = \int_{Q_{0}^{ν, ξ}} f \cdot φ d x d t$

(B.2.31)

for all $φ \in C_{0, div}^{\infty} ([0, T) \times R_{ν, ξ}^{3})$ . Then the results from Theorem B.2.48 and Corollary B.2.1 hold for v for all half balls $B^{ν, ξ} (z) = B (z) \cap [(x - ξ) \cdot ν > 0] \subset R^{3}$ with $(z - ξ) \cdot ν = 0$ .

Proof

The proof follows easily from Corollary B.2.2 by rotation of the coordinate system. There is an orthogonal matrix $V \in R^{3 \times 3}$ such that the mapping $z = V (x - ξ)$ transforms $R_{ν, ξ}^{3}$ to $R_{+}^{3}$ . We define

$\tilde{v} (t, x) = V^{- 1} v (t, V (x - ξ)), \tilde{f} (t, x) = V^{- 1} f (t, V (x - ξ)),$

as well as the bilinear form $\tilde{A}$ by

$\tilde{A} (ζ, ξ) : = A (V ζ V^{- 1}, V ξ V^{- 1}), ζ, ξ \in R^{3 \times 3} .$

Note that the ellipticity constants of $A$ and $\tilde{A}$ coincide as V is an orthogonal matrix. Now it is easy to see that $\tilde{v} \in L^{2} (0, T; W_{0, div}^{1, 2} (R_{+}^{3}))$ satisfies $\tilde{v} |_{x_{3} = 0} = 0$ and is a solution to (B.2.22) with right hand side $\tilde{f}$ and bilinear form $\tilde{A}$ . Hence Corollary B.2.3. □

Theorem B.2.49

Let $Q : = (0, T) \times G$ with a bounded domain $G \subset R^{3}$ having a $C^{2}$ -boundary. Let $f \in L^{q} (Q)$ for some $q > 2$ . Then there is a unique weak solution $v \in L^{\infty} (0, T; L^{2} (G)) \cap L^{q} (0, T; W_{0, div}^{1, q} (G))$ to

$\int_{Q} v \cdot \partial_{t} φ d x d t - \int_{Q} A (ε (v), ε (φ)) d x = \int_{Q} f \cdot φ d x d t$

(B.2.32)

for all $φ \in C_{0, div}^{\infty} ([0, T) \times G)$ such that $\nabla^{2} v \in L^{q} (Q)$ . Moreover, we have

$\int_{Q} | \nabla^{2} v |^{q} d x d t ⩽ c \int_{Q} | f |^{q} d x d t .$

Proof

Due to the local $L^{q}$ -theory for the whole space problem and the half-space problem which follow from Corollary B.2.1 and Corollary B.2.2 (with the right scaling in T) the proof is similar to [133], Thm. 4.1, in the case $A = I$ . Note that $L^{q}$ -estimates for the stationary problem on bounded domains with given divergence are stated in Lemma B.1.1. We want to invert the operator

$\begin{matrix} L & : Y \to L^{q} (I; L_{div}^{q} (G)), \\ v & \mapsto P_{q} (\partial_{t} v - div A ε (v)) . \end{matrix}$

The space $Y$ is given by

$Y : = L^{q} (I; W_{0, div}^{1, q} \cap W^{2, q} (G)) \cap W^{1, q} (I; L^{q} (G)) \cap {v (0, \cdot) = 0, v_{\partial G} = 0}$

and $P_{q}$ is the Helmholtz projection from $L^{q} (G)$ into $L_{div}^{q} (G)$ . The latter one is defined by

$L_{div}^{q} (G) : = {\overline{C_{0, div}^{\infty} (G)}}^{{‖ \cdot ‖}_{q}} .$

The Helmholtz-projection $P_{q} u$ of a function $u \in L^{q} (G)$ can be defined as $P_{q} u : = u - \nabla h$ , where h is the solution to the Neumann-problem

${\begin{matrix} Δ h = div u on G, \\ N_{B} \cdot (\nabla h - u) = 0 on \partial G . \end{matrix}$

We will try to find an operator $R : L^{q} (I; L_{div}^{q} (G)) \to Y$ such that

$L \circ R = I + τ$

(B.2.33)

with $‖ τ ‖ < 1$ . The range of $L \circ R$ (which then is $L^{q} (0, T; L_{div}^{q} (G))$ ) is contained in the range of $L$ . So $L$ is onto.

Let $G_{k}$ , $0 = 1, . . ., N$ be a covering of G such that $G_{0} ⋐ G$ and $G_{k}$ covers a (small) boundary strip of G. There are local coordinates

$z = Z_{k} (y^{k}) = (y_{1}^{k}, y_{2}^{k}, y_{3}^{k} - F_{k} (y_{1}^{k}, y_{2}^{k})), y^{k} = (y_{1}^{k}, y_{2}^{k}) \in B_{λ} (ξ_{k})$

where $F_{k}$ is a $C^{2}$ -function and $0 < λ ⩽ λ_{0} < 1$ . Here $ξ_{k}$ denotes the center point of $S_{k} = \partial G \cap G_{k}$ and $ν_{k}$ the outer unit normal of $S_{k}$ at the point $ξ_{k}$ . In this coordinate system we have a flat boundary which is contained in the plane ${(x - ξ_{k}) \cdot ν_{k} = 0}$ . We consider a decomposition of unity ${(ζ_{k})}_{k = 0}^{N} \subset C_{0}^{\infty} (R^{3})$ with respect to $G_{k}$ such that $spt ζ_{k} \subset G_{k}$ . We can assume that $| \nabla^{l} ζ_{k} | ⩽ c λ^{- l}$ for $l = 1, 2$ and that the multiplicity of the covering of G by the domains $G_{k}$ does not depend on λ.

Furthermore, $M_{0} f$ and $M f$ is the extension of a function f (by zero) to the whole space or the half space respectively. Note that if $f \in L_{div}^{q} (G)$ , then $M_{0} f \in L_{div}^{q} (R^{3})$ . Finally, we denote by $U^{k} f$ (for $f \in L^{q} (R_{+}^{3})$ ) and $U_{0} f$ (for $f \in L^{q} (R^{3})$ ) the solution on the half space (corresponding to the plane ${(x - ξ_{k}) \cdot ν_{k} = 0}$ ) and the whole space respectively (see Corollary B.2.1 and Corollary B.2.3). By $Q^{k} f$ we denote the pressure corresponding to $U^{k} f$ . Now we define the operators

$\begin{matrix} R_{0} f & : = ζ_{0} U_{0} M_{0} f + \sum_{k = 1}^{N} ζ_{k} Z_{k}^{- 1} U^{k} M Z_{k} f, \\ P_{0} f & : = \sum_{k = 1}^{N} Z_{k}^{- 1} σ Q^{k} M Z_{k} f . \end{matrix}$

The idea is in the interior to extend the force to the whole space, compute the whole space solution and localize again. At the boundary it is more tricky since we have to flatten the problem before considering the half space problem (and of course we have to transform back after solving it). Due to the involved cut-off functions $R_{0} f$ is in general not divergence-free. This will be corrected in the following way: we set

$R f = R_{0} f + R_{1} f, P f = P_{0} f + P_{1} f .$

Here $R_{1} f = w$ and $P_{1} f = s$ , where $(w, s)$ is the unique solution to the stationary problem

$- div A ε (w) + \nabla s = 0, div w = div R_{0} f, w |_{\partial G} = 0,$

cf. Lemma B.1.1. Now we clearly have $R f \in Y$ . We need to establish (B.2.33). We abbreviate

$\begin{matrix} u_{k} & : = Z_{k}^{- 1} U^{k} M Z_{k} f, \\ π_{k} & : = Z_{k}^{- 1} Q^{k} M Z_{k} f . \end{matrix}$

We define ${\tilde{\nabla}}_{k} = \nabla_{x} + Z_{k} \nabla F_{k} \partial_{z_{3}}$ and accordingly ${\tilde{div}}_{k}$ as well as ${\tilde{ε}}_{k}$ . We gain on $Q_{k}^{T}$

$\partial_{t} u_{k} - {\tilde{div}}_{k} A ({\tilde{ε}}_{k} (u_{k})) + {\tilde{\nabla}}_{k} π_{k} = Z_{k}^{- 1} Z_{k} f = f .$

There holds

$\partial_{t} R f - div A ε (R f) + \nabla P f = f + S f + \partial_{t} R_{1} f,$

(B.2.34)

$\begin{matrix} S f & = - A ε (U_{0} M_{0} f) \nabla ζ_{0} - div A (ζ_{0} ⊙ U_{0} M_{0} f) - \sum_{k = 1}^{N} A ε (u_{k}) \nabla ζ_{k} \\ - \sum_{k = 1}^{N} div A (\nabla ζ_{k} ⊙ u_{k}) + \sum_{k = 1}^{N} \nabla ζ_{k} π_{k} - \sum_{k = 1}^{N} ζ_{k} ({\tilde{\nabla}}_{k} - \nabla) π_{k} \\ + \sum_{k = 1}^{N} ζ_{k} ({\tilde{div}}_{k} A ({\tilde{ε}}_{k} (\cdot)) - div A (ε (\cdot))) u_{k} . \end{matrix}$

(B.2.35)

From (B.2.34) it follows

$L R f = f + P_{q} S f + P_{q} \partial_{t} R_{1} f$

i.e. (B.2.33) with $τ = P_{q} S + P_{q} \partial_{t} R_{1}$ . We need to estimate the norms of the operators $S$ and $\partial_{t} R_{1}$ . If we choose T small enough the first two terms in (B.2.35) are small in accordance to Corollary B.2.1. The same is true for the first three sums as a consequence of Corollary B.2.3. All together we have

$\sum_{i = 1}^{5} {‖ T_{i} ‖}_{q} ⩽ δ (λ, T) {‖ f ‖}_{q}$

with $δ (λ, T) \to 0$ for $T \to 0$ (and any fixed λ). Note that $δ (λ, T)$ does not depend on N on account of the localization. We will argue similarly for the next three sums assuming that the gradients of the $F_{k}$ are small (meaning that λ is small). Here, we gain

${‖ T_{6} ‖}_{q} + {‖ T_{7} ‖}_{q} ⩽ κ (λ) {‖ f ‖}_{q}$

with $κ (λ) \to 0$ for $λ \to 0$ . Note that $κ (λ)$ does neither depend on T nor on N. By choosing first λ small enough such that $κ (λ) ⩽ \frac{1}{8}$ and then T small enough such that $δ (λ, T) ⩽ \frac{1}{8}$ we can follow

${‖ S f ‖}_{q} ⩽ \frac{1}{4} {‖ f ‖}_{q} .$

(B.2.36)

Now we are going to show the same for $\partial_{t} R_{1}$ . In order to achieve this we consider the function $w^{'} = \partial_{t} R_{1} f$ which is the solution to

$- div A ε (\partial_{t} w^{'}) + \nabla s^{'} = 0, div w^{'} = div \partial_{t} R_{0} f, w^{'} |_{\partial G} = 0 .$

We have the identity

$\begin{matrix} div \partial_{t} R_{0} f & = \sum_{k = 0}^{N} \nabla ζ_{k} \cdot \partial_{t} u_{k} = \sum_{k = 0}^{N} {\tilde{\nabla}}_{k} ζ_{k} \cdot \partial_{t} u_{k} + \sum_{k = 0}^{N} (\nabla - {\tilde{\nabla}}_{k}) ζ_{k} \cdot \partial_{t} u_{k} \\ = \sum_{k = 1}^{N} {\tilde{\nabla}}_{k} ζ_{k} \cdot ({\tilde{div}}_{k} A ({\tilde{ε}}_{k} (u_{k})) - {\tilde{\nabla}}_{k} π_{k}) + \sum_{k = 0}^{N} ({\tilde{\nabla}}_{k} - \nabla) ζ_{k} \cdot f \\ + \sum_{k = 1}^{N} (\nabla - {\tilde{\nabla}}_{k}) ζ_{k} \cdot \partial_{t} u_{k} = : T_{1} + T_{2} + T_{3}, \end{matrix}$

where $u_{0} = U_{0} M_{0} f$ and ${\tilde{\nabla}}_{0} = \nabla$ . We use the formula

$\begin{matrix} T_{1} & = \sum_{k = 1}^{N} {\tilde{div}}_{k} ({\tilde{\nabla}}_{k} ζ_{k} A ({\tilde{ε}}_{k} (u_{k})) - {\tilde{\nabla}}_{k} ζ_{k} π_{k}) \\ - \sum_{k = 1}^{N} ({\tilde{\nabla}}_{k}^{2} ζ_{k} A ({\tilde{ε}}_{k} (u_{k})) - {\tilde{Δ}}_{k} ζ_{k} π_{k}) = : T_{1}^{1} + T_{1}^{2}, \end{matrix}$

as well as

$\begin{matrix} ({\tilde{\nabla}}_{k} - \nabla) g^{k} & = Z_{k} \nabla F_{k} \partial_{z_{3}} g^{k} = Z_{k} \partial_{z_{3}} (\nabla F_{k} g^{k}) \\ = \partial_{ν_{k}} (Z_{k} \nabla F_{k} g^{k}) = ν_{k} \cdot \nabla (Z_{k} \nabla F_{k} g^{k}) \\ = div (ν_{k} Z_{k}^{- 1} (\nabla F_{k} g^{k})) . \end{matrix}$

Now we can apply Corollary B.1.1 with $div g = T_{1}^{1}$ and $g_{0} = T_{1}^{2} + T_{2} + T_{3}$ . By Corollary B.2.2 there are constants $δ^{'} (λ, T), δ^{″} (λ, T)$ with $δ^{'} (λ, T) \to 0$ and $δ^{″} (λ, T) \to 0$ for $T \to 0$ (and any fixed λ) such that

${‖ g ‖}_{q} ⩽ δ^{'} (λ, T) {‖ f ‖}_{q}, {‖ g_{0} ‖}_{q} ⩽ c (1 + δ^{″} (λ, T)) {‖ f ‖}_{q} .$

As a consequence of Corollary B.1.1 this yields

${‖ \partial_{t} R_{1} f ‖}_{q} ⩽ c (λ^{β} + δ^{'} (λ, T) + δ^{'} (λ, T)) {‖ f ‖}_{q} .$

Choosing first λ and then T small enough we gain

${‖ \partial_{t} R_{1} f ‖}_{q} ⩽ \frac{1}{4} {‖ f ‖}_{q} .$

(B.2.37)

Combining (B.2.36) and (B.2.37) implies $‖ τ ‖ ⩽ \frac{1}{2}$ . Hence $L$ is onto (recall (B.2.33)). This means we have shown the claim for T sufficiently small, say $T = T_{0} ≪ 1$ . It is easy to extend it to the whole interval. Let $(v, π)$ be the solution on $[0, T_{0}]$ . We extend it in an even manner to the interval $[0, 2 T_{0}]$ . On the interval $[T_{0}, 2 T_{0}]$ we define $(v^{'}, π^{'})$ as solution to the $A$ -Stokes system with right-hand-side

$f^{'} (t, x) = f (t, x) - f (x, 2 T_{0} - t) + 2 \partial_{t} v (x, 2 T_{0} - t) .$

If we set $v^{'} = 0, π^{'} = 0$ on $[0, T_{0}]$ then $(v + v^{'}, π + π^{'})$ is the solution on $[0, 2 T_{0}]$ . This can be repeated to construct the solution on $[0, T]$ . □

B.3 The non-stationary problem in divergence form

In order to treat problems with right hand side in divergence form we consider the $A$ -Stokes operator

$A_{q} : = - P_{q} div A (ε (\cdot)) .$

The $A$ -Stokes operator $A_{q}$ enjoys the same properties than the Stokes operator $A_{q}$ (see for instance [87]).

For the $A$ -Stokes operator it holds $D (A_{q}) = W_{0, div}^{1, q} \cap W^{2, q} (G)$ , where D denotes the domain, and

${‖ u ‖}_{2, q} ⩽ c_{1} {‖ A_{q} u ‖}_{q} ⩽ c_{2} {‖ u ‖}_{2, q}, u \in D (A_{q}),$

(B.3.38)

$\int_{G} A_{q} u \cdot w d x = \int_{G} u \cdot A_{q^{'}} w d x u \in D (A_{q}), w \in D (A_{q^{'}}) .$

(B.3.39)

Inequality (B.3.38) is a consequence of Lemma B.1.1 a) and the continuity of $P_{q}$ .

Since $A_{q}$ is positive its root $A_{q}^{\frac{1}{2}}$ is well-defined with $D (A_{q}^{\frac{1}{2}}) = W_{0, div}^{1, q} (G)$ and

${‖ u ‖}_{1, q} ⩽ c_{1} {‖ A_{q}^{\frac{1}{2}} u ‖}_{q} ⩽ c_{2} {‖ u ‖}_{1, q}, u \in D (A_{q}^{\frac{1}{2}}),$

(B.3.40)

$\int_{G} A_{q}^{\frac{1}{2}} u \cdot w d x = \int_{G} u \cdot A_{q^{'}}^{\frac{1}{2}} w d x u \in D (A_{q}^{\frac{1}{2}}), w \in D (A_{q^{'}}^{\frac{1}{2}}) .$

(B.3.41)

Finally, the inverse operator $A_{q}^{- \frac{1}{2}} : L_{div}^{q} (G) \to W_{0, div}^{1, q} (G)$ is defined and it holds

${‖ \nabla A_{q}^{- \frac{1}{2}} u ‖}_{q} ⩽ c {‖ u ‖}_{q}, u \in D (A_{q}^{- \frac{1}{2}}),$

(B.3.42)

$\int_{G} A_{q}^{- \frac{1}{2}} u \cdot w d x = \int_{G} u \cdot A_{q^{'}}^{- \frac{1}{2}} w d x u \in D (A_{q}^{- \frac{1}{2}}), w \in D (A_{q^{'}}^{- \frac{1}{2}}) .$

(B.3.43)

From the definition of the square root of a positive self-adjoint operator follows also that

$\begin{matrix} A_{q^{'}}^{\frac{1}{2}} & : W^{2, q^{'}} \cap W_{0, div}^{1, q^{'}} (G) \to W_{0, div}^{1, q^{'}} (G), \\ A_{q^{'}}^{- \frac{1}{2}} & : W_{0, div}^{1, q^{'}} (G) \to W^{2, q^{'}} \cap W_{0, div}^{1, q^{'}} (G), \end{matrix}$

together with

${‖ \nabla A_{q}^{\frac{1}{2}} u ‖}_{q} ⩽ c {‖ u ‖}_{2, q}, u \in W^{2, q^{'}} \cap W_{0, div}^{1, q^{'}} (G),$

(B.3.44)

${‖ \nabla A_{q}^{- \frac{1}{2}} u ‖}_{q} ⩽ c {‖ u ‖}_{q}, u \in W_{0, div}^{1, q^{'}} (G) .$

(B.3.45)

Finally we state the main result of this section.

Theorem B.3.50

Let $Q : = (0, T) \times G$ with a bounded domain $G \subset R^{3}$ having a $C^{2}$ -boundary. Let $F \in L^{q} (Q)$ , where $q \in (1, \infty)$ . There is a unique solution $w \in L^{q} (0, T; W_{0, div}^{1, q} (G))$ to

$\begin{matrix} \int_{Q} w \cdot \partial_{t} φ d x d t - & \int_{Q} A (ε (w), ε (φ)) d x d t = \int_{Q} F : \nabla φ \end{matrix}$

(B.3.46)

for all $φ \in C_{0, div}^{\infty} ([0, T) \times G)$ . Moreover we have

$\underset{Q}{⨍} | \nabla w |^{q} d x d t ⩽ c \underset{Q}{⨍} | F |^{q} d x d t,$

where c only depends on $A$ and q.

Proof

Let us first assume that $q > 2$ . Then Theorem B.2.49 applies. We set $f : = A_{q}^{- \frac{1}{2}} div F$ which is defined via the duality

$\int_{G} A_{q}^{- \frac{1}{2}} div F \cdot φ d x = \int_{G} F : \nabla A_{q^{'}}^{- \frac{1}{2}} φ d x, φ \in C_{0, div}^{\infty} (G),$

using (B.3.43). So we gain $f \in L_{div}^{q} (G)$ with

${‖ f ‖}_{q} ⩽ c {‖ F ‖}_{q} .$

(B.3.47)

We define $\tilde{w} \in L^{q} (0, T; W_{0, div}^{1, q} (G))$ as the unique solution to

$\begin{matrix} \int_{Q} \tilde{w} \cdot \partial_{t} φ d x d t - & \int_{Q} A (ε (\tilde{w}), ε (φ)) d x d t = \int_{Q} f \cdot φ d x d t \end{matrix}$

(B.3.48)

for all $φ \in C_{0, div}^{\infty} ([0, T) \times G)$ . Theorem B.2.49 yields $\tilde{w} \in L^{q} (0, T; W^{2, q} (G))$ and

${‖ \tilde{w} ‖}_{2, q} ⩽ c {‖ f ‖}_{q} .$

(B.3.49)

We want to return to the original problem and set $w : = A_{q}^{\frac{1}{2}} \tilde{w}$ thus we have $w \in L^{q} (0, T; W_{0, div}^{1, q} (G))$ . Since $A_{q^{'}}^{\frac{1}{2}} : W_{0, div}^{1, q^{'}} \cap W^{2, q^{'}} (G) \to W_{0, div}^{1, q^{'}} (G)$ we can replace φ by $A_{q^{'}}^{\frac{1}{2}} φ$ in (B.3.48). This implies using (B.3.41) and the definition of f

$\int_{Q} w \cdot \partial_{t} φ d x d t + \int_{Q} div A (ε (\tilde{w})) : A_{q^{'}}^{\frac{1}{2}} φ d x d t = \int_{Q} F : \nabla φ$

for all $φ \in C_{0, div}^{\infty} (Q)$ . On account of $A_{q^{'}}^{\frac{1}{2}} φ \in W_{0, div}^{1, q^{'}} (G)$ and $A_{q}^{\frac{1}{2}} \tilde{w} \in W_{0, div}^{1, q} (G)$ we gain due to (B.3.41)

$\begin{matrix} \int_{Q} div A (ε (\tilde{w})) : A_{q^{'}}^{\frac{1}{2}} φ d x d t \\ = \int_{Q} A_{q} \tilde{w} : A_{q^{'}}^{\frac{1}{2}} φ d x d t = \int_{Q} A_{q}^{\frac{1}{2}} \tilde{w} : A_{q^{'}} φ d x d t \\ = \int_{Q} w \cdot div A (ε (φ)) d x d t = - \int_{Q} A (ε (w), ε (φ)) d x d t \end{matrix}$

using (B.3.41) and $w \in W_{0, div}^{1, q} (G)$ . This shows that w is the unique solution to (6.2.27). Moreover, we obtain the desired regularity estimate via

$\begin{matrix} \int_{Q} | \nabla w |^{q} d x d t & ⩽ c \int_{Q} | A_{q}^{\frac{1}{2}} w |^{q} d x d t = c \int_{Q} | A_{q} \tilde{w} |^{q} d x d t \\ ⩽ c \int_{Q} | \nabla^{2} \tilde{w} |^{q} ⩽ c \int_{Q} | f |^{q} d x d t \\ ⩽ c \int_{Q} | F |^{q} d x d t \end{matrix}$

as a consequence of (B.3.40), the definition of w, (B.3.38), (B.3.49), and (B.3.47). A simple scaling argument shows that the inequality is independent of the diameter of I and B. So we have shown the claim for $q > 2$ .

The case $q = 2$ follows easily from a priori estimates and Korn's inequality. So let us assume that $q < 2$ . Duality arguments show that

$\frac{1}{q} \underset{Q}{⨍} | \nabla w |^{q} d x d t = \sup_{G \in L^{q^{'}} (Q)} [\underset{Q}{⨍} \nabla w : G d x d t - \frac{1}{q^{'}} \underset{Q}{⨍} | G |^{q^{'}} d x d t] .$

For a given $G \in L^{q^{'}} (Q)$ let $z_{G}$ be the unique $L^{q^{'}} (0, T; W_{0, div}^{1, q^{'}} (G))$ -solution to

$\underset{Q}{⨍} z \cdot \partial_{t} ξ d x d t + \int_{Q} A (ε (z), ε (ξ)) d x d t = \int_{Q} G : \nabla ξ d x d t$

(B.3.50)

for all $ξ \in C_{0, div}^{\infty} ((0, T] \times G)$ . This is a backward parabolic equation with end datum zero. We have that $\partial_{t} z_{G} \in L^{q^{'}} (0, T; W_{div}^{- 1, q^{'}} (G))$ such that test-functions can be chosen from the space $L^{q} (0, T; W_{0, div}^{1, q} (G))$ . Due to $q^{'} > 2$ the first part of the proof (applied to ${\tilde{z}}_{\tilde{G}} (t, \cdot) = z_{G} (T - t, \cdot)$ , where $\tilde{G} (t, \cdot) = G (T - t, \cdot)$ ) yields

$\underset{Q}{⨍} | \nabla z_{G} |^{q^{'}} d x d t ⩽ c \underset{Q}{⨍} | G |^{q^{'}} d x d t .$

This and $w (0, \cdot) = 0$ implies (using w as a test-function in (B.3.50))

$\begin{matrix} \underset{Q}{⨍} | \nabla w |^{q} d x d t \\ ⩽ c \sup_{G \in L^{q^{'}} (Q)} [\underset{Q}{⨍} A (ε (w), ε (z_{G})) d x d t - \underset{Q}{⨍} \partial_{t} z_{G} \cdot w d x d t - \underset{Q}{⨍} | \nabla z_{G} |^{q^{'}} d x d t] \\ ⩽ c \sup_{ξ \in C_{0, div}^{\infty} (Q)} [\underset{Q}{⨍} A (ε (w), ε (ξ)) d x d t - \underset{Q}{⨍} w \cdot \partial_{t} ξ d x d t - \underset{Q}{⨍} | \nabla ξ |^{q^{'}} d x d t] . \end{matrix}$

The equation for w and Young's inequality finally give

$\begin{matrix} \underset{Q}{⨍} | \nabla w |^{q} d x d t & ⩽ c \sup_{ξ \in C_{0, div}^{\infty} (Q)} [\underset{Q}{⨍} F : \nabla ξ d x d t - \underset{Q}{⨍} | \nabla ξ |^{q^{'}} d x d t] \\ ⩽ c \underset{Q}{⨍} | F |^{q} d x d t \end{matrix}$

and hence the claim. □

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Appendix B: The A-Stokes system

Create new playlist

Sign In

Sign Up

B.1 The stationary problem

B.2 The non-stationary problem

B.3 The non-stationary problem in divergence form

Table of Contents for
Appendix B: The A-Stokes system