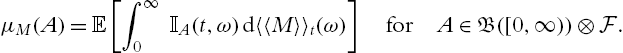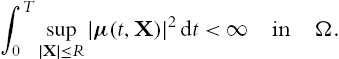Preliminaries
Abstract
In this chapter we revise some basic concepts from stochastic analysis. We begin with the properties of stochastic processes before defining the stochastic integral in the sense of Itô. The third section is concerned with the chain rule in stochastic integration which is known as Itô's formula. Finally we present classical as well as more recent results on stochastic ordinary differential equations. These will be used in the finite dimensional approximation of stochastic PDEs in chapter 10.
Keywords
Stochastic analysis; Stochastic processes; Stochastic integration; Stochastic differential equations; Itô's formula
8.1 Stochastic processes
We consider random variables on a probability space ![]() . Let
. Let ![]() be a filtration such that
be a filtration such that ![]() for
for ![]() . A real-valued stochastic process is a set of random variables
. A real-valued stochastic process is a set of random variables ![]() on
on ![]() with values in
with values in ![]() . A stochastic process can be interpreted as a function of t and ω, where t can be interpreted as time. For fixed
. A stochastic process can be interpreted as a function of t and ω, where t can be interpreted as time. For fixed ![]() the mapping
the mapping ![]() is called path or trajectory of X. We follow the presentation from [100] where the interested reader may also find details of the proofs.
is called path or trajectory of X. We follow the presentation from [100] where the interested reader may also find details of the proofs.
The most important process is the Wiener process.
8.2 Stochastic integration
The aim of this section is to define stochastic integrals of the form
Here M is a square integrable martingale, X a stochastic process and ![]() . Throughout the section we assume that
. Throughout the section we assume that ![]()
![]() -a.s. Moreover, we suppose that M is a quadratically integrable
-a.s. Moreover, we suppose that M is a quadratically integrable ![]() -adapted martingale where
-adapted martingale where ![]() is a filtration which satisfies the usual conditions (see Definition 8.1.6). A process
is a filtration which satisfies the usual conditions (see Definition 8.1.6). A process ![]() could be of unbounded variation in any finite subinterval of
could be of unbounded variation in any finite subinterval of ![]() . Hence integrals of the form (8.2.1) cannot be defined pointwise in
. Hence integrals of the form (8.2.1) cannot be defined pointwise in ![]() . However, M has finite quadratic variation given by the continuous and increasing process
. However, M has finite quadratic variation given by the continuous and increasing process ![]() (see Theorem 8.1.31). Due to this fact, the stochastic integral can be defined with respect to continuous integrable martingales M for an appropriate class of integrands X.
(see Theorem 8.1.31). Due to this fact, the stochastic integral can be defined with respect to continuous integrable martingales M for an appropriate class of integrands X.
The definition of the stochastic integral goes back to Itô. He studied the case where M is a Wiener process. His students Kunita and Watanabe considered the general case ![]() . In the following we have a look at the class of integrands which are allowed in (8.2.1). We define a measure
. In the following we have a look at the class of integrands which are allowed in (8.2.1). We define a measure ![]() on
on ![]() by
by
We call two ![]() -adapted stochastic processes
-adapted stochastic processes ![]() and
and ![]() equivalent with respect to M, if
equivalent with respect to M, if ![]()
![]() -a.e. This leads to the following equivalence relation: for a
-a.e. This leads to the following equivalence relation: for a ![]() -adapted process X we define
-adapted process X we define
provided the right-hand-side exists. So ![]() is the
is the ![]() -norm of X as a function of
-norm of X as a function of ![]() with respect to the measure
with respect to the measure ![]() . We define the equivalence relation
. We define the equivalence relation
Our definition of the stochastic integral will imply that ![]() and
and ![]() coincide provided X and Y are equivalent.
coincide provided X and Y are equivalent.
For ![]() we define
we define ![]() as the space of processes
as the space of processes ![]() with
with ![]() for all
for all ![]() and a.e.
and a.e. ![]() and set
and set
A process ![]() can be identified with a process only defined on
can be identified with a process only defined on ![]() . In particular we have that
. In particular we have that ![]() is a closed subspace of the Hilbert space
is a closed subspace of the Hilbert space
In order to define the stochastic integral for ![]() we have to approximate the elements of
we have to approximate the elements of ![]() in an appropriate way by step processes, i.e. by processes in
in an appropriate way by step processes, i.e. by processes in ![]() . This can be done thanks to the following theorem.
. This can be done thanks to the following theorem.
8.3 Itô's Lemma
One of the most important tools in stochastic analysis is Itô's Lemma. It is a chain-rule for paths of stochastic processes. In contrast to the deterministic case it can only be interpreted as an integral equation because the stochastic processes we are interested in (for instance the Wiener process) are in general not differentiable.
8.4 Stochastic ODEs
In this section we are concerned with stochastic differential equations. We seek a real-valued process ![]() on a probability space
on a probability space ![]() with filtration
with filtration ![]() such that
such that
which holds true ![]() -a.s. and for all
-a.s. and for all ![]() . Here W is a Wiener process with respect to
. Here W is a Wiener process with respect to ![]() . The functions
. The functions ![]() are assumed to be continuous. As in Remark 8.3.20, equation (8.4.11)1 is only an abbreviation for the integral equation
are assumed to be continuous. As in Remark 8.3.20, equation (8.4.11)1 is only an abbreviation for the integral equation
There are two different concepts of solutions to (8.4.12).
i) We talk about strong solution (in the probabilistic sense) if the solution exists on a given probability space ![]() with a given Wiener process W. A strong solution exists for a given initial datum
with a given Wiener process W. A strong solution exists for a given initial datum ![]() and there holds
and there holds ![]() a.s.
a.s.
ii) We talk about weak solution (in the probabilistic sense) or martingale solution if there is a probability space and a Wiener process such that (8.4.12) holds true. The solution is usually written as
This means that when seeking a weak solution, constructing the probability space (and the Wiener process on it) is part of the problem. A solution typically exists for a given initial law ![]() and we have
and we have ![]() . Even if an initial datum
. Even if an initial datum ![]() is given it might live on a different probability space. Hence
is given it might live on a different probability space. Hence ![]() and
and ![]() can only coincide in law.
can only coincide in law.
The existence of a strong solution in the sense of Theorem 8.4.35 is classical, see e.g. [12] and [82,83]. If the assumptions on the coefficients are weakened, strong solutions might not exist, see [17]. In this case we can only hope for a weak solution. We refer to [95] for a nice proof and further references.
The stochastic ODEs which appear later all have strong solutions. However, the concept of martingale solutions will be important for the SPDEs.
The stochastic ODEs we considered so far have two drawbacks. First, we need vector valued processes and, secondly, we have to weaken the assumptions on the drift μ (Lipschitz-continuity in X and linear growth is too strong). Everything in this chapter can be obviously extended to the multi-dimensional setting. Here a standard Wiener process in ![]() is a vector valued stochastic process and each of its components is a real valued Wiener process (recall Definition 8.1.4). Moreover, the components are independent. Getting rid of the assumed Lipschitz continuity is more difficult. Now seek a
is a vector valued stochastic process and each of its components is a real valued Wiener process (recall Definition 8.1.4). Moreover, the components are independent. Getting rid of the assumed Lipschitz continuity is more difficult. Now seek a ![]() -valued process
-valued process ![]() on a probability space
on a probability space ![]() with filtration
with filtration ![]() such that
such that
Here W is a standard ![]() -valued Wiener process with respect to
-valued Wiener process with respect to ![]() and
and ![]() is some initial datum. The functions
is some initial datum. The functions
are continuous in ![]() for each fixed
for each fixed ![]() ,
, ![]() . Moreover, they are assumed to be progressively measurable. The application in Chapter 10 requires weaker assumptions as in the classical existence theorems mentioned above. In our application we only have local Lipschitz continuity of μ. Fortunately, some more recent results apply. In the following we state the assumptions which are in fact a special case of the assumptions in [124, Thm. 3.1.1.].
. Moreover, they are assumed to be progressively measurable. The application in Chapter 10 requires weaker assumptions as in the classical existence theorems mentioned above. In our application we only have local Lipschitz continuity of μ. Fortunately, some more recent results apply. In the following we state the assumptions which are in fact a special case of the assumptions in [124, Thm. 3.1.1.].
(A1) We assume that the following integrability condition on μ for all ![]()
(A2) μ is weakly coercive, i.e. for all ![]() we have that
we have that
where ![]() is
is ![]() -adapted.
-adapted.
(A3) μ is locally weakly monotone, i.e. for all ![]() and all
and all ![]() the following holds
the following holds
(A4) Σ is Lipschitz continuous, i.e. for all ![]() and all
and all ![]() the following holds
the following holds