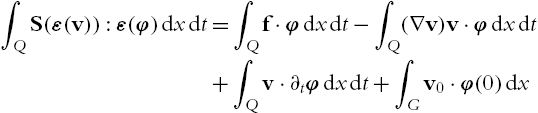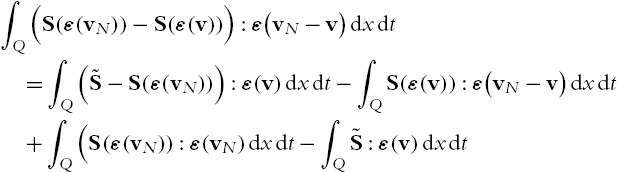Power law fluids
Abstract
We study non-stationary motions of power law fluids in a bounded Lipschitz domain. Based on the solenoidal Lipschitz truncation from Chapter 6 we show the existence of weak solutions to the generalized Navier–Stokes system for p>2dd+2![]() . Our approach completely avoids the appearance of the pressure function.
. Our approach completely avoids the appearance of the pressure function.
Keywords
Generalized Newtonian fluids; Power law fluids; Non-stationary flows; Weak solutions; Existence theory; Solenoidal Lipschitz truncation
The flow of a homogeneous incompressible fluid in a bounded body G⊂Rd![]() (d=2,3
(d=2,3![]() ) during the time interval (0,T)
) during the time interval (0,T)![]() is described by the following set of equations
is described by the following set of equations
{ρ∂tv+ρ(∇v)v=divS−∇π+ρfinQ,divv=0inQ,v=0on∂G,v(0,⋅)=v0inG,
see for instance [23]. Here the unknown quantities are the velocity field v:Q→Rd![]() and the pressure π:Q→R
and the pressure π:Q→R![]() . The function f:Q→Rd
. The function f:Q→Rd![]() represents a system of volume forces and v0:G→Rd
represents a system of volume forces and v0:G→Rd![]() the initial datum, while S:Q→Rd×dsym
the initial datum, while S:Q→Rd×dsym![]() is the stress deviator and ρ>0
is the stress deviator and ρ>0![]() is the density of the fluid. Equation (7.0.1)1 and (7.0.1)2 describe the conservation of balance and the conservation of mass respectively. Both are valid for all homogeneous incompressible liquids and gases. Very popular among rheologists is the power law model
is the density of the fluid. Equation (7.0.1)1 and (7.0.1)2 describe the conservation of balance and the conservation of mass respectively. Both are valid for all homogeneous incompressible liquids and gases. Very popular among rheologists is the power law model
S(ε(v))=ν0(1+|ε(v)|)p−2ε(v)
where ν0>0![]() and p∈(1,∞)
and p∈(1,∞)![]() , cf. [13,23]. We recall that the case p∈[32,2]
, cf. [13,23]. We recall that the case p∈[32,2]![]() covers many interesting applications. For further comments on the physical background we refer to Section 1.4.
covers many interesting applications. For further comments on the physical background we refer to Section 1.4.
The first mathematical results concerning (7.0.1), (7.0.2) were achieved by Ladyshenskaya and Lions for p⩾3d+2d+2![]() (see [106] and [109]). They show the existence of a weak solution in the space
(see [106] and [109]). They show the existence of a weak solution in the space
Lp(0,T;W1,p0,div(G))∩L∞(0,T;L2(G)).
The weak formulation reads as
∫QS(ε(v)):ε(φ)dxdt=∫Qf⋅φdxdt−∫Q(∇v)v⋅φdxdt+∫Qv⋅∂tφdxdt+∫Gv0⋅φ(0)dx
for all φ∈C∞0,div([0,T)×G)![]() with S given by (7.0.2). In this case it follows from parabolic interpolation that (∇v)v⋅v∈L1(Q)
with S given by (7.0.2). In this case it follows from parabolic interpolation that (∇v)v⋅v∈L1(Q)![]() . So the solution is also a test-function and the existence proof is based on monotone operator theory and compactness arguments. These results have been improved by Wolf to the case p>2d+2d+2
. So the solution is also a test-function and the existence proof is based on monotone operator theory and compactness arguments. These results have been improved by Wolf to the case p>2d+2d+2![]() via L∞
via L∞![]() -truncation. Wolf's result was improved to p>2dd+2
-truncation. Wolf's result was improved to p>2dd+2![]() in [65] by the Lipschitz truncation method. Under this restriction on p we have v⊗v∈L1(Q)
in [65] by the Lipschitz truncation method. Under this restriction on p we have v⊗v∈L1(Q)![]() . Hence we can test by Lipschitz continuous functions. So we have to approximate v by a Lipschitz continuous function vλ
. Hence we can test by Lipschitz continuous functions. So we have to approximate v by a Lipschitz continuous function vλ![]() which is quite challenging in the parabolic situation. For further historical comments we refer to Section 5.3.
which is quite challenging in the parabolic situation. For further historical comments we refer to Section 5.3.
We will revise the existence proof from [65]. Using the solenoidal Lipschitz truncation constructed in section 6.1 we can completely avoid the appearance of the pressure and therefore highly simplify the method. For simplicity we only consider the case d=3![]() but all results of this chapter extend to the general case. The main result is as follows.
but all results of this chapter extend to the general case. The main result is as follows.
In the next section we show the existence of weak solutions to (7.0.3) in case p>115![]() . Due to this bound on q the space of test functions coincides with the space where the solution is constructed and the convective term becomes a compact perturbation. The result of Section 7.1 will later be used to obtain an approximate solution in the proof of Theorem 7.0.27, see Section 7.2.
. Due to this bound on q the space of test functions coincides with the space where the solution is constructed and the convective term becomes a compact perturbation. The result of Section 7.1 will later be used to obtain an approximate solution in the proof of Theorem 7.0.27, see Section 7.2.
7.1 The approximated system
Throughout this section we assume that S∈C0(Rd×dsym)∩C1(Rd×dsym∖{0})![]() and for some κ⩾0
and for some κ⩾0![]()
λ(κ+|ε|)q−2|σ|2⩽DS(ε)(σ,σ)⩽Λ(κ+|ε|)q−2|σ|2
for all ε,σ∈Rd×dsym∖{0}![]() with some positive constants λ,Λ
with some positive constants λ,Λ![]() .
.
7.2 Non-stationary flows
In this section we show how the solenoidal Lipschitz truncation can be used to simplify the existence proof for weak solutions to the power law model for non-Newtonian fluids. We are able to work completely in the pressure free formulation and establish the existence of a solution v∈L∞(0,T;L2(G))∩Lp(0,T;W1,p0,div(G))![]() to
to
∫QS(ε(v)):ε(φ)dxdt=∫Qf⋅φdxdt+∫Qv⊗v:ε(φ)dxdt+∫Qv∂tφdxdt+∫Gv0φ(0)dx
for all φ∈C∞0,div([0,T)×G)![]() .
.