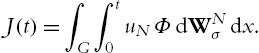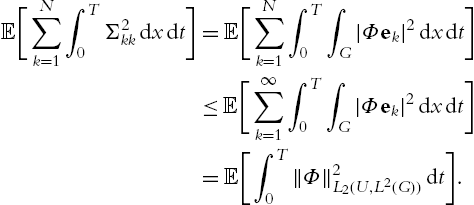Stochastic PDEs
Abstract
In this chapter we revise some well-known tools for SPDEs. In the first section we collect methods from infinite dimensional stochastic analysis, in particular stochastic integration in Hilbert spaces. After this, we give an introduction to the variational approach to SPDEs by considering the stochastic heat equation. Finally, we present the theorems of Prokhorov and Skorokhod which are essential for the stochastic compactness method.
Keywords
Infinite dimensional stochastic analysis; Stochastic PDEs; Stochastic heat equation; Variational approach; Galerkin method; Compactness; Skorokhod's Theorem
9.1 Stochastic analysis in infinite dimensions
In the following we extend the setup from the previous chapter to the case of Banach or Hilbert space valued stochastic processes (see [55]).
Let ![]() be a Banach space and
be a Banach space and ![]() . We denote by
. We denote by ![]() the Banach space of all measurable mappings
the Banach space of all measurable mappings ![]() such that
such that
where the expectation is taken with respect to ![]() . The measurability has to be understood via the approximation by step functions similar to Section 5.1. Regarding the reflexivity and the dual spaces we have the same results as in the case of Bochner spaces (see Lemma 5.1.1). The definitions of adaptivity and progressive measurability (see Chapter 8) extend in a straightforward manner to Banach space valued processes. The definition of the stochastic integral can be extended to Hilbert spaces, where the process X as well as the stochastic integral take values in some Hilbert spaces
. The measurability has to be understood via the approximation by step functions similar to Section 5.1. Regarding the reflexivity and the dual spaces we have the same results as in the case of Bochner spaces (see Lemma 5.1.1). The definitions of adaptivity and progressive measurability (see Chapter 8) extend in a straightforward manner to Banach space valued processes. The definition of the stochastic integral can be extended to Hilbert spaces, where the process X as well as the stochastic integral take values in some Hilbert spaces ![]() . Let U be a Hilbert space with orthonormal basis
. Let U be a Hilbert space with orthonormal basis ![]() and let
and let ![]() be the set of Hilbert–Schmidt operators from U to
be the set of Hilbert–Schmidt operators from U to ![]() . Recall that a bounded linear operator
. Recall that a bounded linear operator ![]() is called Hilbert–Schmidt operator iff
is called Hilbert–Schmidt operator iff
We consider a cylindrical Wiener process ![]() which has the form
which has the form
with a sequence ![]() of independent real valued Brownian motions on
of independent real valued Brownian motions on ![]() . Define further the auxiliary space
. Define further the auxiliary space ![]() as
as
thus the embedding ![]() is Hilbert–Schmidt and trajectories of W belong
is Hilbert–Schmidt and trajectories of W belong ![]() -a.s. to the class
-a.s. to the class ![]() (see [55]).
(see [55]).
For ![]() progressively
progressively ![]() measurable we see that the equality
measurable we see that the equality
defines a ![]() -a.s. continuous
-a.s. continuous ![]() -valued
-valued ![]() -martingale. Moreover, we can multiply the above with test-functions since
-martingale. Moreover, we can multiply the above with test-functions since
is well-defined and ![]() -a.s. continuous.
-a.s. continuous.
In the following we define the quadratic variation of a stochastic process with values in a Hilbert space.
Very useful is also the Burkholder–Davis–Gundi inequality.
Now we present an infinite dimensional version of Itô's formula which is appropriate at least to obtain energy estimates for linear SPDEs, see [105, Theorem 3.1] or [127, Chapter 4.2, Theorem 2].
In Lemma C.0.1 in Appendix C we will establish a version of Itô's formula which is appropriate for nonlinear PDEs, in particular for stochastic Navier–Stokes equations and problems with polynomial nonlinearities.
In some applications we need fractional time derivatives of stochastic integrals. The following lemma is concerned with fractional derivatives of stochastic integrals in Hilbert spaces (see [73, Lemma 2.1] for a proof).
If we have higher moments it is possible to improve the fractional time differentiability to Hölder-continuity.
The following lemma is very useful in order to pass to the limit in stochastic integrals (see [56, Lemma 2.1])
9.2 Stochastic heat equation
As a preparation for the stochastic models for power law fluids we will study the stochastic heat equation by means of a Galerkin–Ansatz. So we seek for a ![]() -adapted process
-adapted process ![]() satisfying
satisfying
Here W is a cylindrical ![]() -Wiener process (see (9.1.1)),
-Wiener process (see (9.1.1)), ![]() is some initial datum and Φ is a progressively
is some initial datum and Φ is a progressively ![]() -measurable process taking values in the space of Hilbert–Schmidt operators. More precisely, we assume
-measurable process taking values in the space of Hilbert–Schmidt operators. More precisely, we assume
Typically one supposes some (nonlinear) dependence of Φ on u. But we neglect this here for simplicity. The Hilbert space U on which W is defined will most naturally be ![]() . As in the case of stochastic ODEs (9.2.4) is an abbreviation for the integral equation
. As in the case of stochastic ODEs (9.2.4) is an abbreviation for the integral equation
The stochastic integral has to be understood as in (9.1.3). The integral ![]() makes sense in case of a strong solution, i.e. if
makes sense in case of a strong solution, i.e. if ![]() a.s. In order to understand the weak formulation (weak in the PDE-sense) we multiply the above with test-functions
a.s. In order to understand the weak formulation (weak in the PDE-sense) we multiply the above with test-functions ![]() , thereby obtaining the following equality, which holds
, thereby obtaining the following equality, which holds ![]() -a.s.:
-a.s.:
for a.e. ![]() . Due to (9.2.5) this can be equivalently formulated using test-functions for
. Due to (9.2.5) this can be equivalently formulated using test-functions for ![]() . The natural solution space for this is obviously
. The natural solution space for this is obviously
9.3 Tools for compactness
In this section we present some (mainly basic) tools from probability theory which are quite crucial to obtain compactness for SPDE. Let ![]() be a topological space. The smallest σ-field
be a topological space. The smallest σ-field ![]() on
on ![]() which contains all open sets is called topological σ-field. A random variable with values in the topological space
which contains all open sets is called topological σ-field. A random variable with values in the topological space ![]() is a measurable map
is a measurable map ![]() . The probability law μ of X on
. The probability law μ of X on ![]() will be given by
will be given by ![]() . An important concept for applications is the pre-compactness of families of random variables. We will need the following definition.
. An important concept for applications is the pre-compactness of families of random variables. We will need the following definition.
The proof of Lemma 9.3.2 in the general case is not very long but quite technical and it is hard to grasp the main ideas. We will therefore briefly outline the case of real-valued random variables, i.e. ![]() and
and ![]() . Let
. Let ![]() be a probability law on
be a probability law on ![]() such that
such that ![]() weakly in the sense of measures as
weakly in the sense of measures as ![]() . We denote by
. We denote by ![]() and F the distribution functions of
and F the distribution functions of ![]() and μ respectively. Let us assume for simplicity that they are injective (otherwise one can argue via their generalized inverse functions). In this case we have
and μ respectively. Let us assume for simplicity that they are injective (otherwise one can argue via their generalized inverse functions). In this case we have ![]() pointwise. Now we set
pointwise. Now we set ![]() . Let us assume for simplicity that the distribution functions
. Let us assume for simplicity that the distribution functions ![]() (
(![]() ) and F are continuous. We define random variables (for
) and F are continuous. We define random variables (for ![]() )
)
Now one can easily see that for ![]()
and similarly ![]() . Moreover, we have
. Moreover, we have
for every ![]() . In the general case this convergence only holds true in points where
. In the general case this convergence only holds true in points where ![]() is continuous (which is in
is continuous (which is in ![]() -a.e. ω).
-a.e. ω).
Lemma 9.3.2 only applies to metric spaces. Unfortunately, this does not cover Banach spaces with the weak topology. Therefore we need the following generalization.