On the Numerical Solution of Equilibria in Auction Models with Asymmetries within the Private-Values Paradigm
Timothy P. Hubbarda and Harry J. Paarschb, aDepartment of Economics, Colby College, USA, bDepartment of Economics, University of Melbourne, Australia, [email protected], [email protected]
Abstract
We describe and compare numerical methods used to approximate equilibrium bid functions in models of auctions as games of incomplete information. In such games, private values are modeled as draws from bidder-specific type distributions and pay-your-bid rules are used to determine transactions prices. We provide a formal comparison of the performance of these numerical methods (based on speed and accuracy) and suggest ways in which they can be improved and extended as well as applied to new settings.
Keywords
First-price auctions; Asymmetric auctions; Private-values model; Numerical solutions
JEL Classification Codes
C20; D44; L1
1 Motivation and Introduction
During the past half century, economists have made considerable progress in understanding the theoretical structure of strategic behavior under market mechanisms, such as auctions, when the number of potential participants is relatively small; see Krishna (2010) for a comprehensive presentation and evaluation of progress.
Perhaps the most significant breakthrough in understanding behavior at auctions was made by Vickrey (1961) who modeled auctions as noncooperative games of incomplete information where bidders have private information concerning their type that they exploit when tendering offers for the good for sale. One analytic device commonly used to describe bidder motivation at auctions is a continuous random variable that represents individual-specific heterogeneity in types, which is typically interpreted as heterogeneity in valuations. The conceptual experiment involves each potential bidder receiving an independent draw from a distribution of valuations. Conditional on his draw, a bidder is assumed to act purposefully, maximizing either the expected profit or the expected utility of profit from winning the good for sale. Another frequently made assumption is that the bidders are ex ante symmetric, their independent draws coming from the same distribution of valuations, an assumption that then allows the researcher to focus on a representative agent’s decision rule when characterizing the Bayes-Nash equilibrium to the auction game, particularly under the pay-your-bid pricing rule, often referred to as first-price auctions, at least by economists.1
The assumption of symmetry is made largely for computational convenience. When the draws of potential bidders are independent, but from different distributions—urns, if you like—then the system of first-order differential equations that characterizes a Bayes-Nash equilibrium usually does not have a convenient closed-form solution: typically, approximate solutions can only be calculated numerically.2
Asymmetries may exist in practice for any number of reasons in addition to the standard heterogeneous-distributions case. For example, an asymmetric first-price model is relevant when bidders are assumed to draw valuations from the same distribution, but have different preferences (for instance, risk-averse bidders might differ by their Arrow-Pratt coefficient of relative risk aversion), when bidders collude and form coalitions, and when the auctioneer (perhaps the government) grants preference to a class of bidders. Bid preferences are particularly interesting because the auctioneer, for whatever reason, deliberately introduces an asymmetry when evaluating bids, even though bidders may be symmetric. In addition, admitting several objects complicates matters considerably; see, for example, Weber (1983). In fact, economic theorists distinguish between multi-object and multi-unit auctions. At multi-unit auctions, it matters not which unit a bidder wins, but rather the aggregate number of units he wins, while at multi-object auctions it matters which specific object(s) a bidder wins. An example of a multi-object auction would involve the sale of an apple and an orange, while an example of a multi-unit auction would involve the sale of two identical apples. At the heart of characterizing Bayes-Nash equilibria in private-values models of sequential, multi-unit auctions (under either first-price or second-price rules) are the solution to an asymmetric-auction game of incomplete information.
When asymmetries exist, canonical and important results from auction theory are not guaranteed to hold. For example, asymmetries can lead to inefficient allocations—outcomes in which the bidder who values the item most does not win the auction, which violates a condition required of the important Revenue Equivalence Theorem; see Myerson (1981). Identifying conditions under which auction mechanisms can be ranked in terms of expected revenue for the seller is an active area of theoretical research; Kirkegaard (2012) has recently shown that the first-price auction yields more revenue than the second-price auction when (roughly) the strong bidder’s distribution is “flatter” and “more dispersed” than the weak bidder’s distribution. Likewise, borrowing elements from first-price auctions, Lebrun (2012) demonstrated that introducing a small pay-your-bid element into second-price auctions can increase expected revenues garnered by the seller in asymmetric settings. Solving various asymmetric models and calculating expected revenue (perhaps through simulations) can provide other directions in which to investigate. Thus, understanding how to solve for equilibria in models of asymmetric auctions is of central importance to economic theory as well as empirical analysis and policy evaluation.
Computation time is of critical importance to structural econometricians who often need to solve for the equilibrium (inverse-) bid functions within an estimation routine for each candidate vector of parameters when recovering the distributions of the latent characteristics, which may be conditioned on covariates as well.3 Most structural econometric work is motivated by the fact that researchers would like to consider counterfactual exercises to make policy recommendations. Because users of auctions are interested in raising as much revenue as possible (or, in the case of procurement, saving as much money as possible), the design of an optimal auction is critical to raising (saving) money. If applied models can capture reality sufficiently well, then they can influence policies at auctions in practice.4 Unfortunately poor approximations to the bidding strategies can lead to biased and inconsistent estimates of the structural elements of the model. Consequently, both accuracy and speed are important when solving for equilibria in models of asymmetric first-price auctions. It will be important to keep both of these considerations in mind as we investigate ways for solving such models.
Our chapter is in six additional sections: in the next, we develop the notation that is used in the remainder of the chapter, then introduce some known results, and, finally, demonstrate how things work within a well-understood environment. We apologize in advance for abusing the English language somewhat: specifically, when we refer to a first-price auction, we mean an auction at which either the highest bidder wins the auction and pays his bid or, in the procurement context, the lowest bidder wins the auction and is paid his bid. This vocabulary is standard among researchers concerned with auctions; see, for example, Paarsch and Hong (2006). When the distinction is important, we shall be specific concerning what we mean.
Subsequently, in Section 3, we describe some well-known numerical strategies that have been used to solve two-point boundary-value problems that are similar to ones researchers face when investigating models of asymmetric first-price auctions. We use this section not just as a way of introducing the strategies, but so we can refer to them later when discussing what researchers concerned with solving for equilibrium (inverse-) bid functions at asymmetric first-price auctions have done. In Section 4, we then discuss research that either directly or indirectly contributed to improving computational strategies to solve for bidding strategies at asymmetric first-price auctions. In particular, we focus on the work of Marshall et al. (1994), Bajari (2001), Fibich and Gavious (2003), Li and Riley (2007), Gayle and Richard (2008), Hubbard and Paarsch (2009), Fibich and Gavish (2011) as well as Hubbard et al. (2013). In Section 5, we depict the solutions to some examples of asymmetric first-price auctions to illustrate how the numerical strategies can be used to investigate problems that would be difficult to analyze analytically. In fact, following Hubbard and Paarsch (2011), we present one example that has received very little attention thus far—asymmetric auctions within the affiliated private-values paradigm (APVP). In Section 6, we compare the established strategies and suggest ways in which they can be extended or improved by future research. We summarize and conclude our work in Section 7. We have also provided the computer code used to solve the examples of asymmetric first-price auctions presented below at the following website: http://www.colby.edu/economics/faculty/thubbard/code/hpfpacode.zip.
2 Theoretical Model
In this section, we first develop our notation, then introduce some known results, and finally demonstrate how the methods work within a well-understood environment.
2.1 Notation
Suppose that potential bidders at the auction are members of a set ![]() where the letter
where the letter ![]() indexes the members. Because the main focus in auction theory is asymmetric information, which economic theorists have chosen to represent as random variables, the bulk of our notation centers around a consistent way to describe random variables. Typically, we denote random variables by uppercase Roman letters—for example,
indexes the members. Because the main focus in auction theory is asymmetric information, which economic theorists have chosen to represent as random variables, the bulk of our notation centers around a consistent way to describe random variables. Typically, we denote random variables by uppercase Roman letters—for example, ![]() or
or ![]() . Realizations of random variables are then denoted by lowercase Roman letters; for example,
. Realizations of random variables are then denoted by lowercase Roman letters; for example, ![]() is a realization of
is a realization of ![]() . Probability density and cumulative distribution functions are denoted
. Probability density and cumulative distribution functions are denoted ![]() and
and ![]() , respectively. When there are different distributions (urns), we again use the subscript to refer to a given bidder’s distribution, but use the set
, respectively. When there are different distributions (urns), we again use the subscript to refer to a given bidder’s distribution, but use the set ![]() numbering. Hence,
numbering. Hence, ![]() and
and ![]() for specific bidders, but
for specific bidders, but ![]() and
and ![]() , in general. If necessary, a vector
, in general. If necessary, a vector ![]() of random variables is denoted
of random variables is denoted ![]() , while a realization, without bidder
, while a realization, without bidder ![]() , is denoted
, is denoted ![]() . The vectors
. The vectors ![]() and
and ![]() are denoted
are denoted ![]() and
and ![]() , respectively.
, respectively.
The lowercase Greek letters ![]() and
and ![]() are used to denote equilibrium bid functions:
are used to denote equilibrium bid functions: ![]() for a bid at a first-price auction where the choice variable is
for a bid at a first-price auction where the choice variable is ![]() . Again, if necessary, we use
. Again, if necessary, we use ![]() to collect all strategies, and
to collect all strategies, and ![]() to collect the choice variables, while
to collect the choice variables, while ![]() is used to collect all the strategies except that of bidder
is used to collect all the strategies except that of bidder ![]() and
and ![]() collects all the choices except that of bidder
collects all the choices except that of bidder ![]() . We use
. We use ![]() to denote the inverse-bid function and
to denote the inverse-bid function and ![]() to collect all of the inverse-bid functions. Now,
to collect all of the inverse-bid functions. Now, ![]() denotes a tender at a low-price auction, where the choice variable is
denotes a tender at a low-price auction, where the choice variable is ![]() . We use
. We use ![]() to collect all strategies and
to collect all strategies and ![]() to collect the choice variables, while
to collect the choice variables, while ![]() is used to collect all the strategies except that of bidder
is used to collect all the strategies except that of bidder ![]() and
and ![]() collects all the choices except that of bidder
collects all the choices except that of bidder ![]() .
.
We denote by ![]() a general family of polynomials, and use
a general family of polynomials, and use ![]() for Chebyshev polynomials, and
for Chebyshev polynomials, and ![]() for Bernstein polynomials.
for Bernstein polynomials.
We use ![]() to collect the parameters of the approximate equilibrium inverse-bid functions.
to collect the parameters of the approximate equilibrium inverse-bid functions.
2.2 Derivation of Symmetric Bayes-Nash Equilibrium
Consider a seller who seeks to divest a single object at the highest price. The seller invites sealed-bid tenders from ![]() potential buyers. After the close of tenders, the bids are opened more or less simultaneously and the object is awarded to the highest bidder. The winner then pays the seller what he bid.
potential buyers. After the close of tenders, the bids are opened more or less simultaneously and the object is awarded to the highest bidder. The winner then pays the seller what he bid.
Suppose each potential buyer has a private value for the object for sale. Assume that each potential buyer knows his private value, but not those of his competitors. Assume that ![]() , the value of potential buyer
, the value of potential buyer ![]() , is an independent draw from the cumulative distribution function
, is an independent draw from the cumulative distribution function ![]() , which is continuous, having an associated probability density function
, which is continuous, having an associated probability density function ![]() that is positive on the compact interval
that is positive on the compact interval ![]() where
where ![]() is weakly greater than zero. Assume that the number of potential buyers
is weakly greater than zero. Assume that the number of potential buyers ![]() as well as the cumulative distribution function of values
as well as the cumulative distribution function of values ![]() and the support
and the support ![]() are common knowledge. This environment is often referred to as the symmetric independent private-value paradigm (IPVP).
are common knowledge. This environment is often referred to as the symmetric independent private-value paradigm (IPVP).
Suppose potential buyers are risk neutral. Thus, when buyer ![]() , who has valuation
, who has valuation ![]() , submits bid
, submits bid ![]() , he receives the following pay-off:
, he receives the following pay-off:
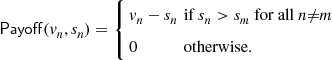 (1)
(1)
Assume that buyer ![]() chooses
chooses ![]() to maximize his expected profit
to maximize his expected profit
![]() (2)
(2)
What is the structure of ![]() ? Within this framework, the identity of bidders (their subscript
? Within this framework, the identity of bidders (their subscript ![]() ) is irrelevant because all bidders are ex ante identical. Thus, without loss of generality, we can focus on the problem faced by bidder
) is irrelevant because all bidders are ex ante identical. Thus, without loss of generality, we can focus on the problem faced by bidder ![]() . Suppose the opponents of bidder
. Suppose the opponents of bidder ![]() use a bid strategy that is a strictly increasing, continuous, and differentiable function
use a bid strategy that is a strictly increasing, continuous, and differentiable function ![]() . Bidder
. Bidder ![]() will win the auction with tender
will win the auction with tender ![]() when all of his opponents bid less than him because their valuations of the object are less than his. Thus,
when all of his opponents bid less than him because their valuations of the object are less than his. Thus,
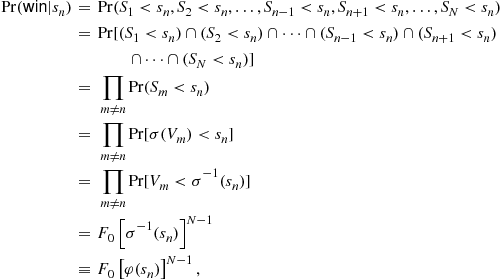
so Eq. (2) can be written as
![]() (3)
(3)
where ![]() is the inverse-bid function. Differentiating Eq. (3) with respect to
is the inverse-bid function. Differentiating Eq. (3) with respect to ![]() yields the following first-order condition:
yields the following first-order condition:
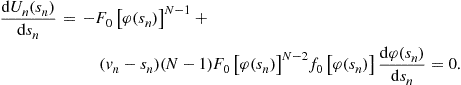 (4)
(4)
In a Bayes-Nash equilibrium, ![]() equals
equals ![]() . Also, under monotonicity, we know from the inverse function theorem that
. Also, under monotonicity, we know from the inverse function theorem that ![]() equals
equals ![]() , so dropping the
, so dropping the ![]() subscript yields
subscript yields
![]() (5)
(5)
Note that, within the symmetric IPVP, optimal behavior is characterized by a first-order ordinary differential equation (ODE); that is, the differential equation involves only the valuation ![]() , the bid function
, the bid function ![]() , and the first derivative of the bid function
, and the first derivative of the bid function ![]() , which we shall often denote in short-hand by
, which we shall often denote in short-hand by ![]() , below. Although the valuation
, below. Although the valuation ![]() enters nonlinearly through the functions
enters nonlinearly through the functions ![]() and
and ![]() , the differential equation is considered linear because
, the differential equation is considered linear because ![]() can be expressed as a linear function of
can be expressed as a linear function of ![]() . These features make the solution to this differential equation tractable, but as we shall see in the subsection that follows, they only hold within the symmetric IPVP.
. These features make the solution to this differential equation tractable, but as we shall see in the subsection that follows, they only hold within the symmetric IPVP.
Equation (5) is among the few differential equations that have a closed-form solution. Following Boyce and DiPrima (1977) and using a notation that will be familiar to students of calculus, we note that when differential equations are of the following form:
![]()
there exists a function ![]() such that
such that
![]()
Thus,
![]()
When ![]() is positive, as it will be in the auction case because it is the ratio of two positive functions multiplied by a positive integer,
is positive, as it will be in the auction case because it is the ratio of two positive functions multiplied by a positive integer,
![]()
so
![]()
whence
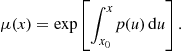
Therefore,
![]()
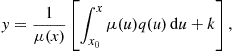
where ![]() is chosen to satisfy an initial condition
is chosen to satisfy an initial condition ![]() equals
equals ![]() .
.
To solve Eq. (5) in a closed-form, a condition relating ![]() and
and ![]() must be known. Fortunately, economic theory provides us with this known relationship at one critical point: in the absence of a reserve price, the minimum price that must be bid,
must be known. Fortunately, economic theory provides us with this known relationship at one critical point: in the absence of a reserve price, the minimum price that must be bid, ![]() equals
equals ![]() . That is, a potential buyer having the lowest value
. That is, a potential buyer having the lowest value ![]() will bid his value. In the presence of a reserve price
will bid his value. In the presence of a reserve price ![]() , one has
, one has ![]() equals
equals ![]() . The appropriate initial condition, together with the differential equation, constitute an initial-value problem which has the following unique solution:
. The appropriate initial condition, together with the differential equation, constitute an initial-value problem which has the following unique solution:
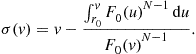 (6)
(6)
This is the symmetric Bayes-Nash equilibrium bid function of the ![]() th bidder; it was characterized by Holt (1980) as well as Riley and Samuelson (1981).
th bidder; it was characterized by Holt (1980) as well as Riley and Samuelson (1981).
We next consider the case where bidders are ex ante asymmetric, proceeding in stages. In an asymmetric environment, a number of complications arise. In particular, unlike the model with identical bidders presented above, typically no closed-form expression for the bidding strategies exists in an asymmetric environment (except in a few special cases described below), so numerical methods are required.
2.3 Bidders from Two Different Urns
Consider a first-price auction with just two potential buyers in the absence of a reserve price and assuming risk neutrality. We present the two-bidder case first to highlight the interdependence among bidders and to characterize explicitly many features of the first-price auction within the IPVP when bidders are asymmetric. In particular, we contrast features of this problem with those of the symmetric case presented in the previous subsection. Suppose that bidder 1 gets an independent draw from urn 1, denoted ![]() , while bidder 2 gets an independent draw from urn 2, denoted
, while bidder 2 gets an independent draw from urn 2, denoted ![]() . Assume that the two valuation distributions have the same support
. Assume that the two valuation distributions have the same support ![]() . The largest of the two bids wins the auction, and the winner pays what he bid.
. The largest of the two bids wins the auction, and the winner pays what he bid.
Now, ![]() , the expected profit of bid
, the expected profit of bid ![]() to player 1, can be written as
to player 1, can be written as
![]()
while ![]() , the expected profit of bid
, the expected profit of bid ![]() to player 2, can be written as
to player 2, can be written as
![]()
Assuming each potential buyer ![]() is using a bid
is using a bid ![]() equal to
equal to ![]() that is monotonically increasing in his value
that is monotonically increasing in his value ![]() , we can write the probability of winning the auction as
, we can write the probability of winning the auction as
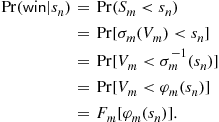
Thus, the expected profit function for bidder 1 is
![]()
while the expected profit function for bidder 2 is
![]()
As in the symmetric case, the presence of bidder ![]() ’s inverse-bid function in bidder
’s inverse-bid function in bidder ![]() ’s objective makes clear the trade-off bidder
’s objective makes clear the trade-off bidder ![]() faces: by submitting a lower bid, he increases the profit he receives when he wins the auction, but he decreases his probability of winning the auction.
faces: by submitting a lower bid, he increases the profit he receives when he wins the auction, but he decreases his probability of winning the auction.
To construct the pair of Bayes-Nash equilibrium bid functions, first maximize each expected profit function with respect to its argument. The necessary first-order condition for these maximization problems are:
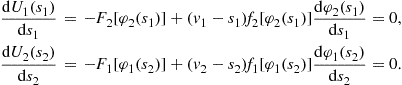
Now, a Bayes-Nash equilibrium is characterized by the following pair of differential equations:5
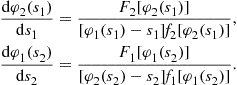 (7)
(7)
These differential equations allow us to describe some essential features of the problem. First, as within the symmetric IPVP, each individual equation constitutes a first-order differential equation because the highest derivative term in each equation is the first derivative of the function of interest. Unlike within the symmetric IPVP, however, we now have a system of differential equations, one for each bidder. Moreover, note that the functions in this system are the inverse-bid functions ![]() , not the bid functions
, not the bid functions ![]() themselves. Within the symmetric IPVP, however, we were concerned with an equilibrium in which all (homogeneous) bidders adopted the same bidding strategy
themselves. Within the symmetric IPVP, however, we were concerned with an equilibrium in which all (homogeneous) bidders adopted the same bidding strategy ![]() . This, together with monotonicity of the bid function, allowed us to map the first-order condition from a differential equation characterizing the inverse-bid function
. This, together with monotonicity of the bid function, allowed us to map the first-order condition from a differential equation characterizing the inverse-bid function ![]() to a differential equation characterizing the bid function
to a differential equation characterizing the bid function ![]() .6 In the asymmetric environment, it is typically impossible to do this because, in general,
.6 In the asymmetric environment, it is typically impossible to do this because, in general,
![]()
While we would like to solve for the bid functions, it is typically impossible to do this directly within the asymmetric IPVP.
The inverse-bid functions ![]() are helpful because they allow us to express the probability of winning the auction for any choice
are helpful because they allow us to express the probability of winning the auction for any choice ![]() ; bidder
; bidder ![]() considers the probability that the other bidder will draw a valuation that will induce him to submit a lower bid in equilibrium than the bid player
considers the probability that the other bidder will draw a valuation that will induce him to submit a lower bid in equilibrium than the bid player ![]() submits. Because the bidders draw valuations from different urns, they do not use the same bidding strategy; the valuation for which it is optimal to submit a bid
submits. Because the bidders draw valuations from different urns, they do not use the same bidding strategy; the valuation for which it is optimal to submit a bid ![]() is, in general, different for the two bidders. Furthermore, the differential equations we obtain are no longer linear. Finally, note that each differential equation involves a bid
is, in general, different for the two bidders. Furthermore, the differential equations we obtain are no longer linear. Finally, note that each differential equation involves a bid ![]() , the derivative of the inverse-bid function for one of the players, which we shall denote hereafter by
, the derivative of the inverse-bid function for one of the players, which we shall denote hereafter by ![]() , and the inverse-bid functions of each of the bidders
, and the inverse-bid functions of each of the bidders ![]() as well as
as well as ![]() . Mathematicians would refer to this system of ODEs as nonautonomous because the system involves the bid
. Mathematicians would refer to this system of ODEs as nonautonomous because the system involves the bid ![]() explicitly.7 This last fact highlights the interdependence among players that is common to game-theoretic models. Thus, in terms of deriving the equilibrium inverse-bid functions within the asymmetric IPVP, we must solve a nonlinear system of first-order ODEs.
explicitly.7 This last fact highlights the interdependence among players that is common to game-theoretic models. Thus, in terms of deriving the equilibrium inverse-bid functions within the asymmetric IPVP, we must solve a nonlinear system of first-order ODEs.
The case in which each of two bidders draws his valuation from a different urn has allowed us to contrast the features of the problem with those of the symmetric environment in a transparent way. There are also conditions that the equilibrium bid functions must satisfy, and which allow us to solve the pair of differential equations, but we delay that discussion until after we present the ![]() -bidder case.
-bidder case.
2.4 General Model
We now extend the model of the first-price auction presented above to one with ![]() potential buyers in the absence of a reserve price and assuming risk neutrality. Suppose that bidder
potential buyers in the absence of a reserve price and assuming risk neutrality. Suppose that bidder ![]() gets an independent draw from urn
gets an independent draw from urn ![]() , denoted
, denoted ![]() . Assume that all valuation distributions have a common, compact support
. Assume that all valuation distributions have a common, compact support ![]() .8 Then the largest of the
.8 Then the largest of the ![]() bids wins the auction, and the bidder pays what he bid.
bids wins the auction, and the bidder pays what he bid.
Again, ![]() , the expected profit of bid
, the expected profit of bid ![]() to player
to player ![]() , can be written as
, can be written as
![]()
Assuming each potential buyer ![]() is using a bid
is using a bid ![]() that is monotonically increasing in his value
that is monotonically increasing in his value ![]() , we can write the probability of winning the auction as
, we can write the probability of winning the auction as
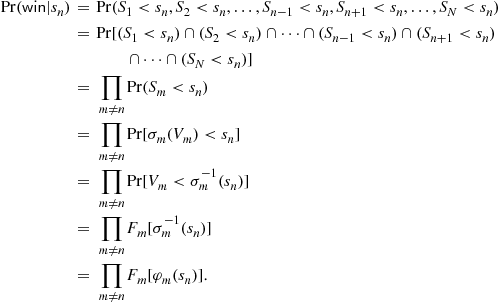
Thus, the expected profit function for bidder ![]() is
is
![]()
To construct the Bayes-Nash equilibrium bid functions, first maximize each expected profit function with respect to its argument. The necessary first-order condition for a representative maximization problem is:
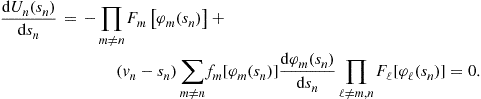
Replacing ![]() with a generic bid
with a generic bid ![]() and noting that
and noting that ![]() equals
equals ![]() , we can rearrange this first-order condition as
, we can rearrange this first-order condition as
![]() (8)
(8)
which can be summed over all ![]() bidders to yield
bidders to yield
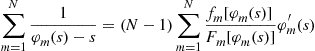
or
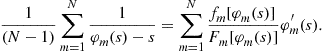
Subtracting Eq. (8) from this latter expression yields
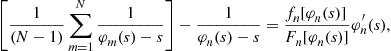
which leads to the, perhaps traditional, differential equation formulation
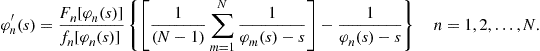 (9)
(9)
In addition to this system of differential equations (or system (7) in the two-bidder case presented above), two types of boundary conditions exist. The first generalizes the initial condition from the symmetric environment to an asymmetric one:
Left-Boundary Condition on Bid Functions: ![]() for all
for all ![]() .This left-boundary condition simply requires any bidder who draws the lowest valuation possible to bid his valuation. It extends the condition from the environment where there was only one type of bidder to one where there are
.This left-boundary condition simply requires any bidder who draws the lowest valuation possible to bid his valuation. It extends the condition from the environment where there was only one type of bidder to one where there are ![]() types of bidders.9 We shall need to use the boundary condition(s) with the system of differential equations to solve for the inverse-bid functions, as discussed above. Specifically, we shall be interested in solving for a monotone pure-strategy equilibrium (MPSE) in which each bidder adopts a bidding strategy that maximizes expected pay-offs given the strategies of the other players. Given this focus, we can translate the left-boundary condition defined above into the following boundary condition which involves the inverse-bid functions:
types of bidders.9 We shall need to use the boundary condition(s) with the system of differential equations to solve for the inverse-bid functions, as discussed above. Specifically, we shall be interested in solving for a monotone pure-strategy equilibrium (MPSE) in which each bidder adopts a bidding strategy that maximizes expected pay-offs given the strategies of the other players. Given this focus, we can translate the left-boundary condition defined above into the following boundary condition which involves the inverse-bid functions:
Left-Boundary Condition on Inverse-Bid Functions: ![]() for all
for all ![]() . The second type of condition obtains at the right-boundary. Specifically,
. The second type of condition obtains at the right-boundary. Specifically,
Right-Boundary Condition on Bid Functions: ![]() for all
for all ![]() . The reader may find this condition somewhat surprising: even though the bidders may adopt different bidding strategies, all bidders will choose to submit the same bid when they draw the highest valuation possible. For specific details and proofs of this condition, see part (2) of Theorem 1 of Lebrun (1999), Lemma 10 of Maskin and Riley (2003), and, for a revealed preference-style argument, Footnote 12 of Kirkegaard (2009).10 Informally, at least in the two-bidder case, no bidder will submit a bid that exceeds the highest bid chosen by his opponent because the bidder could strictly decrease the bid by some small amount
. The reader may find this condition somewhat surprising: even though the bidders may adopt different bidding strategies, all bidders will choose to submit the same bid when they draw the highest valuation possible. For specific details and proofs of this condition, see part (2) of Theorem 1 of Lebrun (1999), Lemma 10 of Maskin and Riley (2003), and, for a revealed preference-style argument, Footnote 12 of Kirkegaard (2009).10 Informally, at least in the two-bidder case, no bidder will submit a bid that exceeds the highest bid chosen by his opponent because the bidder could strictly decrease the bid by some small amount ![]() and still win the auction with certainty, and increase his expected profits. This right-boundary condition also has a counterpart which involves the inverse-bid functions.
and still win the auction with certainty, and increase his expected profits. This right-boundary condition also has a counterpart which involves the inverse-bid functions.
Right-Boundary Condition on Inverse-Bid Functions: ![]() for all
for all ![]() .
.
A few comments are in order here: first, because we now have conditions at both low and high valuations (bids), the problem is no longer an initial-value problem, but rather a boundary-value problem. Thus, we are interested in the solution to the system of differential equations which satisfies both the left-boundary condition on the inverse-bid function and the right-boundary condition on the inverse-bid function. In the mathematics literature, this is referred to as a two-point boundary-value problem. The critical difference between an initial-value problem and a boundary-value problem is that auxiliary conditions concern the solution at one point in an initial-value problem, while auxiliary conditions concern the solution at several points (in this case, two) in a boundary-value problem. The other challenging component of this problem is that the common high bid ![]() is unknown a priori, and is determined endogenously by the behavior of bidders. This means that the high bid
is unknown a priori, and is determined endogenously by the behavior of bidders. This means that the high bid ![]() must be solved for as part of the solution to the system of differential equations. That is, we have a system of differential equations that are defined over a domain (because we are solving for the inverse-bid functions) that is unknown a priori. In this sense, the problem is considered a free boundary-value problem. Note, too, that this system is overidentified: while there are
must be solved for as part of the solution to the system of differential equations. That is, we have a system of differential equations that are defined over a domain (because we are solving for the inverse-bid functions) that is unknown a priori. In this sense, the problem is considered a free boundary-value problem. Note, too, that this system is overidentified: while there are ![]() differential equations, there are
differential equations, there are ![]() boundary conditions as well. In addition, some properties of the solution are known beforehand: bidders should not submit bids that exceed their valuations and the (inverse-) bid functions must be monotonic.
boundary conditions as well. In addition, some properties of the solution are known beforehand: bidders should not submit bids that exceed their valuations and the (inverse-) bid functions must be monotonic.
One feature of this system of differential equations that makes them interesting to computational economists, and challenging to economic theorists, is that the Lipschitz condition does not hold. A function ![]() satisfies the Lipschitz condition on a
satisfies the Lipschitz condition on a ![]() -dimensional interval
-dimensional interval ![]() if there exists a Lipschitz constant
if there exists a Lipschitz constant ![]() (greater than zero) such that
(greater than zero) such that
![]()
for a given vector norm ![]() and for all
and for all ![]() and
and ![]() . To get a better understanding of this, assume
. To get a better understanding of this, assume ![]() and rewrite the Lipschitz condition as
and rewrite the Lipschitz condition as
![]()
where ![]() equals
equals ![]() and we have chosen to use the
and we have chosen to use the ![]() norm.11 If we assume that
norm.11 If we assume that ![]() is differentiable and we let
is differentiable and we let ![]() , then the Lipschitz condition means that
, then the Lipschitz condition means that
![]()
so the derivative is bounded by the Lipschitz constant.12 The system (9) does not satisfy the Lipschitz condition in a neighborhood of ![]() because a singularity obtains at
because a singularity obtains at ![]() . To see this, note that the left-boundary condition requires that
. To see this, note that the left-boundary condition requires that ![]() equals
equals ![]() for all bidders
for all bidders ![]() equal to
equal to ![]() . This condition implies that the denominator terms in the right-hand side of these equations which involve
. This condition implies that the denominator terms in the right-hand side of these equations which involve ![]() go to zero. Note, too, that the numerators contain
go to zero. Note, too, that the numerators contain ![]() s, which equal zero at
s, which equal zero at ![]() . Because the Lipschitz condition is not satisfied for the system, much of the theory concerning systems of ODEs no longer applies.
. Because the Lipschitz condition is not satisfied for the system, much of the theory concerning systems of ODEs no longer applies.
While not the focus of this research, our presentation would be incomplete were we to ignore the results concerning existence and uniqueness of equilibria developed by economic theorists. The issue of existence is critical to resolve before solution methods can be applied. While computational methods could be used to approximate numerically a solution that may not exist, the value of a numerical solution is far greater when we know a solution exists than when not. The issue of uniqueness is essential to empirical researchers using data from first-price auctions. Without uniqueness, an econometrician would have a difficult task justifying that the data observed are all derived from the same equilibrium. Because the Lipschitz condition fails, one of the sufficient conditions of the Picard-Lindelöf theorem, which guarantees that a unique solution exists to an initial-value problem, does not hold. Consequently, fundamental theorems for systems of differential equations cannot be applied to the system (9).
Despite this difficulty, Lebrun (1999) proved that the inverse-bid functions are differentiable on ![]() and that a unique Bayes-Nash equilibrium exists when all valuation distributions have a common support (as we have assumed above) and a mass point at
and that a unique Bayes-Nash equilibrium exists when all valuation distributions have a common support (as we have assumed above) and a mass point at ![]() . He also provided sufficient conditions for uniqueness when there are no mass points, under assumptions which are quite mild and easy for a researcher to verify. Existence was also demonstrated by Maskin and Riley (2000b), while Maskin and Riley (2000a) investigated some equilibrium properties of asymmetric first-price auctions. The discussion above is most closely related to the approach taken by Lebrun (1999) as well as Lizzeri and Persico (2000), for auctions with two asymmetric bidders; these researchers established existence by showing that a solution exists to the system of differential equations.13 Reny (1999) proved existence in a general class of games, while Athey (2001) proved that a pure strategy Nash equilibrium exists for first-price auctions with heterogeneous bidders under a variety of circumstances, some of which we consider below. For a discussion on the existence of an equilibrium in first-price auctions, see Appendix G of Krishna (2002).
. He also provided sufficient conditions for uniqueness when there are no mass points, under assumptions which are quite mild and easy for a researcher to verify. Existence was also demonstrated by Maskin and Riley (2000b), while Maskin and Riley (2000a) investigated some equilibrium properties of asymmetric first-price auctions. The discussion above is most closely related to the approach taken by Lebrun (1999) as well as Lizzeri and Persico (2000), for auctions with two asymmetric bidders; these researchers established existence by showing that a solution exists to the system of differential equations.13 Reny (1999) proved existence in a general class of games, while Athey (2001) proved that a pure strategy Nash equilibrium exists for first-price auctions with heterogeneous bidders under a variety of circumstances, some of which we consider below. For a discussion on the existence of an equilibrium in first-price auctions, see Appendix G of Krishna (2002).
2.5 Special Case
As we noted above, an explicit solution to the system (9), or system (7) in the two-bidder case, exists only in a few special cases. The special case we present here involves two bidders who draw valuations from asymmetric uniform distributions.14 For two uniform distributions to be different, they must have different supports, which requires us to modify slightly the model we presented above. Specifically, consider a first-price auction involving two risk-neutral bidders at which no reserve price exists. Suppose that bidder ![]() gets an independent draw from a uniform distribution
gets an independent draw from a uniform distribution ![]() having support
having support ![]() . For convenience, we assume the lowest possible valuation
. For convenience, we assume the lowest possible valuation ![]() is zero, and is common to all bidders: the bidders only differ by the highest possible valuation they can draw. The largest of the two bids wins the auction, and the bidder pays what he bid.
is zero, and is common to all bidders: the bidders only differ by the highest possible valuation they can draw. The largest of the two bids wins the auction, and the bidder pays what he bid.
Within this environment,
![]()
so the probability of bidder ![]() winning the auction with a bid
winning the auction with a bid ![]() equals
equals
![]()
Thus, the expected profit function for bidder 1 is
![]()
while the expected profit function for bidder 2 is
![]()
Taking the first-order conditions for maximization of each bidder’s expected profit and setting them equal to zero yields:
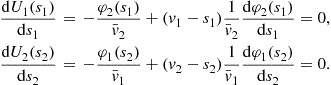
The following pair of differential equations characterizes the Bayes-Nash equilibrium:
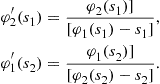 (10)
(10)
As described above, the equilibrium inverse-bid functions solve this pair of differential equations, subject to the following boundary conditions:
![]()
and
![]()
Together, these conditions imply that, while the domains of the bid functions differ, the domains of the inverse-bid functions are the same for both bidders.
This system can be solved in closed-form. The first step is to find the common and, a priori unknown, high bid ![]() . To do this, following Krishna (2002), we can rewrite the equation describing
. To do this, following Krishna (2002), we can rewrite the equation describing ![]() by subtracting one from both sides and rearranging to obtain
by subtracting one from both sides and rearranging to obtain
![]()
Adding the two equations yields
![]()
Note, however, that
![]()
so
![]()
Integrating both sides yields
![]() (11)
(11)
where we have used the left-boundary condition that ![]() equals zero to determine the constant of integration. This equation can be used to solve for
equals zero to determine the constant of integration. This equation can be used to solve for ![]() using the right-boundary condition
using the right-boundary condition
![]()
so
![]()
Following Krishna (2002), we can use a change of variables by setting
![]()
for which
![]()
Note, too, that the change of variables implies
![]()
The key to solving the system of differential equations is that each differential equation in the system (10) can be expressed as an alternative differential equation which depends only on the inverse-bid function, and its derivative, for a single bidder: it does not involve the other bidder’s inverse-bid function. To see this, solve for ![]() using Eq. (11) and substitute it into the equation defining
using Eq. (11) and substitute it into the equation defining ![]() in the system (10) to obtain
in the system (10) to obtain
![]()
Now, using the change of variables proposed above, as well as the relationships obtaining from it, this differential equation can be written as
![]()
which can be rewritten as
![]()
The solution to this differential equation is
![]()
where ![]() is the constant of integration. Using the change of variables, the inverse-bid function is
is the constant of integration. Using the change of variables, the inverse-bid function is
![]()
where
![]()
is determined by the right-boundary condition that ![]() equals
equals ![]() . Likewise,
. Likewise,
![]()
where
![]()
which completes the closed-form solution for the inverse-bid functions in this special case. The associated bid functions for the case where ![]() is Uniform[0,1] and
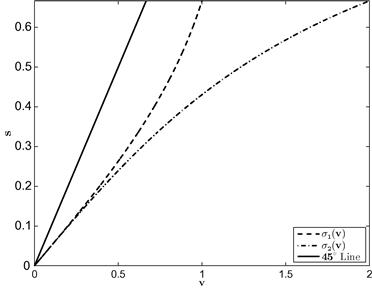
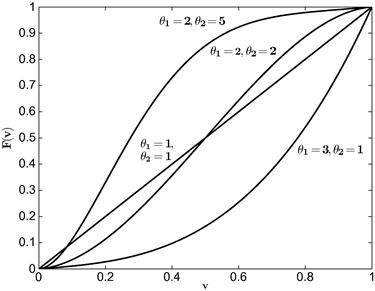
is Uniform[0,1] and ![]() is Uniform[0, 2] are depicted in Figure 1.
is Uniform[0, 2] are depicted in Figure 1.
In this example, tractability obtains because ![]() , the inverse of the Mills’ ratio, is a convenient function of the inverse-bid function: it equals
, the inverse of the Mills’ ratio, is a convenient function of the inverse-bid function: it equals ![]() . Thus, the pair of differential equations in the two-bidder case can be expressed as a pair of independent ODEs. That is, the relationship among bidders is so special we can use the approach we used to solve for the equilibrium at a symmetric first-price auction. In short, we are able to derive closed-form expressions for the inverse-bid functions (or, likewise, for the bid functions). In general, inverses of the Mills’ ratio will involve terms that prevent such isolation and will require using numerical methods.
. Thus, the pair of differential equations in the two-bidder case can be expressed as a pair of independent ODEs. That is, the relationship among bidders is so special we can use the approach we used to solve for the equilibrium at a symmetric first-price auction. In short, we are able to derive closed-form expressions for the inverse-bid functions (or, likewise, for the bid functions). In general, inverses of the Mills’ ratio will involve terms that prevent such isolation and will require using numerical methods.
2.6 Extensions
The model presented above is relevant to a number of different research questions. In this subsection, we discuss some extensions to the model which also require the use of computational methods.15 While it may seem reasonable empirically to assume that there may exist more than one type of bidder at auction, the asymmetric first-price model we have presented can arise even when bidders draw valuations from the same distribution. In particular, we consider first the case of risk-averse bidders and then the case in which bidders collude and form coalitions. We then cast the model presented above in a procurement environment in which the lowest bidder is awarded the contract. Finally, given this procurement setting, we consider a case in which the auctioneer (in this case, the government) grants preference to a class of bidders.
2.6.1 Risk Aversion
In the discussion of asymmetric first-price auctions that we presented above, we assumed (as researchers most commonly do) that the asymmetry was relevant because bidders drew valuations from different distributions. Alternatively, we could assume that bidders are symmetric in that they all draw valuations from the same distribution, but asymmetric in that they have heterogeneous preferences. Assume that buyer ![]() ’s value
’s value ![]() is an independent draw from the (common) cumulative distribution function
is an independent draw from the (common) cumulative distribution function ![]() , which is continuous, having an associated positive probability density function
, which is continuous, having an associated positive probability density function ![]() that has compact support
that has compact support ![]() where
where ![]() is weakly greater than zero. Assume that the number of potential buyers
is weakly greater than zero. Assume that the number of potential buyers ![]() as well as the cumulative distribution function of values
as well as the cumulative distribution function of values ![]() and the support
and the support ![]() are common knowledge.
are common knowledge.
We relax the assumption that bidders are risk neutral and, instead, assume that the bidders have different degrees of risk aversion. While individual valuations are private information, all bidders know that valuations are drawn from ![]() and know each bidder’s utility function. Consider the case in which bidders have constant relative risk aversion (CRRA) utility functions but differ in their Arrow-Pratt coefficient of relative risk aversion
and know each bidder’s utility function. Consider the case in which bidders have constant relative risk aversion (CRRA) utility functions but differ in their Arrow-Pratt coefficient of relative risk aversion
![]()
where ![]() for all bidders
for all bidders ![]() .16 Thus, when buyer
.16 Thus, when buyer ![]() submits bid
submits bid ![]() , he receives the following pay-off:
, he receives the following pay-off:
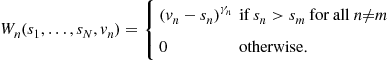 (12)
(12)
Under risk neutrality the profit bidder ![]() receives when he wins the auction is linear in his bid
receives when he wins the auction is linear in his bid ![]() so the pay-off is additively separable from the bidder’s valuation. This breaks down under risk aversion as utility becomes nonlinear—utility is concave in the CRRA case.17
so the pay-off is additively separable from the bidder’s valuation. This breaks down under risk aversion as utility becomes nonlinear—utility is concave in the CRRA case.17
Assuming each potential buyer ![]() is using a bid
is using a bid ![]() that is monotonically increasing in his value
that is monotonically increasing in his value ![]() , the expected utility function for bidder
, the expected utility function for bidder ![]() is
is
![]()
The necessary first-order condition for a representative utility maximization problem is:
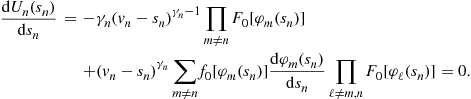
Replacing ![]() with a general bid
with a general bid ![]() and noting that
and noting that ![]() equals
equals ![]() , we can rearrange this first-order condition as
, we can rearrange this first-order condition as
![]() (13)
(13)
which can be summed over all ![]() bidders to yield
bidders to yield
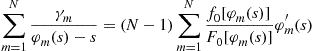
or
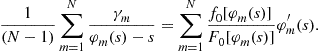
Subtracting Eq. (13) from this latter expression yields
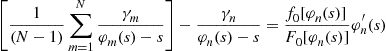
which leads to the following differential equation formulation:
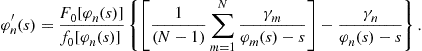 (14)
(14)
In addition to this system of ODEs, there are two types of boundary conditions on the equilibrium (inverse-) bid functions which mirror those of the asymmetric first-price auction:
Left-Boundary Condition (on Inverse-Bid Functions): ![]() for all
for all ![]() .
.
We are interested in the solution to the system (14) which satisfies the right- and left-boundary conditions on the inverse-bid functions. In general, no closed-form solution exists and the Lipschitz condition does not hold in a neighborhood around ![]() because of a singularity. Consequently, numerical methods are again required.
because of a singularity. Consequently, numerical methods are again required.
2.6.2 Collusion or Presence of Coalitions
Consider instead a model in which all ![]() potential bidders have homogeneous, risk-neutral preferences. Furthermore, assume that all bidders draw independent valuations from the same distribution
potential bidders have homogeneous, risk-neutral preferences. Furthermore, assume that all bidders draw independent valuations from the same distribution ![]() , having an associated positive probability density function
, having an associated positive probability density function ![]() that has compact support
that has compact support ![]() . Suppose, however, subsets of bidders join (collude to form) coalitions. Introducing collusion into an otherwise symmetric auction is what motivated the pioneering research of Marshall et al. (1994). Bajari (2001) proposed using numerical methods to understand better collusive behavior in a series of comparative static-like computational experiments. We discuss the contributions of these researchers later in this chapter. First, however, it is important to recognize that the symmetric first-price auction with collusion, as is typically modeled, is equivalent to the standard asymmetric first-price auction model presented above. Specifically, if the bidders form coalitions of different sizes, a distributional asymmetry is created and the model is just like the case in which each coalition is considered a bidder which draws its valuation from a different distribution.
. Suppose, however, subsets of bidders join (collude to form) coalitions. Introducing collusion into an otherwise symmetric auction is what motivated the pioneering research of Marshall et al. (1994). Bajari (2001) proposed using numerical methods to understand better collusive behavior in a series of comparative static-like computational experiments. We discuss the contributions of these researchers later in this chapter. First, however, it is important to recognize that the symmetric first-price auction with collusion, as is typically modeled, is equivalent to the standard asymmetric first-price auction model presented above. Specifically, if the bidders form coalitions of different sizes, a distributional asymmetry is created and the model is just like the case in which each coalition is considered a bidder which draws its valuation from a different distribution.
The ![]() potential bidders form
potential bidders form ![]() coalitions with a representative coalition
coalitions with a representative coalition ![]() having size
having size ![]() with
with
![]()
and
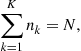
where ![]() is less than or equal to
is less than or equal to ![]() . We are not concerned with how the coalition divides up the profit if it wins the item at auction. Instead, we are simply concerned with how each coalition behaves in this case. Note, too, that we allow for coalitions to be of size 1; that is, a bidder may choose not to belong to a coalition, and thus behaves independently (noncooperatively).
. We are not concerned with how the coalition divides up the profit if it wins the item at auction. Instead, we are simply concerned with how each coalition behaves in this case. Note, too, that we allow for coalitions to be of size 1; that is, a bidder may choose not to belong to a coalition, and thus behaves independently (noncooperatively).
Assume that each coalition ![]() chooses its bid
chooses its bid ![]() to maximize its (aggregate) expected profit
to maximize its (aggregate) expected profit
![]()
Coalition ![]() will win the auction with tender
will win the auction with tender ![]() when all other coalitions bid less than
when all other coalitions bid less than ![]() because the highest valuation of the object for each rival coalition induces bids that are less than that of coalition
because the highest valuation of the object for each rival coalition induces bids that are less than that of coalition ![]() . Assuming each coalition
. Assuming each coalition ![]() adopts a bidding strategy
adopts a bidding strategy ![]() that is monotonically increasing in its value
that is monotonically increasing in its value ![]() , we can write the probability of winning the auction as
, we can write the probability of winning the auction as
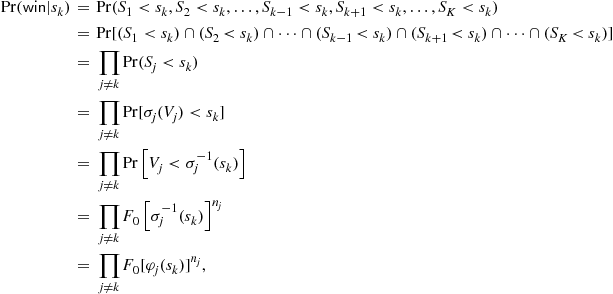
where, again, ![]() is the inverse-bid function. Thus, the expected profit function of coalition
is the inverse-bid function. Thus, the expected profit function of coalition ![]() is
is
![]()
When the number of bidders in each coalition is different for at least two coalitions (when ![]() for some
for some ![]() ), then even though all bidders draw valuations from the same distribution, an asymmetry obtains. Thus, for a given bid, each coalition faces a different probability of winning the auction. This probability of winning differs across coalitions because, when choosing its bid, each coalition
), then even though all bidders draw valuations from the same distribution, an asymmetry obtains. Thus, for a given bid, each coalition faces a different probability of winning the auction. This probability of winning differs across coalitions because, when choosing its bid, each coalition ![]() must consider the distribution of the maximum of
must consider the distribution of the maximum of ![]() draws for each rival coalition
draws for each rival coalition ![]() . If all coalitions are of the same size, then this model collapses to the symmetric IPVP with
. If all coalitions are of the same size, then this model collapses to the symmetric IPVP with ![]() bidders for which we can solve for the (common) bidding strategy which has a closed-form solution, as shown above. When, however, the number of bidders in each coalition is different for at least two of the coalitions, the model is just like the asymmetric first-price model.
bidders for which we can solve for the (common) bidding strategy which has a closed-form solution, as shown above. When, however, the number of bidders in each coalition is different for at least two of the coalitions, the model is just like the asymmetric first-price model.
Each coalition will choose its bid, given its (highest) valuation, to maximize its expected profit. The necessary first-order condition for a representative maximization problem is:
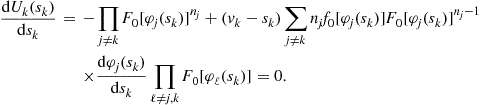
Replacing ![]() with a general bid
with a general bid ![]() and noting that
and noting that ![]() equals
equals ![]() , we can rearrange this first-order condition as
, we can rearrange this first-order condition as
![]() (15)
(15)
which can be summed over all ![]() coalitions to yield
coalitions to yield
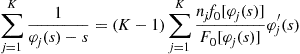
or
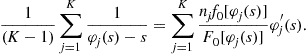
Subtracting Eq. (15) from this latter expression yields
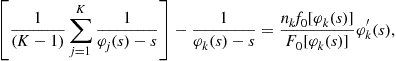
which leads to the, perhaps traditional, differential equation formulation
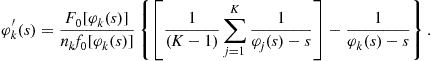
In addition to this system of ODEs, there are two types of boundary conditions on the equilibrium (inverse-) bid functions which mirror those of the asymmetric first-price auction:
Left-Boundary Condition (on Inverse-Bid Functions): ![]() for all
for all ![]() .
.
In this collusive environment, where bidders form coalitions, there is almost never a closed-form solution to the system of ODEs: one exception is when the bidders all draw valuations from a common uniform distribution. In such an environment, it is as if each coalition ![]() receives a draw from a power distribution with parameter (power)
receives a draw from a power distribution with parameter (power) ![]() and the coalition game is like an asymmetric first-price auction in which each bidder (coalition) receives a draw from a different power distribution. Plum (1992) derived the explicit equilibrium bid functions within an environment when there are two bidders (or, in this case, coalitions of equal size) at auction with different valuation supports.18 This uniform/power distribution example constitutes another very special case of an asymmetric auction. In general, no closed-form solution exists and the Lipschitz condition does not hold in a neighborhood around
and the coalition game is like an asymmetric first-price auction in which each bidder (coalition) receives a draw from a different power distribution. Plum (1992) derived the explicit equilibrium bid functions within an environment when there are two bidders (or, in this case, coalitions of equal size) at auction with different valuation supports.18 This uniform/power distribution example constitutes another very special case of an asymmetric auction. In general, no closed-form solution exists and the Lipschitz condition does not hold in a neighborhood around ![]() because of a singularity. Again, numerical methods are required.
because of a singularity. Again, numerical methods are required.
2.6.3 Procurement
We can modify the above analysis of the first-price auction with ![]() potential buyers to analyze a procurement environment in which a government agency seeks to complete an indivisible task at the lowest cost. The agency invites sealed-bid tenders from
potential buyers to analyze a procurement environment in which a government agency seeks to complete an indivisible task at the lowest cost. The agency invites sealed-bid tenders from ![]() potential suppliers—firms. The bids are opened more or less simultaneously and the contract is awarded to the lowest bidder who wins the right to perform the task. The agency then pays the winning firm its bid on completion of the task. Assume that there is no price ceiling—a maximum acceptable bid that has been imposed by the buyer—and assume bidders (firms) are risk neutral. Suppose that bidder
potential suppliers—firms. The bids are opened more or less simultaneously and the contract is awarded to the lowest bidder who wins the right to perform the task. The agency then pays the winning firm its bid on completion of the task. Assume that there is no price ceiling—a maximum acceptable bid that has been imposed by the buyer—and assume bidders (firms) are risk neutral. Suppose that bidder ![]() gets an independent cost draw
gets an independent cost draw ![]() from urn
from urn ![]() , denoted
, denoted ![]() . Assume that all cost distributions have a common, compact support
. Assume that all cost distributions have a common, compact support ![]() .
.
Now, ![]() , the expected profit of bid
, the expected profit of bid ![]() to player
to player ![]() , can be written as
, can be written as
![]()
Assuming each potential buyer ![]() is using a bid
is using a bid ![]() that is monotonically increasing in his cost
that is monotonically increasing in his cost ![]() , we can write the probability of winning the auction as
, we can write the probability of winning the auction as
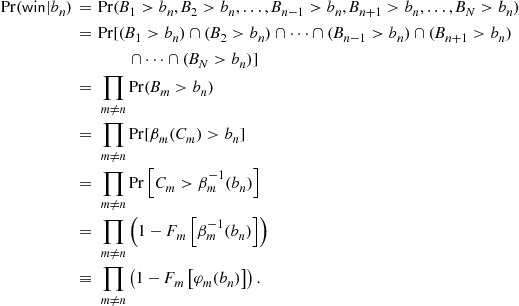
Thus, the expected profit function for bidder ![]() is
is
![]()
To construct the Bayes-Nash, equilibrium bid functions, first maximize each expected profit function with respect to its argument. The necessary first-order condition for a representative maximization problem is:
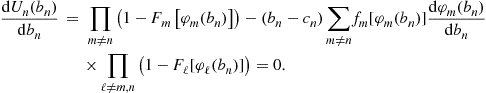
Replacing ![]() with a general bid
with a general bid ![]() and noting that
and noting that ![]() equals
equals ![]() , we can rearrange this first-order condition as
, we can rearrange this first-order condition as
![]() (16)
(16)
which can be summed over all ![]() bidders to yield
bidders to yield
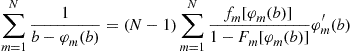
or
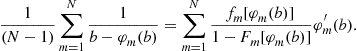
Subtracting Eq. (16) from this latter expression yields
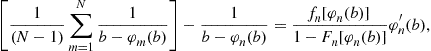
which leads to the, perhaps traditional, differential equation formulation
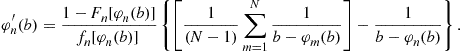 (17)
(17)
In addition to this system of differential equations, as in the asymmetric first-price auction, there are two types of boundary conditions on the equilibrium bid functions at an asymmetric procurement auction.
Right-Boundary Condition on Bid Functions: ![]() for all
for all ![]() . This right-boundary condition requires any bidder who draws the highest cost possible to bid his cost.19 We shall use the boundary condition(s) with the system of differential equations to solve for the MPSE inverse-bid functions, as discussed above. Given this focus, we can translate this right-boundary condition into the following boundary condition which involves the inverse-bid functions:
. This right-boundary condition requires any bidder who draws the highest cost possible to bid his cost.19 We shall use the boundary condition(s) with the system of differential equations to solve for the MPSE inverse-bid functions, as discussed above. Given this focus, we can translate this right-boundary condition into the following boundary condition which involves the inverse-bid functions:
Right-Boundary Condition on Inverse-Bid Functions: ![]() for all
for all ![]() . The second type of condition obtains at the left-boundary and is analogous to the right-boundary conditions from the asymmetric first-price auction. Specifically,
. The second type of condition obtains at the left-boundary and is analogous to the right-boundary conditions from the asymmetric first-price auction. Specifically,
Left-Boundary Condition on Bid Functions: ![]() for all
for all ![]() . This condition requires that, even though the bidders may adopt different bidding strategies, all bidders will choose to submit the same bid if they draw the lowest cost possible. Consider two firms: any bid by one that is below
. This condition requires that, even though the bidders may adopt different bidding strategies, all bidders will choose to submit the same bid if they draw the lowest cost possible. Consider two firms: any bid by one that is below ![]() would be suboptimal because the firm could strictly increase the bid by some small amount
would be suboptimal because the firm could strictly increase the bid by some small amount ![]() and still win the auction with certainty, while at the same time increasing its profits. See the formal arguments provided in the citations given above for the asymmetric first-price model. This left-boundary condition also has a counterpart which involves the inverse-bid functions,
and still win the auction with certainty, while at the same time increasing its profits. See the formal arguments provided in the citations given above for the asymmetric first-price model. This left-boundary condition also has a counterpart which involves the inverse-bid functions,
Thus, we are interested in the solution to the system of differential equations which satisfies both the right-boundary condition on the inverse-bid functions and the left-boundary condition on the inverse-bid functions. Because we have conditions on the inverse-bid functions at both ends of the domain, we have a two-point boundary-value problem. In the procurement environment, because the common low bid is unknown a priori, the lower boundary constitutes the free boundary.
The system (17) does not satisfy the Lipschitz condition in a neighborhood of ![]() because a singularity obtains at
because a singularity obtains at ![]() . To see this, note that right-boundary condition requires that
. To see this, note that right-boundary condition requires that ![]() equals
equals ![]() for all bidders
for all bidders ![]() equal to
equal to ![]() . This condition implies that the denominator terms in the right-hand side of these equations which involve
. This condition implies that the denominator terms in the right-hand side of these equations which involve ![]() vanish. Likewise, the numerators involve a survivor function which equals zero at
vanish. Likewise, the numerators involve a survivor function which equals zero at ![]() . Thus, again, because the Lipschitz condition is not satisfied, much of the theory concerning systems of ODEs no longer applies.
. Thus, again, because the Lipschitz condition is not satisfied, much of the theory concerning systems of ODEs no longer applies.
2.6.4 Bid Preferences
Even when bidders draw valuations or costs from the same distribution, buyers (sellers) sometimes invoke policies or rules that introduce asymmetries. Bid preference policies are a commonly studied example; see, for example, Marion (2007), Hubbard and Paarsch (2009) as well as Krasnokutskaya and Seim (2011). We shall continue with the procurement model by considering the effect of a bid preference policy. Specifically, consider the most commonly used preference program under which the bids of preferred firms are treated differently for the purposes of evaluation only. In particular, the bids of preferred firms are typically scaled by some discount factor which is one plus a preference rate denoted ![]() . Suppose there are
. Suppose there are ![]() preferred bidders and
preferred bidders and ![]() typical (nonpreferred) bidders, where
typical (nonpreferred) bidders, where ![]() equals
equals ![]() . The preference policy reduces the bids of class 1 firms for the purposes of evaluation only; a winning firm is still paid its bid, on completion of an awarded contract.
. The preference policy reduces the bids of class 1 firms for the purposes of evaluation only; a winning firm is still paid its bid, on completion of an awarded contract.
Each bidder draws a firm-specific cost independently from a potentially asymmetric cost distribution ![]() where
where ![]() corresponds to the class the firm belongs to
corresponds to the class the firm belongs to ![]() . Each firm then chooses its bid
. Each firm then chooses its bid ![]() to maximize
to maximize
![]()
Suppose that all bidders of class ![]() use a (class-symmetric) monotonically increasing strategy
use a (class-symmetric) monotonically increasing strategy ![]() . This assumption imposes structure on the probability of winning an auction, conditional on a particular strategy
. This assumption imposes structure on the probability of winning an auction, conditional on a particular strategy ![]() , which then determines the bid
, which then determines the bid ![]() given a class
given a class ![]() firm’s cost draw. In particular, for a class 1 bidder,
firm’s cost draw. In particular, for a class 1 bidder,
![]()
while for a class 2 bidder
![]()
where ![]() equals
equals ![]() . These probabilities follow the derivations we have presented above after accounting for the fact that preferred (nonpreferred) bidders inflate (discount) tenders from bidders in the rival class in considering the valuation required of opponents from that class to induce a bid that would win the auction. Substituting these probabilities into the expected profit for a firm belonging to class
. These probabilities follow the derivations we have presented above after accounting for the fact that preferred (nonpreferred) bidders inflate (discount) tenders from bidders in the rival class in considering the valuation required of opponents from that class to induce a bid that would win the auction. Substituting these probabilities into the expected profit for a firm belonging to class ![]() and taking first-order conditions yields
and taking first-order conditions yields
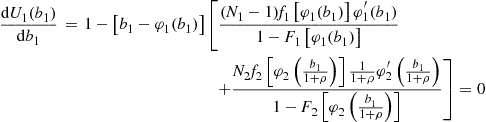
and
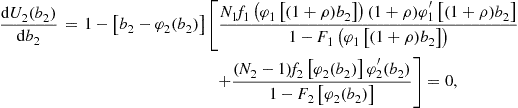
which characterize equilibrium behavior for bidders who choose to participate in such auctions.20
Most observed preference policies use a constant preference rate to adjust the bids of qualified firms for the purposes of evaluation only. To incorporate bid preferences in the model, using this common preference rule, the standard boundary conditions must be adjusted to depend on the class of the firm. Reny and Zamir (2004) have extended the results concerning existence of equilibrium bid functions in a general asymmetric environment; these results apply to the bid-preference case. Under the most common preference policy, the equilibrium inverse-bid functions will satisfy the class-specific conditions which are revised from the general procurement model presented above. Specifically,
Right-Boundary Conditions (on Inverse-Bid Functions):
a. for all nonpreferred bidders of class ![]() ;
;
b. for all preferred bidders of class ![]() , where
, where ![]() if
if ![]() , but when
, but when ![]() , then
, then ![]() is determined by
is determined by
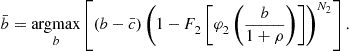
These right-boundary conditions specify that with a preference policy a nonpreferred bidder will bid its cost when it has the highest cost. When just one preferred firm competes with nonpreferred firms, that firm finds it optimal to submit a bid that is greater than the highest cost because the preference rate will reduce the bid and allow the preferred firm to win the auction with some probability. When, however, more than one firm receives preference, it is optimal for preferred firms to bid their costs at the right-boundary. These arguments are demonstrated in Appendix A of Hubbard and Paarsch (2009).
The left-boundary conditions will also be class-specific when the preference rate ![]() is positive. Specifically,
is positive. Specifically,
Left-Boundary Conditions (on Inverse-Bid Functions): there exists an unknown bid ![]() such that
such that
These left-boundary conditions require that, when a nonpreferred firm draws the lowest cost, it tenders the lowest possible bid ![]() , whereas a preferred firm submits
, whereas a preferred firm submits ![]() . This condition can be explained by a similar argument to the standard left-boundary condition, taking into account that preferred bids get adjusted using
. This condition can be explained by a similar argument to the standard left-boundary condition, taking into account that preferred bids get adjusted using ![]() .
.
Note, too, that to ensure consistency across solutions, Hubbard and Paarsch (2009) as well as Krasnokutskaya and Seim (2011) assumed that nonpreferred players bid their costs if those costs are in the range ![]() . Because of the preferential treatment (and assuming more than one bidder receives preferential treatment), nonpreferred players cannot win the auction when they bid higher than
. Because of the preferential treatment (and assuming more than one bidder receives preferential treatment), nonpreferred players cannot win the auction when they bid higher than ![]() . Thus, any bidding strategy will be acceptable in a Bayes-Nash equilibrium, which is why the assumption is needed for consistency.21
. Thus, any bidding strategy will be acceptable in a Bayes-Nash equilibrium, which is why the assumption is needed for consistency.21
In the above model, we have allowed the firms to draw costs from different distributions. If the bidders draw costs from symmetric distributions, but are treated asymmetrically, then we still must solve an asymmetric (low-price) auction as the discrimination among classes of bidders induces them to behave in different ways. Note, too, that unlike the canonical asymmetric auctions presented above, where the asymmetry is exogenously fixed (the distributions and utility functions are set for the bidders), in an environment with bid preferences and symmetric bidders, an asymmetry obtains which is endogenous as the preference rate ![]() is typically a choice variable of the procuring agency. Regardless of the reason, no closed-form solution exists. The Lipschitz condition again does not hold in a neighborhood around
is typically a choice variable of the procuring agency. Regardless of the reason, no closed-form solution exists. The Lipschitz condition again does not hold in a neighborhood around ![]() , so numerical methods are required.
, so numerical methods are required.
3 Primer on Relevant Numerical Strategies
In this section, we describe several numerical strategies that have been used to solve two-point boundary-value problems that are similar to the ones researchers face in models of asymmetric first-price auctions. We use this section not just as a way of introducing the strategies, but so we can refer to them later when discussing what researchers concerned with solving for (inverse-) bid functions at asymmetric first-price auctions have done.
3.1 Shooting Algorithms
A common way to solve boundary-value problems is to treat them like initial-value problems, solving them repeatedly, until the solution satisfies both boundary conditions. This approach often involves algorithms that are referred to as shooting.22 To understand how shooting algorithms work, consider firing an object at a target some distance away. Suppose that one does not hit the target on the first try. Presumably, if hitting the target is important, then one will learn from the first miss, make appropriate adjustments, and fire again. One can continue this process until the target is hit. The key characteristics which make success possible, eventually, are that one knows how to fire an object (using whatever mechanism is used to send the object at the target) and that one recognizes the types of adjustments that need to be made so that successive shots at the target improve. This story provides an analogy for the procedure used in a shooting algorithm to solve boundary-value problems.
Two features are attractive when solving a system of ODEs which constitute a two-point boundary-value problem, like in the asymmetric first-price auctions. First, an efficient, accurate solution method can be used to solve the system of differential equations on the relevant interval. Second, the researcher knows how to make adjustments to a given solution in a way that the next iteration improves on the previous. In a two-point boundary-value problem, conditions are imposed on either end of the interval. The shooting algorithm treats one of the boundaries like an initial value. Given that initial value, well-known ways exist to solve a system of differential equations. After solving the system and arriving at the other boundary, we check to see whether the other (target) condition is satisfied. If not, then we need to understand how to adjust the initial condition, so that when we re-solve the system of equations, we get closer to satisfying our target condition. Note that, if we do not make the proper adjustment, then we obviously have little hope of converging to a solution. We discuss the shooting algorithm in the first-price auction as well as the low-price (procurement) auction and then include a discussion of potential solution techniques that can be used within the shooting algorithm to solve the initial-value problem at each iteration.
First, consider solving for the equilibrium inverse-bid functions at an asymmetric first-price auction. Recall the two boundary conditions we have concerning the equilibrium inverse-bid functions that must hold in this case:
![]()
and
![]()
Our first decision is to determine which condition should serve as the initial condition and which should serve as a terminal condition. Note the difference between the two conditions—for the left-boundary, we know both the bid as well as the valuation a priori, while for the right-boundary we know only the valuation ![]() , but not the common high bid
, but not the common high bid ![]() for which we must solve. Because we do not know the value of
for which we must solve. Because we do not know the value of ![]() a priori, the right-boundary makes a poor target: after solving the system, we shall not know whether our solution involves the correct value for the high bid
a priori, the right-boundary makes a poor target: after solving the system, we shall not know whether our solution involves the correct value for the high bid ![]() or how to interpret whether the value(s) obtained were too high or too low (since the truth is unknown) in order to make proper adjustments. Ignoring the issue that the Lipschitz condition does not hold for the system at the lower boundary, the left-boundary condition makes for a good target: we know the bid as well as its corresponding valuation for all players. Thus, we want to use the condition that
or how to interpret whether the value(s) obtained were too high or too low (since the truth is unknown) in order to make proper adjustments. Ignoring the issue that the Lipschitz condition does not hold for the system at the lower boundary, the left-boundary condition makes for a good target: we know the bid as well as its corresponding valuation for all players. Thus, we want to use the condition that ![]() equals
equals ![]() as our “initial” value. As such, using a shooting algorithm at a first-price auction involves using a backwards or reverse shooting algorithm in which the initial value is actually the “terminal” value.
as our “initial” value. As such, using a shooting algorithm at a first-price auction involves using a backwards or reverse shooting algorithm in which the initial value is actually the “terminal” value.
For a given ![]() , the proposed solution can fail in one of two ways, both of which involve evaluating the solution at the target condition and recognizing that the proposed solution (shot) did not hit the target. One type of failure is that the value of at least one of the
, the proposed solution can fail in one of two ways, both of which involve evaluating the solution at the target condition and recognizing that the proposed solution (shot) did not hit the target. One type of failure is that the value of at least one of the ![]() approximated inverse-bid functions at
approximated inverse-bid functions at ![]() is a value that is “too far” from the true (known) value which is
is a value that is “too far” from the true (known) value which is ![]() ; that is,
; that is, ![]() is too large. This failure obtains when the guess for
is too large. This failure obtains when the guess for ![]() is too low. In this case, the inverse-bid functions are well behaved in that they are monotonic, but they do not satisfy the target condition. Consequently, the guess for the unknown high bid
is too low. In this case, the inverse-bid functions are well behaved in that they are monotonic, but they do not satisfy the target condition. Consequently, the guess for the unknown high bid ![]() must be increased; that is how to adjust from the missed shot. The other type of failure involves the solution “blowing up” or diverging. Specifically, the solutions explode toward minus infinity as the bids approach
must be increased; that is how to adjust from the missed shot. The other type of failure involves the solution “blowing up” or diverging. Specifically, the solutions explode toward minus infinity as the bids approach ![]() . In this case, the guess for the high bid
. In this case, the guess for the high bid ![]() is too high and the candidate solution never reaches the target condition. Under this type of failure, the appropriate modification involves decreasing the guess for the unknown high bid
is too high and the candidate solution never reaches the target condition. Under this type of failure, the appropriate modification involves decreasing the guess for the unknown high bid ![]() . We illustrate these two failures in Figure 2, in which we depict a situation in which the candidate solutions involve the true value
. We illustrate these two failures in Figure 2, in which we depict a situation in which the candidate solutions involve the true value ![]() , a value in which the high bid is too low
, a value in which the high bid is too low ![]() , and a value in which the high bid is too high
, and a value in which the high bid is too high ![]() .23 Note that when
.23 Note that when ![]() is too high, the system approaches the
is too high, the system approaches the ![]() line and singularity obtains. To see this, recall system (9) and note that the denominators of each of the terms in brackets involve
line and singularity obtains. To see this, recall system (9) and note that the denominators of each of the terms in brackets involve ![]() . As the inverse-bid function approaches the
. As the inverse-bid function approaches the ![]() line, players’ bids approach their valuations causing the singularities. Thus, to obtain convergence, bids must be kept below their valuations. Consequently, convergence will obtain from the left of the
line, players’ bids approach their valuations causing the singularities. Thus, to obtain convergence, bids must be kept below their valuations. Consequently, convergence will obtain from the left of the ![]() line.24
line.24
In a model of a first-price auction, the shooting algorithm for a representative iteration ![]() can be summarized as follows:
can be summarized as follows:
1. Take a guess for the common high bid ![]() .
.
2. Solve the system of differential equations backwards on the interval ![]() .
.
3. Use the value that a valid (monotonic) solution takes at ![]() to gauge whether to increase or to decrease the guess
to gauge whether to increase or to decrease the guess ![]() . Specifically,
. Specifically,
a. if the solution at ![]() blows up, then set
blows up, then set ![]() (decrease
(decrease ![]() ) in step 1 and try again;
) in step 1 and try again;
b. if the approximated solution at ![]() is in
is in ![]() , but does not meet pre-specified tolerance criteria for at least one bidder (
, but does not meet pre-specified tolerance criteria for at least one bidder (![]() for some bidder
for some bidder ![]() ), then set
), then set ![]() (increase
(increase ![]() ) in step 1 and try again.
) in step 1 and try again.
![]()
for some pre-specified norm ![]() and pre-specified tolerance level
and pre-specified tolerance level ![]() .
.
Of course, the algorithm can be modified and improved. For example, once one iteration has been considered with a high bid that was too high and one has been considered with a high bid that was too low, then the actual highest bid lies somewhere in between and a bisection routine can be used to speed-up convergence. Of course, bisection is generally considered to have a slow rate of convergence, so Newton’s method or another root-finding procedure may be preferred.
Solving for the inverse-bid functions at an asymmetric low-price auction is essentially the mirror image of the first-price shooting algorithm. Recall the two boundary conditions we have concerning the inverse-bid functions that must hold in this case:
![]()
and
![]()
In this case, the right-boundary makes for a good target as it allows us to evaluate how close the candidate solution is to the true solution. Because, in the procurement environment, the common low bid is unknown a priori, we can use this low bid as the initial value in a (forward) shooting algorithm.
The candidate solution can again fail in two ways which correspond to the preceding discussion concerning first-price auctions. One type of failure involves the cost of at least one of the ![]() approximated inverse-bid functions at
approximated inverse-bid functions at ![]() being too far below the true (known) value which is
being too far below the true (known) value which is ![]() ; that is,
; that is, ![]() is too large. This failure obtains when the guess for
is too large. This failure obtains when the guess for ![]() is too high. In this case, the inverse-bid functions are well behaved in that they are monotonic, but they do not satisfy the target condition. Consequently, the guess for the unknown low bid
is too high. In this case, the inverse-bid functions are well behaved in that they are monotonic, but they do not satisfy the target condition. Consequently, the guess for the unknown low bid ![]() must be decreased. The other type of failure again involves the system diverging, this time toward infinity as the bid approaches
must be decreased. The other type of failure again involves the system diverging, this time toward infinity as the bid approaches ![]() . In this case, the guess for the low bid
. In this case, the guess for the low bid ![]() is too low and the proposed solution never reaches the target condition. Under this type of failure, the appropriate modification involves increasing the guess for the unknown low bid
is too low and the proposed solution never reaches the target condition. Under this type of failure, the appropriate modification involves increasing the guess for the unknown low bid ![]() . A formal argument for this procurement setting is provided in Appendix B of Bajari (2001); see Lemmata 7 and 8 of that paper.
. A formal argument for this procurement setting is provided in Appendix B of Bajari (2001); see Lemmata 7 and 8 of that paper.
The shooting algorithm at a low-price auction for a representative iteration ![]() can be summarized as follows:
can be summarized as follows:
1. Take a guess for the common low bid ![]() .
.
2. Solve the system of differential equations on the interval ![]() .
.
3. Use the value that a valid (monotonic) solution takes at ![]() to gauge whether to increase or decrease the guess
to gauge whether to increase or decrease the guess ![]() . Specifically,
. Specifically,
a. if the solution at ![]() blows up, then set
blows up, then set ![]() (increase
(increase ![]() ) in step 1 and try again;
) in step 1 and try again;
b. if the approximated solution at ![]() is in
is in ![]() , but does not meet pre-specified tolerance criteria for at least one bidder (
, but does not meet pre-specified tolerance criteria for at least one bidder (![]() for some bidder
for some bidder ![]() ), then set
), then set ![]() (decrease
(decrease ![]() ) in step 1 and try again.
) in step 1 and try again.
![]()
for some pre-specified norm ![]() and pre-specified tolerance level
and pre-specified tolerance level ![]() .
.
As we suggested earlier, a root-finding routine can be used to complement this approach, to improve efficiency.
Throughout this subsection, we have taken for granted that the researcher has a viable and stable way of solving the system of ODEs which is subject to initial conditions. Any textbook concerning ODEs (and, most likely, any numerical analysis textbook) will document a number of common ways to approximate the solution to a system of first-order initial-value problems. For a discussion of these methods, with emphasis on applications to problems encountered by economists, see Judd (1998), although there is no discussion of auctions in that book. As such, we summarize them only briefly here because the approach taken is often what distinguishes among research concerning asymmetric first-price auctions. Typically, these methods involve approximating the solution to the system of ODEs at a grid of points and then interpolating these values to provide a continuous approximation. This approach means that the system of differential equations is treated like a system of difference equations. The distance between grid points is referred to as the step size.
For ease of presentation, let us describe the system of ![]() first-order ODEs for which a representative equation for bidder
first-order ODEs for which a representative equation for bidder ![]() was given by system (9) as
was given by system (9) as
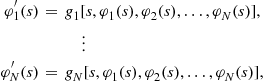
which we shall express succinctly as
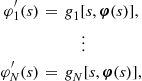
where ![]() collects all of the inverse-bid functions, each evaluated at bid
collects all of the inverse-bid functions, each evaluated at bid ![]() , and
, and ![]() represents the right-hand side of the differential equation for bidder
represents the right-hand side of the differential equation for bidder ![]() . Consider approximating the solution to this system of ODEs at a grid of bids
. Consider approximating the solution to this system of ODEs at a grid of bids
![]()
where ![]() is the number of points in the grid and
is the number of points in the grid and
![]()
for step size ![]() . Let
. Let ![]() be the bid relevant for the initial condition and let
be the bid relevant for the initial condition and let ![]() be the bid that is relevant for the target (terminal) condition.25 Our solution to this system will involve a value
be the bid that is relevant for the target (terminal) condition.25 Our solution to this system will involve a value ![]() which approximates the inverse-bid function for player
which approximates the inverse-bid function for player ![]() at bid
at bid ![]() for each bid in the grid space and for each bidder at auction; that is, we need to approximate
for each bid in the grid space and for each bidder at auction; that is, we need to approximate
![]()
The solution methods we discuss involve first fixing the initial condition to be satisfied for each bidder
![]()
and, then, approximating the difference equation for ![]() , in sequence.
, in sequence.
Taylor’s method is one of the most intuitively easy ways to understand how to solve such a system. Under the explicit (forward) Taylor’s method of order ![]() , the approximate value of the inverse-bid function for player
, the approximate value of the inverse-bid function for player ![]() at a bid (step)
at a bid (step) ![]() can be expressed as
can be expressed as
![]() (18)
(18)
where ![]() collects
collects ![]() . This scheme is motivated by a Taylor-series argument. Suppose
. This scheme is motivated by a Taylor-series argument. Suppose ![]() is the true inverse-bid function for player
is the true inverse-bid function for player ![]() . Expanding
. Expanding ![]() around
around ![]() then yields
then yields
![]() (19)
(19)
for some ![]() . Dropping the
. Dropping the ![]() term and assuming
term and assuming ![]() equals
equals ![]() as well as
as well as ![]() equals
equals ![]() yields Taylor’s method proposed in Eq. (18). Note, too, that Euler’s method which would approximate
yields Taylor’s method proposed in Eq. (18). Note, too, that Euler’s method which would approximate ![]() by
by
![]()
is Taylor’s method of order one.
An alternative to the explicit (forward) Taylor’s method proposed above is the implicit (backward) Taylor’s method (of order ![]() ). In the explicit Taylor’s method, we used a Taylor-series expansion of
). In the explicit Taylor’s method, we used a Taylor-series expansion of ![]() around
around ![]() , but we could have considered an expansion around
, but we could have considered an expansion around ![]() , instead. Thus,
, instead. Thus,
![]()
which motivates the implicit Taylor’s method
![]()
Thus, ![]() is defined only implicitly in terms of
is defined only implicitly in terms of ![]() and
and ![]() . This scheme requires an
. This scheme requires an ![]() -dimensional system of nonlinear equations to be solved at each step to approximate
-dimensional system of nonlinear equations to be solved at each step to approximate ![]() . While this approach is more expensive in terms of computing time, the approximations are typically much better than those obtained under the explicit Taylor’s method. Intuitively, the value
. While this approach is more expensive in terms of computing time, the approximations are typically much better than those obtained under the explicit Taylor’s method. Intuitively, the value ![]() depends not only on
depends not only on ![]() and
and ![]() , but also on the behavior of
, but also on the behavior of ![]() at
at ![]() . Implicit Taylor’s methods have superior stability properties and these methods are effective for stiff systems, while the explicit Taylor’s method is not.
. Implicit Taylor’s methods have superior stability properties and these methods are effective for stiff systems, while the explicit Taylor’s method is not.
A system is referred to as stiff when its candidate solutions are sensitive to small changes in the chosen step size ![]() . To solve stiff differential equations accurately using Euler’s method (for example),
. To solve stiff differential equations accurately using Euler’s method (for example), ![]() must be very small, which means that such methods will take a long time to compute an accurate solution.26 While this may not be an issue when one just wants to do this once, in empirical work concerning auctions, one may need to solve the differential equation thousands (even millions) of times.
must be very small, which means that such methods will take a long time to compute an accurate solution.26 While this may not be an issue when one just wants to do this once, in empirical work concerning auctions, one may need to solve the differential equation thousands (even millions) of times.
As one might expect, both the explicit and implicit Taylor’s methods of order ![]() have local truncation error of
have local truncation error of ![]() , which means that as the step size
, which means that as the step size ![]() , the local truncation error is proportional to
, the local truncation error is proportional to ![]() for some unknown constant
for some unknown constant ![]() . To see this, note that a Taylor-series expansion around some point
. To see this, note that a Taylor-series expansion around some point ![]() for the explicit Taylor’s method (or
for the explicit Taylor’s method (or ![]() for the implicit Taylor’s method) involves dropping a term
for the implicit Taylor’s method) involves dropping a term
![]()
for some ![]() for each
for each ![]() in the grid space. Equation (18) implies
in the grid space. Equation (18) implies
![]()
and, assuming ![]() is
is ![]() over
over ![]() and given
and given
![]()
then Eq. (19) implies
![]()
Each step in Taylor’s method incurs local truncation error ![]() and we require
and we require ![]() steps, so the global truncation error is
steps, so the global truncation error is
![]()
Taylor’s methods are attractive in that, given a step size ![]() , the truncation error can be reduced by using higher-order methods.27 Taylor’s methods of higher orders, however, require computing and evaluating higher-order derivatives. One way to avoid this, but still maintain the relationship between order of the method and truncation error, is to use Runge-Kutta methods, which are the most commonly used methods in practice.
, the truncation error can be reduced by using higher-order methods.27 Taylor’s methods of higher orders, however, require computing and evaluating higher-order derivatives. One way to avoid this, but still maintain the relationship between order of the method and truncation error, is to use Runge-Kutta methods, which are the most commonly used methods in practice.
Runge-Kutta methods are classified by their order, which corresponds to the order of their (global) truncation error. A Runge-Kutta method of order ![]() has local truncation error of
has local truncation error of ![]() and global truncation error of
and global truncation error of ![]() . Here, we present only the classical Runge-Kutta method which is of order 4, and use this as a point of discussion for a number of extensions that researchers have developed. Specifically, the fourth-order Runge-Kutta method, sometimes referred to as RK4, approximates
. Here, we present only the classical Runge-Kutta method which is of order 4, and use this as a point of discussion for a number of extensions that researchers have developed. Specifically, the fourth-order Runge-Kutta method, sometimes referred to as RK4, approximates
![]()
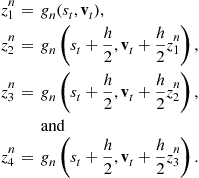
For brevity, we have exploited our notation using
![]()
Thus, the next value (dropping superscripts) ![]() is determined by the current one
is determined by the current one ![]() , plus the product of the step size
, plus the product of the step size ![]() and an estimated slope. The estimated slope is a weighted average of slopes:
and an estimated slope. The estimated slope is a weighted average of slopes: ![]() is the slope at the left endpoint of the interval;
is the slope at the left endpoint of the interval; ![]() is the slope at the midpoint of the interval, using Euler’s method along with slope
is the slope at the midpoint of the interval, using Euler’s method along with slope ![]() to determine the value at the point
to determine the value at the point ![]() is again the slope at the midpoint, but now the slope
is again the slope at the midpoint, but now the slope ![]() is used to determine its
is used to determine its ![]() argument; and
argument; and ![]() is the slope at the right endpoint of the interval, with its
is the slope at the right endpoint of the interval, with its ![]() value determined using
value determined using ![]() . Note, too, that if instead of a system there is one equation
. Note, too, that if instead of a system there is one equation ![]() which does not depend on
which does not depend on ![]() , so the differential equation is equivalent to a simple integral, then RK4 is simply Simpson’s rule, a well-known and commonly used quadrature rule.28
, so the differential equation is equivalent to a simple integral, then RK4 is simply Simpson’s rule, a well-known and commonly used quadrature rule.28
Many different modifications or extensions of Runge-Kutta methods exist. In the classical Runge-Kutta method presented above, the step size is equal between all grid points. Some extensions (for example, the Runge-Kutta-Fehlberg method and the Dormand-Prince method) allow for an adaptive step size by varying the number and position of steps to ensure that truncation error is below some bound. While Runge-Kutta methods achieve a higher rate of convergence with fewer calculations per step, like Euler’s method, they do not always perform well on stiff problems; see Hairer and Wanner (1996). Note, too, that neither the method of Euler nor the methods of Runge-Kutta use past information to improve the approximation as one works along in constructing a solution.
In response to these limitations, numerical analysts have pursued a variety of other strategies. For a given ![]() , these alternative methods are more accurate than Euler’s method and may have a smaller error constant than Runge-Kutta methods as well. The classical Runge-Kutta method presented above also uses only information at
, these alternative methods are more accurate than Euler’s method and may have a smaller error constant than Runge-Kutta methods as well. The classical Runge-Kutta method presented above also uses only information at ![]() to compute
to compute ![]() : methods with this feature are referred to as one-step methods. Methods that use
: methods with this feature are referred to as one-step methods. Methods that use ![]() grid points to approximate a function at the next point are referred to as multi-step methods. Under multi-step methods, one again begins at an initial point and then takes a small step
grid points to approximate a function at the next point are referred to as multi-step methods. Under multi-step methods, one again begins at an initial point and then takes a small step ![]() forward in calculating the next value. The difference is that, unlike one-step methods, multi-step methods use some intermediate points to obtain a higher-order approximation of the next value. Multi-step methods gain efficiency by keeping track of as well as using the information from previous steps rather than discarding it. Specifically, multi-step methods use the values of the function at several previous points as well as the derivatives (or some of them) at those points.
forward in calculating the next value. The difference is that, unlike one-step methods, multi-step methods use some intermediate points to obtain a higher-order approximation of the next value. Multi-step methods gain efficiency by keeping track of as well as using the information from previous steps rather than discarding it. Specifically, multi-step methods use the values of the function at several previous points as well as the derivatives (or some of them) at those points.
Linear multi-step methods are special cases in the class of multi-step methods. As the name suggests, under these methods, a linear combination of previous points and derivative values is used to approximate the solution. Denote by ![]() the number of previous steps used to calculate the next value. Denote the desired value at the current stage by
the number of previous steps used to calculate the next value. Denote the desired value at the current stage by ![]() . A linear multi-step method has the following general form:
. A linear multi-step method has the following general form:
![]()
The values chosen for ![]() and
and ![]() determine the solution method; a numerical analyst must choose these coefficients. Often, many of the coefficients are set to zero. Sometimes, the numerical analyst chooses the coefficients so they will interpolate
determine the solution method; a numerical analyst must choose these coefficients. Often, many of the coefficients are set to zero. Sometimes, the numerical analyst chooses the coefficients so they will interpolate ![]() exactly when
exactly when ![]() is a
is a ![]() th order polynomial. When
th order polynomial. When ![]() is nonzero, the value of
is nonzero, the value of ![]() depends on the value of
depends on the value of ![]() , and the equation for
, and the equation for ![]() must be solved iteratively, using fixed-point iteration or, alternatively, using variants of Newton’s method.
must be solved iteratively, using fixed-point iteration or, alternatively, using variants of Newton’s method.
A simple linear, multi-step method is the Adams-Bashforth two-step method. Under this method,
![]()
That is, ![]() is
is ![]() , while
, while ![]() is zero, and
is zero, and ![]() is
is ![]() , while
, while ![]() is
is ![]() . To implement Adams-Bashforth, however, one needs two values (
. To implement Adams-Bashforth, however, one needs two values (![]() and
and ![]() ) to compute the next value
) to compute the next value ![]() . In a typical initial-value problem, only one value is provided. One way to circumvent this lack of information is to use the
. In a typical initial-value problem, only one value is provided. One way to circumvent this lack of information is to use the ![]() computed by Euler’s method as the second value. With this choice, the Adams-Bashforth two-step method yields a candidate approximating solution.
computed by Euler’s method as the second value. With this choice, the Adams-Bashforth two-step method yields a candidate approximating solution.
For other values of ![]() , Butcher (2003) has provided explicit formulas to implement the Adams-Bashforth methods. Again, assuming the Lipschitz condition is satisfied, the local truncation error of the Adams-Bashforth two-step method is
, Butcher (2003) has provided explicit formulas to implement the Adams-Bashforth methods. Again, assuming the Lipschitz condition is satisfied, the local truncation error of the Adams-Bashforth two-step method is ![]() , while the global truncation error is
, while the global truncation error is ![]() . (Other Adams-Bashforth methods have local truncation errors that are
. (Other Adams-Bashforth methods have local truncation errors that are ![]() and global truncation errors that are
and global truncation errors that are ![]() , and are, thus, competitive with RK4.)
, and are, thus, competitive with RK4.)
In addition to Adams-Bashforth, two other families are also used: first, Adams-Moulton methods and, second, backward differentiation formulas (BDFs).
Like Adams-Bashforth methods, the Adams-Moulton methods have ![]() equal
equal ![]() and the other
and the other ![]() s equal to zero. Where, however, Adams-Bashforth methods are explicit, Adams-Moulton methods are implicit. For example, when
s equal to zero. Where, however, Adams-Bashforth methods are explicit, Adams-Moulton methods are implicit. For example, when ![]() is zero, under Adams-Moulton,
is zero, under Adams-Moulton,
![]() (20)
(20)
which is sometimes referred to as the backward Euler method, while when ![]() is one,
is one,
![]() (21)
(21)
which is sometimes referred to as the trapezoidal rule. Note that these equations only define the solutions implicitly; that is, Eqs. (20) and (21) must be solved numerically for ![]() and
and ![]() , respectively.
, respectively.
BDFs constitute the main other way to solve ODEs. BDFs are linear multi-step methods which are especially useful when solving stiff differential equations. We know that, given a symmetric auction setting (one differential equation)
![]()
for step size ![]() , a linear multi-step method can, in general, be written as
, a linear multi-step method can, in general, be written as
![]()
BDFs involve setting ![]() to zero for any
to zero for any ![]() other than
other than ![]() , so a general BDF is
, so a general BDF is
![]()
Note that, like Adams-Moulten methods, BDFs are implicit methods as well: one must solve nonlinear equations at each step—again, using fixed-point iteration or variants of Newton’s method. Thus, the methods can be computationally burdensome. The evaluation of ![]() at
at ![]() in
in ![]() is, however, an effective way in which to discipline approximate solutions to stiff differential equations.
is, however, an effective way in which to discipline approximate solutions to stiff differential equations.
3.2 Projection Methods
An alternative to the shooting algorithms described in the previous subsection are projection methods. A projection method is a general strategy of approximating a true, but unknown, function by a finite number of approximating functions. That is, the true solution is approximated by a finite combination of simple, known functions. For economists, projection methods are, perhaps, more intuitive than the other approaches described above. Specifically, a researcher would first choose a basis to approximate the solutions to each inverse-bid function. The full basis for the space of candidate solutions should be rich (flexible) enough to approximate any function relevant to the problem (which will be represented and approximated as a linear combination of basis functions). This choice specifies the structure of the approximation. The researcher would then fix the flexibility of the approximation by deciding how many basis elements to include. In short, the researcher must fix the order of the approximation. This transforms an infinite-dimensional problem into a finite-dimensional one, where only the coefficients of the basis functions need then to be found. Generally, the only “correct” choice is to use an approximation of infinite order. If the choice of basis is good, then higher orders will yield better approximations. The researcher must also decide on an appropriate residual function to evaluate how closely the approximation represents the true solution. The goal of projection methods is to find a set of coefficients which make some norm of the residual function as close to zero as possible or solves some projection using test functions. Obtaining these coefficients involves solving a set of nonlinear, simultaneous equations or solving a minimization problem. After this has been accomplished, the researcher can verify the quality of the candidate solution and choose either to increase the order of the approximation or, failing that, to begin with a different basis.
Projection methods provide approximate solutions in the form of linear combinations of continuous functions. Some families of projection methods are known by their method of approximation. Spectral methods use bases where each element is nonzero almost everywhere, as with trigonometric bases and orthogonal polynomials. Specifically, Judd (1998) has advocated using orthogonal polynomials instead of trigonometric bases because solutions to economics problems generally are not periodic in nature: periodic approximations to nonperiodic functions require many terms to achieve accuracy.
In the case of an asymmetric first-price auction problem, consider approximating each inverse-bid function by a truncated series expansion
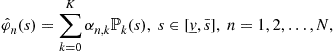 (22)
(22)
where ![]() are some basis functions (which are typically chosen to be polynomials) and the
are some basis functions (which are typically chosen to be polynomials) and the ![]() s are sometimes referred to as the spectral coefficients. Spectral methods often converge exponentially as the order of the approximating polynomial increases. In the finite-element method (nonoverlapping), subdomains are constructed over the domain of interest based on piecewise polynomial interpolation. For the asymmetric first-price auction problem introduced above, consider partitioning the interval
s are sometimes referred to as the spectral coefficients. Spectral methods often converge exponentially as the order of the approximating polynomial increases. In the finite-element method (nonoverlapping), subdomains are constructed over the domain of interest based on piecewise polynomial interpolation. For the asymmetric first-price auction problem introduced above, consider partitioning the interval ![]() into
into ![]() regions, then the inverse-bid function for player
regions, then the inverse-bid function for player ![]() can be approximated by
can be approximated by
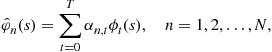
where ![]() is some basis function (for example, piecewise linear polynomials, cubic spline, and so forth) and
is some basis function (for example, piecewise linear polynomials, cubic spline, and so forth) and ![]() s are now bidder-specific coefficients for subinterval
s are now bidder-specific coefficients for subinterval ![]() . As such, finite-element methods use basis functions where each element has a small support, typically involving piecewise functions that are nonzero almost everywhere on the subdomain. Thus, spectral methods use global basis functions in which each term in the series is a polynomial (and the last term is of high order). Finite-element methods use local basis functions on the subdomains (of fixed order), which are then aggregated to approximate the function(s) over the full domain.
. As such, finite-element methods use basis functions where each element has a small support, typically involving piecewise functions that are nonzero almost everywhere on the subdomain. Thus, spectral methods use global basis functions in which each term in the series is a polynomial (and the last term is of high order). Finite-element methods use local basis functions on the subdomains (of fixed order), which are then aggregated to approximate the function(s) over the full domain.
For economists, perhaps the most intuitive spectral method is that of least squares. Consider, again, the set of ![]() first-order ODEs for which a representative equation for bidder
first-order ODEs for which a representative equation for bidder ![]() was given by system (9), which we shall express as
was given by system (9), which we shall express as
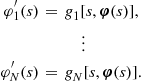
Under the spectral method considered above, each inverse-bid function is approximated by a truncated series expansion of some basis functions. The problem is to estimate ![]() as well as the
as well as the ![]() s for all
s for all ![]() and
and ![]() . Consider selecting a large number
. Consider selecting a large number ![]() of grid points from the interval
of grid points from the interval ![]() . The system can be evaluated at each grid point and the parameters can be chosen to minimize the following criterion function:
. The system can be evaluated at each grid point and the parameters can be chosen to minimize the following criterion function:
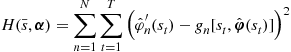
where ![]() denotes a vector that collects the
denotes a vector that collects the ![]() coefficients of the polynomials. To economists, the least-squares approach is compelling: we have reduced the problem of solving a functional equation to solving a nonlinear minimization problem, a problem with which we have considerable experience. In many problems, boundary conditions can be satisfied by the choice of the basis. A challenge in the context of an asymmetric first-price auction is the presence of the free boundary. In this formulation, the boundary conditions must enter the objective function directly or be imposed as constraints, which leads to a constrained optimization problem. We shall investigate and formalize these alternatives below when summarizing the previous research. The method of least squares is an attractive way of approximating these solutions. In fact, some have argued that it is a safe way of generating approximations that depend nonlinearly on the unknowns; see, for example, Boyd (2001).
coefficients of the polynomials. To economists, the least-squares approach is compelling: we have reduced the problem of solving a functional equation to solving a nonlinear minimization problem, a problem with which we have considerable experience. In many problems, boundary conditions can be satisfied by the choice of the basis. A challenge in the context of an asymmetric first-price auction is the presence of the free boundary. In this formulation, the boundary conditions must enter the objective function directly or be imposed as constraints, which leads to a constrained optimization problem. We shall investigate and formalize these alternatives below when summarizing the previous research. The method of least squares is an attractive way of approximating these solutions. In fact, some have argued that it is a safe way of generating approximations that depend nonlinearly on the unknowns; see, for example, Boyd (2001).
In contrast to the method of least squares, collocation (pseudospectral) methods work under the assumption that the solution can be represented by a candidate family of functions (typically polynomials); collocation involves selecting a candidate which solves the system exactly at a set of points on the interval of interest. These points are referred to as the collocation points. Specifically, each component of the residual is set to equal zero exactly by choosing the number of collocation points (including the boundary conditions) ![]() to equal the number of unknown coefficients
to equal the number of unknown coefficients ![]() . Of course, the common high bid
. Of course, the common high bid ![]() is also unknown, so there are
is also unknown, so there are ![]() unknowns in total. Collocation is akin to interpolating a known function by requiring the approximation to coincide with the true function at a collection of points, so it is also referred to as an interpolating spectral method. Substituting the approximations for the true, but unknown, inverse-bid functions and computing the gradient yields a system of equations which must be solved for the spectral coefficients. Orthogonal collocation involves choosing the grid points to correspond with the
unknowns in total. Collocation is akin to interpolating a known function by requiring the approximation to coincide with the true function at a collection of points, so it is also referred to as an interpolating spectral method. Substituting the approximations for the true, but unknown, inverse-bid functions and computing the gradient yields a system of equations which must be solved for the spectral coefficients. Orthogonal collocation involves choosing the grid points to correspond with the ![]() zeros of the
zeros of the ![]() th orthogonal polynomial basis element and the basis elements are orthogonal with respect to the inner product. Provided the residual is smooth in the bids, the Chebyshev interpolation theorem says that these zero conditions will force the residual to be close to zero for all
th orthogonal polynomial basis element and the basis elements are orthogonal with respect to the inner product. Provided the residual is smooth in the bids, the Chebyshev interpolation theorem says that these zero conditions will force the residual to be close to zero for all ![]() . Likewise, the optimality of Chebyshev interpolation also says that if one is going to use collocation, then these are the best possible points to use.
. Likewise, the optimality of Chebyshev interpolation also says that if one is going to use collocation, then these are the best possible points to use.
Solving for the spectral coefficients requires either a minimization algorithm or a nonlinear algebraic equation solver. If the system of equations is overidentified, or if one is minimizing the sum of squared residuals, then a nonlinear least-squares algorithm may be used. Good initial guesses are important because projection methods involve either a system of nonlinear equations or optimizing a nonlinear objective. Judd (1998) has advocated a two-stage approach. In the first stage, the method of least squares is used, along with a loose convergence criterion, to compute quickly a low-quality approximation, while in the second stage, this approximation is used as an initial guess for a projection method involving a higher-order approximation. Sometimes, the finite-dimensional problem generated by a projection method will not have a solution, even when the original problem does have a solution. If solving the system for a particular basis and a particular order ![]() is proving difficult, then using another basis or order may resolve the issue. Regardless, one way to ensure existence of a solution is to construct a least-squares objective (which may overidentify the problem) as an approximation is assured as long as the objective(s) are continuous and optimization methods are reliable.
is proving difficult, then using another basis or order may resolve the issue. Regardless, one way to ensure existence of a solution is to construct a least-squares objective (which may overidentify the problem) as an approximation is assured as long as the objective(s) are continuous and optimization methods are reliable.
4 Previous Research Concerning Numerical Solutions
In this section, we discuss research that either directly or indirectly contributed to improving computational methods to solve for bidding strategies at asymmetric first-price auctions.
4.1 Marshall et al. (1994)
The first researchers to propose using numerical algorithms to solve for the equilibrium (inverse-) bid functions at asymmetric auctions were Marshall et al. (1994). The authors investigated a model in which all bidders draw valuations from a uniform distribution. An asymmetry obtained because two coalitions existed at the auction, each with a different number of bidders; that is, the coalitions were of different sizes.29 Thus, as described above, the model of Marshall et al. simplifies to an asymmetric auction with two bidders who each draw valuations from a different power distribution.30
Marshall et al. applied l’Hôpital’s rule to the first-order conditions to derive
![]()
where ![]() is the number of bidders in coalition
is the number of bidders in coalition ![]() and
and ![]() is coalition
is coalition ![]() ’s inverse-bid function. They found that successive (higher) derivatives of
’s inverse-bid function. They found that successive (higher) derivatives of ![]() are zero at
are zero at ![]() . Because of this, forward numerical integration produces a linear solution described by
. Because of this, forward numerical integration produces a linear solution described by
![]()
This “nuisance” solution is incorrect because it does not satisfy the appropriate right-boundary condition that all coalitions submit the same bid ![]() when they have the highest valuation
when they have the highest valuation ![]() . This fact motivated them to use a backward shooting algorithm, like the ones we described above, in which they assumed a “terminal” (right-boundary) point
. This fact motivated them to use a backward shooting algorithm, like the ones we described above, in which they assumed a “terminal” (right-boundary) point ![]() , integrated backwards, and then used the “initial” (left-boundary) condition that all coalitions bid
, integrated backwards, and then used the “initial” (left-boundary) condition that all coalitions bid ![]() when they have the lowest valuation
when they have the lowest valuation ![]() to check the validity of the solution. What drives the shooting algorithm is the notion that the assumed value of
to check the validity of the solution. What drives the shooting algorithm is the notion that the assumed value of ![]() needs to be increased or decreased at a given iteration based on the value that the candidate solution takes at
needs to be increased or decreased at a given iteration based on the value that the candidate solution takes at ![]() .
.
In practice, for stability reasons, Marshall et al. advocated normalizing the inverse-bid functions by the bid at which they are being evaluated; that is, solving for
![]()
rather than ![]() . They approximated the
. They approximated the ![]() values by Taylor-series expansions of order
values by Taylor-series expansions of order ![]() (chosen to be five) around each point
(chosen to be five) around each point ![]() where
where ![]() represents one of
represents one of ![]() equally spaced (in this case, 10,000) grid points. In doing so, they used analytic functions for the successive derivatives of the transformed inverse-bid functions to avoid inaccuracy of high-order numerical derivatives. Their approach requires an efficient algorithm for evaluating the Taylor-series expansions and a reasonable convergence criterion. Marshall et al. considered the approximate solution valid when
equally spaced (in this case, 10,000) grid points. In doing so, they used analytic functions for the successive derivatives of the transformed inverse-bid functions to avoid inaccuracy of high-order numerical derivatives. Their approach requires an efficient algorithm for evaluating the Taylor-series expansions and a reasonable convergence criterion. Marshall et al. considered the approximate solution valid when
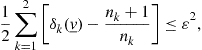
where ![]() was chosen to be of the order
was chosen to be of the order ![]() . They adapted this convergence criterion somewhat to deal with cases involving greater numerical instability in the neighborhood of
. They adapted this convergence criterion somewhat to deal with cases involving greater numerical instability in the neighborhood of ![]() ; see Appendix B of their paper. While Marshall et al. only considered the case of two coalitions competing at auction with bidders in each coalition receiving uniform draws, they suggested that their approach could be adapted to general distributions. Their uniform/power distributional assumption was convenient in that there was no need to evaluate nonlinear cumulative distribution (and probability density) functions at each inverse-bid function because these terms canceled each other out in the first-order conditions. Extending their approach to general distributions means that terms involving
; see Appendix B of their paper. While Marshall et al. only considered the case of two coalitions competing at auction with bidders in each coalition receiving uniform draws, they suggested that their approach could be adapted to general distributions. Their uniform/power distributional assumption was convenient in that there was no need to evaluate nonlinear cumulative distribution (and probability density) functions at each inverse-bid function because these terms canceled each other out in the first-order conditions. Extending their approach to general distributions means that terms involving ![]() enter the first-order conditions. A practical difficulty with this is that Taylor-series expansions for these functions must be included in the algorithm via implementation of an appropriate chain rule; see Appendix C of Marshall et al. (1994).
enter the first-order conditions. A practical difficulty with this is that Taylor-series expansions for these functions must be included in the algorithm via implementation of an appropriate chain rule; see Appendix C of Marshall et al. (1994).
4.2 Bajari (2001)
Bajari (2001) observed that bid-rigging (collusive bidding) was a serious problem at procurement auctions. He sought to provide empirical researchers with a way to assess whether observed bidding behavior was consistent with competitive bidding. Empirical researchers have argued, however, that models of bidding should admit asymmetric bidders; for example, Bajari (1997) found that 75% of the highway construction contracts he observed were awarded to the firm located closest to the project: location was clearly an important source of asymmetry.31 To deal with this, Bajari proposed algorithms for computing equilibrium (inverse-) bid functions when asymmetric bidders competed at auction. In doing so, his research extended that of Marshall et al. (1994) by allowing for ![]() bidders, each of whom draws his valuation from a different, arbitrary distribution that satisfies some regularity conditions. For us, this research is relevant because Bajari (2001) proposed three different approaches to computing equilibria in these models, although we present only two of them.32 While Bajari considered a procurement setting in his research, we maintain our discussion of first-price asymmetric auctions.
bidders, each of whom draws his valuation from a different, arbitrary distribution that satisfies some regularity conditions. For us, this research is relevant because Bajari (2001) proposed three different approaches to computing equilibria in these models, although we present only two of them.32 While Bajari considered a procurement setting in his research, we maintain our discussion of first-price asymmetric auctions.
Bajari’s first algorithm is essentially a straightforward application of the shooting algorithm we discussed above.33 He provided a formal proof that the convergence-divergence behavior of the inverse-bid functions and the known boundary ![]() (
(![]() in his case) at a first-price (procurement) auction can be used to adjust the starting, unknown bid
in his case) at a first-price (procurement) auction can be used to adjust the starting, unknown bid ![]() ; see Lemmata 7 and 8 in Appendix B of his paper which informed our earlier discussion of this procedure. Bajari suggested that “standard methods in the numerical analysis of ordinary differential equations” can be used to solve the system and adopted a Runge-Kutta algorithm.34,35
; see Lemmata 7 and 8 in Appendix B of his paper which informed our earlier discussion of this procedure. Bajari suggested that “standard methods in the numerical analysis of ordinary differential equations” can be used to solve the system and adopted a Runge-Kutta algorithm.34,35
Under Bajari’s third algorithm, the inverse-bid functions are approximated by flexible functional forms. Specifically, he assumed that the inverse-bid function for bidder ![]() can be represented by a linear combination of ordinary polynomials. Although Bajari considered the procurement case, here we consider the case of sale, so
can be represented by a linear combination of ordinary polynomials. Although Bajari considered the procurement case, here we consider the case of sale, so
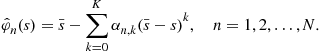 (23)
(23)
Note that Eq. (8) implies that the first-order condition for bidder ![]() can be expressed as
can be expressed as
![]()
Define ![]() as
as
![]() (24)
(24)
where ![]() denotes a vector that collects the
denotes a vector that collects the ![]() coefficients of the polynomials. In an exact solution,
coefficients of the polynomials. In an exact solution, ![]() should equal zero for all bidders and at any bid
should equal zero for all bidders and at any bid ![]() . In addition, an exact solution must satisfy the left-boundary condition
. In addition, an exact solution must satisfy the left-boundary condition
![]()
and the right-boundary condition
![]()
for each bidder ![]() .
.
Because the common high bid ![]() is unknown a priori, there are
is unknown a priori, there are ![]() unknowns that must be found. Bajari proposed selecting a large number
unknowns that must be found. Bajari proposed selecting a large number ![]() of grid points uniformly spaced over the
of grid points uniformly spaced over the ![]() interval and choosing these unknown parameters to minimize
interval and choosing these unknown parameters to minimize
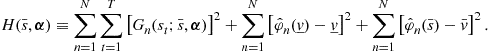 (25)
(25)
If all the first-order conditions as well as the boundary conditions are satisfied, then the objective ![]() will equal zero. Bajari reported finding accurate solutions (to five or more significant digits) when only third- or fourth-order polynomials were used. In practice, Bajari chose
will equal zero. Bajari reported finding accurate solutions (to five or more significant digits) when only third- or fourth-order polynomials were used. In practice, Bajari chose ![]() to equal five and used a nonlinear least-squares algorithm to select
to equal five and used a nonlinear least-squares algorithm to select ![]() and
and ![]() by minimizing a modified version of Eq. (25)
by minimizing a modified version of Eq. (25)
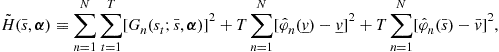
which adds weight to the boundary conditions.
An advantage of the polynomial approximation approach is that it is extremely fast. This is particularly important to econometricians who often need to recompute the solution within some estimation routine at each iteration. Researchers who wish to simulate dynamic models involving asymmetric auctions can also benefit from using this algorithm. To realize this gain in speed relative to shooting algorithms, the user must provide good starting values for the algorithm.
4.3 Fibich and Gavious (2003)
Fibich and Gavious (2003) recognized that while it is impossible to obtain closed-form solutions to the equilibrium bid functions in models of asymmetric first-price auctions, the equilibrium in a model of a symmetric first-price auction has a well-known closed-form solution. The authors suggested using perturbation analysis to calculate an explicit approximation to the asymmetric first-price solution to gain insight into revenue and efficiency questions in settings in which the asymmetry is small. Specifically, Fibich and Gavious defined the average distribution among ![]() bidders at a valuation
bidders at a valuation ![]() as
as
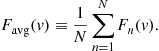
Let ![]() be a parameter that measures the level of asymmetry which is defined as
be a parameter that measures the level of asymmetry which is defined as
![]()
Given these two definitions, auxiliary functions ![]() can be constructed as
can be constructed as
![]()
These auxiliary functions have the property that
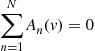
and, for all ![]()
![]()
Since valuations are drawn from a common, compact support ![]() ,
,
![]()
and
![]()
as the average value of the distribution equals the value of each distribution at the endpoints of the interval.
They noted that, by construction,
![]()
where ![]() represents the perturbation from the average distribution for player
represents the perturbation from the average distribution for player ![]() . Within this framework, Fibich and Gavious proved that the equilibrium bid functions can be solved for explicitly.36 In particular, they demonstrated the following:
. Within this framework, Fibich and Gavious proved that the equilibrium bid functions can be solved for explicitly.36 In particular, they demonstrated the following:
![]()
where ![]() is the equilibrium bid function at a first-price auction when all bidders draw valuations from
is the equilibrium bid function at a first-price auction when all bidders draw valuations from ![]() and
and
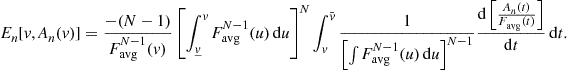
The perturbation approach of Fibich and Gavious is attractive because explicit expressions for the equilibrium bids can be derived; these allow researchers to extend theoretical results when asymmetries are sufficiently small, provided certain conditions (typically on the auxiliary functions) are satisfied.37
While the perturbation approach has been shown to be theoretically useful in deriving explicit approximations, the user sacrifices “exactness.” Another concern is the size ![]() must be for the approximations to be valid. To consider this, Fibich and Gavious used a shooting algorithm to compare the explicit approximations to those computed numerically, which they referred to as the exact solutions. They demonstrated that the approximations are quite good when
must be for the approximations to be valid. To consider this, Fibich and Gavious used a shooting algorithm to compare the explicit approximations to those computed numerically, which they referred to as the exact solutions. They demonstrated that the approximations are quite good when ![]() is less than 0.25; the approximations of the bidding functions are, however, visually distinct for
is less than 0.25; the approximations of the bidding functions are, however, visually distinct for ![]() greater than 0.50. Thus, the perturbation approach is helpful to researchers using numerical methods in that it can inform the researcher concerning a good initial guess which will speed up convergence by reducing the number of required iterations. Specifically, algorithms built-off a shooting approach require an initial guess for the a priori unknown high bid
greater than 0.50. Thus, the perturbation approach is helpful to researchers using numerical methods in that it can inform the researcher concerning a good initial guess which will speed up convergence by reducing the number of required iterations. Specifically, algorithms built-off a shooting approach require an initial guess for the a priori unknown high bid ![]() . The results of Fibich and Gavious suggest the following initial guess:
. The results of Fibich and Gavious suggest the following initial guess:
![]()
While this may seem like a minor point, a common difficulty encountered when using shooting algorithms to solve boundary-value problems is that obtaining convergence in an efficient way (for example, by using Newton’s method) requires accurate initial estimates of (in this case) ![]() .
.
4.4 Gayle and Richard (2008)
Gayle and Richard (2008) presented perhaps the most practical contribution to the field. They generalized the backwards-shooting algorithm of Marshall et al. (1994) to allow for ![]() bidders, each of whom draws his valuation (cost) from one of four commonly used distributions. Gayle and Richard also provided a user-friendly computer program, which is available free of charge to researchers.38 Gayle and Richard claimed, too, that researchers could specify arbitrary (parametric, semiparametric, or nonparametric) distributions which their program could accommodate by constructing local Taylor-series expansions of (the inverse of) the (truncated) distributions automatically.
bidders, each of whom draws his valuation (cost) from one of four commonly used distributions. Gayle and Richard also provided a user-friendly computer program, which is available free of charge to researchers.38 Gayle and Richard claimed, too, that researchers could specify arbitrary (parametric, semiparametric, or nonparametric) distributions which their program could accommodate by constructing local Taylor-series expansions of (the inverse of) the (truncated) distributions automatically.
Gayle and Richard adjusted the Marshall et al. algorithm in two ways: first, they approximated functions of the inverse-bid functions; second, they incorporated a minimization routine to search for the unknown high bid ![]() . Recall that Eq. (8) can be written as
. Recall that Eq. (8) can be written as
![]()
Gayle and Richard defined
![]()
and rewrote this first-order condition for player ![]() as
as
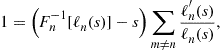
where we have applied the chain rule to derive ![]() . Rather than approximate the inverse-bid functions, they used Taylor-series expansions of
. Rather than approximate the inverse-bid functions, they used Taylor-series expansions of ![]() and generated expansions of
and generated expansions of ![]() , as well as
, as well as ![]() for each
for each ![]() ; that is, each of these three components was approximated by a Taylor-series expansion. The coefficients of each expansion are computed recursively with the
; that is, each of these three components was approximated by a Taylor-series expansion. The coefficients of each expansion are computed recursively with the ![]() term providing the link between coefficients of one order and those of the next. Once the piecewise approximation is finished at one point
term providing the link between coefficients of one order and those of the next. Once the piecewise approximation is finished at one point ![]() , the algorithm proceeds (backwards) to
, the algorithm proceeds (backwards) to ![]() which equals
which equals ![]() where
where ![]() is the uniform step size. Rather than specify convergence criteria, Gayle and Richard chose the high bid
is the uniform step size. Rather than specify convergence criteria, Gayle and Richard chose the high bid ![]() by solving the following minimization problem:
by solving the following minimization problem:
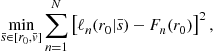
where ![]() denotes a potential reserve price and equals
denotes a potential reserve price and equals ![]() when no reservation price exists.
when no reservation price exists.
The program that Gayle and Richard have provided computes the bid functions without the presence of a reserve price as well as with the optimal reserve price. The algorithm also computes expected profits, probabilities of winning, expected revenues to the seller, and the probability the seller receives no bids in the presence of a reserve price. These statistics are computed for second-price auctions as well. Many of these values are expressed as the solution to integrals which the authors computed numerically via univariate quadrature: they used the extended Simpson’s rule.
The approach of Gayle and Richard relies on equally spaced subdivisions of the valuation support. They warned that “occasional pathologies” would require adaptive selection of the step size, and addressed this issue by increasing the number of points in the grid space as needed, showing in an example that, for a given order Taylor-series expansion, increasing the number of grid points (creating a finer grid) reduced the root mean squared error (RMSE) which was computed using each player’s first-order condition. The reduction of RMSE was marginal, but the cost (as measured by the increase in computational time) was substantial.39 This suggests there is little to gain by considering a finer grid within the algorithm. Furthermore, for a given number of grid points, higher-order Taylor-series expansions did not reduce the RMSE but did increase the computational time.40 In fact, Gayle and Richard cautioned readers that “an order of approximation that is too high can lead to significant numerical pathologies.” This conclusion may obtain because computing higher-order derivatives is often numerically unstable and, thus, prone to error.
4.5 Hubbard and Paarsch (2009)
One downside to the shooting algorithms of Marshall et al. (1994) and the first method of Bajari (2001) as well as of Gayle and Richard (2008) is that they take a long time to compute. Higher accuracy clearly comes at the cost of increased computational time. In fact, Gayle and Richard warned that, if the model involves bidders of many different types, then “the potential computational time increases significantly.” Computation time is of critical importance to empirical researchers who often need to solve for the equilibrium (inverse-) bid functions for each candidate vector of parameters when estimating the underlying distributions of private values, which may be conditioned on covariates as well. Empirical researchers also need to be concerned with the errors associated with computing the equilibrium (inverse-) bid functions which might bias estimates. Likewise, if researchers need to simulate dynamic games that require computing the inverse-bid functions at each period, then speed is crucial as this may require solving for the inverse-bid functions thousands of times. For example, Saini (2012) solved for a Markov Perfect Bayesian Equilibrium (MPBE) in a dynamic, infinite-horizon, procurement auction in which asymmetries obtain endogenously because of capacity constraints and utilization. Likewise, Saini (2010) admitted entry and exit and allowed firms to invest in capacity in a dynamic oligopoly model. In that model, firms compete at auction in each period, so the evolution of market structure as well as its optimality and efficiency under first-price and second-price auctions can be investigated. This required him to solve for the inverse-bid functions for each firm, at each state (described by each firm’s capacity), at each iteration in computing the MPBE.
Typically, with spectral methods, researchers use either Fourier basis functions or orthogonal polynomials. Judd (1998) has warned against using ordinary polynomials as a basis. While the Stone-Weierstraß theorem guarantees that ordinary polynomials are complete in the ![]() norm, given our interest in bounded, measurable functions on a compact set, this does not help when a least-squares objective is used. They will not be orthogonal in any natural inner product on
norm, given our interest in bounded, measurable functions on a compact set, this does not help when a least-squares objective is used. They will not be orthogonal in any natural inner product on ![]() . Furthermore, these polynomials may not be a good choice for a basis given that their behavior is too similar—that is, collinear; for example, they are all monotonically increasing and positive on
. Furthermore, these polynomials may not be a good choice for a basis given that their behavior is too similar—that is, collinear; for example, they are all monotonically increasing and positive on ![]() . Finally, they can vary dramatically over an interval
. Finally, they can vary dramatically over an interval ![]() .
.
For example, see Figure 3 which depicts several examples of Chebyshev polynomials; these are used in auctions because they are defined on a closed interval. In Figure 4, we depict the corresponding standard polynomials. The standard polynomials are very similar: all are monotonically increasing and positive over the positive real numbers. In contrast, the Chebyshev polynomials are orthogonal with respect to the inner product, something we suggested might be helpful in our earlier discussion of projection methods.
Hubbard and Paarsch (2009) modified the polynomial approximation approach of Bajari (2001) in three ways: first, instead of regular polynomials, they employed Chebyshev polynomials, which are orthogonal polynomials and thus more stable numerically. In addition to an orthogonal basis, Hubbard and Paarsch recommended coupling this choice with a grid defined by the roots of the ![]() th order Chebyshev polynomial—the Chebyshev nodes—which can be computed as
th order Chebyshev polynomial—the Chebyshev nodes—which can be computed as
![]()
The Chebyshev nodes lie on the interval ![]() , the domain of the Chebyshev polynomials. The points
, the domain of the Chebyshev polynomials. The points ![]() are found via the following transformation:
are found via the following transformation:
![]()
Second, Hubbard and Paarsch cast the problem within the Mathematical Programs with Equilibrium Constraints (MPEC) approach advocated by Su and Judd (2012); for more on the MPEC approach, see Luo et al. (1996). Specifically, they used the MPEC approach to discipline the estimated Chebyshev coefficients in the approximations so that the first-order conditions defining the inverse equilibrium bid functions are approximately satisfied, subject to constraints that the boundary conditions defining the equilibrium strategies are satisfied. Finally, they imposed monotonicity on candidate solutions. We make explicit the constrained optimization problem below when discussing the work of Hubbard et al. (2013) who have extended this line of research.
4.6 Fibich and Gavish (2011)
While most researchers who have employed shooting algorithms to solve asymmetric auctions have noticed their instability, Fibich and Gavish (2011) proved that this was not a “technical issue,” but rather an inherent property of backward integration in this setting.41 Fibich and Gavish demonstrated this instability by first considering a very controlled, well-understood setting—the symmetric first-price auction. As we noted above, the equilibrium bid function in this case can be solved in closed-form. Fibich and Gavish showed that a solution obtained via backward integration that involves being ![]() away from the true high bid (which can also be calculated analytically in a symmetric setting) involves an absolute error that increases monotonically from
away from the true high bid (which can also be calculated analytically in a symmetric setting) involves an absolute error that increases monotonically from ![]() (at the high bid, by construction) to infinity as
(at the high bid, by construction) to infinity as ![]() . Furthermore, the sensitivity of the backwards-shooting solution becomes worse as the number of players increases. Given this instability obtains in a symmetric setting, it is not surprising that the results extend to one involving heterogeneous bidders.
. Furthermore, the sensitivity of the backwards-shooting solution becomes worse as the number of players increases. Given this instability obtains in a symmetric setting, it is not surprising that the results extend to one involving heterogeneous bidders.
Not only did Fibich and Gavish document the problem of instability formally, but they also suggested an alternative approach to solving asymmetric auctions. Specifically, they transformed the free boundary-value problem involving ![]() to one in which one player’s valuation is written explicitly as a function of the other player’s valuation.42 In doing so, they obtained a standard (although still nonlinear) boundary-value problem which they proposed solving via fixed-point iteration. For example, in the two-player case, using a change of variables, the system (7), can be rewritten as
to one in which one player’s valuation is written explicitly as a function of the other player’s valuation.42 In doing so, they obtained a standard (although still nonlinear) boundary-value problem which they proposed solving via fixed-point iteration. For example, in the two-player case, using a change of variables, the system (7), can be rewritten as
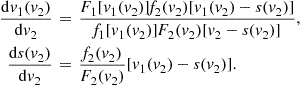
An advantage of this transformation is that the dependent variable ![]() is known to be in the range
is known to be in the range ![]() . In the canonical system of ODEs, the dependent variable
. In the canonical system of ODEs, the dependent variable ![]() has an unknown support as
has an unknown support as ![]() is unknown a priori. Under this transformation, the left-boundary condition can be expressed as
is unknown a priori. Under this transformation, the left-boundary condition can be expressed as
![]()
while the known right-boundary condition becomes
![]()
Note that ![]() remains unknown a priori, but it can be recovered once the system has been solved. Fibich and Gavish suggested solving this system using fixed-point iteration: discretize
remains unknown a priori, but it can be recovered once the system has been solved. Fibich and Gavish suggested solving this system using fixed-point iteration: discretize ![]() and construct an initial guess for the solutions
and construct an initial guess for the solutions ![]() and
and ![]() over the grid of
over the grid of ![]() points; then solve a modified version of the system above which provides new values for
points; then solve a modified version of the system above which provides new values for ![]() and
and ![]() , respectively. Of course, the
, respectively. Of course, the ![]() and
and ![]() values feed into the equation determining the other as any modification of the system still involves both variables. Use the new
values feed into the equation determining the other as any modification of the system still involves both variables. Use the new ![]() and
and ![]() values in the next iteration and continue this procedure. A researcher can incorporate tolerance criteria based on a norm involving the changes in
values in the next iteration and continue this procedure. A researcher can incorporate tolerance criteria based on a norm involving the changes in ![]() and
and ![]() between iterations to determine when to stop cycling through the iterative procedure. Since fixed-point problems can be expressed as root-finding problems, it is perhaps not surprising that Fibich and Gavish also suggested using Newton’s method to solve their transformed system. While an advantage of this technique is that it can speed up convergence, a disadvantage is that Newton’s method would be very complicated to implement with more than two bidders.
between iterations to determine when to stop cycling through the iterative procedure. Since fixed-point problems can be expressed as root-finding problems, it is perhaps not surprising that Fibich and Gavish also suggested using Newton’s method to solve their transformed system. While an advantage of this technique is that it can speed up convergence, a disadvantage is that Newton’s method would be very complicated to implement with more than two bidders.
Fibich and Gavish also investigated some interesting applications of their method to problems that cannot be solved using backwards shooting (even if the shooting algorithm were reliable) simply because it is too time-consuming. In particular, they first presented an example with a large number of heterogeneous bidders, and argued that, as ![]() increases (tends to infinity), asymmetric auctions “become symmetric.” Bali and Jackson (2002) showed that all symmetric mechanisms, which in equilibrium award objects to a highest signal observer and only have payments conditional on winning, generate the same limiting revenue, which is equal to the expected value of the best-use of the object. Given that Fibich and Gavish found that asymmetric auctions become symmetric, they employed the result of Bali and Jackson to examine the rate at which asymmetric auctions become revenue equivalent as the number of players increases.
increases (tends to infinity), asymmetric auctions “become symmetric.” Bali and Jackson (2002) showed that all symmetric mechanisms, which in equilibrium award objects to a highest signal observer and only have payments conditional on winning, generate the same limiting revenue, which is equal to the expected value of the best-use of the object. Given that Fibich and Gavish found that asymmetric auctions become symmetric, they employed the result of Bali and Jackson to examine the rate at which asymmetric auctions become revenue equivalent as the number of players increases.
4.7 Hubbard et al. (2013)
Hubbard et al. (2013) expanded on the suggestions proposed by Hubbard and Paarsch (2009) by using economic theory to constrain approximations further and to guide them in determining the quality of the solutions. Of the research discussed so far, theirs relies most on connecting economic theory with numerical analysis and leveraging this interdependence. Although it is typically impossible to solve the system of differential equations that characterizes equilibrium bidding in closed-form, some properties can be deduced by studying the system at the endpoints as ![]() approaches
approaches ![]() or
or ![]() . Fibich et al. (2002) proved the following properties concerning the high and low types, the first of which follows directly from system (9):
. Fibich et al. (2002) proved the following properties concerning the high and low types, the first of which follows directly from system (9):
The second condition generalizes the Marshall et al. (1994) result as ![]() in their restricted model. This second condition holds if the probability density functions for each bidder are strictly greater than zero and if
in their restricted model. This second condition holds if the probability density functions for each bidder are strictly greater than zero and if ![]() is differentiable at
is differentiable at ![]() . Because Hubbard et al. represented the inverse-bid functions by (Chebyshev) polynomials, this latter condition will hold in their approximations. Thus, these two properties imply two conditions in addition to the right-boundary and left-boundary conditions that will characterize each inverse-bid function.
. Because Hubbard et al. represented the inverse-bid functions by (Chebyshev) polynomials, this latter condition will hold in their approximations. Thus, these two properties imply two conditions in addition to the right-boundary and left-boundary conditions that will characterize each inverse-bid function.
For each bidder, the authors imposed four equality constraints on the equilibrium inverse-bid functions, which they approximated by Chebyshev polynomials of order ![]() . Specifically, Hubbard et al. (2013) approximated the solution to system (9) by solving
. Specifically, Hubbard et al. (2013) approximated the solution to system (9) by solving
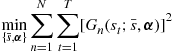
subject to the following conditions for each bidder ![]() :
:
where ![]() was defined in Eq. (23). The last condition is imposed to preserve shape; that is, monotonicity is imposed on the solution at a grid of
was defined in Eq. (23). The last condition is imposed to preserve shape; that is, monotonicity is imposed on the solution at a grid of ![]() additional points not considered in the objective function. The MPEC approach is used to discipline the estimated Chebyshev coefficients in the approximations so that the first-order conditions defining the equilibrium inverse-bid functions are approximately satisfied, subject to constraints that the boundary conditions defining the equilibrium strategies hold.
additional points not considered in the objective function. The MPEC approach is used to discipline the estimated Chebyshev coefficients in the approximations so that the first-order conditions defining the equilibrium inverse-bid functions are approximately satisfied, subject to constraints that the boundary conditions defining the equilibrium strategies hold.
Under this approach, ![]() equality constraints exist and
equality constraints exist and ![]() points enter the objective function; in contrast, there are
points enter the objective function; in contrast, there are ![]() unknowns—the parameters in
unknowns—the parameters in ![]() plus
plus ![]() . For the number of conditions (boundary and first-order together) to equal the number of unknowns
. For the number of conditions (boundary and first-order together) to equal the number of unknowns
![]()
or
![]() (26)
(26)
Since at auctions, ![]() weakly exceeds two, and
weakly exceeds two, and ![]() and
and ![]() are integers, this equality cannot hold for any
are integers, this equality cannot hold for any ![]() choice. When comparing the
choice. When comparing the ![]() unknowns with the
unknowns with the ![]() conditions, note that, if
conditions, note that, if ![]() equals three and all the conditions are satisfied, then only one degree of freedom remains. One criticism of the polynomial approximation approach (and projection methods, in general) is that it works well, if the practitioner has a good initial guess. When
equals three and all the conditions are satisfied, then only one degree of freedom remains. One criticism of the polynomial approximation approach (and projection methods, in general) is that it works well, if the practitioner has a good initial guess. When ![]() equals three, the researcher obtains an initial guess that already satisfies some theoretical properties at essentially no cost because there is only one free parameter,
equals three, the researcher obtains an initial guess that already satisfies some theoretical properties at essentially no cost because there is only one free parameter, ![]() , to minimize the nonlinear least-squares objective.
, to minimize the nonlinear least-squares objective.
This approach is related to the spectral methods used to solve partial differential equations; see the discussion above as well as a book-length treatment by Gottlieb and Orszag (1993). Recall that, under collocation methods, it is assumed that the solution can be represented by a candidate approximation, typically a polynomial; a solution is selected that solves the system exactly at a set of (collocation) points over the interval of interest. Because equality (26) cannot hold, collocation is infeasible in this case, but the MPEC approach can be thought of as a hybrid between collocation and least squares as some constraints are explicitly imposed, leading to a constrained nonlinear optimization problem. It will be impossible to make all residual terms equal to zero: the fit is necessarily imperfect in a quantitative sense.
When the order of the polynomial used in the approximation is too small, Hubbard et al. demonstrated that the approach may deliver approximations that are qualitatively inadequate as well. Specifically, the authors used theoretical results from Kirkegaard (2009) to evaluate the quality of an approximation. Kirkegaard proved that if ![]() crosses
crosses ![]() , then the equilibrium bid functions must cross as well.43 Under certain conditions, he determined the exact number of times the bid functions will cross. Let
, then the equilibrium bid functions must cross as well.43 Under certain conditions, he determined the exact number of times the bid functions will cross. Let
![]()
measure bidder ![]() ’s strength (power) relative to bidder
’s strength (power) relative to bidder ![]() at a given value
at a given value ![]() . Similarly, define
. Similarly, define
![]()
as bidder ![]() ’s equilibrium expected pay-off (profit) at an auction if his value is
’s equilibrium expected pay-off (profit) at an auction if his value is ![]() , and let
, and let
![]()
denote bidder ![]() ’s equilibrium pay-off relative to bidder
’s equilibrium pay-off relative to bidder ![]() ’s equilibrium pay-off at a given value. Note that
’s equilibrium pay-off at a given value. Note that ![]() is exogenous, while
is exogenous, while ![]() is endogenous—we shall use this language to refer to these ratios.
is endogenous—we shall use this language to refer to these ratios.
Kirkegaard (2009) demonstrated that the two ratios can be used to make predictions concerning the properties of ![]() and
and ![]() or, equivalently,
or, equivalently, ![]() and
and ![]() . At
. At ![]() equal
equal ![]() , the two bids coincide and so too do the two ratios, or
, the two bids coincide and so too do the two ratios, or ![]() equals
equals ![]() and
and ![]() equals
equals ![]() , which is one. In fact, comparing the two ratios at any
, which is one. In fact, comparing the two ratios at any ![]() is equivalent to comparing the equilibrium bids at
is equivalent to comparing the equilibrium bids at ![]() , or
, or
![]() (27)
(27)
Moreover, it turns out that the motion of the endogenous ratio ![]() , is determined by how it compares to the exogenous ratio
, is determined by how it compares to the exogenous ratio ![]() . Specifically,
. Specifically,
![]() (28)
(28)
The standard right-boundary condition can be written in terms of these ratios as
![]() (29)
(29)
while the left-boundary condition, so long as the second condition from Fibich et al. (2002) is satisfied, becomes
![]() (30)
(30)
Recall that Fibich et al. maintained ![]() for all
for all ![]() . These observations allow one to make a number of predictions. In Figure 5, we depict the exogenous and endogenous ratios for an example in which
. These observations allow one to make a number of predictions. In Figure 5, we depict the exogenous and endogenous ratios for an example in which ![]() and
and ![]() cross twice in the interior, so
cross twice in the interior, so ![]() equals one twice in the interior.
equals one twice in the interior.
Based on the approximate equilibrium bid functions, denoted ![]() , the ratio of expected pay-offs can be computed. Denote the estimated ratio by
, the ratio of expected pay-offs can be computed. Denote the estimated ratio by ![]() . If
. If ![]() and
and ![]() are plotted in the same figure, then they should interact in a manner consistent with these observations, as illustrated in Figure 5. Comparing these ratios provides a visual “test” of the adequacy of the approximation. Specifically, the steepness of
are plotted in the same figure, then they should interact in a manner consistent with these observations, as illustrated in Figure 5. Comparing these ratios provides a visual “test” of the adequacy of the approximation. Specifically, the steepness of ![]() at a point of intersection with
at a point of intersection with ![]() and the location of the intersections can be used to eliminate inaccurate solutions. In particular, any acceptable solution should respect the following:
and the location of the intersections can be used to eliminate inaccurate solutions. In particular, any acceptable solution should respect the following:
1. Slope: At any point where ![]() and
and ![]() intersect (i.e., where
intersect (i.e., where ![]() equals
equals ![]() ), the latter should be flat, have a derivative that equals zero. If
), the latter should be flat, have a derivative that equals zero. If ![]() is steep at such a point, then this is an indication that the approximate equilibrium bid function is inaccurate as the first-order conditions are not close to being satisfied. Note, too, that this is true any time bids coincide (for any
is steep at such a point, then this is an indication that the approximate equilibrium bid function is inaccurate as the first-order conditions are not close to being satisfied. Note, too, that this is true any time bids coincide (for any ![]() , including
, including ![]() ).
).
2. Location: The location of the intersections of ![]() and
and ![]() must also be consistent with theory. In particular,
must also be consistent with theory. In particular, ![]() and
and ![]() can cross at most once between any two peaks of
can cross at most once between any two peaks of ![]() ; when the diminishing wave property is satisfied (see Kirkegaard, 2009), they must cross between any two peaks (not counting
; when the diminishing wave property is satisfied (see Kirkegaard, 2009), they must cross between any two peaks (not counting ![]() equals
equals ![]() ). In Figure 5, for example,
). In Figure 5, for example, ![]() and
and ![]() must cross once to the left of the point where
must cross once to the left of the point where ![]() is minimized, and once between the two interior stationary points.
is minimized, and once between the two interior stationary points.
Although Hubbard et al. chose to use the projection approach, the “tests” they proposed to check the validity of a candidate solution can be used regardless of the approximation method used by a researcher.
Hubbard et al. also considered a Monte Carlo study using various orders of approximations to solve some examples of asymmetric auctions. They found that poor approximations (those which involved polynomials of too low an order and, thus, failed the visual test suggested above) led to incorrect expected-revenue rankings between first-price and second-price auctions, incorrect insights concerning the number of inefficiencies that obtain, and incorrect conclusions concerning which auction format favors different bidders as well as how auction formats affect the ex ante probability of a given bidder winning the auction. In short, at the risk of belaboring the obvious, it is important that researchers use good approximations.
5 Some Examples
In this section, we present the approximate solutions to some examples of equilibrium inverse-bid functions. Our approach mirrors our previous presentation: we begin by considering a problem to which we know the solution, and then consider increasingly more difficult problems. Specifically, we first consider approximating the solution to a symmetric auction, but treating it like an asymmetric auction. This is something we should expect any numerical approach to do successfully; doing this also allows us to benchmark a given method since the bidding strategy can be computed in closed-form. We then consider a common example studied by economic theorists in which there are two bidders at auction and the private-values distribution of one bidder first-order stochastically dominates that of the other. In the third example, we examine a problem that, until recently, had not been investigated, one which involves value distributions that cross. Finally, in the last example, we investigate a problem that has been neglected (relative to the independence case), one in which bidders draw valuations from different marginal distributions, but (following Hubbard and Paarsch, 2011) we allow these valuations to be dependent by choosing a copula that imposes affiliation.
Given that we have solved a symmetric auction with some confidence, we next consider a small modification to this problem. Specifically, we change the distribution from which one bidder draws valuations. A convenient setting for our examples involves the (standard) Beta distribution which has support ![]() . The Beta probability density function can be expressed as
. The Beta probability density function can be expressed as
![]()
where
![]()
when ![]() is an integer. The cumulative distribution function is then
is an integer. The cumulative distribution function is then
![]()
which is often referred to as the regularized Beta function, while the integral term is referred to as the incomplete Beta function. Note that when ![]() and
and ![]() both equal one, the Beta distribution is simply a uniform distribution. This distribution is attractive to use because the probability density functions can capture a wide array of shapes. Unfortunately, for many parameterizations, the probability density function takes the value zero at
both equal one, the Beta distribution is simply a uniform distribution. This distribution is attractive to use because the probability density functions can capture a wide array of shapes. Unfortunately, for many parameterizations, the probability density function takes the value zero at ![]() equal zero. To ensure the probability density function is strictly positive, we avoid this difficulty by mixing the Beta distribution with a uniform distribution and choosing the weight on the uniform distribution to be small—to preserve the properties that make the Beta distribution attractive. We depict some Beta-Uniform mixed probability density functions in Figure 7 under various parameterizations.44 In Figure 8, we depict the corresponding cumulative distribution functions as we shall reference them in the two examples that follow.
equal zero. To ensure the probability density function is strictly positive, we avoid this difficulty by mixing the Beta distribution with a uniform distribution and choosing the weight on the uniform distribution to be small—to preserve the properties that make the Beta distribution attractive. We depict some Beta-Uniform mixed probability density functions in Figure 7 under various parameterizations.44 In Figure 8, we depict the corresponding cumulative distribution functions as we shall reference them in the two examples that follow.
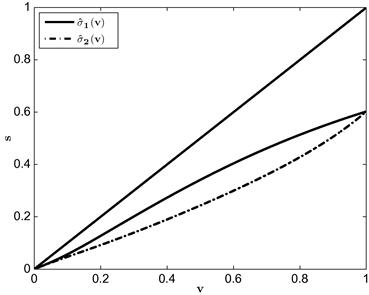
Figure 9 Approximate equilibrium bid functions at asymmetric auction for Example 2.
Although the sharp predictions of the model with strong and weak bidders make it an attractive one, little reason exists to suggest that the model is necessarily an accurate description of real-world bidder asymmetries. As we discussed above, recently, Kirkegaard (2009) derived results under much weaker assumptions concerning the primitives of the economic environment. For example, he has shown that when first-order stochastic dominance does not hold so the cumulative distribution functions of bidders cross, the equilibrium bid functions must cross as well. In the next example, we consider a situation where the cumulative distribution functions of the bidders cross. As shown by Hubbard et al. (2013), the guidance that theory provides in such settings is extremely helpful to researchers interested in approximating an asymmetric first-price auction as it allows for further qualitative “checks” on the approximate solution.
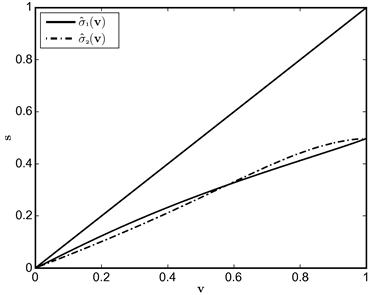
Figure 10 Approximate equilibrium bid functions at asymmetric auction for Example 3.
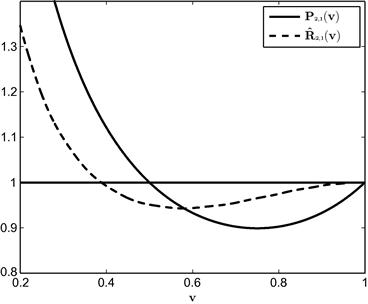
Figure 11 Exogenous and endogenous ratios for Example 3.
Thus far, our focus—both in the examples and in our earlier presentation—has solely concerned the IPVP. The symmetric IPVP model involves bidders whose valuations are independent and identically distributed. While our research has been motivated by relaxing the commonly adopted symmetry assumption (valuations are no longer identically distributed), the methods we have discussed can also be used to examine models in which valuations are dependent as well. In auction theory, dependence has been typically assumed to satisfy a property referred to as affiliation, a term coined by Milgrom and Weber (1982). Affiliation is a condition concerning the joint distribution of signals. In the case of continuous random variables, following Karlin (1968), some refer to affiliation as multivariate total positivity of order two. Under affiliation for continuous random variables, the off-diagonal elements of the Hessian of the logarithm of the joint probability density of signals are all nonnegative: the joint probability density function is log-supermodular. Maskin and Riley (2000b) showed that a monotonic equilibrium exists when bidders draw valuations from heterogeneous distributions within the APVP. Hubbard et al. (2012) used the family of Archimedean copulae to impose affiliation in an econometric model, thus ensuring that an equilibrium is satisfied by the measurement equation. Rather than derive an entirely new model, we refer readers to Hubbard and Paarsch (2011) who investigated the asymmetric APVP in detail. In particular, they solved for the equilibrium (inverse-) bid functions in various theoretical models in which valuations are affiliated. In the following example, we consider asymmetric bidders who draw valuations from a joint distribution that is characterized by a Frank copula involving positive dependence. Within the Archimedean family of copulae, conditions on the dependence parameter(s) can be used to guarantee affiliation.
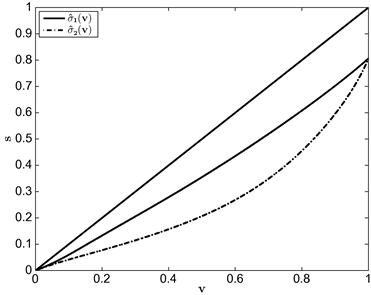
Figure 12 Approximate equilibrium bid functions at asymmetric auction for Example 4.
6 Comparisons of Relative Performance and Potential Improvements
In this section, we do two things: first, we present a practical comparison of the shooting, fixed-point iterative, and polynomial approximation strategies focusing on run time as well as an error analysis of three of the examples described above; second, we discuss ways in which current numerical strategies could be improved. While many of these ideas are preliminary, we think they will make interesting extensions.
6.1 Comparisons of Relative Performance
Using the first three examples presented above, all of which concern the IPVP, we conducted a small error analysis of each of the three numerical strategies. For each example, we evaluated each first-order condition of the system of differential equations at a uniform grid of one thousand points. Thus, given the shooting algorithm and the polynomial approximation approach, we solved for the inverse-bid functions on the relevant grid of ![]() where the
where the ![]() subscripts denote approximated values using solution method
subscripts denote approximated values using solution method ![]() . For the fixed-point iterative method, on the other hand, we used one of the player’s valuations as the dependent variable and solved for that player’s bid function as well as the valuation(s) of the other player(s) as a function of this valuation.47
. For the fixed-point iterative method, on the other hand, we used one of the player’s valuations as the dependent variable and solved for that player’s bid function as well as the valuation(s) of the other player(s) as a function of this valuation.47
For each method, we considered three choices for key decision parameters that a user must choose: for the shooting algorithm, we chose three different tolerance criteria; for the fixed-point iterative method, we chose three different step sizes for the grid; for the polynomial approximation approach, we chose three different orders for the polynomials. To distinguish among these cases, in Tables 1 and 2 below, we denote the shooting algorithms by “Shoot ![]() ” where
” where ![]() denotes some tolerance level (at
denotes some tolerance level (at ![]() ). We denote the fixed-point iterative method by “FPI
). We denote the fixed-point iterative method by “FPI ![]() ” where the value
” where the value ![]() represents the number of points in the uniformly spaced grid.48 Finally, we denote the polynomial approximation approach by “Poly
represents the number of points in the uniformly spaced grid.48 Finally, we denote the polynomial approximation approach by “Poly ![]() ” where the value
” where the value ![]() represents the order of these polynomials; we present three sets of results where we varied the order of the polynomials used to approximate each inverse-bid function.
represents the order of these polynomials; we present three sets of results where we varied the order of the polynomials used to approximate each inverse-bid function.
Because the iterative approach involved solving the system at a grid of points, we evaluated nongrid points using linear interpolation as this is consistent with how the algorithm operates and preserves monotonicity of the solution. Evaluating the first-order conditions required the derivatives of the inverse-bid functions; see, system (7) above for the two-player case as well as Eqs. (19a) and (20a) in Fibich and Gavish (2011). To compute these derivatives, given a grid of points, we used finite differences and report error statistics based on the midpoint of the original grid used to evaluate the solution. This, too, is consistent with the approach of Fibich and Gavish, but in doing this we lose one grid point in the error analysis for the fixed-point iterative method which is actually based on 999 uniformly spaced points.
We present two types of information concerning the performance of the three different numerical strategies. First, in Table 1, we report the low and the high bids as well as the low and the high valuations under each strategy.
The lower and upper points are critical points which all strategies lever and often use as a metric to evaluate convergence. Furthermore, they provide a caveat concerning how the results of the error analysis should be interpreted because the points in the error analysis will lie within these respective intervals, a point we shall return to below. In examining Table 1, the most striking result is that many of the elements concerning the shooting algorithm read “n/a”: in these cases, we could not achieve convergence for the shooting algorithm. This occurred even though, by any standard, very modest tolerance levels were used: the most stringent tolerance level was only ![]() . Convergence could only be achieved at a tolerance of 0.1 for all examples, which is 10% of the high valuation. Because the winning bids tend to cluster at the high end, being off by 10% at this end is disappointing, particularly to those researchers hoping to use the results to inform policy debates. If the theoretical argument made by Fibich and Gavish (2011) against shooting algorithms left the reader unconvinced, then this table should illustrate further how poorly these methods work in practice.
. Convergence could only be achieved at a tolerance of 0.1 for all examples, which is 10% of the high valuation. Because the winning bids tend to cluster at the high end, being off by 10% at this end is disappointing, particularly to those researchers hoping to use the results to inform policy debates. If the theoretical argument made by Fibich and Gavish (2011) against shooting algorithms left the reader unconvinced, then this table should illustrate further how poorly these methods work in practice.
The fixed-point iterative method performs much better than the shooting algorithm. Remember that ![]() is the known interval in this approach. Unfortunately, setting
is the known interval in this approach. Unfortunately, setting ![]() equal to the known value
equal to the known value ![]() (which equals zero in each example) prevents the algorithm from working as a singularity obtains at the low value. The solution used under this approach in practice is to simply avoid it and to start the grid a step size away from the low valuation. Thus,
(which equals zero in each example) prevents the algorithm from working as a singularity obtains at the low value. The solution used under this approach in practice is to simply avoid it and to start the grid a step size away from the low valuation. Thus, ![]() decreases by an order as the step size increases by an order of magnitude. Unfortunately, if a researcher wanted to obtain approximations over the full true interval, then he would have to resort to extrapolation under this method.
decreases by an order as the step size increases by an order of magnitude. Unfortunately, if a researcher wanted to obtain approximations over the full true interval, then he would have to resort to extrapolation under this method.
An advantage of the polynomial approximation approach, as implemented by Hubbard et al. (2013), is that theoretical constraints are imposed at the endpoints explicitly; under the polynomial approximation approach, all approximations span the known interval without error for the case with uniform bidders (Example 1). Furthermore, the only unknown where error can obtain is in approximating ![]() as it is determined endogenously. The polynomial approximation results look promising in achieving this true value: in each example, as the order of the polynomial increases the approximation of
as it is determined endogenously. The polynomial approximation results look promising in achieving this true value: in each example, as the order of the polynomial increases the approximation of ![]() converges in the same direction and, it appears to be the same value as the fixed-point iterative method.
converges in the same direction and, it appears to be the same value as the fixed-point iterative method.
In Table 2, we report the time it took to solve each example for each solution method (and parameter choice) as well as some summary statistics concerning the value of the first-order conditions at the candidate solutions.
All methods do quite well in solving Example 1 for which we know the true solution. Even from this example, however, the shooting algorithm is clearly inferior: with a tolerance of ![]() , the shooting algorithm took over a minute to solve, and this was the only case where this tolerance level could be attained. Remember, too, that when interpreting the error statistics, the interval over which the points were chosen might be a subset of the true interval, as shown by the results in Table 1. For example, in the application of the fixed-point iterative method to Example 1 with 500 points, the maximum error is reported as 0.00001 in Table 2, but the high valuation (for bidder 1) and high bid were approximated to be 0.99801 and 0.49950, respectively, both of which involve errors that exceed the maximum reported as the true high valuation is one and the true high bid is 0.5. Note that these discrepancies have not been factored into the error statistics reported in Table 2. We emphasize this caveat when interpreting the results because it can be avoided when closed-form solution exists, as in Example 1, but this is typically impossible in most cases, as the examples that follow demonstrate.
, the shooting algorithm took over a minute to solve, and this was the only case where this tolerance level could be attained. Remember, too, that when interpreting the error statistics, the interval over which the points were chosen might be a subset of the true interval, as shown by the results in Table 1. For example, in the application of the fixed-point iterative method to Example 1 with 500 points, the maximum error is reported as 0.00001 in Table 2, but the high valuation (for bidder 1) and high bid were approximated to be 0.99801 and 0.49950, respectively, both of which involve errors that exceed the maximum reported as the true high valuation is one and the true high bid is 0.5. Note that these discrepancies have not been factored into the error statistics reported in Table 2. We emphasize this caveat when interpreting the results because it can be avoided when closed-form solution exists, as in Example 1, but this is typically impossible in most cases, as the examples that follow demonstrate.
The choice of grid sizes as well as the order of the polynomials appears to be appropriate in comparing the fixed-point iterative method and polynomial approximation approach. For small grid sizes (low-order polynomials), the approximations take less than a second to calculate, while more accurate approximations (involving a finer grid or higher-order polynomial) take a few seconds to solve.49 Both methods do quite well on Example 2 which involved first-order stochastic dominance, although it is clear that the polynomial approximation approach requires a “sufficiently high” order polynomial be used, which is consistent with the arguments made by Hubbard et al. (2013). Example 3 is clearly the toughest for all approaches as the errors involved in the approximations are higher than in the first two examples. The fixed-point iterative method achieves lower error, on average, but the polynomial approximations have a lower maximum error. Note, too, that as the order of the polynomial approximation increases, all error statistics improve (the average, median, and maximum errors decrease and the standard deviation of the error gets tighter). This does not seem to hold for the fixed-point iterative method as the maximum error increases as the number of points in the grid increases (the step size decreases), the average seems to level off, and the variance in the error solution increases.
6.2 Potential Improvements
Shooting algorithms have been the most well studied and the most criticized of the numerical strategies considered. Even in their original work, Marshall et al. (1994) admitted that the analytic requirements for such shooting algorithms are more stringent than for other numerical strategies. Perhaps the most devastating criticism of (backwards) shooting algorithms was presented by Fibich and Gavish (2011) who showed analytically that backwards-shooting algorithms are inherently unstable for solving asymmetric auctions. One way to mitigate these concerns would be to incorporate checks into each candidate solution that ensure the solutions do not blow up at any point, that the inverse-bid functions are contained on ![]() , and that they are monotonically decreasing (since we shoot backwards). Only if a candidate solution passes these checks should the convergence criteria (how close the inverse-bid functions are to
, and that they are monotonically decreasing (since we shoot backwards). Only if a candidate solution passes these checks should the convergence criteria (how close the inverse-bid functions are to ![]() ) be considered. These checks require more sophisticated programming and seem absent from the methods currently proposed in the literature. Even if the instability concerns could be addressed, however, repeatedly shooting backwards is an expensive procedure in terms of time, as the above comparison illustrates.
) be considered. These checks require more sophisticated programming and seem absent from the methods currently proposed in the literature. Even if the instability concerns could be addressed, however, repeatedly shooting backwards is an expensive procedure in terms of time, as the above comparison illustrates.
Applying fixed-point iteration (or Newton’s method) as suggested by Fibich and Gavish (2011) appears very promising. Although not discussed in their paper, it appears (from the authors’ code) that they use a Gauss-Seidel method in which, within an iteration, the updated values of solutions that have already been considered are used in computing solutions to the remaining equations. This is used to speed up convergence. Two ways exist in which researchers can immediately consider improving the iterative methods. First, a primary concern with the approach is that it requires a transformation of the system of differential equations which seems to depend critically on which variable (player’s valuation) is chosen as the independent variable. Unfortunately, this choice is critical: an incorrect choice can lead to a divergent solution. Future research in this area should provide guidance concerning this choice. For example, perhaps there is a relationship between the distributions each player draws valuations from (which is the reason the asymmetry obtains) that can be used to identify which variable should be used as the independent variable.
A second area for improving the iterative approach involves the initial guess. The importance of a good initial guess has been stressed by all researchers. For example, a classic criticism of Newton’s method is that there is often only a small region of convergence: an initial guess must be quite close to the solution. In finding a zero of a function over a closed interval, researchers might choose the midpoint of the interval. Fibich and Gavish (2011) chose an analogous approach when constructing an initial guess for the iterative methods for solving nonlinear systems of equations. For example, in the two-player case, they used a symmetric bidding strategy (the valuations are equal to each other) and a uniform-based rule in which bids are one-half of the valuation considered as their initial guess. They found this worked to approximate well the solutions in the examples they considered but suggested future research might consider the sensitivity of an initial guess.
Polynomial approximations and other approaches related to spectral methods can also be improved. While the methods are faster than shooting algorithms, a researcher cannot use these methods blindly: solutions need to be inspected to make sure they are reasonable. For example, a common issue with Chebyshev polynomials is that they can be difficult to implement when it comes to enforcing shape constraints. To deal with this, Hubbard et al. (2013) imposed rationality (players cannot bid more than their valuation) and monotonicity constraints on a finer grid of points which were not used in the residual calculation. We believe that other ways exist to improve the performance of these approximation methods. In the discussion that follows, we focus on extensions of or modifications to this approach. Specifically, we believe researchers might have success by changing the norm used in the objective, by choosing different bases or expanding the types of terms involved in the approximation, or by considering a finite-element method.
Bajari (2001) originally considered a least-squares objective and Hubbard and Paarsch (2009) as well as Hubbard et al. (2013) continued this tradition, but some problems might be better approximated using a different norm. Returning to Bajari’s original (third) method, he suggested using ordinary (algebraic) polynomials. These polynomials are very similar (correlated) to each other; as such, the least-squares problem is ill-conditioned. While this basis is probably not a good choice under the least-squares approach, it could be appropriate under a different norm. For example, rather than consider a least-squares objective, which involves an ![]() (Euclidean) norm, a researcher could minimize the sum of the absolute values of the residual function—the
(Euclidean) norm, a researcher could minimize the sum of the absolute values of the residual function—the ![]() norm, which is sometimes referred to as the taxicab norm or the Manhattan distance. This will seem sensible to applied researchers who have found that the method of least squares does not perform well in the presence of outliers and who have, instead, opted to use the method of least-absolute deviations (LAD). In estimation problems, LAD returns the median (as opposed to the mean of least squares) and is robust to outliers. In the auction case, outliers would be poorly approximated regions of an inverse-bid function. While an orthogonal basis has a comparative advantage in an
norm, which is sometimes referred to as the taxicab norm or the Manhattan distance. This will seem sensible to applied researchers who have found that the method of least squares does not perform well in the presence of outliers and who have, instead, opted to use the method of least-absolute deviations (LAD). In estimation problems, LAD returns the median (as opposed to the mean of least squares) and is robust to outliers. In the auction case, outliers would be poorly approximated regions of an inverse-bid function. While an orthogonal basis has a comparative advantage in an ![]() setting, this concept concerns vector spaces and adds nothing when an
setting, this concept concerns vector spaces and adds nothing when an ![]() norm is adopted. For example, maintaining the spirit of the approach suggested by Hubbard et al. (2013), a researcher could choose the unknown parameters (the common high bid and the polynomial coefficients) to minimize
norm is adopted. For example, maintaining the spirit of the approach suggested by Hubbard et al. (2013), a researcher could choose the unknown parameters (the common high bid and the polynomial coefficients) to minimize
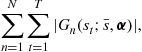
where ![]() was defined in Eq. (24) and the optimization is subject to the four boundary-related constraints we have discussed as well as rationality and monotonicity-related conditions. In practice, this problem can be recast as
was defined in Eq. (24) and the optimization is subject to the four boundary-related constraints we have discussed as well as rationality and monotonicity-related conditions. In practice, this problem can be recast as
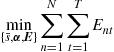
subject to
![]()
as well as the boundary and shape constraints. Of course, since the ![]() terms and constraints are nonlinear in
terms and constraints are nonlinear in ![]() and
and ![]() , this is a nonlinear programming problem whose solution is sensitive to the shape of the region defined by the
, this is a nonlinear programming problem whose solution is sensitive to the shape of the region defined by the ![]() s in the space of
s in the space of ![]() .
.
A researcher might instead opt for an ![]() (maximum) norm which would involve choosing the unknown parameters to minimize
(maximum) norm which would involve choosing the unknown parameters to minimize
![]()
subject to the boundary and shape constraints discussed. Here, the error in the approximation to the system is defined as the largest value, at any given point in the grid, that one of the first-order conditions takes. (Remember, the first-order conditions would all equal zero exactly in a perfect solution.) This strategy is often called a minimax approximation by researchers concerned with numerical analysis and this approach has been used for some time to approximate solutions to systems of ODEs (see, for example, Burton and Whyburn (1952)) as well as boundary-value problems (see, for example, Schmidt and Wiggins (1979)).
Alternatively, an improved approximation could involve choosing a different basis. Judd (1998) has noted that if the choice of basis is good, then increasing the order of the approximation should yield better approximations. He went on to claim that “using a basis that is well-suited to a problem can greatly improve performance.” For additional discussion, see pages 380–382 of Judd’s book. This suggests that a researcher must take care in selecting a basis. While we have advocated Chebyshev polynomials, other orthogonal bases may be better for a given problem. A researcher might also have success in choosing a basis which involves some terms that have characteristics that basis-members are known to have in common with the solution a researcher is trying to approximate. Judd (1998) has alluded to this by suggesting that one could choose basis elements that look something like or have features in common with the solution so that even a few elements can give a good approximation. Outside the class of orthogonal polynomials, there may be gains from choosing Bernstein polynomials, which are defined by
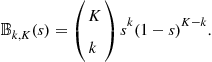
Bernstein polynomials might make for an attractive basis in this problem because the first few polynomials put weight on the approximations near the boundaries, which is often where most of the concerns about the accuracy of approximations exist. Bernstein polynomials are global over the support, but each individual member puts weight on different regions. In fact, each polynomial has a single, unique maximum in the ![]() interval. Another choice could be Laurent polynomials, which are like standard algebraic polynomials, but which admit negative powers in the approximation. Laurent polynomials may be useful in capturing the singularity that obtains at the boundary of these problems. Ultimately, a researcher can include a linear combination of functions from an arbitrary dictionary as projection methods generalize directly to idiosyncratic basis element choices. Tibshirani (1996) proposed a least-absolute deviation shrinkage and selection operator (lasso) technique in an estimation setting. The lasso approach reduces the value of (shrinks) some coefficients like in ridge regression and, hence, is more stable, and sets other values to zero, like in subset selection, if the variable/element is not important. That is, the lasso penalizes adding unnecessary variables. It would seem such an approach could be used to determine which elements of a basis are helpful in approximating the inverse-bid functions via projection methods. Some related research concerned with estimating a function is the basis pursuit approach, which involves minimizing an
interval. Another choice could be Laurent polynomials, which are like standard algebraic polynomials, but which admit negative powers in the approximation. Laurent polynomials may be useful in capturing the singularity that obtains at the boundary of these problems. Ultimately, a researcher can include a linear combination of functions from an arbitrary dictionary as projection methods generalize directly to idiosyncratic basis element choices. Tibshirani (1996) proposed a least-absolute deviation shrinkage and selection operator (lasso) technique in an estimation setting. The lasso approach reduces the value of (shrinks) some coefficients like in ridge regression and, hence, is more stable, and sets other values to zero, like in subset selection, if the variable/element is not important. That is, the lasso penalizes adding unnecessary variables. It would seem such an approach could be used to determine which elements of a basis are helpful in approximating the inverse-bid functions via projection methods. Some related research concerned with estimating a function is the basis pursuit approach, which involves minimizing an ![]() norm of the coefficients; see, for example, Chen et al. (1998).
norm of the coefficients; see, for example, Chen et al. (1998).
Rather than approximating each inverse-bid function by one global function (polynomial), one might instead consider finite-element methods which involve partitioning the domain of interest ([![]() ] in this case) into smaller segments and using splines or piecewise polynomials which are then aggregated to form an approximation over the entire region. This is like an hybrid of the polynomial approach originally suggested by Bajari (2001) that comes closer to capturing the spirit of the Taylor-series expansions suggested by, most recently, Gayle and Richard (2008). This approach, however, avoids the use of backwards integration and would not suffer from the criticisms of Fibich and Gavish (2011) as it involves a nonlinear least-squares (or LAD, depending on the norm) approach. This might be attractive as it can allow the researcher to gain the speed of the polynomial approach but perhaps reduce error and improve stability.
] in this case) into smaller segments and using splines or piecewise polynomials which are then aggregated to form an approximation over the entire region. This is like an hybrid of the polynomial approach originally suggested by Bajari (2001) that comes closer to capturing the spirit of the Taylor-series expansions suggested by, most recently, Gayle and Richard (2008). This approach, however, avoids the use of backwards integration and would not suffer from the criticisms of Fibich and Gavish (2011) as it involves a nonlinear least-squares (or LAD, depending on the norm) approach. This might be attractive as it can allow the researcher to gain the speed of the polynomial approach but perhaps reduce error and improve stability.
7 Summary and Conclusions
In this paper, we have presented a survey of numerical methods used to approximate equilibrium bid functions in models of auctions as games of incomplete information where private values are modeled as draws from bidder-specific type distributions when pay-your-bid rules are used to determine transaction prices. We first outlined a baseline model and demonstrated how things work within a well-understood environment. Subsequently, we described some well-known numerical methods that have been used to solve two-point boundary-value problems that are similar to ones researchers face when investigating asymmetric first-price auctions. Next, we discussed research that either directly or indirectly contributed to improving computational methods to solve for bidding strategies at asymmetric first-price auctions. We also depicted the solutions to some examples of asymmetric first-price auctions to illustrate how the numerical methods can be used to investigate problems that would be difficult to analyze analytically. In fact, we presented a solution to one example that has received very little attention thus far—asymmetric auctions within the APVP. We also compared and contrasted the established methods and suggested ways in which they could be extended or improved by additional future research. Finally, by providing the computer code used to solve the examples of asymmetric first-price auctions, we hope to encourage researchers to apply these methods in their research.
One weakness of all research in this literature is that all evidence concerning the performance of the proposed approach is purely numerical and done via example: no one has considered analytically the efficiency and convergence properties of the proposed solutions. This demonstrates the value of work like Hubbard et al. (2013) which used sound theoretical results to verify numerical solutions. Nonetheless, a shortcoming of this field is that no one has proved that an approach converges to the truth.
Acknowledgments
The authors would like to thank Kenneth L. Judd, René Kirkegaard, Karl Schmedders, Benjamin S. Skrainka, Che-Lin Su, and Will M. Wright as well as two anonymous referees for useful comments and helpful suggestions. Paarsch gratefully acknowledges that some of the research for this Chapter was completed while he was a visiting research scholar at the Collegio Carlo Alberto in Moncalieri, Italy.
References
1. Armantier Olivier, Sbaï Erwann. Estimation and comparison of treasury auction formats when bidders are asymmetric. Journal of Applied Econometrics. 2006;21:745–779.
2. Armantier Olivier, Sbaï Erwann. Comparison of alternative payment mechanisms for French treasury auctions. Annales d’Économie et de Statistique 2009;(93–94):135–160.
3. Armantier Olivier, Florens Jean-Pierre, Richard Jean-François. Approximation of Nash equilibria in Bayesian games. Journal of Applied Econometrics. 2008;23:965–981.
4. Athey Susan C. Single crossing properties and the existence of pure strategy equilibria in games of incomplete information. Econometrica. 2001;69:861–889.
5. Athey Susan C, Haile Philip A. Nonparametric approaches to auctions. In: Heckman James J, Leamer Edward E, eds. New York: Elsevier; 2007:3847–3965. Handbook of Econometrics. vol. 6.
6. Bajari Patrick L. The first price sealed bid auction with asymmetric bidders: theory with applications. doctoral dissertation Department of Economics, University of Minnesota 1997.
7. Bajari Patrick. Comparing competition and collusion in procurement auctions: a numerical approach. Economic Theory. 2001;18:187–205.
8. Bali Valentina, Jackson Matthew. Asymptotic revenue equivalence in auctions. Journal of Economic Theory. 2002;106:161–176.
9. Boyce William E, DiPrima Richard C. Elementary Differential Equations. third ed. New York: John Wiley & Sons; 1977.
10. Boyd John P. Chebyshev and Fourier Spectral Methods. third ed. New York: Dover Publications Inc.; 2001.
11. Burton LP, Whyburn William M. Minimax solutions of ordinary differential systems. Proceedings of the American Mathematical Society. 1952;5:794–803.
12. Butcher John C. Numerical Methods for Ordinary Differential Equations. New York: John Wiley & Sons; 2003.
13. Chen Kay-Yut, Plott Charles R. Nonlinear behavior in sealed bid first price auctions. Games and Economic Behavior. 1998;25:34–78.
14. Chen Scott Shaobing, Donoho David L, Saunders Michael A. Atomic decomposition by basis pursuit. SIAM Journal on Scientific Computing. 1998;20:33–61.
15. Cheng Harrison. Ranking sealed high-bid and open asymmetric auctions. Journal of Mathematical Economics. 2006;42:471–498.
16. Cox James C, Smith Vernon L, Walker James M. Auction market theory of heterogeneous bidders. Economics Letters. 1982;9:319–325.
17. Dalkir Serdar, Logan John W, Masson Robert T. Mergers in symmetric and asymmetric noncooperative auction markets: the effects on prices and efficiency. International Journal of Industrial Organization. 2000;18:383–413.
18. Fibich Gadi, Gavious Arieh. Asymmetric first-price auctions: a perturbation approach. Mathematics of Operations Research. 2003;28:836–852.
19. Fibich Gadi, Gavish Nir. Numerical simulations of asymmetric first-price auctions. Games and Economic Behavior. 2011;73:479–495.
20. Fibich Gadi, Gavious Arieh, Sela Aner. Low and high types in asymmetric first-price auctions. Economics Letters. 2002;75:283–287.
21. Fibich Gadi, Gavious Arieh, Sela Aner. Revenue equivalence in asymmetric auctions. Journal of Economic Theory. 2004;115:309–321.
22. Gayle Wayne-Roy, Richard Jean-François. Numerical solutions of asymmetric, first-price, independent private values auctions. Computational Economics. 2008;32:245–278.
23. Gottlieb David, Orszag Steven A. Numerical Analysis of Spectral Methods: Theory and Applications. Philadelphia: SIAM; 1993.
24. Griesmer James H, Levitan Richard E, Shubik Martin. Toward a study of bidding processes, Part IV: games with unknown costs. Naval Research Logistics Quarterly. 1967;14:415–443.
25. Guerre Emmanuel, Perrigne Isabelle, Vuong Quang. Nonparametric identification of risk aversion in first-price auctions under exclusion restrictions. Econometrica. 2009;77:1193–1227.
26. Hairer Ernst, Wanner Gerhard. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems. second ed. Berlin: Springer-Verlag; 1996.
27. Holt Jr Charles A. Competitive bidding for contracts under alternative auction procedures. Journal of Political Economy. 1980;88:433–445.
28. Hubbard Timothy P, Paarsch Harry J. Investigating bid preferences at low-price, sealed-bid auctions with endogenous participation. International Journal of Industrial Organization. 2009;27:1–14.
29. Hubbard, Timothy P., Paarsch, Harry J., 2011. Asymmetries and affiliation in models of first-price auctions with private values, typescript, Department of Economics, Colby College.
30. Hubbard Timothy P, Li Tong, Paarsch Harry J. Semiparametric estimation in models of first-price, sealed-bid auctions with affiliation. Journal of Econometrics. 2012;168:4–16.
31. Hubbard Timothy P, Kirkegaard R, Paarsch HJ. Using economic theory to guide numerical analysis: Solving for equilibria in models of asymmetric first-price auctions. Computational Economics. 2013;42:241–266.
32. Judd Kenneth L. Numerical Methods in Economics. Cambridge, USA: MIT Press; 1998.
33. Kaplan Todd, Zamir Shmuel. Asymmetric first-price auctions with uniform distributions: analytic solutions to the general case. Economic Theory. 2012;50:269–302.
34. Karlin Samuel. Total Positivity. vol. 1 Stanford, California: Stanford University Press; 1968.
35. Kirkegaard René. Asymmetric first price auctions. Journal of Economic Theory. 2009;144:1617–1635.
36. Kirkegaard René. A mechanism design approach to ranking asymmetric auctions. Econometrica. 2012;80:2349–2364.
37. Krasnokutskaya Elena, Seim Katja. Bid preference programs and participation in highway procurement auctions. American Economic Review. 2011;101:2653–2686.
38. Krishna Vijay. Auction Theory. San Diego: Academic Press; 2002.
39. Krishna Vijay. Auction Theory. second ed. San Diego: Academic Press; 2010.
40. Lebrun Bernard. Existence of an equilibrium in first-price auctions. Economic Theory. 1996;7:421–443.
41. Lebrun Bernard. First-price auctions in the asymmetric n bidder case. International Economic Review. 1999;40:125–142.
42. Lebrun, Bernard, 2012. Revenue-superior variants of the second-price auction, typescript, Department of Economics, York University.
43. Li Huagang, Riley John G. Auction choice. International Journal of Industrial Organization. 2007;25:1269–1298.
44. Lizzeri Alessandro, Persico Nicola. Uniqueness and existence of equilibrium in auctions with a reserve price. Games and Economic Behavior. 2000;30:83–114.
45. Luo Zhi-Quan, Pang Jong-Shi, Ralph Daniel. Mathematical Programs with Equilibrium Constraints. Cambridge, England: Cambridge University Press; 1996.
46. Marion Justin. Are bid preferences benign? The effect of small business subsidies in highway procurement auctions. Journal of Public Economics. 2007;91:1591–1624.
47. Marshall Robert C, Meurer Michael J, Richard Jean-Francois, Stromquist Walter R. Numerical analysis of asymmetric first price auctions. Games and Economic Behavior. 1994;7:193–220.
48. Maskin Eric, Riley John. Optimal auctions with risk averse buyers. Econometrica. 1984;52:1473–1518.
49. Maskin Eric, Riley John. Asymmetric auctions. Review of Economic Studies. 2000a;67:413–438.
50. Maskin Eric, Riley John. Equilibrium in sealed high bid auctions. Review of Economic Studies. 2000b;67:439–454.
51. Maskin Eric, Riley John. Uniqueness of equilibrium in sealed high-bid auctions. Games and Economic Behavior. 2003;45:395–409.
52. Matthews Steven A. Selling to risk averse buyers with unobservable tastes. Journal of Economic Theory. 1983;30:370–400.
53. Matthews Steven A. Comparing auctions for risk averse buyers: a buyer’s point of view. Econometrica. 1987;55:633–646.
54. Milgrom Paul R, Weber Robert J. A theory of auctions and competitive bidding. Econometrica. 1982;50:1089–1122.
55. Myerson Roger B. Optimal auction design. Mathematics of Operations Research. 1981;6:55–73.
56. Paarsch Harry J. Deriving an estimate of the optimal reserve price: an application to British Columbian timber sales. Journal of Econometrics. 1997;78:333–357.
57. Paarsch Harry J, Hong Han. An Introduction to Structural Econometrics of Auctions. Cambridge, MA: MIT Press; 2006.
58. Plum Michael. Characterization and computation of Nash-equilibria for auctions with incomplete information. International Journal of Game Theory. 1992;20:393–418.
59. Reny Philip J. On the existence of pure and mixed strategy Nash equilibria in discontinuous games. Econometrica. 1999;67:1029–1056.
60. Reny Philip J, Zamir Shmuel. On the existence of pure strategy monotone equilibria in asymmetric first-price auctions. Econometrica. 2004;72:1105–1125.
61. Riley John G, Samuelson William F. Optimal auctions. American Economic Review. 1981;71:381–392.
62. Saini, Viplav, 2010. Investment incentives in a dynamic procurement auction, typescript, Department of Economics, Oberlin College.
63. Saini Viplav. Endogenous asymmetry in a dynamic procurement auction. RAND Journal of Economics. 2012;43:726–760.
64. Schmidt Darrell, Wiggins Kenneth L. Minimax approximate solutions of linear boundary value problems. Mathematics of Computation. 1979;145:139–148.
65. Su Che-Lin, Judd Kenneth L. Constrained optimization approaches to estimation of structural models. Econometrica. 2012;80:2213–2230.
66. Tibshirani Robert. Regression shrinkage and selection via the lasso Journal of the Royal Statistical Society. Series B (Methodological). 1996;58:267–288.
67. Vickrey William S. Counterspeculation, auctions, and competitive sealed tenders. Journal of Finance. 1961;16:8–37.
68. Weber Robert J. Multiple-object auctions. In: Engelbrecht-Wiggans Richard, Shubik Martin, Stark Richard M, eds. Auctions, Bidding, Contracting: Uses and Theory. New York: New York University Press; 1983.
1Within the private-values environment, under the pricing rule used at oral, ascending-price (English) or second-price, sealed-bid (Vickrey) formats, it is a weakly dominant strategy for a bidder to tender his valuation, so computing the equilibrium is relatively straightforward.
2Under the second-price rule, again within the private-values environment, it remains a weakly dominant strategy for a bidder to tender his valuation, so computing the equilibrium remains straightforward.
3Likewise, if researchers need to simulate dynamic games that require computing the inverse-bid functions in each period, then speed is crucial because this may require solving for the inverse-bid functions thousands of times.
4For example, Paarsch (1997) determined the reserve prices set at timber auctions conducted by the British Columbian Ministry of Forests in the 1990s and beyond.
5Armantier et al. (2008) have proposed solving for a constrained strategic equilibrium to approximate strategies in games for which the Nash equilibrium is computationally intractable. As an example, they considered solving a first-price auction within the asymmetric IPVP. This approach has also been applied to multi-unit settings, in particular, Treasury bill auctions; see, for example, Armantier and Sbaï (2006, 2009). We refer readers to Armantier et al. (2008) for a comparison of this approach to the methods we describe here.
6Essentially, this was just an application of the implicit function theorem.
7A nonautonomous ODE is also referred to as time-dependent, although, for our purposes, bid-dependent is a better characterization.
8Note that the assumption of a common support is often employed by auction theorists and almost always by empirical researchers. Throughout this chapter we maintain the assumption of a common valuation (or, in a procurement setting, cost) support unless we explicitly state otherwise; for example, we shall not assume this in the example we consider in Section 2.5. It is important to bear in mind because the boundary conditions we present below may not hold in settings where the support differs when there are more than two bidders at the auction.
9If a reserve price ![]() existed, then
existed, then ![]() would be the relevant condition: the marginal bidder would bid the reserve price
would be the relevant condition: the marginal bidder would bid the reserve price ![]() .
.
10Athey and Haile (2007) also provided a proof that the bid support is the same for all bidders (which, thus, nests the left- and right-boundary conditions) under the assumptions we have adopted; see Theorem 2.2 of their paper.
11All norms are equivalent in finite-dimensional spaces, so if a function satisfies the Lipschitz condition in one norm, it satisfies the Lipschitz condition in all norms. The Lipschitz constant ![]() , however, does depend on the choice of norm.
, however, does depend on the choice of norm.
12In this example, we have assumed that ![]() is differentiable, but this is unnecessary; we have made the assumption for illustrative purposes only. We do not claim that the inverse-bid functions are differentiable everywhere, something we discuss below.
is differentiable, but this is unnecessary; we have made the assumption for illustrative purposes only. We do not claim that the inverse-bid functions are differentiable everywhere, something we discuss below.
13In contrast, Lebrun (1996), Maskin and Riley (2000b) as well as Athey (2001) proved the existence of a MPSE under the restriction that bidders can only bid in discrete amounts, that is, the bids must belong to a finite set. These researchers then used a limiting argument, which involves shrinking the minimum bid increment and showing that a sequence of pure-strategy equilibria converges uniformly almost everywhere to a pure strategy in which bids are unrestricted.
14Our example follows Krishna (2002) as well as Maskin and Riley (2000a); these researchers compared revenue and efficiency at an asymmetric first-price auction with that of a second-price auction. The derivation of this example was originally provided by Griesmer et al. (1967). Kaplan and Zamir (2012) generalized this work by considering two bidders at auction (with or without a reserve price) who each draw valuations from uniform distributions with any asymmetric, bounded supports. Another example, which involves power distributions, was originally derived by Plum (1992). We postpone a discussion of this case until later, when we discuss bidder collusion.
15In addition to the examples considered here, one can imagine other models which generate the intractable property of asymmetric first-price auctions. For example, if bidders have different budget constraints or, in the case of procurement auctions, different capacity constraints; if bidders must pay an entry fee before they are able to bid and entry fees differ across bidders. Our approach would apply to any type of relaxation of the assumptions or extension to the model we have presented above that will lead bidders to behave differently from one another.
16While we restrict attention to asymmetric bidders with CRRA utility, Krishna (2002) has presented the case with symmetric risk-averse bidders having arbitrary utility functions. Our presentation of this model does not mirror those of others, but similar models have been investigated by Cox et al. (1982), Matthews (1983, 1987), Maskin and Riley (1984) as well as Chen and Plott (1998). For results concerning econometric identification (under various exclusion restrictions) of a model with asymmetric, risk-averse buyers see Section 4.3 of Guerre et al. (2009).
17In the limit case, where ![]() equals one for all bidders, this model simplifies to the symmetric IPVP model with risk-neutral bidders.
equals one for all bidders, this model simplifies to the symmetric IPVP model with risk-neutral bidders.
18Marshall et al. (1994) have also provided a partial characterization of the equilibrium bid functions in such an environment in Appendix A of their paper. See, too, Cheng (2006) for such a derivation, which includes a nice discussion of the relationship between the uniform and power distributions as well as revenue comparisons across auction models.
19If a price ceiling ![]() existed, then
existed, then ![]() would be the relevant condition: the marginal bidder would bid the price ceiling
would be the relevant condition: the marginal bidder would bid the price ceiling ![]() .
.
20Note that, depending on the preference rate, some nonpreferred types will not be able to win the auction even if bidders tender their cost.
21More than anything, the standard model with bid preferences illustrates that relaxing the assumption concerning the common support of valuations (costs) is important. Although the policy explicitly alters the distribution of submitted bids, players internalize this when submitting equilibrium bids, so the policy can be thought of as affecting the type support(s). See Footnote 8 above and the discussion at the end of Section 5.1 of Athey and Haile (2007) which, although framed with an empirical focus, contains insight concerning this issue. For sufficiently large preference rates and with more than one of each class of bidder at auction, it is likely that, the boundary conditions presented would need to be adjusted. Intuitively, when the discount rate gets large enough, preferred types disregard competition from nonpreferred types and the conditions on the bid support change.
22As we discuss in the next section of the paper, using shooting algorithms was first proposed by Marshall et al. (1994) for the case of two bidders who draw valuations from asymmetric power distributions, and generalized by Bajari (2001) to the ![]() -bidder case for arbitrary distributions.
-bidder case for arbitrary distributions.
23In this example, there are two asymmetric bidders, which is why there are two functions with the same line style for each legend entry, with ![]() equal to
equal to ![]() . We depict the intuition in
. We depict the intuition in ![]() -space as the algorithm is used to find the inverse-bid functions.
-space as the algorithm is used to find the inverse-bid functions.
24See Appendix B of Li and Riley (2007).
25Note that in an asymmetric first-price auction model the initial bid ![]() would be
would be ![]() and the terminal bid
and the terminal bid ![]() would be
would be ![]() . Since the system is solved backwards, the grid would descend from
. Since the system is solved backwards, the grid would descend from ![]() to
to ![]() .
.
26Hairer and Wanner (1996) have noted that explicit methods do not work well on stiff problems: stability rather than accuracy governs the choice of step size.
27Of course, it is possible for a low-order method with a small step size to outperform a high-order method with larger step size, at least in terms of truncation error.
28Consider the following integral:
![]()
To implement Simpson’s rule, take the interval ![]() and subdivide it into
and subdivide it into ![]() subintervals each of width
subintervals each of width ![]() , so
, so ![]() . Replace
. Replace ![]() by a quadratic polynomial that takes the same values as the integrand at the endpoints of each subinterval and at each midpoint. On any subinterval,
by a quadratic polynomial that takes the same values as the integrand at the endpoints of each subinterval and at each midpoint. On any subinterval, ![]() ,
,
![]()
For the entire interval ![]() , the formula is
, the formula is
![]()
29Marshall et al. discussed how their research could be extended to a model in which two types of bidders draw valuations from any two arbitrary distributions. The presentation is similar to the section “Bidders from Two Different Urns” that we presented earlier which involved two bidders, although they allowed for more than one bidder from each class.
30While Marshall et al. characterized this closed-form solution partially (in their Appendix A), they proposed numerical methods as being applicable to a general class of problems noting that this (power distribution) case “seems to be the exception rather than the rule.”
31It would also be reasonable to think that the firms have different managerial ability, capacity constraints, capabilities, and so forth.
32We do not discuss the second method Bajari proposed which involves assuming initially that firms bid their cost and then solving iteratively for the best-response (at each bid) of rival firms to this strategy profile until each firm is best-responding to all other firms’ strategies.
33Although published 6 years later, Bajari (2001) credits Li and Riley (2007) (although his reference is to a paper by Riley and Li with the same title) as generalizing this shooting algorithm. While Marshall et al. (1994) used Taylor-series expansions to integrate backwards, Li and Riley (2007) used the Bulirsch-Stoer method. The Bulirsch-Stoer method uses a modified midpoint method in integration. A large interval is spanned by different sequences of fine substeps and extrapolation uses rational functions; see Appendix B of Li and Riley (2007). Li and Riley also introduced a bisection algorithm to speed up search for the high bid ![]() .
.
34We thank Patrick L. Bajari for providing us with his original computer program and a user guide. While he did not advocate explicitly a method for approximating the solution, the program shows that a Runge-Kutta algorithm was used, but Bajari warned users in his accompanying guide that results are sensitive to the tolerance criterion, something we have found as well.
35Dalkir et al. (2000) also used a (fourth-order) explicit Runge-Kutta method. They considered a procurement environment in which bidders each draw a cost from a uniform distribution. The asymmetry enters their model when the effects of a merged firm are introduced.
36Unlike the numerical methods we have described, which require solving for the inverse-bid functions, Fibich and Gavious characterized the bid functions directly; see Propositions 1 and 3 of their paper.
37Fibich and Gavious (2003) extended results concerning expected revenue and the probability of inefficiency obtaining. Typically, the results hold within ![]() accuracy. Fibich et al. (2004) extended the Revenue Equivalence Theorem using a perturbation approach.
accuracy. Fibich et al. (2004) extended the Revenue Equivalence Theorem using a perturbation approach.
38Gayle and Richard also cited the working paper of Li and Riley (2007) (also as Riley and Li) who introduced ![]() software which can compute bid functions under restricted scenarios.
software which can compute bid functions under restricted scenarios.
39In their example, in which just two bidders were considered, each of whom drew valuations from asymmetric Weibull distributions, and a fifth-order Taylor-series expansion was used, it took 37 s to solve the problem with 500 grid points, and 202 s to solve the problem with 2000 grid points, while the RMSE fell by only 0.45%. Instead of creating a finer grid, Li and Riley (2007) used a step size that depended on the allowed error tolerance and used more steps for problems with more curvature in the inverse-bid functions.
40The lowest computation time involved a second-order expansion with 500 grid points which took 18 s. Holding fixed the number of grid points, the RMSE was constant for all orders of Taylor-series expansions between 2 and 5 which is what Gayle and Richard recommended.
41For example, Marshall et al. (1994) as well as Li and Riley (2007) made explicit statements concerning the poor behavior of the solutions in the neighborhood of the lower endpoint.
42Fibich and Gavish noted that the choice of which valuation to use as the independent variable is ad hoc and can lead to divergence; see Footnote 7 as well as the conclusion of their paper, where they suggested this choice might be worth pursuing in future research.
43Kirkegaard’s results hold for any number of bidders ![]() (but assume a common support).
(but assume a common support).
44We chose the weight on the uniform distribution to be 0.1, so the weight on the Beta distribution was 0.9.
45See Corollary 2 and Corollary 3 of Kirkegaard (2009).
46Additional details concerning this example can be found in Hubbard and Paarsch (2011).
47The function can be thought of in this way: if bidder 2 has type ![]() , then he will bid exactly the same as bidder 1 does when bidder 1 has type
, then he will bid exactly the same as bidder 1 does when bidder 1 has type ![]() . Thus,
. Thus, ![]() is a “tying” function which relates the values of each player that lead to ties (bidding the same).
is a “tying” function which relates the values of each player that lead to ties (bidding the same).
48We thank Nir Gavish for providing us with the MAtlab code used by Fibich and Gavish (2011). This code is now available as supplementary material to the electronic version of the published article. Aside from varying the step size of the grid and altering the distributions used, we also let the dependent variable span ![]() , where
, where ![]() is the step size in the grid used, rather than
is the step size in the grid used, rather than ![]() as this seemed to improve performance at the upper end. We let all other parameters in the code take on the values recommended by the authors. In particular, the results we present are based on 50 iterations and initial guesses of
as this seemed to improve performance at the upper end. We let all other parameters in the code take on the values recommended by the authors. In particular, the results we present are based on 50 iterations and initial guesses of ![]() and
and ![]() .
.
49These calculations were performed on a MacBook Pro having 4 GB of memory and a 2.3 GHz dual-core Intel Core i5 processor—in short, a modest computer.