CHAPTER 10
Binary Search Trees
In Chapter 9, you studied an important conceptual tool: the binary tree. This chapter presents the binary search tree data type and a corresponding data structure, the BinarySearchTree class. BinarySearchTree objects are valuable collections because they require only logarithmic time, on average, for inserting, removing, and searching (but linear time in the worst case). This performance is far better than the linear average-case time for insertions, removals and searches in an array, ArrayList or LinkedList object. For example, if n = 1,000,000,000, log2 n < 30.
The BinarySearchTree class is not part of the Java Collections Framework. The reason for this omission is that the framework already includes the TreeSet class, which boasts logarithmic time for inserting, removing, and searching even in the worst case. The BinarySearchTree class requires linear-in-n time, in the worst case, for those three operations. So the BinarySearchTree class should be viewed as a "toy" class that is simple enough for you to play with and will help you to better understand the TreeSet class. The implementation of the TreeSet class is based on a kind of "balanced" binary search tree, namely, the red-black tree.
To further prepare you for the study of red-black trees and the TreeSet class, this chapter also explains what it means to say that a binary search tree is balanced. To add some substance to that discussion, we introduce the AVL tree data type, which is somewhat simpler to understand than the red-black tree data type.
CHAPTER OBJECTIVES
- Compare the time efficiency of the BinarySearchTree class's insertion, removal and search methods to that of the corresponding methods in the ArrayList and LinkedList classes.
- Discuss the similarities and differences of the BinarySearchTree class's contains method and the binarySearch methods in the Arrays and Collections classes.
- Explain why the BinarySearchTree class's remove method and the TreeIterator class's next method are somewhat difficult to define.
- Be able to perform each of the four possible rotations.
- Understand why the height of an AVL tree is always logarithmic in n.
10.1 Binary Search Trees
We start with a recursive definition of a binary search tree:
A binary search tree t is a binary tree such that either t is empty or
- each element in leftTree(t) is less than the root element of t;
- each element in rightTree(t) is greater than the root element of t;
- both leftTree(t) and rightTree(t) are binary search trees.
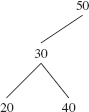
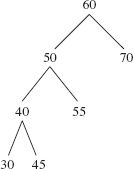
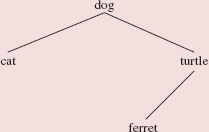
Figure 10.1 shows a binary search tree.
An inOrder traversal of a binary search tree accesses the items in increasing order. For example, with the binary search tree in Figure 10.1, an inOrder traversal accesses the following sequence:
15 25 28 30 32 36 37 50 55 59 61 68 75
As we have defined a binary search tree, duplicate elements are not permitted. Some definitions have "less than or equal to" and "greater than or equal to" in the above definition. For the sake of consistency with some classes in the Java Collections Framework that are based on binary search trees, we opt for strictly less than and strictly greater than.
Section 10.1.1 describes the BinarySearchTree class. As we noted at the beginning of this chapter, this is a "toy" class that provides a gentle introduction to related classes in the Java Collections Framework. Much of the code for the BinarySearchTree class is either identical to or a simplification of code in the TreeMap class of the Java Collections Framework. Overall, the BinarySearchTree class's performance is not good enough for applications—because its worst-case height is linear in n —but you will be asked to add new methods and to modify existing methods.
FIGURE 10.1 A binary search tree
10.1.1 The BinarySearchTree Implementation of the Set Interface
We will study the binary-search-tree data type through the method specifications of the Binary SearchTree class. The BinarySearchTree class is not part of the Java Collections Framework, but it implements the Collection interface. In fact, the BinarySearchTree class implements a slight extension of the Collection interface: the Set interface. The Set interface does not provide any new methods. The only difference between the Collection and Set interfaces is that duplicate elements are not allowed in a Set, and this affects the specifications of the default constructor and the add method in the BinarySearchTree class. We will see these differences shortly.
Another feature that distinguishes the BinarySearchTree class from previous Collection classes we have seen is that the elements in a BinarySearchTree must be maintained in order. For simplicity, we assume that the elements are instances of a class that implements the Comparable interface, which was introduced in Section 5.5. Thus, null elements are not allowed in a BinarySearchTree object. Here is that interface:
public interface Comparable { /** * Returns an int less than, equal to or greater than 0, depending on * whether the calling object is less than, equal to or greater than a * specified object. * * @param obj - the specified object that the calling object is compared to. * * @return an int value less than, equal to, or greater than 0, depending on * whether the calling object is less than, equal to, or greater than * obj, respectively. * * @throws ClassCastException - if the calling object and obj are not in the * same class. * */ public int compareTo (T obj) } // interface Comparable
From now on, when we refer to the "natural" order of elements, we assume that the element's class implements the Comparable interface; then the natural order is the order imposed by the compareTo method in the element's class. For example, the Integer class implements the Comparable interface, and the "natural" order of Integer objects is based on the numeric comparison of the underlying int values. To illustrate this ordering, suppose we have the following:
Integer myInt = 25; System.out.println (myInt.compareTo (107));
The output will be less than 0 because 25 is less than 107. Specifically, the output will be −1 because when the compareTo method is used for numeric comparisons, the result is either —1, 0, or 1, depending on whether the calling object is less than, equal to, or greater than the argument.
For a more involved example, the following Student class has name and gpa fields. The compareTo method will use the alphabetical ordering of names; for equal names, the ordering will be by decreasing grade point averages. For example,
new Student ("Lodato", 3.8).compareTo (new Student ("Zsoldos", 3.5))
returns −1 because "Lodato" is, alphabetically, less than "Zsoldos". But
new Student ("Dufresne", 3.4).compareTo (new Student ("Dufresne", 3.6))
returns 1 because 3.4 is less than 3.6, and the return value reflects decreasing order. Similarly,
new Student ("Dufresne", 3.8).compareTo (new Student ("Dufresne", 3.6))
returns −1, because 3.8 is greater than 3.6.
Here is the Student class:
public class Student implements Comparable<Student> { public final double DELTA = 0.0000001; protected String name; protected double gpa; public Student() { } /** * Initializes this Student object from a specified name and gpa. * * @param name - the specified name. * @param gpa - the specified gpa. * */ public Student (String name, double gpa) { this.name = name; this.gpa = gpa; } // constructor /** * Compares this Student object with a specified Student object. * The comparison is alphabetical; for two objects with the same name, * the comparison is by grade point averages. * * @param otherStudent - the specified Student object that this Student * object is being compared to. * * @return −1, if this Student object's name is alphabetically less than * otherStudent's name, or if the names are equal and this * Student object's grade point average is at least DELTA * greater than otherStudent's grade point average; * 0, if this Student object's name the same as * otherStudent's name and the grade point * averages are within DELTA; * 1, if this Student object's name is alphabetically greater * than otherStudent's name, or if the names are equal and * this Student object's grade point average is at least DELTA * less than otherStudent's grade point average; * */ public int compareTo (Student otherStudent) { final double DELTA = 0.0000001; if (name.compareTo (otherStudent.name) < 0) return −1; if (name.compareTo (otherStudent.name) > 0) return 1; if (gpa - otherStudent.gpa > DELTA) return −1; if (otherStudent.gpa - gpa > DELTA) return 1; return 0; } // method compareTo /** * Determines if this Student object's name and grade point average are * the same as some specified object's. * * @param obj - the specified object that this Student object is being * compared to. * * @return true - if obj is a Student object and this Student object has the * same name and almost (that is, within DELTA) the same point average as obj. * */ public boolean equals (Object obj) { if (! (obj instanceof Student)) return false; return this.compareTo ((Student)obj) == 0; } // method equals /** * Returns a String representation of this Student object. * * @return a String representation of this Student object: name, blank, * grade point average. * */ public String toString() { return name+"" + gpa; } // method toString } // class Student
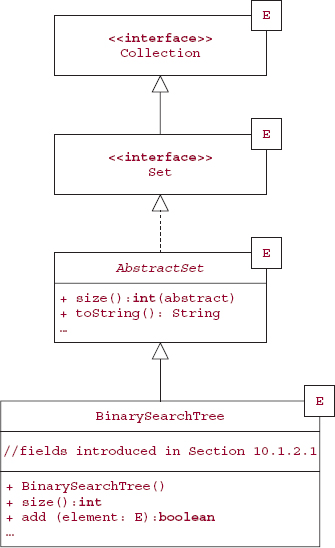
Rather than starting from scratch, we will let the BinarySearchTree class extend some class already in the Framework. Then we need implement only those methods whose definitions are specific to the BinarySearchTree class. The AbstractSet class is a good place to start. That class has garden-variety implementations for many of the Set methods: isEmpty, toArray, clear, and the bulk operations (addAll, containsAll, removeAll and retainAll). So the class heading is
public class BinarySearchTree<E> extends AbstractSet <E>
Figure 10.2 shows the relationships among the classes and interfaces we have discussed so far.
FIGURE 10.2 A UML diagram that includes part of the BinarySearchTree class
Here are the method specifications for the methods we will explicitly implement:
/** * Initializes this BinarySearchTree object to be empty, to contain only elements * of type E, to be ordered by the Comparable interface, and to contain no * duplicate elements. * */ public BinarySearchTree() /** * Initializes this BinarySearchTree object to contain a shallow copy of * a specified BinarySearchTree object. * The worstTime(n) is O(n), where n is the number of elements in the * specified BinarySearchTree object. * * @param otherTree - the specified BinarySearchTree object that this * BinarySearchTree object will be assigned a shallow copy of. * */ public BinarySearchTree (BinarySearchTree<? extends E> otherTree) /** * Returns the size of this BinarySearchTree object. * * @return the size of this BinarySearchTree object. * */ public int size( ) /** * Returns an iterator positioned at the smallest element in this * BinarySearchTree object. * * @return an iterator positioned at the smallest element (according to * the element class's implementation of the Comparable * interface) in this BinarySearchTree object. * */ public Iterator<E> iterator() /** * Determines if there is an element in this BinarySearchTree object that * equals a specified element. * The worstTime(n) is O(n) and averageTime(n) is O(log n). * * @param obj - the element sought in this BinarySearchTree object. * @return true - if there is an element in this BinarySearchTree object that * equals obj; otherwise, return false. * * @throws ClassCastException - if obj is not null but cannot be compared to the * elements already in this BinarySearchTree object. * @throws NullPointerException - if obj is null. * */ public boolean contains (Object obj) /** * Ensures that this BinarySearchTree object contains a specified element. * The worstTime(n) is O(n) and averageTime(n) is O(log n). * * @param element - the element whose presence is ensured in this * BinarySearchTree object. * * @return true - if this BinarySearchTree object changed as a result of this * method call (that is, if element was actually inserted); otherwise, * return false. * * @throws ClassCastException - if element is not null but cannot be compared * to the elements of this BinarySearchTree object. * @throws NullPointerException - if element is null. * */ public boolean add (E element) /** * Ensures that this BinarySearchTree object does not contain a specified * element. * The worstTime(n) is O(n) and averageTime(n) is O(log n). * * @param obj - the object whose absence is ensured in this * BinarySearchTree object. * * @return true - if this BinarySearchTree object changed as a result of this * method call (that is, if obj was actually removed); otherwise, * return false. * * @throws ClassCastException - if obj is not null but cannot be compared to the * elements of this BinarySearchTree object. * @throws NullPointerException - if obj is null. * */ public boolean remove (Object obj)
These method specifications, together with the method specifications of methods not overridden from the AbstractSet class, constitute the abstract data type Binary Search Tree: all that is needed for using the BinarySearchTree class. For example, here is a small class that creates and manipulates three BinarySearchTree objects: two of String elements and one of Student elements (for the Student class declared earlier in this section):
public class BinarySearchTreeExample { public static void main (String[ ] args) { new BinarySearchTreeExample().run(); } // method main public void run() { BinarySearchTree<String> tree1 = new BinarySearchTree<String>(); tree1.add ("yes"); tree1.add ("no"); tree1.add ("maybe"); tree1.add ("always"); tree1.add ("no"); // not added: duplicate element if (tree1.remove ("often")) System.out.println ("How did that happen?"); else System.out.println (tree1.remove ("maybe")); System.out.println (tree1); BinarySearchTree<String> tree2 = new BinarySearchTree<String> (tree1); System.out.println (tree2); BinarySearchTree<Student> tree3 = new BinarySearchTree<Student>(); tree3.add (new Student ("Jones", 3.17)); tree3.add (new Student ("Smith", 3.82)); tree3.add (new Student ("Jones", 3.4)); if (tree3.contains (new Student ("Jones", 10.0 - 6.6))) System.out.println ("The number of elements in tree3 is " + tree3.size()); System.out.println (tree3); } // method run } // class BinarySearchTreeExample
The output is
true [always, no, yes] [always, no, yes] The number of elements in tree3 is 3 [Jones 3.4, Jones 3.17, Smith 3.82]
Here is part of the BinarySearchTreeTest class:
protected BinarySearchTree<String> tree; @Before public void RunBeforeEachTest() { tree = new BinarySearchTree<String>(); } // method RunBeforeEachTest @Test public void testAdd() { tree.add ("b"); tree.add ("a"); tree.add ("c"); tree.add ("e"); tree.add ("c"); tree.add ("d"); assertEquals ("[a, b, c, d, e]", tree.toString()); } // method testAdd @Test public void testContains() { tree.add ("a"); tree.add ("b"); tree.add ("c"); assertEquals (true, tree.contains ("a")); assertEquals (true, tree.contains ("b")); assertEquals (true, tree.contains ("c")); assertEquals (false, tree.contains ("x")); assertEquals (false, tree.contains ("")); } // method testContains @Test (expected = NullPointerException.class) public void testContainsNull() { tree.add ("a"); tree.add ("b"); tree.add ("c"); tree.contains (null); } // method testContainsNull @Test public void testRemove() { tree.add ("b"); tree.add ("a"); tree.add ("c"); assertEquals (true, tree.remove ("b")); assertEquals (2, tree.size()); assertEquals (false, tree.remove ("b")); assertEquals (2, tree.size()); } // method testRemove
The complete test class, available from the book's website, includes an override of the Abstract Set class's equals (Object obj) method to return false when comparing two BinarySearchTree objects that have the same elements but different structures.
10.1.2 Implementation of the BinarySearchTree Class
In this section, we will develop an implementation of the BinarySearchTree class. To confirm that Binary Search Tree is an abstract data type that has several possible implementations, you will have the opportunity in Project 10.1 to develop an array-based implementation.
The only methods we need to implement are the seven methods specified in Section 10.1.1. But to implement the iterator() method, we will need to develop a class that implements the Iterator interface, with hasNext(), next() and remove() methods. So we will create a TreeIterator class embedded within the BinarySearchTree class.
The definitions of the default constructor, size(), iterator(), and hasNext() are one-liners. Also, the definition of the copy constructor is fairly straightforward, and the TreeIterator class's remove method is almost identical to the BinarySearchTree class's remove method. But the remaining four methods—contains, add, and remove in BinarySearchTree, and next in TreeIterator—get to the heart of how the implementation of the BinarySearchTree class differs from that of, say, the LinkedList class.
10.1.2.1 Fields and Nested Classes in the BinarySearchTree Class
What fields and embedded classes should we have in the BinarySearchTree class? We have already noted the need for a TreeIterator class. From the fact that a binary search tree is a binary tree—with a root item and two subtrees—and from our earlier investigation of the LinkedList class, we can see the value of having an embedded Entry class. The only fields in the BinarySearchTree class are:
protected Entry<E> root; protected int size;
The Entry class, as you may have expected, has an element field, of type (reference to) E, and left and right fields, of type (reference to) Entry<E>. To facilitate going back up the tree during an iteration, the Entry class will also have a parent field, of type (reference to) Entry<E>. Figure 10.3 shows the representation of a BinarySearchTree object with elements of type (reference to) String. To simplify the figure, we pretend that the elements are of type String instead of reference to String. Here is the nested Entry class:
protected static class Entry<E> { protected E element; protected Entry<E> left = null,
FIGURE 10.3 A BinarySearchTree object with four elements
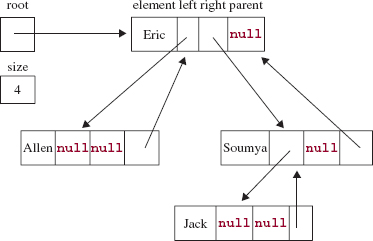
right = null, parent; /** * Initializes this Entry object. * * This default constructor is defined for the sake of subclasses of * the BinarySearchTree class. */ public Entry() { } /** * Initializes this Entry object from element and parent. * */ public Entry (E element, Entry<E> parent) { this.element = element; this.parent = parent; } // constructor } // class Entry
Recall, from Section 7.3.5, that the Entry class nested in the Java Collection Framework's LinkedList class was given the static modifier. The BinarySearchTree's nested Entry class is made static for the same reason: to avoid the wasted time and space needed to maintain a reference back to the enclosing object.
Now that we have declared the fields and one of the nested classes, we are ready to tackle the BinarySearchTree method definitions.
10.1.2.2 Implementation of Simple Methods in the BinarySearchTree Class
We can immediately develop a few method definitions:
public BinarySearchTree()
{
We could have omitted the assignments to the root and size fields because each field is given a default initial value (null for a reference, 0 for an int, false for a boolean, and so on) just prior to the invocation of the constructor. But explicit assignments facilitate understanding; default initializations do not.
public int size() { return size; } // method size() public Iterator<E> iterator() { return new TreeIterator(); } // method iterator
It is easy enough to define a copy constructor that iterates through otherTree and adds each element from otherTree to the calling object. But then the iteration over otherTree will be inOrder, so the new tree will be a chain, and worstTime(n) will be quadratic in n. To obtain linear-in-n time, we construct the new tree one entry at a time, starting at the root. Because each entry has an element, a parent, a left child, and a right child, we create the new entry from otherTree's entry and the new entry's parent. The new entry's left (or right) child is then copied recursively from otherTree's left (or right) child and from the new entry—the parent of that child.
We start with a wrapper method that calls the recursive method:
public BinarySearchTree (BinarySearchTree<? extends E> otherTree) { root = copy (otherTree.root, null); size = otherTree.size; } // copy constructor protected Entry<E> copy (Entry<<? extends E> p, Entry<E> parent) { if (p != null) { Entry<E> q = new Entry<E> (p.element, parent); q.left = copy (p.left, q); q.right = copy (p.right, q); return q; } // if return null; } // method copy
10.1.2.3 Definition of the contains Method
The elements in a binary search tree are stored in the "natural" order, that is, the order imposed by the compareTo method in the element class. The definition of the contains (Object obj) method takes advantage of that fact that by moving down the tree in the direction of where obj is or belongs. Specifically, an Entry object temp is initialized to root and then obj is compared to temp.element in a loop. If they are equal, true is returned. If obj is less than temp.element, temp is replaced with temp.left. Otherwise, temp is replaced with temp.right. The loop continues until temp is null. Here is the complete definition:
public boolean contains (Object obj) { Entry<E> temp = root; int comp; if (obj == null) throw new NullPointerException(); while (temp != null) { comp = ((Comparable)obj).compareTo (temp.element); if (comp == 0) return true; else if (comp < 0) temp = temp.left; else temp = temp.right; } // while return false; } // method contains
The cast of obj to a Comparable object is necessary for the compiler because the Object class does not have a compareTo method.
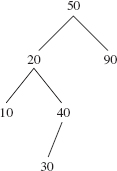
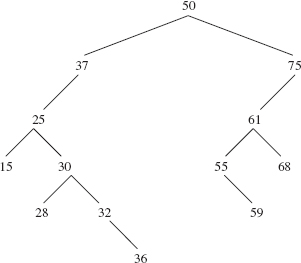
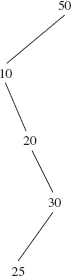
How long does this method take? For this method, indeed, for all of the remaining methods in this section, the essential feature for estimating worstTime(n) or averageTime(n) is the height of the tree. Specifically, for the contains method, suppose the search is successful; a similar analysis can be used for an unsuccessful search. In the worst case, we will have a chain, and will be seeking the leaf. For example, suppose we are seeking 25 in the binary search tree in Figure 10.4.
In such a case, the number of loop iterations is equal to the height of the tree. In general, if n is the number of elements in the tree, and the tree is a chain, the height of the tree is n - 1, so worstTime(n) is linear in n for the contains method.
We now determine averageTime(n) for a successful search. Again, the crucial factor is the height of the tree. For binary search trees constructed through random insertions and removals, the average height H is logarithmic in n —(see Cormen, [2002]). The contains method starts searching at level 0, and each loop iteration descends to the next lower level in the tree. Since averageTime(n) requires no more than H iterations, we immediately conclude that averageTime(n) is O(logn). That is, averageTime(n) is less than or equal to some function of log n.
FIGURE 10.4 A binary search tree
To establish that averageTime(n) is logarithmic in n, we must also show that averageTime(n) is greater than or equal to some function of log n. The average—over all binary search trees—number of iterations is greater than or equal to the average number of iterations for a complete binary search tree with n elements. In a complete binary tree t, at least half of the elements are leaves (see Concept Exercise 9.11), and the level of each leaf is at least height(t) - 1. So the average number of iterations by the contains method must be at least (height(t) - 1)/2, which, by Concept Exercise 9.7, is (floor(log2(n(t)) - 1)/2. That is, the average number of iterations for the contains method is greater than or equal to a function of log n. So averageTime(n) is greater than or equal to some function of log n.
We conclude from the two previous paragraphs that averageTime(n) is logarithmic in n. Incidentally, that is why we defined the contains method above instead of inheriting the one in the AbstractCollection class (the superclass of AbstractSet). For that version, an iterator loops through the elements in the tree, starting with the smallest, so its averageTime(n) is linear in n.
The binary search tree gets its name from the situation that arises when the contains method is invoked on a full tree. For then the contains method accesses the same elements, in the same order, as a binary search of an array with the same elements. For example, the root element in a full binary search tree corresponds to the middle element in the array.
You may have been surprised (and even disappointed) that the definition of the contains method was not recursive. Up to this point in our study of binary trees, most of the concepts—including binary search tree itself—were defined recursively. But when it comes to method definitions, looping is the rule rather than the exception. Why is that? The glib answer is that left and right are of type Entry, not of type BinarySearchTree, so we cannot call
left.contains(obj) // illegal
But we can make contains a wrapper method for a protected, recursive containsElement method:
public boolean contains (Object obj) { return containsElement (root, obj); } // method contains protected boolean containsElement (Entry<E> p, Object obj) { if (p == null) return false; int comp = ((Comparable)obj).compareTo (p.element); if (comp == 0) return true; if (comp < 0) return containsElement (p.left, obj); return containsElement (p.right, obj); } // method containsElement
This recursive version would be nominally less efficient—in both time and space—than the iterative version. And it is this slight difference that sinks the recursive version. For the iterative version is virtually identical to one in the TreeMap class, part of the Java Collections Framework, where efficiency is prized above elegance. Besides, some of the luster of recursion is diminished by the necessity of having a wrapper method.
10.1.2.4 Definition of the add Method
The definition of the add (E element) method is only a little more complicated than the definition of contains (Object obj). Basically, the add method starts at the root and branches down the tree searching for the element; if the search fails, the element is inserted as a leaf.
Specifically, if the tree is empty, we construct a new Entry object and initialize that object with the given element and a null parent, then increment the size field and return true. Otherwise, as we did in the definition of the contains method, we initialize an Entry object, temp, to root and compare element to temp.element in a loop. If element equals temp.element, we have an attempt to add a duplicate, so we return false. If element is less than temp.element, replace temp with temp.left unless temp.left is null, in which case we insert element in an Entry object whose parent is temp. The steps are similar when element is greater than temp.element.
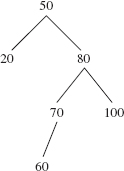
For example, suppose we are trying to insert 45 into the binary search tree in Figure 10.5:
FIGURE 10.5 A binary search tree into which 45 will be inserted
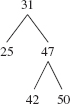
The insertion is made in a loop that starts by comparing 45 to 31, the root element. Since 45 > 31, we advance to 47, the right child of 31. See Figure 10.6.
Because 45 < 47, we advance to 42, the left child of 47, as indicated in Figure 10.7.
At this point, 45 > 42, so we would advance to the right child of 42 if 42 had a right child. It does not, so 45 is inserted as the right child of 42. See Figure 10.8.
FIGURE 10.6 The effect of comparing 45 to 31 in the binary search tree of Figure 10.5
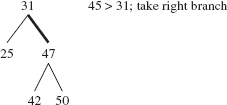
FIGURE 10.7 The effect of comparing 45 to 47 in the binary search tree of Figure 10.6
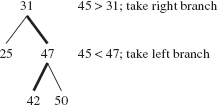
FIGURE 10.8 The effect of inserting 45 into the binary search tree in Figure 10.7
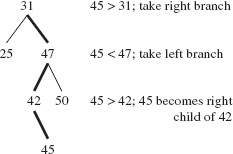
In general, the search fails if the element to be inserted belongs in an empty subtree of temp. Then the element is inserted as the only element in that subtree. That is, the inserted element always becomes a leaf in the tree. This has the advantage that the tree is not re-organized after an insertion.
Here is the complete definition (the loop continues indefinitely until, during some iteration, true or false is returned):
public boolean add (E element) { if (root == null) { if (element == null) throw new NullPointerException(); root = new Entry<E> (element, null); size++; return true; } // empty tree else { Entry<E> temp = root; int comp; while (true) { comp = ((Comparable)element).compareTo (temp.element); if (comp == 0) return false; if (comp < 0) if (temp.left != null) temp = temp.left; else { temp.left = new Entry<E> (element, temp); size++; return true; } // temp.left == null else if (temp.right != null) temp = temp.right; else { temp.right = new Entry<E> (element, temp); size++; return true; } // temp.right == null } // while } // root not null } // method add
The timing estimates for the add method are identical to those for the contains method, and depend on the height of the tree. To insert at the end of a binary search tree that forms a chain, the number of iterations is one more than the height of the tree. The height of a chain is linear in n, so worstTime(n) is linear in n. And, with the same argument we used for the contains method, we conclude that averageTime(n) is logarithmic in n.
In Programming Exercise 10.4, you get the opportunity to define the add method recursively.
10.1.2.5 The Definition of the remove Method
The only other BinarySearchTree method to be defined is
public boolean remove (Object obj)
The definition of the remove method in the BinarySearchTree class is more complicated than the definition of the add method from Section 10.1.2.4. The reason for the extra complexity is that the remove method requires a re-structuring of the tree—unless the element to be removed is a leaf. With the add method, the inserted element always becomes a leaf, and no re-structuring is needed.
The basic strategy is this: we first get (a reference to) the Entry object that holds the element to be removed, and then we delete that Entry object. Here is the definition:
public boolean remove (Object obj) { Entry<E> e = getEntry (obj); if (e == null) return false; deleteEntry (e); return true; } // method remove
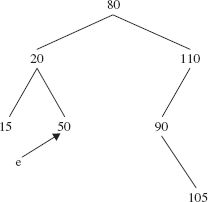
Of course, we need to postpone the analysis of the remove method until we have developed both the getEntry and deleteEntry methods. The protected method getEntry searches the tree—in the same way as the contains method defined in Section 10.1.2.3—for an Entry object whose element is obj. For example, Figure 10.9 shows what happens if the getEntry method is called to get a reference to the Entry whose element is 50.
FIGURE 10.9 The effect of calling the getEntry method to get a reference to the Entry whose element is 50. A copy of the reference e is returned
Here is the definition of the getEntry method:
/** * Finds the Entry object that houses a specified element, if there is such an Entry. * The worstTime(n) is O(n), and averageTime(n) is O(log n). * * @param obj - the element whose Entry is sought. * * @return the Entry object that houses obj - if there is such an Entry; * otherwise, return null. * * @throws ClassCastException - if obj is not comparable to the elements * already in this BinarySearchTree object. * @throws NullPointerException - if obj is null. * */ protected Entry<E> getEntry (Object obj) { int comp; if (obj == null) throw new NullPointerException(); Entry<E> e = root; while (e != null) { comp = ((Comparable)obj).compareTo (e.element); if (comp == 0) return e; else if (comp < 0) e = e.left; else e = e.right; } // while return null; } // method getEntry
The analysis of the getEntry method is the same as for the contains method in Section 10.1.2.3: worstTime(n) is linear in n and averageTime(n) is logarithmic in n.
The structure of the while loop in the getEntry method is identical to that in the contains method. In fact, we can re-define the contains method to call getEntry. Here is the new definition, now a one-liner:
public boolean contains (Object obj) { return (getEntry (obj) != null); } // method contains
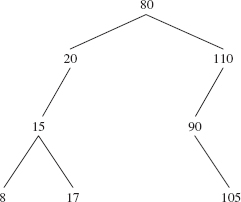
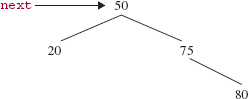
For the deleteEntry method, let's start with a few simple examples of how a binary search tree is affected by a deletion; then we'll get into the details of defining the deleteEntry method. As noted, removal of a leaf requires no re-structuring. For example, suppose we remove 50 from the binary search tree in Figure 10.10:
FIGURE 10.10 A binary search tree from which 50 is to be removed
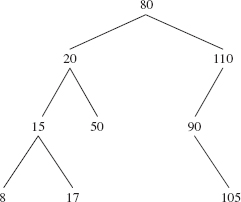
To delete 50 from the tree in Figure 10.10, all we need to do is change to null the right field of 50's parent Entry—the Entry object whose element is 20. We end up with the binary search tree in Figure 10.11.
In general, if p is (a reference to) the Entry object that contains the leaf element to be deleted, we first decide what to do if p is the root. In that case, we set
FIGURE 10.11 The binary search tree from Figure 10.10 after the removal of 50
Otherwise, the determination of which child of p.parent gets the value null depends on whether p is a left child or a right child:
if (p == p.parent.left) p.parent.left = null; else p.parent.right = null;
Notice how we check to see if p is a (reference to) a left child: if p equals p's parent's left child.
It is almost as easy to remove an element that has only one child. For example, suppose we want to remove 20 from the binary search tree in Figure 10.11. We cannot leave a hole in a binary search tree, so we must replace 20 with some element. Which one? The best choice is 15, the child of the element to be removed. So we need to link 15 to 20's parent. When we do, we get the binary search tree shown in Figure 10.12.
FIGURE 10.12 The binary search tree from Figure 10.11 after 20 was removed by replacing 20's entry with 15's entry
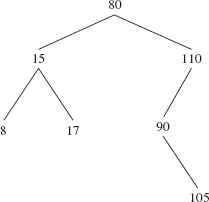
In general, let replacement be the Entry that replaces p, which has exactly one child. Then replacement should get the value of either p.left or p.right, whichever is not empty—they cannot both be empty because p has one child. We can combine this case, where p has one child, with the previous case, where p has no children:
Entry<E> replacement; if (p.left != null) replacement = p.left; else replacement = p.right; // If p has at least one child, link replacement to p.parent. if (replacement != null) { replacement.parent = p.parent; if (p.parent == null) root = replacement; else if (p == p.parent.left) p.parent.left = replacement; else p.parent.right = replacement; } // p has at least one child else if (p.parent == null) // p is the root and has no children root = null; else // p has a parent and has no children { if (p == p.parent.left) p.parent.left = null; else p.parent.right = null; } // p has a parent but no children
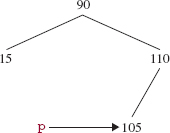
Finally, we come to the interesting case: when the element to be removed has two children. For example, suppose we want to remove 80 from the binary search tree in Figure 10.12.
As in the previous case, 80 must be replaced with some other element in the tree. But which one? To preserve the ordering, a removed element should be replaced with either its immediate predecessor (in this case, 17) or its immediate successor (in this case, 90). We will, in fact, need a successor method for an inOrder iterator. So assume we already have a successor method that returns an Entry object's immediate successor. In general, the immediate successor, s, of a given Entry object p is the leftmost Entry object in the subtree p.right. Important: the left child of this leftmost Entry object will be null. (Why?)
The removal of 80 from the tree in Figure 10.12 is accomplished as follows: first, we copy the successor's element to p.element, as shown in Figure 10.13.
Next, we assign to p the value of (the reference) s. See Figure 10.14.
Then we delete p's Entry object from the tree. As noted earlier, the left child of p must now be null, so the removal follows the replacement strategy of removing an element with one no children or one child. In this case, p has a right child (105), so 105 replaces p's element, as shown in Figure 10.15.
Because the 2-children case reduces to the 0-or-1-child case developed earlier, the code for removal of any Entry object starts by handling the 2-children case, followed by the code for the 0-or-1-child case.
As we will see in Section 10.2.3, it is beneficial for subclasses of BinarySearchTree if the deleteEntry method returns the Entry object that is actually deleted. For example, if the deleteEntry method is called to delete an entry that has two children, the successor of that entry is actually removed from the tree and returned.
FIGURE 10.13 The first step in the removal of 80 from the binary search tree in Figure 10.12: 90, the immediate successor of 80, replaces 80
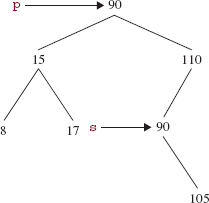
FIGURE 10.14 The second step in the removal of 80 in the binary search tree of Figure 10.12: p points to the successor entry
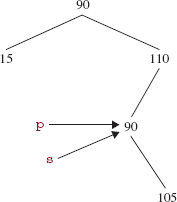
FIGURE 10.15 The final step in the removal of 80 from the binary search tree in Figure 10.12: p's element (90) is replaced with that element's right child (105)
Here is the complete definition:
/** * Deletes the element in a specified Entry object from this BinarySearchTree. * * @param p - the Entry object whose element is to be deleted from this * BinarySearchTree object. * * @return the Entry object that was actually deleted from this BinarySearchTree * object. * */ protected Entry<E> deleteEntry (Entry<E> p) { size-; // If p has two children, replace p's element with p's successor's // element, then make p reference that successor. if (p.left != null && p.right != null) { Entry<E> s = successor (p); p.element = s.element; p = s; } // p had two children // At this point, p has either no children or one child. Entry<E> replacement; if (p.left != null) replacement = p.left; else replacement = p.right; // If p has at least one child, link replacement to p.parent. if (replacement != null) { replacement.parent = p.parent; if (p.parent == null) root = replacement; else if (p == p.parent.left) p.parent.left = replacement; else p.parent.right = replacement; } // p has at least one child else if (p.parent == null) root = null; else { if (p == p.parent.left) p.parent.left = null ; else p.parent.right = null; } // p has a parent but no children return p; } // method deleteEntry
We still have the successor method to develop. Here is the method specification:
/**
* Finds the successor of a specified Entry object in this BinarySearchTree.
* The worstTime(n) is O(n) and averageTime(n) is constant.
*
* @param e - the Entry object whose successor is to be found.
*
* @return the successor of e, if e has a successor; otherwise, return null.
*
*/
protected Entry<E> successor (Entry<E> e)
This method has protected visibility to reflect the fact that Entry—the return type and parameter type—has protected visibility.
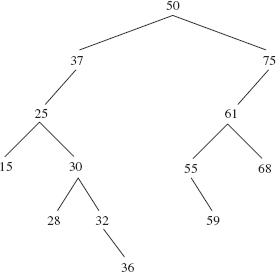
How can we find the successor of an Entry object? For inspiration, look at the binary search tree in Figure 10.16.
In the tree in Figure 10.16, the successor of 50 is 55. To get to this successor from 50, we move right (to 75) and then move left as far as possible. Will this always work? Only for those entries that have a non-null right child. What if an Entry object—for example, the one whose element is 36—has a null right child? If the right child of an Entry object e is null, we get to e's successor by going back up the tree to the left as far as possible; the successor of e is the parent of that leftmost ancestor of e. For example, the successor of 36 is 37. Similarly, the successor of 68 is 75. Also, the successor of 28 is 30; since 28 is a left child, we go up the tree to the left zero times—remaining at 28—and then return that Entry object's parent, whose element is 30. Finally, the successor of 75 is null because its leftmost ancestor, 50, has no parent.
Here is the method definition:
protected Entry<E> successor (Entry<E> e) { if (e == null ) return null;
FIGURE 10.16 A binary search tree
else if (e.right != null) { // successor is leftmost Entry in right subtree of e Entry<E> p = e.right; while (p.left != null) p = p.left; return p; } // e has a right child else { // go up the tree to the left as far as possible, then go up // to the right. Entry<E> p = e.parent; Entry<E> ch = e; while (p != null && ch == p.right) { ch = p; p = p.parent; } // while return p; } // e has no right child } // method successor
To estimate worstTime(n) for the successor method, suppose the following elements are inserted into an initially empty binary search tree: n,1,2,3,…, n - 1. The shape of the resulting tree is as shown in Figure 10.17.
FIGURE 10.17 A binary search tree in which finding the successor of n — 1 requires n — 3 iterations
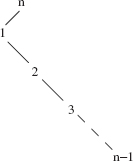
For the binary search tree in Figure 10.17, obtaining the successor of n - 1 requires n - 3 iterations, so worstTime(n) is linear in n. For averageTime(n), note that an element in the tree will be reached at most 3 times: once to get to its left child, once as the successor of that left child, and once in going back up the tree to get the successsor of its rightmost descendant. So the total number of loop iterations to access each element is at most 3n, and the average number of loop iterations is 3n/n = 3. That is, averageTime(n) is constant.
We can briefly summarize the steps needed to delete an entry:
- If the entry has no children, simply set to null the corresponding subtree-link from the entry's parent (if the entry is the root, set the root to null).
- If the entry has one child, replace the parent-entry link and the entry-child link with a parent-child link.
- If the entry has two children, copy the element in the entry's immediate successor into the entry to be deleted, and then delete that immediate successor (by part a or part b).
Finally, we can estimate the time for the remove method. The remove method has no loops or recursive calls, so the time for that method is determined by the time for the getEntry and deleteEntry methods called by the remove method. As noted above, for the getEntry method, worstTime(n) is linear in n and averageTime(n) is logarithmic in n. The deleteEntry method has no loops or recursive calls, but calls the successor method, whose worstTime(n) is linear in n and whose averageTime(n) is constant. We conclude that for the remove method, worstTime(n) is linear in n and averageTime(n) is logarithmic in n.
To complete the development of the BinarySearchTree class, we develop the embedded TreeIterator class in Section 10.1.2.6.
10.1.2.6 The TreeIterator Class
All we have left to implement is the TreeIterator class, nested in the BinarySearchTree class. The method specifications for hasNext(), next(), and remove() were given in the Iterator interface back in Chapter 4. The only fields are a reference to the element returned by the most recent call to the next() method, and a reference to the element to be returned by the next call to the next() method. The declaration of the TreeIterator class starts out with
protected class TreeIterator implements Iterator<E> { protected Entry<E> lastReturned = null, next;
Before we get to defining the three methods mentioned above, we should define a default constructor. Where do we want to start? That depends on how we want to iterate. For a preOrder or breadthFirst iteration, we would start at the root Entry object. For an inOrder or postOrder iteration, we would start at the leftmost Entry object. We will want to iterate over the elements in a BinarySearchTree in ascending order, so we want to initialize the next field to the leftmost (that is, smallest) Entry object in the BinarySearchTree. To obtain that first Entry object, we start at the root and go left as far as possible:
/** * Positions this TreeIterator to the smallest element, according to the Comparable * interface, in the BinarySearchTree object. * The worstTime(n) is O(n) and averageTime(n) is O(log n). * */ protected TreeIterator() { next = root; if (next != null) while (next.left != null) next = next.left; } // default constructor
To estimate the time for this default constructor, the situation is the same as for the contains and add methods in the BinarySearchTree class: worstTime(n) is linear in n (when the tree consists of a chain of left children), and averageTime(n) is logarithmic in n.
The hasNext() method simply checks to see if the next field has the value null:
/** * Determines if there are still some elements, in the BinarySearchTree object this * TreeIterator object is iterating over, that have not been accessed by this * TreeIterator object. * * @return true - if there are still some elements that have not been accessed by * this TreeIterator object; otherwise, return false. * */ public boolean hasNext() { return next != null; } // method hasNext
The definition of the next() method is quite simple because we have already defined the successor method:
/** * Returns the element in the Entry this TreeIterator object was positioned at * before this call, and advances this TreeIterator object. * The worstTime(n) is O(n) and averageTime(n) is constant. * * @return the element this TreeIterator object was positioned at before this call. * * @throws NoSuchElementException - if this TreeIterator object was not * positioned at an Entry before this call. * */ public E next() { if (next == null) throw new NoSuchElementException(); lastReturned = next; next = successor (next); return lastReturned.element; } // method next
Finally, the TreeIterator class's remove method deletes the Entry that was last returned. Basically, we call deleteEntry (lastReturned). A slight complication arises if lastReturned has two children. For example, suppose lastReturned references the Entry object whose element is (the Integer whose value is) 40 in the BinarySearchTree object of Figure 10.18.
For the BinarySearchTree object of Figure 10.18, if we simply call then next will reference an Entry object that is no longer in the tree. To avoid this problem, we set
deleteEntry (lastReturned);
FIGURE 10.18 A binary search tree from which 40 is to be removed
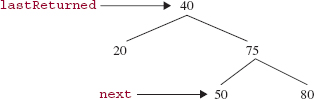
next = lastReturned;
before calling
deleteEntry (lastReturned);
Then the tree from Figure 10.18 would be changed to the tree in Figure 10.19.
FIGURE 10.19 A binary search tree in which the element referenced by lastReturned is to be removed. Before deleteEntry (lastReturned) is called, next is assigned the value of lastReturned

After deleteEntry (lastReturned) is called for the tree in Figure 10.19, we get the tree in Figure 10.20.
FIGURE 10.20 The tree from Figure 10.19 after deleteEntry (lastReturned) is called
For the tree in Figure 10.20, next is positioned where it should be positioned. We then set lastReturned to null to preclude a subsequent call to remove() before a call to next(). Here is the method definition:
/** * Removes the element returned by the most recent call to this TreeIterator * object's next() method. * The worstTime(n) is O(n) and averageTime(n) is constant. * * @throws IllegalStateException - if this TreeIterator's next() method was not * called before this call, or if this TreeIterator's remove() method was * called between the call to the next() method and this call. * */ public void remove() { if (lastReturned == null) throw new IllegalStateException(); if (lastReturned.left != null && lastReturned.right != null) next = lastReturned; deleteEntry(lastReturned); lastReturned = null; } // method remove
Lab 17 provides run-time support for the claim made earlier that the average height of a Binary SearchTree is logarithmic in n.
You are now prepared to do Lab 17:
A Run-Time Estimate of the Average Height of a BinarySearchTree Object
10.2 Balanced BinarySearch Trees
Keep in mind that the height of a BinarySearchTree is the determining factor in estimating the time to insert, remove or search. In the average case, the height of a BinarySearchTree object is logarithmic in n (the number of elements), so inserting, removing, and searching take only logarithmic-in-n time. This implies that BinarySearchTree objects represent an improvement, on average, over ArrayList objects and LinkedList obects, for which inserting, removing, or searching take linear time.1 But in the worst case, a BinarySearchTree object's height can be linear in n, which leads to linear-in-n worstTime(n) for inserting, removing, or searching.
We do not include any applications of the BinarySearchTree class because any application would be superseded by re-defining the tree instance from one of the classes in Chapter 12: TreeMap or TreeSet. For either of those classes, the height of the tree is always logarithmic in n, so insertions, removals, and searches take logarithmic time, even in the worst case. As we noted at the beginning of this chapter, the TreeMap and TreeSet classes are based on a somewhat complicated concept: the red-black tree. This section and the following two sections will help prepare you to understand red-black trees.
A binary search tree is balanced if its height is logarithmic in n, the number of elements in the tree. Three widely known data structures in this category of balanced binary search trees are AVL trees, red-black trees and splay trees. AVL trees are introduced in Section 10.3. Red-black trees are investigated in Chapter 12. For information on splay trees, the interested reader may consult Bailey [2003].
For all of these balanced binary search trees, the basic mechanism that keeps a tree balanced is the rotation. A rotation is an adjustment to the tree around an element such that the adjustment maintains the required ordering of elements. The ultimate goal of rotating is to restore some balance property that has temporarily been violated due to an insertion or removal. For example, one such balance property is that the heights of the left and right subtrees of any element should differ by at most 1. Let's start with a simple classification of rotations: left and right.
In a left rotation, some adjustments are made to the element's parent, left subtree and right subtree. The main effect of these adjustments is that the element becomes the left child of what had been the element's right child. For a simple example, Figure 10.21 shows a left rotation around the element 50. Note that before and after the rotation, the tree is a binary search tree.
FIGURE 10.21 A left rotation around 50
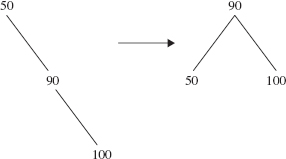
Figure 10.22 has another example of a left rotation, around the element 80, that reduces the height of the tree from 3 to 2.
The noteworthy feature of Figure 10.22 is that 85, which was in the right subtree of the before-rotation tree, ends up in the left subtree of the after-rotation tree. This phenomenon is common to all left rotations around an element x whose right child is y. The left subtree of y becomes the right subtree of x. This adjustment is necessary to preserve the ordering of the binary search tree: Any element that was in y's left subtree is greater than x and less than y. So any such element should be in the right subtree of x (and in the left subtree of y). Technically, the same phenomenon also occurred in Figure 10.21, but the left subtree of 50's right child was empty.
FIGURE 10.22 A left rotation around 80
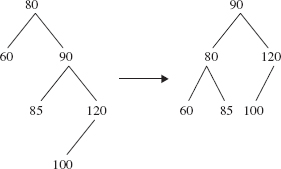
Figure 10.23 shows the rotation of Figure 10.22 in a broader context: the element rotated around is not the root of the tree. Before and after the rotation, the tree is a binary search tree.
FIGURE 10.23 The left rotation around 80 from Figure 10.22, but here 80 is not the root element
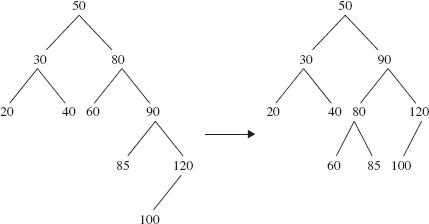
Figure 10.23 illustrates another aspect of all rotations: all the elements that are not in the rotated element's subtree are unaffected by the rotation. That is, in both trees, we still have:
If we implement a rotation in the BinarySearchTree class, no elements are actually moved; only the references are manipulated. Suppose that p (for "parent") is a reference to an Entry object and r (for "right child") is a reference to p's right child. Basically, a left rotation around p can be accomplished in just two steps:
p.right = r.left; // for example, look at 85 in Figure 10.22 r.left = p;
Unfortunately, we also have to adjust the parent fields, and that adds quite a bit of code. Here is the complete definition of a leftRotate method in the BinarySearchTree class (a similar definition appears in the TreeMap class in Chapter 12):
/** * Performs a left rotation in this BinarySearchTre object around a specified * Entry object. * * @param p - the Entry object around which the left rotation is performed * * @throws NullPointerException - if p is null or p.right is null. * * @see Cormen, 2002. protected void rotateLeft (Entry<E> p) { Entry<E> r = p.right; p.right = r.left; if (r.left != null) r.left.parent = p; r.parent = p.parent; if (p.parent == null) root = r; else if (p.parent.left == p) p.parent.left = r; else p.parent.right = r; r.left = p; p.parent = r; } // method rotateLeft
This indicates how much of a bother parents can be! But on the bright side, no elements get moved, and the time is constant.
What about a right rotation? Figure 10.24 shows a simple example: a right rotation around 50.
FIGURE 10.24 A right rotation around 50
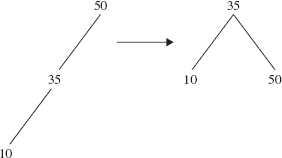
Does this look familiar? Figure 10.24 is just Figure 10.21 with the direction of the arrow reversed. In general, if you perform a left rotation around an element and then perform a right rotation around the new parent of that element, you will end up with the tree you started with.
Figure 10.25 shows a right rotation around an element, 80, in which the right child of 80's left child becomes the left child of 80. This is analogous to the left rotation in Figure 10.22.
FIGURE 10.25 A right rotation around 80
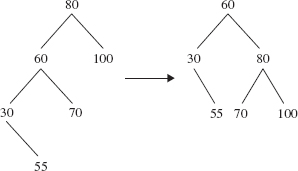
Here are details on implementing right rotations in the BinarySearchTree class. Let p be a reference to an Entry object and let l (for "left child") be a reference to the left child of p. Basically, a right rotation around p can be accomplished in just two steps:
p.left = l.right; // for example, look at 70 in the rotation of Figure 10.8 l.right = p;
Of course, once we include the parent adjustments, we get a considerably longer—but still constant time—method. In fact, if you interchange "left" with "right" in the definition of the leftRotate method, you get the definition of rightRotate.
In all of the rotations shown so far, the height of the tree was reduced by 1. That is not surprising; in fact, reducing height is the motivation for rotating. But it is not necessary that every rotation reduce the height of the tree. For example, Figure 10.26 shows a left rotation—around 50—that does not affect the height of the tree.
FIGURE 10.26 A left rotation around 50. The height of the tree is still 3 after the rotation
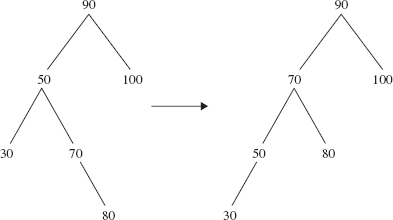
It is true that the left rotation in Figure 10.26 did not reduce the height of the tree. But a few minutes of checking should convince you that no single rotation can reduce the height of the tree on the left side of Figure 10.26. Now look at the tree on the right side of Figure 10.26. Can you figure out a rotation that will reduce the height of that tree? Not a right rotation around 70; that would just get us back where we started. How about a right rotation around 90? Bingo! Figure 10.27 shows the effect.
FIGURE 10.27 A right rotation around 90. The height of the tree has been reduced from 3 to 2
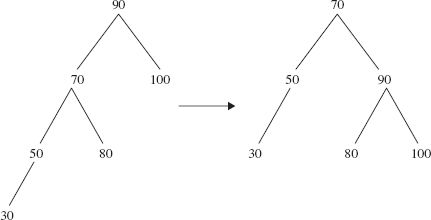
The rotations in Figures 10.26 and 10.27 should be viewed as a package: a left rotation around 90's left child, followed by a right rotation around 90. This is referred to as a double rotation. In general, if p is a reference to an Entry object, then a double rotation around p can be accomplished as follows:
leftRotate (p.left); rightRotate (p);
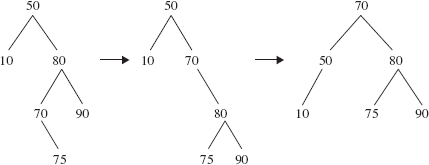
Figure 10.28 shows another kind of double rotation: a right rotation around the right child of 50, followed by a left rotation around 50.
FIGURE 10.28 Another kind of double rotation: a right rotation around 50's right child, followed by a left rotation around 50
Before we move on to Section 10.2.1 with a specific kind of balanced binary search tree, let's list the major features of rotations:
- There are four kinds of rotation:
- Left rotation;
- Right rotation;
- A left rotation around the left child of an element, followed by a right rotation around the element itself;
- A right rotation around the right child of an element, followed by a left rotation around the element itself.
- Elements not in the subtree of the element rotated about are unaffected by the rotation.
- A rotation takes constant time.
- Before and after a rotation, the tree is still a binary search tree.
- The code for a left rotation is symmetric to the code for a right rotation: simply swap the words "left" and "right".
Section 10.2.1 introduces the AVL tree, a kind of binary search tree that employs rotations to maintain balance.
10.2.1 AVL Trees
An AVL tree is a binary search tree that either is empty or in which:
- the heights of the root's left and right subtrees differ by at most 1, and
- the root's left and right subtrees are AVL trees.
AVL trees are named after the two Russian mathematicians, Adelson-Velski and Landis, who invented them in 1962. Figure 10.29 shows three AVL trees, and Figure 10.30 shows three binary search trees that are not AVL trees.

FIGURE 10.30 Three binary search trees that are not AVL trees
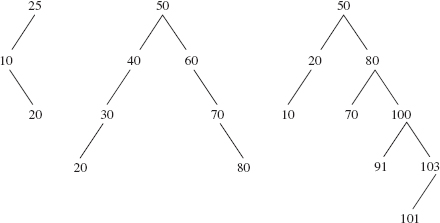
The first tree in Figure 10.30 is not an AVL tree because its left subtree has height 1 and its right subtree has height −1. The second tree is not an AVL tree because its left subtree is not an AVL tree; neither is its right subtree. The third tree is not an AVL tree because its left subtree has height 1 and its right subtree has height 3.
In Section 10.2.2, we show that an AVL tree is a balanced binary search tree, that is, that the height of an AVL tree is always logarithmic in n. This compares favorably to a binary search tree, whose height is linear in n in the worst case (namely, a chain). The difference between linear and logarithmic can be huge. For example, suppose n = 1,000,000,000,000. Then log2 n is less than 40. The practical import of this difference is that insertions, removals and searches for the AVLTree class take far less time, in the worst case, than for the BinarySearchTree class.
10.2.2 The Height of an AVL Tree
We can prove that an AVL tree's height is logarithmic in n, and the proof relates AVL trees back to, of all things, Fibonacci numbers.
Claim If t is a non-empty AVL tree, height(t) is logarithmic in n, where n is the number of elements in t.
Proof We will show that, even if an AVL tree t has the maximum height possible for its n elements, its height will still be logarithmic in n. How can we determine the maximum height possible for an AVL tree with n elements? As Kruse (see Kruse [1987]) suggests, rephrasing the question helps us get the answer. Given a height h, what is the minimum number of elements in any AVL tree of that height?
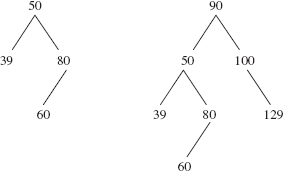
For h = 0,1,2 let minh be the minimum number of elements in an AVL tree of height h. Clearly, min0 = 1and min1 = 2. The values of min2 and min3 can be seen from the AVL trees in Figure 10.31.
In general, if h1 > h2, then minh1 is greater than the number of elements needed to construct an AVL tree of height h2. That is, if h1 >h2, then minh1 > minh2. In other words, minh is an increasing function of h.
Suppose that t is an AVL tree with h height and minh elements, for some value of h > 1. What can we say about the heights of the left and right subtrees of t? By the definition of height, one of those subtrees must have height h - 1. And by the definition of an AVL tree, the other subtree must have height of h - 1or h - 2. In fact, because t has the minimum number of elements for its height, one of its subtrees must have height h - 1and minh-1 elements, and the other subtree must have height h - 2and minh-2 elements.
A tree always has one more element than the number of elements in its left and right subtrees. So we have the following equation, called a recurrence relation:
minh = minh-1 + minh-2 +1, for any integer h > 1
Now that we can calculate minh for any positive integer h, we can see how the function minh is related to the maximum height of an AVL tree. For example, because min6 = 33 and min7 = 54, the maximum height of an AVLtree with 50 elements is six.
The above recurrence relation looks a lot like the formula for generating Fibonacci numbers (see Lab 7). The term Fibonacci tree refers to an AVL tree with the minimum number of elements for its height. From the above recurrence relation and the values of min0 and min1, we can show, by induction on h, that
minh = fib(h + 3) - 1, for any nonnegative integer h.
We can further show, by induction on h (see Concept Exercise 10.8),
fib(h + 3) - 1 ≥ (3/2)h, for any nonnegative integer h.
Combining these results,
minh ≥ (3/2)h, for any nonnegative integer h.
Taking logs in base 2 (but any base will do), we get
log2(minh) ≥ h * log2(3/2), for any nonnegative integer h.
FIGURE 10.31 AVL trees of heights 2 and 3 in which the number of elements is minimal
Rewriting this in a form suitable for a Big-O claim, with 1 / log2(3/2) < 1.75:
h ≤ 1.75 * log2(minh), for any nonnegative integer h.
If t is an AVL tree with h height and n elements, we must have minh ≤ n, so for any such AVL tree,
h ≤ 1.75 * log2(n).
This implies that the height of any AVL tree is O(logn). Is O(logn) a tight upper bound; that is, is the height of any AVL tree logarithmic in n? Yes, and here's why. For any binary tree of height h with n elements,
h ≥ log2(n + 1) - 1
by part 2 of the Binary Tree Theorem. We conclude that any AVL tree with n elements has height that is logarithmic in n, even in the worst case.
To give you a better idea of how AVL trees relate to binary search trees, we sketch the design and implementation of the AVLTree class in Section 10.2.3. To complete the implementation, you will need to tackle Programming Projects 10.3 and 10.4. Those projects deal with some of the details of the add and remove methods, respectively.
10.2.3 The AVLTree Class
The AVLTree class will be developed as a subclass of the BinarySearchTree class. There will not be any additional fields in the AVLTree class, but each entry object has an additional field:
char balanceFactor = '=';
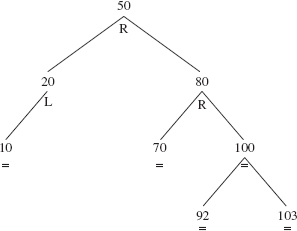
The purpose of this additional field in the Entry class is to make it easier to maintain the balance of an AVLTree object. If an Entry object has a balanceFactor value of '=', the Entry object's left subtree has the same height as the Entry object's right subtree. If the balanceFactor value is 'L', the left subtree's height is one greater than the right subtree's height. And a balanceFactor value of 'R' means that the right subtree's height is one greater than the left subtree's height. Figure 10.32 shows an AVL tree with each element's balance factor shown below the element.
FIGURE 10.32 An AVL tree with the balance factor under each element
Here is the new entry class, nested in the AVLTree class:
protected static class AVLEntry<E> extends BinarySearchTree.Entry<E> { protected char balanceFactor = '='; /** * Initializes this AVLEntry object from a specified element and a * specified parent AVLEntry. * * @param element - the specified element to be housed in this * AVLEntry object. * @param parent - the specified parent of this AVLEntry object. * */ protected AVLEntry (E element, AVLEntry<E> parent) { this.element = element; this.parent = parent; } // constructor } // class AVLEntry
The only methods that the AVLTree class overrides from the BinarySearchTree class are those that involve the AVLEntry class's balanceFactor field. Specifically, the AVLTree class will override the add and deleteEntry methods from the BinarySearchTree class. The re-balancing strategy is from Sahni (see Sahni [2000]).
One intriguing feature of the AVLTree class is that the contains method is not overridden from the BinarySearchTree class, but worstTime(n) is different: logarithmic in n, versus linear in n for the BinarySearchTree class. This speed reflects the fact that the height of an AVL tree is always logarithmic in n.
The definition of the add method in the AVLTree class resembles the definition of the add method in the BinarySearchTree class. But as we work our way down the tree from the root to the insertion point, we keep track of the inserted AVLEntry object's closest ancestor whose balanceFactor is 'L' or 'R'. We refer to this Entry object as imbalanceAncestor. For example, if we insert 60 into the AVLTree object in Figure 10.33, imbalanceAncestor is the Entry object whose element is 80:
FIGURE 10.33 An AVLTree object
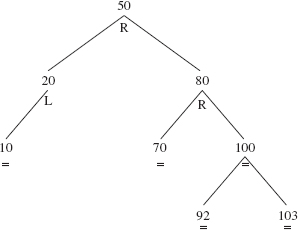
After the element has been inserted, BinarySearchTree-style, into the AVLTree object, we call a fix-up method to handle rotations and balanceFactor adjustments. Here is the definition of the add method:
public boolean add (E element) { if (root == null) { if (element == null) throw new NullPointerException(); root = new AVLEntry<E> (element, null ); size++; return true ; } // empty tree else { AVLEntry<E> temp = (AVLEntry<E>)root, imbalanceAncestor = null; // nearest ancestor of // element with // balanceFactor not '=' int comp; while (true ) { comp = ((Comparable)element).compareTo (temp.element); if (comp == 0) return false; if (comp < 0) { if (temp.balanceFactor != '=') imbalanceAncestor = temp; if (temp.left != null) temp = (AVLEntry<E>)temp.left; else { temp.left = new AVLEntry<E> (element, temp); fixAfterInsertion ((AVLEntry<E>)temp.left, imbalanceAncestor); size++; return true; } // temp.left == null } // comp < 0 else { if (temp.balanceFactor != '=') imbalanceAncestor = temp; if (temp.right != null) temp = (AVLEntry<E>)temp.right; else { temp.right = new AVLEntry<E>(element, temp); fixAfterInsertion ((AVLEntry<E>)temp.right, imbalanceAncestor); size++; return true; } // temp.right == null } // comp > 0 } // while } // root not null } // method add
This code differs from that of the BinarySearchTree class's add method in three respects:
- The new entry is an instance of AVLEntry.
- The imbalanceAncestor variable is maintained.
- The fixAfterlnsertion method is called to re-balance the tree, if necessary.
The definition of the fixAfterlnsertion method is left as Programming Project 10.3. The bottom line is that, for the add method, worstTime(n) is O(logn). In fact, because the while loop in the add method can require as many iterations as the height of the AVL tree, worstTime(n) is logarithmic in n.
The definition of the deleteEntry method (called by the inherited remove method) starts by performing a BinarySearchTree -style deletion, and then invokes a fixAfterDeletion method. Fortunately, for the sake of code re-use, we can explicitly call the BinarySearchTree class's deleteEntry method, so the complete definition of the AVLTree class's deleteEntry method is simply:
protected Entry<E> deleteEntry (Entry<E> p) { AVLEntry<E> deleted = (AVLEntry<E>)super.deleteEntry (p); fixAfterDeletion (deleted.element, (AVLEntry<E>)deleted.parent); return deleted; } // method deleteEntry
Of course, we are not done yet; we are not even close: The definition of the fixAfterDeletion method is left as Programming Project 10.4. For the remove method, worstTime(n) is O(logn). In fact, because we start with a BinarySearchTree -style deletion, worstTime(n) is logarithmic in n.
The book's website includes an applet that will help you to visualize insertions in and removals from an AVLTree object.
10.2.4 Runtime Estimates
We close out this chapter with a brief look at some run-time issues. For the AVLTree class's add method, worstTime(n) is logarithmic in n, whereas for the BinarySearchTree class's add method, worstTime(n) is linear in n. And so, as you would expect, the worst case run-time behavior of the AVLTree class's add method is much faster than that of the BinarySearchTree class's add method. Programming Exercise 10.5 confirms this expectation.
What about averageTime(n)? The averageTime(n) is logarithmic in n for the add method in those two classes. Which do you think will be faster in run-time experiments? Because quite a bit of effort goes into maintaining the balance of an AVLTree object, the average height of a BinarySearchTree object is about 50% larger than the average height of an AVLTree object: 2.1 log2 n versus 1.44 log2 n. But the extra maintenance makes AVLTree insertions slightly slower, in spite of the height advantage, than BinarySearchTree insertions.
In Chapter 12, we present another kind of balanced binary search tree: the red-black tree. Insertions in red-black trees are slightly faster (but less intuitive), on average, than for AVLtrees, and that is why the red-black tree was selected as the underlying structure for the Java Collection Framework's TreeMap and TreeSet classes. Both of these classes are extremely useful; you will get some idea of this from the applications and Programming Projects in Chapter 12.
SUMMARY
A binary search tree t is a binary tree such that either t is empty or
- each element in leftTree(t) is less than the root element of t;
- each element in rightTree(t) is greater than the root element of t;
- both leftTree(t) and rightTree(t) are binary search trees.
The BinarySearchTree class maintains a sorted collection of Comparable elements. The time estimates for searching, inserting, and deleting depend on the height of the tree. In the worst case—if the tree is a chain—the height is linear in n, the number of elements in the tree. The average height of a binary search tree is logarithmic in n. So for the contains, add, and remove methods, worstTime(n) is linear in n and averageTime(n) is logarithmic in n.
A binary search tree is balanced if its height is logarithmic in n, the number of elements in the tree. The balancing is maintained with rotations. A rotation is an adjustment to the tree around an element such that the adjustment maintains the required ordering of elements. This chapter introduced one kind of balanced binary search tree: the AVL tree. An AVL tree is a binary search tree that either is empty or in which:
- the heights of the root's left and right subtrees differ by at most 1, and
- the root's left and right subtrees are AVL trees.
The AVLTree class is a subclass of the BinarySearchTree class. The only overridden methods are those related to maintaining balance: add and delete Entry.
CROSSWORD PUZZLE
| ACROSS | DOWN |
| 1. An AVL tree with the minimum number of elements for its height | 2. The given definitions of the contains, add and remove methods in the BinarySearchTree class are ________ . |
| 4. The feature of a BinarySearchTree object most important in estimating worstTime(n) and averageTime(n) for the contains, add and remove methods | 3. An adjustment to a binary search tree around an element that maintains the required ordering of elements. |
| 6. The only field in the AVLEntry class that is not inherited from the nested Entry class of the BinarySearchTree class | 5. The fourth field in the nested Entry class of the BinarySearchTree class. The other three fields are element, left and right. |
| 10. A binary search tree is if _________ its height is logarithmic in n, the number of elements in the tree. | 7. A balanced binary search tree in which, if the tree is not empty, the heights of the left and right subtrees differ by at most one |
| 8. The only field, other than size, in the BinarySearchTree class | |
| 9. The worstTime(n) for the copy method in the BinarySearchTree class is ________ in n. |
CONCEPT EXERCISES
10.1
- Show the effect of making the following insertions into an initially empty binary search tree:
30, 40, 20, 90, 10, 50, 70, 60, 80
- Find a different ordering of the above elements whose insertions would generate the same binary search tree as in part a.
10.2 Describe in English how to remove each of the following from a binary search tree:
- an element with no children
- an element with one child
- an element with two children
10.3
- For any positive integer n, describe how to arrange the integers 1, 2, …, n so that when they are inserted into a BinarySearchTree object, the height of the tree will be linear in n.
- For any positive integer n, describe how to arrange the integers 1, 2, …, n so that when they are inserted into a BinarySearchTree object, the height of the tree will be logarithmic in n.
- For any positive integer n, describe how to arrange the integers 1, 2, …, n so that when they are inserted into an AVLTree object, the height of the tree will be logarithmic in n.
- For any positive integer n, is it possible to arrange the integers 1,2,…, n so that when they are inserted into an AVLTree object, the height of the tree will be linear in n? Explain.
10.4 In each of the following binary search trees, perform a left rotation around 50.
a.
b.
10.5 In each of the following binary search trees, perform a right rotation around 50.
a.
b.
c.
10.6 In the following binary search tree, perform a double rotation (a left rotation around 20 and then a right rotation around 50) to reduce the height to 2.
10.7 In the following binary search tree, perform a "double rotation" to reduce the height to 2:
10.8 Show that for any nonnegative integer h,
fib(h + 3) - 1 ≥ (3/2)h
Hint: Use the Strong Form of the Principle of Mathematical Induction and note that, for h > 1,
(3/2)h-1 + (3/2)h-2 = (3/2)h-2 * (3/2 + 1)≥(3/2)h-2 * 9/4.
10.9 Suppose we define maxh to be the maximum number of elements in an AVL tree of height h.
- Calculate max3.
- Determine the formula for maxh for any h ≥ 0.
Hint: Use the Binary Tree Theorem from Chapter 9.
- What is the maximum height of an AVL tree with 100 elements?
10.10 Show that the height of an AVL tree with 32 elements must be exactly 5.
Hint: calculate max4 (see Concept Exercise 10.9) and min6.
10.11 For the contains method in the BinarySearchTree class, worstTime(n) is linear in n. The AVLTree class does not override that method, but for the contains method in the AVLTree class, worstTime(n) is logarithmic in n. Explain.
10.12 The following program generates a BinarySearchTree object of n elements. Draw the tree when n = 13. For any n ≥ 0, provide a @ (that is, Big Theta) estimate of height(n), that is, the height of the BinarySearchTree object as a function of n.
import java.util.*; public class weirdBST { public static void main (String[] args) { new weirdBST().run(); } // method main public void run() { BinarySearchTree<Double> tree = new BinarySearchTree<Double>(); LinkedList<Double> list =new LinkedList<Double>(); System.out.println ("Enter n > 0"); int n = new Scanner (System.in).nextInt(); tree.add (1.0); list.add (1.0); int k = 2; while (tree.size() < n) addLevel (tree, n, k++, list); System.out.println (tree.height()); } // method run public void addLevel (BinarySearchTree<Double> tree, int n, int k, LinkedList<Double> list) { final double SMALL = 0.00000000001; LinkedList<Double> newList = new LinkedList<Double>(); Iterator<Double> itr = list.iterator(); double d = itr.next(); tree.add (d - 1.0); newList.add (d - 1.0); for (int i = 0; i < k && tree.size() < n; i++) { tree.add (d + SMALL ); newList.add (d + SMALL); if (itr.hasNext()) d = itr.next(); } // for list.clear(); list.addAll (newList); } // method addLevel } // class weirdBST
PROGRAMMING EXERCISES
10.1 In the BinarySearchTree class, test and develop a leaves method. Here is the method specification:
/**
* Returns the number of leaves in this BinarySearchTree object.
* The worstTime(n) is O(n).
*
* @return - the number of leaves in this BinarySearchTree object.
*
*/
public int leaves()
Test your method by adding tests to the BinarySearchTreeTest class available from the book's website. Hint: A recursive version, invoked by a wrapper method, can mimic the definition of leaves(t) from Section 9.1. Or, you can also develop an iterative version by creating a new iterator class in which the next method increments a count for each Entry object whose left and right fields are null.
10.2 Modify the BinarySearchTree class so that the iterators are fail-fast (see Appendix 1 for details on fail-fast iterators). Test your class by adding tests to the BinarySearchTreeTest class available from the book's website.
10.3 Modify the BinarySearchTree class so that BinarySearchTree objects are serializable (see Appendix 1 for details on serializability). Test your class by adding tests to the BinarySearchTreeTest class available from the book's website.
10.4 Create a recursive version of the add method.
Hint: Make the add method a wrapper for a recursive method. Test your version with the relevant tests in the BinarySearchTreeTest class available from the book's website.
10.5 In the BinarySearchTree class, modify the getEntry method so that it is a wrapper for a recursive method. Test your version with the relevant tests in the BinarySearchTreeTest class available from the book's website.
10.6 (This exercise assumes you have completed Programming Projects 10.3 and 10.4.) Create a test suite for the AVLTree class.
Hint: Make very minor modifications to the BinarySearchTreeTest class available from the book's website. Use your test suite to increase your confidence in the correctness of the methods you defined in Programming Projects 10.3 and 10.4.
10.7 (This exercise assumes you have completed Programming Projects 10.3 and 10.4.) In the AVLTree class, test and define the following method:
/** * The height of this AVLTree object has been returned. * The worstTime(n) is O(log n). * * @return the height of this AVLTree object. * */ public int height()
Hint: Use the balanceFactor field in the AVLEntry class to guide you down the tree. Test your method by adding tests to the BinarySearchTreeTest class available from the book's website.
Programming Project 10.1: An Alternate Implementation of the Binary-Search-Tree Data Type
This project illustrates that the binary-search-tree data type has more than one implementation. You can also use the technique described below to save a binary search tree (in fact, any binary tree) to disk so that it can be subsequently retrieved with its original structure.
Develop an array-based implementation of the binary-search-tree data type. Your class, BinarySearchTreeArray<E>, will have the same method specifications as the BinarySearchTree<E> class but will use indexes to simulate the parent, left, and right links. For example, the fields in your embedded Entry<E> class might have:
E element;
int parent,
left,
right;
Similarly, the BinarySearchTreeArray<E> class might have the following three fields:
Entry<E> [ ] tree;
int root,
size;
The root Entry object is stored in tree [0], and a null reference is indicated by the index —1. For example, suppose we create a binary search tree by entering the String objects "dog", "turtle", "cat", "ferret". The tree would be as follows:
The array representation, with the elements stored in the order in which they are entered, is
The method definitions are very similar to those in the BinarySearchTree class, except that an expression such as
root.left
is replaced with
tree [root].left
For example, here is a possible definition of the getEntry method:
protected Entry<E> getEntry (Object obj) { int temp = root, comp; while (temp != -1) { comp = ((Comparable)obj).compareTo (tree [temp].element); if (comp == 0) return tree [temp]; else if (comp < 0) temp = tree [temp].left; else temp = tree [temp].right; } // while return null; } // method getEntry
You will also need to modify the TreeIterator class.
Programming Project 10.2: Printing a BinarySearchTree Object
In the BinarySearchTree class, implement the following method:
/**
* Returns a String representation of this BinarySearchTree object.
* The worstTime(n) is linear in n.
*
* @return a String representation - that incorporates the structure-of this
* BinarySearchTree object.
*
*/
public String toTreeString()
Note 1: The String returned should incorporate the structure of the tree. For example, suppose we have the following:
BinarySearchTree<Integer> tree = new BinarySearchTree<Integer>();
tree.add (55);
tree.add (12);
tree.add (30);
tree.add (97);
System.out.println (tree.toTreeString());
The output would be:
In what sense is the above approach better than developing a printTree method in the BinarySearchTree class?
Programming Project 10.3: The fixAfterInsertion Method
Test and define the fixAfterInsertion method in the AVLTree<E> class. Here is the method specification:
/** * Restores the AVLTree properties, if necessary, by rotations and balance * factor adjustments between a specified inserted entry and the specified nearest * ancestor of inserted that has a balanceFactor of 'L' or 'R'. * The worstTime(n) is O(log n). * * @param inserted - the specified inserted AVLEntry object. * @param imbalanceAncestor - the specified AVLEntry object that is the * nearest ancestor of inserted. * */ protected void fixAfterInsertion (AVLEntry<E> inserted, AVLEntry<E> imbalanceAncestor)
Hint: If imbalanceAncestor is null, then each ancestor of the inserted AVLEntry object has a balanceFactor value of '='. For example, Figure 10.34 shows the before-and-after for this case.
There are three remaining cases when the balanceFactor value of imbalanceAncestor is 'L'. The three cases when that value is 'R' can be obtained by symmetry.
Case 1: imbalanceAncestor.balanceFactor is 'L' and the insertion is made in the right subtree of imbal anceAncestor. Then no rotation is needed. Figure 10.35 shows the before-and-after for this case.
Case 2: imbalanceAncestor.balanceFactor is 'L' and the insertion is made in the left subtree of the left subtree of imbalanceAncestor. The restructuring can be accomplished with a right rotation around imbalanceAncestor. Figure 10.36 shows the before-and-after in this case.
Case 3: imbalanceAncestor.balanceFactor is 'L' and the inserted entry is in the right subtree of the left subtree of imbalanceAncestor. The restructuring can be accomplished with a left rotation around the left child of imbalanceAncestor followed by a right rotation around imbalanceAncestor. There are three subcases to determine the adjustment of balance factors:
3a: imbalanceAncestor's post-rotation parent is the inserted entry. Figure 10.37 shows the before-and-after in this case.
FIGURE 10.34 On the left-hand side, an AVLTree object just before the call to fixAfterInsertion; the element inserted was 55, and all of its ancestors have a balance factor of '='. On the right-hand side, the AVLTree object with adjusted balance factors
FIGURE 10.35 On the left-hand side, an AVL tree into which 55 has just been inserted. The balance factors of the other entries are pre-insertion. On the right-hand side, the same AVL tree after the balance factors have been adjusted. The only balance factors adjusted are those in the path between 55 (exclusive) and 50 (inclusive)
FIGURE 10.36 On the left side, what was an AVL tree has become imbalanced by the insertion of 13. The balance factors of the other entries are pre-insertion. In this case, imbalanceAncestor is the AVLEntry object whose element is 50. On the right side, the restructured AVL tree with adjusted balanced factors
FIGURE 10.37 On the left side, what was an AVL tree has become imbalanced by the insertion of 40. The balance factors of the other entries are pre-insertion. In this sub-case, imbalanceAncestor is the AVLEntry object whose element is 50. On the right side, the restructured AVL tree with adjusted balanced factors
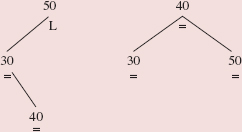
3b: The inserted element is less than imbalanceAncestor's post-rotation parent. Figure 10.38 shows the before-and-after in this subcase.
3c: The inserted element is greater than imbalanceAncestor's post-rotation parent. Figure 10.39 shows the before-and-after in this subcase.
FIGURE 10.38 On the left side, what was an AVL tree has become imbalanced by the insertion of 35. The balance factors of the other entries are pre-insertion. In this case, imbalanceAncestor is the AVLEntry object whose element is 50. On the right side, the restructured AVL tree with adjusted balanced factors
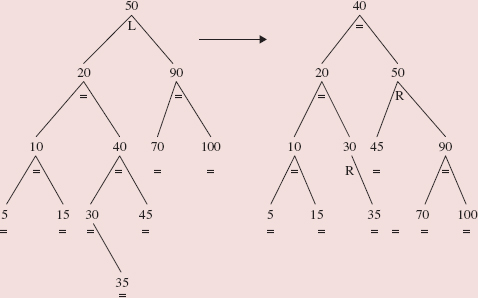
FIGURE 10.39 On the left side, what was an AVL tree has become imbalanced by the insertion of 42. The balance factors of the other entries are pre-insertion. In this case, imbalanceAncestor is the AVLEntry object whose element is 50. On the right side, the restructured AVL tree with adjusted balanced factors
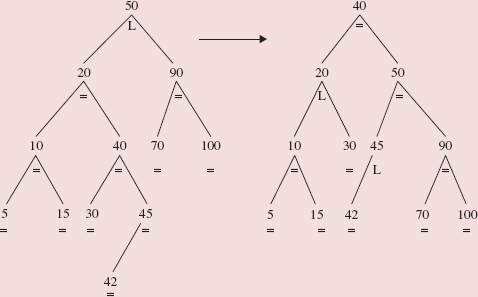
Programming Project 10.4: The fixAfterDeletion Method
Test and define the fixAfterDeletion method in the AVLTree<E> class. Here is the method specification:
/**
* Restores the AVL properties, if necessary, by rotations and balance-factor
* adjustments between the element actually deleted and a specified ancestor
* of the AVLEntry object actually deleted.
* The worstTime(n) is O(log n).
*
* @param element - the element actually deleted from this AVLTree object.
* @param ancestor - the specified ancestor (initially, the parent) of the
* element actually deleted.
*
*/
protected void fixAfterDeletion (E element, AVLEntry<E> ancestor)
Hint: Loop until the tree is an AVL tree with appropriate balance factors. Within the loop, suppose the element removed was in the right subtree of ancestor (a symmetric analysis handles the left-subtree case). Then there are three subcases, depending on whether ancestor.balanceFactor is '=', 'R', or 'L'. In all three subcases, ancestor.balanceFactor must be changed. For the '=' subcase, the loop then terminates. For the 'R' subcase, ancestor is replaced with ancestor.parent and the loop continues. For the 'L' subcase, there are three sub-subcases, depending on whether ancestor.left.balanceFactor is '=', 'R', or 'L'. And the 'R' sub-subcase has three sub-sub-subcases.
1 The corresponding methods in the ArrayList and LinkedList classes are add (int index, E element), remove (Object obj) and contains (Object obj). Note that ArrayList objects and LinkedList objects are not necessarily in order.