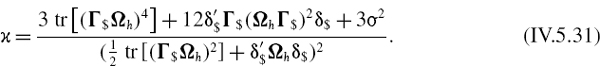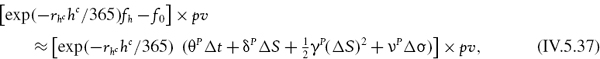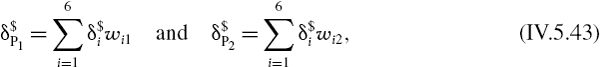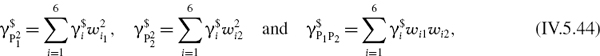IV.5

Value at Risk for Option Portfolios

IV.5.1 INTRODUCTION

The previous chapters in this book have focused on two aspects of VaR modelling: the risk characteristics of portfolios with different types of risk factors, and the modelling of the risk factors. Until now we have only applied the models that we have developed to simple portfolios where the portfolio mapping is a linear function of their risk factors. Now we extend the analysis to discuss how to estimate VaR and expected tail loss for option portfolios.

The most important risk factors for an option are the change in price of the underlying asset, the square of this price change and the change in the implied volatility. The squared price change is necessary because an option price is non-linearly related to the underlying price. This introduces an extra degree of complexity into the construction of a VaR model for an option portfolio.

When VaR estimates for option portfolios are scaled over different risk horizons we are making an implicit assumption that the portfolio is being dynamically rebalanced at the end of each day, to keep its risk factor sensitivities constant. For this reason, we call such a VaR estimate a dynamic VaR estimate. Then, even though the portfolio returns cannot be normal and i.i.d., it is common practice to scale the daily VaR to longer risk horizons using a square-root scaling rule. Indeed, it is admissible under banking regulations, although the Basel Committee indicates that this practice may ultimately be disallowed.¹ Dynamic VaR estimates are suitable for actively traded portfolios, in particular for assessing the risk of a portfolio that is always delta–gamma–vega neutral and for assessing the VaR when the portfolio is held at its risk limits, if these limits are defined in terms of risk factor sensitivities. However the use of a square-root scaling rule can be a significant source of model risk.

The alternative is to measure the VaR directly from the h-day P&L, without scaling up a 1-day VaR estimate to a longer risk horizon. In this case we are assuming the portfolio is not traded during the risk horizon, and so we call such a VaR estimate a static VaR estimate. Static VaR is suitable for estimating the risk of a single structured product that is not intended to be dynamically rebalanced. In practice, assuming no rebalancing over the risk horizon is not realistic for option portfolios. Option traders write options because they think they know how to hedge their risks, and they believe they can make a profit after accounting for their hedging costs, often rebalancing their hedged portfolio several times per day.

If the risk factor returns are normal and i.i.d. it makes no difference to a linear portfolio whether we scale the daily VaR to longer risk horizons using the square-root scaling rule, or measure the VaR directly from the h-day return or P&L distribution. That is, the static and dynamic VaR estimates are the same. But this is not the case for option portfolios. Static VaR estimates have gamma, vega and theta effects that are much more pronounced than they are in dynamic VaR, with the gamma effect being the greatest.

Our focus in this chapter will be on modelling the non-linear characteristics of portfolios, rather than on the precision of the VaR methodology. Nevertheless, from the many empirical examples given in this chapter we are able to draw some strong general conclusions about the appropriate type of VaR model to apply to option portfolios.

Whilst analytic approximations to options VaR based on delta–gamma mapping may seem attractive, the option portfolio P&L resulting from this approximation is highly skewed and bimodal so it is very difficult capture with a parametric model. Moreover, accurate VaR estimation requires a precise fit in the tails of this distribution, and even small discrepancies between the parametric form and the empirical distribution can lead to large errors in the analytic approximation to VaR.

We shall show that standard historical simulation is suitable for dynamic VaR estimation, but there are problems with trying to use a non-parametric model for static VaR estimation. Typically, the precision of a standard historical VaR estimate relies on using daily risk factor returns in a very large number of simulations. From these we could estimate a 1-day VaR non-parametrically and scale up this estimate to longer risk horizons, under the assumption that the option portfolio has stable, i.i.d. returns. But this approach assumes that the portfolio is rebalanced daily to return the risk factor sensitivities to their values at the time the VaR is estimated, so it gives an estimate of dynamic VaR, not static VaR. For a static portfolio that is not traded over the risk horizon we need to estimate the h-day VaR as a quantile of the h-day P&L distribution. Standard historical simulation based on overlapping data will distort the tail behaviour of the P&L distribution in such as way that VaR estimates at extreme quantiles can be seriously underestimated. In fact, the only way that we can estimate the static h-day VaR in the context of historical simulation is by introducing a parametric model for the conditional distributions of the portfolio returns, such as a GARCH model.²

A strong conclusion that is drawn from this chapter is that the only viable method for estimating the static VaR for option portfolios is parametric simulation, using either Monte Carlo or the filtered historical simulation method of Barone-Adesi et al. (1998, 1999). Either way, option portfolio VaR estimates must be based on a suitable risk factor returns model, not only a non-normal multivariate distribution for risk factor returns but also a model that captures the dynamic properties of risk factor returns. Our empirical examples demonstrate how important it is to include volatility clustering effects in price risk factors. Mean reversion in volatility risk factors is also of some importance, except over very short risk horizons.

Even if efficient Monte Carlo simulation algorithms are based on an appropriate model for risk factor returns, there is another important source of error in VaR for an option portfolio. This is the risk factor mapping. For a portfolio of options it is standard to base the risk factor mapping on a Taylor expansion, where the risk factor sensitivities are given by the portfolio Greeks. But a Taylor expansion is only a local approximation, meaning that it is only accurate for small changes in risk factors. However, because VaR is a loss that we are fairly confident will not occur, to assess VaR we need to consider large movements in risk factors. Thus the Greeks approximations only give a crude approximation to the VaR. In particular, these approximations are of limited use when stress testing a portfolio because, in stress testing, risk factors are set to very extreme values.

On the other hand, to estimate VaR for a large complex option portfolio without using a risk factor mapping may take a considerable amount of time. The Greeks approximations have the major advantage that they facilitate real-time VaR calculations, and these are necessary when traders are operating under VaR limits. Typically, limits might be set at the 95% confidence level, over a daily risk horizon. Real time VaR calculations could then be based on delta–gamma–vega approximation in a Monte Carlo or historical dynamic VaR model.

The outline of this chapter is as follows. Section IV.5.2 discusses the characteristics that differentiate option portfolios from linear portfolios, for the purposes of VaR measurement. We briefly summarize the risk factor mappings for option portfolios and then provide a critical review of the practice of scaling VaR for option portfolios from a daily risk horizon to longer risk horizons.

Section IV.5.3 describes some simple analytic approximations to VaR estimates for option portfolios. We focus on a large complex portfolio where exact evaluation is impractical, so that a risk factor mapping must be applied. First we derive a simple delta – normal VaR approximation that treats an option portfolio as if it were linear. Then a quasi-analytical method for calculating the VaR, based on a delta–gamma mapping, is explained. The method relies on fitting quantiles, or better still the whole P&L distribution, to the moments of a multi-factor delta–gamma representation.

In Section IV.5.4 we explain how historical simulation could be applied to options and option portfolios. The section begins with empirical examples of VaR when options are revalued exactly, using the pricing model, starting with a standard European option but also including an example based on an analytic approximation to the price of an option with a path-dependent pay-off. Then we move on to option portfolios, first with exact repricing of the options at the risk horizon and then when the portfolio P&L is mapped to risk factors. Of particular interest is the study of historical VaR for a delta–gamma-hedged option portfolio. Such a portfolio has minimal price risk only if it is continually rebalanced to maintain delta–gamma neutrality. This section concludes with a case study on measuring the historical dynamic VaR of a hedged energy options trading book.

Section IV.5.5 describes the application of Monte Carlo VaR to options and option portfolios. The basic steps of Monte Carlo VaR for options are understood in the context of a simple application: measuring the VaR and ETL of a standard European index option.³ The core of the model is the simulation of two negatively correlated risk factors, i.e. the underlying equity index price and its implied volatility. We use this example to demonstrate the difference between static and dynamic VaR. That is, we measure the h-day VaR directly from an h-day P&L distribution, which is the correct way to estimate the VaR of a static portfolio such as a simple European option, and then we measure it from the simulated daily P&L distribution and then scaling by the square root of h. The second method makes some strong assumptions about portfolio rebalancing over the risk horizon, which are not appropriate for a fixed position in a single option, and hence it ignores the crucial gamma, vega and theta effects that are very important to capture in a VaR estimate for an option.

Thereafter Section IV.5.5 considers Monte Carlo VaR based on risk factor mapping of an option portfolio. We explain how delta–gamma–vega mapping is used to revalue the option at the risk horizon and then examine the Monte Carlo VaR model for portfolios of options on several underlyings, applying a multivariate Taylor expansion for the mapping to risk factors. We conclude with a case study on the development of an appropriate risk factor returns model for a large portfolio of energy options. Section IV.5.6 summarizes and concludes.

The material in this chapter assumes knowledge of the analytic, historical and Monte Carlo VaR models described in previous chapters of this volume. Readers should also be familiar with the option theory in Chapter III.3 and the option portfolio mapping methodologies described in detail in Sections III.5.5 and III.5.6.

IV.5.2 RISK CHARACTERISTICS OF OPTION PORTFOLIOS

The value of an option is a non-linear function of its risk factors. Even if we ignore volatility and other less important risk factors, the price of an option is always a non-linear function of the underlying asset price S. This section begins by reviewing the essential details about mapping option portfolios, then we discuss the implications of non-linear risk factor mapping for VaR assessment.

IV.5.2.1 Gamma Effects

In Section III.5.5 we developed the simplest possible mapping of a single option to its price risk factor, the delta – gamma approximation. This may be written:

where R = ΔS/S is the return on the underlying asset and δ^$ and γ^$ denote the value delta and value gamma of the option.⁴ More precisely,

where N is the number of units of the underlying that the option contracts to trade and pv is the point value of the option.

The P&L of a portfolio of options on the same underlying may also be represented by (IV.5.1), but now δ^$ and γ^$ denote the net value delta and value gamma of the portfolio. For all options on the same underlying we can simply add up the value deltas to find the net value delta, and similarly the net value gamma is just the sum of the individual gammas.

When an option portfolio has several underlying price risk factors there are two alternative approaches to price risk factor mapping. Either we use a simple approximation like (IV.5.1) based on price beta mapping or we use a multivariate delta – gamma approximation. It is also possible to combine both approaches. Below we extract the relevant formulae from Section III.5.5 to summarize the possibilities.

The price beta mapping approach is described in Section III.5.5.5. It depends on representing each underlying price risk factor return R_i in terms of a single index risk factor return R. From the model derivation we know that formula (IV.5.1) still applies, but now

where and are the net value delta and gamma for each price risk factor and

Thus we perform a regression of each underlying return on an index return and use the regression betas in (IV.5.4) to estimate the value delta and gamma.

In Section III.5.5.6 we developed an alternative mapping for portfolios with several underlying price risk factors. This is the multivariate delta – gamma approximation, which takes the form

Here R = (R₁,…, R_n)′ is the vector of the underlying assets' discounted returns,

and

where P is the price of the portfolio. The multivariate mapping is more complex but more accurate than the price beta mapping approach. It is also possible to combine the two approaches using more than one index risk factor in the beta mapping, thus reducing dimensions of the multivariate delta–gamma approximation.

From our discussion in Section III.5.5.4 we know that a position with positive gamma (e.g. a long position on a standard call or put) has a convex pay-off, so that losses are less and profits are more than they would be under a corresponding linear position; and a position with negative gamma (e.g. a short position on a standard call or put) has a concave pay-off, so that losses are greater and profits are less than they would be under a corresponding linear position. An option portfolio with positive delta and gamma (e.g. a long call) gains more from an upward price move and loses less from a downward price move than a linear portfolio with the same delta. But an option portfolio with positive delta and negative gamma (e.g. a short put) will gain less from an upward price move and lose more from a downward price move than a linear portfolio with the same delta.⁵ Thus positive gamma reduces the risk and negative gamma increases the risk of an option portfolio, relative to the delta-equivalent exposure. This is termed the gamma effect on the risk of an option portfolio.

IV.5.2.2 Delta and Vega Effects

The general expression for the delta – gamma– vega approximation to the P&L of a portfolio of options, possibly on different underlyings, is

where Δσ is a vector of changes in implied volatilities, and the value delta and gamma are defined in (IV.5.7), but how is the value vega vector ν_$ calculated? Each option in the portfolio has its own implied volatility as a risk factor. So in large portfolios it is necessary to reduce the number of volatility risk factors. Typically this will be achieved by either vega bucketing or volatility beta mapping.

Under volatility beta mapping, Section III.5.6.4 explains how to calculate the portfolio's position vega, ν^P, with respect to a reference volatility such as the 3-month at-the-money (ATM) volatility or a volatility index. We use the formula

where N_i denotes the number of units of the underlying that the ith option contracts to buy or sell, ν_i denotes the vega of the ith option and is the volatility beta of the ith option. This volatility beta may be estimated by regressing the ith option implied volatilities on the reference volatility. Then, the portfolio's value vega with respect to this reference volatility is the sum of the position vegas multiplied by the point values of the options.

If the underlying price and volatility are negatively and symmetrically related, then the vega effect reinforces the delta effect for a put and offsets the delta effect for a call. To see this, first suppose the price falls dramatically, and so the volatility jumps up. Now consider these positions:

• long call – the call price decreases due to the underlying price fall, but increases due to volatility increasing, thus compensating the loss on the long position;
• short put – the put price increases due to the underlying price fall, so you make a loss on the short position, and the put price increases due to volatility increasing and this compounds the loss.

Now suppose the price increases, so the volatility decreases, and consider these positions:

• short call – the call price increases due to the underlying price increase, but the loss on the short position is offset by a compensatory decrease in the call price due to volatility decreasing;
• long put – the put price decreases due to the underlying price increase, and the loss on the long position is compounded by a decrease in the put price due to volatility decreasing.

The situation is summarized in Table IV.5.1, which shows that the delta–vega effects are most prominent in put options.

However, in stock and equity index option portfolios, there is an asymmetric negative price– volatility relationship. That is, volatility tends to increase considerably when there is a large fall in the underlying price, but following a large rise in the underlying price of the same magnitude volatility tends to decrease only a little, if at all. Thus the vega effect on a long put or short call is negligible. Therefore the most important vega effect to account for in VaR estimation is on a short put, since here it augments the delta effect. By contrast, the vega effect on a long call offsets the delta effect. The situation is summarized in Table IV.5.2, where we see that short put positions have the most pronounced delta–vega effects.

Table IV.5.1 Delta and vega effects (symmetric negative price–volatility relationship)

Table IV.5.2 Delta and vega effects (asymmetric negative price–volatility relationship)

Finally, suppose the underlying price and volatility are asymmetrically and positively related, as they often are for commodity options. That is, volatility increases considerably following a price rise, but does not decrease very much following a price fall of the same magnitude. Then the vega effect reinforces the delta effect on a long put, offsets the delta effect on a short call and is negligible for a long call or a short put. The situation is summarized in Table IV.5.3, where it is now the long put positions that have the most pronounced delta–vega effects.

Table IV.5.3 Delta and vega effects (asymmetric positive price–volatility relationship)

IV.5.2.3 Theta and Rho Effects

Here we summarize the Taylor expansions that approximate the P&L of an option portfolio when interest rate and time risk factors are included in the mapping.⁶ Later in this chapter we shall use these approximations to estimate the VaR of option portfolios.

The general expression for the delta – gamma– vega– theta– rho approximation to the P&L of a portfolio of options, possibly on different underlyings, is

where the value delta and gamma are defined in (IV.5.7).⁷ The value theta θ^$ is the sum of each position theta multiplied by the point value of the option. Since option prices generally decrease as they approach expiry, the maturity or theta effect is to increase the risk of long positions, and decrease the risk of short positions.

The value rho vector π_$ is calculated as the sum of each position rho multiplied by the point value of the option. Note that there is a curve of interest rate risk factors r unless all the options in the portfolio have the same maturity. But unless the underlying of the option is an interest rate or bond, changes in interest rates only affect the discounting of future expected pay-offs. Hence, the rho effect on portfolio risk that stems from changes in interest rates is typically very small.

IV.5.2.4 Static and Dynamic VaR Estimates

Static VaR is calculated over an h-day risk horizon on the assumption that the current portfolio is held over the next h days. Of course, when no trading takes place the risk factor sensitivities are not constant during the risk horizon. In dynamic VaR we assume the risk factor sensitivities are constant over the risk horizon. Then the portfolio must be rebalanced each time a risk factor changes.

For portfolios containing very long-dated options, and a risk horizon of only a few days, a constant risk factor sensitivities assumption is feasible even without rebalancing. Otherwise the use of constant risk factor sensitivities over the risk horizon assumes that the portfolio is rebalanced at the end of each day to return risk factor sensitivities to their values at the beginning of the day. For instance, the portfolio may be rebalanced daily to be delta–gamma neutral, or to keep the position Greeks at their limit values. When a trader operates under limits on his net value delta, gamma, vega and possibly other Greeks, it is very informative to estimate the VaR assuming the trader is at his limits.

The assumption we make about rebalancing affects the way we compute an h-day VaR, for h > 1. We shall now explain exactly how our rebalancing assumption affects the option's VaR estimate, in the theoretical context of the delta–gamma approximation (IV.5.1) of the portfolio's P&L where the underlying log returns are assumed to be normal and i.i.d. The delta–gamma mapping gives an approximate change in the portfolio value as a quadratic function of the underlying return, with coefficients determined by the value delta and value gamma of the portfolio. Our assumption that the log returns on the underlying are normal and i.i.d. implies that they scale in distribution with the square root of time. We now consider two cases.

Static VaR

Denote by R the daily log return on the underlying price risk factor. Assuming this is i.i.d. and normal, the h-day log return on the underlying price has the same distribution as the random variable h^½R.⁸ Hence, the h-day P&L on the option portfolio, as represented by the delta–gamma mapping, may be written

where δ^$ and γ^$ are the value delta and value gamma at the time that the VaR is measured.

Note that the presence of the gamma term in (IV.5.14) implies that the P&L will not scale with the square root of h, hence

We conclude that under the no rebalancing assumption it is not correct to compute the 1-day portfolio VaR of an option portfolio and simply scale this to an h-day horizon, using a square-root law or any other power scaling law. The correct procedure is to use the h-day risk factor returns to derive the portfolio's P&L distribution, and then derive the VaR.

The no rebalancing assumption has the advantage that the proper theta effect and gamma effect are captured by the VaR estimate if the position is not traded during the risk horizon. When revaluing the portfolio h days ahead, the time to expiry of each option is decreased by h days. Option prices generally decrease as they approach expiry, so the theta effect is to increase the VaR for long positions, and decrease the VaR for short positions. By contrast, the gamma effect decreases the VaR for long positions, and increases the VaR for short positions on standard options, as explained in Section IV.5.2.1.

It is easy to estimate static VaR using Monte Carlo simulations. This is because Monte Carlo VaR models are flexible enough to generate h-day log returns R_h directly. One simply obtains the structured Monte Carlo simulations using the assumed statistical model for h-day risk factor returns. The 100α% h-day delta–gamma VaR, based on the Monte Carlo approach then uses the approximation

However, there are two problems here. First, the Taylor approximation is only valid for small changes in the underlying returns, and the potential size of these returns increases with h. So is it inadvisable to apply Taylor expansion to estimate static VaR over long risk horizons. A second problem is that to adopt the assumption of no rebalancing with standard historical VaR calculations,⁹ we can only use overlapping data on the h-day risk factor returns, since non-overlapping data of frequency equal to the risk horizon are not usually available in sufficient quantity to estimate VaR accurately. But the use of overlapping data on risk factor returns will truncate the tails of the P&L distributions, as discussed in Section IV.3.2.7. This will be illustrated empirically in Section IV.5.4.

Dynamic VaR

Dynamic VaR assumes that the portfolio is rebalanced during the risk horizon to maintain constant risk factor sensitivities. If simulations are at the daily frequency, it must be assumed that the portfolio is rebalanced once a day over a period of h days, each time returning δ^$ and γ^$ to the value delta and value gamma at the time that the VaR is estimated. This type of VaR estimate is used to estimate the VaR of a dynamically hedged portfolio, or to estimate the VaR at a trader's sensitivity-based limits.

Assume that the daily log returns on the risk factors are i.i.d. Then, under the constant risk factor sensitivity assumption, the trader faces the same risk at the beginning of each day during the risk horizon. In this case, the h-day P&L for the option portfolio is just the sum of h independent and identical 1-day P&Ls. However, although i.i.d., the portfolio P&L distribution will not be normal even if the risk factor returns are, because the portfolio mapping is a quadratic and not a linear transformation of a normal variable. Hence, it may not be very accurate to scale the 1-day VaR to longer risk horizons using a square-root scaling rule. If the P&L distribution is stable then a different power law scaling rule may be applied (see Section IV.3.2) and then VaR_h,α = h^1/ξVaR_{1, α} for some constant ξ, not necessarily equal to 2.

Although the P&L of an option portfolio is definitely not normally distributed, it is sometimes assumed nevertheless that ξ = 2, and hence that

But this assumes the gamma, vega and theta effects on h-day P&L also scale with , which is not the case. The theta effect is captured by the term θΔt in the Greeks approximation, so when a 1-day horizon is scaled up to 10 days using (IV.5.17) the effect is θ/365, whereas based on a 10-day P&L it should be 10 θ/365. And even if the delta effect scales with , the gamma effect should scale with h. The vega effect is more complex: if there is asymmetry in the price–volatility relationship this is only likely to be apparent at the daily frequency, so scaling up 1-day VaR by the square root of time could be augmenting or diminishing the VaR, depending on the market, the type of option and the sign of our position.

The daily rebalancing assumption is approximate for two main reasons. First, the square-root scaling rule may not be appropriate, if it is used. Whilst the P&L of an option might conceivably have a stable distribution, it highly unlikely to be normal. Secondly, the daily P&L distribution is estimated by decreasing the maturity of each option by only 1 day and discounting the portfolio price by only 1 day, so scaling up a VaR that is estimated this way diminishes the theta effect, i.e. that option prices tend to decrease as they approach expiry. Daily rebalancing also diminishes the gamma effect, which can be considerable for short dated options;¹⁰ and it distorts the vega effect, which can be considerable for long dated options.

Over one day the underlying price and volatility tend to move much less than they would over a 10-day or longer risk horizon. Hence, when VaR is estimated over one day, and then scaled up, the gamma, vega and theta effects will be too small. As a result, we expect the VaR estimate for positive gamma positions (e.g. a long call or put option) to be greater when based on daily rebalancing than it is when we estimate VaR from a directly computed h-day P&L distribution. And the opposite is the case for positions with negative gamma.

We shall be comparing the static and dynamic VaR estimates in several empirical examples and case studies in this chapter, to highlight the effect that the assumption we make about rebalancing will have on the VaR estimate. And we shall specifically focus on this issue in Examples IV.5.3 and IV.5.7, in the context of the historical VaR model. As explained above the static VaR is more sensitive to the portfolio gamma, vega and theta than dynamic VaR. Although they are the same at the daily horizon, the two assumptions can lead to totally different VaR estimates when the risk horizon is more than a few days, and so it is important to choose the assumption that is closest to the trading practice of the particular portfolio.

IV.5.3 ANALYTIC VALUE-AT-RISK APPROXIMATIONS

This section begins with a description of the mapping of option portfolios to the underlying prices, interest rates, time – and indeed any risk factor except volatility. Mapping to volatility risk factors is quite a challenge, and is covered in the next section. We then describe how these mappings allow an analytic approximation to the VaR of an option portfolio. However, for more complex risk factor mappings, and in particular those that include volatility as a risk factor, we must estimate VaR using simulation.

IV.5.3.1 Delta Approximation and Delta–Normal VaR

For a portfolio of options on a single underlying the first order Taylor approximation to the portfolio's discounted P&L is

where δ^$ is the value delta of the portfolio and R is the discounted return on the underlying.

Since (IV.5.18) is a simple linear transformation the VaR based on (IV.5.18) is very easy to calculate. For instance, suppose the discounted h-day returns on the underlying asset are normally distributed with mean and standard deviation μ_h and σ_h. Thus

where R_h denotes the discounted h-day return on the underlying. By (IV.5.18) the approximate distribution of the h-day P&L on the portfolio is

Option pricing theory is based on the assumption that the expected return on the underlying asset is the risk free discount rate. To be consistent with this assumption we set μ_h = 0. Now, from (IV.5.20) it follows that we can apply the normal linear VaR formula given in Section IV.2.2.1 to approximate the 100α% h-day VaR of the option portfolio as

where Φ⁻¹(1 − α) is the 1 − α quantile of the standard normal distribution. In other words, the portfolio has a VaR that is approximately δ^$ times the VaR of the underlying asset.

More generally, we can apply a delta mapping to portfolios of options on several underlyings. The mapping is

where P is the portfolio price, is the vector of net position deltas and ΔS = (ΔS₁,…, ΔS_n)' is the vector of changes in the underlying prices. Equivalently,

where is the vector of value deltas and r = (R₁,…, R_n)′ is the vector of returns on the underlying prices.

This is just a linear mapping based on risk factor returns that we might assume to have a multivariate normal distribution. So, following the usual reasoning (see Section IV.1.6.3, for instance) we have

where Ω_h is the h-day covariance matrix of the discounted returns on the underlying asset. We might also assume they have a multivariate Student t distribution, as explained in Section IV.2.8, in which case (IV.5.24) would be modified to

EXAMPLE IV.5.1: DELTA–NORMAL VAR

A portfolio of options on the FTSE 100, S&P 500 and DJ Eurostoxx 50 indices has the characteristics shown in Table IV.5.4. The options are for £10 per point on the FTSE 100, $100 per point on the S&P 500 and €10 per point on the DJ Eurostoxx. Calculate the value deltas in sterling terms and hence compute the delta–normal approximation to the 1% 10-day VaR for a UK investor, under the assumption that exchange rates are constant.

Table IV.5.4 Characteristics of equity indices and their options

SOLUTION The net value deltas in sterling terms are as follows:

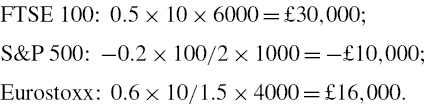
The 10-day covariance matrix of the daily risk factor returns is

and so the 10-day variance of the portfolio P&L is

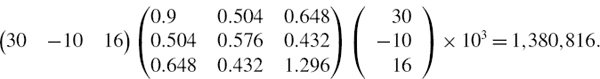
Using (IV.5.24) this gives a 1% 10-day VaR of .

Because the portfolio is assumed to be linear in the above example, we get the same answer from static and dynamic VaR estimation. That is, we get the same answer whether we assume that the portfolio is:

• rebalanced daily to maintain the current values of the net position deltas, in which case we can multiply the 1-day VaR by to get the 10-day VaR; or
• not traded during the 10-day period, in which case we base the VaR on the 10-day covariance matrix.

This is true for a linear portfolio with i.i.d. normal returns, but when we include gamma effects we obtain different results depending on the assumption about rebalancing.

Several extensions to the normal linear VaR have been described in Chapter IV.2 of this volume. We can measure the VaR and the ETL of any portfolio with a linear risk factor mapping using a Student t distribution or a normal mixture distribution, for instance. All these generalizations can be carried over to option portfolios when their risk factor mapping is the basic delta map given by (IV.5.22). However, a linear risk factor mapping such as (IV.5.22) is extremely inaccurate as an approximation for the P&L for an option portfolio. The values of most option portfolios will be a highly non-linear function of the underlying asset prices. As a result, the delta–normal VaR model should not be used, even for simple option portfolios.

IV.5.3.2 P&L Distributions for Option Portfolios

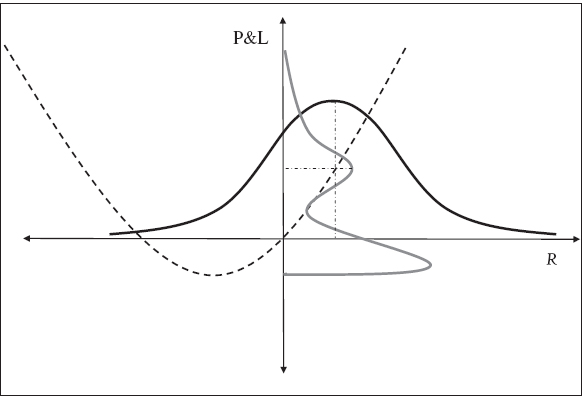
Figure IV.5.1 illustrates how the delta–gamma approximation translates the distribution of risk factor changes into a distribution of price changes for the option portfolio. We assume there is a single risk factor with return R. The distribution of R is assumed to be normal and its density is shown by the black curve. The vertical axis represents the option portfolio P&L given by the delta–gamma approximation (IV.5.1). The delta–gamma approximation is a quadratic function of R that is indicated by the dashed curve, and the option portfolio P&L density that is derived by applying this approximation to each value of R is shown by the grey curve drawn relative to the vertical axis.

Figure IV.5.1 The P&L distribution resulting from delta–gamma approximation

On the figure we have indicated the mean return, assumed positive, using a dot-dashed vertical line. We also indicate, using a horizontal dot-dashed line, that the delta–gamma approximation translates the mean return into a local maximum of the P&L density. Another local maximum is obtained when the return is negative, and this time the maximum occurs at a negative value for P&L.

The figure shows that even when we use a simple delta–gamma approximation to the portfolio P&L, its distribution is highly non-normal. This is because the delta–gamma approximation gives the P&L as a weighted sum of the return and the squared return, and if the returns are normally distributed the squared returns have a chi-squared distribution. Also, the expectation of the squared return is not zero. Hence, the expected P&L is not zero even when the expected return on the underlying is zero.¹¹ The P&L distribution induced by the delta–gamma approximation is therefore positively skewed, bimodal and may also be highly leptokurtic.

IV.5.3.3 Delta–Gamma VaR

We now derive an analytic approximation to the VaR of a portfolio of options on several underlyings. To do this we need to fit a distribution with density function such as that shown by the grey, skewed, bimodal curve in Figure IV.5.1.

Consider the h-day P&L given by the delta–gamma representation (IV.5.6), where the returns on the underlying assets have a multivariate normal distribution with covariance matrix Ω_h. Of course the option portfolio P&L will not have a normal distribution, since it includes sums of squared normal variables. But we can use (IV.5.6) to estimate the mean, variance, skewness and kurtosis of the P&L distribution, assuming the approximation (IV.5.6) is reasonably accurate.

The expectation of the right-hand side of (IV.5.6) is given by¹²

where tr is the trace of a matrix, i.e. the sum of its diagonal elements. After some calculations, we derive the following expressions for the higher moments of the distribution of the discounted P&L:

Hence, the skewness and kurtosis of the delta–gamma representation are

Although the above expressions look complicated, they allow one to calculate the mean, variance, skewness and kurtosis of the delta–gamma P&L distribution (IV.5.6) for an option portfolio with many underlyings. If we know the price risk factor sensitivities δ_$ and Γ_$ that characterize the portfolio, and the covariance matrix Ω_h of h-day returns on the underlying prices, then we can derive the moments of the P&L distribution.

Now suppose we have calculated the first four moments as explained above. How do we estimate the VaR? One possibility is to apply a Cornish – Fisher expansion to approximate a quantile from these moments using the methodology explained in Section IV.3.4.3. However, we know from our empirical studies in Section IV.3.4 that for highly leptokurtic distributions this is will not provide results that are as accurate as those derived by fitting a Johnson SU distribution to the moments. The method is illustrated in the next example. It uses Tuenter's algorithm for fitting the Johnson SU distribution, as explained in Section IV.3.4.4.¹³

EXAMPLE IV.5.2: DELTA–GAMMA VAR WITH JOHNSON DISTRIBUTION

Consider a portfolio of options on bonds and on equities with a P&L that has the delta–gamma approximation

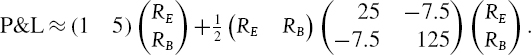
The units of measurement are millions of US dollars. Thus the net value delta is $1 million with respect to the bond index and $5 million with respect to the equity index. The value gamma matrix is also measured in millions of dollars. Suppose that the returns on the bond and equity indices are normally distributed with volatilities of 30% and 20% and a correlation of −0.25. Fit a Johnson distribution to the distribution of the portfolio P&L. Hence, estimate the 1% 10-day VaR of the portfolio and compare your result with the delta–normal VaR based on (IV.5.25).

SOLUTION We have

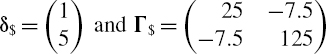
The 10-day covariance matrix of the risk factor returns is

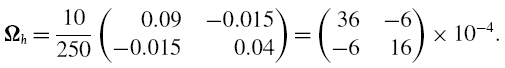
In the spreadsheet for this example we calculate the moments of the 10-day P&L distribution based on (IV.5.26)– (IV.5.31) and the results are: mean $0.150 million, standard deviation $0.256 million, skewness 1.1913, and excess kurtosis 47.153. Since the excess kurtosis is positive, we can fit a Johnson SU distribution to these parameters using Tuenter's algorithm.¹⁴ The result is a delta–gamma 1% 10-day VaR of $261,024. The corresponding delta–normal VaR is $451,096. Clearly, ignoring the gamma effect leads to considerable error when computing VaR. The portfolio has a positive gamma, so we know from our discussion in Section IV.5.2.3 that the VaR will be considerably reduced when we take the gamma effect into account.

Because it is not bimodal the Johnson distribution that was applied in the above example is not the best way to fit the first four moments of the option portfolio P&L distribution. We have used it because it is practical, and because Section IV.3.4 demonstrated that if the P&L distribution is very leptokurtic, as it is in the example, it is better than using a four moment Cornish–Fisher expansion.¹⁵ However, the P&L distribution is bimodal and highly skewed as well. The VaR at extreme quantiles is heavily influenced by the tail behaviour of the P&L distribution, and it is difficult to capture this well with any analytic approximation.

IV.5.4 HISTORICAL VALUE AT RISK FOR OPTION PORTFOLIOS

This section presents several empirical examples on the computation of historical VaR for option portfolios. We begin by studying the simplest possible portfolio: a position on a standard European option on the S&P 500 index. The position requires revaluing for every historical scenario of underlying price and volatility risk factor changes. This is easy when we just apply the Black–Scholes–Merton formula to revalue the portfolio at the risk horizon, but the portfolio revaluation can take considerable time for portfolios of exotic, path-dependent options.

We shall also discuss how to apply historical VaR to the risk assessment of path-dependent options, but since our focus is on the methodology rather than computational details, the position considered will be a simple European look-back option. Although its pay-off is path-dependent, under the constant volatility assumption we still have an analytic formula for its price.¹⁶ If numerical methods have to be applied to price a large complex option portfolio this will be very time-consuming. VaR with exact revaluation can usually be estimated overnight, but for high frequency risk assessment purposes such portfolios are often better represented by a risk factor mapping. Hence, another empirical example in this section illustrates the historical VaR approach for a portfolio of options that have been mapped to their risk factors, where all the options are on a single underlying. We then extend this to portfolios of options on several underlyings and end the section with a case study on the historical VaR for a trading book of energy options.

Various enhancements of standard historical simulation (e.g. to account for volatility adjustment, or to apply parametric filtering based on a GARCH model) that improve its accuracy have been described in Section IV.3.3. However, to include these in the empirical examples of this section – which already require quite complex Excel workbooks – would obscure the main purpose of this section. We therefore examine the application of standard historical simulation only, showing that it can usefully be applied to estimate the dynamic VaR of an option portfolio, but it is not the best VaR model to use for static options positions, except when the risk horizon is short.¹⁷

IV.5.4.1 VaR and ETL with Exact Revaluation

How does one calculate the historical VaR and ETL of an option that can be priced analytically? In this section we consider a very simple portfolio, i.e. a short position on a 30-day European put on the S&P 500 index. These options are very actively traded on the CME. Each option is for $250 per index point, i.e. the pay-off function is

where ω is 1 for a call and −1 for a put and the strike K and S&P 500 index futures price S are measured in index points.¹⁸

Data

The risk factors of this portfolio are the S&P 500 futures price, the option's implied volatility, and the 30-day US LIBOR rate. For convenience, and specifically to avoid concatenating a very long series of 30-day index futures prices, we apply variations in the spot index price to the current index futures price. This only induces a very tiny error in our calculations because the basis risk between the S&P 500 spot index and its futures contract is negligible.¹⁹ Similarly, we shall apply variations in the S&P 500 volatility index, i.e. the Vix index, to the current implied volatility of the option. This assumes the option has a volatility beta of 1 with respect to the Vix index.²⁰ Finally, for the interest rate we use the 1-month LIBOR rate.²¹

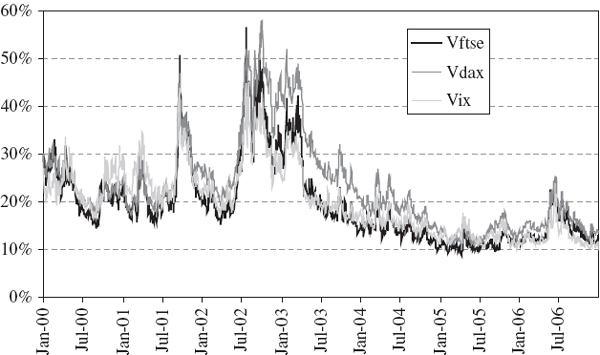
Daily data on these risk factors from 3 January 1990 until 25 April 2008 are displayed in Figure IV.5.2. The Vix and LIBOR are measured on the left hand scale and the index is measured on the right hand scale. The VaR will be measured on 25 April 2008, when the index futures price stood at almost 1400 and the Vix was at almost 20%. The main influence on the markets at this time, not just in the US but also in Europe and Asia, was the credit crunch that was precipitated by the sub-prime mortgage crisis in the US during 2007. To ease the credit squeeze, US interest rates had been cut considerably so that the 1-month LIBOR rate stood at only 2.86% at this time.

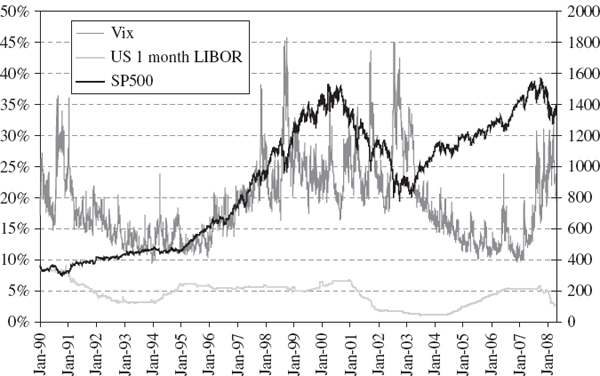
Figure IV.5.2 S&P 500 index price, Vix and 1-month US LIBOR, 1990–2008

Simulating Risk Factor Values

How should we simulate the risk factor values in the historical model? We know from our discussion in Section IV.3.2 that we need to use daily or even higher frequency returns on the risk factors so that we have enough data to measure VaR at the 99% or higher confidence level. This means that for h > 1 we have a choice between the following approaches, each having its own advantages and limitations.

(i) Estimate the VaR for a dynamically rebalanced position, and scale up the 1-day VaR estimate. This assumes that we rebalance the position each day to keep the Greeks constant.

(ii) Estimate the VaR for a static position using h-day simulations based on overlapping samples.

(iii) First estimate a parametric model for the conditional distributions of the returns in multi-step simulation, and then employ this model in the filtered historical simulation model of Barone-Adesi et al. (1998, 1999).²²

The first two approaches have the advantage of simplicity but the disadvantage of inaccuracy. In case (i) the error stems from an assumption that the position has stable, i.i.d. returns and that we know the appropriate power law for scaling,²³ and in case (ii) the error arises from the distortion of the tail behaviour of the portfolio return distribution.²⁴ The third approach is more complex than the others, requiring the estimation of a GARCH model on the position's daily log returns and the application of the statistical bootstrap for simulation over the risk horizon.

We now ask how we should model the evolution of an option's risk factor returns in the framework of standard historical simulation. We shall answer this question in the context of a 1-day VaR estimate. Given T historical daily returns (or changes) on a risk factor, the first step in historical simulation is to derive the set,

of 1-day-ahead risk factor prices. For i = 1,…, n, each price _it, is based on the current value _i of the risk factor when the VaR is measured and, under the assumption that the risk factor X_i follows a geometric process, we set

where r_it = ln(X_it) − ln(X_i,t−1) is the daily log return on the risk factor, in the historical sample, at time t. But under the assumption that the risk factor X_i follows an arithmetic process, we use the daily changes x_it = X_it − X_{i,t − 1} and simulate the risk factor prices as

Should we use arithmetic or geometric stochastic processes to model the evolution of risk factors? Since we have a European option that is priced using the Black–Scholes–Merton formula, we should assume the underlying asset price follows a geometric Brownian motion. Thus the log return on the underlying price is a normally distributed random variable, and we should simulate prices using (IV.5.32). But what about the volatility and interest rate processes? It is not entirely clear whether these are governed by arithmetic or geometric processes in the real world. However, following our empirical results in Section II.5.3.6, I would advise that we assume the real-world processes for interest rates and volatility are also geometric. Hence, in all the case studies for this section we have used simulated interest rates and volatilities that are also based on (IV.5.32). This also has the advantage that simulated volatilities and interest rates cannot be negative.

Another reason to use log returns rather than absolute changes in risk factors is that over a long historical period there could be significant trends in the risk factors. In that case, an absolute change of 100 index points (or 100 basis points) ten years ago could have had quite a different significance compared to a similar change today.

It is also convenient to use log returns since the sum of h consecutive log returns is the h-day log return. Then, for a static VaR estimate, we use the h-day log return at time t, r_hit to simulate the ith risk factor price h days ahead as

The result of the historical simulation of the underlying risk factors will be a set of 1-day ahead or h-day ahead values for the risk factors. The time ordering implicit in these values is not important, although it is important to couple the simulations of the values of different risk factors, to retain the implicit correlation between them. However, the time ordering of the returns that are used to generate these values can be important, to adjust for volatility clustering. In that case, the simulated risk factor values are generated from the volatility-adjusted returns.

Building the P&L Distribution and Estimating VaR

In the case of our simple S&P 500 option the risk factors are just the index futures price, the option's implied volatility, and the US LIBOR rate. In static VaR, the simulated values for the risk factors are used to revalue the option at the risk horizon. If the risk horizon is h days, the maturities of the simulated futures price, implied volatility and interest rate must be reduced by h days.

By way of illustration, consider a single standard European option position, and denote the price of the option at time t by²⁵

Suppose the VaR is estimated at time t = 0. Then the forward looking discounted P&L from a long position on the option in h trading days, i.e. in h^c calendar days, is

where f₀ is the current value of the option, pv is the point value for the position and r_hc is the h^c-day continuously compounded discount rate. We know everything on the right-hand side of (IV.5.35) except for the option price f_h in h trading days' (i.e. in h^c calendar days') time.²⁶ To simulate this, we apply the Black–Scholes–Merton pricing formula to a simulated pair (S_h, σ_h) of values for the underlying price S_h and for the option's implied volatility σ_h, in h trading days' time.

Taking each vector of simulated values of the risk factors in turn, we obtain the VaR estimate as follows:²⁷

• With no rebalancing (i.e. static VaR) we obtain many simulated h-day-ahead portfolio values, from which we build an empirical distribution of the h-day portfolio P&L, and discount this to today. The 100α% h-day VaR is minus the α quantile of this distribution.
• With rebalancing to constant sensitivities (i.e. dynamic VaR) we obtain many simulated 1-day-ahead portfolio values, from which we build an empirical distribution of the daily portfolio P&L, and discount this to today. The 100α% 1-day VaR is minus the α quantile of this distribution. Then, to extrapolate this figure to an 100α% h-day VaR, we apply the square-root-of-time or some other power law scaling rule.

The next example compares the application of standard historical simulation to static and dynamic VaR estimates for a single option. Note that both approaches have errors: errors in static historical VaR arise from the use of historical overlapping samples, and errors in dynamic historical VAR arise from the use of a square-root scaling law. But these errors are unlikely to affect our decision about whether to apply static or dynamic VaR measures in the first place. This decision only depends on our assumptions about the position. If we are estimating the VaR of a non-traded position we use should static VaR, and if we are estimating the VaR of a trader's limits, or of his current position (assuming it is rebalanced to maintain constant risk factor sensitivities over the risk horizon) we should use dynamic VaR.

EXAMPLE IV.5.3: STATIC AND DYNAMIC HISTORICAL VAR FOR AN OPTION

Use standard historical simulation to estimate the 1% 10-day VaR for an unhedged position on a standard European call or put on the S&P 500 index. Estimate both

• static VaR, using 10-day overlapping returns on the risk factors, and
• dynamic VaR, scaling up the daily VaR to a 10-day horizon using the square-root-of-time rule.

Consider long and short positions on a 30-day call and a 30-day put, both with strike 1400. The VaR is estimated on 25 April 2008 when the index is at 1400 and the index volatility is at 20%. For clarity, and since this will have very little effect on the result, assume the discount rate is 0%.²⁸ Use the same historical scenarios on the S&P 500 index and the Vix volatility that were used in the previous example.

SOLUTION The spreadsheet for this example generates scenarios based on the daily log returns on the S&P 500 and Vix between 3 January 1990 and 25 April 2008, as we have described above. It prices the option using each of the simulated {price, volatility} scenarios. Then it calculates the P&L as the difference between the discounted scenario price and the current price of the option. This is the P&L for a long position, and the opposite difference is the P&L for the short position. Multiplying the lower 1% quantile of the distribution of these price changes by the index point value of $250 gives the 1% 10-day VaR of the unhedged position as in Table IV.5.5.

Long positions. Since the options have only 30 days to maturity the long positions have quite a large positive gamma; the gamma effect will decrease the static VaR considerably and the application of a square-root scaling rule to 1-day VaR would underestimate this gamma effect considerably. This is why the 10-day dynamic VaR estimates for the long positions, which are based on the square-root scaling rule, are considerably larger than the static VaR estimates. However, since the simulations based on overlapping data can truncate the tails of the P&L distribution, the static VaR estimates based on overlapping data may be too low at high confidence levels (see the discussion following this example).

Table IV.5.5 1% 10-day VaR under different rebalancing assumptions

Why is the dynamic VaR for the long put so much larger than the dynamic VaR for the long call? The reason is the vega effect. The option's positive vega has the effect of offsetting the VaR for a long call, but augmenting (or at least not offsetting) the VaR for a long put, as explained in Section IV.5.2.2. The dynamic VaR is assumed to be based on a square-root scaling rule, and this could understate or overstate the vega effect, depending on the option and the risk factor characteristics. In stock index options dynamic VaR estimates tend to overstate the vega effect. This is because the daily changes in volatility have a small, negative autocorrelation and at the daily level there is a pronounced asymmetry in the index price– volatility relationship which is not present in 10-day returns (see Section IV.4.4.4). For both of these reasons, the square-root scaling rule tends overstate the vega risk of stock index options.

Short positions. We already know from the previous example that short positions on naked options are much more risky than long positions. This is why their VaR estimates in Table IV.5.5 are much larger than the VaR estimates for the long positions. The short positions have a large negative gamma, which should increase the static VaR, but in the dynamic VaR estimates the portfolio is rebalanced to keep the gamma constant over the risk horizon, so the gamma effect is diminished.

If the gamma effect were the only effect to consider we might suppose that the dynamic VaR will be less than the static VaR, and this is certainly the case for the short call, but this is not the case for the short put. Again, the reason lies with the vega effect, which we know from our discussion in Section IV.5.2.2 will augment the VaR for the short put position. Since dynamic VaR estimates overstate the vega effect in stock index options, the dynamic VaR estimate for the short put position is larger than the static VaR estimate.

We know from our discussion in Section IV.3.2.7 that a potential problem with using overlapping data to estimate static VaR in the historical model is that the tail behaviour of the risk factor returns can be distorted so that VaR estimates at extreme quantiles may be too low. On the other hand, the use of a square-root scaling rule for dynamic VaR estimates also introduces errors, because at least one of the risk factors (i.e. volatility) is unlikely to scale with a square-root law.²⁹ To illustrate these two sources of model risk, Table IV.5.6 shows the VaR estimates for the previous example, but now based on the 10% and 0.1% significance levels. Because we have a daily sample size of about 5000, there are only 500 non-overlapping 10-day P&Ls. This means that we can estimate the 10% quantile (by taking the 50th largest 10-day loss), and the 0.2% quantile is the largest loss. But we cannot measure the 0.1% quantile empirically, unless we use a statistical bootstrap, and the bootstrap merely increases the number of observations by repeating them. It introduces no new information to the data. So we only have an upper bound for the 0.1% quantile, i.e. the largest loss, which translates to a lower bound for the 0.1% VaR.

Using overlapping samples will generate about 5000 observations, but there is no new information in these data. Now it becomes possible to estimate the 0.1% quantile (as the 5th largest 10-day loss), but we would still underestimate the 0.1% quantile because the size of the 10-day losses is limited by the largest loss in the sample.

Table IV.5.6 Comparison of 10% and 0.1% 10-day VaR under different rebalancing assumptions

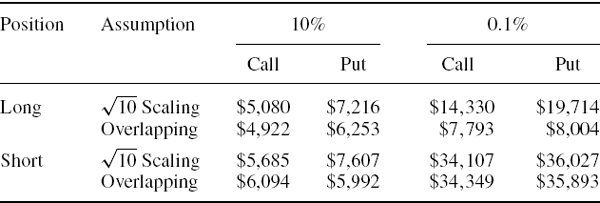
Looking at the results in Table IV.5.6, the 0.1% VaR estimates of long options exposures are far too low when based on overlapping data. This is evident from the estimates of only $7793 for the call and $8004 for the put. These 0.1% VaR estimates are not very much greater than the 10% VaR estimates! On the other hand, since we have a static position the VaR estimates based on the square-root scaling rule are too high for the long positions, and too low for the short positions, because they virtually ignore the gamma effects. They are also too high for the put relative to the call, because they overstate the vega effect, as discussed above.

In summary, there is a considerable amount of model risk in standard historical simulation when applying this methodology to measure static options VaR, even though there is no parametric model to estimate.

EXAMPLE IV.5.4: HISTORICAL VAR AND ETL OF A DELTA-HEDGED OPTION

On 25 April 2008 you sell a European put on the S&P 500 index futures with strike 1400 and maturity 30 days. The index futures price is at 1398, the market price of the option is 32, its delta is −0.4991 and its implied volatility is 19.42%. Use the historical data shown in Figure IV.5.2 to estimate the 1% 1-day VaR and ETL of the unhedged short put option position and of the delta hedged portfolio. Then compare the results with those for a long position on the put, and for both short and long positions on a call with the same strike and maturity, and the same market price as the put.³⁰

SOLUTION Note that these options are on the futures rather than the index, although we use the index to generate scenarios for the futures price as described earlier. So we price the options on the futures using each of the {futures price, volatility, interest rate} simulations.³¹ Then the unhedged P&L is calculated as the difference between the simulated option price, discounted by 1 day, and the current price of the option (i.e. 32). This is the P&L for a long position, and the opposite difference is the P&L for the short position. Multiplying the lower 1% quantile of the distribution of these price changes by the index point value of $250 gives the 1% 1-day VaR of the unhedged short put position as $6467. Clearly the VaR for naked short options position is huge, and that is why traders must hedge the options that they write.

Now consider a delta hedge that is held for a period of 1 day, offsetting the short put position by purchasing δ = −0.4980 (i.e. taking a short position) on the index futures.³² This time, the discounted price changes on the hedged portfolio are calculated for each of the historical scenarios. Multiplying the lower 1% quantile of the distribution of these price changes by the index point value gives the 1% 1-day VaR of the hedged short put position as $1873. This not small because we have not hedged the gamma or vega risk of the option.

For the ETL calculations we record the daily losses that exceed the 1% quantile of the daily P&L distribution.³³ Then the estimate of the daily ETL is the average of these excess losses, i.e. $8413 for the naked short put position and $2818 for the delta-hedged portfolio. These figures represent the expected loss given that the VaR is exceeded, so they provide some idea of the potential for extreme losses on options positions.

Now we use the spreadsheet to estimate the 1% 1-day VaR and ETL for the long put, and for a short and a long position on a call with the same strike and maturity, i.e. 1400 and 30 days, a market price of 32 and an implied volatility of 20.67%.³⁴ The results, which are displayed in Table IV.5.7, show that the long positions have much less risk than the short positions. This is because they have positive gamma. The gamma for 30-day near ATM options is relatively large, and that is why there is so much difference between the risk from going long and short these call and put options, even after delta-hedging.

Table IV.5.7 Comparison of VaR and ETL for long and short calls and puts

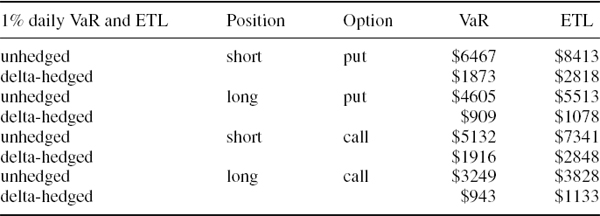
The historical P&L distribution has a very large excess kurtosis.³⁵A long position also has a large positive skewness and a short position has a large negative skewness. The ETL increases with kurtosis in the P&L distribution but decreases with positive skewness. Hence the ETL is not very much greater than the VaR for a long position, but it is substantially greater than the VaR for a short position, particularly for the delta-hedged short positions. The long positions have an ETL that is approximately 20% greater than the VaR, whereas the delta-hedged short positions have an ETL that is about 50% greater than the VaR.

This example illustrates the huge risks taken by option traders and the clear need for accurate and active hedging. The 1% 1-day VaR of the unhedged short put is $6467, relative to a position value of 32 × $250 = $7750, and at $8413 the 1% 1-day ETL exceeds the position value. However, the delta-hedged short put has much lower VaR and ETL, and this is relative to an initial position value of (32 + 0.4980 × 1398) × $250 = $182,062.

We have already mentioned, several times, that ignoring the discount rate as a risk factor would have a negligible effect on the VaR. The next example justifies this statement empirically.

EXAMPLE IV.5.5: INTEREST RATE, PRICE AND VOLATILITY RISKS OF OPTIONS

Decompose the total historical VaR of the unhedged short put position in Example IV.5.4 into the VaR due to uncertainty in the underlying price, uncertainty in volatility and uncertainty in the discount rate. Then scale these figures up, using a square-root law, to estimate the dynamic VaR over the life of the option.

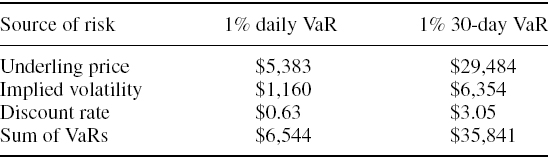
SOLUTION From Example IV.5.4 the total 1% 1-day VaR of the unhedged short put is $6467. To disaggregate this into stand-alone components we must create three separate historical simulations of the P&L where, instead of changing all three risk factors as in the previous example, we change only one of them. Thus the price risk is measured by a quantile of the P&L distribution generated by changing the underlying price but keeping volatility and discount rate constant at their current levels. Similarly, the volatility risk is measured by a quantile of the P&L distribution generated by changing the volatility but keeping price and discount rate constant at their current levels. And the interest rate risk is measured by a quantile of the P&L distribution generated by changing the discount rate but keeping price and volatility constant at their current levels. The results for the 1% 1-day VaR decomposition of the unhedged short put are shown in the first column of Table IV.5.8, and in the second column we have scaled these figures up to a 30-day risk horizon, using a square-root rule.³⁶

These results show that by far the most important risk factor for an option is the underlying price. The volatility risk is substantial but still, the stand-alone price risk is almost four times the stand-alone volatility risk. The only inconsequential risk is that due to uncertainty in the discount rate.

Table IV.5.8 Disaggregation of option VaR into price, volatility and interest rate VaRs

IV.5.4.2 Dynamically Hedged Option Portfolios

Typically option traders will hold portfolios that are delta–gamma–vega neutral. Of course, as the underlying risk factors change, the hedges will have to be rebalanced. Rebalancing too frequently will erode any profits from writing options because of the transactions costs. It is therefore common to rebalance positions on a daily basis, to set the delta, gamma and vega back to zero. But the trader still runs substantial risks; and these risks would not be detected in daily VaR calculations based on delta–gamma–vega portfolio mapping, since the delta, gamma and vega will always be zero when the VaR is measured.³⁷

To assess such risks we consider a simple European option that is gamma and vega hedged with other options on the same underlying and then delta hedged with the underlying, as explained in Section III.3.4.6. We compute the 1-day VaR of the hedged portfolio based on exact revaluation and then, assuming the portfolio is rebalanced to be delta–gamma–vega neutral at the end of each day, the 10-day dynamic VaR is estimated as times the 1-day VaR.

EXAMPLE IV.5.6: VAR AND ETL FOR A DELTA–GAMMA–VEGA HEDGED PORTFOLIO

A trader writes a standard 60-day European call on the S&P 500 index futures with strike 1400 when the current index futures is at 1398. The call has a price of 50 and an implied volatility of 22.67%. To gamma–vega hedge he buys two other S&P 500 futures options: a 30-day put with strike 1375 and a 90-day call with strike 1425. The 30-day put has price 30 and implied volatility 25.58% and the 90-day call has price 55 and implied volatility 24.38%. Using the same historical {price, volatility, interest rate} simulations that were used in Example IV.5.4, estimate the 1% 10-day VaR and ETL of the delta–gamma–vega neutral portfolio assuming it is rebalanced at the end of each day to return the delta, gamma and vega to zero. Assume the discount rate is 2.75% at all maturities up to 90 days.

SOLUTION First, gamma–vega neutral positions are computed in the spreadsheet. Then the position delta of the gamma–vega hedged portfolio is used to determine the delta hedge position on the S&P 500 index. The resulting option positions and their risk factor sensitivities are shown in Table IV.5.9.

For gamma–vega neutrality we have a position of 0.4843 on the 30-day put and 0.5472 on the 90-day call. The resulting position in all three options has a net delta of −0.5293 −0.1858 + 0.2628 = −0.4523. We assume we can buy exactly this amount of the underlying in the delta neutral hedge, so that there is no residual position risk.

Table IV.5.9 Characteristics of European options on S&P 500 futures

The spreadsheet revalues each option on every historical simulation, computes the discounted total P&L on the gamma–vega neutral portfolio, and also computes the discounted P&L on the delta–gamma–vega neutral portfolio that includes the position on the S&P 500 index futures. Since we are assuming daily rebalancing to constant risk factor sensitivities, the 10-day historical VaR for the delta–gamma–vega neutral portfolio is calculated as − times the lower 1% quantile of this P&L distribution, and the ETL is times the average of the losses that exceed the 1% quantile of the distribution.

The VaR is not zero: the 1% 10-day VaR is $871. And the 1% 10-day ETL is $968. We conclude that even when traders rebalance daily to delta–gamma–vega neutral positions they can run significant risks. This is because we have only hedged against small changes in the price and volatility risk factors. A delta–gamma–vega hedged portfolio would have a much smaller risk if it were rebalanced more frequently than once per day, but then the transactions costs could erode any benefit from hedging.

Readers may verify that the result in the above example is not unusual. Changing the options in the spreadsheet leads to similar results, i.e. the dynamic VaR for a delta–gamma–vega neutral portfolio is not insignificantly different from zero. As already mentioned, this is because the VaR estimate is based on exact revaluation: of course the dynamic VaR estimate would be zero if we based it on a delta–gamma–vega mapping, because the portfolio is rebalanced daily to set the delta, gamma and vega to zero.

IV.5.4.3 Greeks Approximation

The aim of this section is to illustrate the method for computing historical VaR when options have been mapped to risk factors. For an option portfolio on a single underlying, mapped to a single volatility risk factor, a delta-gamma–vega–theta representation allows us to approximate the price of the portfolio h trading days (and h^c calendar days) ahead as

where f₀ is the price of the portfolio today, Δt = h^c/365, ΔS is the difference between an underlying price in h trading days' time, derived from a simulated daily log return on S, and the price today, σ is the difference between the simulated volatility in h trading days' time and the volatility today, and θ^P, δ^P, γ^P and ν^P are the position Greeks of the portfolio. Now the approximate discounted P&L on the portfolio may be written

where pv is the point value for options on this underlying.³⁸

More detailed risk factor mappings could add other Greeks, such as rho (the sensitivity to changes in interest rates) or higher order sensitivities like vanna and volga. But the minor Greeks such as rho, vanna and volga usually have little effect on the portfolio VaR, as we demonstrate in this section, so delta–gamma–vega–theta mapping is often sufficient.

When using standard historical simulation for options we are always faced with the choice between, on the one hand, estimating static VaR and using overlapping data for ΔS and Δσ, and, on the other hand, estimating the dynamic VaR by basing (IV.5.37) on a risk horizon of 1 day and then scaling up the result to a risk horizon of h days. The following example illustrates the effect of this decision, and also examines the accuracy of VaR estimates based on Greeks approximations.

EXAMPLE IV.5.7: HISTORICAL VAR WITH GREEKS APPROXIMATION

Estimate the 1% 1-day and 10-day VaR of long and short positions on the put option in Example IV.5.4, and for the 10-day VaR. Assume first that the position is rebalanced daily to return the risk factor sensitivities to their values at the time the VaR is estimated, and then that the position is held static. Compare the results for a long and a short position on the put, based on delta-only, delta–gamma, delta–gamma–vega, delta–gamma–vega–theta and delta–gamma–vega–theta–vanna–volga–rho approximations.

SOLUTION In the spreadsheet for this example, the dollar Greeks are held constant and applied to the same historical {futures price, volatility, interest rate} simulations as in Example IV.5.4.³⁹ The results are displayed in the top half of Table IV.5.10. Note that the results based on exact revaluation were already obtained in Table IV.5.5, Example IV.5.4.

The ‘delta only’ VaR is imprecise because it is a linear approximation to a highly non-linear relationship. The delta only approximation behaves like a linear portfolio, and as we know from previous chapters, the VaR can be greatly affected by non-constant volatility. The put has a positive gamma and so the delta–gamma VaR for the long position is less than the VaR based on the delta only approximation. But the opposite is the case for the short put position: there were many large negative price changes in the S&P 500 futures during the historical period, and the negative gamma increases the sensitivity of the option to such moves.

The delta–gamma–vega VaR figures include the portfolio's price changes due to changes in volatility. Changes in volatility have two effects on the portfolio's VaR. One effect is that the VaR increases due to the addition of another risk factor. If this were the only effect then VaR would increase, whatever the sign of the portfolio vega. But there is a second effect that is due to the correlation between the index price changes and the volatility changes, which is negative in this case. The net effect of adding the volatility risk factor to the delta–gamma representation is therefore indeterminate; it could increase or decrease the VaR.

Table IV.5.10 Historical VaR with Greeks approximation

It is clear from our results that once a delta–gamma–vega approximation is used, adding further Greeks has little effect on the VaR. But the most striking thing about these results is that the 1% VaR based on the Greeks approximation is considerably less than the VaR based on exact revaluation. Why is this difference so large? The main reason is that the historical VaR estimate is driven by some very large changes in the risk factors during the historical period. Specifically, there were some large price rises and volatility falls which have affected the long put, and some very large price falls and volatility rises which have affected the short put. A Greeks approximation is only accurate for small changes in the risk factors.

Now consider the 10-day VaR figures in the lower part of Table IV.5.10. When we assume daily rebalancing we approximate the 10-day VaR in the spreadsheet labelled ‘Dynamic VaR’ as the square root of 10 times the 1-day VaR. Under the no rebalancing assumption, we evaluate the 10-day VaR directly, in the spreadsheet labelled ‘Static VaR’, using overlapping data. The delta–gamma VaR is again less than the delta only VaR, for a long position, and greater than the delta only VaR for a short position. But now we can see that the gamma effect is much larger in the static VaR estimate than it is in the dynamic VaR estimate. This is because the dynamic VaR captures only a very small gamma effect, over a 1-day horizon only, and this is much smaller than the gamma effect over an h-day horizon.

This example shows that if we try to estimate VaR for a static options position or portfolio, by scaling up 1-day VaR estimates to a longer risk horizon, we will seriously underestimate the gamma effect on VaR. We would also underestimate the theta effect and distort the vega effect.⁴⁰ Instead we should compute static VaR estimates, i.e. we should estimate VaR directly from the h-day P&L distribution, without scaling up a short-term VaR estimate to a longer-term risk horizon, and use exact revaluation if possible. However, the problem with using standard historical simulation here is that the tails of the h-day P&L distribution become truncated, so the VaR at extreme percentiles, and the ETL, are underestimated.

The exact revaluation of complex options without analytic expressions for the price requires a significant computational effort. Hence, it is often necessary to use a Greeks approximation to compute historical VaR. But the above example highlights a major problem with the application of Greeks approximation in the estimation of historical VaR for an option portfolio. Historical scenarios on daily changes in the risk factors are not always small changes; indeed, it is precisely the large changes in the risk factors that influence the VaR estimates, especially at extreme quantiles. Hence the application of standard historical simulation to obtain VaR estimates based on Greeks approximations is prone to imprecision.

The next example shows how delta–gamma–vega approximation is applied to estimate the VaR of a large portfolio containing options on several correlated underlyings. We consider an options trading book held by a UK bank on 31 December 2006, containing standard European options on UK, US and German stocks. The risk factors are the stock index futures and their respective volatility indices. To avoid having to concatenate constant maturity futures time series over a long historical period, we again infer the changes in the futures from the changes in the spot index. Hence, we assume the basis risk is zero, which introduces a small error in the calculation, but this is a very minor source of model risk in VaR models for portfolios of options on major indices.

Figures IV.5.3 and IV.5.4 depict the historical data that will be used in the next example. They are the daily index prices and the corresponding volatility indices, from 4 January 2000 until 31 December 2006 (a total of 1666 observations on each risk factor).⁴¹ Clearly we are estimating the VaR during a relatively tranquil period, compared with the previous examples which measured the VaR on 25 April 2008.

Figure IV.5.3 FTSE 100, DAX 30 and S&P 500 indices

Figure IV.5.4 Vftse, Vdax and Vix volatility indices

The position delta and gamma of each sub-portfolio in UK, US and German stocks may be calculated as described in Section IV.5.3.2. But the position vega is more difficult to estimate, and we refer the interested reader to Section III.5.6 for further details. In the next example we do not compute the position Greeks, and instead we start from the delta–gamma–vega representation of each sub-portfolio.

EXAMPLE IV.5.8: HISTORICAL VAR FOR OPTIONS ON SEVERAL UNDERLYINGS

A portfolio contains various options on the FTSE 100, S&P 500 and DAX 30 futures. The portfolio has not been fully hedged and the position delta, gamma for each sub-portfolio, its position vega with respect to the relevant volatility index, and the point values of the index futures options, are shown in Table IV.5.11. The mark-to-market value of the portfolio is £1 million. Based on the data shown in Figures IV.5.3 and IV.5.4, estimate the 1% 1-day historical VaR of the portfolio on 31 December 2006. Assume that the forex rates are fixed at £/$ = 0.5 and €/$ = 0.75, and that the UK LIBOR curve is flat at 5%.⁴²

Table IV.5.11 Position Greeks of large international stock option portfolio

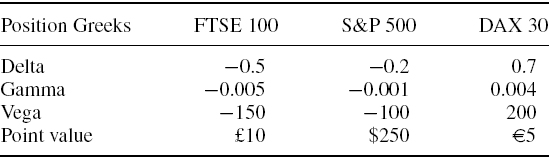
SOLUTION First we compute the value delta, value gamma and value vega for each sub-portfolio, expressing these in pounds sterling. Thus we multiply each position Greek by the point value for each index and then by the relevant forex rate. The results are shown in Table IV.5.12.

Table IV.5.12 Value Greeks of a large international stock option portfolio

Using the daily data on the equity index closing prices and their volatility indices shown, in Figures IV.5.3 and IV.5.4, we estimate VaR by taking the daily returns on the price and volatility risk factors to simulate a discounted daily P&L due to delta, delta–gamma and delta– gamma–vega approximations. The results for the 1% 1-day VaR are shown in Table IV.5.13.⁴³

Table IV.5.13 Historical VaR for a large international stock option portfolio

---

1% 1-day VaR
Delta-only	£1,493
Delta–gamma	£2,281
Delta–gamma–vega	£2,405

---

The net value gamma is large and negative, so adding the gamma effect increases the delta-only VaR considerably. In the absence of any dependence between price and volatility, the effect of adding the volatility risk factor is to increase VaR when vega is positive and to decrease it when vega is negative. In our case the net vega is negative, so adding vega risk would decrease the VaR if the price and volatility risk factors were independent. However, the price and volatility have a negative relationship, and this offsets the decrease in VaR. In fact, in our case the addition of vega risk gives a small increase in VaR.

IV.5.4.4 Historical VaR for Path-Dependent Options

The price of a path-dependent option at the risk horizon depends on the simulations of the risk factors over the risk horizon. For instance, the price of a barrier option depends on whether the underlying price has hit or crossed a barrier at any time before or at the risk horizon. This means that to assess the risk of a path-dependent product, multi-step historical simulation must be used, as described in Section IV.3.2.7.

In the following we shall use a look-back call for illustration. The price of a look-back call depends on the minimum of the underlying price between inception and maturity. Its pay-off is max(S_T − m, 0), where S_T is the underlying price at maturity T, and the strike m is the minimum underlying price achieved between the issue and the expiry of the option.

Under the assumption of geometric Brownian motion with constant volatility for the dynamics of the underlying price S, the price at time t of a look-back call on a non-dividend-paying asset is given in Section III.3.9.9. The option price is exp

where T is the expiry date of the option, F_t = S_t expr(T − t), m_t is the current strike of the option, i.e. the minimum price on the underlying achieved between the time of issue and time t, r is the discount rate of maturity T − t,⁴⁴ λ = 2rσ⁻², σ is the volatility in the underlying price process, and

EXAMPLE IV.5.9: HISTORICAL VAR FOR A PATH-DEPENDENT OPTION

Estimate the 1% 10-day historical VaR of a European look-back call on the S&P 500 index with 90 days to expiry. Suppose the current strike of the call is 1375 and that the VaR is estimated when the index price is 1400, the volatility is 20% and the 90-day US LIBOR rate is 3%. Base your calculations on the same {price, volatility, interest rate} simulations that were used in Example IV.5.4. How does the VaR for the look-back call compare with the VaR for a standard call option on the S&P 500 index with the same maturity and strike 1375? Use multi-step historical simulation on a static position in each case.

SOLUTION The current price of the look-back call is calculated using S = 1400, m = 1375,σ = 20% and r = 3% in (IV.5.38), giving the current price of the call as 114.23. The option is on the S&P 500 index so we assume its point value is $250, as it is for the CME options. Hence, the current mark-to-market value of the option is $28,558.

We now use the historical simulations to price the look-back call in 10 days' time. First we calculate the strike of the look-back call as the minimum underlying price achieved between the issue of the option and 10 days forward in time, decreasing the option's maturity by 10 days when we value it. Unless the underlying price drops below 1375 over the next 10 days, this will remain at 1375. Note that we use 10 consecutive historical price, volatility and interest rate changes when calculating this minimum price. In this way we capture the dynamic properties of the historical scenarios, including any autocorrelated changes in prices, interest rates and volatilities.

Then the 10-day discounted P&L on the option is calculated as the point value times the difference between the discounted simulated option price and the current option price. Finally, the 1% VaR is estimated as −1 times the 1% quantile of the distribution of discounted P&L. The result is a 1% 10-day VaR of only $5249 for a long position and $17,633 for a short position.

We now compare this with the VaR of a 90-day call on the S&P 500 index, with strike equal to the current strike of the look-back call, i.e. 1375. Since the underlying is currently at 1400, the call is deep in the money (ITM) and has a current price of 74.10. In the spreadsheet for this example we use multi-step historical simulation over a 10-day risk horizon, finding that the standard European call has a 1% 10-day VaR of $10,345 for a long position and $19,071 for a short position. These are greater than the corresponding VaRs for the look-back call. This is because the higher delta and the lower gamma of the standard call both augment its VaR.

The advantage of using historical scenarios to estimate the VaR of path-dependent options is that they capture the observed behaviour of the markets. Relying only on the empirical dependence between the risk factors is a clear advantage over using covariance matrices, and historical simulations also provide a natural model for autocorrelation in risk factors (in their returns and/or their squared returns) which can be an important effect to include when assessing the risks of path-dependent options. In the above example we used consecutive historical scenarios, that capture volatility clustering and autocorrelation in price and interest rate changes in an entirely natural way. This has the advantage of requiring no parametric model to capture price and volatility dynamics, but also the disadvantage that VaR at high confidence levels would be underestimated if the sample size is not sufficiently large. When VaR and ETL must be assessed at extreme quantiles and the historical sample size is not very large, then it would be better to use a parametric model such as a GARCH model for the evolution of returns over the risk horizon. That is, instead of standard historical simulation in a multi-step framework based on overlapping samples, the filtered historical simulation method that was described in Section IV.3.3.4 would be preferred.

IV.5.4.5 Case Study: Historical VaR for an Energy Options Trading Book

The case study in this section calculates the historical VaR of a portfolio of options on crude oil futures, using an exposure that represents the commodity options trading desk of a large bank, where there is at least some delta hedging with the underlying futures. In our case the risk factors will be the prices of futures with monthly maturities from 1 month to 6 months, and their ATM implied volatilities. The VaR of the trading book will be calculated on 1 August 2006 using daily closing prices from 2 January 1996 until that date, and the risk factor prices in US dollars per barrel are illustrated in Figures IV.5.5 and IV.5.6.

Figure IV.5.5 NYMEX WTI crude oil futures prices

Figure IV.5.6 NYMEX WTI at-the-money volatilities

Risk Factors

Since the Iraq war in 2003 the prices of crude oil have been tremendously volatile, from around $25 per barrel at the time of the war, rising to a high of almost $150 per barrel in June 2008 then falling back to less than $100 per barrel at the time of writing. The volatility of the futures options has fluctuated within the region of 25–60%, with peaks after the terrorist attacks in the US in September 2001 and at the outbreak of the Iraq war. Interesting features of the ATM volatility series are their huge daily variations and the many spikes in volatility; in fact the 1-month ATM volatility has so many spikes that we have omitted it from the graph. These features are apparent in many energy options.

The Portfolio

We shall examine the risk taken by a trader in crude oil options of different maturities. We assume he rebalances his portfolio to keep a net delta, gamma and vega of zero, but he has permission to trade within his portfolio up to the limits shown in Table IV.5.14. These limits reflect the belief that oil prices will fall over the next few months, since the value delta up to 3 months ahead is negative. We shall assume the portfolio is rebalanced daily over the risk horizon, to return the value Greeks to their limit values. Even though the net value delta, gamma and vega of the portfolio are all zero, the portfolio may still run substantial risks from any non-parallel movements in the futures and volatility term structures. The futures price risk factors are very highly correlated with each other, as are the implied volatility risk factors, but they are not perfectly correlated, and so some movements will be non-parallel shifts.

Table IV.5.14 Limits on value Greeks of the crude oil option portfolio

To keep the analysis simple we are ignoring the cross-gamma effects, i.e. we assume the sensitivities to the second order products of returns on futures of different maturities are zero, so we have specified only a vector for the value gamma, rather than a matrix.

Historical VaR

The calculation of the historical VaR is based on a multivariate delta–gamma–vega representation with six price and six volatility risk factors. Figure IV.5.6 shows that even though the option's volatilities were lower than average at the time VaR is measured, it is quite possible that the volatilities could jump above 40% or more, over a reasonably short time horizon. Hence, we make no volatility adjustment to the portfolio P&L series.

Since we have a dynamically rebalanced portfolio, the 1% 10-day VaR is approximated as minus the lower 1% quantile of the P&L distribution, multiplied by the square root of 10.⁴⁵ The results are shown in Table IV.5.15. Whilst the gamma risk appears to be relatively small, quite a different picture might emerge if we assumed a static portfolio over a 10-day horizon. The vega risk is substantial. In commodity option portfolios the price–volatility correlation is usually positive. Hence, the addition of the volatility risk factors increases the VaR. In this case it appears to increase the VaR substantially, because the portfolio is only hedged against parallel movements in the volatility term structure, and crude oil volatility term structures often tilt or change convexity. We shall return to this case study in Section IV.5.5.8, when we explain the use of Monte Carlo simulation to estimate the VaR of the same portfolio.

Table IV.5.15 Historical VaR of the crude oil option portfolio

Delta only	$14,103
Delta–gamma	$14,547
Delta–gamma–vega	$17,940

---

IV.5.5 MONTE CARLO VALUE AT RISK FOR OPTION PORTFOLIOS

The main purpose of this section is to demonstrate how the repricing algorithm for an option, or an option portfolio, is applied to Monte Carlo simulations. Monte Carlo has the major advantage of generating many thousands of forward looking returns on the risk factors; there are no limitations on sample size as there are with standard historical simulation. To avoid complexity, many of our examples in this section will use an i.i.d. multivariate normal risk factor log returns assumption. However, very often this distributional assumption is not appropriate, and we know from the previous chapter that many other conditional and unconditional risk factor return distributions could be applied instead. We do need to build a model for risk factor return distributions that accurately represents their empirical behaviour. So another aim of this section is to quantify the impact of the risk factor returns model on the Monte Carlo VaR estimate, and to compare this source of model risk with other sources of error, such as the error induced by the risk factor mapping.

Although options are priced in the risk neutral world, where the futures price is a martingale and therefore has zero expected return, VaR is an assessment of risk in the real world. Therefore, we need not assume that the expected return on a futures price is a martingale, or that a spot price returns the risk free rate. In particular, we need not assume that the standard deviation of the underlying returns simulations is derived from the implied volatility of the option, since the option typically has a different maturity than the risk horizon for the VaR. It is the process volatility over the risk horizon that we must use in the Monte Carlo simulations for the underlying price. The implied volatility is therefore treated like any other stochastic risk factor, having its own expected return and volatility. Simulations for the underlying price and volatility must also take account of their dependence. For instance, an equity index option price and volatility might be assumed to have an asymmetric negative dependence.

This section adopts an approach that is very similar to that in the previous section, where we first explain the VaR methodology and then derive practical, general results in the context of increasingly complex but realistic examples. The CD-ROM is not large enough to contain many thousands of correlated simulations on all the risk factors for every example. Hence, I have set each workbook to have only 100 simulations. After copying the workbook for each example, readers should extend the number of simulations by filling down the last row of the simulations, and all calculations based on these, in all the spreadsheets of the workbook.⁴⁶

IV.5.5.1 Monte Carlo VaR and ETL with Exact Revaluation

We first explain the steps involved with the computation of Monte Carlo VaR and ETL for a single-asset option assuming that the price and volatility risk factors are i.i.d. with multivariate normal distributions:

1. State the covariance matrix of the h-day risk factor returns. For instance, for a single option there are two main risk factors: the underlying price and its implied volatility. Their covariance matrix has three distinct elements: two h-day variances of the underlying and the implied volatility, and the covariance term, which depends on the price–volatility correlation.⁴⁷
2. Simulate a very large number N of uncorrelated pairs of standard normal draws. As described in the previous chapter, we take kN random numbers, where k is the number of risk factors, so k = 2 in this case, transform them into independent simulations from a standard normal distribution and arrange these into columns in Excel.
3. Use the expected returns and the Cholesky matrix to transform these columns into correlated simulations on the underlying price S_h and volatility σ_h in h trading days' time, with the targeted expected returns, volatilities and correlation. First compute the Cholseky matrix of the h-day covariance matrix.⁴⁸ Then pre-multiply each pair of uncorrelated simulations by this Cholesky matrix. Also, in the simulated data, use the discounted expected returns on the risk factor, if these are assumed to be non-zero.⁴⁹
4. Apply each simulated return to the current values of the risk factors. For instance, consider a simple option having only two risk factors, the underlying price and the implied volatility, with current values 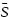and . We shall simulate N pairs {S_h, σ_h} at this stage. We often assume that the simulated returns r_Sh and r_σh on the underlying price and the implied volatility are log returns, so that

   

5. Apply the option pricing model to each set of simulated risk factor values and hence simulate a discounted P&L distribution for the option. For instance, with a simple European option apply the Black–Scholes–Merton formula to each pair {S_h, σ_h}. This gives N possible h-trading-day-ahead option prices f_h. The discounted P&L is then

   

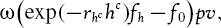
   where f₀ is the current value of the option, ω = 1 for a long position and −1 for a short position, h^c is the number of calendar days corresponding to h trading days and r_hc is the h^c-day continuously compounded discount rate. We now have N possible discounted P&L values from which we build the empirical distribution.

6. Obtain the 100α%h-day VaR and ETL. The 100α% h-day VaR is −1 times the lower α quantile of the distribution of discounted P&L and the 100α% h-day ETL is the average of all the losses that exceed –VaR.

The following example estimates the Monte Carlo VaR of the same European option on the S&P 500 index futures that was considered in the previous examples. In the workbook for this example the reader should follow through the calculation of each of the six steps above.⁵⁰

EXAMPLE IV.5.10: MONTE CARLO VAR FOR A STANDARD EUROPEAN OPTION

On 25 April 2008 you sell a European put on the S&P 500 index with strike 1400 and maturity 30 days. The index futures price is at 1398, the market price of the option is 32, and its implied volatility is 19.42%.⁵¹ Assume that the expected return on the risk factors over the next 10 days is zero, except for the futures price which we expect to have the risk free rate of return.⁵² Estimate the 1% 10-day Monte Carlo VaR for this static position using the following risk factor returns covariance matrices:

(a)the historical, equally weighted average covariance matrix for the price–volatility process that is estimated using the data shown in Figure IV.5.2;

(b)the option's implied volatility for the futures price volatility, an interest rate volatility of 15% and a volatility of volatility of 50%, a price–volatility correlation of −0.7, and the other risk factor correlations are zero.

How do the results compare with each other, and with the historical 1% 10-day VaR of the same option?

SOLUTION

(a) Using exactly the same data as in Example IV.5.4 allows some comparison between the historical simulation VaR and the multivariate normal Monte Carlo VaR for a simple option. Hence, we shall keep the discount rate as a risk factor, as we did in Example IV.5.4. This also serves to illustrate the Monte Carlo algorithm when there are more than two underlying risk factors, but otherwise we know from Example IV.5.5 that there is little point in assuming that the discount rate is stochastic, except perhaps for measuring VaR for very long term options over a risk horizon of many months, in currencies where interest rates are high.

So, the first step is to compute the risk factor covariance matrix using the historical data shown in Figure IV.5.2. This is calculated in the spreadsheet for that figure and the results are shown in Table IV.5.16.

Table IV.5.16 Historical volatilities and correlations for risk factors of S&P 500 option

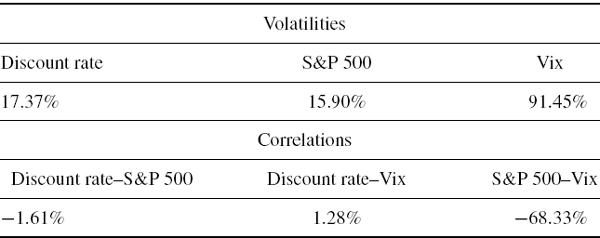
When simulations are based on the historical covariance matrix, the 1% 10-day VaR is about $18,000 based on N = 10,000 possible future values for the option. From Example IV.5.3, the 1% 10-day historical VaR of the short put based on a square-root scaling rule is $20,407. There are two reasons why this is larger than the Monte Carlo VaR.

• The first reason is that Monte Carlo VaR assumes the risk factors have a multivariate normal distribution, whereas the risk factor returns are highly skewed and leptokurtic. The multivariate normality assumption is a significant source of model risk in this case.
• The second reason is that the historical VaR in this example uses a square-root scaling rule, which distorts the gamma and vega effects. In this case both of these effects would decrease the VaR, if they were properly accounted for.

Recall that, when the 1% 10-day historical VaR is based on overlapping data, the gamma and vega effects are not distorted, but then the distorted tails of the P&L distribution depress the historical VaR estimate. The 1% 10-day historical static VaR estimate (previously calculated in Example IV.5.3) is $18,709. This is still greater than the Monte Carlo VaR estimate, because in this example Monte Carlo VaR assumes the risk factors are i.i.d. normal.

(b) We now use the option implied data to obtain the h-day covariance matrix.⁵³ This gives a 1% 10-day VaR of the written put option of around $23,500 based on N = 10,000 possible future values for the option. This is much greater than in case (a) because we are using the implied volatility in the simulations of the major risk factor, i.e. the underlying futures prices, and this implied volatility happened to be very high at the time when the VaR was measured. However, since VaR estimates are based on a real-world risk factor return distribution, there is no particular reason why we should use the implied volatility for the process volatility in the simulations, especially since the option's maturity is not the same as the risk horizon.

Recall from Table IV.5.2 that the VaR from a long option position, call or put, was very much less than the VaR from a short position on the same option. In the workbook for the above example, change the position to ‘long’ instead of ‘short’. Also change the option to a call with price 32, and therefore with implied volatility 20.67%. Based on the historical covariance matrix, the 1% 10-day VaR from buying the put option is about $7950 and that from buying the call is about $7300. Comparison with Table IV.5.16 shows that these results are similar to the historical VaR results based on overlapping data, but they are very far from the historical VaR estimates based on a square-root scaling rule.⁵⁴

The main learning point from this example is that only Monte Carlo simulation can capture the proper theta, gamma and vega effects on VaR for static option portfolios, because we can estimate the h-day Monte Carlo VaR directly from a simulated h-day P&L distribution. The overriding problem with applying standard historical simulation to static option portfolios is that we need to use overlapping samples (otherwise we do not have enough data) and, as a result, the historical model will underestimate VaR at high confidence levels.

IV.5.5.2 Risk Factor Models for Simulating Options VaR

Monte Carlo simulation of risk factor returns requires assuming some parametric form for their joint distribution. In the simplest case the risk factor dynamics are assumed to be governed by an i.i.d. multivariate normal process. Multivariate Student t simulations, which still rely on a covariance matrix to capture the highly non-linear price–volatility relationship, could also be used. And, in more general Monte Carlo frameworks, the risk factor returns could have a joint distribution with different marginals and with risk factor dependency represented by a copula. Also, multi-step Monte Carlo techniques could be applied to simulate realistic dynamic features such as volatility clustering in risk factors.⁵⁵

How important are all these ‘bells and whistles’ for Monte Carlo VaR models applied to option portfolios? It is an established empirical fact that most risk factor returns have highly non-normal, dynamic joint distributions – when returns are measured at a high frequency. But as the frequency of the returns diminishes, the distributions move closer to i.i.d. multivariate normality. In some markets, when risk factor returns are simulated over a 10-day horizon or longer, multivariate normality may not be such an unreasonable assumption to make.

The remainder of this section studies the importance of formulating an appropriate model for the risk factor return distribution, and the importance of theta, gamma and vega effects for different types of portfolio. Using a series of examples based on the same S&P 500 futures options studied in the previous examples of this chapter, we shall verify the following:

• It is important to capture non-normality in the distribution of risk factor returns, but only when risk factor returns have a horizon of no more than a few days.
• It is also important to capture the correct gamma and vega effects in static VaR.
• Asymmetric relationships between risk factors can be important for dynamic VaR estimates.
• Multi-step Monte Carlo VaR estimates should be based on a risk factor model with volatility clustering.

If any of the above features are lacking from the model that underpins Monte Carlo simulations, a substantial model risk will be introduced. However,

• the theta effect is important only when the static VaR is estimated over a very long risk horizon;
• it seems unimportant to capture non-linearity in the price–volatility relationship even for a daily risk horizon.

IV.5.5.3 Capturing Non-normality and Non-linearity

In this subsection we consider the effect of using a multivariate Student t distribution in Monte Carlo VaR. We also examine the effect on VaR of introducing non-linearity into the price– volatility relationship. Potentially, both of these effects will be important, even for a simple portfolio of vanilla options.

To use a multivariate Student t distribution for risk factor returns we simply use standardized Student t simulations rather standard normal simulations at step 2 of the Monte Carlo simulation algorithm. The risk factor returns dependency is still modelled using a correlation matrix. However, such dependency is linear and we know that price and volatility usually have an asymmetric, non-linear relationship. To capture this in the VaR estimate it is possible to derive simulations on the volatility risk factor via an estimated price–volatility model. That is, instead of using the Cholesky matrix to simulate correlated returns on two risk factors, we just take each simulated return on the underlying asset, and use an assumed or empirical non-linear relationship between price and implied volatility to infer the corresponding change in the implied volatility.

It is important to recognize that the extent of non-normality and non-linearity will depend on the frequency for the simulations (e.g. whether simulations are on daily or weekly returns). For instance, if we wish to measure dynamic VaR we should base simulations on the behaviour of the risk factor returns over a short interval such as 1 day. At this frequency the price and volatility returns could be highly non-normal and have a non-linear relationship. But if we wish to measure static VaR over a horizon of a couple of weeks or longer, the risk factor returns are likely to have distributions that are close to normality and an almost linear price–volatility relationship.

For example, consider two samples on S&P 500 index returns and the Vix between 2 January 2000 and 25 April 2008, one with daily and the other with weekly frequency.⁵⁶ The sample excess kurtosis of the S&P 500 daily log return was 2.42 and that of the S&P 500 weekly log return was 3.12. There is a highly significant leptokurtosis in both samples,⁵⁷ so it seems appropriate to model either daily or weekly log returns on the S&P 500 index price using a Student t distribution.⁵⁸ On the other hand, we saw in Section IV.4.4.4 that a nonlinear price–volatility relationship is only a feature of these data at the daily frequency, not at the weekly frequency.

One of our aims is to investigate the importance of capturing a non-linear price–volatility relationship in the VaR estimate, so we shall keep the model as simple as possible. Based on the results in Section IV.4.4.4, in the next two examples we shall apply the relationship

to each of the simulated log returns X_t on the S&P 500 index, and hence simulate a corresponding value for Y_t, the log return on the Vix. Also based on the results in Section IV.4.4.4, we assume the error has standard deviation 3.75% at the daily frequency, and standard deviation 7.5% at the weekly frequency. Now we can investigate the effect on VaR when we remove the non-linearity from the price–volatility relationship, by removing the quadratic term from (IV.5.39).⁵⁹

EXAMPLE IV.5.11: NON-LINEAR, NON-NORMAL MONTE CARLO VAR

Consider the same European option positions on the S&P 500 index futures as in our previous examples. That is, the call and the put have strike 1400 and maturity 30 days on 25 April 2008. The index futures price is at 1398, the market price of both options is 32, so the put implied volatility is 19.42% and the call implied volatility is 20.67%. Estimate the 1% daily VaR of long and short positions on the put option, and on the call option. Base your results on the non-linear model (IV.5.39) of daily log returns and then, to investigate the effect of non-linearity (i.e. an asymmetric price–volatility relationship) on the VaR estimates, drop the quadratic term from the relationship. Also, to investigate the effect of non-normality, compare the results from using price simulations from a Student t distribution with 6 degrees of freedom with those from assuming a normal distribution for daily returns on the S&P 500.

SOLUTION In the spreadsheet labelled ‘Daily P&L Simulations’, we simulate 1-day-ahead futures prices using a normal distribution for the S&P 500 daily log returns. Then we use the model (IV.5.39) to derive the corresponding log return on the Vix, and hence simulate 1-day-ahead call and put implied volatilities. Then the prices of the call and the put are computed for each set of simulated risk factors, and hence the daily P&L distribution is simulated. The 1% daily VaR for a long position is estimated as −1 times the 1% quantile of the daily P&L distribution, and the 1% daily VaR for a short position is the 99% quantile of the daily P&L distribution.⁶⁰

We then change the model (IV.5.39) to remove the quadratic term, thus assuming a symmetric linear price–volatility relationship, and proceed as before. Finally, we repeat both the above, but now we assume a Student t distribution with 6 degrees of freedom for the S&P 500 returns.⁶¹ Table IV.5.17 displays some results, based on two different sets of 5,000 simulations.⁶²

Table IV.5.17 Effect of non-linearity and non-normality on 1% daily Monte Carlo VAR

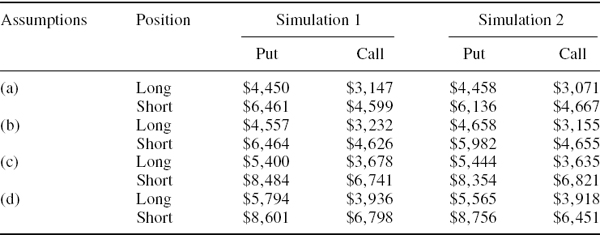
(a) Non-linear daily model, normal S&P 500 returns

(b) Linear daily model, normal S&P 500 returns

(c) Non-linear daily model, Student t distributed S&P 500 returns

(d) Linear daily model, Student t distributed S&P 500 returns.

It is to be expected that the VaR estimates based on a normal distribution for the S&P returns are less than the corresponding VaR estimates based on a Student t distribution having 6 degrees of freedom. For a long position the VaR estimates based on a Student t distribution are about 20% greater than the normal VaR estimates, and for a short position they are about 40% greater than the corresponding normal VaR estimates. This validates the assertion made in the previous section, i.e. that it is very important that the Monte Carlo VaR model captures any leptokurtosis in the underlying returns, particularly for positions with negative gamma.

Compared with the non-normality effect, the effect of using a non-linear price–volatility relationship for VaR estimation is insignificant. The non-linear model (IV.5.39) induces an asymmetric negative price–volatility relationship, so compared with the symmetric negative relationship in the linear model the VaR estimates based on the non-linear model should be slightly less for a long position and slightly more for a short position. Whilst the results in Table IV.5.17 do show these features, the differences between the non-linear and linear model VaR estimates are so small that they are well within the simulation error.

IV.5.5.4 Capturing Gamma, Vega and Theta Effects

It is not necessary to assume daily rebalancing with Monte Carlo VaR. Indeed, we did not make this assumption in Example IV.5.10 precisely because it does not capture the proper gamma, vega and theta effects for a static option position. Usually, by far the most important effect to capture is the delta effect, but this assumes a linear relationship between the option portfolio's P&L and that of the underlying. Introducing gamma, vega and theta effects allows one to build a better representation of the option portfolio's P&L distribution.

We already know the following:

• For standard options, the gamma effect decreases the VaR of a long position, and increases the VaR of a short position, and if the gamma is large (e.g. for short dated ATM options) this is the most important effect to capture, over any risk horizon.
• The vega effect depends on the price–volatility correlation. In equity markets, where there is a strong negative relationship between price and volatility (which we believe is also asymmetric but only at a high frequency) the main effect of vega risk is to increase the VaR for a short put position and indeed for any position with positive delta and negative vega, as explained in Section IV.5.2.2.
• The theta effect increases the VaR of a long position, and decreases the VaR of a short position, but this is only important when VaR is measured over a long risk horizon.

The next example compares these three different effects.

EXAMPLE IV.5.12: GAMMA, VEGA AND THETA EFFECTS IN SHORT TERM VAR

Continue the previous example, but this time compute the 1% 5-day VaR for a long and a short position on the call and the put. Compare your results based on the usual alternatives for the rebalancing of the position over the risk horizon, i.e. use

(a)the daily rebalancing assumption, where the weekly dynamic VaR is the daily VaR multiplied by the square root of 5; and

(b)the no-rebalancing assumption, where the static VaR is estimated from the P&L distribution that is derived from weekly returns on the risk factors.

In both cases assume the returns on the S&P index have a Student t distribution with 6 degrees of freedom.

SOLUTION The results are summarized in Table IV.5.18. Comparing the results in (a) with (c), and (b) with (d), we see that it does not matter much whether we use a linear or a non-linear price–volatility relationship. In either case we find that the static VaR is considerably lower than the dynamic VaR, for a long position in either the put or the call. This observation implies that the gamma effect dominates the theta effect for a long position. For the short positions, the gamma effect also dominates the theta effect. This is obvious for the short call, since its static VaR is greater than its dynamic VaR. But the VaR for the short put is also heavily influenced by the vega effect, and with a non-linear daily model the vega effect is distorted by the square-root scaling. That is, the daily rebalancing assumption is overstating the vega effect for this position, especially when based on the non-linear model, so the short put VaR estimates in cases (a) and (c) are too high.

Table IV.5.18 Student t Monte Carlo VAR with and without daily rebalancing

(a) Dynamic VaR: daily rebalancing over risk horizon, linear daily model,

(b) Static VaR: no rebalancing over risk horizon, linear weekly model

(c) Dynamic VaR: daily rebalancing over risk horizon, non-linear daily model

(d) Static VaR: no rebalancing over risk horizon, non-linear weekly model.

In the above example the options had a large gamma, because they were near ATM and relatively short-dated, and the theta effect was small because we considered only a very short risk horizon. Hence, the gamma effect dominated the VaR. The final example in this subsection demonstrates that the trade-off between gamma, vega and theta effects is quite different when we estimate the VaR for long dated options over a long risk horizon. Again we shall isolate the influence of each effect by comparing the VaR estimates under the assumptions of daily rebalancing over the risk horizon, where the VaR estimate virtually ignores theta and gamma effects and distorts the vega effects for static positions, and the VaR estimate under the static, no rebalancing assumption.

EXAMPLE IV.5.13: THETA EFFECTS IN LONG-TERM VAR

Consider a standard European option on the S&P 500 futures with 500 calendar days to maturity, a strike of 1400, and where both put and call implied volatilities are 20%. The futures price is currently at 1398, and the 1-year LIBOR rate is 3%. The put price is 126.062 and the call price is 124.143. Using the historical covariance matrix of Example IV.5.10, compare the 1% 250-day VaR estimates for long and short positions on the call and the put in turn, that are obtained by

(a)estimating the static VaR from the 250-day P&L distribution directly, and

(b)estimating the dynamic VaR from the daily P&L distribution and scaling this by the square root of 250.

SOLUTION The results are computed in the spreadsheet for this example, and the VaR estimates based on one set of 10,000 simulations are displayed in Table IV.5.19. In case (a) the 1% 250-day VaR is much greater for a long position than it is for a short position. Hence, the theta effect, which increases the VaR for long positions on standard calls and puts, dominates the gamma effect, which decreases the VaR for long positions and increases the VaR for short positions on standard calls and puts. In case (b) both theta and gamma effects are minimal, because the VaR is measured over a 1-day horizon before scaling to a 250-day risk horizon. Here there is some evidence of a small gamma effect, but the main influence on the VaR is the delta effect. That is, when the VaR of an option is measured over a daily horizon and then scaled to a longer horizon, it behaves almost like the VaR of a linear position on the underlying, and this is why the estimates for case (b) are so much greater than they are for case (a).

Table IV.5.19 Long-term VaR estimates for static and dynamic portfolios

The above example illustrates that the scaling of a daily VaR for an option portfolio to a long-term VaR produces VaR estimates that are very high indeed. If the VaR relates to a position that is truly static, so there is no trading on the option portfolio over the risk horizon, the practice of scaling short-term VaR estimates up to longer-term estimates would very seriously overestimate the risk. We re-iterate that, due to data limitations, dynamic VaR estimation is usually the only alternative that is available with the standard historical VaR model. It is only with Monte Carlo simulation, or a hybrid method based on filtered historical simulation, that we can obtain realistic estimates of VaR for a static position over a long-term risk horizon.

IV.5.5.5 Path Dependency

Our next two examples investigate whether volatility clustering and autocorrelation effects in risk factor returns are important to include in the Monte Carlo simulation model. In Section IV.5.4.4, Example IV.5.9, we investigated the use of consecutive historical returns to estimate VaR for an option with path-dependent pay-off. There we noted that an advantage of using historical simulation based on h consecutive risk factor returns is that it captures, in a simple and natural way, the complex dependencies between risk factor returns, and the autoregressive behaviour in risk factor returns (and volatility clustering in particular). But it is possible that this entirely non-parametric approach may lead to underestimation of static VaR at very high confidence levels over long risk horizons, due to historical sample size limitations.

Monte Carlo simulation is not limited in sample size, and there are no problems caused by overlap between any two simulated series of consecutive returns. Our next example illustrates the effect on VaR of moving from one-step to multi-step Monte Carlo simulations over the risk horizon. We do not introduce the effect of volatility clustering and autocorrelation in the multi-step simulations until Example IV.5.15.

EXAMPLE IV.5.14: ONE-STEP VERSUS MULTI-STEP MONTE CARLO VAR

Estimate the 1% 10-day Monte Carlo VaR of a European call on the S&P 500 index with 90 days to expiry. Suppose that the current strike of the call is 1375 and that the VaR is estimated when the index price is 1400, the implied volatility is 20% and the 90-day US LIBOR rate is currently at 3%. Hence, the current market price of the call is 74.1. Estimate the VaR of both long and short positions on this option, based on a discounted 10-day P&L distribution that is obtained:

(a)in one step, i.e. by applying the 10-day covariance matrix of the risk factor returns to Monte Carlo simulations of 10-day log returns;

(b)in multi-steps, by applying the 1-day covariance matrix of the risk factor returns to Monte Carlo simulations of 1-day log returns, summing the 1-day log returns along a path to obtain a 10-day log return.

Base your covariance matrix on the same historical data that were used in Example IV.5.9, which is the matrix shown in Table IV.5.22. In each case use the 10-day log returns to simulate values of the risk factors in 10 days' time, hence revalue the option, and simulate a P&L by taking the difference between the discounted value of the simulated option price and the current option price.

SOLUTION The workbook for this example is a modification of the workbook for Example IV.5.9. When Monte Carlo simulations are performed in one step, we obtain VaR estimates of approximately $9800 for the long call and $19,000 for the short call position. When multi-step simulations are used the Monte Carlo VaR changes only marginally, as readers can see in the spreadsheet.⁶³ The VaR is slightly less than when based on one step of normal simulations, and this makes sense since normal h-day log returns can be consistent with non-normal daily returns.⁶⁴ Forcing multi-step Monte Carlo to use normal daily returns could therefore understate the VaR.

The next example extends the above analysis to include volatility clustering and mean-reversion in volatility in the multi-step Monte Carlo VaR model.⁶⁵ Recall that Example IV.4.7 generated Monte Carlo simulations on a price risk factor whose volatility is modelled using an asymmetric GARCH process. This captures mean reversion and asymmetric volatility clustering in volatility, and the first of these effects is particularly important. We now implement a symmetric bivariate GARCH process to generate correlated price and volatility simulations, and subsequently we re-estimate the VaR of the option considered in the previous example.⁶⁶

EXAMPLE IV.5.15: GARCH MONTE CARLO VAR FOR OPTIONS

Estimate the 1% 10-day Monte Carlo VaR of a European call on the S&P 500 index with 90 days to expiry. As in Example IV.5.14, the current strike of the call is 1375 and the VaR is estimated when the index price is 1400 and the implied volatility is 20%. However, here we assume that the 90-day US LIBOR rate is constant.⁶⁷ Estimate the VaR of both long and short positions on this option, based on a discounted 10-day P&L distribution that is obtained using multi-step Monte Carlo with a bivariate GARCH model. Assume a constant price– volatility correlation of −0.8 and use the conditional variance equation parameters shown in Table IV.5.20. Compare the result with the simulations based on i.i.d. price and implied volatility log returns, with the same unconditional volatilities as those given in the last row of the table.

Table IV.5.20 Bivariate GARCH model parameters

SOLUTION The first spreadsheet in the workbook for this example generates two sets of random numbers to use for the price and the implied volatility simulations. The second spreadsheet simulates 10-day correlated returns for price and for volatility, based first on the i.i.d. assumption and then on the GARCH volatility models. For comparison, these simulations utilize the same two sets of random numbers. The third spreadsheet prices the option and derives the 10-day discounted P&L under each of the models. The parameters and results are shown in the spreadsheet labelled ‘VaR’. In this spreadsheet readers may change the size of the shock to the current price return and see the effect on the GARCH VaR. The results based on one set of 10,000 simulations are summarized in Table IV.5.21.

Table IV.5.21 Monte Carlo VaR for option based on constant volatility and GARCH

Even without a shock to the current underlying return the GARCH VaR is marginally greater than the constant volatility VaR, as expected since we have more uncertainty in the model when volatility clusters. As the size of the shock increases so does the difference between the GARCH VaR and the constant volatility VaR. As expected, the VaR of the short call is the most affected by volatility clustering. The same comment applies for a short put option, as readers can see by changing the option type in the spreadsheet.

Having discussed the importance of path-dependent behaviour in price and volatility risk factor returns, we now explain how Monte Carlo simulations are used to price path-dependent products. We shall illustrate the approach by estimating the Monte Carlo VaR of the same look-back call option that was considered in Example IV.5.9. For comparison we use a risk factor covariance matrix based on the same daily historical data as was previously used to estimate the historical VaR for this option.

EXAMPLE IV.5.16: MONTE CARLO VAR FOR A PATH-DEPENDENT OPTION

In Example IV.5.9 we estimated the historical VaR of a 90-day look-back call. The result was a 1% 10-day VaR of $5249 for a long position and $17,633 for a short position. Estimate the 1% 10-day Monte Carlo VaR of the same option under the assumption that the risk factor returns are i.i.d. and multivariate normal. Base your covariance matrix on same historical data that were used in Example IV.5.9, which is the matrix shown in Table IV.5.22.

Table IV.5.22 Risk factor covariance matrix (×10⁴)

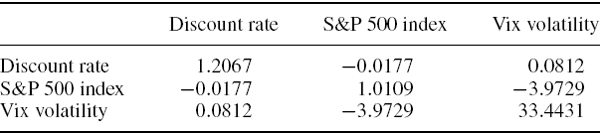
SOLUTION The general method for evaluating VaR for a path-dependent option, and the look-back call pricing formula, are given in Section IV.5.4.4. This example is similar to Example IV.5.9, with one important difference: the underlying price, volatility and interest rates that are used to revalue the option are not taken from consecutive days in a historical data set. Instead they are obtained using correlated Monte Carlo simulations.⁶⁸ Even though simulations are only over one day, we may still include a trend in each variable in the simulations, and we shall do this to ensure that we are matching the features of the historical data as closely as possible. Hence, the average daily log return on each risk factor over the historical period is added to each simulated log return. However, readers can verify, by setting them to zero, that these trends have very little effect on the result.

Each revaluation requires the simulation of daily values for all the risk factors over the next 10 days. Only this way can we find the minimum underlying price that is used to value the look-back call 10 days ahead. There is a size limit on the number of such simulations one can perform in Excel. With 5000 simulations of price, volatility and interest rate paths, the 1% 10-day VaR for this option is approximately $6,700 if long and $11,500 if short.

Thus the Monte Carlo VaR estimate of the long position on the look-back call option is higher than the historical VaR, and the opposite is the case for a short position. This is because the historical VaR captures the empirical relationship between price and volatility, which may be non-linear and not i.i.d., whereas our Monte Carlo simulations are using a simple correlation to model their relationship. In the historical data, a long call benefits from the additional effect of a volatility increase following an underlying price fall, so the Monte Carlo VaR of a long look-back call will be greater than its historical VaR. And a short call does not benefit from the offsetting effect of a volatility decrease following an underlying price rise in the historical data, so its Monte Carlo VaR will be lower than its historical VaR.

IV.5.5.6 Option Portfolios with a Single Underlying

To assess the risk of a portfolio of options, we could value each option exactly for every simulation of the risk factors. However, for large portfolios of exotic and path dependent products on several underlyings, this takes considerable computation time, especially if we wish to decompose the VaR into stand-alone components due to the underlying price and volatility market factors. For this reason a Taylor approximation to the portfolio P&L is commonly used.

In this subsection we illustrate the direct estimation of Monte Carlo VaR, with and without a risk factor mapping based on a Taylor approximation, when all the options are on the same underlying. In this case the same simulations for the underlying price can be applied to all options, but each option will still have its own implied volatility risk factor. Without a portfolio mapping, the high correlation between the implied volatilities of different options needs to be taken into account in the VaR estimate.

The following example illustrates the direct estimation of Monte Carlo VaR, without risk factor mapping, using an extremely simple portfolio containing two standard European options.

EXAMPLE IV.5.17: MONTE CARLO VAR OF STRANGLE: EXACT REVALUATION

A speculator takes a short strangle position on S&P 500 index futures options with maturity 60 days.⁶⁹ That is, he sells two 60-day options, an ITM call and an ITM put. Suppose that the call has strike 1350 and implied volatility 25%, and that the put has strike 1450 and implied volatility 20%. The 60-day US LIBOR rate is 5%, the futures price is currently at 1400 and risk factor volatilities and correlations are shown in Table IV.5.23. Estimate the 1% 10-day VaR of the short strangle position.

Table IV.5.23 Risk factor volatilities and correlations

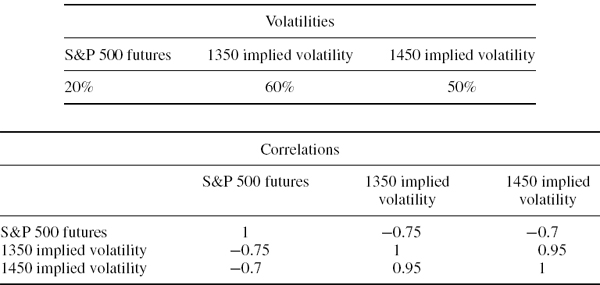
SOLUTION In this example there are three major risk factors: the underlying price and two implied volatilities. Hence, the covariance and Cholesky matrices are 3 × 3 matrices. For each triple of simulated values for {price, 1350 implied volatility, 1450 implied volatility} we calculate the discounted P&L on the strangle position by adding the discounted P&L on the call to that of the put. Since we have a short strangle position, each P&L is estimated by taking the simulated option value from the current value of the option. All prices are, as usual, calculated using the Black–Scholes–Merton formula and the current values are 83.42 for the call and 23.67 for the put.

Based on 10,000 simulations the 1% 10-day VaR estimate for the short strangle position is about $20,000. Of course, because of its strong negative gamma, a short strangle has much greater VaR than a long strangle: the 1% 10-day VaR of the corresponding long strangle is about $4500.

When a portfolio contains many options there are a very large number of risk factors, even when all the options are on the same underlying. A portfolio with n options has n + 1 major risk factors – the underlying price and n different implied volatilities – excluding the minor risk factors such as discount rates and dividends. We also know that when VaR is estimated over long risk horizons it is important to include maturity effects.

To apply Monte Carlo VaR with risk factor mapping we follow steps 1–6 of the algorithm outlined in Section IV.5.5.1, but at step 5 we revalue the position using the risk factor mapping rather than the option pricing model. For instance, under a delta–gamma–vega–theta approximation the (undiscounted) price of a single option in h trading days' time is simulated as

where ΔS is the difference between the simulated underlying price (derived from a simulated h-day log return on S) and the price today, Δσ is the difference between the option's implied volatility (derived from a simulated h-day log return on σ) and the volatility today, and δ, γ, ν and θ are the option's delta, gamma, vega and theta. Having revalued the portfolio approximately, we obtain an approximate discounted P&L which is, as before, given by (IV.5.37).

We can extend this to an approximation where there is more than one option in the portfolio, if all the options' implied volatilities are vega-mapped to a single reference implied volatility, σ. Then we simply use the net position delta, gamma, vega and theta in (IV.5.40). More generally, there may be several position vegas and implied volatility risk factors in the vega mapping, and correspondingly there will be several vega terms in the expression for the discounted P&L.

One of the advantages of Monte Carlo VaR is that we do not require a long data history. Multivariate normal or Student t Monte Carlo VaR only requires the risk factor returns covariance matrix and this could be estimated using daily returns over the past six months or even less. In fact, it need not be estimated from historical data at all. Nevertheless, in the next example we use the risk factor returns covariance matrix derived from the risk factor volatilities and correlations in Table IV.5.16, which are based on over 18 years of data. This is only because we want to compare the results from the next example with those obtained for the same portfolio using historical VaR, in Example IV.5.7. The portfolio is very simple: in fact we have just a single option on the S&P 500 index and we measure the Monte Carlo VaR based on different Taylor expansions for the change in portfolio value. The underlying risk factors are the S&P 500 index price, the Vix implied volatility index and the risk free interest rate of maturity equal to that of the option.

EXAMPLE IV.5.18: MONTE CARLO VAR WITH DELTA–GAMMA–VEGA MAPPING

Consider a European put on the S&P 500 index with strike 1400 and maturity 30 days. The index futures price is at 1398, the market price of the option is 32, its delta is −0.4980 and its implied volatility is 19.42%.⁷⁰ Use the covariance matrix derived from Table IV.5.16 to estimate the 1% 10-day Monte Carlo VaR and ETL of the option under the assumption that the risk factor log returns are i.i.d. with a multivariate normal distribution. Base the P&L on delta-only, delta–gamma, delta–gamma–vega and delta–gamma–vega–theta approximations and compare results with the historical VaR results for the same option, shown in Table IV.5.10.

SOLUTION There are three risk factors, the price, the volatility and the discount rate. By contrast with historical VaR, Monte Carlo VaR only uses the covariance matrix of the returns; all the other information in the returns is disregarded. Moreover, we shall assume that the risk factors have a multivariate lognormal distribution, so we use correlated normal simulations for the log returns on the risk factors. As well as the 10-day static VaR (derived directly from the 10-day log returns, simulated using the 10-day covariance matrix) we shall simulate daily log returns using the 1-day risk factor covariance matrix, and multiply the daily VaR estimate by the square root of 10 to obtain a 10-day dynamic VaR estimate.⁷¹

The only difference between the VaR estimates in this example and those in Example IV.5.7 is that the correlated risk factor changes used in the Taylor expansion are generated by Monte Carlo simulation, as explained above, rather than being based on historical data. The workbook has two spreadsheets for P&L calculations, one for daily P&L and the other for h-day P&L. Table IV.5.24 displays the results based on 10,000 simulations. The P&L simulations are based on various Greeks approximations, shown in the first column of this table, and taking the appropriate quantile of the simulated P&L distributions gives the Monte Carlo VaR estimates in the columns headed (a) and (b). For comparison, in columns (c) and (d) we include the historical VaR results from Table IV.5.10.

Table IV.5.24 Comparison of Monte Carlo and historical VaR

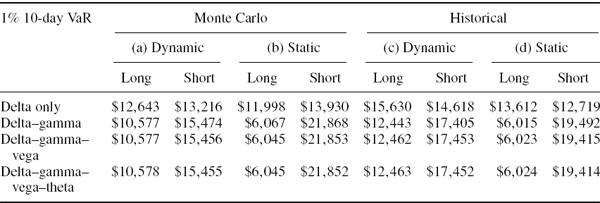
For reasons already explained, the gamma effect is much larger in the static VaR estimates than in the dynamic VaR estimates. Comparing the first two results in column (b), the 1% 10-day VaR of a long position on the put is virtually halved when the gamma effect is included, and the corresponding VaR for a short position is increased by approximately 50% when we include the gamma effect from a static position. Comparing columns (a) and (c), the dynamic Monte Carlo VaR estimates (i.e. those that assume rebalancing over the risk horizon) are less than the corresponding historical VaR estimates; this is because the empirical P&L distribution is heavy-tailed. Comparing columns (b) and (d), the static Monte Carlo VaR estimates can be greater than or less than the historical static VaR estimates. However, we know the historical VaR based on overlapping data in column (d) is likely to underestimate the risk of both long and short positions at high confidence levels, because the tail behaviour is distorted. Without this distortion the Monte Carlo estimates, being based on i.i.d. normal risk factors, would no doubt be less than the historical VaR estimates.

The most important feature of this example is the difference between the static and dynamic VaR results. It provides yet another illustration that, whilst this may be acceptable for linear portfolios, for option portfolios we cannot just scale up a 1-day VaR to an h-day VaR, using the square-root-of-time rule or some other power law for scaling, unless it is appropriate to assume the portfolio is rebalanced daily to keep its risk factor sensitivities constant over the risk horizon. For static positions we need to simulate h-day risk factor returns, and the only way we can do this without using overlapping data is to use Monte Carlo methods.

IV.5.5.7 Option Portfolios with Several Underlyings

The major risk factors of a portfolio containing options on n underlying assets are the asset prices {S₁,…, S_n}. There are also many implied volatility risk factors that are important, and these need mapping to a reduced set of implied volatility risk factors. In the simplest form of vega mapping we would assume the implied volatilities of all the options on S_i are mapped to a single volatility risk factor σ_i, so that there are only n volatility risk factors, which we denote by {σ₁,…, σ_n}.⁷² Using only the price risk factors, a multivariate delta – gamma approximation of the form (IV.5.6) may be used to approximate the P&L of an option portfolio resulting from small changes in all the risk factors. As usual, we shall illustrate the method with an empirical example.

EXAMPLE IV.5.19: MONTE CARLO VAR WITH MULTIVARIATE DELTA–GAMMA MAPPING

Consider a portfolio of options on bonds and on equities with a P&L that has the delta–gamma approximation

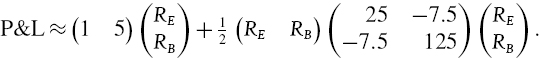
The units of measurement are millions of dollars. Thus the net value delta is $1 million with respect to the bond index and $5 million with respect to the equity index. The value gamma matrix is also measured in millions of dollars. Suppose that the returns on the bond and equity indices are normally distributed with volatilities of 30% and 20% and a correlation of −0.25. Estimate the 1% 10-day VaR of the static portfolio using Monte Carlo simulation based on a delta–gamma mapping, assuming zero discounting. How does your result compare with the Monte Carlo VaR based on a delta-only mapping?

SOLUTION The 10-day risk factor covariance matrix has the Cholesky decomposition shown in the spreadsheet, and this is applied to simulate correlated returns on bonds and equities. Then, for each pair of simulations, the delta–gamma approximation (IV.5.6) is applied; discounting this gives the delta–gamma approximation to the portfolio's 10-day P&L; then taking the 1% quantile of this distribution gives the 1% 10-day delta–gamma VaR as −1 times this quantile. Dropping the three second order terms in the delta–gamma approximation gives the corresponding VaR estimate based on delta approximation only. Averaging results over several sets of 10,000 simulations, we obtain a 1% 10-day delta-only VaR estimate that is very close to $450,000. But when based on delta–gamma approximation, the 1% 10-day VaR estimate falls to approximately $130,000.

We can compare our results with those obtained in Example IV.5.2, where we used a Johnson SU distribution to estimate the 1% 10-day VaR of this same portfolio. We found that the delta-only VaR was $451,096, which is very close to the Monte Carlo result, but the delta–gamma VaR was $261,024. Since gamma effects give rise to a highly non-normal P&L distribution for the portfolio (as seen in Figure IV.5.1), our results show that the Johnson distribution does not capture as much of a gamma effect as the Monte Carlo approach. The VaR at extreme quantiles such as 1% is very much influenced by the tail behaviour of the P&L distribution, and it is not easy to capture this with an analytic approximation.

Finally, we illustrate the use of a multivariate delta – gamma– vega approximation to estimate the VaR of an option portfolio using Monte Carlo simulation. The Taylor approximation is of the form

where the risk factor sensitivities are measured in value terms, R is the vector of returns on the underlying assets and σ is a vector of volatility risk factors. Taking a portfolio that we have already considered (in Example IV.5.8) the last example of this chapter uses a multivariate delta–gamma–vega approximation to compare the Monte Carlo VaR with the historical VaR. We shall make the following assumptions:

• Exchange rates are constant and we ignore discounting.
• The risk factor returns have a multivariate normal distribution.
• Their covariance matrix is based on the same historical data as that used in Example IV.5.7.

EXAMPLE IV.5.20: MONTE CARLO VAR WITH MULTIVARIATE DELTA–GAMMA–VEGA MAPPING

A portfolio contains various options on the FTSE 100, S&P 500 and DAX 30 futures. The portfolio has not been hedged and the position delta, the gamma for each sub-portfolio, its position vega with respect to the relevant volatility index, and the point values of the index futures options, were shown in Table IV.5.11. The mark-to-market value of the portfolio is £1 million. Assume that the forex rates are fixed at £/$ = 0.5 and €/$ = 0.75, and that the UK LIBOR curve is flat at 5%.⁷³ The volatilities and correlations of the risk factor returns, derived from the data shown in Figures IV.5.3 and IV.5.4, are given in Table IV.5.25.⁷⁴ Estimate the 10-day Monte Carlo VaR of the static portfolio.

Table IV.5.25 Risk factor volatilities and correlations

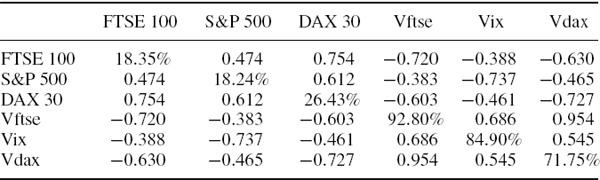
SOLUTION The workbook for this example is very similar to the workbook for Example IV.5.8, except that we have used Monte Carlo simulation instead of historical simulation to generate the 10-day returns on the price risk factors and the changes in the volatility risk factors. Table IV.5.26 compares the results, averaged over several sets of 10,000 simulations, with the historical 1% 10-day VaR results based on Example IV.5.8.⁷⁵

Table IV.5.26 Monte Carlo versus historical VaR for a large international stock option portfolio

With only a delta approximation, the Monte Carlo VaR is smaller than the historical VaR. This is because the model assumes that risk factor returns have a multivariate normal distribution, whereas their empirical distributions are in fact highly leptokurtic. But when the gamma effects are included the Monte Carlo VaR is greater than the historical VaR. This is because the historical VaR is dynamic, so it underestimates gamma effects, and in our case the gamma effect will increase the VaR because the net value gamma of the portfolio is negative.

In general the inclusion of volatility as a second risk factor would decrease the VaR of this portfolio, because the net vega of the portfolio is negative. However, the negative price– volatility correlation offsets this decrease. With a strong negative correlation between the price and volatility risk factors, such as is apparent mainly in daily data, the VaR could increase when vega effects are added. Indeed, we see this in the historical VaR estimates. By contrast, the inclusion of vega effects marginally reduces the Monte Carlo VaR, compared with the delta–gamma approximation. Well, we already know that correlation is too crude a statistical tool for capturing the empirical characteristics of the price–volatility relationship!

IV.5.5.8 Case Study: Monte Carlo VaR for an Energy Options Trading Book

In Section IV.5.4.5 we estimated the historical VaR of a portfolio of options on crude oil futures on 1 August 2006, using daily closing prices from 2 January 1996 until that date. This section calculates the Monte Carlo VaR of the same portfolio, using the same historical data to compute the risk factor model parameters. When specifying the risk factor returns model, a series of workbooks explain how we move from a basic i.i.d. multivariate normal risk factor return distribution to one that includes the features that are known to be exhibited by empirical risk factor returns.

The portfolio was characterized by its delta, gamma and vega limits, shown in Table IV.5.14. For comparison, we shall estimate both static and dynamic Monte Carlo VaR estimates, over a 10-day horizon. The dynamic VaR measures the risk if the trader stays at his limits, whereas the static VaR assumes the positions are left unmanaged for a 10-day period.

Twelve-Dimensional Multivariate Normal Distribution

Table IV.5.27 shows the correlations between daily returns on the futures (below the diagonal) and between daily changes in volatility (above the diagonal, shaded). The returns correlations are extremely high, and they decrease as the maturity gap increases, just as in any highly correlated term structure. The correlations between the implied volatility risk factor returns are lower than the correlations between the price risk factor returns, although they do increase with the options' maturities.

Table IV.5.27 Risk factor correlations

The full 12 × 12 covariance matrix of price returns and volatility changes may be used to simulate values for the option portfolio; to these we apply a delta–gamma–vega mapping, and from the simulated P&L distribution we estimate the portfolio VaR. Unlike historical simulation, we are not constrained to assume the portfolio is rebalanced to constant risk factor sensitivities over the risk horizon. We may assume this, for instance if we want to estimate the VaR of the portfolio if the trader stayed at the limits shown in Table IV.5.14. Alternatively, we can examine the risk of an unmanaged ‘static’ portfolio, keeping the holdings constant over the risk horizon, and in that case we would simulate h-day risk factor changes to obtain a distribution for h-day P&L.

In workbook (a) the spreadsheet labelled ‘Static’ uses the Cholesky matrix of the h-day covariance matrix to simulate multivariate normal risk factor changes and then applies the risk factor mapping for the h-day P&L; and the spreadsheet labelled ‘Dynamic’ uses the same random numbers but applies the Cholesky matrix of the 1-day covariance matrix to obtain the daily P&L distribution. Then the results are shown, along with the (adjustable) holdings for the portfolio, in the sheet labelled ‘VaR’. Some results for a 1% 10-day VaR based on 10,000 simulations are shown in Table IV.5.28, and the results from the historical VaR case study in Section IV.5.4.5 are also shown for comparison.

Table IV.5.28 Monte Carlo VaR of the crude oil option portfolio

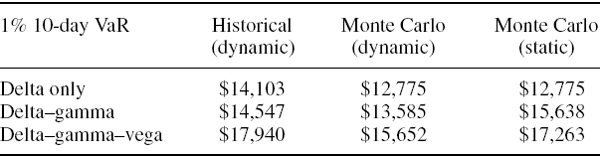
The delta-equivalent Monte Carlo VaR is the same under the rebalancing (dynamic) or no rebalancing (static) assumptions, because the delta-only VaR assumes the portfolio is linear. The historical VaR figures in the first column may be compared with the Monte Carlo VaR estimates for a dynamic portfolio. Due to the normality assumption, the Monte Carlo model underestimates the delta-equivalent VaR, relative to the historical VaR.

The size of the gamma effect is about the same in both of the dynamic models, but much larger in the static model, for reasons we have discussed many times in this chapter. The influence of the vega effect is more difficult to predict. In this case it is large according to the historical model, but smaller in the Monte Carlo models, again because these assume multivariate normality when other distributions for volatility changes would be a better choice. The static Monte Carlo model predicts the smallest vega effect of all, but since this also has the largest gamma effect the delta–gamma–vega Monte Carlo static VaR estimate lies between the VaR estimates from the two dynamic models.

The i.i.d. multivariate normal Monte Carlo model cannot represent many important empirical characteristics of the market, and so it should be improved to allow non-normal risk factor returns. For example, the multivariate Student t, mixture or copula distributions for underlying returns would be a better choice than a multivariate normal. The risk factor returns model should also be extended to allow for volatility clustering, as we know this has an important influence on results in markets such as this.

In practice, it is not easy to use better statistical models for the risk factor returns of such large portfolios, because the price and volatility risk factors are so numerous. A typical energy options portfolio will have many different future prices as underlyings, and each underlying will have a whole surface of associated implied volatility risk factors. Hence, using advanced dynamic statistical models for risk factor return distributions in the simulations can become complex and time-consuming. How much accuracy would be lost if we applied standard techniques such as principal component analysis and vega mapping to reduce the dimension of the risk factor space? This would achieve a very effective reduction in dimensionality if the trader is trading right across the term structure, but how accurate will the results be?

Principal Component Analysis

The high correlations between crude oil futures returns indicate that little accuracy would be lost by using PCA to reduce the dimension of the price risk factor space. We now show that the VaR computations may be simplified, with very little loss of accuracy, by simulating the values for two or three principal component factors rather than the entire term structure of futures prices. Additionally, using PCA has the advantage of identifying the main sources of risk. That is, we can decompose the VaR into components corresponding to trends, tilts and convexity changes in the term structure of futures prices.

The results of applying PCA to the 10-day historical covariance matrix are obtained in workbook (b) and are displayed in Tables IV.5.29 and IV.2.30. Since the eigenvalues scale with h, the eigenvalues of the daily covariance matrix are one-tenth of the values shown in Table IV.2.29. This eigenvalue analysis shows that the first principal component alone explains over 97% of the total variation in the futures prices over the historical period. One might be tempted to represent the futures price returns using only one component, i.e. to assume the returns are perfectly correlated along the term structure. Alternatively, using two principal components in our delta–gamma representation does not assume the returns are perfectly correlated in our simulations, which is more realistic, and hardly any accuracy will be lost because the two components together explain 99.58% of the historical variation in the system. We shall report results using first one and then two components in the representation.

Table IV.5.29 Eigenvalues of 10-day historical covariance matrix for crude oil futures

The normalized eigenvectors that generate the first two components are shown in Table IV.5.30.⁷⁶ Note that the first eigenvector, which captures the common trend in the futures term structure, is not a parallel shift.

Table IV.5.30 Normalized eigenvectors for first two eigenvalues in Table IV.5.29

ω1	ω2
0.48457	0.80597
0.44399	0.05473
0.40981	−0.14720
0.38441	−0.26294
0.36371	−0.33402
0.34651	−0.38084

---

The eigenvectors are used to compute the net value delta and gamma of the portfolio with respect to the first two principal components. The net value deltas are given by⁷⁷

where is the value delta on the i-month futures, shown in Table IV.5.14, and w_ij is the ith element of the j th eigenvector shown in Table IV.5.30.

Even though the value gammas in Table IV.5.14 ignored the cross-gamma effects, so we only had a vector rather than a matrix of value gammas with respect to the futures prices, we cannot ignore cross-gamma effects in the principal component representation. The net value gammas with respect to the first two components and their cross-gamma are given by

where is the value gamma on the i-month futures, shown in Table IV.5.14.

Given these formulae, we can now calculate the net value deltas and gammas corresponding to the two principal components as

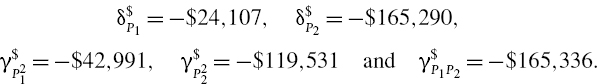
This shows that although the portfolio has a net value delta of zero and a net value gamma of zero, the portfolio is not immune to the most likely movements in the futures term structure. The most common movement, i.e. the common trend, is represented by the first eigenvector, and this is not a parallel shift. The large exposures to the second component, a tilt, reflects the fact that these movements, which ensure the futures prices are less than perfectly correlated, explain less than 3% of the historical movements.

The advantages of using PCA in Monte Carlo simulations are the identification of the key risks in a portfolio, the reduction in dimension of the risk factor space and the use of orthogonal risk factors. It is simple to translate the deltas and gammas with respect to the futures price changes into deltas and gammas with respect to the principal components, and it is straightforward to simulate values for two orthogonal components, with variances given by the first two eigenvalues shown in Table IV.5.29.⁷⁸ Then we just apply the delta-only or delta– gamma mapping to the principal components, with the value delta and gamma shown above, to simulate the portfolio P&L distribution.

Table IV.5.31 reports the 1% 10-day VaR based on independent normal, and then independent Student t, simulations of the principal component risk factors. For comparison, a common set of random numbers is used to generate the results, which are based first on the net delta and then on the net delta-gamma representation of the portfolio. First we assume daily rebalancing to the limit values, and so we can compare our results with the centre column of Table IV.5.28, i.e. $12,775 for the delta-only VaR and $13,585 for the delta–gamma VaR. Then we assume the portfolio is static, so we can compare our results with those shown in the last column of Table IV.5.28, i.e. the same delta-only VaR but $15,638 for the delta–gamma VaR.

The first two columns of Table IV.5.31 report the 1% 10-day VaR of the portfolio when the futures prices are assumed to be perfectly correlated, and represented by the common trend component with eigenvector w₁ in Table IV.5.30. The second two columns present the same results but modified with the addition of a second component. Comparison with our earlier results shows that the delta-only VaR is substantially underestimated unless we use both components. Only then are they capturing the essential features of dynamic and static VaR estimates. And, as expected, the use of a leptokurtic distribution for the principal components increases the VaR. The results shown in Table IV.5.31 are for 6 degrees of freedom in the Student t distribution. The further enhancement of the simulations for two principal components, for instance to include volatility clustering, is left as an exercise to the experienced reader.

Table IV.5.31 Monte Carlo PC VaR for the portfolio of crude oil options

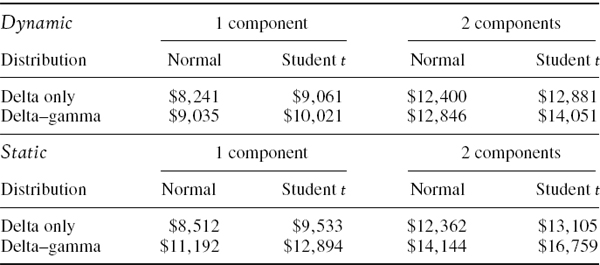
Vega Mapping

We now turn to the problem of the volatility risk factors. Should we reduce the dimension of this risk factor space, and if so how? The original mapping of vega to ATM implied volatilities is already introducing a considerable model risk. What sort of additional modelling errors might be introduced by using only one or two volatility risk factors in total?

We already know that PCA on volatilities is unlikely to work as well as it does for the price risk factors, because the ATM implied volatilities are not as highly correlated as the prices. Readers could try applying PCA to the volatilities, but if we aim to reduce dimensions in this way (as we did for the price risk factors) there will be large approximation errors. So to illustrate a different type of mapping now – which could also have been applied to the price risk factors, as explained in Section III.5.5.5, though perhaps with less success than the principal component mapping – we shall use a volatility beta mapping, as explained in Section III.5.6.4.

An ad hoc choice of the 3-month volatility as the reference volatility is made. Although it may be advisable to use volatility betas relative to this reference volatility that are more risk sensitive than OLS estimates, we can quickly look at the performance of the simple volatility OLS beta estimators

where Δσ_i denotes the i-month ATM volatility. If these perform badly relative to the historical model, it may not be worth the effort trying to refine this approach with more sensitive beta estimates. The volatility beta estimates based on the entire historical sample are shown in Table IV.5.32. The differing sizes of these betas reflects the lack of correlation in the behaviour of the implied volatilities.

Table IV.5.32 Volatility beta estimates relative to 3-month volatility

Given these volatility beta estimates, the net value vega of the portfolio relative to the 3-month reference volatility is given by

where denotes the value vega of the portfolio relative to the i-month volatility, shown in the last column of Table IV.5.14. Workbook (c) for this case study calculates the net vega for the portfolio as −$70,700.

Then we use the sample standard deviation of the 3-month implied volatility to simulate normally distributed changes in the reference volatility risk factor, and apply the vega adjustment based on these changes and the net value vega. It then proceeds in a similar fashion to workbook (a), which contains the 12-dimensional multivariate normal risk factor model, but replaces the volatility part of the model by the volatility beta mapping. The 1% 10-day VaR results are shown in Table IV.5.33.

Table IV.5.33 Influence of vega mapping on VaR for a portfolio of crude oil options

(a) Twelve-dimensional multivariate normal i.i.d. returns, dynamic portfolio

(b) Six-dimensional multivariate normal i.i.d. price returns, vega mapping, dynamic portfolio

(c) Twelve-dimensional multivariate normal i.i.d. returns, static portfolio

(d) Six-dimensional multivariate normal i.i.d. price returns, vega mapping, static portfolio.

For both static and dynamic portfolios, the application of the vega mapping underestimates the vega effect. This is to be expected, since we have reduced the uncertainty in the model by reducing the number of volatility risk factors. It may be worth investigating whether the use of a more risk sensitive volatility beta vector would improve the accuracy of these results.

IV.5.6 SUMMARY AND CONCLUSIONS

Option portfolios range from small baskets of vanilla options on the same underlying asset to very large collections of complex products on many underlying assets. Usually option portfolios that are held by banks are managed to be delta neutral. It is the banks' business to accept risks, for instance by writing options, because they know how to hedge them. Banks need to assess the risks they are taking before and after hedging. But the numerous empirical examples in this chapter have shown that it is all too easy for risk managers to produce highly inaccurate measurements of the risks that face option traders. Even the accurate estimation of VaR for a simple basket of vanilla options on a single underlying is a difficult task that must be properly designed, as we have taken care to demonstrate in this chapter. Readers should not underestimate the very significant investment of resources necessary to implement a VaR model that is capable of producing accurate estimates for all the options positions in a large bank.

This chapter has addressed the problem of measuring the risk of option portfolios using both direct valuation and risk factor mapping. We know that risk factor mapping of any type of portfolio provides a useful method to allocate portfolio risk to different sources and to hedge these risks. And for option portfolios there is another reason to use risk factor mapping: it reduces the computation time taken for VaR calculations of complex portfolios. However, risk factor mapping of option portfolios is far less accurate than risk factor mapping of other portfolios. There are two main reasons for this. Firstly, it is based on Taylor approximation. But this is only accurate for small changes in the risk factors, and VaR is a loss in the lower tail of the portfolio return distribution, so large changes in risk factors are required to estimate it. Secondly, typical option portfolios have a huge number of risk factors. The underlying price and the implied volatility are the main risk factors for each individual option but, even if all the options are on the same underlying, we have a whole volatility surface as risk factors. Hence, we must use techniques to reduce the number of volatility risk factors, and this introduces further inaccuracies into the Taylor approximation.

Positive gamma reduces VaR and negative gamma increases VaR, relative to the delta-only VaR. We call this the gamma effect. To be more precise, when the net value gamma is positive the portfolio's VaR based on a delta–gamma approximation is less than its VaR based on a delta approximation, irrespective of the sign of delta. The opposite is the case when the net value gamma is negative. Similarly, adding a volatility risk factor increases VaR if the net value vega is positive, and reduces VaR if the value vega is negative. But the vega effect is more complex, because the net effect of adding vega risk to the mapping depends on the price–volatility correlation as well as the sign of vega. For instance, when the net position vega is positive and the price–volatility correlation is also positive (e.g. in commodity options) the delta–gamma–vega VaR will exceed the delta–gamma VaR. But when the net position vega is positive and the price–volatility correlation is negative (e.g. in equity options) there are two effects of opposite sign so the delta–gamma–vega VaR may be greater than or less than the delta–gamma VaR. Finally, since option prices generally decrease as the option approaches expiry, the maturity effect increases the risk of long positions and decreases the risk of short positions. However, this theta effect only has a significant influence on VaR for long-term option portfolios when risk is assessed over a risk horizon of a few weeks or more.

It is possible to approximate the VaR of an option portfolio analytically, but these approximations are not very accurate. The simplest (and least accurate) of these is the delta – normal VaR, which is a normal linear VaR model. Here a normal distribution for the underlying asset returns translates into a normal distribution for the delta approximation to the option portfolio's P&L. The delta–gamma approximation is not linear, so a normal distribution for the underlying asset returns does not translate into a normal distribution for the delta–gamma approximation to the option portfolio's P&L. In fact the P&L distribution resulting from the delta–gamma approximation is often bimodal, and highly positively skewed and leptokurtic. The moments of the distribution can be computed directly from the delta and gamma of the portfolio, knowing only the covariance matrix of the underlying asset returns. We showed how to fit a Johnson distribution to the moments and hence estimate the VaR. However, by comparing the result with the Monte Carlo VaR based on delta–gamma approximation, we find that the analytic approximation is not able to capture the tail behaviour that is so important for VaR estimation.

Most of the text in this chapter has focused on the historical VaR and Monte Carlo VaR models as applied to individual options and option portfolios. We have illustrated each point in an empirical example or case study, and the CD-ROM contains almost 30 interactive workbooks for this chapter alone. To reduce the size of the workbooks containing Monte Carlo simulations, readers will need to fill down all simulations and calculations after copying the file to the hard drive. Also, for clarity, no enhancements for advanced sampling and variance reduction have been applied. Our purpose in the Monte Carlo section of this chapter is to identify the effects that different choices of risk factor model are likely to have on our VaR estimates, rather than on the accuracy of our simulation results.

We have been very careful to state the assumptions about rebalancing that are implicit in the way we scale the VaR for an option portfolio. There are two alternatives. First, we could compute the dynamic VaR, i.e. the VaR of a dynamically rebalanced portfolio which is traded at the end of each day over the risk horizon, to return the risk factor sensitivities to their original values at the time the VaR is estimated. For example, this type of assumption is relevant if we wish to estimate the VaR of a portfolio that was at its trading limits. Then, if the risk factor returns are i.i.d., the same risk is faced every day during the risk horizon. In this case we can compute 1-day VaR, and scale this to an approximate h-day VaR using the square-root-of-time rule or some other power scaling rule.

The other alternative, applicable when we have a fixed position such as a single structured product, is to assume the portfolio is not traded during the risk horizon. We call this the static VaR. Then the correct way to estimate an h-day VaR is to use h-day risk factor returns in the simulation. We have shown, using many numerical examples, that scaling up a daily VaR estimate to a longer risk horizon would seriously distort the theta, gamma and vega effects if the portfolio is not traded during the risk horizon.

The dynamic and static VaR estimates are the same for a linear portfolio when the risk factor returns are i.i.d., but they are not the same for an option portfolio. For this reason, we must be very clear about what type of VaR estimate we require – static or dynamic. This choice depends on the trading environment, and on the purpose of the VaR estimation.

Standard historical simulation is suited to dynamic VaR estimation, but its application to static VaR estimation is limited. The problem with historical simulation is the sample size constraint: there are insufficient historical data to obtain accurate estimates of extreme quantiles, which is exactly what we need for VaR estimation. So if a standard historical VaR model is applied to an option portfolio we must either assume we have a dynamic portfolio that is rebalanced daily over the risk horizon, to keep its risk factor sensitivities constant, and therefore scale up the daily VaR using some power law; or, for a static portfolio, we must use overlapping h-day returns on the risk factors in the simulation. However, the use of overlapping data distorts the tail behaviour in the risk factor return distribution. For these reasons standard historical VaR is not recommended for static VaR estimation for option portfolios. The model needs to be augmented using a parametric model of volatility clustering, as in the filtered historical simulation model of Barone-Adesi et al. (1998, 1999).

For dynamic VaR estimation standard historical simulation has one distinct advantage over Monte Carlo simulation, and this is that it captures the empirical dynamic properties and non-linear dependence between risk factors in a simple and very natural fashion. There is no need to build a complex dynamic model for risk factor returns, as there is with Monte Carlo simulation. However, we know from the previous chapter that Monte Carlo simulation is flexible enough to be adapted to many multivariate distributions, and to include dynamic properties such as volatility clustering and mean reversion in risk factor returns. We have demonstrated empirically that volatility clustering in price risk factors is a very important effect to capture for accurate VaR estimates of option portfolios.

Monte Carlo VaR is also applicable to both dynamic and static portfolios, and therefore provides a means to compare the impact that our portfolio rebalancing assumption has on the VaR estimates. Static portfolios have more pronounced gamma, vega and theta effects. However, capturing these effects with a Greeks approximation to the portfolio P&L should be done with caution, since the risk factor changes over the risk horizon could be too large to be compatible with a local approximation.

This chapter has contained a sequence of progressively more sophisticated empirical examples. We have computed VaR using analytic approximations, historical simulation and Monte Carlo simulation for a standard European option, an option with path-dependent pay-off, a hedged portfolio, general portfolios of options on the same underlying asset and, finally, portfolios of options on several underlying assets. We have demonstrated that the risk of unhedged short options positions is very much greater than the risk of unhedged long options positions, and that even delta-gamma-vega hedged portfolios could have a fairly large VaR when they are not continually rebalanced. Moreover, some hedged portfolios are only hedged against certain types of movements in risk factors. For instance, the net value Greeks of our portfolio of crude oil options were all zero. But this only hedges the portfolio against parallel movements in the term structures of crude oil futures prices and implied volatilities, whereas non-parallel movements are actually very common. Thus a portfolio can run some very significant risks even when it appears to be fully hedged.

A certain degree of estimation risk, linked to sample size limitations, is usually unavoidable in historical VaR model. But estimation risk in Monte Carlo VaR is something that we can do our best to eliminate because simulation errors can be controlled by advanced sampling techniques. So the main source of model risk in Monte Carlo VaR stems from an inappropriate model of the risk factor returns. The chapter ends with a detailed case study that demonstrates the effect that different risk model enhancements are likely to have on the Monte Carlo VaR estimates for an energy option portfolio. The multivariate i.i.d. normal model has been used as a benchmark against which to measure the loss of accuracy induced by reducing the dimension of the underlying price and implied volatility risk factor space.

¹ BCBS (2006, p. 196) states that ‘Banks are expected to ultimately move towards the application of a full 10-day price shock to options positions or positions that display option-like characteristics.’

² Section IV.3.3.4 explains how filtered historical simulation applies the statistical bootstrap to combine a parametric dynamic model for portfolio returns with standard historical simulation.

³ This is the only subsection where we consider the ETL of an option portfolio. Once VaR has been estimated, obtaining the ETL estimate is straightforward. See Sections IV.2.10 and IV.3.6 for further details.

⁴ These are also called dollar delta and dollar gamma by some authors. We use the value delta and value gamma because they are additive across different options. Position Greeks are only additive when the portfolio contains options on only one underlying, but value Greeks are additive for any option portfolio. For VaR assessment, we assume the returns are discounted, so that (IV.5.1) represented the discounted P&L.

⁵ Similarly, an option portfolio with negative delta and positive gamma (e.g. a long put) gains more from a downward price move and loses less from an upward price move than a linear portfolio with the same delta. But an option portfolio with negative delta and negative gamma (e.g. a short call) will gain less from a downward price move and lose more from an upward price move than a linear portfolio with the same delta.

⁶ Again the material here is drawn from Chapter III.5 to which readers are referred for further explanation.

⁷ Higher order Taylor approximations for the volatility risk may be used, such as the delta–gamma–vega–vanna–volga approximation. However, this commonly has little effect on the VaR of the portfolio. See Example IV.5.5 for an empirical illustration.

⁸ See Section I.3.3.11 for further details.

⁹ That is, in the absence of some parametric filtering based on a dynamic model for portfolio returns.

¹⁰ For large price moves VaR tends to decrease for positions with positive gamma but increase for positions with negative gamma. However, daily price variations are smaller than h-day price variations for h > 1, hence the gamma effect is diminished by the use of dynamic VaR.

¹¹ Since we have omitted the theta effect, a zero realized return would lead to a zero realized P&L; but a zero expected return does not give a zero expected P&L.

¹² Note that option pricing usually assumes each underlying assset is expected to return the risk free rate, i.e. that the expectation of the discounted return is zero. Hence E(R) = 0. Also note that the gamma matrix is symmetric, so that it is equal to its transpose. If a delta–gamma–theta approximation is used the theta term should be added to the trace here.

¹³ The P&L, X, of an option portfolio when approximated with a delta–gamma representation often has a positive skewness as well as a positive excess kurtosis. In this case, we fit a Johnson SU distribution to − X and compute the VaR from the upper tail of the fitted distribution. Note that if the excess kurtosis is negative we cannot use the Johnson SU distribution, but other types of Johnson distribution are available. See Mina and Ulmer (1999).

¹⁴ But since the skewness is positive we fit the Johnson distribution to the distribution with a mean of −$0.150 million and a skewness of −1.913 and estimate the VaR from the upper tail of this distribution.

¹⁵ A six-moment Cornish–Fisher expansion has been considered by some authors, but the tail behaviour of the distribution is still unlikely to be well represented.

¹⁶ Many exotic options such as Asians and barrier options also have analytic price approximations. See Section III.3.9.9 for the look-back option pricing formula.

¹⁷ As already stated, this is because simulations cannot be based on overlapping h-day risk factor returns because the tail of the portfolio return distribution will be truncated, leading to imprecision of VaR estimates at high levels of confidence.

¹⁸ The CBOE S&P 500 index options contract is for $100 per index point, but trading volume on this contract is minor compared to the trading volume on the CME contract. European and American index options are priced on the index futures contract with the same maturity as the option. See Section III.3.6 for further details.

¹⁹ See Alexander and Barbosa (2007).

²⁰ Both index and index volatility data may be downloaded from Yahoo! Finance: symbols ∘GSPC and ∘VIX.

²¹ These data may be downloaded from the British Bankers' Association website. See www.bba.org.uk.

²² This approach is described in Section IV.3.3.4.

²³ Option portfolios have volatility as a major risk factor and so their returns are unlikely to scale by the square-root-of-time rule. See Section IV.3.2.4 for a discussion of this point.

²⁴ See Section IV.3.2.2 for an explanation why overlapping h-day returns produces a truncation of the tail.

²⁵ Here the option strike is K and its maturity date is T, the underlying price is S and its implied volatility is σ. We know that the discount rate r is such a minor risk factor that in the following we shall assume this is the same for all maturities.

²⁶ In our empirical examples, to avoid counting calendar days for different assumptions about the risk horizon (measured in trading days) we shall either assume the discount rate is zero or that h^c =h. This introduces only a very small error in the VaR calculations, since even ignoring the discount rate completely has a negligible effect on the VaR for option portfolios, as demonstrated in Example IV.5.5.

²⁷ Since we are only considering one-step historical simulation here, the simulated risk factor prices, and hence also the simulated portfolio P&L data, could be displayed in any order, provided only that the risk factor price series are ‘shuffled’ as one if the ordering is changed. That is, the changes in price, volatility and interest rate on a given day must remain linked. The reason is that the connection between price and volatility is incredibly important: an increase in volatility is far more likely to occur on a day when the price jumps than on a day when the price remains constant.

²⁸ Readers can change this in the spreadsheet, but note that we maintain some simplifying assumptions, i.e. that the changes in the relevant continuously compounded discount rate are identical to the changes in the discretely compounded 1-month discount rate and that the number of trading days in the risk horizon is equal to the number of calendar days. The errors that these assumptions introduce are very small.

²⁹ As demonstrated empirically in Section IV.3.2.4.

³⁰ You will need to back-out the implied volatility for this call using Goal Seek or Solver, as shown in the spreadsheet. Readers can change the spreadsheet to compute the VaR of other European call or put options. Just input the strike and maturity and read off the VaR, but first follow the Goal Seek instructions to compute the correct implied volatility.

³¹ This time, use the historical data on the 1 month US Treasury bill as a proxy for movements in the 10-day continuously compounded discount rate.

³² Of course we cannot sell a non-integer number of futures, but we shall not consider the consequent position risk here.

³³ As before, the P&L is discounted by 1 day, although this has very little effect on the daily ETL.

³⁴ When you change cell B14 of the spreadsheet labelled ‘VaR’ to a call option, do not forget to apply Goal Seek or Solver to compute the correct implied volatility.

³⁵ The excess kurtosis is 5.11 for the unhedged put, 7.37 for the unhedged call, 17.51 for the hedged put and 15.88 for the hedged call. This is the same for long and short positions. For long positions the skewness is 1.08 for the unhedged put, 1.45 for the unhedged call, 2.69 for the hedged put and 2.52 for the hedged call. For short positions, multiply the skewness by −1.

³⁶ For simplicity, we also use 30 calendar days for the discounting.

³⁷ Similarly, the delta-only approximation to the VaR of the delta-hedged portfolio in Example IV.5.4 would be zero. Yet with exact re-valuation, the 1% 10-day VaR of the delta-hedged portfolio is $1,198.

³⁸ We have ignored a second term f₀(exp(−r_hch^c/365) − 1) on the right-hand side, since this is negligible unless h is very large, so it will not affect the accuracy of the Greeks approximation.

³⁹ For simplicity, in the static VaR calculations we assume h^c/365 h/250 so that for the 10-day VaR, Δt = 0.4 instead of 0.3836. The theta effect is so small here that this approximation leads to inconsequential errors.

⁴⁰ The vega and theta effects are small for this particular option and risk horizon, but would not be small for long term ATM options held over long risk horizons.

⁴¹ In Figure IV.5.3 the S&P index is measured on the right-hand scale and the FTSE 100 and DAX 30 indices are measured on the left-hand scale. All data were downloaded from Yahoo! Finance except for the Vftse index, which was calculated from option prices by my PhD student Stamatis Leontsinis.

⁴² So that there is no forex risk and no interest rate risk on the portfolio. Note that these fixed values can be changed by the user.

⁴³ In the spreadsheet readers may scale up the daily VaR estimates to longer horizons using the square-root scaling rule, bearing in mind that the theta, gamma and vega effects will be distorted if the position is in fact static. See Section IV.5.4.1, and Example IV.5.3 in particular.

⁴⁴ This also changes with time t but, like volatility, we assume it is constant for the derivation of the price formula.

⁴⁵ And to reduce complexity we ignore the discounting, since this has only a minor effect on the VaR over a 10-day period.

⁴⁶ For your convenience I have also switched from automatic to manual calculations. With manual calculations just press F9 to repeat the simulations.

⁴⁷ We could also include the discount rate, but this is a very minor risk factor. We shall keep the discount rate as a risk factor for our first empirical example in this section, but since the simulation error is so large, there seems no point in increasing the size and complexity of the subsequent workbooks by keeping the discount rate risk as a risk factor. Hence we shall assume this is constant from Example IV.5.10 onward.

⁴⁸ This requires the Excel add-in ‘Matrix.xla’.

⁴⁹ As already mentioned, although options are priced in the risk neutral measure we assess risk in the physical or real-world measure. Hence, the drift used in the simulations should be the real-world expected return. We could assume that the underlying price returns the risk free rate, but we need not do so in the real world. Also, the implied volatility may be assumed to have an expected return of zero. But our assumption about expected returns usually makes very little difference, since market VaR is typically measured (at least initially) over short risk horizons.

⁵⁰ In the spreadsheet the uncorrelated simulations are row vectors, so we post-multiply the row vector by the transpose of the Cholesky matrix, which is equivalent to step 3.

⁵¹ To compute the VaR of other European call or put options copy the option price and volatility calculations to a different spreadsheet. Even when calculations are set to manual the simulations will be repeated when you apply Solver or Goal Seek to derive the new implied volatility. I recommend you to calculate the implied volatility in another workbook, and close any workbooks that are using Monte Carlo simulation before doing so.

⁵² VaR is estimated in the real-world measure, not the risk neutral measure in which of course a futures price would be a martingale.

⁵³ Thus the 10-day variance of the futures price is σ²/25 where σ is the option's implied volatility, the 10-day variance of the implied volatility is ξ²/25 where ξ is the assumed volatility of volatility, the price–volatility covariance is σ ξ/25 where is the assumed price–volatility correlation, etc.

⁵⁴ In fact, the historical VAR estimates based on overlapping data are slightly less than the Monte Carlo estimates. The i.i.d. normal assumption may lead one to suppose that the Monte Carlo VaR estimates will be less than the historical VaR estimates, but the use of overlapping data truncates the tails of the historical h-day risk factor return distribution. This truncation can lead to a significant underestimation of the historical static VaR for option portfolios over long risk horizons and at very high confidence levels.

⁵⁵ See Sections IV.4.3.1 and IV.4.4.1.

⁵⁶ Data downloaded from Yahoo! Finance, symbol ∘GSPC and ∘VIX.

⁵⁷ The approximate standard errors for skewness and excess kurtosis are 6n^−1/2 for the skewness and 24n^−1/2 for the excess kurtosis, where n is the sample size.

⁵⁸ Based on a sample excess kurtosis of 2.42, the method of moments estimate of the degrees of freedom in a Student t distribution for S&P 500 daily log returns is 6.48. Similarly, the weekly return distribution has degrees of freedom parameter 5.92, for an excess kurtosis of 3.12. For simplicity, we shall assume the degree of freedom parameter is 6 for both daily and weekly log returns.

⁵⁹ For simplicity we assume the error process is normally distributed in each case.

⁶⁰ Because the P&L for a short position is minus the P&L for a long position.

⁶¹ To generate results for the assumption that the returns are normally distributed, just set the degrees of freedom parameter in the ‘Risk Factor Simulations’ spreadsheet to about 200. Remember to press F9 to recalculate, when the automatic calculation option is turned off.

⁶² Of course, with only 5000 simulations there is a considerable sampling error in these results, but the workbook is already very large. Readers may like to increase the number of simulations when they have loaded the workbook on to their hard disk.

⁶³ Excel may have size problems extending all simulations in all spreadsheets so I recommend that only 5000 simulations are used in this spreadsheet. Notice that our estimates are quite close to the historical VaR estimates that were based on multi-step simulation in Example IV.5.9. Those estimates were approximately $10,300 for the long call and $19,000 for the short call position.

⁶⁴ Even when they are skewed and leptokurtic, if we sum h consecutive daily log returns we obtain an h-day log return that has an approximately normal distribution. Provided only that they are i.i.d., the central limit theorem holds, as explained in Section I.3.5.2. Normality ‘kicks in’ very quickly so, for example for h =10, a normal approximation for the log return distributions is often appropriate even though daily log returns may be far from normal.

⁶⁵ Mean-reversion in underlying prices is often negligible, so we shall ignore this.

⁶⁶ Following Example IV.4.7, readers should find it relatively straightforward to extend Example IV.5.1.5 to an asymmetric bivariate GARCH process if required.

⁶⁷ This assumption helps to simplify the workbook, and it make little difference to the results because stochastic discount rates have only a very small effect on 10-day VaR.

⁶⁸ Here we are using correlated i.i.d. simulations simply because the workbook would become too complex if we used a bivariate GARCH process for volatility clustering, as in the previous example.

⁶⁹ See Section III.3.5 for a description of the strangle and other options strategies.

⁷⁰ To compute the VaR of other European call or put options copy the option price and volatility calculations to a different spreadsheet. Even when calculations are set to manual, simulations will be repeated when you apply Solver or Goal Seek to derive the new implied volatility, and it will take a very long time unless you use another workbook!

⁷¹ That is, the position is first assumed to be held static, and then assumed to be rebalanced daily to return the risk factor sensitivities to their values at the time the VaR is measured.

⁷² Of course, many other methods of vega mapping are possible (see Section III.5.5.2 for further details) and we adopt this simple mapping here only because our purpose is to illustrate the Monte Carlo VaR methodology, not the pros and cons of different vega mappings.

⁷³ But as usual, these can be changed in the spreadsheet.

⁷⁴ In this table volatilities are along the diagonal and correlations are on the off-diagonals.

⁷⁵ The historical VaR estimates are times the figures displayed in Table IV.5.13.

⁷⁶ We use eigenvectors that are normalized to have unit length, i.e. the sum of the squared elements of each eigenvector is one. Note that these eigenvectors are invariant under scaling the covariance matrix. Also, the diagonal matrix of eigenvalues Λ is recovered using the spectral decomposition, i.e. Λ = W′ΩW, as demonstrated in the spreadsheet labelled ‘PCA’. This is important, since these eigenvalues are the variances of the principal components in the simulations, and without such normalization the futures returns that are implicit in the simulations will not have the correct variance.

⁷⁷ This is mathematically the same as mapping deltas and gammas under price beta mapping. See Sections IV.5.2.1 and III.5.5.5 for further details.

⁷⁸ In general, we could of course use more than two principal components if this is needed for an acceptable degree of accuracy.