Now that you are familiar with lists and queues, it's time to move on to describing stacks. You are probably familiar with some real-world examples of stacks: Plates are usually stacked—you place the first one on the shelf and add to the top. If you need a plate, you remove the top one first. The newspapers at your local convenience store are stacked, as are the books on your desk that you've been meaning to read.
Stacks can also be used to implement a simple Most-Recently-Used (MRU) cache and are often used for parsing programming languages.
This "everything stacks" chapter will familiarize you with the following topics:
What stacks are
What stacks look like
How you use stacks
How stacks are implemented
We start by introducing the basic operations of a stack. We then cover the tests required to validate the correctness of any stack implementation. Finally, you'll look at the most common form of stack, based on a list.
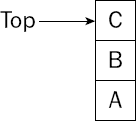
A stack is like a list with access restricted to one end. Figure 5-1 shows a graphical representation of a stack.
You'll notice that whereas lists and queues are usually thought of as running from left to right, stacks are pictured vertically—hence, the term "top" to refer to the first and only directly accessible element of a stack. A stack both inserts (pushes) and deletes (pops) from the top.
A stack is also known as a last-in-first-out (LIFO) queue, as it guarantees that the next element removed will be the one that has been on the stack for the least amount of time.
Table 5-1 describes the operations provided by a stack.
Table 5.1. Operations on a Stack
Operation | Description |
|---|---|
| Adds a value to the top of the stack. The size of the stack will increase by one. |
| Deletes and returns the value at the top of the stack. The size of the stack will decrease by one. Throws |
| Obtains the number of elements in the stack. |
| Returns but does not delete the value at the top of the stack. Throws |
| Determines whether a stack is empty. Returns |
| Deletes all elements from a stack. The size of the stack is reset to zero. |
Pushing a value on a stack adds it to the top. Figure 5-2 shows what happens when the value D is pushed onto the stack shown in Figure 5-1.
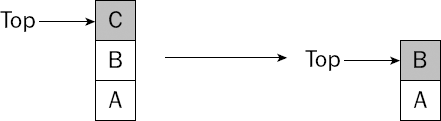
Popping a value from a stack removes it from the top. Figure 5-3 shows what happens when a value is popped from the stack shown in Figure 5-1.
The last three operations—peek(), isEmpty(), and clear()—are technically provided for convenience, as they can all be implemented on top of the first three.
Now take the operation definitions and convert these into a combination of Java interfaces and tests:
package com.wrox.algorithms.stacks;
import com.wrox.algorithms.queues.Queue;
public interface Stack extends Queue {
public void push(Object value);
public Object pop() throws EmptyStackException;
public Object peek() throws EmptyStackException;
public void clear();
public int size();
public boolean isEmpty();
}The Java interface is quite simple because of the relatively small number of operations. The two methods pop() and peek() both declare that they throw an EmptyStackException anytime an attempt is made to access a stack that has no elements, so you also need to define this exception class as well:
package com.wrox.algorithms.stacks;
public class EmptyStackException extends RuntimeException {
}Note
Notice that, like the EmptyQueueException from Chapter 4, it has been defined as extending RuntimeException. This is because we consider it to be indicative of a programming error—an error in the application logic. There is no legitimate reason that one of these should ever occur during the normal course of application execution, and as such you don't want to force the developer to have to needlessly catch them.
Lastly, note that the Stack interface extends the Queue interface. That's because, as previously discussed, a stack is really a LIFO queue (and you'd like it to be plug-compatible as such), with enqueue() and dequeue() acting as synonyms for push() and pop(), respectively.
Now we can proceed to create the test cases necessary to ensure the correct operation of a stack. You will define separate test cases for each of the push(), pop(), peek(), and clear() methods. The size() and isEmpty() methods have no explicit tests of their own because they are tested as part of the others just mentioned.
Although we will only describe one stack implementation in this chapter, it is entirely possible to create your own variations. For that reason, you will create a generic test class that can be extended by concrete test classes specific to each implementation.
The stack interface is very simple, as reflected in the small number of test cases. Still, it is important not to become complacent and presume that due to the simplicity, no testing is required.
You also need to ensure that any attempt to call pop() on an empty list results in an appropriate exception being thrown:
public void testCantPopFromAnEmptyStack() {
Stack stack = createStack();
assertEquals(0, stack.size());
assertTrue(stack.isEmpty());
try {
stack.pop();
fail();
} catch (EmptyStackException e) {
// expected
}
}This test pushes the three values B, A, and C onto the stack and then pops them off one at a time, ensuring that they are removed in the correct order: C; then A; and finally B.
After first ensuring the stack is empty, you attempt to pop a value. If the call to pop() is successful, you fail the test because this is incorrect behavior—you shouldn't be able to pop from an empty stack. If instead an EmptyStackException is thrown, the stack is working as expected.
To test peek, you push two values—C and then A—and ensure that not only does peek() return the last value pushed—in this case, an A—but also that nothing has been removed from the stack as a consequence:
public void testCantPeekIntoAnEmptyStack() {
Stack stack = createStack();
assertEquals(0, stack.size());
assertTrue(stack.isEmpty());
try {
stack.peek();
fail();} catch (EmptyStackException e) {
// expected
}
}Last but not least, you confirm that clear() performs as expected and removes all elements from the stack:
public void testClear() {
Stack stack = createStack();
stack.push(VALUE_A);
stack.push(VALUE_B);
stack.push(VALUE_C);
assertFalse(stack.isEmpty());
assertEquals(3, stack.size());
stack.clear();
assertTrue(stack.isEmpty());
assertEquals(0, stack.size());
try {
stack.pop();
fail();
} catch (EmptyStackException e) {
// expected
}
}
}Although you could try to implement a stack from first principles, there is really no need to. Instead, in the same way you did during the chapter on queues, you can take advantage of the fact that a list provides you with everything you need to implement a stack.
You'll see that it is trivial to implement a stack based on the methods already provided by a list. This being the case, anything you could implement with a stack could be done with a list instead. However, by using a specific construct for the purpose, you enforce a clean separation between the concept of a list and that of a stack. This separation of concerns is critically important when designing software.
Having chosen to use a list to implement the stack, you now need to decide how best this can be achieved. You have a few options here: Enhance an existing list implementation, extend an existing list implementation, or create a new class altogether.
Each of these solutions has pros and cons. Enhancing or extending an existing implementation would be trivial—you would simply have the class implement the Stack in addition to the List interface, and add the methods necessary to satisfy the requirements of a stack. However, this approach has one major drawback: Given that there are at least two known, and no doubt countless unknown, list implementations, you would need to repeat the process for each different type of list you wished to use. Clearly, this is not a particularly elegant solution.
Your other option, and the one discussed here, is to write an entirely new class, ListStack, that uses composition. That is, your new class will hold and wrap an instance of a list. This has a number of advantages, not the least of which is that, if implemented wisely, your stack should be capable of operating on top of any type of list you choose, with no code changes.
At this point in the book, it should be clear to you how important we deem tests to be, so as always, we need a concrete test class:
package com.wrox.algorithms.stacks;
public class ListStackTest extends AbstractStackTestCase {
protected Stack createStack() {
return new ListStack();
}
}Pushing a value onto the stack is as easy as adding to the end of the list:
public void push(Object value) {
_list.add(value);
}
public void enqueue(Object value) {
push(value);
}The only thing this class needs to hold is a list to use as the underlying data structure. A linked list has been used because it is very efficient at adding and removing items from the ends—something a stack does. Having said this, you could easily substitute an array list without much worry. The main thing to understand is that rather than extend a particular list implementation, you've instead used composition to "wrap" a list. This prevents the list methods from "leaking" out, which may cause users of your ListStack class to believe that they can use the methods on the list interface as well as those defined for the stack.
As you can see, push() just adds the value to the underlying list, while enqueue() simply delegates to push().
Notice also that you haven't checked for a null value here because you can delegate that responsibility to the underlying list implementation.
The performance of push() and pop() as implemented here relies entirely on the performance of the underlying list's add() and delete() methods, respectively.
The peek() method allows access to the value at the top of the stack without removing it:
public Object peek() throws EmptyStackException {
Object result = pop();
push(result);
return result;
}To complete the class, you can delegate the remaining methods to the underlying list, as the expected behavior is identical:
public void clear() {
_list.clear();
}
public int size() {
return _list.size();}
public boolean isEmpty() {
return _list.isEmpty();
}This time you are being a little more cautious. Without the defensive check, the list's delete() method might well throw an IndexOutOfBoundsException—not what the caller would have expected. Instead, you explicitly check the size of the stack and throw EmptyStackException as specified in the Stack interface, before removing and returning the last element in the underlying list.
Also notice that even though dequeue() can delegate most of its behavior to pop(), it still needs to convert an EmptyStackException into an EmptyQueueException.
Then, using the peek() method, you call pop() to retrieve the next item, record its value, and push it back on again before returning the value to the caller. In this way, you have effectively returned the value at the top of the stack without actually removing it.
You should now be able to compile and run the tests against the completed, list-based stack. As satisfying as this no doubt is, once all your tests are passing, you'll probably want to use your stack for something a bit more constructive.
It is actually surprisingly difficult to find an example of using a stack that is not overly academic in nature. The usual examples involve solving the Towers of Hanoi puzzle, implementing a Reverse-Polish-Notation (RPN) calculator, reversing a list of values, and so on, none of which are particularly useful or relate particularly well to the applications with which you will likely be involved.
Some real-world examples that you are more likely to encounter include XML processing, screen flow management (such as the back and forward buttons in your browser), and undo/redo. It is this last item, undo, that is used in the example.
Imagine an application that holds a list—maybe a shopping list, a list of e-mail messages, or whatever. The user interface, which we will not detail here, displays this list and enables users to add, and possibly remove, items.
Now let's say that you wish to allow users to undo their actions. Each time the user performs an action, you would need to record some information about the state of the list (see Memento [Gamma, 1995]) that will allow us to undo the action sometime in the future. This state information could be pushed onto a stack. When the user requests to undo an action, you could then pop the information off the top of the stack and use it to restore the list to the state it was in just prior to the action being performed.
The most obvious way to implement this would be to store a copy of the list before each action is performed. While this works, it's not really an ideal solution. For one thing, you would need to make an entire copy of the list each time. Instead, you can take advantage of the fact that insert is the inverse of delete—if you insert an element at position 5, you can "undo" this by simply deleting the value at position 5. Conversely, if you delete an element from position 3, inserting the original value back into position 3 will have the effect of "undoing" the deletion.
Although a complete discussion is beyond the scope of this book, the example presented could easily be extended to support a single undo stack across multiple lists, or any data structure for that matter, by encapsulating the undo functionality in external classes.
To demonstrate what we mean and at the same time build reliable production code, why not use some tests? Take the requirements described in the preceding section and turn them into test cases.
package com.wrox.algorithms.stacks;
import com.wrox.algorithms.lists.AbstractListTestCase;
import com.wrox.algorithms.lists.ArrayList;
import com.wrox.algorithms.lists.List;
public class UndoableListTest extends AbstractListTestCase {
protected List createList() {
return new UndoableList(new ArrayList());
}
...
}After a value is inserted into the list, you should be able to call undo() to restore the list to its original state:
public void testUndoInsert() {
UndoableList list = new UndoableList(new ArrayList());
assertFalse(list.canUndo());
list.insert(0, VALUE_A);
assertTrue(list.canUndo());
list.undo();
assertEquals(0, list.size());
assertFalse(list.canUndo());
}
public void testUndoAdd() {UndoableList list = new UndoableList(new ArrayList());
assertFalse(list.canUndo());
list.add(VALUE_A);
assertTrue(list.canUndo());
list.undo();
assertEquals(0, list.size());
assertFalse(list.canUndo());
}Neither of the two methods
undoandcanUndoare part of theListinterface. They are methods that you will add to theUndoableListclass later.
When you call delete() to remove a value, you should be able to call undo() to have the value restored to its original position:
public void testUndoDeleteByPosition() {
UndoableList list = new UndoableList(
new ArrayList(new Object[] {VALUE_A, VALUE_B}));
assertFalse(list.canUndo());
assertSame(VALUE_B, list.delete(1));
assertTrue(list.canUndo());
list.undo();
assertEquals(2, list.size());
assertSame(VALUE_A, list.get(0));
assertSame(VALUE_B, list.get(1));
assertFalse(list.canUndo());
}
public void testUndoDeleteByValue() {
UndoableList list = new UndoableList(
new ArrayList(new Object[] {VALUE_A, VALUE_B}));
assertFalse(list.canUndo());
assertTrue(list.delete(VALUE_B));
assertTrue(list.canUndo());
list.undo();
assertEquals(2, list.size());
assertSame(VALUE_A, list.get(0));
assertSame(VALUE_B, list.get(1));
assertFalse(list.canUndo());
}Although calling set() doesn't change the size of a list, it does modify the contents. Therefore, you can expect that after changing the value of an element, a call to undo() should cause the same element to revert to its previous value:
public void testUndoSet() {
UndoableList list = new UndoableList(new ArrayList(new Object[]
{VALUE_A}));
assertFalse(list.canUndo());
assertSame(VALUE_A, list.set(0, VALUE_B));
assertTrue(list.canUndo());
list.undo();
assertEquals(1, list.size());
assertSame(VALUE_A, list.get(0));
assertFalse(list.canUndo());
}For the purposes of this example, we have chosen to have clear() differ slightly from the other methods shown so far in that it won't record state for a subsequent undo. This decision was made purely on the grounds of simplicity. There is no reason you couldn't implement undo functionality for clear() yourself, possibly by taking an entire copy of the list prior to it being cleared:
public void testClearResetsUndoStack() {
UndoableList list = new UndoableList(new ArrayList());
assertFalse(list.canUndo());
list.add(VALUE_A);
assertTrue(list.canUndo());
list.clear();
assertFalse(list.canUndo());
}So far, you've only tested individual actions and their corresponding undo behavior. If you only wanted to undo one level, you wouldn't need a stack. In fact, you want to be able to roll back any number of actions in the appropriate order. You should at least have a test to demonstrate that this actually works:
public void testUndoMultiple() {
UndoableList list = new UndoableList(new ArrayList());
assertFalse(list.canUndo());
list.add(VALUE_A);
list.add(VALUE_B);
list.undo();
assertEquals(1, list.size());
assertSame(VALUE_A, list.get(0));assertTrue(list.canUndo());
list.delete(0);
list.undo();
assertEquals(1, list.size());
assertSame(VALUE_A, list.get(0));
assertTrue(list.canUndo());
list.undo();
assertEquals(0, list.size());
assertFalse(list.canUndo());
}The tests first ensure that an empty list starts off with nothing to undo. A single value is then inserted in or added to the list. Because the test class itself extends AbstractListTestCase, you can be confident that the actual behavior of inserting a value into the list works. Therefore, all you need to ensure next is that calling undo removes the inserted value.
In both the undo and delete cases, the tests are relatively simple, as you need not concern yourself with the behavior of the actual delete() method—this has been tested by the methods in the superclass. The list is first initialized with some predefined values. Then, delete a value and, after calling undo(), ensure that it has reappeared in the expected location.
The final test starts off with an empty list and variously adds and removes values, invoking undo() along the way. In particular, you will see that the very first add is never undone until right at the end of the test, even though two other actions are undone in the meantime. This proves that the stack-based undo is working as expected.
Tests in place, it's time to actually implement the UndoableList class, as shown in the following Try It Out.
To get going, you need to start capturing state information each time a value is inserted in or added to the list by intercepting calls to insert():
private final class UndoInsertAction implements Action {
private final int _index;
public UndoInsertAction(int index) {
_index = index;
}
public void execute() {
_list.delete(_index);
}
}
public void insert(int index, Object value) throws IndexOutOfBoundsException {
_list.insert(index, value);
_undoStack.push(new UndoDeleteAction(index));
}
public void add(Object value) {
insert(size(), value);
}Next you need to intercept calls to delete() so that you can restore the deleted value at some later stage:
private final class UndoDeleteAction implements Action {
private final int _index;
private final Object _value;
public UndoDeleteAction(int index, Object value) {
_index = index;
_value = value;
}
public void execute() {
_list.insert(_index, _value);
}
}
public Object delete(int index) throws IndexOutOfBoundsException {
Object value = _list.delete(index);
_undoStack.push(new UndoInsertAction(index, value));
return value;}
public boolean delete(Object value) {
int index = indexOf(value);
if (index == −1) {
return false;
}
delete(index);
return true;
}The method first calls indexOf() to determine the position of the value within the list. Then, if the value isn't found, false is returned; otherwise, the delete() method that takes an index is called, which will record the necessary state to perform an undo operation later. Calling set() also modifies the state of the list, so you need a way to restore its effect as well:
private final class UndoSetAction implements Action {
private final int _index;
private final Object _value;
public UndoSetAction(int index, Object value) {
_index = index;
_value = value;
}
public void execute() {
_list.set(_index, _value);
}
}
public Object set(int index, Object value) throws IndexOutOfBoundsException {
Object originalValue = _list.set(index, value);
_undoStack.push(new UndoSetAction(index, originalValue));
return originalValue;
}Now that you have defined the necessary infrastructure to record the undo state, you can write the code for the undo() method:
public void undo() throws EmptyStackException {
((Action) _undoStack.pop()).execute();
}As a convenience, you might also enable callers to determine whether there are any more actions to undo. This would be handy, for example, if you wanted to enable/disable an undo button in a user interface:
public boolean canUndo() {
return !_undoStack.isEmpty();
}To determine whether there are any more actions to undo, you can just query the undo stack: If it's empty, then there is no more to undo and vice-versa.
Even though clear() modifies the list, it was decided that for this example, no undo state would be recorded and the list would be reset:
public void clear() {
_list.clear();
_undoStack.clear();
}Besides clearing the underlying list, the undo stack is also cleared, thereby resetting the entire structure.
Completing the interface requirements for this class is somewhat of a formality:
public Object get(int index) throws IndexOutOfBoundsException {
return _list.get(index);
}
public int indexOf(Object value) {
return _list.indexOf(value);
}
public Iterator iterator() {
return _list.iterator();
}
public boolean contains(Object value) {
return _list.contains(value);
}
public int size() {
return _list.size();
}
public boolean isEmpty() {
return _list.isEmpty();
}
public String toString() {
return _list.toString();
}
public boolean equals(Object object) {
return _list.equals(object);
}None of the remaining methods make any modifications to the state of the list, so it is sufficient that they simply delegate to the underlying instance.
Aside from the underlying list, the class also holds the undo stack, which will hold instances of the inner interface UndoAction (also shown), which defines a single method, execute(), that will eventually be called to perform most of the work involved in implementing the undo functionality.
The
UndoActionclass is an example of the command pattern [Gamma, 1995]. In this case, the command pattern makes it simple to encapsulate all the undo behavior so that the action itself is responsible for performing whatever is needed to get the job done. An effective but rather less elegant—and much less extensible—alternative would be to use aswitchstatement, and route according to some constant defined for each action.
The action UndoDeleteAction class implements the UndoAction interface and, of course, more important, the execute() method. To undo an insert is to delete, so when execute() is called, it uses the recorded position to delete a value from the underlying list.
The insert() method calls insert() on the underlying list and then pushes an undo action. The add() method can then call insert(). You could have created a special action to delete from the end of the list, but calling insert(), passing in the position, has exactly the same effect and requires much less code.
The UndoDeleteAction class implements the UndoAction interface and holds the recorded position and value for later use. To undo a deletion is to insert, so when execute() is called, the action reinserts the value into the underlying list.
The first delete() calls delete() on the underlying list and retrieves the deleted value before pushing an insert action and returning to the caller. Deleting by value is a little trickier. Because you have no way of knowing where in the list the value was deleted, you must re-implement delete by value based on delete by position—not a particularly efficient solution, but your only option.
A call to set() on the underlying list always returns the original value contained at the specified position, so in this case, the UndoSetAction's execute() method stores the old value, together with the position in order to perform the undo. Notice again that, as was the case for the previous two undo actions, the execute() method makes calls on the underlying list in order to prevent the undo from pushing additional undo action onto the stack.
As you can see, there's not a lot of code to actually write for the actual undo() method. All the hard work has already been done by each of the UndoAction classes, so making it all come together is a simple matter of popping the next action (if any) off the stack and calling execute().
And there you have it. You now have a fully tested and implemented list that supports undo functionality.
Although conceptually very simple, stacks underpin the operation of most computers. In this chapter you've learned the following:
Most CPUs, and therefore most programming languages, including Java, are stack-based.
Stacks always add and remove from the top—thus, they are often referred to as FIFO queues.
Stacks can easily be implemented on top of lists without constraining the implementation to one particular type of list.
There are many possible uses for stacks. This chapter demonstrated how easy it is to augment another data structure—in this case, a list—with an undo feature.
Now that you have seen some simple algorithms for string searching, and are familiar with managing your data using basic data structures such as lists, queues, and stacks, it is time to move on to solving more complex problems.