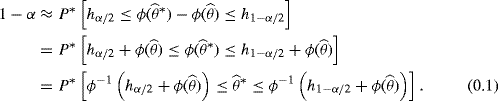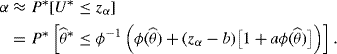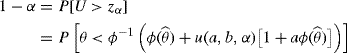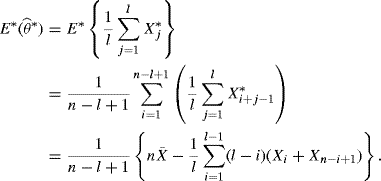Chapter 9

Bootstrapping

9.1 The Bootstrap Principle

Let θ = T(F) be an interesting feature of a distribution function, F, expressed as a functional of F. For example, T(F) = ∫ z dF(z) is the mean of the distribution. Let x₁, . . ., x_n be data observed as a realization of the random variables X₁, . . ., X_n ~ i . i . d . F. In this chapter, we use X ~ F to denote that X is distributed with density function f having corresponding cumulative distribution function F. Let X={X_1,. . .,X_n} denote the entire dataset.

If is the empirical distribution function of the observed data, then an estimate of θ is . For example, when θ is a univariate population mean, the estimator is the sample mean, .

Statistical inference questions are usually posed in terms of or some , a statistical function of the data and their unknown distribution function F. For example, a general test statistic might be , where S is a functional that estimates the standard deviation of .

The distribution of the random variable may be intractable or altogether unknown. This distribution also may depend on the unknown distribution F. The bootstrap provides an approximation to the distribution of derived from the empirical distribution function of the observed data (itself an estimate of F) [175, 177]. Several thorough reviews of bootstrap methods have been published since its introduction [142, 181, 183].

Let denote a bootstrap sample of pseudo-data, which we will call a pseudo-dataset. The elements of are i.i.d. random variables with distribution . The bootstrap strategy is to examine the distribution of , that is, the random variable formed by applying R to . In some special cases it is possible to derive or estimate the distribution of through analytical means (see Example 9.1 and Problems 9.1 and 9.2). However, the usual approach is via simulation, as described in Section 9.2.1.

Example 9.1 (Simple Illustration) Suppose n = 3 univariate data points, namely {x₁, x₂, x₃} = {1, 2, 6}, are observed as an i.i.d. sample from a distribution F that has mean θ. At each observed data value, places mass . Suppose the estimator to be bootstrapped is the sample mean , which we may write as or , where R does not depend on F in this case.

Let consist of elements drawn i.i.d. from . There are 3³ = 27 possible outcomes for . Let denote the empirical distribution function of such a sample, with corresponding estimate . Since does not depend on the ordering of the data, it has only 10 distinct possible outcomes. Table 9.1 lists these.

Table 9.1 Possible bootstrap pseudo-datasets from {1, 2, 6} (ignoring order), the resulting values of , the probability of each outcome in the bootstrapping experiment (), and the observed relative frequency in 1000 bootstrap iterations.

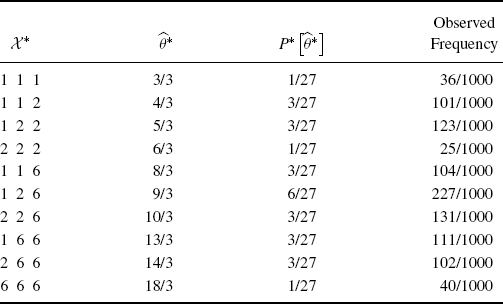
In Table 9.1, represents the probability distribution for with respect to the bootstrap experiment of drawing conditional on the original observations. To distinguish this distribution from F, we will use an asterisk when referring to such conditional probabilities or moments, as when writing .

The bootstrap principle is to equate the distributions of and . In this example, that means we base inference on the distribution of . This distribution is summarized in the columns of Table 9.1 labeled and . So, for example, a simple bootstrap (roughly 93%) confidence interval for θ is () using quantiles of the distribution of . The point estimate is still calculated from the observed data as .

9.2 Basic Methods

9.2.1 Nonparametric Bootstrap

For realistic sample sizes the number of potential bootstrap pseudo-datasets is very large, so complete enumeration of the possibilities is not practical. Instead, B independent random bootstrap pseudo-datasets are drawn from the empirical distribution function of the observed data, namely . Denote these for i = 1, . . ., B. The empirical distribution of the for i = 1, . . ., B is used to approximate the distribution of , allowing inference. The simulation error introduced by avoiding complete enumeration of all possible pseudo-datasets can be made arbitrarily small by increasing B. Using the bootstrap frees the analyst from making parametric assumptions to carry out inference, provides answers to problems for which analytic solutions are impossible, and can yield more accurate answers than given by routine application of standard parametric theory.

Example 9.2 (Simple Illustration, Continued) Continuing with the dataset in Example 9.1, recall that the empirical distribution function of the observed data, , places mass on 1, 2, and 6. A nonparametric bootstrap would generate by sampling , , and i.i.d. from . In other words, draw the with replacement from {1, 2, 6} with equal probability. Each bootstrap pseudo-dataset yields a corresponding estimate . Table 9.1 shows the observed relative frequencies of the possible values for resulting from B = 1000 randomly drawn pseudo-datasets, . These relative frequencies approximate . The bootstrap principle asserts that in turn approximates the sampling distribution of .

For this simple illustration, the space of all possible bootstrap pseudo-datasets can be completely enumerated and the exactly derived. Therefore there is no need to resort to simulation. In realistic applications, however, the sample size is too large to enumerate the bootstrap sample space. Thus, in real applications (e.g., Section 9.2.3), only a small proportion of possible pseudo-datasets will ever be drawn, often yielding only a subset of possible values for the estimator.

A fundamental requirement of bootstrapping is that the data to be resampled must have originated as an i.i.d. sample. If the sample is not i.i.d., the distributional approximation of by will not hold. Section 9.2.3 illustrates that the user must carefully consider the relationship between the stochastic mechanism generating the observed data and the bootstrap resampling strategy employed. Methods for bootstrapping with dependent data are described in Section 9.5.

9.2.2 Parametric Bootstrap

The ordinary nonparametric bootstrap described above generates each pseudo-dataset by drawing i.i.d. from . When the data are modeled to originate from a parametric distribution, so X₁, . . ., X_n ~ i.i.d. F(x, θ), another estimate of F may be employed. Suppose that the observed data are used to estimate θ by . Then each parametric bootstrap pseudo-dataset can be generated by drawing . When the model is known or believed to be a good representation of reality, the parametric bootstrap can be a powerful tool, allowing inference in otherwise intractable situations and producing confidence intervals that are much more accurate than those produced by standard asymptotic theory.

In some cases, however, the model upon which bootstrapping is based is almost an afterthought. For example, a deterministic biological population model might predict changes in population abundance over time, based on biological parameters and initial population size. Suppose animals are counted at various times using various methodologies. The observed counts are compared with the model predictions to find model parameter values that yield a good fit. One might fashion a second model asserting that the observations are, say, lognormally distributed with mean equal to the prediction from the biological model and with a predetermined coefficient of variation. This provides a convenient—if weakly justified—link between the parameters and the observations. A parametric bootstrap from the second model can then be applied by drawing bootstrap pseudo-datasets from this lognormal distribution. In this case, the sampling distribution of the observed data can hardly be viewed as arising from the lognormal model.

Such an analysis, relying on an ad hoc error model, should be a last resort. It is tempting to use a convenient but inappropriate model. If the model is not a good fit to the mechanism generating the data, the parametric bootstrap can lead inference badly astray. There are occasions, however, when few other inferential tools seem feasible.

9.2.3 Bootstrapping Regression

Consider the ordinary multiple regression model, , for i = 1, . . ., n, where the _i are assumed to be i.i.d. mean zero random variables with constant variance. Here, x_i and β are p-vectors of predictors and parameters, respectively. A naive bootstrapping mistake would be to resample from the collection of response values a new pseudo-response, say , for each observed x_i, thereby generating a new regression dataset. Then a bootstrap parameter vector estimate, , would be calculated from these pseudo-data. After repeating the sampling and estimation steps many times, the empirical distribution of would be used for inference about β. The mistake is that the Y_i x_i are not i.i.d.—they have different conditional means. Therefore, it is not appropriate to generate bootstrap regression datasets in the manner described.

We must ask what variables are i.i.d. in order to determine a correct bootstrapping approach. The _i are i.i.d. given the model. Thus a more appropriate strategy would be to bootstrap the residuals as follows.

Start by fitting the regression model to the observed data and obtaining the fitted responses and residuals . Sample a bootstrap set of residuals, , from the set of fitted residuals, completely at random with replacement. (Note that the are actually not independent, though they are usually roughly so.) Create a bootstrap set of pseudo-responses, , for i = 1, . . ., n. Regress Y^∗ on x to obtain a bootstrap parameter estimate . Repeat this process many times to build an empirical distribution for that can be used for inference.

This approach is most appropriate for designed experiments or other data where the x_i values are fixed in advance. The strategy of bootstrapping residuals is at the core of simple bootstrapping methods for other models such as autoregressive models, nonparametric regression, and generalized linear models.

Bootstrapping the residuals is reliant on the chosen model providing an appropriate fit to the observed data, and on the assumption that the residuals have constant variance. Without confidence that these conditions hold, a different bootstrapping method is probably more appropriate.

Suppose that the data arose from an observational study, where both response and predictors are measured from a collection of individuals selected at random. In this case, the data pairs z_i = (x_i, y_i) can be viewed as values observed for i.i.d. random variables Z_i = (X_i, Y_i) drawn from a joint response–predictor distribution. To bootstrap, sample completely at random with replacement from the set of observed data pairs, {z₁, . . ., z_n}. Apply the regression model to the resulting pseudo-dataset to obtain a bootstrap parameter estimate . Repeat these steps many times, then proceed to inference as in the first approach. This approach of bootstrapping the cases is sometimes called the paired bootstrap.

If you have doubts about the adequacy of the regression model, the constancy of the residual variance, or other regression assumptions, the paired bootstrap will be less sensitive to violations in the assumptions than will bootstrapping the residuals. The paired bootstrap sampling more directly mirrors the original data generation mechanism in cases where the predictors are not considered fixed.

There are other, more complex methods for bootstrapping regression problems [142, 179, 183, 330].

Example 9.3 (Copper–Nickel Alloy) Table 9.2 gives 13 measurements of corrosion loss (y_i) in copper–nickel alloys, each with a specific iron content (x_i) [170]. Of interest is the change in corrosion loss in the alloys as the iron content increases, relative to the corrosion loss when there is no iron. Thus, consider the estimation of θ = β₁/β₀ in a simple linear regression.

Table 9.2 Copper–nickel alloy data for illustrating methods of obtaining a bootstrap confidence interval for β₁/β₀.

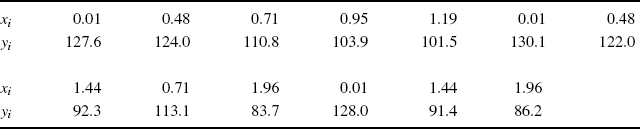
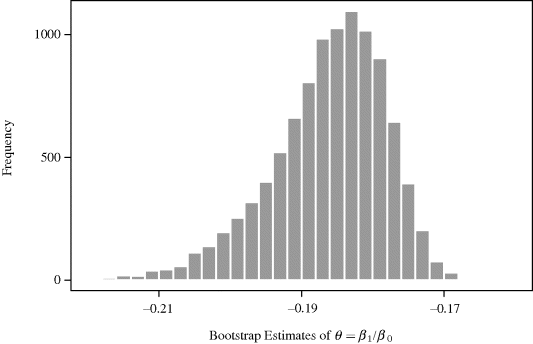
Letting z_i = (x_i, y_i) for i = 1, . . ., 13, suppose we adopt the paired bootstrapping approach. The observed data yield the estimate . For i = 2, . . ., 10, 000, we draw a bootstrap dataset by resampling 13 data pairs from the set {z₁, . . ., z₁₃} completely at random with replacement. Figure 9.1 shows a histogram of the estimates obtained from regressions of the bootstrap datasets. The histogram summarizes the sampling variability of as an estimator of θ.

Figure 9.1 Histogram of 10,000 bootstrap estimates of β₁/β₀ from the nonparametric paired bootstrap analysis with the copper–nickel alloy data.

9.2.4 Bootstrap Bias Correction

A particularly interesting choice for bootstrap analysis when T(F) = θ is the quantity . This represents the bias of , and it has mean equal to . The bootstrap estimate of the bias is .

Example 9.4 (Copper–Nickel Alloy, Continued) For the copper–nickel alloy regression data introduced in Example 9.3, the mean value of among the bootstrap pseudo-datasets is −0.00125, indicating a small degree of negative bias. Thus, the bias-corrected bootstrap estimate of β₁/β₀ is −0.18507 − (− 0.00125) = − 0.184. The bias estimate can naturally be incorporated into confidence interval estimates via the nested bootstrap of Section 9.3.2.4.

An improved bias estimate requires only a little additional effort. Let denote the empirical distribution of the jth bootstrap pseudo-dataset, and define . Then is a better estimate of bias. Compare this strategy with bootstrap bagging, discussed in Section 9.7. Study of the merits of these and other bias corrections has shown that has superior performance and convergence rate [183].

9.3 Bootstrap Inference

9.3.1 Percentile Method

The simplest method for drawing inference about a univariate parameter θ using bootstrap simulations is to construct a confidence interval using the percentile method. This amounts to reading percentiles off the histogram of values produced by bootstrapping. It has been the approach implicit in the preceding discussion.

Example 9.5 (Copper–Nickel Alloy, Continued) Returning to the estimation of θ = β₁/β₀ for the copper–nickel alloy regression data introduced in Example 9.3, recall that Figure 9.1 summarizes the sampling variability of as an estimator of θ. A bootstrap 1 − α confidence interval based on the percentile method could be constructed by finding the [(1 − α/2)100]th and [(α/2)100]th empirical percentiles in the histogram. The 95% confidence interval for β₁/β₀ using the simple bootstrap percentile method is (−0.205, −0.174).

Conducting a hypothesis test is closely related to estimating a confidence interval. The simplest approach for bootstrap hypothesis testing is to base the p-value on a bootstrap confidence interval. Specifically, consider a null hypothesis expressed in terms of a parameter whose estimate can be bootstrapped. If the (1 − α)100% bootstrap confidence interval for the parameter does not cover the null value, then the null hypothesis is rejected with a p-value no greater than α. The confidence interval itself may be obtained from the percentile method or one of the superior approaches discussed later.

Using a bootstrap confidence interval to conduct a hypothesis test often sacrifices statistical power. Greater power is possible if the bootstrap simulations are carried out using a sampling distribution that is consistent with the null hypothesis [589]. Use of the null hypothesis sampling distribution of a test statistic is a fundamental tenet of hypothesis testing. Unfortunately, there will usually be many different bootstrap sampling strategies that are consistent with a given null hypotheses, with each imposing various extra restrictions in addition to those imposed by the null hypothesis. These different sampling models will yield hypothesis tests of different quality. More empirical and theoretical research is needed to develop bootstrap hypothesis testing methods, particularly methods for appropriate bootstrap sampling under the null hypothesis. Strategies for specific situations are illustrated by [142, 183].

Although simple, the percentile method is prone to bias and inaccurate coverage probabilities. The bootstrap works better when θ is essentially a location parameter. This is particularly important when using the percentile method. To ensure best bootstrap performance, the bootstrapped statistic should be approximately pivotal: Its distribution should not depend on the true value of θ. Since a variance-stabilizing transformation g naturally renders the variance of independent of θ, it frequently provides a good pivot. Section 9.3.2 discusses several approaches that rely on pivoting to improve bootstrap performance.

9.3.1.1 Justification for the Percentile Method

The percentile method can be justified by a consideration of a continuous, strictly increasing transformation ϕ and a distribution function H that is continuous and symmetric [i.e., H(z) = 1 − H(− z)], with the property that

(9.1)

where h_α is the α quantile of H. For instance, if ϕ is a normalizing, variance-stabilizing transformation, then H is the standard normal distribution. In principle, when F is continuous we may transform any random variable X ~ F to have any desired distribution G, using the monotone transformation G⁻¹(F(X)). There is therefore nothing special about normalization. In fact, the remarkable aspect of the percentile approach is that we are never actually required to specify explicitly ϕ or H.

Applying the bootstrap principle to (9.1), we have

(9.2)

Since the bootstrap distribution is observed by us, its percentiles are known quantities (aside from Monte Carlo variability which can be made arbitrarily small by increasing the number of pseudo-datasets, B). Let ξ_α denote the α quantile of the empirical distribution of . Then and .

Next, the original probability statement (9.1) from which we hope to build a confidence interval is reexpressed to isolate θ. Exploiting symmetry by noting that h_α/2 = − h_1−α/2 yields

(9.3)

The confidence limits in this equation happily coincide with the limits in (9.2), for which we already have estimates ξ_α/2 and ξ_1−α/2. Hence we may simply read off the quantiles for from the bootstrap distribution and use these as the confidence limits for θ. Note that the percentile method is transformation respecting in the sense that the percentile method confidence interval for a monotone transformation of θ is the same as the transformation of the interval for θ itself [183].

9.3.2 Pivoting

9.3.2.1 Accelerated Bias-Corrected Percentile Method, BC_a

The accelerated bias-corrected percentile method, BC_a, usually offers substantial improvement over the simple percentile approach [163, 178]. For the basic percentile method to work well, it is necessary for the transformed estimator to be unbiased with variance that does not depend on θ. BC_a augments ϕ with two parameters to better meet these conditions, thereby ensuring an approximate pivot.

Assume there exists a monotonically increasing function ϕ and constants a and b such that

(9.4)

has a N(0, 1) distribution, with 1 + aϕ(θ) > 0. Note that if a = b = 0, this transformation leads us back to the simple percentile method.

By the bootstrap principle,

(9.5)

has approximately a standard normal distribution. For any quantile of a standard normal distribution, say z_α,

(9.6)

However, the α quantile of the empirical distribution of , denoted ξ_α, is observable from the bootstrap distribution. Therefore

(9.7)

In order to use (9.7), consider U itself:

(9.8)

where u(a, b, α) = (b − z_α)/[1 − a(b − z_α)]. Notice the similarity between (9.6) and (9.8). If we can find a β such that u(a, b, α) = z_β − b, then the bootstrap principle can be applied to conclude that θ < ξ_β will approximate a 1 − α upper confidence limit. A straightforward inversion of this requirement yields

(9.9)

where Φ is the standard normal cumulative distribution function and the last equality follows from symmetry. Thus, if we knew a suitable a and b, then to find a 1 − α upper confidence limit we would first compute β and then find the βth quantile of the empirical distribution of , namely ξ_β, using the bootstrap pseudo-datasets.

For a two-sided 1 − α confidence interval, this approach yields , where

(9.10)

(9.11)

and and are the corresponding quantiles from the bootstrapped values of .

As with the percentile method, the beauty of the above justification for BC_a is that explicit specification of the transformation ϕ is not necessary. Further, since the BC_a approach merely corrects the percentile levels determining the confidence interval endpoints to be read from the bootstrap distribution, it shares the transformation-respecting property of the simple percentile method.

The remaining question is the choice of a and b. The simplest nonparametric choices are and

(9.12)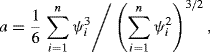

where

(9.13)

with denoting the statistic computed omitting the ith observation, and . A related alternative is to let

(9.14)

where δ_i represents the distribution function that steps from zero to one at the observation x_i (i.e., unit mass on x_i). The ψ_i in (9.14) can be approximated using finite differences. The motivation for these quantities and additional alternatives for a and b are described by [589].

Example 9.6 (Copper–Nickel Alloy, Continued) Continuing the copper–nickel alloy regression problem introduced in Example 9.3, we have a = 0.0486 [using (9.13)] and b = 0.00802. The adjusted quantiles are therefore β₁ = 0.038 and β₂ = 0.986. The main effect of BC_a was therefore to shift the confidence interval slightly to the right. The resulting interval is (−0.203, −0.172).

9.3.2.2 The Bootstrap t

Another approximate pivot that is quite easy to implement is provided by the bootstrap t method, also called the studentized bootstrap [176, 183]. Suppose θ = T(F) is to be estimated using , with estimating the variance of . Then it is reasonable to hope that will be roughly pivotal. Bootstrapping yields a collection of .

Denote by and the distributions of and , respectively. By definition, a 1 − α confidence interval for θ is obtained from the relation

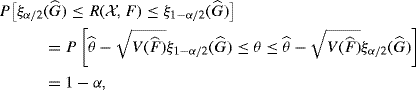
where is the α quantile of . These quantiles are unknown because F (and hence ) is unknown. However, the bootstrap principle implies that the distributions and should be roughly equal, so for any α. Thus, a bootstrap confidence interval can be constructed as

(9.15)

where the percentiles of are taken from the histogram of bootstrap values of . Since these are percentiles in the tail of the distribution, at least several thousand bootstrap pseudo-datasets are needed for adequate precision.

Example 9.7 (Copper–Nickel Alloy, Continued) Continuing the copper–nickel alloy regression problem introduced in Example 9.3, an estimator of the variance of based on the delta method is

(9.16)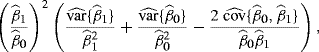

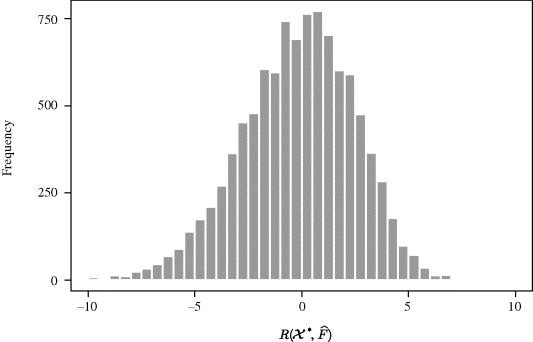
where the estimated variances and covariance can be obtained from basic regression results. Carrying out the bootstrap t method then yields the histogram shown in Figure 9.2, which corresponds to . The 0.025 and 0.975 quantiles of are −5.77 and 4.44, respectively, and . Thus, the 95% bootstrap t confidence interval is (− 0.197, − 0.169).

Figure 9.2 Histogram of 10,000 values of from a studentized bootstrap analysis with the copper–nickel alloy data.

This method requires an estimator of the variance of , namely . If no such estimator is readily available, a delta method approximation may be used [142].

The bootstrap t usually provides confidence interval coverage rates that closely approximate the nominal confidence level. Confidence intervals from the bootstrap t are most reliable when is approximately a location statistic in the sense that a constant shift in all the data values will induce the same shift in . They are also more reliable for variance-stabilized estimators. Coverage rates for bootstrap t intervals can be sensitive to the presence of outliers in the dataset and should be used with caution in such cases. The bootstrap t does not share the transformation-respecting property of the percentile-based methods above.

9.3.2.3 Empirical Variance Stabilization

A variance-stabilizing transformation is often the basis for a good pivot. A variance-stabilizing transformation of the estimator is one for which the sampling variance of the transformed estimator does not depend on θ. Usually a variance-stabilizing transformation of the statistic to be bootstrapped is unknown, but it can be estimated using the bootstrap.

Start by drawing B₁ bootstrap pseudo-datasets for j = 1, . . ., B₁. Calculate for each bootstrap pseudo-dataset, and let be the empirical distribution function of the jth bootstrap pseudo-dataset.

For each , next draw B₂ bootstrap pseudo-datasets from . For each j, let denote the parameter estimate from the kth subsample, and let be the mean of the . Then

(9.17)

is an estimate of the standard error of given .

Fit a curve to the set of points , j = 1, . . ., B₁. For a flexible, nonparametric fit, Chapter 11 reviews many suitable approaches. The fitted curve is an estimate of the relationship between the standard error of the estimator and θ. We seek a variance-stabilizing transformation to neutralize this relationship.

Recall that if Z is a random variable with mean θ and standard deviation s(θ), then Taylor series expansion (i.e., the delta method) yields var {g(Z)} ≈ g′(θ)²s²(θ). For the variance of g(Z) to be constant, we require

(9.18)

where a is any convenient constant for which 1/s(u) is continuous on [a, z]. Therefore, an approximately variance-stabilizing transformation for may be obtained from our bootstrap data by applying (9.18) to the fitted curve from the previous step. The integral can be approximated using a numerical integration technique from Chapter 5. Let denote the result.

Now that an approximate variance-stabilizing transformation has been estimated, the bootstrap t may be carried out on the transformed scale. Draw B₃ new bootstrap pseudo-datasets from , and apply the bootstrap t method to find an interval for . Note, however, that the standard error of is roughly constant, so we can use for computing the bootstrap t confidence interval. Finally, the endpoints of the resulting interval can be converted back to the scale of θ by applying the transformation .

The strategy of drawing iterated bootstrap pseudo-datasets from each original pseudo-dataset sample can be quite useful in a variety of settings. In fact, it is the basis for the confidence interval approach described below.

9.3.2.4 Nested Bootstrap and Prepivoting

Another style of pivoting is provided by the nested bootstrap [26, 27]. This approach is sometimes also called the iterated or double bootstrap.

Consider constructing a confidence interval or conducting a hypothesis test based on a test statistic , given observed data values x₁, . . ., x_n from the model X₁, . . ., X_n ~ i.i.d. F. Let . The notation for F₀ makes explicit the dependence of the distribution of R₀ on the distribution of the data used in R₀. Then a two-sided confidence interval can be fashioned after the statement

(9.19)

and a hypothesis test based on the statement

(9.20)

Of course, these probability statements depend on the quantiles of F₀, which are not known. In the estimation case, F is not known; for hypothesis testing, the null value for F is hypothesized. In both cases, the distribution of R₀ is not known. We can use the bootstrap to approximate F₀ and its quantiles.

The bootstrap begins by drawing B bootstrap pseudo-datasets, , from the empirical distribution . For the jth bootstrap pseudo-dataset, compute the statistic . Let , where 1_{A} = 1 if A is true and zero otherwise. Thus estimates , which itself estimates according to the bootstrap principle. Thus, the upper limit of the confidence interval would be estimated as , or we would reject the null hypothesis if . This is the ordinary nonparametric bootstrap.

Note, however, that a confidence interval constructed in this manner will not have coverage probability exactly equal to 1 − α, because is only a bootstrap approximation to the distribution of . Similarly, the size of the hypothesis test is , since .

Not knowing the distribution F₀ also deprives us of a perfect pivot: The random variable has a standard uniform distribution independent of F. The bootstrap principle asserts the approximation of F₀ by , and hence the approximation of by . This allows bootstrap inference based on a comparison of to the quantiles of a uniform distribution. For hypothesis testing, this amounts to accepting or rejecting the null hypothesis based on the bootstrap p-value.

However, we could instead proceed by acknowledging that , for some nonuniform distribution F₁. Let . Then the correct size test rejects the null hypothesis if . A confidence interval with the correct coverage probability is motivated by the statement . As before, F₁ is unknown but may be approximated using the bootstrap. Now the randomness comes from two sources: (1) The observed data were random observations from F, and (2) given the observed data (and hence ), is calculated from random resamplings from . To capture both sources of randomness, we use the following nested bootstrapping algorithm:

1. Generate bootstrap pseudo-datasets , each as an i.i.d. random sample from the original data with replacement.

2. Compute for j = 1, . . ., B₀.

3. For j = 1, . . ., B₀:

a. Let denote the empirical distribution function of . Draw B₁ iterated bootstrap pseudo-datasets, , each as an i.i.d. random sample from .

b. Compute the for k = 1, . . ., B₁.

c. Compute

(9.21)

4. Denote the empirical distribution function of the resulting sample of as .

5. Use and the quantiles of to construct the confidence interval or hypothesis test.

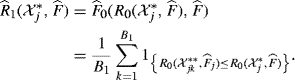
Steps 1 and 2 capture the first source of randomness by applying the bootstrap principle to approximate F by . Step 3 captures the second source of randomness introduced in when R₀ is bootstrapped conditional on .

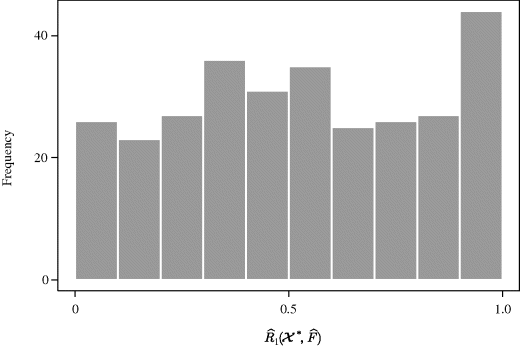
Example 9.8 (Copper–Nickel Alloy, Continued) Returning to the regression problem introduced in Example 9.3, let . Figure 9.3 shows a histogram of values obtained by the nested bootstrap with B₀ = B₁ = 300. This distribution shows that differs noticeably from uniform. Indeed, the nested bootstrap gave 0.025 and 0.975 quantiles of as 0.0316 and 0.990, respectively. The 3.16% and 99.0% percentiles of are then found and used to construct a confidence interval for β₁/β₀, namely (−0.197, −0.168).

Figure 9.3 Histogram of 300 values of from a nested bootstrap analysis with the copper–nickel alloy data.

With its nested looping, the double bootstrap can be much slower than other pivoting methods: In this case nine times more bootstrap draws were used than for the preceding methods. There are reweighting methods such as bootstrap recycling that allow reuse of the initial sample, thereby reducing the computational burden [141, 484].

9.3.3 Hypothesis Testing

The preceding discussion about bootstrap construction of confidence intervals is relevant for hypothesis testing, too. A hypothesized parameter value outside a (1 − α)100% confidence interval can be rejected at a p-value of α. Hall and Wilson offer some additional advice to improve the statistical power and accuracy of bootstrap hypothesis tests [302].

First, bootstrap resampling should be done in a manner that reflects the null hypothesis. To understand what this means, consider a null hypothesis about a univariate parameter θ with null value θ₀. Let the test statistic be . The null hypothesis would be rejected in favor of a simple two-sided alternative when is large compared to a reference distribution. To generate the reference distribution, it may be tempting to resample values via the bootstrap. However, if the null is false, this statistic does not have the correct reference distribution. If θ₀ is far from the true value of θ, then will not seem unusually large compared to the bootstrap distribution of . A better approach is to use values of to generate a bootstrap estimate of the null distribution of . When θ₀ is far from the true value of θ, the bootstrap values of will seem quite small compared to . Thus, comparing to the bootstrap distribution of yields greater statistical power.

Second, we should reemphasize the importance of using a suitable pivot. It is often best to base the hypothesis test on the bootstrap distribution of , where is the value of a good estimator of the standard deviation of computed from a bootstrap pseudo-dataset. This pivoting approach is usually superior to basing the test on the bootstrap distribution of , , , or , where estimates the standard deviation of from the original dataset.

9.4 Reducing Monte Carlo Error

9.4.1 Balanced Bootstrap

Consider a bootstrap bias correction of the sample mean. The bias correction should equal zero because is unbiased for the true mean μ. Now, , and the corresponding bootstrap values are for j = 1, . . ., B. Even though is unbiased, random selection of pseudo-datasets is unlikely to produce a set of values whose mean is exactly zero. The ordinary bootstrap exhibits unnecessary Monte Carlo variation in this case.

However, if each data value occurs in the combined collection of bootstrap pseudo-datasets with the same relative frequency as it does in the observed data, then the bootstrap bias estimate must equal zero. By balancing the bootstrap data in this manner, a source of potential Monte Carlo error is eliminated.

The simplest way to achieve this balance is to concatenate B copies of the observed data values, randomly permute this series, and then read off B blocks of size n sequentially. The jth block becomes . This is the balanced bootstrap—sometimes called the permutation bootstrap [143]. More elaborate balancing algorithms have been proposed [253], but other methods of reducing Monte Carlo error may be easier or more effective [183].

9.4.2 Antithetic Bootstrap

For a sample of univariate data, x₁, . . ., x_n, denote the ordered data as x₍₁₎, . . ., x_(n), where x_(i) is the value of the ith order statistic (i.e., the ith smallest data value). Let π(i) = n − i + 1 be a permutation operator that reverses the order statistics. Then for each bootstrap dataset , let denote the dataset obtained by substituting X_(π(i)) for every instance of X_(i) in . Thus, for example, if has an unrepresentative predominance of the larger observed data values, then the smaller observed data values will predominate in .

Using this strategy, each bootstrap draw provides two estimators: and . These two estimators will often be negatively correlated. For example, if R is a statistic that is monotone in the sample mean, then negative correlation is likely [409].

Let . Then R_a has the desirable property that it estimates the quantity of interest with variance

(9.22)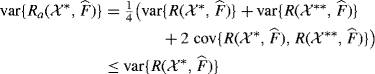

if the covariance is negative.

There are clever ways of establishing orderings of multivariate data, too, to permit an antithetic bootstrap strategy [294].

9.5 Bootstrapping Dependent Data

A critical requirement for the validity of the above methods is that it must be reasonable to assume that the bootstrapped quantities are i.i.d. With dependent data, these approaches will produce a bootstrap distribution that does not mimic F because it fails to capture the covariance structure inherent in F.

Assume that data x₁, . . ., x_n comprise a partial realization from a stationary time series of random variables X₁, . . ., X_n, . . . with the finite dimensional joint distribution function of the random variables {X₁, . . ., X_n} denoted F. For a time series (X₁, . . ., X_n, . . .), stationarity implies that the joint distribution of {X_t, X_t+1, . . ., X_t+k} does not depend on t for any k ≥ 0. We also assume that the process is weakly dependent in the sense that {X_t : t ≤ τ} is independent of {X_t : t ≥ τ + k} in the limit as k→ ∞ for any τ. Let denote the time series we wish to bootstrap, and hereafter we denote series with (·) and unordered sets with { · }.

Since the elements of are dependent, it is inappropriate to apply the ordinary bootstrap for i.i.d. data. This is obvious since under dependence. As a specific example, consider bootstrapping with mean μ. In the case of dependent data, equals var{X₁} plus many covariance terms. However as n→ ∞ where var^∗ represents the variance with respect to the distribution . Thus the covariance terms would be lost in the i.i.d. bootstrap. Also see Example 9.9. Hence, applying the i.i.d. bootstrap to dependent data cannot even ensure consistency [601].

Several bootstrap methods have been developed for dependent data. Bootstrap theory and methods for dependent data are more complex than for the i.i.d. case, but the heuristic of resampling the data to generate values of for approximating the sampling distribution of is the same. Comprehensive discussion of bootstrapping methods for dependent data is given by [402]. A wide variety of methods have been introduced by [81, 93, 94, 396, 425, 498, 512, 513, 529, 590, 591].

9.5.1 Model-Based Approach

Perhaps the simplest context for bootstrapping dependent data is when a time series is known to be generated from a specific model such as the first-order stationary autoregressive process, that is, the AR(1) model. This model is specified by the relation

(9.23)

where |α| < 1 and the _t are i.i.d. random variables with mean zero and constant variance. If the data are known to follow or can be assumed to follow an AR(1) process, then a method akin to bootstrapping the residuals for linear regression (Section 9.2.3) can be applied.

Specifically, after using a standard method to estimate α (see, e.g., [129]), define the estimated innovations to be for t = 2, . . ., n, and let be the mean of these. The can be recentered to have mean zero by defining . Bootstrap iterations should then resample n + 1 values from the set with replacement with equal probabilities to yield a set of pseudo-innovations . Given the model (and ), a pseudo-data series can be reconstructed using and for t = 1, . . ., n.

When generated in this way, the pseudo-data series is not stationary. One remedy is to sample a larger number of pseudo-innovations and to start generating the data series “earlier,” that is, from for k much less than 0. The first portion of the generated series (t = k, . . ., 0) can then be discarded as a burn-in period [402]. As with any model-based bootstrap procedure, good performance for this approach is dependent on the model being appropriate.

9.5.2 Block Bootstrap

Most often, a model-based approach should not be applied, so a more general method is needed. Many of the most common approaches to bootstrapping with dependent data rely on notions of blocking the data in order to preserve the covariance structure within each block even though that structure is lost between blocks once they are resampled. We begin by introducing the nonmoving and moving block bootstraps. It is important to note that our initial presentation of these methods omits several refinements like additional blocking, centering and studentizing that help ensure the best possible performance. We introduce those topics in Sections 9.5.2.3 and 9.5.2.4.

9.5.2.1 Nonmoving Block Bootstrap

Consider estimating an unknown quantity θ = T(F) using the statistic where is the empirical distribution function of the data. A bootstrap resampling approach will be used to estimate the sampling distribution of by obtaining a collection of bootstrap pseudo-estimates for i = 1, . . ., m. Each is computed as where denotes the empirical distribution function of a pseudo-dataset . These must be generated in a manner that respects the correlation structure in the stochastic process that produced the original data . A simple approximate method that attempts to achieve this goal is the nonmoving block bootstrap [93].

Consider splitting = (X₁,. . .,X_n) into b nonoverlapping blocks of length l, where for simplicity hereafter we assume lb = n. Denote these blocks as = (X_(i-1)l+1,. . .,X_il) for i = 1, . . ., b. The simplest nonmoving block bootstrap begins by sampling independently from with replacement. These blocks are then concatenated to form a pseudo-dataset . Replicating this process B times yields a collection of bootstrap pseudo-datasets denoted for i = 1, . . ., B. Each bootstrap pseudo-value is computed from a corresponding and the distribution of is approximated by the distribution of these B pseudo-values. Although this bootstrap procedure is simple, we will discuss shortly why it is not the best way to proceed.

First, however, let us consider a simple example. Suppose n = 9, l = 3, b = 3, and = (X₁,. . ., X₉)=(1,2,3,4,5,6,7,8,9). The blocks would be = (1,2,3), = (4,5,6), and = (7,8,9). Independently sampling these blocks with replacement and reassembling the result might yield = (4,5,6,1,2,3,7,8,9). The order within blocks must be retained, but the order in which the blocks are reassembled doesn't matter because is stationary. Another possible bootstrap sample is = (1,2,3,1,2,3,4,5,6).

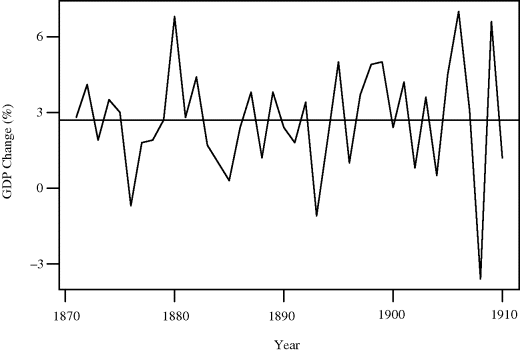
Example 9.9 (Industrialized Countries GDP) The website for this book contains data on the average percent change in gross domestic product (GDP) for 16 industrialized countries for the n = 40 years from 1871 to 1910, derived from [431]. The data are shown in Figure 9.4.

Figure 9.4 Time series of mean changes in gross domestic product (GDP) for 16 industrialized countries for 1871–1910. The horizontal line is the overall mean, .

Let estimate the mean GDP change over the period. The variance of this estimator is

(9.24)

Let b = 5 and l = 8. Figure 9.5 shows a histogram of B = 10,000 bootstrap estimates for i = 1, . . ., B using the nonmoving block bootstrap. The sample standard deviation of these values is 0.196.

Figure 9.5 Histogram of B = 10,000 bootstrap estimates from Example 9.9.

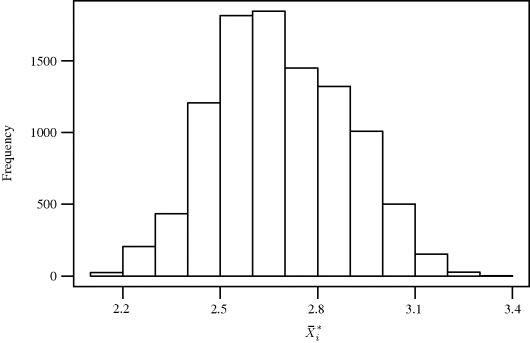
Because most of the dominant covariance terms in Equation (9.24) are negative, the sample standard deviation generated by the i.i.d. approach will be larger than the one from the block bootstrap approach. In this example, the i.i.d. approach (which corresponds to l = 1, b = 40) yields 0.332.

9.5.2.2 Moving Block Bootstrap

The nonmoving block bootstrap uses sequential disjoint blocks that partition . This choice is inferior to the more general strategy employed by the moving block bootstrap [396]. With this approach, all blocks of l adjacent X_t are considered, regardless of whether the blocks overlap. Thus we define = (X_i,. . .,X_i+l-1) for i = 1, . . ., n − l + 1. Resample these blocks independently with replacement, obtaining where again we make the convenient assumption that n = lb. After arranging the end to end in order to assemble , a pseudo-estimate is produced. Replicating this process B times provides a bootstrap sample of values for i = 1, . . ., B. For the case where = (1,. . .,9), a possible bootstrap series is (1, 2, 3, 2, 3, 4, 6, 7, 8), formed from the two overlapping blocks (1, 2, 3) and (2, 3, 4) and the additional block (6, 7, 8).

Example 9.10 (Industrialized Countries GDP, Continued) For the previous GDP dataset, the moving blocks bootstrap with l = 8 yields an estimated standard deviation of 0.188. For comparison, the moving and nonmoving bootstrap applications were replicated 20,000 times to assess the expected performance of the two procedures. The medians (and standard deviations) of the bootstrap estimates of the standard deviation were 0.187 (0.00125) and 0.196 (0.00131) for the nonmoving and moving block approaches, respectively. In principle, the moving block bootstrap should outperform its nonmoving block counterpart; see Section 9.6.2.

9.5.2.3 Blocks-of-Blocks Bootstrapping

Above we have sidestepped a key issue for the block bootstrap. Our example using is not sufficiently general because the distribution of the sample mean depends only on the univariate marginal distribution of X_t. For dependent data problems, many important parameters of interest pertain to the covariance structure inherent in the joint distribution of several X_t.

Notice that the serial correlation in will (usually) be broken in at each point where adjacent resampled blocks meet as they are assembled to construct . If the parameter θ = T(F) is related to a p-dimensional distribution, a naive moving or nonmoving block bootstrap will not replicate the targeted covariance structure because the pseudo-dataset will resemble white noise more than the original series did.

For example, consider the lag 2 autocovariance ρ₂ = E{(X_t − EX_t)(X_t+2 − EX_t)}. This depends on the distribution function of the trivariate random variable (X_t, X_t+1, X_t+2). An appropriate block bootstrapping technique would ensure that each pseudo-estimate is estimated only from such triples. This would eliminate the instances in where and are not lag 2 adjacent to each other in the original data. Without such a strategy, there would be as many as b − 1 inappropriate contributions to .

The remedy is the blocks-of-blocks bootstrap. Let Y_j = (X_j, . . ., X_j+p−1) for j = 1, . . ., n − p + 1. These Y_j now constitute a new series of p-dimensional random variables to which a block bootstrap may be applied. Furthermore, the sequence ={Y_t} is stationary and we may now reexpress θ and as T_Y(F_Y) and , respectively. Here F_Y is the distribution function of and T_Y is a reexpression of T that enables the functional to be written in terms of so that the estimator is calculated using rather than .

For a nonmoving block bootstrap, then, = (Y₁,. . ., Y_n-p+1) is partitioned into b adjacent blocks of length l. Denote these blocks as . These blocks are resampled with replacement, and appended end-to-end to form a pseudo-dataset . Each yields a pseudo-estimate , where is the empirical distribution function of .

For example, let n = 13, b = 4, l = 3, p = 2, and =(1,2,. . .,13). Then

For the nonmoving blocks-of-blocks approach, the four nonoverlapping blocks of blocks would be

One potential blocks-of-blocks nonmoving bootstrap dataset would be

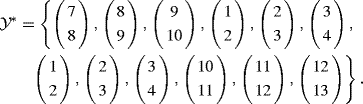
The blocks-of-blocks approach for the moving block bootstrap proceeds analogously. In this case, there are n − p + 1 blocks of size p. These blocks overlap, so adjacent blocks look like (X_t, . . ., X_t+p−1) and (X_t+1, . . ., X_t+p). In the above example, the first two of 10 blocks of blocks would be

One potential pseudo-dataset would be

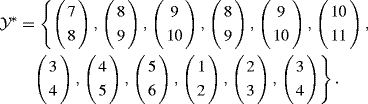
The blocks-of-blocks strategy is implicit in the rest of our block bootstrap discussion. However, there are situations where vectorizing the data to work with the Y_t or reexpressing T as T_Y is difficult or awkward. When these challenges become too great an impediment, a pragmatic solution is to adopt the naive approach corresponding to p = 1.

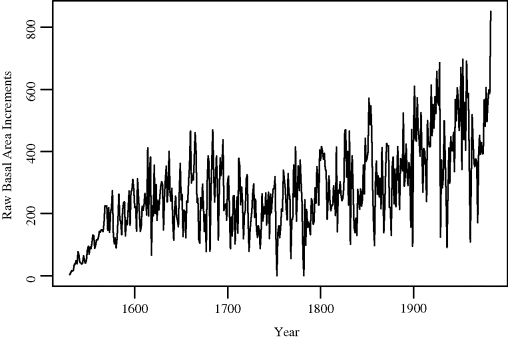
Example 9.11 (Tree Rings) The website for this book provides a dataset related to tree rings for the long-lived bristlecone pine Pinus longaeva at Campito Mountain in California. Raw basal area growth increments are shown in Figure 9.6 for one particular tree with rings corresponding to the n = 452 years from 1532 to 1983. The time series considered below has been detrended and standardized [277].

Figure 9.6 Raw bristlecone pine basal area growth increments for the years 1532–1983 discussed in Example 9.11.

Consider estimating the standard error of the lag 2 autocorrelation of the basal area increments, that is, the correlation between X_t and X_t+2. The sample lag 2 autocorrelation is . To apply the blocks-of-blocks method we must use p = 3 so that each small block includes both X_t and X_t+2 for t = 1, . . ., 450.

Thus yields 450 triples Y_t = (X_t, X_t+1, X_t+2) and the vectorized series is = (Y₁,. . .,Y₄₅₀). From these 450 blocks, we may resample blocks of blocks. Let each of these blocks of blocks be comprised of 25 of the small blocks. The lag 2 correlation can be estimated as

where Y_t,j is the jth element in Y_t and M is the mean of X₁, . . ., X_n. The denominator and M are expressed here in terms of for brevity, but they can be reexpressed in terms of so that .

Applying the moving blocks-of-blocks bootstrap by resampling the Y_t and assembling a pseudo-dataset yields a bootstrap estimate for each i = 1, . . ., B. The standard deviation of the resulting , that is, the estimated standard error of , is 0.51. A bootstrap bias estimate is −0.008 (see Section 9.2.4).

9.5.2.4 Centering and Studentizing

The moving and nonmoving block bootstrap methods yield different bootstrap distributions for . To see this, consider when θ = EX_t and . For the nonmoving block bootstrap, assume that n = lb and note that the blocks are i.i.d., each with probability 1/b. Let E^∗ represent expectation with respect to the block bootstrap distribution. Then

(9.25)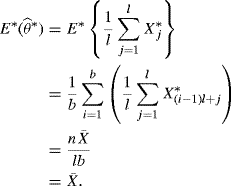

However, for the moving block bootstrap it can be shown that

(9.26)

The second term in the braces in (9.26) accounts for the fact that observations within l positions of either end of the series occur in fewer blocks and hence contribute fewer terms to the double sum above. In other words, the moving block bootstrap exhibits edge effects. Note, however, that the mean squared difference between bootstrap means is so the difference vanishes as n→ ∞.

There is an important implication of the fact that is unbiased for the nonmoving block bootstrap but biased for the moving block approach. Suppose we intend to apply the moving block bootstrap to a pivoted quantity such as . One would naturally consider the bootstrap version . However, , and this error converges to zero at a slow rate that is unnecessary given the approach described in the next paragraph.

The improvement is to center using . For the sample mean, is given in (9.26). This alternative centering could present a significant new hurdle for applying the moving blocks bootstrap to a more general statistic because the calculation of can be challenging. Fortunately, it can be shown that under suitable conditions it suffices to apply the pivoting approach when bootstrapping any statistic that can be expressed as if is a smooth function [140, 275, 398]. This is called the smooth function model, which is a common context in which to study and summarize asymptotic performance of block bootstrap methods.

Studentizing the statistic by scaling it with its estimated standard deviation suffers from an analogous problem. Recognizing the smooth function result above, let us make the simplifying assumption that and limit consideration to the nonmoving bootstrap. A natural studentization would be seem to be where s^∗ is the standard deviation of the bootstrap data X^∗. However, s^∗ is not a good approximation to [296, 312]. The improvements

(9.27)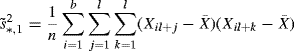

and

(9.28)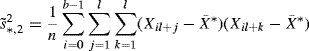

are suggested alternatives [275, 312, 399]. Either is adequate.

Another way to correct for edge effects is the circular block bootstrap [512]. This approach extends the observed time series by defining “new” observations for 1 ≤ i ≤ b − 1, which are concatenated to the end of the original series. Then overlapping blocks are formed from the “wrapped” series in the same manner as for the moving blocks bootstrap. These blocks are resampled independently with replacement with equal probabilities. Since each X_i (1 ≤ i ≤ n) in the original now occurs exactly n times in the extended collection of blocks, the edge effect is eliminated.

The stationary block bootstrap tackles the same edge effect issue by using blocks of random lengths [513]. The block starting points are chosen i.i.d. over {1, . . ., n}. The ending points are drawn according to the geometric distribution given by P[endpoint = j] = p(1 − p)^j−1. Thus block lengths are random with a conditional mean of 1/p. The choice of p is a challenging question; however, simulations show that stationary block bootstrap results are far less sensitive to the choice of p than is the moving blocks bootstrap to the choice of l [513]. Theoretically, it suffices that p → 0 and np→ ∞ as n→ ∞. From a practical point of view, p = 1/l can be recommended. The term stationary block bootstrap is used to describe this method because it produces a stationary time series, whereas the moving and nonmoving block bootstraps do not.

9.5.2.5 Block Size

Performance of a block bootstrap technique depends on block length, l. When l = 1, the method corresponds to the i.i.d. bootstrap and all correlation structure is lost. For very large l, the autocorrelation is mostly retained but there will be few blocks from which to sample. Asymptotic results indicate that, for the block bootstrap, block length should increase as the length of the time series increases if the method is to produce consistent estimators of moments, correct coverage probabilities for confidence intervals, and appropriate error rates for hypothesis tests (see Section 9.6.2). Several approaches for choosing block length in practice have been suggested. We limit discussion here to two methods relevant for the moving block bootstrap.

A reasonable basis for choosing block length is to consider the MSE of the bootstrap estimator. In this chapter, we have considered θ = T(F) as an interesting feature of a distribution F, and as an estimator of this quantity. The statistic will have certain properties (features of its sampling distribution) that depend on the unknown F, such as or . The bootstrap is used to estimate such quantities. Yet, the bootstrap estimator itself has its own bias, variance, and mean squared error that again depend on F. These serve as criteria to evaluate the performance of the block bootstrap and consequently to compare different choices for block length.

The MSE of a bootstrap estimator can be estimated by bootstrapping the bootstrap estimator. Although neither of the methods discussed below implements a nesting strategy as explicit as the one described in Section 9.3.2.4, they both adopt the heuristic of multilevel resampling for estimation of the optimal block length, denoted l_opt. An alternative approach is explored by [83].

Subsampling Plus Bootstrapping

The approach described here is based on an estimate of the mean squared error of a block bootstrap estimate when is the mean or a smooth function thereof [297]. Define and . Let and be block bootstrap estimates of ϕ_b and . For example, under the smooth function model with μ denoting the true mean and θ = H(μ), where is the mean of the ith pseudo-dataset and H is the smooth function. Note that each ϕ_j for depends on l, so we may write these quantities as ϕ_j(l). Under suitable conditions, one can show that

(9.29)

(9.30)

and therefore

(9.31)

for , although c₁ and c₂ depend on j. Differentiating this last expression and solving for the l that minimizes the MSE, we find

(9.32)

where the symbol ~ is defined by the relation a_n ~ b_n if lim _n→∞a_n/b_n = 1. For simplicity in the rest of this section, let us focus on bias estimation, letting ϕ = ϕ_b. We will note later that the same result holds for variance estimation. The goal is to derive the block length that minimizes with respect to l. We will do this by estimating for several candidate values of l and select the best. Begin by choosing a pilot block size l₀ and performing the usual block bootstrap to obtain . Next, consider a smaller sub-dataset of size m < n for which we can obtain an analogous estimate, for some l′. The estimate of will depend on a collection of these and the original .

Let denote a subsequence of of length m, for i = 1, . . ., n − m + 1. Applying the block bootstrap to using B iterations and trial block length l′ produces a point estimate of ϕ, denoted , for each i. For the bias example above, where is the mean of and is the mean of the jth bootstrap pseudo-dataset generated from for j = 1, . . ., B. Then an estimate of the mean squared error of the block bootstrap estimator based on the subset of size m is

(9.33)

recalling that is the estimate obtained by bootstrapping the full dataset using a pilot block length l₀.

Let minimize with respect to l′. This minimum may be found by trying a sequence of l′ and selecting the best. Then estimates the best block size for a series of length m. Since the real data series is length n and since optimal block size is known to be of order n^1/3, we must scale up accordingly to yield .

The procedure described here applies when ϕ is the bias or variance functional. For estimating a distribution function, an analogous approach leads to an appropriate scaling factor of .

Good choices for m and l₀ are unclear. Choices like m ≈ 0.25n and l₀ ≈ 0.05n have produced reasonable simulation results in several examples [297, 402]. It is important that the pilot value l₀ is plausible, but the effect of l₀ can potentially be reduced through iteration. Specifically, after applying the procedure with an initial pilot value l₀, the result may be iteratively refined by replacing the previous pilot value with the current estimate and repeating the process.

Jackknifing Plus Bootstrapping

An empirical plug-in approach has been suggested as an alternative to the above method [404]. Here, an application of the jackknife-after-bootstrap approach [180, 401] is applied to estimate properties of the bootstrap estimator. Recall the expressions for and l_opt in Equations (9.31) and (9.32). Equation (9.32) identifies the optimal rate at which block size should grow with increasing sample size, namely proportionally to n^1/3. However, a concrete choice for l_opt cannot be made without determination of c₁ and c₂. Rearranging terms in Equations (9.29) and (9.30) yields

(9.34)

(9.35)

Thus if and can be approximated by convenient estimators and , then we can estimate c₁, c₂, and hence . Moreover, Equation (9.32) can be applied to estimate l_opt.

The crux of this strategy is crafting the estimators and . One can show that the estimator

(9.36)

is consistent for under suitable conditions where l′ is a chosen block length. The choice of l′ determines the accuracy of the estimator .

Calculation of relies on a jackknife-after-bootstrap strategy [180]. Applied within the blocks-of-blocks context, this approach deletes an adjacent set of blocks and resamples the remainder. From this resample, is calculated. Repeating this process sequentially as the set of deleted blocks progresses from one end of to the other, one block at a time, yields the complete set of bootstrap pseudo-values whose variance may be calculated and scaled up to estimate .

The details are as follows. When the moving block bootstrap is applied to a data sequence (X₁, . . ., X_n), there are n − l + 1 blocks B₁, . . ., B_n−l+1 available for resampling. The blocks are B_j = (X_j, . . ., X_j+l−1) for j = 1, . . ., n − l + 1. Suppose that we delete d adjacent blocks from this set of blocks. There are n − l − d + 2 possible ways to do this, deleting (B_i, . . ., B_i+d−1) for i = 1, . . ., n − l − d + 2. The ith such deletion leads to the ith reduced dataset of blocks, called a block-deleted dataset. By performing a moving block bootstrap with block length l′ on the ith block-deleted dataset, the ith block-deleted value can be computed via where is the empirical distribution function of the sample from this moving block bootstrap of the ith block-deleted dataset. However, the n − l − d + 2 separate block-deleted bootstraps considered above can be carried out without explicitly conducting the block deletion steps. For each i in turn, the collection of original bootstrap pseudo-datasets can be searched to identify all X^∗ in which none of the ith set of deleted blocks are present. Then this subcollection of the original bootstrap pseudo-datasets can be used to calculate . An appropriate variance estimator based on the block-deleted data is

(9.37)

where

(9.38)

and is the estimate of ϕ resulting from the original application of the bootstrap. Finally, l_opt can be found using Equation (9.32). In this manner, the computational effort associated with repeated resampling is replaced by increased coding complexity needed to keep track of (or search for) the appropriate pseudo-datasets for each i. Note that the choice of d will strongly affect the performance of as an estimator of .

Under suitable conditions, is consistent for and is consistent for when d→ ∞ and d/n → 0 as n→ ∞ [404]. Yet a key part of this method remains to be specified: the choices for d and l₀. The values of l₀ = n^1/5 and d = n^1/3l^2/3 are suggested on the basis of heuristic arguments and simulation [401, 403, 404]. An iterative strategy to refine l₀ is also possible.

These results pertain to cases when estimating the best block length for bootstrap estimation of bias or variance. Analogous arguments can be used to address the situation when ϕ represents a quantile. In this case, assuming studentization, and suggested starting values are l₀ = n^1/6 and d = 0.1n^1/3l^2/3 [404].

9.6 Bootstrap Performance

9.6.1 Independent Data Case

All the bootstrap methods described in this chapter rely on the principle that the bootstrap distribution should approximate the true distribution for a quantity of interest. Standard parametric approaches such as a t-test and the comparison of a log likelihood ratio to a χ² distribution also rely on distributional approximation.

We have already discussed one situation where the i.i.d. bootstrap approximation fails: for dependent data. The bootstrap also fails for estimation of extremes. For example, bootstrapping the sample maximum can be catastrophic; see [142] for details. Finally, the bootstrap can fail for heavy-tailed distributions. In these circumstances, the bootstrap samples outliers too frequently.

There is a substantial asymptotic theory for the consistency and rate of convergence of bootstrap methods, thereby formalizing the degree of approximation it provides. These results are mostly beyond the scope of this book, but we mention a few main ideas below.

First, the i.i.d. bootstrap is consistent under suitable conditions [142]. Specifically, consider a suitable space of distribution functions containing F, and let denote a neighborhood of F into which eventually falls with probability 1. If the distribution of a standardized is uniformly weakly convergent when the elements of are drawn from any , and if the mapping from G to the corresponding limiting distribution of R is continuous, then for any and any q as n→ ∞.

Edgeworth expansions can be used to assess the rate of convergence [295]. Suppose that is standardized and asymptotically pivotal, when is asymptotically normally distributed. Then the usual rate of convergence for the bootstrap is given by . Without pivoting, the rate is typically only . In other words, coverage probabilities for confidence intervals are accurate for the basic, unpivoted percentile method, but accurate for BC_a and the bootstrap t. The improvement offered by the nested bootstrap depends on the accuracy of the original interval and the type of interval. In general, nested bootstrapping can reduce the rate of convergence of coverage probabilities by an additional multiple of n^−1/2 or n⁻¹. Most common inferential problems are covered by these convergence results, including estimation of smooth functions of sample moments and solutions to smooth maximum likelihood problems.

It is important to note that asymptotic approaches such as the normal approximation via the central limit theorem are accurate. This illustrates the benefit of standardization when applying bootstrap methods because the convergence rate for the bootstrap in that case is superior to what can be achieved using ordinary asymptotic methods. Accessible discussions of the increases in convergence rates provided by BC_a, the nested bootstrap, and other bootstrap improvements are given in [142, 183]. More advanced theoretical discussion is also available [47, 295, 589].

9.6.2 Dependent Data Case

Under suitable conditions, the dependent data bootstrap methods discussed here are also consistent. The convergence performance of these methods depends on whether block length l is the correct order (e.g., l ∝ n^1/3 for bias and variance estimation). In general, performance of block bootstrap methods when incorporating studentization is superior to what is achieved by normal approximation via the central limit theorem, but not as good as the performance of the bootstrap for i.i.d. data.

Not all dependent data bootstrap methods are equally effective. The moving block bootstrap is superior to the nonmoving block approach in terms of mean squared error. Suppose that bootstrapping is focused on estimating the bias or variance of an underlying estimator. Then the asymptotic mean squared error (AMSE) is 1 . 5^2/3≈ 31 % larger for the nonmoving blocks bootstrap than for the moving blocks method when the asymptotically optimal block sizes are used for each approach [297, 400]. The difference is attributable to the contribution of variances to AMSE; the bias terms for the two methods are the same. Both AMSEs converge to zero at the same rate.

More sophisticated bootstrapping methods for dependent data can offer better asymptotic performance but are considerably more cumbersome and sometimes limited to applications that are less general than those that can be addressed with one of the block methods described above. The tapered block bootstrap seeks to reduce the bias in variance estimation by down-weighting observations near the edges of blocks [498, 499]. The sieve bootstrap aims to approximate the data generation process by initially fitting an autoregressive process. Recentered residuals are then resampled and used to generate bootstrap datasets X^∗ from the fitted model via a recursion method for which the impact of initializing the process is washed away as iterations increase [81, 82, 393]. The dependent wild bootstrap shares the superior asymptotic properties of the tapered block bootstrap and can be extended to irregularly spaced time series [590].

9.7 Other Uses of the Bootstrap

By viewing X^∗ as a random sample from a distribution with known parameter , the bootstrap principle can be seen as a tool used to approximate the likelihood function itself. Bootstrap likelihood [141] is one such approach, which has connections to empirical likelihood methods. By ascribing random weights to likelihood components, a Bayesian bootstrap can be developed [558]. A generalization of this is the weighted likelihood bootstrap, which is a powerful tool for approximating likelihood surfaces in some difficult circumstances [485].

The bootstrap is generally used for assessing the statistical accuracy and precision of an estimator. Bootstrap aggregating, or bagging, uses the bootstrap to improve the estimator itself [63]. Suppose that the bootstrapped quantity, , depends on F only through θ. Thus, the bootstrap values of are . In some cases, θ is the result of a model-fitting exercise where the form of the model is uncertain or unstable. For example, classification and regression trees, neural nets, and linear regression subset selection are all based on models whose form may change substantially with small changes to the data.

In these cases, a dominant source of variability in predictions or estimates may be the model form. Bagging consists of replacing with , where is the parameter estimate arising from the jth bootstrap pseudo-dataset. Since each bootstrap pseudo-dataset represents a perturbed version of the original data, the models fit to each pseudo-dataset can vary substantially in form. Thus provides a sort of model averaging that can reduce mean squared estimation error in cases where perturbing the data can cause significant changes to . A review of the model-averaging philosophy is provided in [331].

A related strategy is the bootstrap umbrella of model parameters, or bumping approach [632]. For problems suitable for bagging, notice that the bagged average is not always an estimate from a model of the same class as those being fit to the data. For example, the average of classification trees is not a classification tree. Bumping avoids this problem.

Suppose that is some objective function relevant to estimation in the sense that high values of h correspond to θ that are very consistent with . For example, h could be the log likelihood function. The bumping strategy generates bootstrap pseudo-values via . The original dataset is included among the bootstrap pseudo-datasets, and the final estimate of θ is taken to be the that maximizes with respect to θ. Thus, bumping is really a method for searching through a space of models (or parameterizations thereof) for a model that yields a good estimator.

9.8 Permutation Tests

There are other important techniques aside from the bootstrap that share the underlying strategy of basing inference on “experiments” within the observed dataset. Perhaps the most important of these is the classic permutation test that dates back to the era of Fisher [194] and Pitman [509, 510]. Comprehensive introductions to this field include [173, 271, 439]. The basic approach is most easily explained through a hypothetical example.

Example 9.12 (Comparison of Independent Group Means) Consider a medical experiment where rats are randomly assigned to treatment and control groups. The outcome X_i is then measured for the ith rat. Under the null hypothesis, the outcome does not depend on whether a rat was labeled as treatment or control. Under the alternative hypothesis, outcomes tend to be larger for rats labeled as treatment.

A test statistic T measures the difference in outcomes observed for the two groups. For example, T might be the difference between group mean outcomes, having value t₁ for the observed dataset.

Under the null hypothesis, the individual labels “treatment” and “control” are meaningless because they have no influence on the outcome. Since they are meaningless, the labels could be randomly shuffled among rats without changing the joint null distribution of the data. Shuffling the labels creates a new dataset: Although one instance of each original outcome is still seen, the outcomes appear to have arisen from a different assignment of treatment and control. Each of these permuted datasets is as likely to have been observed as the actual dataset, since the experiment relied on random assignment.

Let t₂ be the value of the test statistic computed from the dataset with this first permutation of labels. Suppose all M possible permutations (or a large number of randomly chosen permutations) of the labels are examined, thereby obtaining t₂, . . ., t_M.

Under the null hypothesis, t₂, . . ., t_M were generated from the same distribution that yielded t₁. Therefore, t₁ can be compared to the empirical quantiles of t₁, . . ., t_M to test a hypothesis or construct confidence limits.

To pose this strategy more formally, suppose that we observe a value t for a test statistic T having density f under the null hypothesis. Suppose large values of T indicate that the null hypothesis is false. Monte Carlo hypothesis testing proceeds by generating a random sample of M − 1 values of T drawn from f. If the observed value t is the kth largest among all M values, then the null hypothesis is rejected at a significance level of k/M. If the distribution of the test statistic is highly discrete, then ties found when ranking t can be dealt with naturally by reporting a range of p-values. Barnard [22] posed the approach in this manner; interesting extensions are offered in [38, 39].

There are a variety of approaches for sampling from the null distribution of the test statistic. The permutation approach described in Example 9.12 works because “treatment” and “control” are meaningless labels assigned completely at random and independent of outcome, under the null hypothesis. This simple permutation approach can be broadened for application to a variety of more complicated situations. In all cases, the permutation test relies heavily on the condition of exchangeability. The data are exchangeable if the probability of any particular joint outcome is the same regardless of the order in which the observations are considered.

There are two advantages to the permutation test over the bootstrap. First, if the basis for permuting the data is random assignment, then the resulting p-value is exact (if all possible permutations are considered). For such experiments, the approach is usually called a randomization test. In contrast, standard parametric approaches and the bootstrap are founded on asymptotic theory that is relevant for large sample sizes. Second, permutation tests are often more powerful than their bootstrap counterparts. However, the permutation test is a specialized tool for making a comparison between distributions, whereas a bootstrap tests hypotheses about parameters, thereby requiring less stringent assumptions and providing greater flexibility. The bootstrap can also provide a reliable confidence interval and standard error, beyond the mere p-value given by the permutation test. The standard deviation observed in the permutation distribution is not a reliable standard error estimate. Additional guidance on choosing between a permutation test and a bootstrap is offered in [183, 271, 272].

problems

9.1. Let X₁, . . ., X_n ~ i.i.d. Bernoulli(θ). Define and , where X^∗ is a bootstrap pseudo-dataset and is the empirical distribution of the data. Derive the exact analytically.

9.2. Suppose θ = g(μ), where g is a smooth function and μ is the mean of the distribution from which the data arise. Consider bootstrapping .

a. Show that and , where .

b. Use Taylor series to show that

and

9.3. Justify the choice of b for BC_a given in Section 9.3.2.1.

9.4. Table 9.3 contains 40 annual counts of the numbers of recruits and spawners in a salmon population. The units are thousands of fish. Recruits are fish that enter the catchable population. Spawners are fish that are laying eggs. Spawners die after laying eggs.

The classic Beverton–Holt model for the relationship between spawners and recruits is

where R and S are the numbers of recruits and spawners, respectively [46]. This model may be fit using linear regression with the transformed variables 1/R and 1/S.

Consider the problem of maintaining a sustainable fishery. The total population abundance will only stabilize if R = S. The total population will decline if fewer recruits are produced than the number of spawners who died producing them. If too many recruits are produced, the population will also decline eventually because there is not enough food for them all. Thus, only some middle level of recruits can be sustained indefinitely in a stable population. This stable population level is the point where the 45° line intersects the curve relating R and S.

9.5. Patients with advanced terminal cancer of the stomach and breast were treated with ascorbate in an attempt to prolong survival [87]. Table 9.4 shows survival times (days). Work with the data on the log scale.

Table 9.3 Forty years of fishery data: numbers of recruits (R) and spawners (S).

Table 9.4 Survival Times (Days) for Patients with Two Types of Terminal Cancer.

9.6. The National Earthquake Information Center has provided data on the number of earthquakes per year exceeding magnitude 7.0 for the years from 1900 to 1998 [341]. These data are available from the website for this book. Difference the data so that the number for each year represents the change since the previous year.

9.7. Use the problem of estimating the mean of a standard Cauchy distribution to illustrate how the bootstrap can fail for heavy-tailed distributions. Use the problem of estimating θ for the Unif(0, θ) distribution to illustrate how the bootstrap can fail for extremes.

9.8. Perform a simulation experiment on an artificial problem of your design, to compare the accuracy of coverage probabilities and the widths of 95% bootstrap confidence intervals constructed using the percentile method, the BC_a method, and the bootstrap t. Discuss your findings.

9.9. Conduct an experiment in the same spirit as the previous question to study block bootstrapping for dependent data, investigating the following topics.