Chapter 7
Vanilla FX Derivatives Pricing
This chapter introduces two primary responsibilities of a vanilla FX derivatives trader: maintaining volatility surfaces and quoting vanilla price requests.
Maintaining Volatility Surfaces
In some financial markets, all relevant market prices can be observed directly in the market. However, in OTC (over-the-counter) derivatives markets, prices are very often requested for contracts that have not been directly observed in the market. This flexibility is a key advantage of the OTC market structure.
To quote consistent vanilla option prices for any expiry date and strike, traders keep a volatility surface updated in each currency pair. Exhibit 7.1 shows a three-dimensional representation of the volatility surface in one currency pair.

Exhibit 7.1 Example volatility surface
The volatility surface can be split into two components: the ATM (at-the-money) curve and the volatility smile.
ATM Curve
ATM contracts are the backbone of the volatility surface; they define the term structure of implied volatility. ATM contracts are vanilla contracts quoted to a specific maturity and they have a strike near (or at) the forward to the same maturity.
ATM contracts are the most important price reference points within the FX derivatives market. In the interbank broker market ATM contracts are often quoted in a run of prices at the market tenors, the most liquid expiry dates within the market. For example, Exhibit 7.2 gives a run of ATM prices at market tenors: O/N (overnight, i.e., tomorrow), 1wk (one week), 2wk, 1mth (one month), 2mth, 3mth, 6mth, 1yr (one year), and 2yr.
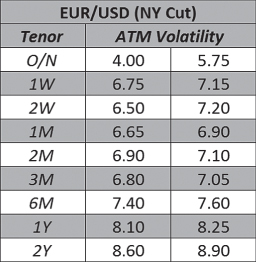
Exhibit 7.2 Example ATM run
The run shows the best bid and best offer that the broker currently has for the ATM contract at each tenor. These are tradable rates that have been made (contributed) by other banks. Therefore, in Exhibit 7.2, the EUR/USD 1mth ATM NY cut two-way implied volatility price is 6.65/6.9%: The contract will cost 6.9% volatility to buy while selling it will earn 6.65% volatility.
When traders talk, ATM implied volatility is often spoken about in terms of its “vol base,” meaning the approximate level of implied volatility in that currency pair. The “handle” is a similar term (e.g., “EUR/USD vol trades off a six handle” means the implied volatility in EUR/USD is 6-point-something-%). When written down, traders often use, for example, 61 to mean 6.1% implied volatility.
It is important to understand how this structure based around fixed market tenors works in practice. As the horizon date changes, the expiry date for each market tenor changes accordingly (the methodology for calculating tenor expiry dates is given in Chapter 10 and implemented in Practical D). Therefore, the contracts liquidly quoted in the market today have different expiry dates from those quoted yesterday or those quoted tomorrow. Plus as spot (and hence the forward outright) moves, the strike of the ATM contract changes too. This is the nature of an OTC market: Contracts are not standardized, although note that strikes are often rounded to the nearest five or ten pips so the ATM strike does not exactly change pip for pip as spot moves.
ATM implied volatilities at different tenors are plotted in a curve in Exhibit 7.3.

Exhibit 7.3 Example ATM curve
ATM curves are described as upward sloping if back-end (e.g., 1yr) ATM volatility is higher than front-end (e.g., 1mth) ATM volatility and as downward sloping if front-end ATM volatility is higher than back-end ATM volatility. In quiet markets, back-end ATM volatility tends to be higher than front-end ATM volatility. In stressed market conditions, ATM curves can become “inverted,” with higher front-end volatility.
In general, ATM curves move in an orderly manner: Single tenors rarely move in isolation and changes in the ATM curve are often characterized as either parallel or weighted shifts.
Within a parallel ATM shift, the ATM volatility at all maturities moves the same amount up or down as demonstrated in Exhibit 7.4.

Exhibit 7.4 Parallel ATM curve shift
Within a weighted ATM shift, ATM volatility at near maturities moves more than ATM volatility at far maturities as demonstrated in Exhibit 7.5.

Exhibit 7.5 Weighted ATM curve shift
Volatility Smile
The volatility smile defines how strikes away from the ATM strike are priced relative to the ATM implied volatility at a given tenor. Slicing through the volatility surface at a particular maturity produces a volatility smile as shown in Exhibit 7.6.

Exhibit 7.6 Example volatility smile
In the interbank broker market, the butterfly and risk reversal contracts are the instruments used to describe the volatility smile:
- The butterfly contract describes the wings of the volatility smile (i.e., how steep the sides of the volatility smile are).
- The risk reversal contract describes the skew of the volatility smile (i.e., how tilted the volatility smile is).
Butterfly and risk reversal contracts are quoted at market tenors like the ATM curve. In equity derivatives, lower strikes tend to have higher implied volatility than higher strikes at a given maturity because equities tend to rally slowly and drop quickly, but in FX different currency pairs have differently shaped volatility smiles. Some volatility smiles are tilted such that downside strikes have higher implied volatility than topside strikes (e.g., 1yr EUR/USD in July 2014) as shown in Exhibit 7.7.

Exhibit 7.7 Example downward-sloping volatility smile
Some volatility smiles are tilted such that topside strikes have higher volatility than downside strikes (e.g., 6mth USD/ZAR [South African Rand] in July 2014) as shown in Exhibit 7.8.

Exhibit 7.8 Example upward-sloping volatility smile
Some volatility smiles are symmetric and/or have low volatility (e.g., 1mth USD/HKD in July 2014) as shown in Exhibit 7.9.

Exhibit 7.9 Example symmetric volatility smile
Some volatility smiles are highly skewed and/or have high volatility (e.g., 1yr AUD/JPY at the height of the 2008 financial crisis) as shown in Exhibit 7.10.

Exhibit 7.10 Example extreme volatility smile
Volatility smiles have higher implied volatility on the “weaker” side of spot (i.e., the direction in which spot is more likely to jump or generally will be more volatile). For example, in major emerging market currency pairs quoted as USD/CCY, the main risk is a sharp EM currency devaluation that causes spot to jump higher. For this reason, USD versus EM currency pair volatility smiles are usually tilted so topside strikes cost more in implied volatility terms than downside strikes (see, e.g., the USD/ZAR example in Exhibit 7.8).
Updating the Volatility Surface
Traders watch for new volatility market information in the currency pairs for which they are responsible. The primary source for this information is the interbank broker market.
When a new price appears or a trade occurs in the broker market, the trader compares that volatility level with the midmarket volatility generated by the desk volatility surface for the same contract. If differences are observed, either the trader updates the volatility surface inputs such that the midmarket volatility hits the market price or the trader may conclude that the price/trade represents a trading opportunity.
Example 1: The USD/CAD 1mth ATM contract two-way price is quoted at 4.8/5.0%. In the trader's volatility surface the current 1mth ATM is marked at 5.0%. The trader takes this as a signal that implied volatility at shorter tenors is reducing and therefore the near end of the ATM curve must be moved lower as shown in Exhibit 7.11.
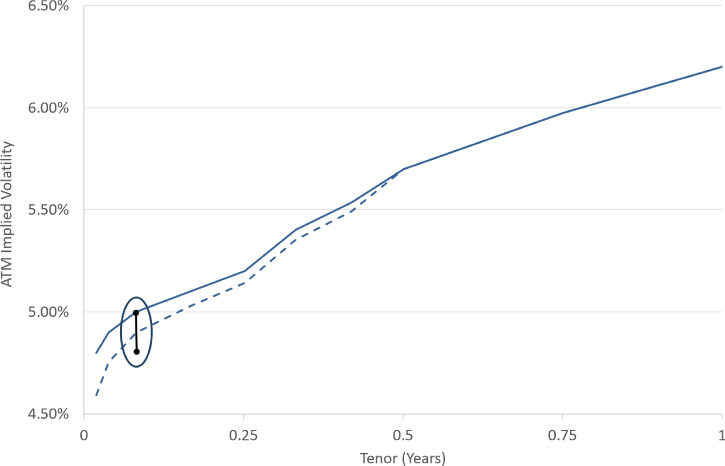
Exhibit 7.11 Changing the ATM curve to match new volatility market information
Example 2: A vanilla trade occurs in the market which suggests that the market is pricing topside strikes at higher implied volatility than before. The volatility smile at the same tenor as the trade is shown in Exhibit 7.12.

Exhibit 7.12 Existing volatility smile plus new volatility market information
The volatility smile at this tenor must be updated to hit this trading level but there are different ways in which this can be achieved. For example:
- The ATM can be moved higher, hence moving the entire volatility smile higher as shown in Exhibit 7.14.
- The wings of the volatility smile can be moved higher (i.e., strikes away from the ATM are priced relatively higher than the ATM) as shown in Exhibit 7.13.
- The skew of the volatility smile can be moved more “for the topside” (i.e., the volatility smile is tilted such that strikes above the ATM are priced higher while strikes below the ATM are priced lower). Note that the ATM stays unchanged in Exhibit 7.15.
Exhibit 7.13 Changing the ATM to match new volatility market information

Exhibit 7.14 Changing the wings of the volatility smile to match new volatility market information

Exhibit 7.15 Changing the skew of the volatility smile to match new volatility market information
The trader chooses between these three possibilities (or maybe a combination of them) when updating the volatility smile. As mentioned, single tenors within the volatility surface rarely move in isolation so the volatility smile is usually updated over multiple tenors at once. By observing many prices and trades in the market, the trader determines how best to update the entire volatility surface.
Vanilla Bid–Offer Spreads
The volatility surface generates a midmarket implied volatility. A bid–offer spread is then applied around the mid-rate to give a two-way price. The bid–offer spread for a particular vanilla contract changes depending on its maturity and the proximity of the strike to the ATM.
In practice, standard market bid–offer spreads are observed in the interbank market. Bid–offer spreads for ATM contracts at market tenors in liquid G10 pairs under “normal” market conditions often look similar to Exhibit 7.16. Simple interpolation can be used to generate bid–offer spreads for expiry dates between tenors. In general there is also a strong relationship between spot bid-offer spread and ATM bid-offer spread because the spot bid-offer spread must be crossed when delta hedging the ATM contract to maturity.
Exhibit 7.16 Standard ATM Bid–Offer Volatility Spreads
| Tenor | ATM Volatility Spread |
| O/N | 3.0% |
| 1wk | 1.0% |
| 2wk | 0.6% |
| 1mth to 1yr | 0.3% |
| 2yr | 0.35% |
| 3yr | 0.4% |
| 4yr | 0.45% |
| 5yr | 0.5% |
ATM volatility spreads are wide in short-dates, reduce to a minimum from 1mth to 1yr, then go wider again at longer tenors, but why? To get a better intuition, vega is used to go from ATM volatility spread to ATM premium spread in Exhibit 7.17.
Exhibit 7.17 Standard ATM Bid–Offer Volatility Spreads and Premium Spreads
| Tenor | ATM Volatility Spread | Vega (CCY1% 2 d.p.) | ATM Premium Spread (CCY1% 2 d.p.) |
| O/N | 3% | 0.02% | 0.06% |
| 1wk | 1% | 0.06% | 0.06% |
| 2wk | 0.6% | 0.08% | 0.05% |
| 1mth | 0.3% | 0.10% | 0.03% |
| 2mth | 0.3% | 0.16% | 0.05% |
| 3mth | 0.3% | 0.20% | 0.06% |
| 6mth | 0.3% | 0.28% | 0.08% |
| 1yr | 0.3% | 0.40% | 0.12% |
| 2yr | 0.35% | 0.56% | 0.20% |
| 3yr | 0.4% | 0.69% | 0.28% |
| 4yr | 0.45% | 0.79% | 0.36% |
| 5yr | 0.5% | 0.87% | 0.44% |
Recall from Chapter 6 that vega is the first derivative of option value with respect to implied volatility:
Therefore the ATM premium spread at a given tenor is calculated by multiplying the ATM volatility spread by the vega. Note that this calculation assumes that vega is unchanged as implied volatility changes.
Exhibit 7.17 shows that looking at ATM volatility spread alone is misleading when comparing bid–offer spreads at different tenors because shorter maturities have lower vega. In most currency pairs the 1mth ATM is the most liquid ATM contract and it therefore has the tightest bid–offer premium spread. Bid–offer spreads in less liquid currency pairs will be wider than those shown in Exhibit 7.17, and the most liquid currency pairs will be tighter, but the relative shape of the bid–offer spread curve is fairly consistent across currency pairs.
For strikes away from the ATM at a given maturity, consider two possible methods of generating the bid–offer spread:
- Constant premium spread
- Constant volatility spread
At a given maturity, the maximum vega exposure occurs on ATM strikes. Strikes away from the ATM have lower vega as shown in Exhibit 7.18.

Exhibit 7.18 Vega versus put strike delta
A 1yr ATM option has 0.40% vega so a 0.25% ATM bid–offer volatility spread equates to a 0.10% bid–offer premium spread. If all strikes at the 1yr tenor had the same premium bid–offer spread, wing strikes would have a wider bid–offer volatility spread due to lower vega as shown in Exhibit 7.19.

Exhibit 7.19 Volatility spread versus put strike delta
If all strikes at the 1yr tenor had the same volatility bid–offer spread, wing strikes would have a tighter bid–offer premium spread due to lower vega as shown in Exhibit 7.20.

Exhibit 7.20 Premium spread versus put strike delta
In practice, for strikes away from the ATM in liquid currency pairs, the bid–offer spread widens in volatility terms, but not as much as constant premium spread. For example, if the 1yr ATM has 0.25% volatility spread and 0.10% premium spread, a 1yr 10 delta vanilla option might have 0.35% volatility spread and hence 0.06% premium spread.
Vanilla Price Making
When price making vanilla FX derivatives, traders adjust their prices based on market sentiment, plus contracts can either be transacted delta hedged or live.
Price Making Overview
When a new vanilla price request is received, the FX derivatives trader views the contract in their desk pricing tool. The price shown in the tool takes the midmarket volatility from the desk volatility surface and applies a default bid–offer spread.
For example, a client requests a GBP/USD 2mth 1.6800 GBP call in GBP20m. The default mid on the contract is 6.45% and the system two-way price is 6.25/6.65%. This is called a neutral rate because neither the bid nor the offer has been improved.
The task of the trader is then to go from the default system rate to a rate they are happy to quote. One of the main factors within the adjustment is the position preference of the trader. As described in Chapter 3, price making is performed with reference to the current trading position. If a trader aims to change their position (for example, by selling vega, buying gamma, or buying options with topside strikes), these preferences are reflected within price making.
The other important factor within vanilla option price making is market sentiment. There are two types of market sentiment: structural and temporary:
- Structural market sentiment involves market-wide preferences to, for example, buy very low-premium options on the high side of the volatility smile or buy options near the ATM on the low side of the volatility smile. These effects usually apply over and above the default modeling of the volatility surface and therefore need to be adjusted for within price making.
- Temporary market sentiment is the current market preference for various types of contract—that is, is the market currently neutral, bid (the market prefers to buy), or offered (the market prefers to sell) for specific event dates? short-dates? back-dates? skew? wings? For example, suppose the 1mth ATM is 7.5/7.7% but it last traded at 7.6% and was bid on at the time. If there is then a new client price request in something similar to 1mth ATM (i.e., a contract with a similar expiry date and similar strike for which the 1mth ATM would be a reasonable hedge), it is appropriate to show a better bid on the contract. If the default system two-way rate on the new contract is 8.0/8.25%, an appropriate quoted rate might be 8.1/8.25%.
Market sentiment is most easily judged by observing the interbank broker market. Traders learn how the normal transaction process for different vanilla contracts works. For example, the implied volatility rate on an ATM contract will start relatively wide—12.45/12.75%—and over time it will tighten up as better bids and offers are shown—12.55/12.7%…12.6/12.7%…12.6/12.65%—before eventually trading somewhere within the original rate. This process usually takes around 30 minutes but it can take anything from a few minutes to a few hours.
The trading level and the speed of transaction are linked and they give information about the current market sentiment:
- If traders can wait to transact and want to deal at the best possible level, they will work slowly toward a midmarket trading level.
- If traders need to transact quickly, they will usually need to cross a larger spread from midmarket.
At the extreme, if the opening bid is hit straightaway, that constitutes a strong sell signal, and if the opening offer is paid straightaway, that constitutes a strong buy signal.
Market sentiment should be reflected within price making because it makes risk easier to recycle and enables better (tighter) prices to be quoted for clients. Occasionally prices will be quoted with either a midmarket bid (i.e., the bid shown is equal to the system midmarket) or a midmarket offer (i.e., the offer shown is equal to the system midmarket).
Transacting Delta Hedged or Live
Vanilla FX derivative price requests are either quoted in volatility or premium terms. FX derivatives traders typically quote prices in volatility terms because this makes the price making process easier. For a vanilla contract with a fixed maturity and strike, each time the spot rate (and therefore the forward) changes, the option premium changes (although the premium is usually rounded so this reduces the impact). However, the implied volatility quoted for a given contract can stay stable for longer, perhaps up to a few minutes in normal market conditions.
Vanilla price requests that are quoted in volatility terms are traded delta hedged. The Black-Scholes formula is used to calculate option premium and option delta, then a spot or forward hedge is transacted at the same rate at which the deal was priced. The interbank broker market and institutional clients who trade FX volatility typically transact in this manner.
Vanilla price requests that are quoted in premium terms are traded live (i.e., without a delta hedge). When a client trades live, the appropriate spot or forward deal must be transacted in the market in order to make the package delta neutral for the FX derivatives trader's position. Corporate clients who want to hedge future FX flows or institutional clients who plan to hold a trade in isolation until maturity typically transact in this manner. Either a salesperson or (increasingly) a machine deals with updating the price as spot moves and then hedges the delta when the client trades.
If the client trades live, the delta must be hedged as the deal is transacted. In this case the two-way premium is calculated using not only a two-way implied volatility but also two-way spot and forward rates, since that spread must be crossed in the market when the trade is delta hedged.
For long-dated options, using the correct two-way forward within pricing is particularly important since a substantial amount of the total premium bid–offer spread can come from the forward spread. Exhibit 7.21 shows the same vanilla option twice in a pricing tool: Leg 1 has choiced market data; appropriate if the counterparty is going to transact delta hedged with a forward hedge. Leg 2 has spread market data; appropriate if the counterparty is going to transact live (i.e., without a delta hedge).

Exhibit 7.21 Vanilla option pricing with and without delta hedge
Market Conventions
It is important that traders know the market conventions in the currency pairs they trade. For example, different ATM contracts are traded in different currency pairs:
- In all G10 (and some EM) currency pairs, the ATM contract is traded as a straddle (i.e., a call and a put with the same maturity and strike; ATM straddles are covered in more detail in Chapter 8).
- In other EM pairs, the ATM contract is traded as a single ATMF (at-the-money-forward) vanilla option with the strike equal to the forward, plus a forward hedge.
- The final ATM contract is ATMS (at-the-money-spot), which is a single vanilla option with the strike equal to current spot.
When trading vanilla options with strikes away from the ATM, the market convention is to always trade the out-of-the-money side (i.e., trade the call or put, whichever has the lower absolute delta). Therefore, if a vanilla option has a strike above the ATM, it will be traded as a CCY1 call/CCY2 put. If the strike is below the ATM, it will be traded as a CCY1 put/CCY2 call. Traded contracts are shown in Exhibit 7.22.

Exhibit 7.22 Traded vanilla option contracts
This is important because, although the Greeks on a delta hedged call and a delta hedged put are the same (due to put–call parity), the out-of-the-money direction has a smaller premium and a smaller expected payoff at maturity and hence has less credit risk than the in-the-money direction. Traders should be careful when in-the-money options are requested by clients: Why wouldn't the conventional side be traded? Some banks tried to sell deep-in-the-money options as a mechanism to earn badly needed cash during the 2008 financial crisis. Although it isn't covered within this book, when trading FX derivatives contracts it is vital that the interest rates used correctly reflect the counterparty credit risk and this is particularly important for high premium in-the-money options.
When quoting in volatility terms, prices are usually rounded to the nearest 0.05% in shorter tenors and 0.025% in longer tenors, with the inflection point usually around the 2mth tenor. This rounding keeps volatility price making clean and ensures that prices quoted in volatility terms can be updated less frequently. When quoting in CCY1% premium terms, prices are usually rounded to the nearest quarter (0.0025%) or half (0.005%) a basis point (0.01%). A basis point is a key concept in derivatives pricing; it is always equal to a hundredth of one percent of the notional.
