Straddle Price Making

Thanks to put–call parity, making a volatility price for a straddle is the same as making a volatility price for a single vanilla option in the combined notional with the same expiry, strike, and cut. A single two-way volatility quote is made and, if dealt, that volatility is used to determine the premiums on both legs.

Zero-Delta ATM Straddles

By far the most commonly traded straddle contracts are zero-delta straddles: a straddle with its strike set such that and therefore . In all G10 and some EM currency pairs, the ATM contract is traded as a zero-delta straddle. Therefore, buying a 1mth ATM contract in EUR/USD actually means transacting a call and put, which forms a straddle.

Zero-Delta Straddle Strike Placement

The zero-delta straddle strike is positioned close to the forward for the same maturity but they are not exactly the same. Recall from Chapter 5 that the forward is derived from spot and interest rates:

where is the forward to time T (measured in years), S is the spot, and and are continuously compounded interest rates (see Chapter 10) to time T in CCY1 and CCY2 respectively.

Dipping briefly into Black-Scholes mathematics:

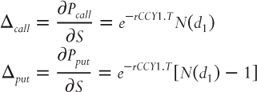
where is the cumulative normal distribution function and σ is volatility.

At the zero-delta straddle strike (K), . Therefore:

Recalling the shape of cumulative normal distribution function from Chapter 5, if , then . So

Therefore, the zero-delta straddle strike is higher than the forward due to the adjustment , which is linked to the Itō correction within the Black-Scholes framework (see Chapter 5).

Unfortunately, this is not quite the end of the story. The above is standard Black-Scholes mathematics, which assumes the premium is paid in CCY2. In, for example, EUR/USD (USD premium), this is the case; but in, for example, USD/JPY (USD premium), the market convention is to pay premium in CCY1.

In CCY1 premium pairs (see Chapter 14 for more details on premium adjusted delta):

which works through as:

Therefore, when the premium is paid in CCY1, the zero-delta straddle strike is lower than the forward due to the adjustment: .

In both cases, the difference between the forward and the ATM zero-delta straddle strike increases as volatility and time to expiry get larger.

Straddle Trading Exposures

Exhibit 8.2 shows the vega profile of a straddle. It is identical to the vega profile of a single vanilla with the same (combined) notional, strike, and maturity. As expected, the vega peak occurs at the strike.

Strangle Price Making

When making a price on a strangle, a single two-way volatility is quoted. If dealt, that volatility is used to determine the premiums on both legs. The bid–offer spread quoted on a strangle in volatility terms will usually be wider than the ATM spread to the same maturity because strikes away from the ATM have less vega (see Chapter 7).

A strangle containing strikes and has (approximate) implied volatility:

where strike has implied volatility and vega while strike has implied volatility and vega . Therefore, if the strangle contains equal delta call and put strikes with roughly equal vega, the strangle volatility will be close to the average of the two individual strike volatilities.

Strangle Trading Exposures

The vega profile of a strangle is similar to the vega profile of a straddle with the same maturity and notional per leg except that the strangle vega profile is wider because the strikes are spread out away from the ATM. At lower deltas the vega profile of the strangle has two distinct peaks from the two strikes as shown in Exhibit 8.4.

Butterfly Price Making

In the interbank market, prices on broker fly contracts are quoted as the volatility differential between the strangle strikes and the ATM strikes. Plus the contract is quoted such that the butterfly notional is the strangle notional.

The broker fly has zero vega and minimal gamma by construction. Therefore, it is quoted significantly tighter than the strangle component in isolation. A bid–offer spread less than half the strangle bid–offer spread will often be shown.

Butterfly Trading Exposures

A long butterfly position is often flat ATM vega by construction and long vega in the wings from the long strangle strikes as shown in Exhibit 8.6.

Risk Reversal Price Making

A risk reversal is a spread contract. It has two legs: one bought, one sold. There are offsetting gamma and vega exposures between the legs and therefore the product is quoted tighter than the equivalent contract where either both legs are bought or both legs are sold. When quoting a price on spread, rather than quoting tighter two-way prices on both legs, the market convention is to quote one leg with a choice price (i.e., a single volatility at which it is possible to buy or sell, often denoted CH) and the other leg with a spread price (i.e., a two-way volatility price). In other words, all the bid–offer spread is put onto one of the legs. Risk reversals are usually quoted with around half the overall bid–offer spread of the equivalent strangle.

For example, USD/BRL 1yr 25d risk reversal:

• Outright 1yr 25d call implied volatility: 14.35 / 14.85%
• Outright 1yr 25d put implied volatility: 10.75 / 11.25%
• 1yr 25d risk reversal implied volatility: 14.35 / 14.85% vs. 11.0% CH

Risk reversals for a given delta are often quoted as an implied volatility differential between the two strikes (e.g., 3.35/3.85% in the above USD/BRL example). This is appropriate when the risk reversals strikes have the same delta and hence there is minimal net vega on the structure. Once the trade is agreed in volatility differential terms, the volatility on one of the strikes is agreed and that determines the volatility of the other strike; hence both premiums can be calculated. The risk reversal product is examined in far more detail in Chapter 12.

Risk Reversal Trading Exposures

The bought leg in the risk reversal generates a long vega exposure with a peak at the long strike while the sold leg generates a short vega exposure with a (negative) peak at the short strike. This is shown in Exhibit 8.9.

ATM Calendar Spread Price Making

Standard vanilla spread pricing rules apply: A spread (two-way) price is shown on the ATM straddle with more vega and the other ATM straddle is shown choice. Therefore, for ATM calendar spreads the far ATM straddle is spread since vega increases at longer maturities. Calendar spreads usually have substantial offsetting vega risk and are therefore quoted tighter than two ATM contracts in the same direction: Perhaps the standard bid–offer spread will be shown on the far leg, with the near leg quoted choice.

ATM Calendar Spread Trading Exposures

ATM calendar spreads give exposures to the shape of the ATM curve since they contain offsetting vega positions in two tenors. Exhibit 8.10 shows the bucketed vega profile from the long 3mth/6mth vega-neutral ATM calendar spread. This position will make money if the 3mth ATM volatility rises more than the 6mth ATM volatility.

Call/Put Spread Price Making

The standard vanilla spread quoting rules apply to call spreads and put spreads too: Spread the leg with more vega and choice the other leg. It is interesting to note that once call/put spreads are placed in a delta hedged trading portfolio, the vega exposures are the same as the vega exposures from a risk reversal with the same strikes; the long strike generates a long vega exposure and the short strike generates a short vega exposure.

Seagull Price Making

On vanilla spreads with more than two legs there are few concrete rules on how to quote prices but generally the price is easier to understand if as many legs as possible are quoted choice. Plus the legs with the most vega should be spread because their price quoted in volatility terms will be the tightest.