Chapter 6
Vanilla FX Derivatives Greeks
It is time to start some derivative analysis. The aim of this chapter is to introduce the basic Greek exposures on European vanilla options. This is stylized Black-Scholes analysis with zero interest rates throughout; hence the forward rate is always equal to the spot rate and discounting considerations can be ignored. The charts within this chapter can be generated in Excel after completing Practical C.
Option Value
A vanilla call option gives the right, but not the obligation, at maturity to buy spot (i.e., buy CCY1 versus sell CCY2) at the strike in the agreed notional. Exhibit 6.1 shows the value at maturity of a long (bought) vanilla call option over different spot levels. This value at maturity is often described as the option payoff.

Exhibit 6.1 Value at maturity of long vanilla call option with 100.00 strike
For a short (sold) vanilla call option, the value at maturity is reflected in the spot-axis resulting in an increasingly negative value above the strike, as shown in Exhibit 6.2. As expected, a long position plus short position in the same contract results in zero value over all spots (i.e., no position).

Exhibit 6.2 Value at maturity of short vanilla call option with 100.00 strike
The initial option premium is sometimes added into these diagrams, as per Exhibit 6.3. Adding the premium into the payoff is appropriate if the plan is to transact the option and then hold it isolated until maturity (see the section on breakevens in Chapter 17). However, in delta hedged trading portfolios, many options are risk managed together. Therefore, it is changes in option value caused by changes in the market data that are most important, called the exposures. This analysis is slightly cleaner if premium is omitted.

Exhibit 6.3 Total P&L at maturity (including initial premium) of long vanilla call option with 100.00 strike
A vanilla put option gives the right, but not the obligation, at maturity to sell spot (i.e., sell CCY1 versus buy CCY2) at the strike in the agreed notional. Exhibit 6.4 shows the value at maturity of a long vanilla put option over different spots.

Exhibit 6.4 Value at maturity of long vanilla put option with 100.00 strike
Again, a short vanilla put option has a value at maturity that is reflected in the spot-axis. This results in increasingly negative value below the strike, as shown in Exhibit 6.5.

Exhibit 6.5 Value at maturity of short vanilla put option with 100.00 strike
So far, so straightforward. Now see how the long vanilla call option value changes prior to maturity in Exhibit 6.6. Call option value prior to maturity is convex in spot, implying a positive second derivative (i.e., positive gamma, discussed later in this chapter).

Exhibit 6.6 Value of long vanilla call option with 100.00 strike and 10% volatility
The value of a vanilla option can be decomposed into intrinsic value plus time value:
- Intrinsic value is the option payoff at maturity.
- Time value is the value expected to be generated from the remaining optionality in the contract.
Optionality is the ability of the contract to transact spot (e.g., buy spot for a call option), or not, depending on the spot level at maturity. In the value at maturity charts, optionality is represented by the change in angle at the strike.
If the forward to maturity is far above or below the strike, the optionality has minimal value since there is little chance of spot going through the strike before maturity. Therefore, option value converges to intrinsic value away from the strike on both sides. Maximum time value occurs when the forward to maturity is equal to the strike; here the optionality is most valuable, as shown in Exhibit 6.7.

Exhibit 6.7 Time value of long vanilla call option with 100.00 strike and 10% volatility
Looking at call option value at higher volatility in Exhibit 6.8 shows how higher volatility leads to higher time value as the distribution widens. Intuitively, if spot is more volatile, it will have more chances to go through the strike.

Exhibit 6.8 Value of long vanilla call option with 100.00 strike and 20% volatility
Therefore, the value of a vanilla option can give information about how much optionality there is within a particular contract. For low-premium vanilla options, there must be minimal intrinsic value and minimal time value on the contract. For high-premium vanilla options, there may be high intrinsic value, high time value, or both.
Within the value charts, the strike of the option is fixed and spot is being changed. If strike were being changed instead for a fixed spot, the diagram would be approximately reflected in the strike level. For example, if the strike moves higher on a call option, the premium decreases because the payoff above the strike is being moved further away from the forward to maturity.
Delta
Taking the first derivative of option value with respect to spot gives one of the most important Greeks: delta, sometimes called spot delta for clarity. In symbols:
where P is option price and S is the spot rate. Note that traders sometimes say they are, e.g., “long spot” to mean “long exposure to spot” (i.e., long delta). In practice, delta is quoted either as a % of the notional amount, or as a cash amount in the notional currency where:
It is important to appreciate that forward delta can also be calculated, but this distinction will be overlooked for now:
where F is the forward rate to the option maturity.
Delta is the exposure of the option value to the spot rate. The delta amount for a given option is therefore the equivalent spot notional that must be transacted (in the opposite delta direction) in order for the option plus the spot hedge to be delta neutral (i.e., zero delta exposure).
For a given option, delta can either be quoted in % terms or cash terms. For example, if an AUD/USD call has 25% spot delta and AUD40m of the contract is bought, AUD10m AUD/USD spot must be sold “on the hedge” in order to leave delta in the trading position unchanged. If the AUD/USD call was sold instead, spot must be bought on the hedge.
When a position is delta neutral, no P&L change results from spot moving higher or lower. However, this only works for small moves in spot if the second derivative (gamma) is non-zero.
Exhibit 6.9 shows the delta of a long vanilla call option with a 100.00 strike. This delta can be calculated by taking the gradient of the call option value profile chart from Exhibit 6.6.
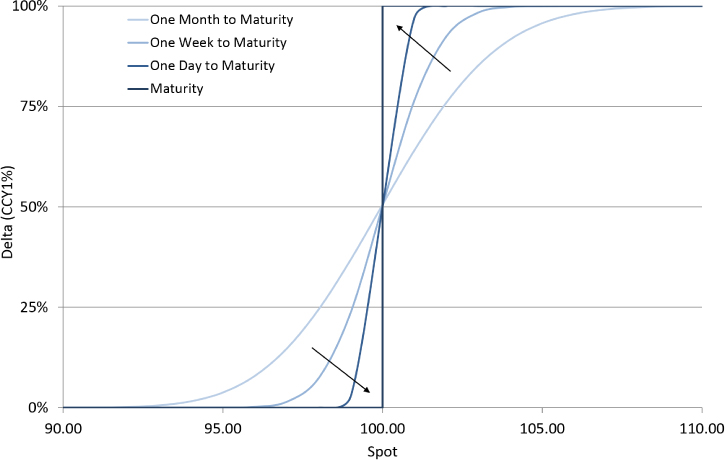
Exhibit 6.9 Delta of long vanilla call option with 100.00 strike
At maturity, there is a discontinuity in delta from 0% below the strike to 100% above caused by either expiring the option below the strike (hence having no position) or exercising the option above the strike (hence buying spot in the full notional amount). Prior to maturity, the delta still goes from 0% to 100% but the change occurs over a wider spot range. Notice that the delta at all maturities is around 50% when spot (or more accurately, the forward to maturity) is equal to the strike.
Intuitively, it shouldn't be a surprise that a long call option position has a positive delta since the value of the call option increases with spot higher, the same as a long spot position.
Delta can also be (approximately) thought of as the % chance of ending up in-the-money (ITM) at maturity. Call options with strikes close to spot (the forward) have a delta of approximately 50% (i.e., a 50/50 chance of ending up ITM at maturity). As spot goes lower, the call option delta reduces as does the chance of ending up in-the-money.
Exhibit 6.10 shows the option value of a long vanilla put option with a 100.00 strike.

Exhibit 6.10 Value of long vanilla put option with 100.00 strike and 10% volatility
Again, taking the first derivative of this option value with respect to spot gives delta. The delta of the option value from Exhibit 6.10 is shown in Exhibit 6.11. Intuitively, put options have negative delta because put option value increases with spot lower, the same as a short spot position.

Exhibit 6.11 Delta of long vanilla put option with 100.00 strike
For example, if an AUD/USD put option has –10% spot delta and AUD80m of the contract is bought, AUD8m AUD/USD spot must be bought on the hedge in order to leave delta in the trading position unchanged. If the option was sold instead, spot must be sold on the hedge.
Put options with strikes close to the forward have a delta of approximately –50% (i.e., 50/50 chance of ending up ITM), and as spot goes lower, the put delta increases negatively. In practice, when traders describe deltas they often leave off the %, so a “twenty-five delta call” actually has a 25% delta. Plus, when describing put options, the negative sign is often omitted, so a “ten delta put” actually has a –10% delta.
The call delta and put delta profiles in Exhibits 6.9 and 6.11 are identical except that the put option delta is 100% lower than the call option delta over all spot values. Put another way, a call option can be converted into a put option simply by selling a notional amount of forward to maturity. In hockey-stick diagram world, a long call option (shown in Exhibit 6.12) plus a short forward with the same strike, maturity, and notional (shown in Exhibit 6.13) gives a long put option (shown in Exhibit 6.14).

Exhibit 6.12 Value at maturity of long call option

Exhibit 6.13 Value at maturity of short forward
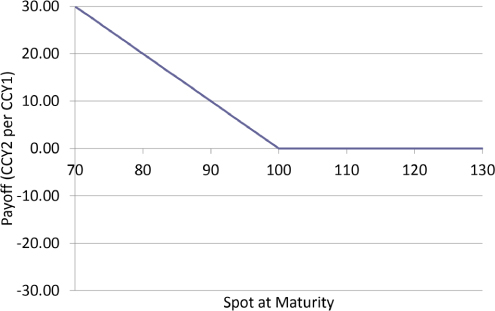
Exhibit 6.14 Value at maturity of long put option
This is a powerful result called put–call parity. In words, a vanilla option can be changed from a call into a put (or a put changed into a call) by trading the forward in the same strike, maturity, and notional:
- Long call + short forward = long put
- Long put + long forward = long call
Additionally, a forward can be constructed from a call option and a put option with all other contract details the same. This is called a synthetic forward:
- Long call + short put = long synthetic forward
- Short call + long put = short synthetic forward
Consider the formula for a long synthetic forward. At maturity, if spot is above the strike, the long call will be exercised (and the short put expired) and spot will be bought at the strike. If spot is below the strike, the short put will be exercised (and the long call expired) and spot will be bought at the strike. No matter where spot ends up at maturity, spot is bought at the strike—exactly the same as owning the forward contract.
One consequence of this is that since the forward has no optionality, delta hedged calls and delta hedged puts with the same maturity and strike have the same Greek exposures. For this reason traders don't usually think in terms of calls or puts once the option is in their trading book; they talk only in terms of strikes and notionals (e.g., “I've got a 1.3250 strike in EUR50m” rather than “I've got a 1.3250 put in EUR50m”).
Another consequence of put–call parity is that call options and put options with the same maturity and strike must always be valued at the same implied volatility; otherwise, arbitrage would be possible via trading the forward. This also explains why approaching the trading desk and asking “who does calls and who does puts?” would be met with wide eyes.
Gamma
Taking the first derivative of delta (or the second derivative of option price) with respect to spot gives another important Greek: gamma. In symbols:
In practice, gamma is quoted either as a % of the notional amount, or as a cash amount in the notional currency where:
Gamma describes how delta changes with spot and is therefore a measure of how stable delta is as spot moves. Due to put–call parity, call and put options with the same strike and maturity have the same gamma profile, shown in Exhibit 6.15. This gamma can be calculated by taking the gradient of either the call option delta profile from Exhibit 6.9 or the put option delta profile from Exhibit 6.11.

Exhibit 6.15 Gamma of long vanilla option with 100.00 strike
As time moves toward the option maturity, gamma increases and concentrates around the strike. Gamma at maturity is not shown on the graph because the discontinuity in delta cannot be neatly differentiated. As discussed previously, gamma can be seen in the curvature of the option value versus spot charts. At longer maturities, when there is a wider spot distribution, delta changes slowly as spot moves, hence low gamma. At shorter maturities, when there is a tighter spot distribution, delta changes quickly as spot moves, hence high gamma.
Long positions in vanilla options always have long gamma exposure because time value leads to a convex option value versus spot relationship. Likewise, short positions in vanilla options always have short gamma exposure. For a given vanilla option, peak gamma occurs at the strike because this is the point at which optionality is maximized.
Vega
Taking the first derivative of option value with respect to implied volatility gives a third important Greek: vega. In symbols:
In practice, vega is usually quoted either as a % of the notional amount, or as a cash amount in the notional currency where:
Note that traders describe their position as, e.g., “long vol” to mean “long exposure to implied volatility” (i.e., long vega).
Exhibit 6.16 shows how the vega profile of a long vanilla option position changes over time. Again, due to put–call parity, since forward contracts have no exposure to implied volatility, call and put options with the same strike and maturity have the same vega profile. The peak vega on a vanilla option reduces over time. Intuitively, vega increases at longer maturities because there is more time for a change in implied volatility to impact the payoff.
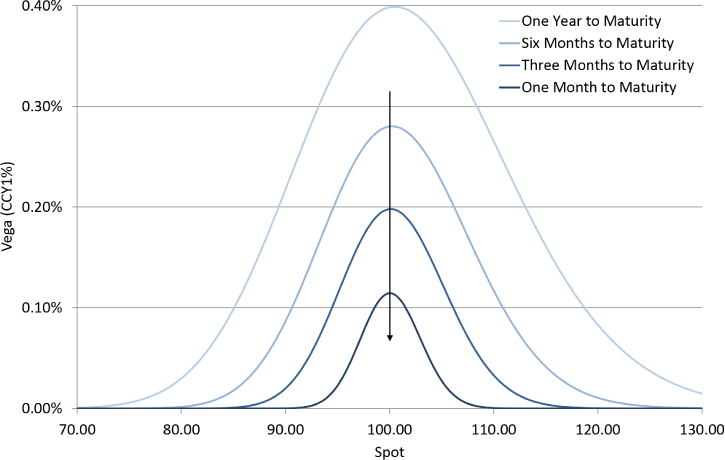
Exhibit 6.16 Vega of long vanilla option with 100.00 strike
For a given vanilla option, peak vega (like gamma) occurs at the strike where optionality and time value is maximized. Far away from the optionality the option is either like a forward (if deep in-the-money) or like no position (if deep out-of-the-money). In either of these cases, changing volatility has minimal impact on option value.
Long vanilla options always have long vega exposure. Intuitively this is because higher volatility widens the distribution and therefore brings larger positive payoffs into play, hence increasing the option value. Likewise, short vanilla options always have short vega exposure.
Summary
When trading FX derivatives, the majority of trading P&L is generated from the three Greek exposures introduced in this chapter: delta, gamma, and vega.
Most often, vanilla options are booked into a trader's position with the appropriate delta hedge so new deals cause no net change to the delta exposure within the position, only the vega and gamma exposures are impacted. Buying delta hedged vanilla options results in longer vega and gamma exposures. Selling delta hedged vanilla options results in shorter vega and gamma exposures.
Gamma and vega both come from the optionality within the derivative contract and both are therefore maximized at the strike for vanilla options. A trading position with a long vega exposure will make money if implied volatility rises and lose money if implied volatility falls while gamma impacts how delta moves with spot. Trading long and short gamma positions is covered in Chapter 9.
Long-dated vanilla options have relatively higher vega and lower gamma exposures while short-dated vanilla options have relatively higher gamma and lower vega exposures. Therefore, the main risk on a given vanilla option changes over time from mainly vega risk to mainly gamma risk. The inflection point between the two types of risk occurs around two-month maturity.
