Constructing a Volatility Smile in Excel

Constructing a volatility smile using the Malz smile model builds understanding of the volatility surface market instruments. The Black-Scholes framework can then be used to calculate strikes for different deltas to show how the market instruments impact strike placement within the volatility smile.

Task A: Set Up the Malz Smile Model

Recall the Malz formula for implied volatility at a given (positive) delta put from Chapter 12:

This formula can be coded up in Excel:

Check that and the 25% put delta and 25% call delta (75% put delta) implied volatility matches up with the standard approximations:

Task B: Plot Implied Volatility versus Delta and Investigate Parameters

The function output can be extended to generate a full volatility smile from 0% to 100% delta:

The volatility smile can then be plotted:

Check that the volatility smile updates as expected when the ATM, risk reversal, and butterfly prices change. This becomes easier if the volatility smile chart is placed next to the inputs on the same Excel sheet, and the low and high values of the implied volatility axis in the chart are fixed rather than automatically rescaling.

Task C: Use Black-Scholes to Get Strike from Delta

The Black-Scholes framework can be used to get the equivalent strike for a given delta. Recall that:

where is spot, is strike, and are continuously compounded interest rates in CCY1 and CCY2, is time to expiry (in years), is implied volatility, is the cumulative normal distribution function, and .

The formula for can be inverted to get the strike from the put delta:

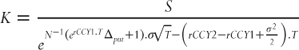
where is the inverse cumulative normal distribution function.

These functions can be implemented first on the Excel sheet using =NORMSDIST(X) for and =NORMSINV(X) for . A strike input is used to generate the put delta, which is itself then used to generate a strike output. If the strike input and output are equal as other inputs change, this confirms that the formulas are correctly implemented:

Note that the put delta used within Black-Scholes formulas is its true (negative) value rather than the positive quoted put delta.

Task D: Switch to VBA Functions and Plot Implied Volatility versus Strike

These functions are long and messy in the sheet but they are much neater as VBA functions. The Malz smile volatility function is simple:

Function MalzSmileVol(ATM As Double, RR25d As Double, Fly25d AsDouble, PutDelta As Double) As Double
    MalzSmileVol = ATM + 2 * RR25d * (PutDelta - 0.5) + 16 *    Fly25d * (PutDelta - 0.5) ^ 2
End Function

The put delta from strike VBA function uses the cumulative normal distribution worksheet function:

Function PutDeltaFromStrike(S As Double, K As Double, rCCY1 AsDouble, rCCY2 As Double, T As Double, v As Double) As Double
    Dim d1 As Double
    d1 = (Log(S / K) + (rCCY2 - rCCY1 + v ^ 2 / 2) * T) / (v * Sqr(T))
    PutDeltaFromStrike = Exp(-rCCY1 * T) *    (Application.WorksheetFunction.NormSDist(d1) - 1)
End Function

The strike from put delta VBA function accesses the inverse cumulative normal distribution worksheet function. The calculation is split into three parts to make it easier to follow and debug:

Function StrikeFromPutDelta(S As Double, PutDelta As Double, rCCY1 AsDouble, rCCY2 As Double, T As Double, v As Double) As Double
    Dim part1 As Double, part2 As Double, part3 As Double
    part1 = Exp(rCCY1 * T) * PutDelta + 1
    part2 = v * Sqr(T)
    part3 = (rCCY2 - rCCY1 + 0.5 * v ^ 2) * T
    StrikeFromPutDelta = S / Exp(Application.WorksheetFunction    .NormSInv(part1) * part2 - part3)
End Function

Again, the VBA functions can be tested by placing them alongside the existing Excel functions:

Once matches are confirmed, the VBA functions can be combined to plot implied volatility versus delta and implied volatility versus strike.

It is not possible to find strikes for 0 or 100 delta options, so replace 0% delta with, for example, 0.01% and replace 100% delta with, for example, 99.99%:

Task E: Investigate Volatility Smile Strike Placement

In practice, the most important strikes at a given tenor are 10 delta and 25 delta puts and calls, plus the ATM. In the Malz framework these strikes are equivalent to these put deltas: 10d, 25d, 50d, 75d, 90d. Using the functions developed, strike placement within the volatility smile can be investigated, remembering to use the negative delta to calculate the strike. With no volatility smile, the strikes for these deltas are roughly equally spaced, with relatively slightly larger differences for topside strikes due to the log-normality of the terminal spot distribution:

Reducing implied volatility or time to maturity causes the terminal distribution to tighten and hence the strikes are positioned closer to the ATM:

Increasing implied volatility or time to maturity causes the terminal distribution to widen and hence the strikes are positioned further from the ATM:

Increasing the butterfly causes the strikes to move further from the ATM, with a larger impact at lower delta strikes due to the higher implied volatility:

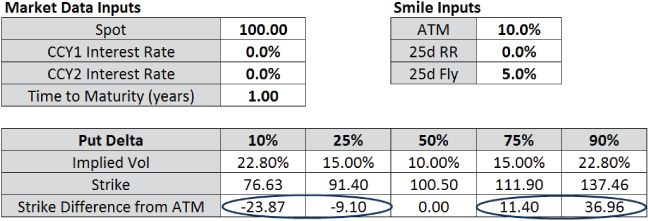
Changing the risk reversal moves the strikes for a given delta further away from the ATM on the high side of the volatility smile and closer to the ATM on the low side of the volatility smile:

Moving CCY1 interest rates higher or CCY2 interest rates lower causes the forward to move lower and hence the whole volatility smile moves lower:

Moving CCY2 interest rates higher or CCY1 interest rates lower has the opposite effect.