Chapter 21
European Digital Options
European digital options are conceptually one of the simplest exotic products; at maturity the option either pays out a fixed cash amount or nothing, depending on whether spot is above or below a specified digital level. However, the risk management of these options, particularly at expiry, can be challenging due to the binary nature of the payout (either receive all the cash or none) over a one-pip spot difference.
A European digital call option pays out cash on the delivery date if spot at maturity is at or above the digital level, as shown in Exhibit 21.1. While a European digital put option pays out cash on the delivery date if spot at maturity is below the digital level.
Exhibit 21.1 100.00 European digital call payoff at maturity
As a technical aside, the European digital call here is defined as paying out at the digital level while the European digital put does not. This is not necessarily the case but it is important that European digital put + European digital call = guaranteed payout at maturity. Put another way, transacting both the digital put and digital call with all other details the same should not result in both contracts paying out. In practice these issues are dealt with via the confirmation documents agreed when trading the contract.
European digital options prices are quoted as a percent of the payout amount, with prices generally rounded to the nearest 0.05% for customers or 0.25% in the interbank broker market. For example, a trader might make a rate of 23.5/24.5 USD% on USD/JPY 3mth 100.00 USD European digital call in USD1m payout (also called USD1m notional). If the client wishes to buy, they must pay USD245k value spot. At expiry, if the spot rate is above 100.00, the client will receive USD1m on the delivery date. Prices cannot be quoted as a percent of the non-payout currency; there is no way to switch between the currencies because the option does not have a strike.
European digital prices are generally between 0% and 100%. If the forward is close to the digital level, the European digital option value will be around 50%. European digital call prices over time are shown in Exhibit 21.2.
Exhibit 21.2 100.00 European digital call value over time
European Digital Replication
European digital calls can be replicated using tight vanilla call spreads and European digital puts can be replicated using tight vanilla put spreads. The vanilla call spread replication for a 100.00 European digital call is shown in Exhibit 21.3.
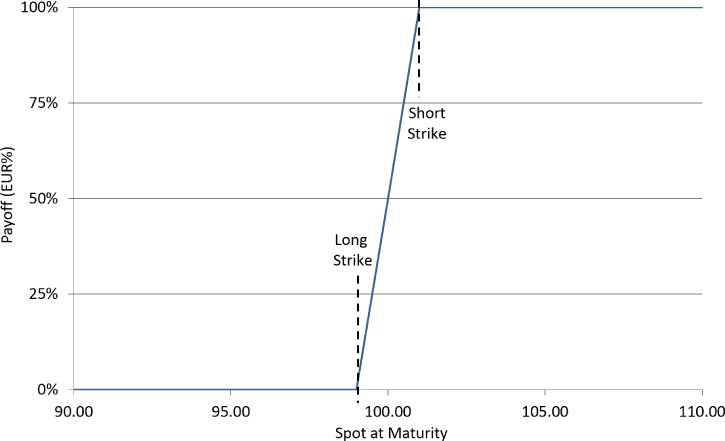
Exhibit 21.3 100.00 European digital call vanilla call spread replication
The tighter the strikes in the replication, the larger the notional required to replicate the digital payout, as shown in Exhibit 21.4. The tightest replication possible would involve trading a one-pip spread with enormous notionals. However, this isn't possible in practice due to the notionals required, plus strike levels are usually rounded to the nearest five or ten pips, particularly in the interbank market.
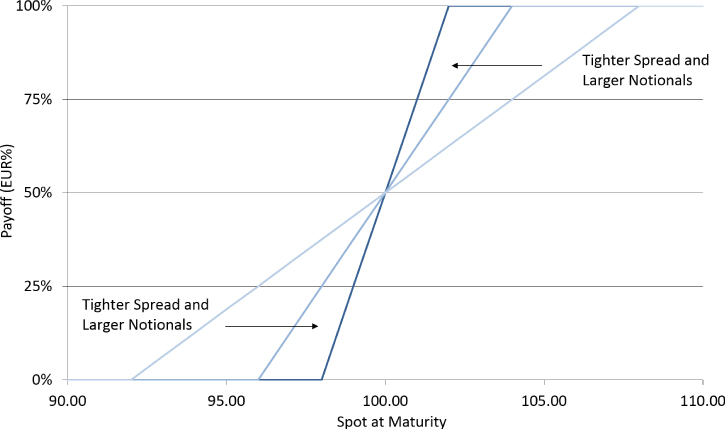
Exhibit 21.4 100.00 European digital call vanilla call spread replication with tighter strikes
The calculation for determining the notionals required within the replication depends on the payout currency of the digital. Recall from Part I that vanilla options naturally generate P&L in the opposite currency to the notional.
European Digital with CCY2 Payout Replication
Given a European digital call with CCY2 payout X at level K, if the call spread replication strikes are long strike 
and short strike 
(symmetrically positioned around K) with CCY1 notional N, a CCY2 payout of 
is generated at 
. Therefore:
that is,
As expected, the closer 
and 
are together 
, the larger the required notional.
Example: Replicating a USD/CNH 1yr 6.1000 USD digital put. A 1yr 6.1250/6.0750 USD vanilla put spread is constructed around the digital level to replicate the payout. The payout of the digital is CNH1m (CCY2) so the USD put 
.
When the digital payout is in CCY2, the replication spread has equal CCY1 notionals but different CCY2 notionals, which in effect generates the payout.
European Digital with CCY1 Payout Replication
Given a European digital call with CCY1 payout X at level K, since a CCY1 payout is required, a CCY2 notional will naturally be calculated within the replication. Therefore, the strikes must be flipped into reciprocal terms.
If the call spread replication strikes are long strike 
and short strike 
with CCY1 notional 
, a CCY1 payout of 
is generated at 
(the strike order in the calculation gets flipped when the reciprocal is taken). Therefore:
that is,
Example: Replicating a USD/CNH 1yr 6.1000 USD digital call. A 1yr 6.0750/6.1250 USD call spread can be constructed around the digital to replicate the payout. The payout of the digital is USD1m (CCY1), so the USD put 
.
This time, when the digital payout is in CCY1, the replication spread has equal CCY2 notionals, but different CCY1 notionals.
European Digital Pricing
Prices for European digital options under Black-Scholes can be calculated directly using cumulative normal distribution function 
. There is a strong link between European digital option prices and the delta of the European vanilla option with the same maturity and the vanilla strike set to the digital level.
Under Black-Scholes, the chance of 
at maturity is given by
where 
is spot, 
is the strike or digital level, 
and 
are continuously compounded interest rates to time 
(measured in years), 
is volatility, 
is the cumulative normal distribution function, and 
.
The CCY2% European digital call price under Black-Scholes discounts this value back to the horizon in the payout currency:
The CCY1% European digital call price under Black-Scholes is calculated by adjusting from 
to 
due to a change of numeraire plus the discounting back to the horizon is changed to CCY1 also:
where 
.
Recall from Practical C that the delta of a European vanilla call option is:
The CCY1% value of a European digital option is equal to the delta of a European vanilla option with the same expiry and strike/digital level (and with payout and quoting conventions aligned). Taking the next derivative with respect to spot implies that the delta of a European digital option is the gamma of a European vanilla with the same expiry and strike/digital level. These relationships are useful for building understanding of the European digital product but note that they hold under Black-Scholes only and not once the volatility smile is included.
Traders price exotic options by calculating the adjustment from the Black-Scholes theoretical value (TV) to a market price. European digital payoffs depend only on the spot at maturity. Hence they have no path dependence and their TV adjustment comes only from the volatility smile. Any well-calibrated volatility smile pricing model could therefore be used to generate a midmarket price for European digital options. Alternatively, the replication strategies examined above are a more direct method of obtaining midmarket prices from the vanilla market:
- If the vanilla options in the replicating spread are priced using the ATM volatility, the replication price approximates the TV of the digital.
- If the vanilla options in the replicating spread are priced on the volatility smile, the replication price approximates the midmarket smile price of the digital.
- The difference between these two values therefore approximates the TV adjustment of the digital. The tighter the replication, the more accurate the valuation.
Therefore, very tight (not practically attainable) vanilla call and put spreads can be constructed within code in order to obtain accurate smile-on mid prices for European digital options.
It is important to note that these “smile-on” digital prices assume the volatility smile at the option maturity matches the market, specifically around the digital level. If this is not the case, for example, in a pegged currency pair, there is no reason to expect that the digital smile-on price will match the market.
The following valuation identities apply to European digital options with the same contract details:
- European digital put TV + European digital call TV = guaranteed payout at maturity.
- European digital put midmarket price + European digital call midmarket price = guaranteed payout at maturity.
This means that the TV adjustment on a European digital call will be equal and negative to the TV adjustment on the equivalent European digital put. Plus taking this a step further, the TV adjustment on a long European digital call option will be the same as the TV adjustment on a short European digital put option with all contract details the same. In the same way that call and put vanilla options are both described as “strikes” within a trading position, European digitals are spoken about in terms of their payout direction and the higher P&L side at maturity.
European Digital Bid–Offer Spread
The vanilla replication of the European digital can also be used to calculate a digital bid–offer spread by multiplying the vanilla option bid–offer spread by the notionals within the replication for strikes set at some fixed width. Alternatively, conservative vanilla spreads can be constructed such that e.g., the full digital payout is generated at the barrier level in order to calculate bid or offer prices directly.
In practice, trading desks more often maintain grids of digital bid–offer spreads for different maturities. Bid–offer spreads for European digitals in liquid G10 currency pairs often have a term structure that looks similar to Exhibit 21.5. Less liquid G10 currency pair and EM currency pair digital bid–offer spreads will typically be quoted wider but the relative shape of the bid–offer spread function over different tenors often remains unchanged.
Exhibit 21.5 Typical EUR/USD European Digital Bid–Offer Spreads
| Tenor | Bid–Offer Spread (CCY1%) |
| O/N | 20% |
| 1wk | 10% |
| 2wk | 7% |
| 1mth | 4% |
| 2mth | 3% |
| 3mth | 2% |
| 6mth | 2% |
| 1yr | 2% |
European Digital Greeks
Many of the Greeks arising from European digital options are similar to the exposures on vanilla options. However, risk management becomes significantly more challenging if spot ends up near the digital level at expiry.
Vega Risk
The European digital vega profile against spot is identical to a risk reversal vega profile that tightens over time. Recalling the replication strategies introduced previously, this should not be a shock. Notice in Exhibit 21.6 how the peak vega stays approximately constant over time. Thinking about the gamma versus vega relationship on a vanilla option, this implies that gamma will pick up sharply on the European digital option into the option maturity.
Exhibit 21.6 100.00 European digital call vega over time
European digital options are:
- Short vega (and short gamma) when the forward is on the higher P&L side of the digital barrier: Lower volatility means an increased chance of staying in the higher P&L area.
- Long vega (and long gamma) when the forward is on the lower P&L side of the digital barrier: Higher volatility means an increased chance of moving to the higher P&L area.
Therefore, if the higher P&L scenario is to the topside, the TV adjustment will be in the same direction as the TV adjustment generated from buying strikes below the digital level and selling strikes above the digital level. Alternatively, if the higher P&L scenario is to the downside, the TV adjustment will be in the same direction as the TV adjustment generated from buying strikes above the digital level and selling strikes below the digital level.
This implies that the TV adjustment on a European digital option depends on the slope of the volatility smile at the digital level to the expiry date. The thought process for traders when asked to price a digital option (with a digital level around current spot) is therefore something like: It's a digital call so the payoff is to topside, so the vega gets longer to the downside. That's a long/short risk reversal position, so I expect this option to trade over/under TV.
Exhibit 21.7 shows TV adjustments for a European digital call with different digital levels in a currency pair with a downside risk reversal.
Exhibit 21.7 European digital call TV adjustment and volatility smile in a currency pair with a downside risk reversal
Hedging European digital vega risk with a vanilla spread or risk reversal works well when there is a fair amount of time until expiry (approximately over a month). On the hedge, a vanilla spread to the same expiry as the digital will be transacted; in the positive P&L region for the bank the strike will be bought and in the negative P&L region for the bank the strike will be sold.
The important decision is how wide apart to place the strikes around the digital level and therefore in what notionals to transact the spread. For example, in EUR/USD, if the digital is at 1.4000 in USD1m payout, either a 1.3500/1.4500 spread in EUR10m or a 1.3900/1.4100 spread in EUR50m could be transacted to replicate the size of the payout and therefore the vega profile.
The wider the strikes in the vanilla hedge, the quicker the hedge breaks down. As a rule of thumb, the hedges will stay relevant until they go beyond 25 delta strike levels. Therefore, price 1mth 25d call and put options with spot set to the digital level. If the vanilla hedge is set up with the strikes around the 25 delta levels, the hedge will remain relevant approximately until the option has one month until expiry. Traders seek the best balance between transaction costs (larger notionals mean higher cost to establish the hedge) and the length of time the hedge stays valid. Note that if spot moves away from the digital level, the hedge is no longer required.
Gamma and Pin Risk
Gamma (and hence theta) from a European digital increases dramatically toward maturity. The gamma profile for a European digital over time is shown in Exhibit 21.8. This presents risk management challenges if spot is near the digital level near expiry as the gamma and theta exposures can overwhelm the rest of the risk in a trading position. Again, this position is hedged by buying options on the positive P&L side and selling options on the negative P&L side of the digital.
Exhibit 21.8 100.00 European digital call gamma over time
At some point, risk management attention turns from managing vega and gamma exposures to the pin risk; The chance of spot ending near the digital level on the expiry date. European digital options generate significant P&L volatility on the expiry date if spot is close to the digital level. Overnight into the expiry date the theta from a USD1m 100.00 digital call is shown in Exhibit 21.9.
Exhibit 21.9 USD1m 100.00 European digital call theta into expiry date
Consider this theta profile: If spot is around the digital level one day prior to expiry, the value of the digital will be around 50%. Then at expiry, the value of the digital is either 0% or 100% depending on whether spot is in-the-money or out-of-the-money (note the similarities with delta bleed on vanilla options). Therefore, the daily theta into the expiry date is at most 50% of the digital value. The practical consequence of this is that, ignoring hedges, the worst-case final-day P&L from a European digital is half the payout amount.
When risk managing a European digital at expiry, traders often work to reduce the worst-case final-day negative P&L to an acceptable level. The worst-case P&L scenario most often occurs with spot one pip away through the digital level on the negative P&L side. To hedge this risk, strikes can be sold at or near the digital level (to the same expiry) and this earns additional theta around that level. However, short strikes generate larger negative P&L in the wings, so traders adjust their delta exposure and buy wing strikes until the best possible P&L distribution is achieved.
If spot is on the negative P&L side of the digital coming up to expiry, risk management is difficult. Into the expiry date, theta will be paid and there will be a P&L gain equal to the payout through the digital level.
If spot is on the positive P&L side of the digital coming up to expiry, risk management is easier. Into the expiry date, theta will be earned and there will be a P&L loss equal to the payout through the digital level. A large delta exposure can therefore be used to generate additional P&L if spot moves toward the digital level (and hence toward the negative P&L side).
In general, it is easier to risk manage a trading position that starts with positive P&L (the theta) but will lose P&L if a certain spot move occurs, rather than a trading position that starts with negative P&L (the theta) but will gain P&L if a certain spot move occurs. Even experienced, well-regarded traders have been known to shout at a spot rate on a screen to encourage it to move.
European Digital Range
Another popular European digital product is a European digital range (also called a European digital spread or a bet spread) that has two digital barriers and pays out if spot at maturity is between the barrier levels. The payoff at maturity of a European digital range is shown in Exhibit 21.10. This product can be replicated with two European digital calls or two European digital puts: one bought and one sold.
Exhibit 21.10 Long USD1m 95.00/105.00 European digital range payoff at maturity
The vega profile of this European digital range is shown in Exhibit 21.11. With spot between the barriers, the option increases in value if implied volatility falls since there will be more chance of spot ending up inside the range, hence short vega. With spot outside the barriers, the option increases in value if implied volatility rises since there will be more chance of spot moving into the range, hence long vega.
Exhibit 21.11 Long USD1m 95.00/105.00 European digital range vega profile
This long-wings vega profile implies a long volga and long convexity exposure that is confirmed in Exhibit 21.12. Therefore, European digital ranges often have positive TV adjustments.
Exhibit 21.12 Long USD1m 95.00/105.00 European digital range volga profile
European digital ranges can be used to estimate the probability of spot being within a certain range on a given date in the future. For example, it is anticipated that significant risk management challenges will occur if spot is between 1.6250 and 1.6350 at the end of February next year. A European digital range for the expiry date and spot levels in question can be constructed. The price of the contract gives the approximate probability of spot being within that range.