Chapter 31
Miscellaneous Options
Exotic FX derivative option types not yet examined include “volatility” products like volatility swaps, variance swaps, and forward volatility agreements, plus forward start options, and compound options.
Volatility and Variance Swaps
In FX derivatives:
- A volatility (vol) swap is a forward contract on the realized volatility of spot over an agreed period.
- A variance (var) swap is a forward contract on the realized variance of spot over an agreed period.
Most commonly, daily spot fixings are used to determine realized volatility and variance. Mathematically, for daily spot fixings, realized variance ![]() is calculated using this formula:
is calculated using this formula:

where ![]() are spot log returns, that is,
are spot log returns, that is, ![]() ,
, ![]() is spot fixing number
is spot fixing number ![]() , and in total there are N log returns.
, and in total there are N log returns.
The mean return is usually not included in the realized variance formula and usually this will not significantly impact the result. However, clients sometimes request it and it is important to check whether it is required. If the mean return is added, the calculation becomes:

where ![]() is the mean of the log returns.
is the mean of the log returns.
In a vol swap, the strike is quoted in volatility terms and the notional is effectively a vega amount:
In a var swap, the strike is quoted in volatility-squared terms and the notional is a cash amount per volatility point squared:
The variance notional is usually linked to vega with this formula:
This formula ensures that if realized volatility is 1 percent away from the volatility strike at maturity, the variance swap payoff is approximately equal to the volatility swap payoff. When volatility swaps and variance swaps are quoted for institutional clients, a two-way volatility or variance strike is quoted for zero upfront payment. When traders talk about the vol swap or var swap “price”, this is what they mean.
The classic quantitative research document on vol swaps and var swaps is a Goldman Sachs paper by Demeterfi, Derman, Kamal, and Zou from 1999 entitled “More Than You Ever Wanted to Know about Volatility Swaps.” The document highlights how variance swaps are theoretically the more natural product because, in a Black-Scholes world (specifically, no spot jumps plus deterministic interest rates), the variance swap payoff can be perfectly replicated by a contract that pays out a log contract at expiry, which in turn can be replicated using a portfolio of vanilla options to the same expiry date.
Volatility swap and variance swap payoffs are shown in Exhibit 31.1 for USD10k vega and a 12% strike. The volatility swap payoff is linear in realized volatility, as expected, while the variance swap payoff is convex in realized volatility, i.e., above the volatility strike the variance swap gains more than the volatility swap, whereas below the volatility strike the variance swap loses less than the volatility swap. Therefore, in a given currency pair and tenor, the rate quoted on the variance swap will be higher than the equivalent rate quoted on the volatility swap. Tracking the vol swap versus var swap strike difference can be used to price volatility swaps, or this “convexity adjustment” can be valued by modeling volatility itself.

Exhibit 31.1 Volatility swap and variance swap payoffs
Vol swaps and var swaps are attractive products for clients because they give a pure payoff based on realized volatility or variance. As has been observed, ATM vanilla options do not give pure exposures because as spot moves, forwards move, or time passes their exposures change.
Variance swaps are a popular product in the equity derivatives market but they are relatively less popular in FX. In FX, both volatility and variance swaps are traded in the interbank broker market but in volumes which are a fraction of vanilla option volumes.
Volatility Swap Greeks
In terms of risk management, the important thing about the volatility swap is that throughout its life, as fixings occur, more is fixed and less is still to be determined. This makes the payoff less sensitive to changes in market data (like Asian options), and hence exposures generally reduce over time.
Prior to any fixings, as spot moves, the value of the vol swap remains constant. This is shown in Exhibit 31.2.

Exhibit 31.2 Volatility swap value prior to any fixings
After spot fixes, as spot then moves away from each fixing, either higher or lower, realized volatility increases and hence the volatility swap value increases as the log return increases. This is shown in Exhibit 31.3.

Exhibit 31.3 Volatility swap value after fixing
Note that this payoff is similar to being long an overnight ATM option; value rises the further spot moves from the strike.
The value profile in Exhibit 31.3 implies a delta position that starts at zero at the fixing, then moves longer with spot higher and shorter with spot lower. The delta profile is shown in Exhibit 31.4.

Exhibit 31.4 Volatility swap delta after fixing
Put another way, the product is long gamma with the peak gamma at the previous fixing as shown in Exhibit 31.5.

Exhibit 31.5 Volatility swap gamma after fixing
The shape of the gamma profile remains approximately unchanged at each fixing except that it moves such that the peak gamma is at the previous fixing.
It is important to dwell for a moment on how these exposures work in practice. As each fixing occurs, the exposures reset. This causes a delta jump at each fixing that will be particularly large if spot is far from the previous fixing. These delta jumps make the gamma exposure harder to trade than the gamma on a standard vanilla option. Plus, at each fixing, gamma jumps back to the peak value.
Before any fixings have been made, the vega of a vol swap is a positive constant across all spot values. When the first fixing occurs, the trade has a reference point and the vega stays unchanged at the fixing rate but moves lower in the wings.
Volatility swaps contain a type of optionality similar to an overnight ATM straddle: If spot moves either higher or lower from the previous fixing, realized volatility increases. In the wings, further away from this “optionality,” vega reduces.
The peak vega reduces at a linear rate over time as more fixings occur. Note that the vega profile shown in Exhibit 31.6 is symmetric because all fixings are set to 100.00.

Exhibit 31.6 Volatility swap vega over time
Vol swap vega is also impacted by the level of implied volatility: At higher implied volatility, the distribution widens and vega is higher in the wings after each fixing. At lower implied volatility, the distribution tightens and vega is lower in the wings after each fixing. This is shown in Exhibit 31.7.
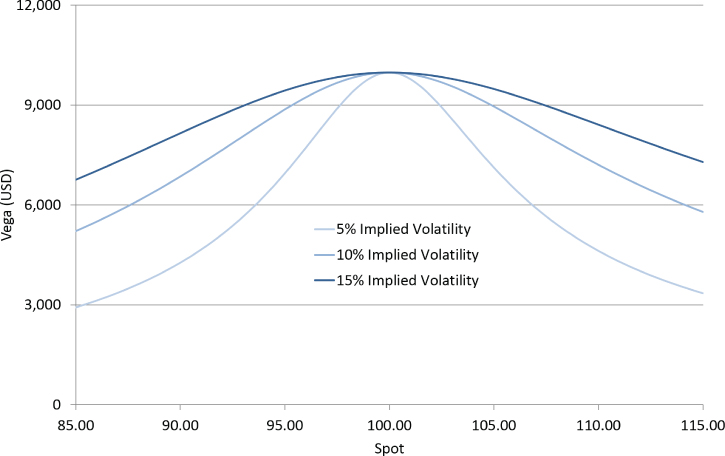
Exhibit 31.7 Volatility swap vega at different levels of implied volatility
Again, it is important to understand how vega evolves in practice. When the volatility swap fixes, vega resets to the peak of the profile, but this vega peak is at a lower level than the peak at the previous fixing. This is one reason why volatility swaps are popular with clients; vega does not permanently reduce as spot moves away from a fixed strike. In a vol swap, it is as if the “strike” keeps resetting back to the ATM at each fixing.
Volatility swaps have no tradable vanna or volga exposures since the position resets the vega position at each fixing. Plus volatility swaps have minimal interest rate exposures, apart from discounting and some minor second-order effects.
Variance Swap Greeks
As with volatility swaps, variance swap value is constant and static over all spot values prior to any fixings occurring. Then, as spot moves away from each fixing, realized variance increases and hence variance swap value increases. This is shown in Exhibit 31.8.

Exhibit 31.8 Variance swap value after fixing
Within a variance swap, delta moves linearly with spot as shown in Exhibit 31.9. This implies a constant gamma exposure that also stays approximately constant as time passes. These are important results:
- Variance swaps can be replicated with a so called “log contract”.
- Variance swaps have constant gamma over all spots.
- The log contract generates a constant gamma exposure over all spots.

Exhibit 31.9 Variance swap delta after fixing
In a similar way, vega on a variance swap is constant over all spots and decays away regularly over time as fixings occur. This is shown in Exhibit 31.10.

Exhibit 31.10 Variance swap vega over time
The vega on a variance swap is linear in implied volatility, which implies a constant long volga exposure over all spots. This is shown in Exhibit 31.11.

Exhibit 31.11 Variance swap vega at different levels of implied volatility
Constant gamma and vega profiles over spot are sometimes called “strikeless gamma” or “strikeless vega.”
Volatility Swap Pricing
In a theoretical Black-Scholes world, the volatility swap price is almost exactly equivalent to the ATM volatility to the same tenor. However, the volatility swap rate is additionally impacted by the number of fixings within the calculation. The standard multiplier used within interbank trades is 252, as quoted in the formulas at the start of the chapter. The holiday calendar most often used for vol swaps is WMR, which has fewer holiday days than the USD and therefore more fixings so it is common to see the quoted rate pulled lower by this effect.
Another important point to be aware of when quoting volatility swaps and variance swaps is the payout currency. The quoted volatility strikes for CCY1 versus CCY2 payouts can be quite different so it is important to confirm which payout currency the client requires. Particularly large valuation differences occur when there is a large skew in the volatility surface. For example, in a currency pair with a large downside risk reversal, higher volatility on downside strikes implies spot has an increased chance of moving further to the downside. With spot lower, CCY2 becomes relatively more valuable than CCY1, so a volatility or variance swap with CCY2 payout will be worth more than the equivalent contract with CCY1 payout.
There is a big difference between pricing vol swaps in liquid G10 currency pairs versus pricing them in managed emerging market currency pairs. In liquid G10 currency pairs, pricing models can be used to generate reference points: Local volatility gives an approximate upper bound for the quoted vol strike and stochastic volatility gives an approximate lower bound for the quoted vol strike. This counterintuitive result occurs because both models (if well-calibrated) have the same variance and since local volatility has a lower vol-of-vol the expectation of the volatility will be higher. A well-calibrated mixed vol model often gives a good indication for short-dated volatility swaps while at longer tenors the effect of stochastic interest rates should additionally be quantified. In practice, traders often track the differential between their models and the interbank broker market prices over time and quote reflecting this adjustment.
In managed emerging market currency pairs it is important to remember that the volatility swap pays out on the realized spot volatility, not the realized forward volatility, so forward volatility must be stripped out of the ATM volatility when pricing a vol swap. This effect can be assessed by calculating historic realized spot volatility using daily fixings and comparing it to the ATM volatility.
It is also important to understand the spot dynamic in the currency pair. This allows a trader to assess the expected spot distribution: Does the central bank intervene in the spot market? Is the fixing an average or a point-in-time fix? How will this impact realized volatility? What else might cause spot to jump?
Volatility swaps and variance swaps need special attention in emerging market currency pairs because the vega stays with spot as it moves. If the emerging market exchange rate jumps and implied volatility spikes, this can cause far larger P&L swings for these products than vanilla options with equivalent vega.
In practice, wing vanilla options are often used to hedge a volatility swap vega profile. Specifically, 10 delta strangles usually hedge vega over a wide enough spot range. However, over time this hedge must be rebalanced as gamma exposure increases if spot moves close to one of the hedge strikes. Plus, if spot jumps a long way through the strikes, the hedge will no longer work.
Variance Swap Pricing
Variance swaps can be perfectly replicated with vanillas to the variance swap expiry date. Specifically, the replication involves transacting a strip of vanilla options that pays out a log contract at maturity. The log contract replication sets up vanilla notionals such that they are inversely proportional to the strike squared. Example notionals are shown in Exhibit 31.12.
Exhibit 31.12 Log Contract Vanilla Replication
| Strike (K) | Strike2 | Notional (CCY1) |
| 60.00 | 3,600 | 2,777,778 |
| 70.00 | 4,900 | 2,040,816 |
| 80.00 | 6,400 | 1,562,500 |
| 90.00 | 8,100 | 1,234,568 |
| 100.00 | 10,000 | 1,000,000 |
| 110.00 | 12,100 | 826,446 |
| 120.00 | 14,400 | 694,444 |
| 130.00 | 16,900 | 591,716 |
| 140.00 | 19,600 | 510,204 |
By trading strikes with these wide gaps between them (10 figures), the accuracy of the replication reduces toward expiry. A perfect replication providing constant gamma exposure over all spots would require vanilla options to be traded at all possible strikes between zero and infinity. (No, that isn't actually possible.)
From a pricing point of view, since the replication involves buying very low delta strikes, it is vital to consider whether the wings of the volatility smile match the market for very low delta options, particularly to the downside since this is where the notionals rise within the replication. At this point, theory meets reality with a bump. The replication method assumes large amounts of low-premium wing options can be traded at midmarket. As mentioned in Chapter 15, in practice, traders are reluctant to sell large amounts of low-premium options due to the leverage in the product. Therefore, the market offer for these strikes is usually higher than the model offer, which in turn causes the market price for variance swaps to be above the theoretical model value.
Transacting a strip of vanilla options will approximately hedge the vega profile from a variance swap, although if spot jumps a long way, the hedge will no longer work. Variance swaps are more dangerous than volatility swaps in this regard because the payoff is based on volatility squared. Therefore, no practically attainable vanilla hedge will provide protection from a short variance swap contract if spot moves far enough. For this reason restrictions are sometimes added to the variance swap contract, e.g., knock-out barriers or maximum daily moves. These considerations are particularly applicable in pegged currency pairs where an exchange rate de-pegging could generate big P&Ls on variance swap contracts.
Forward Volatility Agreements
Forward volatility agreements (FVAs) are another commonly traded volatility product. They are quoted as a forward implied volatility between two expiry dates. At the first expiry date, a spot fixing is taken from an agreed source and the option then becomes an ATM with a fixed strike (calculated from the spot fix) to the final expiry date. Most commonly the dates are specified in terms of market tenors. For example, Exhibit 31.13 shows a “three-month-in-six-month” FVA that turns into a 3mth ATM in six months' time.
Exhibit 31.13 FVA dates structure
Forward vol agreements are closely linked to forward implied volatility, a variance-based calculation given in Chapter 11:

where ![]() is the forward ATM implied volatility between the first and second expiry dates,
is the forward ATM implied volatility between the first and second expiry dates, ![]() is the ATM implied volatility to the first expiry date at time
is the ATM implied volatility to the first expiry date at time ![]() , and
, and ![]() is the ATM implied volatility to the second expiry date at time
is the ATM implied volatility to the second expiry date at time ![]() .
.
The vega exposure from an FVA is flat over different spots until the contract fixes, at which point it becomes a standard ATM vanilla to the final expiry date. This is shown in Exhibit 31.14.

Exhibit 31.14 FVA vega profile change at first fixing
An important point is that the vega exposure is to forward ATM implied volatility and there are therefore vega exposures to both expiry dates within the contract. For a long FVA position, the vega exposure will be short to the first expiry date and long to the final expiry date. Looking at the forward implied volatility calculation:
- Lower ATM volatility at the first expiry date
 increases the forward implied volatility.
increases the forward implied volatility. - Higher ATM volatility at the second expiry date
 increases the forward implied volatility.
increases the forward implied volatility.
Usually, the ATM curve rises at longer tenors due to interest rate volatility but there is no exposure to interest rates (except discounting) on an FVA until it fixes, only forward implied vol exposure. Therefore, on long-dated FVAs, interest rate volatility should be stripped out of the pricing. Put another way, an FVA volatility curve (if such a thing existed) should be much flatter than the equivalent ATM curve.
This overlaps with trader intuition about how attractive an FVA contract is to buy or sell. If the ATM curve is upward sloping, the forward implied volatility will be high and the FVA contract will often be more attractive to sell.
The pricing of an FVA depends mainly on the forward implied volatility within the volatility surface. Therefore, it is preferable that within the pricing model used, volatility itself is random. Local volatility is therefore not a good model choice because (local) volatility is deterministic within the model.
Finally, consider possible vanilla hedges for an FVA. If only the net vega position to the final expiry date is hedged, there will be a significant exposure to the shape of the ATM curve left unhedged. A better hedge for a long FVA would be to buy some 10 delta strangles to the first expiry date and sell some 25 delta strangles to the final expiry date. Notionals should be configured such that the hedge gives matching forward volatility exposures and outright volatility exposure. Although again, over time, the hedge accuracy will reduce and may need to be rebalanced.
Forward Start Options
Forward start options (also called cliquets) are like FVAs in that their structure relies on two expiry dates in the future. Again, these dates can be specified in terms of actual dates or market tenors. A diagram of the dates is shown in Exhibit 31.15.

Exhibit 31.15 Forward start option dates structure
At the first expiry date, rather than settling into an ATM like an FVA, the forward start option can settle into a wider range of options to the final expiry date. The options are most commonly European vanillas but they can also be European digital, European barrier, or American barrier options. Strikes and/or barriers on these options are set with reference to a spot fixing taken on the first expiry date. The strike or barrier levels can generated in one of two ways:
- Strike or barrier level = spot fix on first expiry date + constant
- Strike or barrier level = spot fix on first expiry date × constant
Example: EUR/USD forward start EUR Put/USD Call vanilla from January 23, 2015, into June 23, 2015, with strike set at the ECB fixing × 95%.
The forward start vega exposure is similar to the FVA in that it remains flat until the moment spot fixes on the first expiry date, at which point the option becomes a standard FX derivatives product (e.g., a vanilla option or a barrier option). However, note that the vega may not be at the peak when it fixes. In the case of the EUR/USD forward start example, as spot fixes, the vega position jumps from being flat to having a large vanna/skew exposure from the long downside vanilla as shown in Exhibit 31.16.

Exhibit 31.16 Forward start vega profile
Like an FVA, there are vega exposures to both the first expiry date and the final expiry date but the volatility smile now plays a more important role in the pricing. In the EUR/USD forward start example, pricing will depend on the future expectation of implied volatility for a strike equal to spot × 95%.
Therefore, as well as the full term structure of ATM volatility and interest rates, the forward smile is a key consideration. Different pricing models calibrated to the same vanilla surface produce very different forward smile dynamics. Viewing the forward smile generated by the model enables an opinion on the forward start option price.
Compound Options
The compound option product is an option on an option. Therefore compound options have two expiry dates: a decision date and a final expiry date. These dates can be specified in terms of actual dates or market tenors. A diagram of these dates is shown in Exhibit 31.17.

Exhibit 31.17 Compound option dates structure
At the first expiry date (sometimes called the decision date), the owner of the compound option has either the right to buy or the right to sell a specific vanilla option to the final expiry date at a pre-agreed price (sometimes called the compound strike).
Compounds are either a call (the right to buy) or a put (the right to sell) the vanilla option to the final expiry date. In turn, the underlying vanilla option can be either a call or a put. Compound options are therefore described in terms of their call and put directions:
- Call on a call: the right to buy a vanilla CCY1 call option
- Call on a put: the right to buy a vanilla CCY1 put option
- Put on a call: the right to sell a vanilla CCY1 call option
- Put on a put: the right to sell a vanilla CCY1 put option
Clients trade compound options because they lock in the price of the vanilla while deferring the decision to trade. This is appropriate if the underlying vanilla option is a hedge for an uncertain cash flow. Compounds are generally far cheaper than the equivalent outright vanilla option, although the premium for the underlying vanilla option also must be paid at the decision date.
Example: USD/JPY 3mth compound call option on a 3mth 100.00 strike USD Put/JPY Call option at 0.30 USD%. Therefore, in three months the owner of the compound option decides whether to exercise the compound optionality. Exercising the compound involves paying 0.30 USD% for the 3mth option to the final expiry date. The compound should be exercised if the market price of the vanilla to the final expiry date is higher than 0.30 USD%, otherwise the compound should be expired.
Note that the decision on whether to exercise or expire the compound is based on spot, interest rates, and implied volatility market data for the final expiry date. The consequence of this is that the exercise point moves in spot space.
Compound owners have long vega exposures to both the decision date and the final expiry date because there is optionality at both dates. The peak vega on the decision date is around the spot level at which the option will either be expired or exercised—the center of the optionality. The vega to the final expiry date will have its peak at the strike as usual but that exposure will be weighted by the probability of the compound being exercised on the decision date.
Exhibit 31.18 shows the vega profiles from the above USD/JPY compound option.

Exhibit 31.18 Compound option vega profile
The relative vega exposures between the two dates depend on the probability of compound exercise. For example, if the compound strike on a compound call is 0%, the compound should always be exercised (bought at zero). The vega profile will therefore simply be that of a vanilla to the final expiry date. As the premium strike rises, the total price of the compound plus the final vanilla must always be more expensive than the vanilla option to the final expiry date because the compound contains additional optionality.
Compound option pricing depends on the forward volatility smile and forward interest rates. Like forward start options, as many of these elements as possible should be taken into account when pricing.
Finally, a more general version of a compound is an option on strategy, which is the right to buy or the right to sell a portfolio of (usually) vanilla options.
