Chapter 27
Vanilla Variations
With only minor adjustments to the contract details, the trading risks on European vanilla options can be significantly changed. The adjustments discussed in this chapter are late-delivery, American exercise, and self-quanto payoff.
Late-Delivery Vanilla Options
Consider the options shown in Exhibit 27.1. Leg 1 is a standard European vanilla option with a 1yr expiry. Leg 2 is identical except that the delivery date is one year after the standard delivery date. For a European vanilla option with the standard delivery date, the price of a physically delivered option is the same as the price of a cash-settled option. However, for a late-delivery vanilla option the price difference can get large.

Exhibit 27.1 Pricing tool showing two vanilla option contracts, one with late delivery
In practice, Exhibit 27.1 doesn't contain enough information to price the late-delivery option because these same contract details could represent three different derivative contracts. When pricing late-delivery options it is important to confirm exactly what payoff is required and understand what methodology the pricing model uses so any necessary additional adjustments can be made.
Late Cash Vanilla Options
The late-delivery vanilla option in Exhibit 27.1 could be a late cash vanilla option. At maturity, the option is exercised against a fix. The option is then cash settled on the late delivery date (August 18, 2016).
The price difference between the late cash vanilla and the standard European vanilla depends on discounting in the payout currency between the standard delivery date and the late delivery date. If interest rates in the payout currency are positive, the fixed cash settlement paid further into the future will be worth less and the late cash vanilla option will be cheaper than the regular European vanilla.
The effect of this discounting is included in the pricing tool mid-price shown in Exhibit 27.2. Note the slightly lower price of leg 2 due to small positive USD interest rates.

Exhibit 27.2 Pricing tool showing late cash vanilla option
Prices within Exhibit 27.2 are calculated using a pricing model that assumes interest rates are static, so the effects of stochastic interest rates must be additionally factored in. The most important effect will come from the correlation between spot and payout currency interest rates, which must be considered with reference to the option payoff. This call option pays out more USD with a higher spot. Therefore, if there is a positive correlation between spot and USD interest rates, USD interest rates will likely be higher when the option pays out. This effect will make the market price lower than the static interest rate price generated by the pricing model due to the discounting.
Option on Forwards
The late-delivery vanilla option in Exhibit 27.1 could alternatively be an option on forward, meaning a vanilla option that physically delivers into a forward rather than into spot. At maturity, the option is expired or exercised by comparing the strike (103.00) with the prevailing forward outright to the late delivery date (August 18, 2016). If exercised, the option physically delivers into a 103.00 forward that matures on the late delivery date.
The difference in pricing between this variation and the standard European vanilla depends mainly on the swap points between the standard delivery date and the late delivery date.
- If CCY1 rates are above CCY2 rates, the swap points between the standard delivery date and the late delivery date will be negative. In this case, the CCY1 call option on forward will be cheaper than the European vanilla because the payoff calculated using the forward to the late delivery date will be lower than the payoff calculated using spot at maturity.
- If CCY1 rates are below CCY2 rates, the swap points between the standard delivery date and the late delivery date will be positive. In this case the CCY1 call option on forward will be more expensive than the European vanilla because the payoff calculated using the forward to the late delivery date will be higher than the payoff calculated using spot at maturity.
The option on forward price can be approximated using a 1yr vanilla option with a strike adjusted by the negative of the swap points between the standard delivery date and the late delivery date. For example, if the swap points between August 18, 2015 and August 18, 2016 are –125, the price can be approximated using a 1yr vanilla option with the strike moved higher by 1.25. Note that this causes the option to be priced at a (slightly) different implied volatility than the standard European vanilla.
The effects of swap points are included in leg 2 of the pricing tool mid-price shown in Exhibit 27.3.
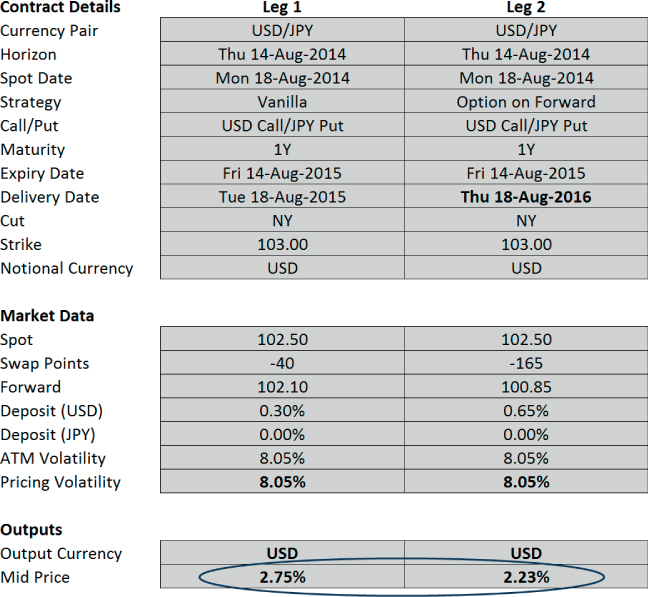
Exhibit 27.3 Pricing tool showing option on forward
Prices within Exhibit 27.3 are calculated using a pricing model that assumes interest rates are static so the effects of stochastic interest rates must be additionally factored in. The most important effect will come from correlations between spot and both interest rates, which must be considered with reference to the option payoff. This CCY1 call option pays out with a higher spot. Therefore, for example, if there is a positive correlation between spot and CCY1 interest rates, when the option pays out, the swap points will have moved more negative. This effect will make the quoted price lower than the static interest rate price generated by the pricing model.
Late-Delivery Vanilla Options
The late-delivery vanilla option in Exhibit 27.1 could, at maturity, be exercised against a fix. But rather than being cash settled on the standard delivery date as usual (August 18, 2015), the option physically delivers into a forward at the strike settling on the late delivery date (August 18, 2016).
The key element in this late-delivery option is non-optimal exercise compared to the option on forward. The late-delivery option is exercised if spot at maturity is above the strike and it is expired if spot at maturity is below the strike. It could therefore be constructed in a pricing tool using a discrete barrier on the expiry date that knocks out below the strike and pays out a forward to the late delivery date.
If interest rates are all statically zero, the price of the late-delivery option would be the same as the standard European vanilla option and the late cash option because the expiry decision would be optimal (since spot = forward). However, as soon as interest rates are non-zero, exercise becomes non-optimal.
If swap points between the standard delivery date and the late delivery date are negative (i.e., CCY1 rates > CCY2 rates) and spot at maturity is above the strike, exercising a call option into the forward at the strike level in the future may result in negative P&L.
Example: On August 14, 2015, USD/JPY spot is 103.25. Therefore, the option exercises into a long forward at 103.00 for August 18, 2016. The forward points are negative and the prevailing forward outright to August 18, 2016 is 102.00. Buying the August 18, 2016 forward at 103.00 leads to negative P&L.
If swap points between the standard delivery date and the late delivery date are positive (i.e., CCY1 rates < CCY2 rates) and spot at maturity is below the strike, not exercising a call option into the forward at the strike level in the future may result in positive P&L being missed.
Example: On August 14, 2015, USD/JPY spot is 102.75. Therefore, the option expires. However, the forward points are positive and the forward outright to August 18, 2016 is 104.00. Buying the August 18, 2016, forward at 103.00 would have lead to positive P&L, which has not been realized due to the exercise decision mechanism.
The pricing reduction from this non-optimal exercise is shown leg 2 of Exhibit 27.4.

Exhibit 27.4 Pricing tool showing late delivery vanilla
This price is calculated assuming interest rates are static so the effects of stochastic interest rates must be additionally factored in. For example, higher interest rate volatility will reduce the quoted price of the late-delivery vanilla because it increases the chances of non-optimal exercise.
American Vanilla Options
European vanilla options can be exercised by the option holder only at the exact option expiry date and cut time. American vanilla options can be exercised by the option holder at any time up to the option expiry date and cut time.
American vanilla options are rarely traded in the OTC FX derivatives market, where the vast majority of vanilla options are traded European-style. If early exercise is required, it is possible to unwind a European vanilla and trade spot to get the same net position change as early exercising the American option. However, American vanilla options are often standard products on exchanges, for example, the Chicago Mercantile Exchange (CME).
No exact closed-form solutions exist for pricing American vanillas and hence they are more complicated to accurately value. Ideally, since they are path dependent, the full interest rate curve, full ATM curve, and potentially even stochastic interest rates should be taken into account within pricing. Several well-established closed-form approximations do exist but they rely on fairly restrictive simplifying assumptions.
American vanilla options contain more optionality than the equivalent European vanilla options. Therefore, American vanillas are always at least as expensive as the equivalent European vanilla, with the value difference increasing with longer time to expiry.
The early exercise feature of an American vanilla should be activated when the value lost from holding the option (mainly due to the forward drift) is more than the value of the remaining optionality.
Consider the value of a 1yr European CCY1 call/CCY2 put vanilla option versus the equivalent early exercise value. The zero interest rate case is shown in Exhibit 27.5.

Exhibit 27.5 European option value versus early exercise value: zero interest rates
With zero interest rates and hence no forward drift or discounting, the European option value is always above the early exercise value. Therefore, it is always optimal to keep the optionality rather than early exercise.
A higher CCY2 interest rate case is shown in Exhibit 27.6. The European option value is again above the early exercise value at all spots, plus this it is further over than the zero interest rate case due to the forward drift. Recall that the forward to time T (![]() ) is given by:
) is given by:

Exhibit 27.6 European option value versus early exercise value: rCCY1 = 0%/rCCY2 = 5%
Higher CCY2 interest rates (rCCY2 > rCCY1) leads to a forward that is above spot. This leads to an expected call option payoff calculated off the higher forward that is always larger than the early exercise value calculated off spot. Therefore, it is always optimal to keep the optionality and hence benefit from the forward drift rather than early exercise.
Higher CCY1 interest rate cases are shown in Exhibits 27.7 and 27.8. Higher CCY1 interest rates (rCCY1 > rCCY2) leads to a forward that is below spot. This leads to an expected call option payoff calculated off the lower forward, which can be lower than the early exercise value calculated off spot.

Exhibit 27.7 European option value versus early exercise value: rCCY1 = 1%/rCCY2 = 0%

Exhibit 27.8 European option value versus early exercise value: rCCY1 = 5%/rCCY2 = 0%
At in-the-money spots beyond a certain level, the European option value is below the early exercise value due to the forward drift. At these spot levels it is optimal to early exercise the American vanilla option.
These examples reveal some important rules:
- The early exercise feature of American vanillas only has value when the payoff is a call on the higher yielding currency (i.e., the currency with higher interest rates).
When the payoff is a CCY1 call, the early exercise feature only has value when CCY1 interest rates are higher than CCY2 interest rates. When the vanilla payoff is not a call on the higher yielding currency, in a static interest rate world, the pricing and Greeks on an American vanilla will be identical to the equivalent European vanilla.
- If it exists, the optimal early exercise level moves closer to the strike the higher the interest rate differential.
This occurs because more value is lost from the forward drift at higher interest rate differential.
- When long an American vanilla, the European vanilla price versus early exercise value difference must be monitored.
Beyond a certain spot level it is optimal to early exercise the American vanilla. This occurs when spot is in-the-money versus the payoff and the forward drift will cause more value to decay away over than is remaining in time value. If this optimal exercise point is not monitored, early exercise optionality has been paid for and then not used; roughly equivalent to throwing money away.
For a client, when the early exercise decision is based on some external trigger rather than on the value of the early exercise optionality, it is usually preferable to trade the standard European vanilla option. However, in currency pairs with limited spot market liquidity, the ability to avoid crossing two option spreads (original deal plus unwind) plus the spot market spread may save money.
American Vanilla Pricing and Greeks
Comparing American and European vanillas in the CCY1 call and higher CCY1 interest rates case demonstrates how early exercise impacts trading risk. Price profiles are shown in Exhibit 27.9.

Exhibit 27.9 1yr 1.3650 EUR call/USD put American vanilla versus European vanilla price
As mentioned, the American vanilla is always more expensive than the equivalent European vanilla. The value of the early exercise optionality (the difference between the lines in Exhibit 27.9) becomes a significant part of the total option value when spot is deep in-the-money.
Delta profiles are shown in Exhibit 27.10. The American vanilla delta picks up more sharply with a higher spot. Beyond the optimal early exercise point, the delta on the American vanilla becomes 100%, equivalent to exercising the vanilla into spot.

Exhibit 27.10 1yr 1.3650 EUR call/USD put American vanilla versus European vanilla delta
Gamma profiles are shown in Exhibit 27.11. The sharper delta pickup generates increased gamma exposure on the American vanilla with spot higher. Beyond the optimal early exercise point, gamma becomes zero as it is assumed the vanilla will be exercised into spot.

Exhibit 27.11 1yr 1.3650 EUR call/USD put American vanilla versus European vanilla gamma
Vega profiles are shown in Exhibit 27.12. Once again, Greeks are curtailed beyond the optimal early exercise point as optionality disappears. At in-the-money spot levels, vega risks on American vanillas move forward to tenors prior to the option expiry, whereas for European vanillas the vega risks are always to expiry. This is key for risk management; To properly assess the trading risk on American vanillas, bucketed vega exposures must be used.

Exhibit 27.12 1yr 1.3650 EUR call/USD put American vanilla versus European vanilla vega
The volga and vanna exposures are significantly larger on an American vanilla option with spot near the optimal early exercise point as shown in Exhibits 27.13 and 27.14.
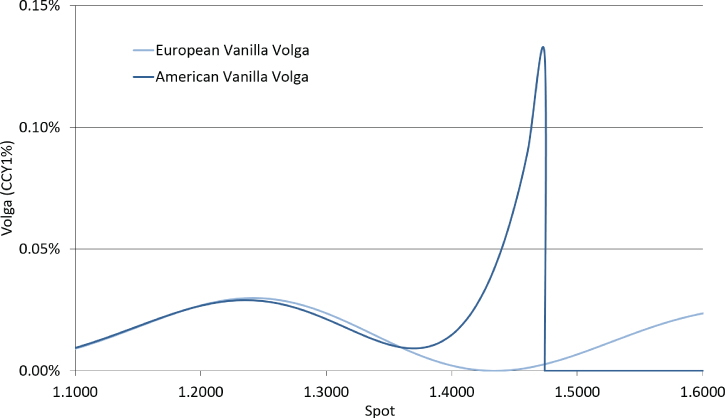
Exhibit 27.13 1yr 1.3650 EUR call/USD put American vanilla versus European vanilla volga

Exhibit 27.14 1yr 1.3650 EUR call/USD put American vanilla versus European vanilla vanna
American Vanilla Pricing
When pricing American vanilla options, traders must understand what methodology is being used to price the option in order to understand which effects are being taken into account and which are being ignored.
At shorter tenors (e.g., under 3mth), where the early exercise optionality has little value, it may be sufficient to price the European vanilla using the volatility smile, and then add in a constant volatility American-style versus European-style price difference.
At longer tenors, stochastic interest rates must be taken into account. If spot and interest rates move in a correlated manner, that will significantly impact the price of American vanilla options. Consider the case where the vanilla option payoff is a CCY1 call but CCY2 interest rates are currently higher than CCY1 interest rates. In the basic analysis, this means that the price will be that of the European vanilla, but the interest rate differential may flip over time, giving the early exercise feature value. This effect is quantified by a stochastic interest rate model.
Finally, the bid–offer spread on American vanillas is generally slightly wider than the equivalent European vanilla (particularly in longer tenors) due to the additional risk management and monitoring they require.
Self-Quanto Vanilla Options
The standard European vanilla option payoff is generated in CCY2 terms, and at maturity it can be converted back to CCY1 terms at the prevailing spot. Self-quanto options have their payout converted back into CCY1 at a fixed rate (usually the strike) rather than at spot. Call and put payoffs react differently to this adjustment and therefore they must be examined separately.
Vanilla CCY1 Call Options
For a CCY1 call option, the European vanilla payoff has a CCY2 P&L at maturity:
The payout can be converted from CCY2 to CCY1 using spot at maturity so:

In the standard self-quanto case, rather than dividing by ST to get back to CCY1 terms, the payout is divided by K:
If spot is in-the-money at maturity on the CCY1 call, then ST > K, which implies the self-quanto payout is larger than the regular vanilla payout and hence:
Exhibit 27.15 shows the payoff at maturity of long 1.3500 EUR call/USD put European and self-quanto vanilla options in EUR1m notional. An intuitive way to think about the self-quanto is that buying a self-quanto CCY1 call can be replicated by buying the CCY1 call European vanilla with same strike plus buying a strip of CCY1 call vanillas above the strike to the same maturity. This strip of options, with notionals far smaller than the self-quanto notional, is visualized in Exhibit 27.16.

Exhibit 27.15 European vanilla versus self-quanto call option payoff at maturity

Exhibit 27.16 European vanilla to self-quanto call option adjustment discrete replication
Therefore, the self-quanto CCY1 call is longer topside vega compared to the European vanilla as shown in Exhibit 27.17.

Exhibit 27.17 European vanilla versus self-quanto call option vega profile
Vanilla CCY1 Put Options
For a CCY1 put European vanilla option, again, the natural vanilla payoff has CCY2 P&L at maturity:
The payout can be converted from CCY2 to CCY1 using spot at maturity so:

In the standard self-quanto case, rather than dividing by ![]() to get back to CCY1 terms, the payout is divided by K:
to get back to CCY1 terms, the payout is divided by K:
If spot is in-the-money at maturity on the CCY1 put, then ![]() , which implies the self-quanto payout is smaller than the regular vanilla payout and hence:
, which implies the self-quanto payout is smaller than the regular vanilla payout and hence:
Exhibit 27.18 shows the payout at maturity of long 1.3500 EUR put/USD call European and self-quanto vanilla options in EUR1m notional.

Exhibit 27.18 European vanilla versus self-quanto put option payoff at maturity
Buying a CCY1 put self-quanto can be replicated by buying the CCY1 put European vanilla with same strike plus selling a strip of CCY1 put vanillas below the strike to the same maturity. Therefore, the self-quanto CCY1 put is shorter downside vega compared to the European vanilla as shown in Exhibit 27.19.

Exhibit 27.19 European vanilla versus self-quanto put option vega profile
Self-Quanto Bid–Offer Spread
For a self-quanto CCY1 call, the replication suggests that it should be quoted wider than the equivalent European vanilla option because there is compounding vega risk from the additional strip of CCY1 calls. However, care must be taken to look at risks beyond just ATM vega; There may be significant optionality in the wings, particularly in high skew currency pairs which should be accounted for within the bid-offer spread.
For a self-quanto CCY1 put, the replication suggests that it should be quoted tighter than the equivalent vanilla option because there is less vega risk due to the offsetting strip of CCY1 puts.
