Chapter 30
Multi-Asset Options
When the payoff from an FX derivatives contract is based on more than one currency pair it is described as a multi-asset option. Having multiple currency pairs within an option structure adds extra dimensions and can significantly increase risk management complexity.
Multi-Asset Trading Risks
Standard Greek exposures are not sufficient for managing multi-asset risk. Single values for delta, gamma, and vega make little sense when the exposures in a given currency pair depend not just on changes in that currency pair but on all the currency pairs within the structure.
It is therefore vital for a trader to understand the methodology used to calculate exposures on multi-asset products within their pricing and risk management systems. If standard Greek exposures are used to risk manage multi-asset options, they certainly rely on strict assumptions about how the underlying assets move together. This can lead to big risk management shocks when the assumptions break down.
Correlations between spot log returns are key parameters within the multi-asset framework. When pricing the two-currency-pair case, for intuition it is often useful to consider how the option payoff is impacted by perfectly positively correlated spots, perfectly negatively correlated spots, and spots with zero correlation. For multi-asset options with more than two currency pairs, correlations are often viewed within a matrix. For example, the following three-asset correlation matrix shows a 25% correlation between asset 1 and asset 2:

Within risk management it is common to flex the correlation matrix and observe how the option price is impacted. However, this flexing process is often easier said than done. The correlation matrix must always be “valid,” meaning positive semi-definite in mathematical terms. This prevents correlation matrices where, for example, assets 1 and 2 are 100% correlated, and assets 1 and 3 are 100% correlated, but assets 2 and 3 are not correlated:

There are also issues around instantaneous correlation versus terminal correlation to worry about. The best material on these issues exists in Riccardo Rebonato's book Volatility and Correlation: The Perfect Hedger and the Fox (John Wiley & Sons, 2nd Edition, 2004).
Unlike Equities, where there is no notion of cross-stocks, in FX there are tradable volatility surfaces in major currency pairs and cross currency pairs. Recalling the ATM volatility triangle framework from Chapter 16, it is therefore possible to view multi-asset risk in vega terms across all relevant currency pairs. Alternatively, cross-volatility risk can be viewed as exposure to correlation between major pairs.
Recall also from Chapter 16 that correlations are quoted between two currency pairs such that the common currency is CCY1 or CCY2 in both cases. If the market convention pair ordering has the common currency as CCY1 in one pair and CCY2 in the other pair, the negative of the correlation must be used within calculations.
Pricing models for multi-asset options are not as well-established as single-asset pricing models. Certainly there is no equivalent to the mixed volatility model. Local and stochastic correlation models have been developed, plus the notion of a correlation smile has been explored, but this is an area in which quants continue to apply their considerable brain power.
Since multi-asset pricing models are generally less sophisticated, scenario analysis becomes a relatively more important risk management tool for trading multi-asset positions. Market data is flexed in different ways and the resultant P&Ls are used to identify the major risks in the position. For example, if USD rates rise by 1% and implied volatilities all drop by 1%, what P&L is generated?
Another complicating factor within multi-asset options is that the fixes used to determine spot at maturity in different currency pairs may be sampled at different times of the day. Additional bid–offer spread should be charged in cases where this issue may arise.
Finally, traders often actively write-off risk (see Chapter 15) and use shadow barriers (see Chapter 25) to simplify multi-asset risk management.
Multi Asset Bid–Offer Spreading
Two standard approaches exist for calculating bid–offer spreads on multi-asset options. The first approach can be thought of as confidence interval spreading. Correlations are flexed up and down to generate a change in option value. By assessing the variability of historical correlation an appropriate correlation flex is determined. As a rough rule of thumb, in G10 pairs for medium tenors (1mth to 1yr), correlation flexes around 10% to 15% are often appropriate. This is a neat and convenient method, plus it gives a good intuitive feel for the risk in the trade. However, it does not take into account the liquidity of the currency pairs within the product and will generate too much spread in some cases and not enough in others. It must also be understood that short-dated correlations are much less stable than long-dated correlations and ![]() is generally lower for short-dated options. Therefore, correlation must be flexed more on contracts with shorter maturities.
is generally lower for short-dated options. Therefore, correlation must be flexed more on contracts with shorter maturities.
The second approach can be thought of as replication spreading. Vega exposures are calculated in all major and cross currency pairs, multiplied by the ATM volatility bid–offer spread in each pair and then summed to get a total bid–offer spread. This approach is appealing because it uses real implied volatility bid–offer spreads but it will usually overestimate bid–offer spread because it does not give any discount for offsetting risk.
A combination of these approaches can also be used, with replication spreading used in major currency pairs and confidence-interval spreading applied in cross-currency pairs.
Basket Options
Basket options contain a number of currency pairs with a common currency between them. Spot moves in the basket pairs are normalized and averaged to create a basket spot move. At maturity, the basket spot is compared to a basket strike and a cash settlement is generated based on a basket vanilla or basket digital payoff.
The following formula can be used to calculate the basket spot. Each currency pair within the basket must be quoted such that CCY1 is the common currency. This may mean, for example, flipping AUD/USD into USD/AUD terms:

where there are n currency pairs in the basket, ![]() is the spot at time t in currency pair i, and therefore
is the spot at time t in currency pair i, and therefore ![]() is the inception spot in currency pair i. Weights
is the inception spot in currency pair i. Weights ![]() sum to 1 and are almost always set to
sum to 1 and are almost always set to ![]() but the flexibility exists to offer different variations. The process of constructing a basket is similar to constructing a financial index. The most well-known FX basket is BRIC, which contains the currencies of Brazil, Russia, India, and China.
but the flexibility exists to offer different variations. The process of constructing a basket is similar to constructing a financial index. The most well-known FX basket is BRIC, which contains the currencies of Brazil, Russia, India, and China.
Within this framework, the basket spot starts at 1 and therefore basket strikes are often quoted as a percentage (e.g., 100%). A basket call payoff at maturity is:
It is also possible to construct an “inverted” or “self-quanto” basket by flipping the formula used to calculate the basket spot:
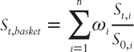
And flipping the payoff at maturity:
Inverted basket payoffs are often preferred by clients because they are cheaper than the standard case.
Example: 1yr EUR/GBP/AUD basket call versus USD with 100% strike. The basket has common currency USD in which the notional is specified and the cash payout at expiry is calculated. Exhibit 30.1 shows realized returns from the individual spot rates plus the basket spot. As with the Asian options seen in Chapter 29, the averaging within the basket reduces the basket spot volatility compared to the component spot volatility.

Exhibit 30.1 Realized component spot and basket spot returns
Like a regular vanilla option, the value of the basket is dependent on the basket forward (i.e., some average of the component forward drift) and the basket spot volatility. The volatility of the basket spot compared to the component spots depends on the correlations between the currency pairs in the basket. If all component spots were 100% correlated, the basket spot would be as volatile as an average of the component spot volatilities. However, as the correlations between pairs move lower than 100%, the basket volatility reduces. Consider a stylized two-pair basket where the spots move in equal and opposite directions; the basket spot would be static.
As noted in Chapter 16, higher correlation between major currency pairs implies lower cross-volatility. Basket options are long vega in the major currency pairs and long correlation between the major currency pairs, hence short vega in the cross-currency pairs.
Basket options are usually quoted with a tighter bid–offer spread than the cumulative spread resulting from vega risk in all major and cross currency pairs within the basket, since the vega risks offset.
Baskets sound complex but in most cases the averaging effect significantly reduces their trading risks. A copula (see Chapter 12) approach can be used to take the volatility surface into account and this generally captures the majority of exposures to the volatility surface. Basket options are commonly traded as an investment product and they are attractive because the basket is usually cheaper than buying the individual vanilla options.
One variation in which the risk management becomes more challenging is a basket digital. If the basket spot is near the basket digital level at expiry, this can be difficult to manage because all spots within the basket impact the payoff, so it is not possible to accurately hedge the digital risk with a standard European digital contract.
Dual Digital Options
Dual digital options are combinations of two European digital options in separate currency pairs but to the same expiry date. The dual digital pays out if both digitals are in-the-money at expiry. For example, a dual digital might payout USD1m if EUR/USD is above 1.3000 and GBP/USD is below 1.6000 at expiry. At inception, if EUR/USD spot is at 1.3000 and GBP/USD spot is at 1.6000 (the digital levels) and there was no significant drift or discounting, each individual digital will cost around 50%. The price of the dual digital then depends on the correlation between EUR/USD and GBP/USD spots.
In a stylized world, if EUR/USD and GBP/USD spots move in a perfectly positively correlated manner, the dual digital will be valued at 0%. There would be no chance for the product to payout since that requires EUR/USD higher and GBP/USD lower. Alternatively, if EUR/USD and GBP/USD spots move in a perfectly negatively correlated manner, the dual digital will be valued at 50% because there is a half chance of EUR/USD higher (and GBP/USD lower) triggering the payout. If there is 0% correlation between the spots, the dual digital will be valued at 25%. The relationship between correlation and dual digital TV is shown in Exhibit 30.2.

Exhibit 30.2 Dual digital TV versus correlation
Exhibit 30.2 shows how this dual digital has a significant short correlation exposure. Recall again the link between correlation and cross volatility: correlation higher = cross-volatility lower. This is demonstrated in Exhibit 30.3, which confirms that this dual digital option has a long exposure to the cross (i.e., EUR/GBP) volatility.

Exhibit 30.3 Dual digital TV versus cross volatility
Dual digital options can be difficult to risk manage because of the implicit leverage within the product. Consider a dual digital product where each digital option has an individual TV of 50% and the dual digital TV is 25%. If a highly correlated spot jump occurs due to an external event in the common currency, each individual digital TV jumps to 80% and the dual digital TV jumps to 64%. This pickup in value from 25% to 64% is difficult to hedge using vanilla options. The risk management challenge from this issue increases for e.g. a triple digital contract.
Trading Risks
The dual digital product pays out if both digitals are in-the-money at maturity. Therefore, the main exposures within the product change depending on relatively how in-the-money each digital is.
If one digital is far in-the-money and the second is at-the-money, the primary trading risk transfers onto the at-the-money digital and the risks will be similar to a standard digital option. Intuitively, one digital is likely to be in-the-money at maturity, hence it is less important than the digital payout which is in the balance. In this case, trading risk is mainly concentrated in one currency pair rather than being dependent on how the currency pairs are moving together.
If one digital is far out-of-the-money and the second is at-the-money, the primary trading risk transfers onto the out-of-the-money digital. Intuitively, to get the payout it is most important that the spot within the out-of-the-money digital currency pair moves in-the-money. Again, trading risk is mainly concentrated in one currency pair rather than being dependent on how the currency pairs are moving together.
If both individual digitals have roughly the same value, the risk is mainly concentrated on how spots in the two currency pairs are moving together (i.e., their correlation).
Vega Risk
Going back to the EUR/USD and GBP/USD dual digital example, consider the vega exposure in EUR/USD with a variable GBP/USD digital level. If the GBP/USD digital level starts very high, with a certain payout, the EUR/USD digital will have a familiar vega profile similar to a risk reversal. Then, as the GBP/USD digital level moves lower, the EUR/USD vega profile moves lower as shown in Exhibit 30.4.

Exhibit 30.4 Dual digital EUR/USD vega for different GBP/USD digital levels
Ponder this for a moment: With the GBP/USD digital level at-the-money-spot, at 1.6000, if EUR/USD implied volatility goes lower, that increases the chance of payout and hence the option value, but why? Intuitively, simply having a less volatile EUR/USD spot does not increase the chance of a payout.
This exposure results from assumptions made within the vega calculation. All implied volatilities within the system are kept constant except for the one that is being flexed. Therefore, EUR/USD volatility does not impact the EUR/GBP cross-volatility and instead correlation is updated to maintain a valid volatility triangle. In this case, lower EUR/USD volatility results in lower EUR/USD versus GBP/USD correlation and therefore a higher price. Within this dual digital contract the main exposure is to correlation, but that correlation exposure is being represented as EUR/USD vega.
Correlation also impacts the GBP/USD vega exposure in the same way. Again, for an at-the-money-spot EUR/USD digital the GBP/USD vega becomes negative at current spot. This is shown in Exhibit 30.5.

Exhibit 30.5 Dual digital GBP/USD vega profile
These examples show why, when risk managing multi-asset options, it is vital to understand what assumptions are used to calculate Greek exposures. Within this example, the exposures calculated are:
- Short EUR/USD vega (with all other implied volatilities held constant but correlation moving)
- Short GBP/USD vega (with all other implied volatilities held constant but correlation moving)
- Long EUR/GBP cross vega (with all other implied volatilities held constant but correlation moving)
But using a different calculation methodology it would be possible to view the same risk as:
- Flat EUR/USD vega (with correlation and the other major volatility held constant but cross-volatility moving)
- Flat GBP/USD vega (with correlation and the other major volatility held constant but cross-volatility moving)
- Short EUR/USD versus GBP/USD correlation exposure
The second formulation is arguably a more intuitive way to view the risks on the trade. It also makes it easier to assess the smile risk in each major currency pair using a vega versus spot chart or vanna exposures.
Best-of and Worst-of Options
Rainbow options have payoffs generated across multiple currency pairs. At maturity, the payoff of the rainbow option is some function of ranked vanilla payoffs. In FX derivatives, best-of (pays out the maximum payoff) and worst-of (pays out the minimum payoff) options are by far the most commonly traded rainbow options. Each payoff has the same expiry date and there must be a common currency between the pairs, Payoffs can be calls or puts and the common currency can be CCY1 or CCY2 in the pair. On the expiry date, only the best- or worst-performing option is exercised and like a normal vanilla option it will only be exercised if it is in-the-money.
In symbols, for options in n currency pairs:
- If the common currency is CCY1 in currency pair i:

- If the common currency is CCY2 in currency pair i:

where the spot at maturity in currency pair i is denoted ![]() .
.
The best-of payout can be reduced where the worst-of cannot:


The following pricing identities give intuitive bounds on best-of and worst-of option prices:

 ≥ any single vanilla option price
≥ any single vanilla option price ≤ any single vanilla option price
≤ any single vanilla option price ≤ sum of all vanilla option prices
≤ sum of all vanilla option prices
Plus, if only two currency pairs are included within the structure:
 = sum of the two vanilla option prices
= sum of the two vanilla option prices
Worst-of options are often a lot cheaper than the equivalent vanilla options. This makes them attractive to institutional investors (particularly hedge funds) with strong directional spot views over multiple currency pairs.
Trading Risks
At different times during the life of a best-of or worst-of option, the main exposure could be to correlation between currency pairs or it could be to implied volatility in one major currency pair. The split between the two types of risk depends on how certain it is which option (if any) will be exercised. If the vanilla options within the rainbow option have similar values, correlation risk is maximized. If one of the vanilla options has a value significantly larger (for best-of) or smaller (for worst-of) than the rest, it becomes clearer which vanilla the trade will become, correlation risk reduces, and vega risk in that currency pair increases.
When pricing a worst-of contract it can be instructive to remove each currency pair in turn and compare the new TVs. This approach shows a trader where the discount within the price is coming from and it is particularly applicable if payouts are deep in-the-money. This technique can also be used when risk managing a short worst-of position: When a particular spot is in-the-money versus the strike, it can often be moved deep in-the-money at very little cost because it has a low probability of being the lowest payout. Moving the strike such that spot is deep in-the-money effectively removes that pair from the worst-of and hence reduces potential future correlation risk.
In general, it is important not to over-hedge best-of and worst-of options. The dynamics of these products mean that their risk profiles change dramatically and keep changing over their life. Initial hedges will almost certainly need to be unwound or rebalanced.
Vega Risk
Example 1: Best-of EUR put/USD call and GBP put/USD call option. In this example, the major pairs are EUR/USD and GBP/USD and the cross-pair is EUR/GBP. This option is long vega in the major pairs since option buyers always like increasing volatility plus the best-of has more value if the two major spots move in opposite directions. Therefore the best-of is long vega in the cross-pair since short correlation exposure implies long cross-vega.
Example 2: Worst-of EUR put/USD call and GBP put/USD call option. This option is long vega in the major pairs since, again, option buyers like increasing volatility. However, this time the worst-of has more value if the two major spots move in the same direction. Therefore the worst-of is short vega in the cross-pair since long correlation implies short cross-vega.
As in the dual digital case, care must be taken to understand the methodology used to calculate vega: What is held constant and what moves within the calculation?
Delta Risk
Delta exposures on best-of and worst-of options need to be treated with caution. The calculation often assumes that each major currency pair moves in isolation. For example, for a worst-of in EUR/USD and AUD/USD, the AUD/USD delta can be calculated assuming AUD/USD moves by itself, EUR/USD does not move, and hence EUR/AUD takes all the strain. This has little chance of being how the spots actually move and hence single-delta numbers have little chance of being correct for risk management purposes.
In practice, a move in one currency pair impacts the delta in other currency pairs. In this example, as EUR/USD moves, the AUD/USD delta will change. Delta exposures in best-of and worst-of options are multidimensional and should therefore be viewed as such.
Payout Direction Risk
One of the key aspects of best-of and worst-of options is the different risks that occur if the option pays out in the same call/put direction on the common currency or it does not.
Consider a simplified two-pair case where the payout on the common currency is the same in both pairs (i.e., EUR put/USD call and AUD put/USD call). Exhibit 30.6 shows the TV versus correlation profiles; higher correlation leads to a higher worst-of price and a lower best-of price.

Exhibit 30.6 TV versus correlation profiles for best-of and worst-of options: Same payoff direction on common currency
Exhibit 30.7 shows the relationship between cross-volatility and TV. The linear relationship implies zero second-order ![]() (cross-volga) exposure within this option.
(cross-volga) exposure within this option.

Exhibit 30.7 TV versus cross-volatility profiles for best-of and worst-of options: Same payoff direction on common currency
Now consider a simplified two-pair case where the payoff direction on the common currency is different (e.g., EUR put/USD call and AUD call/USD put). The TV versus correlation relationship is similar to the same payoff direction case as shown in Exhibit 30.8. Again, higher correlation implies a higher worst-of price and a lower best-of price.

Exhibit 30.8 TV versus correlation profiles for best-of and worst-of options: Different payoff direction on common currency
Exhibit 30.9 shows the relationship between cross-volatility and TV when the payoff direction on the common currency is different. The relationship is different from the same payoff direction case; it is no longer linear, implying a second derivative ![]() (i.e., cross-volga) exposure. This leads to increased risk management challenges plus the different payoff directions on the common currency usually cause the option to have a low valuation and hence the trade has increased leverage that will be difficult to hedge using vanilla options.
(i.e., cross-volga) exposure. This leads to increased risk management challenges plus the different payoff directions on the common currency usually cause the option to have a low valuation and hence the trade has increased leverage that will be difficult to hedge using vanilla options.

Exhibit 30.9 TV versus cross-volatility profiles for best-of and worst-of options: Different payoff direction on common currency
In general, this cross-volga exposure causes worst-of options with different payoff direction on the common currency to trade more over TV than trades with the same payoff direction on the common currency. If no sophisticated stochastic correlation pricing models are available to value the cross-volga exposure, it can be estimated using a simple method that is analogous to the old-school “alpha” method for pricing double-no-touch options: Flex the cross-volatility up and down a fixed amount and find the average TV to put an approximate value on the second-order exposure.
Switching Hedge
Finally, it is interesting to consider a “switching hedge” strategy for best-of or worst-of options. For best-of options, buy the most expensive single vanilla initially and switch it into another currency pair when the most expensive vanilla changes (costing money at each switch). At expiry, this strategy will have the best vanilla payoff as required.
For worst-of options, buy the least expensive single vanilla initially and switch it into another currency pair when the least expensive vanilla changes (earning money at each switch). At expiry, this strategy will have the worst vanilla payoff as required.
These strategies give intuition as to why worst-of options are cheap and best-of options are expensive. It also shows why the risks are more difficult to manage when vanilla values are similar because more switches would be required within the switching hedge.
Quanto Options
Within quanto options, the option payoff is denominated in a third currency, rather than CCY1 or CCY2 within the currency pair. Therefore, these products are sometimes called third currency quanto options to distinguish them from self-quanto options (see Chapter 27).
Example: 1yr EUR/USD EUR call/USD put 1.3500 option that pays out at maturity in GBP. To calculate the payoff, a GBP% payoff must be calculated. This is typically achieved by calculating, for example,

where ![]() is called a quanto-factor and is usually equal to the strike
is called a quanto-factor and is usually equal to the strike ![]() .
.
Quanto options are most often used as investment products where clients require their payout in a specific currency. From a risk management perspective, third-currency quanto options are slightly more complex than regular vanillas due to the third-currency element.
Within a Black-Scholes framework, quanto options are priced by adjusting the drift and applying discounting in the quanto currency. Specifically, the standard stochastic differential equation:
becomes:
where ![]() is the volatility of CCY1/CCY2,
is the volatility of CCY1/CCY2, ![]() is the volatility of CCY3/CCY2, and
is the volatility of CCY3/CCY2, and ![]() is the correlation between CCY1/CCY2 and CCY3/CCY2. The quanto forward therefore shifts such that:
is the correlation between CCY1/CCY2 and CCY3/CCY2. The quanto forward therefore shifts such that:
Therefore, when pricing the example EUR/USD quanto into GBP call option:
- If the correlation is zero or GBP/USD has zero volatility, the only pricing difference between the quanto option and the regular European option will come from the quanto currency discounting.
- If EUR/USD and GBP/USD are positively correlated, the quanto forward moves relatively lower and the price of a quanto call option is lower in the quanto currency (GBP) than the regular European vanilla call option is in USD.
- If EUR/USD and GBP/USD are negatively correlated, the quanto forward moves relatively higher and the price of the quanto call option is higher in the quanto currency (GBP) than the regular European vanilla call option is in USD.
It is possible for any option payoff to be quantoed into a third currency. The forward adjustment and discounting are the main adjustments within the pricing, but in currency pairs with significant skew or wings the volatility surface should also be taken into account using, for example, a quanto local volatility model. Once quanto options are booked into the trading position, they rarely cause any significant pricing or risk management issues unless their notionals are very large. The correlation risk on quanto options is small relative to the risks on dual digital or worst-of options.
