Chapter 14
Vanilla FX Derivatives Trading Exposures
In Part I, Greek exposures were examined within a stylized framework. In practice, even the simplest Greek exposures have additional layers of complexity that must be understood by FX derivatives traders within their risk management.
Delta
Delta 
is one of the most important exposures to a derivatives trader—the sensitivity of price to a change in the underlying. It is a simple concept but there are many possible variations in exactly what the delta exposure represents.
Spot Delta versus Forward Delta
Apologies if this is obvious, but the spot delta on a spot deal is 100% of the notional. Therefore, buying GBP50m GBP/USD spot results in longer GBP50m GBP/USD spot delta exposure within the trading position. For this reason, FX spot traders talk only in terms of net long or short positions, rather than their exposures. The forward delta on a forward outright contract is 100% of the notional. Selling USD100m of 1yr USD/CAD forward outright results in a shorter USD100m USD/CAD 1yr forward delta exposure within the trading position.
Delta exposures can be present valued or future valued like cash flows. Therefore, on a specific trade:
where 
is the discount factor in the delta currency to the forward maturity, 
is the spot delta, and 
is the forward delta. When interest rates in the delta currency are positive (as they usually are), the discount factor is below 1 and 
. For example, buying AUD50m of AUD/USD 5yr forward outright has a spot delta exposure of approximately AUD42m when the 5yr AUD discount factor is around 0.84. This means that, for example, when AUD100m of spot versus AUD100m of forward is traded in an equal notional FX swap, a residual spot delta exposure remains.
Spot delta is the delta exposure most often used within FX derivatives risk management because spot is most often used to hedge delta, particularly in G10 currency pairs. When this is the case, exposures to interest rates and swap points must be additionally monitored.
Delta Quoting Conventions
Traders most often quote option delta in CCY1% or CCY1 cash terms with CCY1 determined by market convention for that currency pair. Spot and forward deals are generally traded in CCY1 terms, so when the option delta is also given in CCY1 terms the hedge amount and direction are immediately clear. For example, an option has long CCY1 delta exposure: Sell spot on the hedge. Quoting delta in CCY2 terms can cause mistakes. For example, if the delta on a GBP/USD option is quoted as short USD16m, the delta hedge at current spot would be to sell GBP10m GBP/USD.
To convert CCY1% spot delta to CCY2% spot delta the following formula is used:
where 
is spot and 
is the strike. Note that when 
, the delta is unchanged between CCY1% and CCY2% terms.
To convert CCY1% forward delta to CCY2% forward delta the following formula is used:
where 
is the forward.
The negative signs are present within these formulas because CCY1 is bought while CCY2 is sold, or vice versa within an FX transaction.
CCY1 versus CCY2 Premium Delta
The standard delta profile for a long vanilla call option goes from 0% (with spot far below the strike) to +100% (with spot far above the strike), hitting +50% around the ATM, as shown in Exhibit 14.1.
Exhibit 14.1 Long vanilla call delta (premium paid in CCY2) with 1.0000 strike
This analysis assumes that the option premium is paid in CCY2 (the domestic currency). If the option premium is paid in CCY1 (the foreign currency), the delta exposure changes.
In USD/JPY, consider a long USD call option with JPY as the natural P&L currency but premium paid in USD by market convention. When buying this option, an additional short USD delta exposure is generated since USD are paid out in the premium.
In general:
where delta and premium are quoted in the same terms.
The intuition that the inclusion of premium moves delta shorter is as follows:
- At lower spot, the USD premium will be relatively cheaper to pay in JPY (domestic) terms.
- At higher spot, the USD premium will be relatively more expensive to pay in JPY (domestic) terms.
The long call CCY1% option premium profile is shown in Exhibit 14.2. The delta adjustment will be particularly large when the option is deep in-the-money and therefore has a large premium. This is shown in Exhibit 14.3. At longer tenors this effect can cause the delta of ATM options to be far away from the stylized 50%.
Exhibit 14.2 Long vanilla call option premium with 1.0000 strike
Exhibit 14.3 Long vanilla call option delta (premium paid in CCY1 or CCY2) with 1.0000 strike
For a long put option, the stylized delta profile goes from –100% (with spot far below the strike) to 0% (with spot far above the strike). Again, a CCY1 premium causes an additional short delta, which this time has a larger impact with spot in-the-money to the downside as shown in Exhibit 14.4.
Exhibit 14.4 Long vanilla put option delta (premium paid in CCY1 or CCY2) with 1.0000 strike
The premium currency in a particular currency pair is determined by market convention. If the currency pair contains USD, then the premium currency will be USD. Other G10 currencies can be approximately ordered: EUR > GBP > AUD > NZD > CAD > CHF > NOK > SEK > JPY.
In G10 versus emerging market currency pairs, the premium is usually paid in the G10 currency.
Delta Bleed
Greek exposures within derivatives trading positions do not stay constant over time. Traders therefore investigate how exposures change (bleed) over the next few trading days. Specifically, traders roll the horizon date forward near the end of the day to see how their position will look on the next trading day. This allows them to assess position bleed, particularly delta bleed.
Exhibit 14.5 shows how delta on a vanilla call option changes over time. Prior to the expiry date there are three possible cases for the relative positioning of spot and the strike of a long vanilla call option:
Exhibit 14.5 Vanilla call option delta with 100.00 strike over time
- For an out-of-the-money (OTM) spot (i.e., spot below strike), delta bleeds shorter.
- For an at-the-money (ATM) spot (i.e., spot close to the strike), delta remains roughly unchanged over time.
- For an in-the-money (ITM) spot (i.e., spot above strike), delta bleeds longer.
Example: EUR/USD spot: 1.3650.
- 7-day 1.3750 EUR call/USD put: 31% delta
- 6-day 1.3750 EUR call/USD put: 29% delta (i.e., –2% delta bleed)
Intuitively this makes sense when delta is thought of as the chance of ending up in-the-money at maturity. Lower time to maturity gives spot less time to move through the strike. Therefore:
- For an OTM option, as time to expiry shortens, the probability of ending up ITM at maturity (and hence the delta) reduces.
- For an ATM option, as time to expiry shortens, the probability of ending up ITM at maturity (and hence the delta) remains roughly unchanged at approximately 50%.
- For an ITM option, as time to expiry shortens, the probability of ending up ITM at maturity (and hence the delta) increases.
For a long put option the ITM versus OTM side is switched (e.g., spot below the strike is OTM for a call but ITM for a put) but additionally, put deltas are negative so the delta bleed on call options and put options ends up being equivalent, as expected due to put–call parity.
Example: EUR/USD spot: 1.3650.
- 7-day 1.3750 EUR put/USD call: –69% delta
- 6-day 1.3750 EUR put/USD call: –71% delta (i.e., –2% delta bleed)
The delta bleed for a particular strike increases as the expiry date approaches with the most dramatic delta bleed occurring into the expiry date itself. On vanilla options with large notionals, traders pay close attention to these delta changes.
Consider a long call option:
- On the day before maturity, if spot is slightly above the strike, delta will be approximately +50%. On the expiry date itself and with spot unchanged delta will be +100% above the strike. Therefore, delta bleed will be +50% of the option notional.
- On the day before maturity, if spot is slightly below the strike, delta will be approximately +50%. On the expiry date itself and with spot unchanged delta will be 0% below the strike. Therefore, delta bleed will be –50% of the option notional.
Generally, delta bleed assists traders with their risk management:
- If the trading position is mainly long downside or short topside vanilla options, delta will bleed longer.
- If the trading position is mainly long topside or short downside vanilla options, delta will bleed shorter.
In each of these scenarios, the delta bleed matches a natural risk management preference to run delta into short gamma areas (i.e., running long delta if short topside gamma) and to run delta away from long gamma areas (i.e., running long delta if long downside gamma). Delta bleed therefore often helps to produce a balanced P&L profile.
Gamma and Theta
As discussed in Chapter 9, buying vanilla options produces long gamma exposures, which costs theta over time. Selling vanilla options produces short gamma exposures, which earns theta over time.
Gamma 
is the rate at which delta changes as spot moves and in risk management tools it is usually quoted for a 1% move in spot.
Theta 
is the rate at which price changes over time and in risk management tools it is usually quoted as the P&L from a one-day shift forward in the horizon date. It therefore represents the net cost (negative theta) or net benefit (positive theta) from holding the trading position for one full trading day. This seems clear enough but it is important that traders know what assumptions are used within the calculation. For example, what happens to the implied volatility and interest rate curves as the horizon date rolls forward?
In practice, cumulative position value changes with time in two different ways. First, when the horizon is rolled forward, there is a P&L jump (i.e., theta). This P&L jump will be particularly large for slightly out-of-the-money vanilla options expiring on the new horizon date. Second, throughout the day, implied volatility moving lower at shorter maturities is an additional source of value change (as per Chapter 11).
Under Black-Scholes, gamma and theta are linked by this formula:
where 
is volatility and 
is spot. The negative sign exists because, for example, long (positive) gamma causes paying (negative) theta.
Looking at the formula, gamma and (negative) theta are proportional 
. This makes intuitive sense because, e.g., long gamma gives the ability to make money out of spot moves and the more delta changes as spot moves, the more money can be made from delta hedging. Put another way, more theta must be paid for the privilege of more long gamma.
Since gamma and theta are proportional, the theta profile shown in Exhibit 14.6 takes an identical shape to the corresponding gamma profile; rising into the strike at maturity.
Exhibit 14.6 Long vanilla option with 100.00 strike theta over time
The next thing to note from the gamma-theta formula is that for the same amount of gamma, higher volatility 
causes theta to rise negatively. Intuitively, vanilla options have higher premium at higher implied volatility and therefore they have more value to decay away.
Additionally, for the same amount of theta, higher volatility causes lower gamma. To understand why, consider the delta profile: If volatility is low, there will be a big delta change over a given spot change, whereas if volatility is high, there will be a much smaller delta change over the same fixed spot change. During the 2008 financial crisis, buying 1mth AUD/JPY ATM at 50% volatility gave 3% gamma while buying 1mth USD/HKD ATM today at 0.25% volatility gives 490% gamma.
Traders actively track the gamma/theta ratio in their trading positions. Within the Black-Scholes framework, theta simply pays for gamma, but in practice theta comes from different aspects of the trading position.
ATM Curve and Volatility Smile Roll Theta
Over time, options roll down the ATM curve as an option maturity goes from, for example, 365 days to 364 days, and so on. If the ATM curve is upward sloping (i.e., 1yr ATM higher than 1mth ATM), this effect causes additional theta to be paid on long vanilla option positions (and additional theta to be earned on short vanilla option positions) as the ATM implied volatility drops over time as the expiry date moves closer to the horizon. If the ATM curve is downward sloping (e.g., 1yr ATM lower than 1mth ATM), the opposite effect occurs. The more steeply sloped the ATM curve, the larger the impact. Exhibit 14.7 demonstrates the ATM curve roll process.
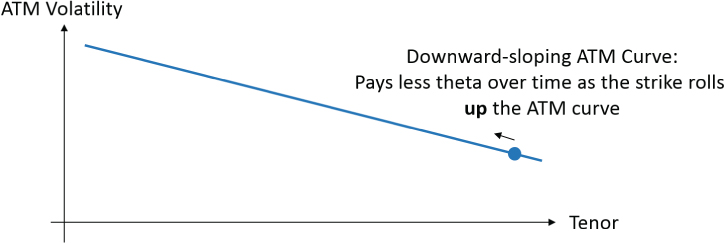
Exhibit 14.7 ATM curve roll
In practice, this effect occurs within the entire volatility surface as all strikes roll to closer maturities.
Forward Roll Theta
With everything else fixed constant, but the horizon shifted forward by one day, the forward outright to a fixed expiry date drifts toward spot. For a given option this is similar to a free spot move equal to the one-day swap points. The P&L impact from this is only a small part of the total option theta, but in high interest rate differential currency pairs it can be important.
Cash Balance Theta
Consider what happens when spot deals in a derivatives trading position settle at maturity. Long AUD10m 0.9500 AUD/USD spot settles into long AUD10m and short USD9.5m on the spot date. Cash balances from settled spot or forward deals, option premiums, or other cash payments accumulate in a trading position over time. These cash balances can be managed by putting long cash balances on deposit, hence earning interest on the cash and borrowing to offset short cash balances, hence paying interest on the cash. Alternatively, FX swaps can be traded, usually against the USD, to push cash balances into the future. It is important that traders know how to monitor these cash balances in their position and understand how they are managed day-to-day.
Smile Gamma
One aspect of a trading position with a significant impact on the gamma/theta ratio is the smile position. Owning options high on the volatility smile results in a lower gamma/theta ratio due to the higher implied volatility (recall the gamma-theta formula). This can be thought of as one of the costs of holding a long smile position. In high-skew currency pairs, long smile positions are expensive to hold over time.
Vanilla traders sometimes look at their gamma exposure calculated from vanilla options valued using the ATM curve (called ATM gamma) and compare it to the gamma exposure calculated from options valued using the full volatility surface. The difference is the smile gamma effect; the amount of gamma coming from the smile:
- If the trading position is mainly long vanilla options priced at higher implied volatility and/or short vanilla options priced at lower implied volatility on the smile, the net smile gamma effect will be negative.
- If the trading position is mainly long vanilla options priced at lower implied volatility and/or short vanilla options priced at higher implied volatility on the smile, the net smile gamma effect will be positive.
A common issue for risk managers is a low gamma/theta ratio within their trading position. To fix this issue, traders search for options in their position with large negative smile gamma effect. It is worth noting that in currency pairs where the smile is high compared to the volatility base, this approach can overlook options that have very low premiums priced using the ATM volatility (e.g., up to 0.02%) but higher premiums priced using the smile volatility (e.g., 0.10% to 0.20%). These options have almost no smile gamma effect (they contain little gamma of any kind because they are low delta), yet long positions in them can contribute significant negative theta.
P&L Distributions from Long Gamma or Short Gamma
On a given trading day in a stylized Black-Scholes world, the maximum P&L that can be lost from a long gamma trading position (ignoring P&L from vega, rho, new deals, etc.) is theta while more (potentially much more) can be made if spot is highly volatile. Exhibit 14.8 shows the P&L distribution from a long gamma position; it contains many small losses and few large gains, although the expectation of the distribution is zero.
Exhibit 14.8 Stylized P&L/theta distribution from long gamma position
Similarly, the most P&L that can be made from a short gamma trading position is theta while (much) more can be lost if spot is highly volatile. Exhibit 14.9 shows the P&L distribution from a short gamma position: It contains many small gains and few large losses, although, again, the expectation of the distribution is zero.
Exhibit 14.9 Stylized P&L/theta distribution from short gamma position
Preference for a long or short gamma P&L distribution impacts how risk managers position their trading books. Some traders prefer to trade long gamma positions while others prefer to trade short gamma positions. In a job interview, though, the correct answer is obviously that you are equally happy trading with whichever gamma position gives the best risk/reward at the time.
Vega and Weighted Vega
The most important exposure on most derivatives contracts is vega. Like delta, vega discounts in the currency it is expressed, so while stylized vega generally changes proportionally to the square root of time, in practice discounting can have a large effect at longer maturities. It is therefore not safe to assume that vega on ATM contracts always increases at longer maturities. For example, Exhibit 14.10 shows long-dated AUD/JPY ATM vega.
Exhibit 14.10 AUD/JPY ATM vega
Traders most often view vega exposures in CCY1 terms, but sometimes vega will be viewed in CCY2 if that is the P&L currency. For example, in EUR/USD, a vega exposure quoted in USD may be preferred.
A standard vega calculation assumes the ATM curve moves in parallel. A weighted vega calculation assumes the ATM curve moves proportional to 
. If the ATM curve moves in a weighted manner, it is therefore expected that, for example, the 3mth ATM moves twice as much as the 1yr ATM. This links to vega exposures where 3mth ATM vega is half that of the 1yr ATM.
The weighted vega calculation folds all exposures into a single reference pillar (usually 1mth or 3mth depending on which tenor is most liquid in a particular currency pair). For example, a 3mth weighted vega of USD400k implies that the full vega exposure in the position is equivalent to a vega exposure of USD400k in the 3mth tenor. It is therefore important to know which reference pillar the weighted vega calculation uses.
The following formula is used to convert vega 
at time 
into weighted vega 
at the weighted reference time 
.
Exhibit 14.11 gives vega multipliers for converting bucketed vega at market tenors into 1mth weighted vega. The same methodology can also be used to calculate weighted vega on each option individually.
Exhibit 14.11 Weighted Vega Multipliers (1mth reference)
| Tenor |  (years) |
 |
Weighted Vega Multipliers (1mth reference) |
| O/N | 0.00274 | 0.052342 | 5.515 |
| 1wk | 0.01923 | 0.138675 | 2.082 |
| 2wk | 0.03846 | 0.196116 | 1.472 |
| 1mth | 0.08333 | 0.288675 | 1.000 |
| 2mth | 0.16667 | 0.408248 | 0.707 |
| 3mth | 0.25000 | 0.500000 | 0.577 |
| 6mth | 0.50000 | 0.707107 | 0.408 |
| 9mth | 0.75000 | 0.866025 | 0.333 |
| 1yr | 1.00000 | 1.000000 | 0.289 |
| 2yr | 2.00000 | 1.414214 | 0.204 |
| 5yr | 5.00000 | 2.236068 | 0.129 |
If the ATM curve is moving in a parallel manner, vega will most accurately predict P&L changes caused by changes to the ATM curve, whereas if the ATM curve is moving in a weighted manner, weighted vega will most accurately predict P&L changes caused by changes to the ATM curve. Most often, the ATM curve moves in neither a parallel nor weighted manner but some combination of the two. Traders therefore view both measures within their risk management and assess how the ATM curve is currently moving when deciding which exposure to pay closest attention to.
Adapted Greeks
Greek exposures for vanilla options can be calculated using a sticky strike or a sticky delta methodology.
Under sticky strike, the implied volatility for a given expiry date and strike stays constant as the forward moves. Standard Black-Scholes Greeks are calculated assuming a sticky strike methodology since only one constant volatility is used within the Black-Scholes framework.
Under sticky delta, the implied volatility for a given expiry date and delta stays constant as the forward moves. These so-called adapted Greeks are calculated assuming a sticky delta methodology.
It is important that traders understand the differences between standard exposures and adapted exposures so they can risk manage using the correct exposures given prevailing market behavior.
Throughout this analysis, Black-Scholes delta refers to the delta calculated under Black-Scholes using the smile volatility and it is easiest to think of the delta on a long vanilla call option when following these logical arguments.
Adapted Delta
Consider a finite difference spot delta calculation in which spot is flexed up and down a small amount and the resultant premium change is divided by the spot flex to calculate delta. In the standard Black-Scholes delta calculation, the implied volatility at which the vanilla is valued remains constant but in an adapted delta calculation the implied volatility for the fixed strike changes as spot flexes up and down: This is the adaption.
Adapted delta is such a well-accepted concept within the FX derivatives market that in some emerging market currency pairs, risk reversals are traded in the interbank broker market with an adapted delta forward hedge.
In symbols:
The formula for adapted delta comes from the chain rule. In words, adapted delta is equal to Black-Scholes delta plus vega 
multiplied by the change in implied volatility for a change in spot. To understand this 
quantity, consider a finite difference delta calculation within a volatility smile with the risk reversal for downside shown in Exhibit 14.12.
Exhibit 14.12 Adapted delta finite difference calculation shown on volatility smile
Within the volatility smile:
- When spot is flexed up, the whole volatility smile moves higher with the flex and the fixed strike rolls up to a higher implied volatility. This makes the vanilla option premium relatively higher.
- When spot is flexed down, the whole volatility smile moves lower with the flex and the fixed strike rolls down to a lower implied volatility. This makes the vanilla option premium relatively lower.
Therefore, 
is positive.
Looking back at the adapted delta formula, vega 
for a long vanilla option is always positive. Therefore, the direction of the adapted delta versus Black-Scholes delta difference comes from the 
quantity. The whole volatility smile moves with spot under the adaption:
- If implied volatility increases at lower strikes, the implied volatility for a fixed strike will rise as spot rises and
will be positive (as in the previous example). - If implied volatility increases at higher strikes, the implied volatility for a fixed strike will fall as spot rises and
will be negative.
In addition, vega decreases away from the strike so Black-Scholes delta versus adapted delta differences reduce to zero in the wings.
Therefore, in a currency pair with relatively higher skew and lower wings:
- If the risk reversal is for topside, adapted delta is usually shorter than Black-Scholes delta.
- If the risk reversal is for downside, adapted delta is usually longer than Black-Scholes delta.
In a currency pair with relatively higher wings and lower skew, adapted delta versus Black-Scholes delta differences change sharply over different spot levels around the ATM. Exhibit 14.13 shows a symmetric volatility smile with zero skew and positive wings.
Exhibit 14.13 Symmetric volatility smile
When an ATM contract is traded, the implied volatility will be at the lowest point of the volatility smile, technically called “at the bottom of the bucket.”
If spot moves higher, the volatility smile at the fixed strike becomes locally sloped higher to the downside, hence 
is positive and:
If spot moves lower, the volatility smile at the fixed strike becomes locally sloping up to the topside, hence 
is negative and:
Adapted Gamma
Adapted gamma takes into account how a fixed strike rolls around the volatility smile in exactly the same way as adapted delta does. The important measure from a risk management perspective is the gamma adaption effect—the difference between adapted gamma and Black-Scholes gamma.
Consider a symmetric volatility smile with no skew but positive wings. The adapted gamma argument is visualized in Exhibit 14.14.
Exhibit 14.14 Adapted gamma finite difference calculation for a symmetric volatility smile
As described in the previous section on adapted delta, for a strike that is initially ATM:
- Spot flexed higher → fixed strike becomes downside →
- Spot flexed lower → fixed strike becomes topside →
Therefore, under adaption, delta moves more for both up and down spot flexes. Hence around the ATM point there is positive gamma adaption effect and the effect is larger the more pronounced the wings of the smile. Exhibit 14.15 shows Black-Scholes gamma and adapted gamma for an ATM strike within a symmetric volatility smile.
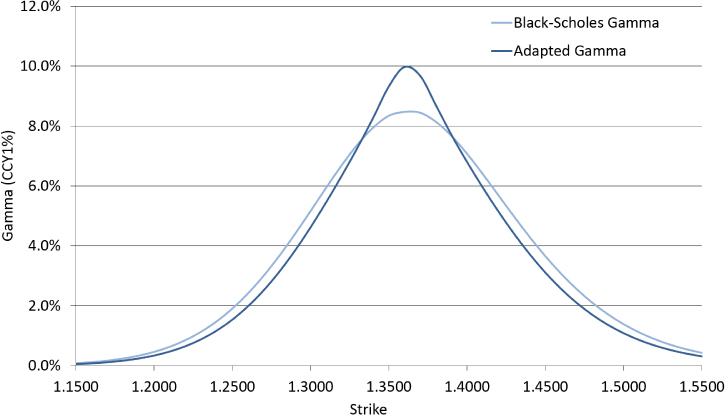
Exhibit 14.15 Adapted gamma versus Black-Scholes gamma in a symmetric volatility smile
The largest positive gamma adaption effect occurs at the point of maximum curvature in the volatility smile (i.e., maximum 
). When a skew component is added into the volatility smile, this point of maximum curvature moves to the lower volatility side of the volatility smile. In Exhibit 14.16, the risk reversal is for downside and the point of maximum curvature has moved to the topside.
Exhibit 14.16 Maximum curvature points for symmetric and non-symmetric volatility smiles
This results in the gamma profiles shown in Exhibit 14.17, which in turn results in the gamma adaption effect profile shown in Exhibit 14.18.
Exhibit 14.17 Adapted gamma versus Black-Scholes gamma profiles for a non-symmetric volatility smile
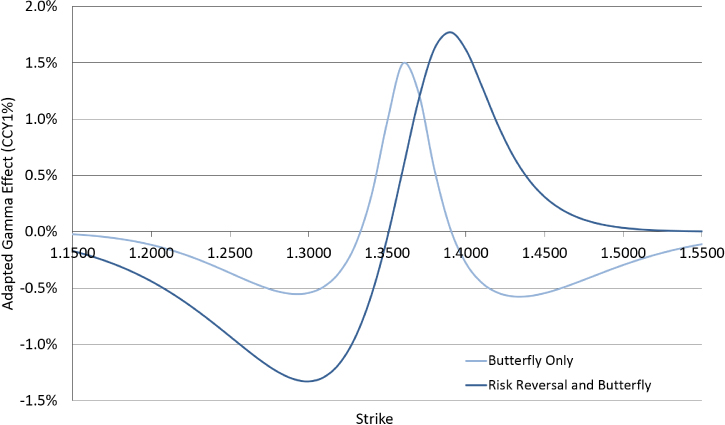
Exhibit 14.18 Gamma adaption effect profile for a non-symmetric volatility smile
In general, the gamma adaption effect follows these rules of thumb:
- Strikes on the high side of the volatility smile usually have a negative gamma adaption effect.
- Strikes on the low side of the volatility smile usually have a positive gamma adaption effect.
Therefore, buying vanillas high on the volatility smile (i.e., at an implied volatility above the ATM) results in a worse gamma/theta ratio under adaption than under Black-Scholes. In extremis it is possible for a trading position to be short adapted gamma yet paying theta—a difficult situation to risk manage.
Adapted Vega
Vega (υ) is the exposure to ATM volatility changes. Consider a finite difference vega calculation in which ATM implied volatility is flexed up and down a small amount and the resultant premium change is divided by the ATM flex to calculate vega. In the standard Black-Scholes vega calculation the implied volatility at which a vanilla is priced changes exactly as much as the ATM flex but in an adapted vega calculation the implied volatility changes differently because the whole volatility curve rebuilds under the adaption.
When the ATM is flexed higher, the strikes for a specific delta move away from the ATM. This pushes the whole volatility smile wider and causes the implied volatility for a specific strike to rise less on the high side of the smile. This effect is shown in Exhibit 14.19.
Exhibit 14.19 Volatility smile adjustment at higher ATM volatility
Therefore, strikes on the high side of the volatility smile have 
and strikes on the low side of the volatility smile have 
. Traders observe this effect most frequently when a bought risk reversal contract gives a short adapted vega exposure and a sold risk reversal contract gives a long adapted vega exposure.
Risk Managing with Adapted Greeks
A trader has done some analysis and concludes that 1yr USD/JPY risk reversals are too high. Therefore they go into the market and sell USD100m/leg of 1yr 25d risk reversal. In USD/JPY the risk reversal is for downside so selling the risk reversal involves selling the downside strike versus buying the topside strike. The risk reversal is delta hedged by selling USD50m of USD/JPY 1yr forward. This results in the trading position shown in Exhibit 14.20. The exposures in Exhibit 14.20 are calculated using the standard Black-Scholes methodology that assumes volatility for a given strike stays unchanged as spot moves (i.e., sticky strike).
Exhibit 14.20 Spot ladder from selling USD/JPY 1yr risk reversal (Black-Scholes exposures)
However, the P&Ls within Exhibit 14.20 are generated by changing spot to each level in the ladder, rebuilding the volatility smile using the new spot level as the reference point, and revaluing all the options within the portfolio. This is equivalent to a sticky delta methodology and therefore the delta exposures and P&L change do not tie in between different spot levels within the spot ladder. For example, delta is roughly flat at 101.38 and yet there is significant positive P&L at 98.33 and significant negative P&L at 104.42.
Put another way, if the method used to calculate P&L within the spot ladder and the method used to calculate the exposures within the ladder are not aligned, delta exposures and P&L changes will not be aligned.
If adapted exposures are displayed in the spot ladder instead as in Exhibit 14.21, delta at 101.38 spot is shorter and P&L changes are aligned with the delta exposures.
Exhibit 14.21 Spot ladder from selling USD/JPY 1yr risk reversal (adapted exposures)
When a spot ladder is constructed as per Exhibit 14.21, volatility surface changes need to be additionally considered. This risk reversal trade therefore will be risk managed based on how implied volatility for the two strikes in the risk reversal is expected to change as spot moves:
- If the implied volatility surface inputs are not changing as spot moves, adapted exposures should be used. Under adaption, the trading position looks too short delta and some spot or forward could be bought back to balance the delta position better.
- If the implied volatility surface inputs are changing as spot moves such that the implied volatility for the transacted strikes remains (roughly) constant, the Black-Scholes exposures should be used and the delta position looks balanced.
Holding the short risk reversal position will cause the trading book to earn money over time if everything stays static as the short smile value decays positively. However, as spot moves, ATM implied volatility changes will probably cost money since in a currency pair with downside risk reversal:
- Spot lower → ATM implied volatility higher while the position gets shorter vega.
- Spot higher → ATM implied volatility lower while the position gets longer vega.
Traders often have a choice whether to risk manage vanilla positions using Black-Scholes exposures or adapted exposures. For risk management it is best to view both exposures and judge how the market is currently trading:
- If the volatility surface is not changing as spot moves, adapted exposures should be used.
- If the volatility surface changes and particularly the ATM changes as suggested by the volatility smile as spot moves, Black-Scholes exposures should be used.
In practice, for small spot moves the volatility surface often remains unchanged (i.e., use adapted exposures), but for larger spot moves the volatility surface often reacts such that the implied volatility for specific strikes remains constant (i.e., use Black-Scholes exposures). The speed of spot moves also matters, since implied volatility reacts more if spot moves more quickly. In some sense, the volatility surface therefore contains information about expected speed of spot moves higher or lower.
Zeta
The zeta of a vanilla option is the premium difference between the value of the option priced using the smile volatility less its value priced using the ATM volatility. Zeta therefore quantifies the value in the option which is due to the volatility smile.
The zeta for a vanilla option is approximately (ignoring second-order effects) vega multiplied by the smile volatility less ATM volatility difference. Therefore:
positive zeta
negative zeta
In AUD/JPY, the risk reversal is for downside as shown in Exhibit 14.22.
Exhibit 14.22 AUD/JPY 1yr volatility smile
The equivalent zeta curve shown in Exhibit 14.23 reflects this. Of course, the zeta for an ATM strike is zero.
Exhibit 14.23 AUD/JPY 1yr zeta profile
In high-skew currency pairs:
- The high point of the zeta curve is often located around the 15d point on the high side of the smile. Being high on the zeta curve causes options to decay more quickly because of their additional value due to the smile.
- The low point of the zeta curve is often located around the 35d point on the low side of the smile.
It is important that traders know approximately where these points are in strike and delta terms because market participants often try to sell vanilla options around the most expensive point on the volatility smile and buy vanilla options around the cheapest point on the volatility smile.
Another popular strategy in high-skew currency pairs is to sell 15 delta vanilla options and buy 2 delta vanilla options, both on the high side of the smile. The idea behind this strategy is as follows:
- If spot doesn't move, the short 15d option decays (positively) more quickly than the long 2d option since the 2d option has a far lower premium.
- If spot blows up to the high side of the volatility smile, the 2d option relatively picks up in value far more than the 15d option as the ATM and risk reversals contracts increase sharply in price.
Unfortunately, the market does not make implementing this strategy easy: Offers on very low delta options on the high side of the risk reversal are often well above their theoretical midmarket (see Chapter 15).
Finally, in a currency pair with no risk reversal, the volatility smile is symmetric and the implied volatility never goes below the ATM as shown in Exhibit 14.24.
Exhibit 14.24 Volatility smile with positive wings and no skew
This results in the zeta profile shown in Exhibit 14.25, which is roughly symmetric and always positive.
Exhibit 14.25 Zeta profile for volatility smile with positive wings and no skew
Interest Rate Risk (Rho)
Within standard Black-Scholes mathematics, rho1 
and rho2 
are sensitivities to changes in the CCY1 and CCY2 continuously compounded risk-free interest rates respectively. In FX derivatives there are always two rho values to consider: one for each currency in the currency pair. Rho is most often quoted in per basis point (pbp) terms—the P&L change for a 0.01% change in interest rates.
The following analysis examines rho exposures for vanilla contracts using stylized Black-Scholes analysis where premiums and hence subtleties around the P&L currency are ignored.
Future Cash and Forwards
Very generally, long-dated contracts have more interest rate risk than short-dated contracts. Future cash payments generate negative rho exposure linearly proportional to notional and tenor. In per basis point terms:
where 
is future cash notional and 
is the time (in years) to the future cash delivery date. The negative sign in the formula indicates that, for example, USD must be sold forward to get longer USD rho. This can be confusing because when USD cash is held, higher return is generated with higher USD rates. The difference comes from holding the cash position versus taking delivery of a fixed cash amount in the future.
The same formula can be applied to forward contracts by considering each currency separately. For example, buying EUR100m EUR/USD 1yr forward at 1.3100 generates short EUR10k pbp EUR rho and long USD13.1k pbp USD rho.
Long Vanilla Call Option
The per basis point rho exposure on a long vanilla call option prior to maturity is shown in Exhibit 14.26:
- If the forward to expiry is far below the strike, the long CCY1 call vanilla has no payoff, no risk, and no rho exposures.
- If the forward to expiry is far above the strike, the long CCY1 call vanilla payoff behaves like a long forward and hence generates negative CCY1 rho and positive CCY2 rho exposures.
Exhibit 14.26 Long 1yr call option with 1.3100 strike rho
The rho exposure on a vanilla option contract is linked to its forward delta exposure. Exhibit 14.27 shows how a long 1yr CCY1 call vanilla has a long forward delta that produces short CCY1 rho and long CCY2 rho:
- At 0% forward delta: Per basis point rho is 0%.
- Around the ATM: Per basis point rho is 0.005%.
- At 100% forward delta: Per basis point rho is 0.01%.
Therefore:
and
where 
is the forward delta expressed in notional currency %.
Exhibit 14.27 Long 1yr call option with 1.3100 strike forward delta
As noted, longer tenor options have higher rho exposure. Therefore, over time the rho exposures on a vanilla reduce as shown in Exhibit 14.28.
Exhibit 14.28 Long 1yr call option with 1.3100 strike rho over time
Long Vanilla Put Option
There are no surprises with the rho for a long vanilla put option. Prior to maturity, if the forward to expiry is far above the strike, the CCY1 put vanilla has no payoff and no risk. If the forward to expiry is far below the strike, the long CCY1 put vanilla is essentially a short forward position and hence generates long CCY1 rho and short CCY2 rho. These rho profiles are shown in Exhibit 14.29.
Exhibit 14.29 Long 1yr put option with 1.3100 strike rho
Long ATM Straddle
Combining long CCY1 call and CCY1 put vanillas with the same ATM strike and maturity gives a long ATM straddle position:
- With a lower forward to maturity, forward delta gets shorter, CCY1 rho gets longer, and CCY2 rho gets shorter.
- With a higher forward to maturity, forward delta gets longer, CCY1 rho gets shorter, and CCY2 rho gets longer.
The crossing point occurs around the ATM as shown in Exhibit 14.30. It is instructive to note that the same rho exposures as Exhibit 14.30 are generated by this straddle, a forward-hedged CCY1 call option or a forward-hedged CCY1 put vanilla option.
Exhibit 14.30 Long 1yr ATM straddle with 1.3100 strike rho
In general, if there is a negative correlation between spot and CCY1 interest rates or a positive correlation between spot and CCY2 interest rates, buying an ATM straddle results in a desirable trading position.
Exhibit 14.31 shows how the ATM straddle rho exposures change with implied volatility:
- At higher implied volatility, the rho exposures stretch out as the distribution widens.
- At lower implied volatility, the rho exposures compress as the distribution tightens.
Exhibit 14.31 Long 1yr ATM straddle with 1.3100 strike rho at different implied volatility levels
Finally, changing interest rates with a fixed spot impacts the forward and this feeds through to the rho exposures on an ATM straddle:
- CCY1 rates higher → forward lower → longer CCY1 rho
- CCY2 rates higher → forward higher → longer CCY2 rho
Hence a long ATM straddle position contains long interest rate gamma, although this effect only becomes significant at longer tenors.