Chapter 22
European Barrier Options
European barrier options have a vanilla payoff at expiry plus they also have a single European barrier. For a European knock-out (EKO) barrier option, if spot at maturity is beyond the barrier level, the contract expires worthless despite being in-the-money. The payoff at maturity of a long European knock-out call with 1.3000 strike and 1.4500 European knock-out barrier is shown in Exhibit 22.1. European barriers must be positioned in-the-money, otherwise they have no impact.

Exhibit 22.1 European knock-out payoff at maturity
European knock-in (EKI) barrier options have a vanilla payoff at expiry only if spot at maturity is beyond the barrier level. The payoff at maturity of a long European knock-in call with 1.3000 strike and 1.4500 European knock-in barrier is shown in Exhibit 22.2.

Exhibit 22.2 European knock-in payoff at maturity
In the European knock-out barrier case, the curtailing of the payoff beyond the barrier can significantly reduce the cost of the European barrier option compared to the equivalent European vanilla option. This is shown in Exhibit 22.3.

Exhibit 22.3 European knock-out barrier versus European vanilla value profiles
Beyond the barrier, the European knock-out contract still has value prior to expiry because there is time remaining for spot to move back inside the barrier. However, as time passes and the probability of such a move occurring reduces, the value of the European knock-out option with spot beyond the barrier level decreases. This is shown in Exhibit 22.4.

Exhibit 22.4 European knock-out barrier value over time
European Knock-out Replication
Like European digital options, a European knock-out has no path dependence: The payoff depends only on spot at maturity. Also like European digital options, European barrier options can be replicated using combinations of simpler products.
A long European knock-out call option with notional N, strike K, and barrier B can be perfectly replicated using a long call spread with notionals N and strikes K and B (shown in Exhibit 22.5) plus a short European digital at B (shown in Exhibit 22.6).

Exhibit 22.5 Long vanilla call spread payoff at maturity

Exhibit 22.6 Short European digital payoff at maturity
Note that the digital in Exhibit 22.6 could itself be replicated using vanilla options so a European knock-out can theoretically be replicated using vanilla options only.
Intrinsic Value
The amount of European digital risk in a European barrier option is given by the intrinsic value. Intrinsic value measures the payoff at maturity at the barrier level, and therefore how much P&L change occurs at maturity if spot ends up one side of the barrier level or the other. The intrinsic value on a European knock-out barrier option is highlighted in Exhibit 22.7.

Exhibit 22.7 Intrinsic value in a European knock-out barrier option
Therefore:
The CCY2 intrinsic value is divided by the barrier level to get it into CCY1 terms rather than current spot because for the P&L jump to be realized spot must be at the barrier level.
Example: USD/JPY USD100m 1yr 100.00 USD Call/JPY Put European knock-out 120.00. ![]() USD 16.7% = USD 16.7m. Therefore, the European knock-out option contains USD16.7m of European digital risk at 120.00.
USD 16.7% = USD 16.7m. Therefore, the European knock-out option contains USD16.7m of European digital risk at 120.00.
Intrinsic value is also called parity, cliff, or spike and it is a key concept that is returned to often within exotic FX derivatives pricing and risk management.
European Knock-in Replication
A long European knock-in call option with notional N, strike K, and barrier B can be perfectly replicated using a long vanilla call option with notional N and strike B (shown in Exhibit 22.8) plus a long European digital at B (shown in Exhibit 22.9).
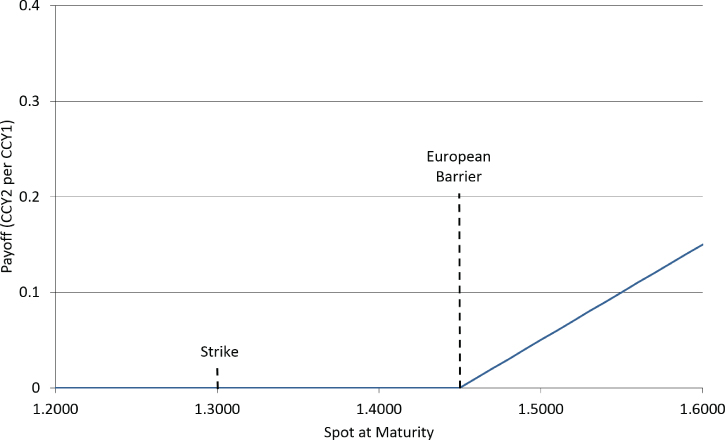
Exhibit 22.8 Long vanilla call payoff at maturity

Exhibit 22.9 Long European digital payoff at maturity
Again, the notional of the European digital in the replication is the intrinsic value of the European knock-in. Intrinsic value can be determined using the same calculation as the European knock-out case. The intrinsic value on a European knock-in barrier option is highlighted in Exhibit 22.10.

Exhibit 22.10 Intrinsic value in a European knock-in barrier option
The replications confirm that, as expected, long European knock-in + long European knock-out = long European vanilla since the digital options and vanilla options at the barrier within the replications cancel each other out.
European Barrier Greeks
European barrier option Greeks exposures can be understood via the replications shown previously.
Vega Risk
If the strike and barrier levels are far enough apart within a European knock-out barrier option, each element can be observed separately within the vega profile as in Exhibit 22.11. At the strike there is a standard vanilla vega profile while the European barrier produces a vanilla spread or risk reversal vega profile.

Exhibit 22.11 European knock-out barrier vega profile with strike and barrier far apart
If the strike and barrier levels are closer together, the vega exposures from the strike and the European barrier merge together as shown in Exhibit 22.12. Also, the proximity of the strike and barrier causes lower option value and vega exposure.

Exhibit 22.12 European knock-out barrier vega profile with strike and barrier close together
These vega profiles match the intuition of the payoff: With spot beyond the barrier, vega exposure is long because higher volatility increases the chance of spot moving back inside the barrier. If spot is between the strike and the barrier, the contract is conflicted: Higher implied volatility allows the optionality from the strike to be used more but it also increases the chance of spot moving beyond the barrier. Therefore, vega exposures from the contract go both positive and negative between the strike and the barrier.
The European knock-in vega profile also matches the intuition of the payoff. With spot beyond the European barrier level, higher volatility increases the chance of spot moving back inside the barrier and hence, like a European digital, European knock-in barrier options have short vega exposures on the positive P&L side of the barrier level and long vega exposures on the negative P&L side of the barrier level. This is shown in Exhibit 22.13.
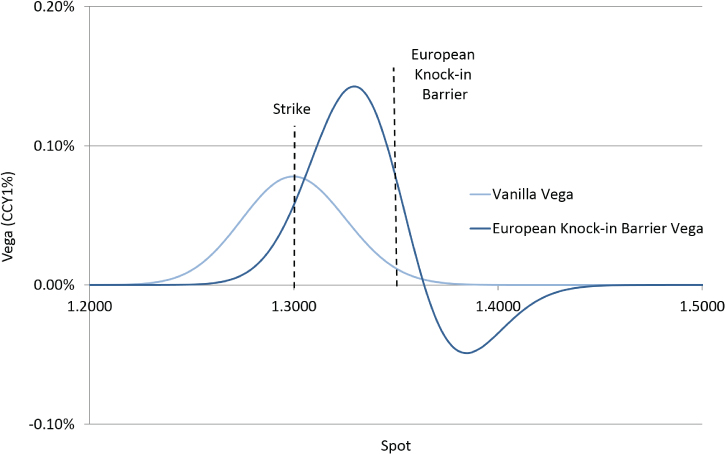
Exhibit 22.13 European knock-in barrier versus vanilla vega profiles
Gamma and Pin Risk
Toward expiry, if spot is close to the strike of a European knock-out barrier, the trading risk is simply that of a regular vanilla option and can be risk managed as such. Alternatively, if spot is close to the European barrier, the trading risk is that of a European digital option in size equal to the intrinsic value.
European Barrier Pricing
Like European digitals, prices for European barrier options incorporating the volatility smile can be generated using vanilla option replication. Alternatively, since European barrier value depends only on the terminal spot distribution, any well-calibrated smile pricing model could be used.
European Barrier Bid–Offer Spread
Intrinsic value is also used to calculate the bid–offer spread on European barrier options. As seen from the replication, a European knock-out consists of vanilla spread risk plus European digital risk. The main risk (and hence the wider spread) usually comes from the digital risk at the barrier. Since spot cannot be close to both the barrier and the strike at maturity it is usually only appropriate to take bid–offer spread from the larger of the strike bid-offer and the barrier digital bid-offer.
Therefore, if the bid–offer spread on the digital risk embedded within the European barrier option is 2%, the European barrier bid–offer spread will be approximately 2% multiplied by the intrinsic value.
