CHAPTER 23
Construction of Phylogenetic Tree: Neighbor‐Joining Method
CS Mukhopadhyay and RK Choudhary
School of Animal Biotechnology, GADVASU, Ludhiana
23.1 INTRODUCTION
The term “neighbors” refers to a node‐pair which is separated by another node. The NJ method (Saitou and Nei, 1987) is a particular case of the “star decomposition method”, where raw data are arranged in a distance matrix and nodes are created (see the example below) whereas, in the NJ method, the separation of nodes is adjusted by average divergence from all other nodes.
23.1.1 Principle
The principle of the neighbor‐joining (NJ) technique is minimum evolution, which selects the tree with minimum branch‐length. It is based on a very fast, greedy heuristic algorithm that generates sub‐trees, and the closest sub‐trees are joined to each other to yield the final tree, in a step‐wise manner. The total branch length is the shortest for the true tree.
- The NJ method can be applied for large datasets relating to the taxa with varying degrees of divergence (hence, the tree will show different lengths for different branches).
- Multiple substitutions can be corrected.
- Some of the sequence information is lost in the NJ method due to the nature of the algorithm.
23.1.2 Assumptions
- Minimum mutational events explain the evolution of the molecular sequences.
- The branch length of the tree with known topology represents the different rate of evolutionary changes.
23.2 OBJECTIVE
To construct a phylogenetic tree, using the neighbor‐joining method, employing a distance matrix obtained from a set of molecular sequences.
23.3 PROCEDURE
The essential points to remember are:
- No preference is exercised in the pairing of sequences.
- It searches to find the pair of sequences that minimizes the branch length.
- The NJ method uses the Fitch–Margoliash Algorithm to create a rate corrected new distance table.
23.3.1 Start with a distance matrix
Let us consider a distance matrix of five sequences (A, B, C, D and E)
23.3.2 Construction of a star tree
A star tree is first drawn, based on the number of input sequences (OTUs). This star tree is a random tree with a central hub that joins all the branches.

23.3.3 Calculation of net divergence
Net divergence (Vi) is calculated for each of the OTUs using the formula  , where, i ≠ j and i, j = 1, 2, …, 5, i.e., the number of OTUs incorporated.
, where, i ≠ j and i, j = 1, 2, …, 5, i.e., the number of OTUs incorporated.
23.3.4 Calculation of new distance values from the original distance and net divergence
The mean divergence (Mi) is calculated by dividing individual net divergence (Vi) by (N – 2), where N is the number of OTUs.
23.3.5 Calculation of new distances
New distances (nij) are calculated by subtracting the mean divergence (Mi, Mj) of the two OTUs which are being studied from the distance (dij) between these two corresponding OTUs (ith and jth OTUs being studied).
| Distance | Equation | Calculation | Value |
| nAB = | dAB – (MA + MB) = | 4 – (8.333 + 9.333) = | – 13.666 |
| nAC = | dAC – (MA + MC) = | 7 – (8.333 + 10.333) = | – 11.666 |
| nAD = | dAD – (MA + MD) = | 6 – (8.333 + 9.333) = | – 11.666 |
| nAE = | dAE – (MA + ME) = | 8 – (8.333 + 12.000) = | – 12.333 |
| nBC = | dBC – (MB + MC) = | 8 – (9.333 + 10.333) = | – 11.666 |
| nBD = | dBD – (MB + MD) = | 7 – (9.333 + 9.333) = | – 11.666 |
| nBE = | dBE – (MB + ME) = | 9 – (9.333 + 12.000) = | – 12.333 |
| nCD = | dCD – (MC + MD) = | 6 – (10.333 + 9.333) = | – 13.666 |
| nCE = | dCE – (MC + ME) = | 10 – (10.333 + 12.000) = | – 12.333 |
| nDE = | dDE – (MD + ME) = | 9 – (9.333 + 12.000) = | – 12.333 |
23.3.6 Construction of new distance matrix from the new distance values (nij)
| A | B | C | D | |
| B | – 13.666 | |||
| C | – 11.666 | – 11.666 | ||
| D | – 11.666 | – 11.666 | – 13.666 | |
| E | – 12.333 | – 12.333 | – 12.333 | – 12.333 |
Here, there are two pairs of OTUs – namely, “A”, “B” and “C”, “D” exhibiting least divergence with value nij = –13.666 (bold). We can select any one of these two pairs. In this example, nCD (shown in bold) is selected.
23.3.7 Calculation of branch length of the internal node
- First, the least distance value is identified from the new distance matrix.
- The two taxa with the minimum nij distance value are taken as neighbors. In the present example, “C” and “D” are the neighbors, with the minimum nij value of –13.666.
- Now, let us assume that “X” is the new node between the neighbors “C” and “D”. The branch lengths from the internal node “X” and the external nodes “C” and “D” (denoted as LCX and LDX, respectively) are calculated.
| Branch length | Equation | Calculation | Value |
| LCX = | (dCD / 2) + ((MC – MD) / (2)) = | (6 / 2) + ((10.333 – 9.333) / (2)) | =3.500 |
| LDX = | dCD – LCX = | (6 – 3.500) | =2.500 |
These values of the branch lengths are now used to construct the tree:

23.3.8 Distance of the other OTUs from internal node (X)
Next, the distances between rest of the terminal nodes (here, “A”, “B” and “E”) with the internal node (“X”) are calculated:
| Equation | Calculation | Value |
| mAX =(dAC + dAD – dCD) / 2 | = (7 + 6 – 6) / 2 | = 3.500 |
| mBX =(dBC + dBD – dCD) / 2 | = (8 + 7 – 6) / 2 | = 4.500 |
| mEX =(dCE + dDE – dCD) / 2 | = (10 + 9 – 6) / 2 | = 6.500 |
Now the first iteration is over, the number of OTUs has been reduced to four (N – 1), where the OTUs “C” and “D” have been merged into “X”. The second iteration will start with the same steps as the first iteration.
23.3.9 New distance matrix to start the second iteration
23.3.10 Calculation of net divergence
23.3.11 Calculation of new distance values from the original distance and net divergence
23.3.12 Calculation of new distances
| Distance | Equation | Calculation | Value |
| nAB = | dAB – (MA + MB) = | 4 – (6.75 + 8.75) = | – 11.500 |
| nAX = | dAX – (MA + MX) = | 3.5 – (6.75 + 7.25) = | – 10.500 |
| nAE = | dAE – (MA + ME) = | 8 – (6.75 + 10.75) = | – 9.500 |
| nBX = | dBX – (MB + MX) = | 4.5 – (8.75 + 7.25) = | – 11.500 |
| nBE = | dBE – (MB + ME) = | 9 – (8.75 + 10.75) = | – 10.500 |
| nXE = | dXE – (MX + ME) = | 6.5 – (7.25 + 10.75) = | – 11.500 |
23.3.13 Construction of new distance matrix from new distance values (nij)
Now we select A and B as the neighbors out of the three pairs with minimum distances.
23.3.14 Calculation of the branch length of the internal node
- The two taxa with the minimum nij distance value are taken as neighbors. In the present example, “A” and “B” are the neighbors with a minimum nij value of –11.500.
- Now, let us assume that “Y” is the new node between the neighbors “A” and “B”. The branch lengths from the internal node “Y” and the external nodes “A” and “B” (denoted as LAY and LBY, respectively) are calculated.
Distance with the internal node (Y):
| Branch Length | Equation | Value |
| LAY = | (dAB / 2) + ((VA – VB) / (2)) | =1.000 |
| LBY = | dAB – LAY | =3.000 |
Next, the distances between the rest of the terminal nodes (here, “E”, “X”) with the internal node (“Y”) is calculated:
| Equation | Calculation | Value |
| mEY =(dAE + dBE – dAB) / 2 = | (8 + 9 – 4) / 2 = | 6.500 |
| mXY =(dAX + dBX – dAB) / 2 = | (3.5 + 4.5 – 4) / 2 = | 2.000 |

Now, a new distance matrix is created in the third iteration (n = 3):
23.3.15 Calculation of net divergence
23.3.16 Calculation of new distance values from the original distance and net divergence
23.3.17 Calculation of new distances
23.3.18 Construction of new distance matrix from the new distance values (nij)
23.3.19 Calculation of branch length of the internal node
- The two taxa with the minimum nij distance values are taken as neighbors. In the present example, “E” and “Y” are the neighbors with a minimum nij value of –15.000.
- Now, let us assume that “Z” is the new node between the neighbors “E” and “Y”. The branch lengths from the internal node “Z” and the external nodes “E” and “Y” (denoted as LEZ and LYZ, respectively) are calculated.
23.3.20 Distance with internal node (Z)
Next, the distances between the rest of the terminal nodes (here, “E”, “Y”) with the internal node (“Z”) are calculated:
| Equation | Calculation | Value |
| mXZ =(dXE + dYX – dEY) / 2 = | ((6.5) + (2) – (6.5)) / 2 = | 1.000 |
The final neighbor‐joining tree obtained is shown below:

The rooted tree can be obtained by positioning the branches in a rectangular format of branches:
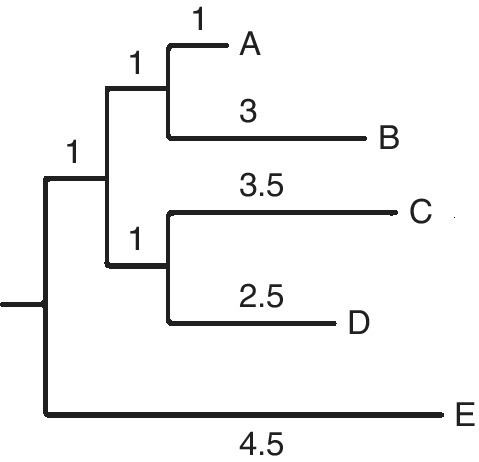
Thus, trees are generated for different topologies, and the tree with the shortest total length is to be selected, as a principle.
23.4 INTERPRETATION OF NJ TREE
The values shown in each branch denote the rate‐corrected distances, which are not proportional to the time‐scale. The inference is thus that the rate of evolution is not the same in different branches, and the distances between two taxa are the sum of the distances indicated in the branches. The distances are calculated using a suitable method (assuming a different rate of substitution).
23.5 QUESTIONS
- 1. Construct a phylogenetic tree using the given distance matrix by applying the NJ method:
- 2. Use the following distance matrix to construct an NJ method‐based phylogenetic tree:
- 3. Given the following distances, construct a phylogenetic tree using the NJ method:
- 4. How is the NJ method principally different from the UPGMA method of phylogeny construction?
- 5. Enumerate the conditions where the NJ method is the best suited for phylogenetic tree construction. Logically explain the reasons why.
