3.3
Equivalence Relations

3.3.1 Introduction

As you well know every fraction has many equivalent forms. For example

equation

are different ways to represent the same number. They may appear different and are called different names, but they are all equal. The idea of grouping things together that appear different, but from a certain perspective are the same which is the fundamental idea behind equivalence relations.

An equivalence relation is a relation that holds between two elements that relaxes the sometimes over‐restrictive “equals relation” and replaces it by “equals from a certain point of view.” This allows one to partition sets into groups called equivalence classes which share common properties. For example, we might say two integers as the same if they have the same remainder when divided by a certain number. For example, from some points of view, we may consider the integers … −5, −2, 1, 4, 7, … “equal” since they all have a remainder of +1 when divided by 3.

3.3.2 Partition of a Set

A partition of a set is a grouping of the members of the set into nonempty sets in such a way that each element is included in one and only one of the subsets. This leads us to the formal definition of a partition of a set.

Diagram displaying an ellipse labeled A with portions labeled A1, A2, A3, A4, and A5.

Figure 3.23 Set partition.

The following theorem reveals the reason equivalences relation play an important role in mathematics.

3.3.3 The Partitioning Property of the Equivalence Relation

We now see how an equivalence relation on a set allows one to create a partition of the set. If the equivalence relation was the equals relation “=,” then the sets in the partition would consist of a single element, but for other equivalence relations the size of the partitions vary.

To show that an equivalence relation “≡” induces a partition of A, note that the reflexive property of an equivalence relation tells us x ≡ x for all x ∈ A, which in turn tells us that every equivalence class is nonempty and that the union of all equivalence classes is the whole set A. Hence, the only remaining thing to show is that distinct equivalence classes do not overlap. In other words, if [x] ∩ [y] ≠ ∅, then [x] = [y]. So we assume [x] ∩ [y] ≠ ∅ and prove [x] = [y]. We begin by doing a little “background” work by picking an element s ∈ [x] ∩ [y] and using properties of an equivalence relation we have x ≡ s and y ≡ s. But ≡ is symmetric so we also have y ≡ s, and by transitivity x ≡ y and by symmetry y ≡ x. We are now ready to start the proof of [x] = [y] by first showing [x] ⊆ [y]. We select an arbitrary d ∈ [x] which implies d ≡ x, but we have seen x ≡ y and so by transitivity we have d ≡ y which means d ∈ [y]. Hence, [x] ⊆ [y]. A similar argument shows that [y] ⊆ [x] and so [x] = [y]. Figure 3.24 gives a broad idea of the players in the proof.

(⇐) If we define members of the set A as equivalent if they belong to the same equivalence class, this defines an equivalence relation on A.▌

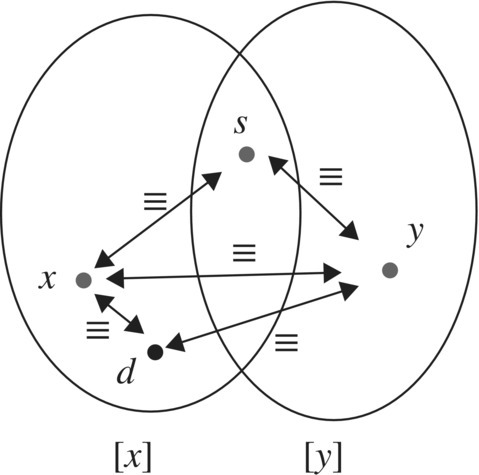
Diagram of disjoint equivalence classes displaying two overlapping ellipses with solid circle markers labeled x, d, s, and y linked to each other by double-headed arrows.

Figure 3.24 Disjoint equivalence classes.

3.3.4 Counting Partitions

Given a set with n members, how many ways are there to subdivide the set into disjoint subsets? The total number of partitions of a set of size n is called the Bell number Bn of the set, and the first few Bell numbers for sets of size n = 0, 1, 2, … are

equation

The set {a, b, c} of three members has a Bell number B3 = 5 and the five partitions of {a, b, c} are drawn in Figure 3.25.

Diagram of partitions of {a, b, c} illustrated by four boxes with portions labeled a, b, and c with their induced equivalence relations that includes a≡a, a≡b, and a≡c, a≡b and c≡c, a≡c and b≡b, etc. from left to right.

Figure 3.25 Partitions of {a, b, c} and their induced equivalence relations.

Note how this partition gives rise to an equivalence relation on {a, b, c}. We say that two elements of the set are equivalent if they belong to the same set in the partition.

3.3.5 Modular Arithmetic

Two integers x, y ∈ ℤ are said to be congruent modulo N, denoted by1

equation

if they have the same remainder when divided by the integer N. Dividing two congruent integers x, y by N, we have

equation

where Q1, Q2 are their respective quotients and r their common remainder. Subtracting the two equations gives

equation

which says if x, y are congruent modulo N, then their difference is divisible by N. In other words,

equation

We now show that the congruence relation is an equivalence relation.

The congruence relation “≡” on ℤ partitions the integers into congruence classes called residue classes, where integers in each residue class have the same remainders when divided by N. For example if N = 5 the residue classes are denoted by [0]5, [1]5, [2]5, [3]5, [4]5, which are listed in Table 3.3.

Table 3.3 Residue classes mod 5.

Residue classes for ℤ modulo (5)
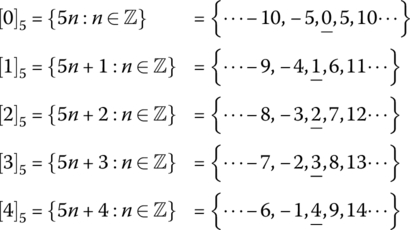images

Note that the residue classes partition the integers into five disjoint sets:

equation

The collection of partitions is called the quotient set of ℤ modulo 5, and denoted by ℤ/5ℤ. In other words

equation

Table 3.4 shows the properties of some common relations.

Table 3.4 Common mathematical relations.

Reflexive Symmetric Transitive Antisymmetric
⊥ No Yes Yes Yes
= Yes Yes Yes Yes
≤ Yes No Yes Yes
< No No Yes Yes
∥ Yes Yes Yes No
⊥ No Yes No No
⊆ Yes No Yes Yes
≡ mod(n) Yes Yes Yes No
≅ Yes Yes Yes No
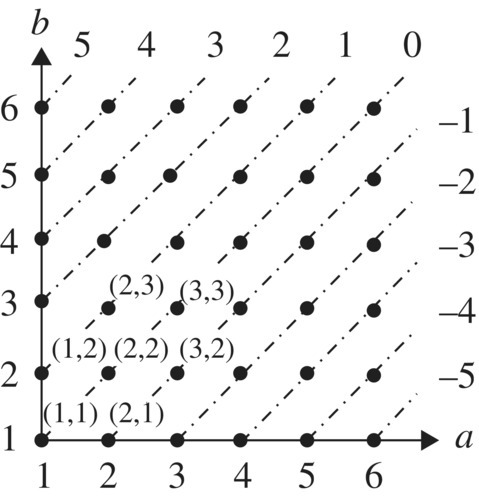
Graph of equivalence classes as grid points on lines y = x + n displaying points with corresponding dotdash line and solid circle marker.

Figure 3.26 Equivalence classes as grid points on lines y = x + n.

Problems

  1. Testing Relations

    Let A denote the student body at a university and individual students by x and y. Determine if the following relations are equivalence relations on A.

    1. x is related to y iff x and y have the same major.
    2. x is related to y iff x and y have the same GPA.
    3. x is related to y iff x and y are from the same country.
    4. x is related to y iff x and y have the same major.
  2. Equivalence Relations

    Which of the following relations R are equivalence relations on the given set A. For those relations that are equivalence relations, find the equivalence classes.

    1. xRy if and only if y = x2. (A = ℝ)
    2. mRn if and only if m is a factor of n. (A = ℕ)
    3. xRy if and only if x and y have the same remainder when divided by 5. (A = ℕ)
    4. xRy if and only if |x − y| ≤ 1. (A = ℝ)
    5. (a, b)R(c, d) if and only if a2 + b2 = c2 + d2. (A = ℝ2)
  3. Not Equivalence Relations

    Determine if the following relations are equivalent relations and if not, which condition: reflexive, symmetric, or transitive fails?

    1. The relation “≤” on the real numbers.
    2. The empty relation on an empty set (i.e. xRy never true)
    3. Relation “⊂” of being a proper subset on a family of sets.
    4. Relation of being perpendicular on lines in the plane.
  4. Finding the Equivalence Relation

    Partition the set A = {a, b, c, d, e} into the equivalence classes {{a, c}, {b, e}, {d}}. Find the equivalence relation induced by this partition.

  5. Finding the Quotient Set

    Show that the relation

    equation

    is an equivalence relation on A = {1, 2, 3, 4, 5}. What is the partition of A induced by this relation?

  6. Finding Equivalence Classes

    The set {1, 2, 3, 4} is partitioned into {{1, 2}, {3, 4}} by an equivalence relation R. Find the following:

    1. [1]
    2. [2]
    3. [3]
    4. [4]
  7. Hmmmmmmmmm

    If an equivalence relation R on a set A has only one equivalence class, what is the relation?

  8. Unusual Equivalence Relation

    Define the relation ≡ on ℤ by m ≡ n if and only if 3 divides m + 2n.

    1. Show that ≡ is an equivalence relation
    2. Find the equivalence classes?
  9. Equivalence Relation in Calculus

    Given the set of continuous functions C[0, 1] defined on the closed interval [0, 1], define R ∈ C[0, 1] × C[0, 1] by

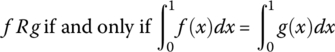
    equation
    1. Show that R is an equivalence relation.
    2. Find g ∈ C [0, 1] equivalent to f(x) = x, but f ≠ g.
  10. Equivalence Relations in Analysis

    Let A = [−1, 1] and define an equivalence relation R on A by xRy if and only if x2 = y2, x, y ∈ [−1, 1]. Find the equivalence classes.

  11. Equivalence Sets of Polynomials

    The set P consists of all polynomials defined on the real line, while I ⊆ P are those polynomials that satisfy p(0) = 0. For f, g ∈ P show that f ≡ g ⇔ f − g ∈ I is an equivalence relation.2

  12. Modular Arithmetic

    If x, y ∈ ℤ we say x ≡ y (mod n) if n divides x − y for a positive integer n. Show the relation ≡ is an equivalence relation.

  13. An Old Favorite

    The equals relation “=” is the most familiar equivalence relation. What are the equivalence classes on the set A = {1, 2, 3, 4, 5} induced by this relation?

  14. Equivalence Classes in Logic

    Define an equivalence relation on logical sentences by saying two sentences are equivalent if they have the same truth value. Place the following sentences in their proper equivalence class.

    images

  15. Similar Matrices

    Two square matrices A, B are equivalent if there is an invertible matrix M that satisfies MAM−1 = B. Show this relation between matrices defines an equivalence relation.

  16. Counting Equivalence Relations
    1. Count the number of equivalence relations on A = {1, 2}.
    2. Count the number of equivalence relations on A = {1, 2, 3}.
  17. Arithmetic in Modular Arithmetic

    Suppose

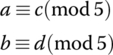
    equation

    Show that

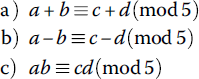
    images

  18. Mapping into the Equivalence Class

    Let X denote student body at your college or university and define the equivalence relation on the student body as “being in the same class,” class referring to freshman, sophomore, junior or senior. Define the mapping f : x → [x] that sends each student x ∈ X into his or her equivalence class [x]. Is this a well‐defined function? What is your own value under this mapping?

  19. Equivalence Classes as Directed Graphs

    Inasmuch as equivalence relations are binary relations, they can be represented by digraphs. Draw a digraph that represents the equivalence classes of the set {0, 1, 2, 3, 4, 5, 6, 7} if two elements are equivalent when they have the same remainder when divided by 3.

  20. Defining Integers from Natural Numbers

    Example 3 shows how the integers can be defined in terms of pairs of positive integers by means of the equivalence relation.

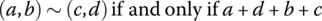
    equation

    Show this relation is an equivalence relation on ℕ × ℕ and describe the different equivalence classes. Observe that the equivalence classes can be placed in a one‐to‐one correspondence with the integers, thus allowing one to define the integers in terms of pairs of natural numbers.

  21. Counting Partitions

    Find the different partitions of the sets

    1. A = {1, 2}
    2. A = {1, 2, 3}
  22. Interesting Equivalence Relation

    Define a relation R on the nonnegative integers

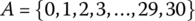
    equation

    by

    mRn⇔ (product of the digits of m= product of the digits of n).

    For example 16R23, 4R14….

    1. Show that R is an equivalence relation on A.
    2. Find the equivalence classes of the relation.
    3. The equivalence classes are listed in Table 3.5.

    Table 3.5 Equivalence classes.

    Product Integers
    0 0,10,20,30
    1 1,11
    2 2,12,21
    3 3,13
    4 4,14,22
    5 5,15
    6 6,16,23
    7 7,17
    8 8,18,24
    9 9,19
    10 25
    12 26
    14 27
    16 28
    18 29
  23. Internet Research

    There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward important equivalence relations in math, important equivalence classes in math, important partitions of a set.

Notes

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.224.0.25