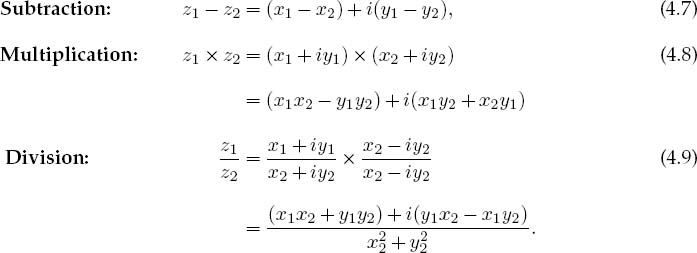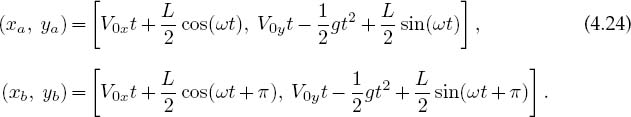4
Object-Oriented Programs: Impedance & Batons
This chapter contains two units dealing with object-oriented programming (OOP) at increasing levels of sophistication. In most of the codes in this book we try to keep our programming transparent to a wide class of users and to keep our Java examples similar to the ones in C and Fortran. Accordingly, we have deliberately avoided the use of advanced OOP techniques. Nevertheless, OOP is a key element in modern programming, and so it is essential that all readers have at least an introductory understanding of it. We recommend that you review Unit I so that you are comfortable declaring, creating, and manipulating both static and dynamic objects. Unit II deals with more advanced aspects of OOP and, while recommended, may be put off for later reading, especially for those who are object-challenged at this stage in their computing careers. (Connelly Barnes helped to prepare Unit II.)
4.1 Unit I. Basic Objects: Complex Impedance
Problem: We are given a circuit containing a resistor of resistance R, an inductor of inductance L, and a capacitor of capacitance C (Figure 4.1 left). All three elements are connected in series to an alternating voltage source V (t) = V0 cos ωt.Determine the magnitude and time dependence of the current in this circuit as a function of the frequency ω.
We solve this RLC circuit for you and assign as your particular problem that you repeat the calculation for a circuit in which there are two RLC circuits in parallel (Figure 4.1 right). Assume a single value for inductance and capacitance, and three values for resistance:
Consider frequencies of applied voltage in the range 0 < ω < 2/ ![]() = 2/s.
= 2/s.
4.2 Complex Numbers (Math)
Complex numbers are useful because they let us double our work output with only the slightest increase in effort. This is accomplished by manipulating them as if they were real numbers and then separating the real and imaginary parts at the end of the calculation. We define the symbol z to represent a number with both real and imaginary parts (Figure 4.2 left):
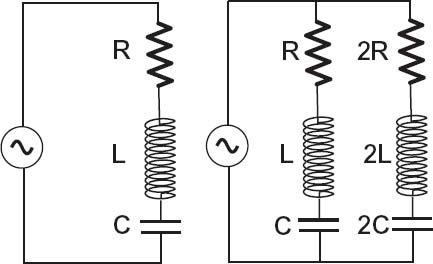
Figure 4.1 Left: An RLC circuit connected to an alternating voltage source. Right: Two RLC circuits connected in parallel to an alternating voltage. Observe that one of the parallel circuits has double the values of R,L, and C as does the other.
Here ![]() is the imaginary number, and the combination of real plus imaginary numbers is called a complex number. In analogy to a vector in an imaginary 2-D space, we also use polar coordinates to represent the same complex number:
is the imaginary number, and the combination of real plus imaginary numbers is called a complex number. In analogy to a vector in an imaginary 2-D space, we also use polar coordinates to represent the same complex number:
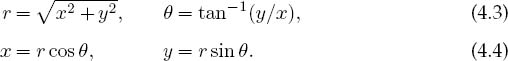
The essence of the computing aspect of our problem is the programming of the rules of arithmetic for complex numbers. This is an interesting chore because while most computer languages contain all the rules for real numbers, you must educate them as to the rules for complex numbers (Fortran being the well-educated exception). Indeed, since complex numbers are not primitive data types like doubles and floats, we will construct complex numbers as objects. We start with two complex numbers, which we distinguish with subscripts:
![]()
Complex arithmetic rules derive from applying algebra to z’s Re and Im parts:
![]()
Figure 4.2 Left: Representation of a complex number as a vector in space. Right: An abstract drawing,or what?
An amazing theorem by Euler relates the base of the natural logarithm system, complex numbers, and trigonometry:
![]()
This leads to the polar representation of complex numbers (Figure 4.2 left),
![]()
Likewise, Euler’s theorem can be applied with a complex argument to obtain
![]()
4.3 Resistance Becomes Impedance (Theory)
We apply Kirchhoff’s laws to the RLC circuit in Figure 4.1 left by summing voltage drops as we work our way around the circuit. This gives the differential equation for the current I(t) in the circuit:
where we have taken an extra time derivative to eliminate an integral over the current. The analytic solution follows by assuming that the voltage has the form V (t) = V0 cos ωt and by guessing that the resulting current I(t) = I0e-iωt will also be complex, with its real part the physical current. Because (4.13) is linear in I, the law of linear superposition holds, and so we can solve for the complex I and then extract its real and imaginary parts:
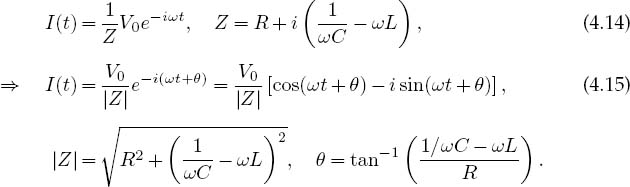
We see that the amplitude of the current equals the amplitude of the voltage divided by the magnitude of the complex impedance, and that the phase of the current relative to that of the voltage is given by θ.
The solution for the two RLC circuits in parallel (Figure 4.1 right) is analogous to that with ordinary resistors. Two impedances in series have the same current passing through them, and so we add voltages. Two impedances in parallel have the same voltage across them, and so we add currents:
![]()
4.4 Abstract Data Structures, Objects (CS)
What do you see when you look at the abstract object on the right of Figure 4.2? Some readers may see a face in profile, others may see some parts of human anatomy, and others may see a total absence of artistic ability. This figure is abstract in the sense that it does not try to present a true or realistic picture of the object but rather uses a symbol to suggest more than meets the eye. Abstract or formal concepts pervade mathematics and science because they make it easier to describe nature. For example, we may define v(t) as the velocity of an object as a function of time. This is an abstract concept in the sense that we cannot see v(t) but rather just infer it from the changes in the observable position. In computer science we create an abstract object by using a symbol to describe a collection of items. In Java we have built- in or primitive data types such as integers, floating-point numbers, Booleans, and strings. In addition, we may define abstract data structures of our own creation by combining primitive data types into more complicated structures called objects. These objects are abstract in the sense that they are named with a single symbol yet they contain multiple parts.
To distinguish between the general structure of objects we create and the set of data that its parts contain, the general object is called a class, while the object with specific values for its parts is called an instance of the class, or just an object. In this unit our objects will be complex numbers, while at other times they may be plots, vectors, or matrices. The classes that we form will not only contain objects (data structures) but also the associated methods for modifying the objects, with the entire class thought of as an object.
In computer science, abstract data structures must possess three properties:
1. Typename: Procedure to construct new data types from elementary pieces.
2. Set values: Mechanism for assigning values to the defined data type.
3. Set operations: Rules that permit operations on the new data type (you would not have gone to all the trouble of declaring a new data type unless you were interested in doing something with it).
In terms of these properties, when we declare a “complex” variable to have real and imaginary parts, we satisfy property 1. When we assign doubles to the parts, we satisfy property 2. And when we define addition and subtraction, we satisfy property 3.
Before we examine how these properties are applied in our programs, let us review the structure we have been using in our Java programs. When we start our programs with a declaration statement such as double x, this tells the Java compiler the kind of variable x is, so that Java will store it properly in memory and use proper operations on it. The general rule is that every variable we use in a program must have its data type declared. For primitive (built-in) data types, we declare them to be double, float, int, char, long, short,or boolean. If our program employs some user-defined abstract data structures, then they too must be declared. This declaration must occur even if we do not define the meaning of the data structure until later in the program (the compiler checks on that). Consequently, when our program refers to a number z as complex, the compiler must be told at some point that there are both a real part x and an imaginary part y that make up a complex number.
The actual process of creating objects in your Java program requires nonstatic class variables and methods. This means we leave out the word static in declaring the class and class variables. If the class and class variables are no longer static, they may be thought of as dynamic. Likewise, methods that deal with objects may be either static or dynamic. The static ones take objects as arguments, much like conventional mathematical functions. In contrast, dynamic methods accomplish the same end by modifying or interacting with the objects. Although you can deal with objects using static methods, you must use dynamic (nonstatic) methods to enjoy the full power of object-oriented programming.
4.4.1 Object Declaration and Construction
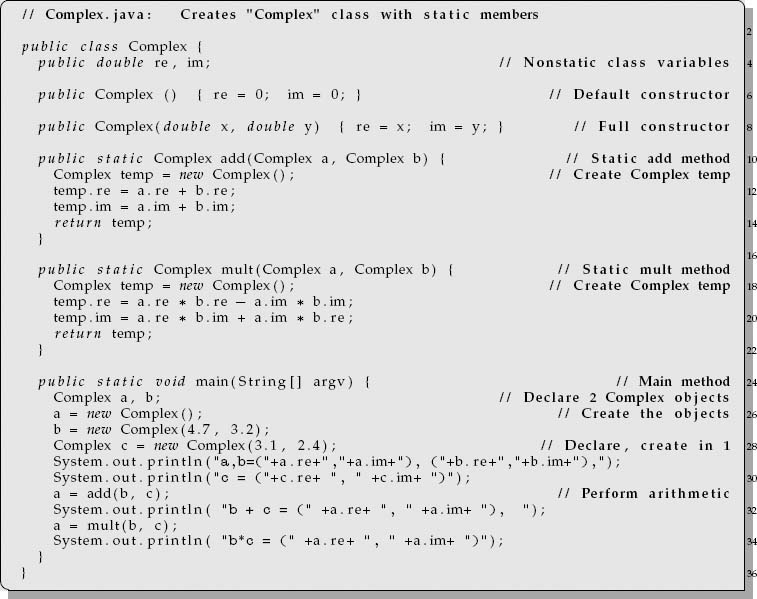
Though we may assign a name like x to an object, because objects have multiple components, you cannot assign one explicit value to the object. It follows then, that when Java deals with objects, it does so by reference; that is, the name of the variable refers to the location in memory where the object is stored and not to the explicit values of the object’s parts. To see what this means in practice, the class file Complex.java in Listing 4.1 adds and multiplies complex numbers, with the complex numbers represented as objects.
Listing 4.1 Complex.java defines the object class Complex. This permits the use of complex data types (objects). Note the two types of Complex constructors.
4.4.2 Implementation in Java
1. Enter the program Complex.java by hand, trying to understand it as best you are able. (Yes, we know that you can just copy it, but then you do not become familiar with the constructs.)
2. Observe how the word Complex is a number of things in this program. It is the name of the class (line 3), as well as the name of two methods that create the object (lines 6 and 10). Methods, such as these, that create objects are called constructors. Although neophytes view these multiple uses of the name Complex as confusing, more experienced users often view it as elegant and efficient. Look closely and take note that this program has nonstatic variables (the word static is not on line 4).
3. Compile and execute this program and check that the output agrees with the results you obtain by doing a hand calculation.
![]()
The first thing to notice about Complex.java is that the class is declared on line 3 with the statement
The main method is declared on line 24 with the statement
![]()
These are the same techniques you have seen before. However, on line 4 we see that the variables re and im are declared for the entire class with the statement
![]()
Although this is similar to the declaration we have seen before for class variables, observe that the word static is absent. This indicates that these variables are interactive or dynamic, that is, parts of an object. They are dynamic in the sense that they will be different for each specific object (instance of the class) created. That is, if we define z1 and z2 to be Complex objects, then the variables re and im each will be different for z1 and z2.
We extract the component parts of our complex object by dot operations, much like extracting the components of a physical vector by taking dot products of it with unit vectors along each axis:
![]()
This same dot notation isused to access the methods of objects, as we will see shortly. On line 6 in Listing 4.1 we see a method Complex declared with the statement
![]()
On line 8 we see a method Complex declared yet again, but with a different statement:
Some explanation is clearly in order! First, notice that both of these methods are nonstatic (the word static is absent). In fact, they are the methods that construct our complex number object, which we call Complex. Second, notice that the name of each of these methods is the same as the name of the class, Complex.1 They are spelled with their first letters capitalized, rather than with the lowercase letters usually used for methods, and because these objects have the same name as the class that contains them.
The two Complex methods are used to construct the object, and for this reason are called constructors. The first Complex constructor on line 6 is seen to be a method that takes no argument and returns no value (yes, this appears rather weird, but be patient). When Complex is called with no argument, as we see on line 18, the real and imaginary parts of the complex number (object) are automatically set to zero. This method is called the default constructor since it does what Java would otherwise do automatically (by default) when first creating an object, namely, set all its component parts initially to zero. We have explicitly included it for pedagogical purposes.
Exercise: Remove the default constructor (on line 6 with no argument) from Complex.java and check that you get the same result for the call to Complex().
![]()
The Complex method on line 8 implements the standard way to construct complex numbers. It is seen to take the two doubles x and y as input arguments, to set the real part of the complex number (object) to x, to set the imaginary part to y, and then to return to the place in the program that called it. This method is an additional constructor for complex numbers but differs from the default constructor by taking arguments. In as much as the non default constructor takes arguments while the default constructor does not, Java does not confuse it with the default constructor even though both methods have the same name.
Okay, let us now take stock of what we have up to this point. On line 4 Complex.java has declared the variables re and im that will be the two separate parts of the created object. As each instance of each object created will have different values for the object’s parts, these variables are referred to as instance variables. Because the name of the class file and the names of the objects it creates are all the same, it is sometimes useful to use yet another word to distinguish one from the other. Hence the phrase instance of a class is used to refer to the created objects (in our example, a, b, and c). This distinguishes them from the definition of the abstract data type.
Look now at the main method to see how to go about creating objects using the constructor Complex. In the usual place for declaring variables (line 25 in the listing) we have the statement
Because the compiler knows that Complex is not one of its primitive (built-in) data types, it assumes that it must be one that we have defined. In the present case, the class file contains the nonstatic class named Complex, as well as the constructors for Complex objects (data types). This means that the compiler does not have to look very far to know what you mean by a complex data type. For this reason, when the statement Complex a, b; on line 25 declares the variables a and b to be Complex objects, the compiler knows that they are manifestly objects since the constructors are not static.
Recall that declaring a variable type, such as double or int, does not assign a value to the variable but instead tells the compiler to add the name of the variable to the list of variables it will encounter. Likewise, the declaration statement Complex a, b; lets the compiler know what type of variables these are without assigning values to their parts. The actual creation of objects requires us to place numerical values in the memory locations that have been reserved for them. Seeing that an object has multiple parts, we cannot give all its parts initial values with a simple assignment statement like a = 0, so something fancier is called for. This is exactly why constructor methods are used. Specifically, on line 26 we have the object a created with the statement
![]()
and on line 27 we have the object b created with the statement
![]()
Look at how the creation of a new object requires the command new to precede the name of the constructor (Complex in this case). Also note that line 26 uses the default constructor method to set both the re and im parts of a to zero, while line 27 uses the second constructor method to set the re part of b to 4.7 and the im part of b to 3.2.
Just as we have done with the primitive data types of Java, it is possible to both declare and initialize an object in one statement. Indeed, line 28 does just that for object c with the statement
![]()
Notice how the data type Complex precedes the variable name c in line 28 because the variable c has not previously been declared; future uses of c should not declare or create it again.
4.4.3 Static and Nonstatic Methods
Once our complex-number objects have been declared (added to the variable list) and created (assigned values), it is easy to do arithmetic with them. First, we will get some experience with object arithmetic using the traditional static methods, and then in §4.4.4 we will show how to perform the same object arithmetic using nonstatic methods.
We know the rules of complex arithmetic and complex trigonometry and now will write Java methods to implement them. It makes sense to place these methods in the same class file that defines the data type since these associated methods are needed to manipulate objects of that data type. On line 31 in our main program we see the statement
This says to add the complex number b to the complex number c and then to store the result “as” (in the memory location reserved for) the complex number a. You may recall that we initially set the re and im parts of a to zero in line 26 using the default Complex constructor. This statement will replace the initial zero values with those computed in line 31. The method add that adds two complex numbers is defined on lines 10–15. It starts with the statement
![]()
and is declared to be static with the two Complex objects (numbers) a and b as arguments. The fact that the word Complex precedes the method’s name add signifies that the method will return a Complex number object as its result. We have the option of defining other names like complex_add or plus for this addition method.
The calculational part of the add method starts on line 11 by declaring and creating a temporary complex number temp that will contain the result of the addition of the complex numbers a and b. As indicated before, the dot operator convention means that temp.re will contain the re part of temp and that temp.im will contain the imaginary part. Thus the statements on lines 12 and 13,
![]()
add the complex numbers a and b by extracting the real parts of each, adding them together, and then storing the result as the re part of temp. Line 13 determines the imaginary part of the sum in an analogous manner. Finally, the statement
![]()
returns the object (complex number) temp as the value of add(Complex a, Complex b). Because a complex number has two parts, both parts must be returned to the calling program, and this is what return temp does.
4.4.4 Nonstatic Methods
The program ComplexDyn.java in Listing 4.2 also adds and multiplies complex numbers as objects, but it uses what are called dynamic, nonstatic, or interactive methods. This is more elegant and powerful, but less like, the traditional procedural programming. To avoid confusion and to permit you to run both the static and nonstatic versions without them interfering with each other, the nonstatic version is called ComplexDyn, in contrast to the Complex used for the static method. Notice how the names of the methods in ComplexDyn and Complex are the same,although they go about their business differently.
Listing 4.2 ComplexDyn.java defines the object class ComplexDyn. This permits the use of dynamic complex data objects,for example,as c.add(b).
Exercise
1. Enter the ComplexDyn.java class file by hand, trying to understand it in the process. If you have entered Complex.java by hand, you may modify that program to save some time (but be careful!).
2. Compile and execute this program and check that the output agrees with the results you obtained in the exercises in §4.2.
![]()
Nonstatic methods go about their business by modifying the properties of the objects to which they are attached (complex numbers in the present case). In fact, we shall see that nonstatic methods are literally appended to the names of objects much as the endings of verbs are modified when their tenses change. In a sense, when the method is appended to an object, it creates a new object. To cite an instance, on line 28 we see the operation
Study the way this statement says to take the complex number object c and modify it using the add method that adds b to the object. This statement results in new values for the parts of object c. Because object c is modified by this action, line 28 is equivalent to our static operation
![]()
Regardless of the approach, since c now contains the sum c + b, if we want to use c again, we must redefine it, as we do on line 31. On line 32 we take object c and multiply it by b via
![]()
This method changes c to c * b. Thus line 32 has the static method equivalence
![]()
We see from these two examples that nonstatic methods are called using the same dot operator used to refer to instance variables of an object. In contrast, static methods take the object as arguments and do not use the dot operator. Thus we called the static methods via add(c,b) and mult(c,b) and called the nonstatic methods via c.add(b) and c.mult(b).
The static methods here do not need a dot operator since they are called from within the class Complex or ComplexDyn that defined them. However, they would need a dot operator if called from another class. For example, you may have seen that the square root method is called Math.sqrt(x). This is actually the static method sqrt from the class Math. You could call the static add(c,b) method of class Complex by using Complex.add(c,b). This works within the program (class)Complex as well but is not required. It is required, however, if add is called from other classes.
Observe now how the object-oriented add method has the distinctive form
![]()
Line 10 tells us that the method add is nonstatic (the word static is absent), that no value or object is returned (the void), and that there is one argument other of the type ComplexDyn. What is unusual about this nonstatic method is that it is supposed to add two complex numbers together, yet there is only one argument given to the method and no object is returned! Indeed, the assumption is that since the method is nonstatic, it will be used to modify only the object to which it will be attached. Hence it literally goes without saying that there is an object around for this method to modify, and the this reference is used to refer to “this” calling object. In fact, the reason the argument to the method is conventionally called other is to distinguish it from the this object that the method will modify. (We are being verbose for clarity’s sake: The word “this” may be left out of these statements without changing their actions.) Consequently, when the object addition is done in line 11 with
it is understood that re refers to the current object being modified (this), while other refers to the “other” object being used to make the modifications.
4.5 Complex Currents (Solution)
1. Extend the class Complex.java or ComplexDyn.java by adding new methods to subtract, take the modulus, take the complex conjugate, and determine the phase of complex numbers.
2. Test your methods by checking that the following identities hold for a variety of complex numbers:
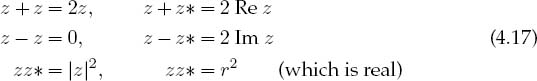
Hint: Compare your output to some cases of pure real, pure imaginary, and simple complex numbers that you are able to evaluate by hand.
3. Equation (4.14) gives the magnitude and phase of the current in a single RLC circuit. Modify the given complex arithmetic program so that it performs the required complex arithmetic.
4. Compute and then make a plot of the magnitude and phase of the current in the circuit as a function of frequency 0 ≤ ω ≤ 2.
5. Construct a z(x, y) surface plot of the magnitude and phase of the current as functions of both the frequency of the external voltage ω and of the resistance R. Observe how the magnitude has a maximum when the external frequency ![]() This is the resonance frequency.
This is the resonance frequency.
6. Another approach is to make a 3-D visualization of the complex Z as a function of a complex argument (Figure 4.3). Do this by treating the frequency ω = x+ iy as a complex number. You should find a sharp peak at x = Re(ω) = 1. Adjust the plot so that you tell where Im(1/Z) changes sign. If you look closely at the graph, you should also see that there is a maximum for a negative imaginary value of ω. This is related to the length of the lifetime of the resonance.
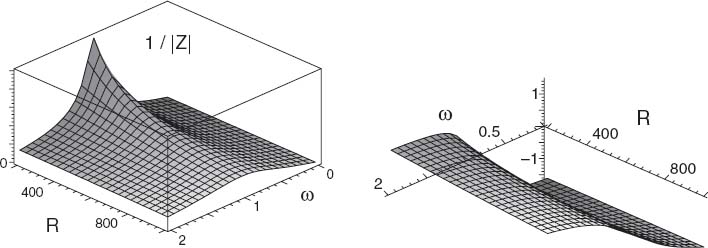
Figure 4.3 Left: A plot of 1/|Z| versus resistance R and frequency ω showing that the magnitude of the current has a maximum at ω = 1. Right: A plot of the current’s phase versus resistance R and frequency ω showing that below resonance,ω < 1,the current lags the voltage, while above resonance the current leads the voltage.
7. Assessment: You should notice a resonance peak in the magnitude at the same frequency for which the phase vanishes. The smaller the resistance R, the more sharply the circuit should pass through resonance. These types of circuits were used in the early days of radio to tune to a specific frequency. The sharper the peak, the better the quality of reception.
8. The second part of the problem dealing with the two circuits in parallel is very similar to the first part. You need to change only the value of the impedance Z used. To do that, explicitly perform the complex arithmetic implied by (4.16), deduce a new value for the impedance, and then repeat the calculation of the current.
4.6 OOP Worked Examples
Creating object-oriented programs requires a transition from a procedural programming mindset, in which functions take arguments as input and produce answers as output, to one in which objects are created, probed, transferred, and modified. To assist you in the transition, we present here two sample procedural programs and their OOP counterparts. In both cases the OOP examples are longer but presumably easier to modify and extend.
4.6.1 OOP Beats
You obtain beats if you add together two sine functions y1 and y2 with nearly identical frequencies,
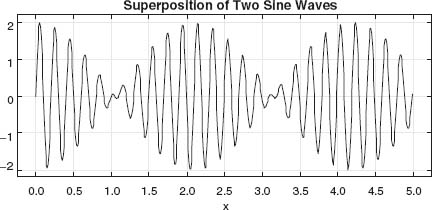
Figure 4.4 Superposition of two waves with similar wave numbers (a PtPlot).
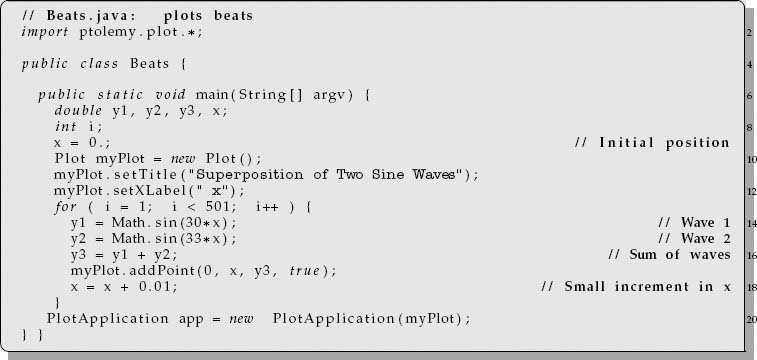
Beats look like a single sine wave with a slowly varying amplitude (Figure 4.4). In Listing 4.3 we give Beats.java, a simple program that plots beats. You see here that all the computation is done in the main program, with no methods called other than those for plotting. On lines 14 and 15 the variables y1 and y2 are defined as the appropriate functions of time and then added together on line 16 to form the beats. Contrast this with the object-oriented program OOPBeats.java in Listing 4.4 that produces the same graph.
Listing 4.3 Beats.java plots beats using procedural programming. Contrast this with the object-oriented program OOPBeats.java in Listing 4.4.
In this OOP version, the main program is at the very end, on lines 26–29. It is short because all it does is create an OOPbeats object named sumsines on line 27 with the appropriate parameters and then on line 28 sums the two waves by having the method sumwaves modify the object. The constructor for an OOPbeats object is given on line 7, followed by the sumwaves method. The sumwaves method takes no arguments and returns no value; the waves are summed on line 19, and the graph plotted all within the method.
Listing 4.4 OOPBeats.java plots beats using OOP. Contrast this with the procedural program Beats.java in Listing 4.3.
4.6.2 OOP Planet
In our second example we add together periodic functions representing positions versus time. One set describes the position of the moon as it revolves around a planet, and the other set describes the position of the planet as it revolves about the sun. Specifically, the planet orbits the sun at a radius R = 4 units with an angular frequency ωp = 1 rad/s, while the moon orbits Earth at a radius r = 1 unit from the planet and an angular velocity ωs = 14 rad/s. The position of the planet at time t relative to the sun is described by
![]()
The position of the satellite, relative to the sun, is given by the sum of its position relative to the planet and the position of the planet relative to the sun:
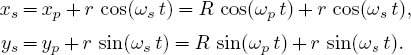
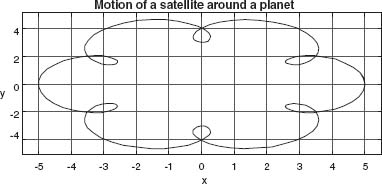
Figure 4.5 The trajectory of a satellite as seen from the sun.
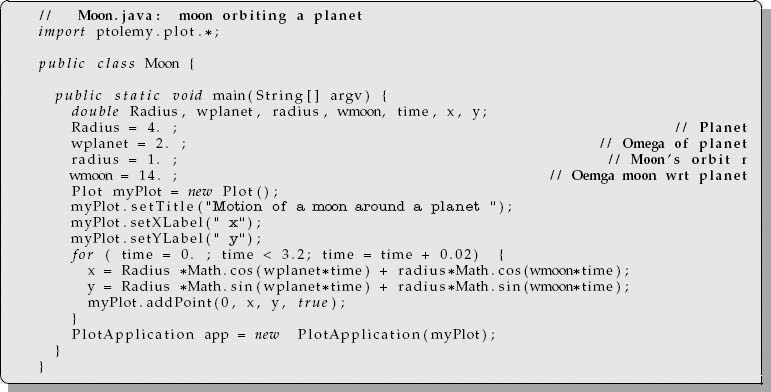
So again this looks like beating (if ωS ![]() ωp and if we plot x or y versus t), except that now we will make a parametric plot of x(t) versus y(t) to obtain a visualization of the orbit. A procedural program Moon.java to do this summation and to produce Figure 4.5 is in Listing 4.5.
ωp and if we plot x or y versus t), except that now we will make a parametric plot of x(t) versus y(t) to obtain a visualization of the orbit. A procedural program Moon.java to do this summation and to produce Figure 4.5 is in Listing 4.5.
Listing 4.5 The procedural program Moon.java computes the trajectory of a satellite as seen from the sun. You need to write your own OOP version of this program.
Exercise: Rewrite the program using OOP.
1. Define a mother class OOPlanet containing:
Radius |
Planet’s orbit radius |
wplanet |
Planet’s orbit ω |
(xp, yp) |
Planet’s coordinates |
getX(double t), getY(double t) |
Planet coordinates methods |
trajectory() |
Method for planet’s orbit |
2. Define a daughter class OOPMoon containing:
radius |
Radius of moon’s orbit |
wmoon |
Frequency of moon in orbit |
(xm, ym) |
Moon’s coordinates |
trajectory() |
Method for moon’s orbit relative to sun |
3. The main program must contain one instance of the class planet and another instance of the class Moon, that is, one planet object and one Moon object.
4. Have each instance call its own trajectory method to plot the appropriate orbit. For the planet this should be a circle, while for the moon it should be a circle with retrogrades (Figure 4.5).
![]()
One solution, which produces the same results as the previous program, is the program OOPlanet.java in Listing 4.6. As with OOPbeats.java, the main program for OOPlanet.java is at the end. It is short because all it does is create an OOPMoon object with the appropriate parameters and then have the moon’s orbit plotted by applying the trajectory method to the object.
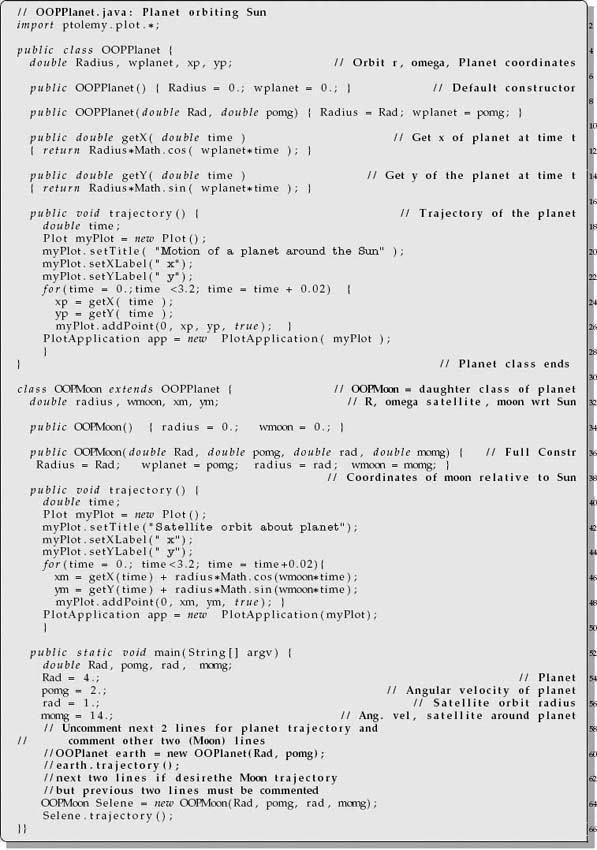
Listing 4.6 OOPPlanet.java creates an OOPMoon object and then plots the moon’s orbit by applying the trajectory method to the object.
What is new about this program is that it contains two classes, OOPlanet beginning on line 4 and OOPMoon beginning on line 31. This means that when you compile the program, you should obtain two class files, OOPlanet.class and OOPMoon.class. Yet because execution begins in the main method and the only main method is in OOPMoon, you need to execute OOPMoon.class to run the program:
![]()
Scan the code to see how the class OOPMoon is within the class OOPlanet and is therefore a subclass. That being the case, OOPMoon is called a daughter class and OOPlanet is called a mother class. The daughter class inherits the properties of the mother class as well as having properties of its own. Thus, on lines 46 and 47, OOPMoon uses the getX(time) and getY(time) methods from the OOPlanet class without having to say OOPlanet.getX(time) to specify the class name.
4.7 Unit II. Advanced Objects: Baton Projectiles
In this unit we look at more advanced aspects of OOP. These aspects are designed to help make programming more efficient by making the reuse of already written components easier and more reliable. The ideal is to permit this even for entirely different future projects for which you will have no memory or knowledge of the internal workings of the already written components that you want to reuse. OOP concepts can be particularly helpful in complicated projects in which you need to add new features without “breaking” the old ones and in which you may be modifying code that you did not write.
4.8 Trajectory of a Thrown Baton (Problem)
We wish to describe the trajectory of a baton that spins as it travels through the air. On the left in Figure 4.6 the baton is shown as as two identical spheres joined by a massless bar. Each sphere has mass m and radius r, with the centers of the spheres separated by a distance L. The baton is thrown with the initial velocity (Figure 4.6 center) corresponding to a rotation about the center of the lower sphere.
Problem: Write an OOP program that computes the position and velocity of the baton as a function of time. The program should
1. plot the position of each end of the baton as a function of time;
2. plot the translational kinetic energy, the rotational kinetic energy, and the potential energy of the baton, all as functions of time;
3. use several classes as building blocks so that you may change one building block without affecting the rest of the program;
4. (optional) then be extended to solve for the motion of a baton with an additional lead weight at its center.
4.8.1 Combined Translation and Rotation (Theory)
Classical dynamics describes the motion of the baton as the motion of its center of mass (CM) (marked with an “X” in Figure 4.6), plus a rotation about the CM. Because the translational and rotational motions are independent, each may be determined separately, and because we ignore air resistance, the angular velocity ω about the CM is constant.
The baton is thrown with an initial velocity (Figure 4.6 center). The simplest way to view this is as a translation of the entire baton with a velocity V0 and a rotation of angular velocity ω about the CM (Figure 4.6 right). To determine ω, we note that the tangential velocity due to rotation is
For the direction of rotation as indicated in Figure 4.6, this tangential velocity is added to the CM velocity at the top of the baton and is subtracted from the CM velocity at the bottom. Because the total velocity equals 0 at the bottom and 2V0 at the top, we are able to solve for ω:
![]()
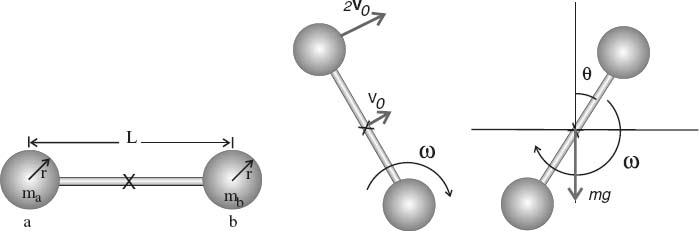
Figure 4.6 Left: The baton before it is thrown. “X” marks the CM. Center: The initial conditions for the baton as it is thrown. Right: The baton spinning in the air under the action of gravity.
If we ignore air resistance, the only force acing on the baton is gravity, and it acts at the CM of the baton (Figure 4.6 right). Figure 4.7 shows a plot of the trajectory [x(t), y(t)] of the CM:
where the horizontal and vertical components of the initial velocity are
![]()
Even though ω = constant, it is a constant about the CM, which itself travels along a parabolic trajectory. Consequently, the motion of the baton’s ends may appear complicated to an observer on the ground (Figure 4.7 right). To describe the motion of the ends, we label one end of the baton a and the other end b (Figure 4.6 left). Then, for an angular orientation φ of the baton,
![]()
where we have taken the initial φ = φ0 = 0. Relative to the CM, the ends of the baton are described by the polar coordinates
![]()
The ends of the baton are also described by the Cartesian coordinates
![]()
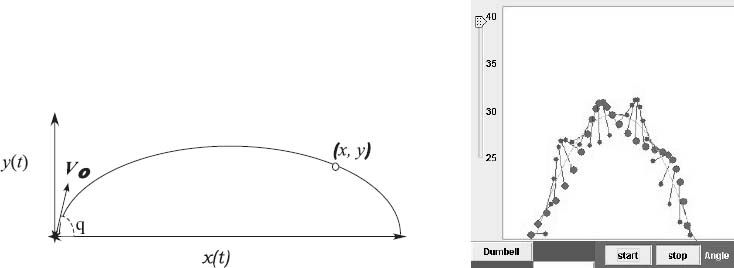
Figure 4.7 Left: The trajectory (x(t), y(t)) followed by the baton’s CM. Right: The applet JParabola.java showing the entire baton as its CM follows a parabola.
The baton’s ends, as seen by a stationary observer, have the vector sum of the position of the CM plus the position relative to the CM:
If La and Lb are the distances of ma and mb from CM, then
![]()
The moment of inertia of the masses (ignoring the bar connecting them) is
![]()
If the bar connecting the masses is uniform with mass m and length L, then it has a moment of inertia about its CM of
![]()
Because the CM of the bar is at the same location as the CM of the masses, the total moment of inertia for the system is just the sum of the two:
![]()
The potential energy of the masses is
while the potential energy of the bar just has ma +mb replaced by m since both share the same CM location. The rotational kinetic energy of rotation is
![]()
with ω the angular velocity and I the moment of inertia for either the masses or the bar (or the sum). The translational kinetic energy of the masses is
![]()
with ma +mb replaced by m for the bar’s translational KE.
To get a feel for the interestingly complicated motion of a baton, we recommend that the reader try out the applet JParabola on the CD (available online: http://press.princeton.edu/landau_survey/) (Fig. 4.7 right).
![]()
![]()
4.9 OOP Design Concepts (CS)
In accord with our belief that much of education is just an understanding of what the words mean, we start by defining OOP as programming containing component objects with four characteristics [Smi 91]:
Encapsulation: The data and the methods used to produce or access data are encapsulated into entities called objects. For our problem, the data are initial positions, velocities, and properties of a baton, and the objects are the baton and its path. As part of the OOP philosophy, data are manipulated only via distinct methods.
Abstraction: Operations applied to objects are assumed to yield standard results according to the nature of the objects. To illustrate, summing two matrices always gives another matrix.By incorporating abstraction into programming, we concentrate more on solving the problem and less on the details of the implementation.
Inheritance: Objects inherit characteristics (including code) from their ancestors yet may be different from their ancestors. A baton inherits the motion of a point particle, which in this case describes the motion of the CM, and extends that by permitting rotations about the CM. In addition, if we form a red baton, it inherits the characteristics of a colorless baton but with the property of color added to it.
Polymorphism: Methods with the same name may affect different objects differently. Child objects may have member functions with the same name but with properties differing from those of their ancestors (analogous to method overload, where the method used depends upon the method’s arguments).
We now solve our baton problem using OOP techniques. Although it is also possible to use the more traditional techniques of procedural programming, this problem contains the successive layers of complexity that make it appropriate for OOP. We will use several source (.java) files for this problem, each yielding a different class file. Each class will correspond to a different physical aspect of the baton, with additional classes added as needed. There will be a class Path.java to represent the trajectory of the CM, a class Ball.java to represent the masses on the ends of the baton, and a class Baton.java to assemble the other classes into an object representing a projected and spinning baton. Ultimately we will combine the classes to solve our problem.
4.9.1 Including Multiple Classes
The codes Ball.java, Path.java, and Baton.java in Listings 4.7–4.9 produce three class files. You may think of each class as an object that may be created, manipulated, or destroyed as needed. (Recall that objects are abstract data types with multiple parts.) In addition, since these classes may be shared with other Java classes, more complicated objects may be constructed by using these classes as building blocks.
Listing 4.7 The class Ball representing the ball on the end of the baton.
To use class files that are not in your working directory, use theimport command to tell Java where to find them.2 For example, in Chapter 3, “Visualization Tools,” we used import ptolemy.plot.* to tell Java to retrieve all class files found in the ptolemy/plot directory. A complication arises here in that multiple class files may contain more than one main method. That being the case, Java uses the first main it finds, starting in the directory from which you issued the java command.
Listing 4.8 The class Path creating an object that represents the trajectory of the center of mass.
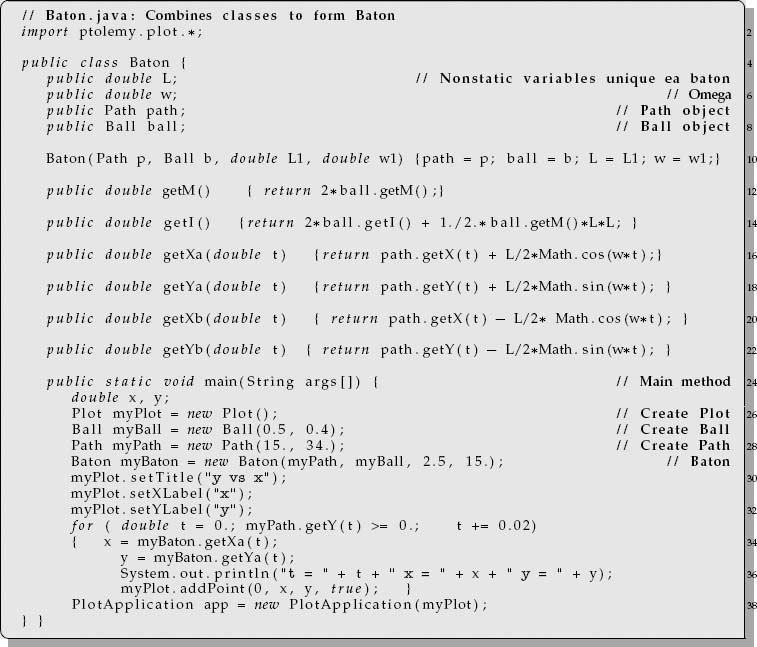
Listing 4.9 Baton.java combines ball and path classes to form a baton.
In a project such as this where there are many different types of objects,it is a good idea to define each object inside its own .java file (and therefore its own .class file) and to place the main method in a file such as Main.java or ProjectName.java. This separates individual objects from the helper codes that glue the objects together. And since reading a well-written main method should give you a fair idea of what the entire program does, you want to be able to find the main methods easily.
4.9.2 Ball and Path Class Implementation
The Ball class in Listing 4.7 creates an object representing a sphere of mass m, radius r, and moment of inertia I. It is our basic building block. Scrutinize the length of the methods in Ball; most are short. Inasmuch as we will be using Ball as a building block, it is a good idea to keep the methods simple and just add more methods to create more complicated objects. Take stock of how similar Ball is to the Complex class in its employment of dynamic (nonstatic) variables. In the present case, m and r behave like the re and im dynamic variables in the Complex class in that they too act by being attached to the end of an object’s name. As an example, myBall.m extracts the mass of a ball object.
In Ball.java we have defined three dynamic methods, getM, getR, and getI. When affixed to a particular ball object, these methods extract its mass, radius, and moment of inertia, respectively. Dynamic methods are like dynamic variables in that they behave differently depending on the object they modify. To cite an instance, ball1.getR() and ball2.getR() return different values if ball1 and ball2 have different radii. The getI method computes and returns the moment of inertia I = 2/5mr2 of a sphere for an axis passing through its center. The methods getM and getR are template methods; that is, they do not compute anything now but are included to facilitate future extensions. To name an instance, if the Ball class becomes more complex, you may need to sum the masses of its constituent parts in order to return the ball’s total mass. With the template in place, you do that without having to reacquaint yourself with the rest of the code first.
Look back now and count all the methods in the Ball class. You should find four, none of which is a main method. This is fine because these methods are used by other classes, one of which will have a main method.
Exercise: Compile the Ball class. If the Java compiler does not complain, you know Ball.java contains valid code. Next try to run the byte code in Ball.class:
You should get an error message of the type java.lang.NoSuchMethodError, with the word main at the end. This is Java’s way of saying you need a main method to execute a class file.
Exercise: Be adventurous and make a main method for the Ball class. Because we have not yet included Path and Baton objects, you will not be able to do much more than test that you have created the Ball object, but that is at least a step in the right direction:
This testing code creates a Ball object and prints out its properties by affixing get methods to the object. Compile and run the modified Ball.java and thereby ensure that the Ball class still works properly.
The class Path in Listing 4.8 creates an object that represents the trajectory [(x(t), y(t)] of the center of mass. The class Path is another building block that we will use to construct the baton’s trajectory. It computes the initial velocity components V0x and V0y and stores them as the dynamic class variables v0x and v0y. These variables need to be dynamic because each new path will have its own initial velocity. The acceleration resulting from gravity is the constant g, which being the same for all objects can be safely declared as a static variable independent of class instance. Survey how Path.java stores g not only as a static variable but also as a class variable so that its value is available to all methods in the class. The constructor method Path () of the class Path takes the polar coordinates (V0, θ) as arguments and computes the components of the initial velocity, (v0x, v0y). This too is a building-block class, so it does not need a main method.
Exercise: Use the main method below to test the class Path. Make a Path object and find its properties at several different times. Remember, since this a test code, it does not need to do anything much. Just making an object and checking that it has the expected properties are enough.
![]()

4.9.3 Composition, Objects Within Objects
A good way to build a complex system is to assemble it from simpler parts. By way of example, automobiles are built from wheels, engines, seats, and so forth, with each of these parts being built from simpler parts yet. OOP builds programs in much the same way. We start with the primitive data types of integers, floatingpoint numbers, and Boolean variables and combine them into more complicated data types called objects (what we did in combining two doubles into a Complex object). Then we build more complicated objects from simpler objects, and so forth.
The technique of constructing complex objects from simpler ones is called composition. As a consequence of the simple objects being contained within the more complex ones, the former are described by nonstatic class variables. This means that their properties change depending upon which object they are within. When you use composition to create more complex objects, you are working at a higher level of abstraction. Ideally, composition hides the distracting details of the simpler objects from your view so that you focus on the major task to be accomplished. This is analogous to first designing the general form of a bridge before worrying about the colors of the cables to be used.
4.9.4 Baton Class Implementation
Now that we have assembled the building-block classes, we combine them to create the baton’s trajectory. We call the combined class Baton.java (Listing 4.9) and place the methods to compute the positions of the ends of the baton relative to the CM in it. Check first how the Baton class and its methods occupy lines 4–22, while the main method is on lines 24–39. Whether the main method is placed first or last is a matter of taste; Java does not care—but some programmers care very much. Look next at how the Baton class contains the four dynamic class variables, L, w, path, and ball. Being dynamic, their values differ for each baton, and since they are class variables (not within any methods), they may be used by all methods in the class without being passed as arguments.
The subobjects used to construct the baton object are created with the statements
These statements tell Java that we are creating the variables path and ball to represent objects of the types Path and Ball. To do this, we must place the methods defining Ball and Path in the directory in which we are creating a Baton. The Java compiler is flexible enough for you to declare class variables in any order or even pass classes as arguments.
The constructor Baton(Path p, Ball b,…) on line 10 takes the Path and Ball objects as arguments and constructs the Baton object from them. On lines 7 and 8 it assigns these arguments to the appropriate class variables path and ball. We create a Baton from a Ball and a Path such that there is a Ball object at each end, with the CM following the Path object:
![]()
Study how the Baton constructor stores the Ball and Path objects passed to it inside the Baton class even though Ball and Path belong to different classes.
On lines 12–22 we define the methods for manipulating baton objects. They all have a get as part of their name. This is the standard way of indicating that a method will retrieve or extract some property from the object to which the method is appended. For instance, Baton.getM returns 2m, that is, the sum of the masses of the two spheres. Likewise, the getI method uses the parallel axes theorem to determine the moment of inertia of the two spheres about the CM,I = 2Im + ½mL2, where m and Im are the mass and moment of inertia of the object about its center of mass. On lines 14–22 we define the methods getXa, getYa, getXb, and getYb. These take the time t as an argument and return the coordinates of the baton’s ends. In each method we first determine the position of the CM by calling path.getX or path.getY and then add on the relative coordinates of the ends. On line 24 we get to the main method. It starts by creating a Plot object myPlot, a Path object myPath, and a Ball object myBall. In each case we set the initial conditions for the object by passing them as arguments to the constructor (what is called after the new command).
4.9.5 Composition Exercise
1. Compile and run the latest version of Baton.java. For this to be successful, you must tell Java to look in the current directory for the class files corresponding to Ball.java and Path.java. One way to do that is to issue the javac and java commands with the -classpath option, with the location of the classes following the option. Here the dot. is shorthand for “the current directory”:
The program should run and plot the trajectory of one end of the baton as it travels through the air (Figure 4.7).
2. If you want to have the Java compiler automatically include the current directory in the classpath (and to avoid the –classpath. option), you need to change your CLASSPATH environment variable to include the present working directory.
3. On line 33 we see that the program executes a for loop over values of t for which the baton remains in the air:
![]()
This says to repeat the loop as long as y(t) is positive, that is, as long as the baton is in the air. Of course we could have had the for loop remain active for times up to the hang time T, but then we would have had to calculate the hang time! The weakness in our approach is that the loop will be repeated indefinitely if y(t) never becomes negative.
4. Plot the trajectory of end b of the baton on the same graph that shows the trajectory of end a. You may do this by copying and pasting the for loop for a and then modifying it for b (making sure to change the data set number in the call to PtPlot so that the two ends are plotted in different colors).
5. Use a PtPlot application to print out your graph.
6. Change the mass of the ball variable to some large number, for instance, 50kg, in the Baton constructor method.Add print statements in the constructor and the main program to show how the ball class variable and the myBall object are affected by the new mass. You should find that ball and myBall both reference the same object since they both refer to the same memory location. In this way changes to one object are reflected in the other object.
![]()
In Java, an object is passed between methods and manipulated by reference. This means that its address in memory is passed and not the actual values of all the component parts of it. On the other hand, primitive data types like int and double are manipulated by value:
At times we may actually say that objects are references. This means that when one object is set equal to another, both objects point to the same location in memory (the start location of the first component of the object). Therefore all three variables myBall, p, and q in the above code fragment refer to the same object in memory. If we change the mass of the ball, all three variables will reflect the new mass value. This also works for object arguments: If you pass an object as an argument to a method and the method modifies the object, then the object in the calling program will also be modified.
4.9.6 Calculating the Baton’s Energy (Extension)
Extend your classes so that they plot the energy of the baton as a function of time. Plot the kinetic energy of translation, the kinetic energy of rotation, and the potential energy as functions of time:
1. The translational kinetic energy of the baton is the energy associated with the motion of the center of mass. Write a getKEcm method in the Baton class that returns the kinetic energy of translation KEcm(t) = mvcm(t)2/2. In terms of pseudocode the method is

Before you program this method, write getVx and getVy methods that extract the CM velocity from a baton. Seeing as how the Path class already computes xcm(t) and ycm(t), it is the logical place for the velocity methods. As a guide, we suggest consulting the getX and getY methods.
2. Next we need the method getKEcm in the Baton class to compute KEcm(t). Inasmuch as the method will be in the Baton class, we may call any of the methods in Baton, as well as access the path and ball subobjects there (sub-objects because they reside inside the Baton object or class). We obtain the velocity components by applying the getV methods to the path sub object within the Baton object:
Even though the method is in a different class than the object, Java handles this. Study how getM(), being within getKEcm, acts on the same object as does getKEcm without explicitly specifying the object.
3. Compile the modified Baton and Path classes.
4. Modify Baton.java to plot the translational kinetic energy of the center of mass as a function of time. Comment out the old for loops used for plotting the positions of the baton’s ends and add the code

Compile the modified Baton.java and check that your plot is physically reasonable. The translational kinetic energy should decrease and then increase as the baton goes up and comes down.
5. Write a method in the Baton class that computes the kinetic energy of rotation about the CM, KEro = ½Iω2. Call getI to extract the moment of inertia of the baton and check that all classes still compile properly.
6. The potential energy of the baton PE(t) = mgycm(t) is that of a point particle with the total mass of the baton located at the CM. Write a method in the Baton class that computes PE. Use getM to extract the mass of the baton and use path.g to extract the acceleration due to gravity g. To determine the height as a function of time, write a method path.getY(t) that accesses the path object. Make sure that the methods getKEcm, getKEr, and getPE are in the Baton class.
7. Plot on one graph the translational kinetic energy, the kinetic energy of rotation, the potential energy, and the total energy. The plots may be obtained with commands such as
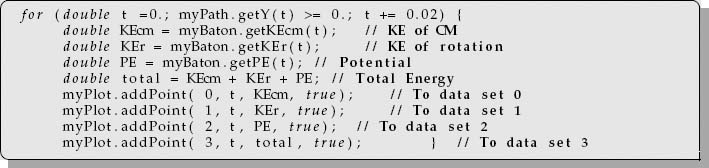
Check that all the plotting commands are object-oriented, with myPlot being the plot object. Label your data sets with a myPlot.addLegend command outside the for loop and check that your graph is physically reasonable. The total energy and rotational energies should both remain constant in time. However, the gravitational potential energy should fluctuate.
4.9.7 Examples of Inheritance and Object Hierarchies
Up until this point we have built up our Java classes via composition, that is, by placing objects inside other objects (using objects as arguments). As powerful as composition is, it is not appropriate in all circumstances. As a case in point, you may want to modify the Baton class to create similar, but not identical, objects such as 3-D batons. A direct approach to extending the program would be to copy and paste parts of the original code into a new class and then modify the new class. However, this is error-prone and leads to long, complicated, repetitive code. The OOP approach applies the concept of inheritance to allow us to create new objects that inherit the properties of old objects but have additional properties as well. This is how we create entire hierarchies of objects.
As an example, let us say we want to place red balls on the ends of the baton. We make a new class RedBall that inherits properties from Ball by using the extend command:
As written, this code creates a RedBall class that is identical to the original Ball class. The key word extends tells Java to copy all the methods and variables from Ball into RedBall. In OOP terminology, the Ball class is the parent class or superclass, and the RedBall class is the child class or subclass. It follows then that a class hierarchy is a sort of family tree for classes, with the parent classes at the top of the tree. As things go, children beget children of their own and trees often grow high.
To make RedBall different from Ball, we add the property of color:

Now we append the getColor method to a RedBall to find out its color. Consider what it means to have the getR method defined in both the Ball and RedBall classes. We do this because the Java compiler assumes that the getR method in RedBall is more specialized, so it ignores the original method in the Ball class. In computer science language, we would say that the new getR method overrides the original method.
4.9.8 Baton with a Lead Weight (Application)
As a second example,we employ inheritance to create a class of objects representing a baton with a weight at its center. We call this new class LeadBaton.java and make it a child of the parent class Baton.java. Consequently, the LeadBaton class inherits all the methods from the parent Baton class, in addition to having new ones of its own:
Here the nondefault constructor LeadBaton(...) takes five arguments, while the Baton constructor takes only three. For the LeadBaton constructor to work, it must call the Baton constructor in order to inherit the properties of a Baton. This is accomplished by use of the key word super, which is shorthand for look in the superclass and which tells Java to look in the parent, or superclass, for the constructor. We may also call methods with the super key word; to illustrate, super.getM() will call the getM method from Baton in place of the getM method from LeadBaton. Finally, because the LeadBaton class assigns new values to the mass, LeadBaton overrides the getM method of Baton.
Exercise:
1. Run and create plots from the LeadBaton class. Start by removing the main method from Baton.java and placing it in the file Main.java. Instead of creating a Baton, now create a LeadBaton with
LeadBaton myBaton = new LeadBaton(myPath, myBall, 2.5, 15., 10.);
Here the argument “10.” describes a 10-kg mass at the center of the baton.
2. Compile and run the main method, remembering to use the option “-classpath.” if needed. You should get a plot of the energies of the lead baton versus time. Compare its energy to an ordinary baton’s and comment on the differences.
3. You should see now how OOP permits us to create many types of batons with only slight modifications of the code. You can switch between a Baton and a LeadBaton object with only a single change to main, a modification that would be significantly more difficult with procedural programming.
![]()
4.9.9 Encapsulation to Protect Classes
In the previous section we created the classes for Ball, Path, and Baton objects. In all cases the Java source code for each class had the same basic structure: class variables, constructors, and get methods. Yet classes do different things, and it is common to categorize the functions of classes as either of the following.
Interface: How the outside world manipulates an object; all methods that are applied to that object; or
Implementation: The actual internal workings of an object; how the methods make their changes.
As applied to our program, the interface for the Ball class includes a constructor Ball and the getM, getR, and getI methods. The interface for the Path class includes a constructor Path and the getX and getY methods.
Pure OOP strives to keep objects abstract and to manipulate them only through methods. This makes it easy to follow and to control where variables are changed and there by makes modifying an existing program easier and lesserror-prone. With this purpose in mind, we separate methods into those that perform calculations and those that cause the object to do things. In addition,to protect our objects from being misused by outsiders, we invoke the private (in contrast to public) key word when declaring class variables. This ensures that these variables may be accessed and changed only from inside the class. Outside code may still manipulate our objects, but it will have to do so by calling the methods we have tested and know will not damage them.
Once we have constructed the methods and made the class variables private, we have objects that are protected by having their internal codes entirely hidden to outside users. As programmers, we may rewrite an object’s code as we want and still have the same working object with a fixed interface for the rest of the world. Furthermore, since the object’s interface is constant, even though we may change the object, there is no need to modify any code that uses the object. This is a great advance in the ability to reuse code and to use other people’s codes properly.
This two-step process of creating and protecting abstract objects is known as encapsulation.Anencapsulated object may be manipulated only in a general manner that keeps the irrelevant details of its internal workings safely hidden within. Just what constitutes an “irrelevant detail” is in the eye of the programmer. In general, you should place the private key word before every nonstatic class variable and then write the appropriate methods for accessing the relevant variables. This OOP process of hiding the object’s variables is called data hiding.
4.9.10 Encapsulation Exercise
1. Place the private key word before all the class variables in Ball.java. This accomplishes the first step in encapsulating an object. Print out myBall.m and myBall.r from the main method. The Java compiler should complain because the variables are now private (visible to Ball class members only) and the main method is outside the Ball class.
2. Create methods that allow you to manipulate the object in an abstract way; for example, to modify the mass of a Ball object and assign it to the private class variable m, include the command myBall.setM(5.0). This is the second step in encapsulation. We already have the methods getM, getR, and getI, and the object constructor Ball, but they do not assign a mass to the ball. Insofar as we have used a method to change the private variable m, we have kept our code as general as possible and still have our objects encapsulated.
3. When we write getM(), we are saying that M is the property to be retrieved from a Ball object. Inversely, the method setM sets the property M of an object equal to the argument that is given. This is part of encapsulation because with both get and set methods on hand, you do not need to access the class variables from outside the class. The use of get and set methods is standard practice in Java. You do not have to write get and set methods for every class you create, but you should create these methods for any class you want encapsulated. If you look back at Chapter 3, “Visualization Tools,” you will see that the classes in the PtPlot library have many get and set methods, for example, getTitle, setTitle, getXLabel, and setXLabel.
4. Java’s interface key word allows us to specify an interface. Here BallInterface defines an interface for Ball-like objects:
This interface does not do anything by itself, but if you modify Ball.java so that public class Ball is replaced by public class Ball implements BallInterface, then the Java compiler will check that the Ball class has all the methods specified in the interface. The Java commands interface and implements are useful in having the compiler check that your classes have all the required methods.
5. Add an arbitrary new method to the interface and compile Ball. If the method is found in Ball.java, then the Ball class will compile without error.
![]()
4.9.11 Complex Object Interface (Extension)
In Listing 4.10 we display KomplexInterface.java, our design for an interface for complex numbers. To avoid confusion with the Complex objects, we call the new objects Komplex. We include methods for addition, subtraction, multiplication, division, negation, and conjugation, as well as get and set methods for the real, imaginary, modulus, and phase. We include all methods in the interface and check that javac compiles the interface without error. Remember, an interface must give the arguments and return type for each method.
Listing 4.10 KomplexInterface.java is an interface for complex numbers and is used in Komplex.java in Listing 4.11.
We still represent complex numbers in Cartesian or polar coordinates:
![]()
Insofar as the complex number itself is independent of representation, we must be able to switch between the rectangular or polar representation. This is useful because certain manipulations are simpler in one representation than in the other; for example, division is easier in polar represenation:
![]()
Listings 4.11 and 4.12 are our implementation of an interface that permits us to use either representation when manipulating complex numbers. There are three files, Komplex, KomplexInterface, and KomplexTest, all given in the listings. Because these classes call each other, each must be in a class by itself. However, for the compiler to find all the classes that it needs, all three classes must be compiled with the same javac command:
![]()
Listing 4.11 Komplex.java manipulates complex numbers using the interface KomplexInterface in Listing 4.10.
Listing 4.12 KomplexTest.java tests Komplex and KomplexInterface. All three classes must be compiled with the same javac command.
You should observe how KomplexInterface requires us to have methods for getting and setting the real and imaginary parts of Komplex objects, as well as adding, subtracting, multiplying, dividing, and conjugating complex objects. (In the comments we see the suggestion that there should also be methods for getting and setting the modulus and phase.)
The class Komplex contains the constructors for Komplex objects. This differs from our previous implementation Complex by having the additional integer variable type. If type = 0, then the complex numbers are in polar representation, else they are in Cartesian representation. So, for example, the method for arithmetic, such as the add method on line 22, is actually two different methods depending upon the value of type. In contrast, the get and set methods for real and imaginary parts are needed only for the polar representation, and so the value of type is not needed.
4.9.12 Polymorphism,Variable Multityping
Polymorphism allows a variable name declared as one type to contain other types as needed while the program runs. The idea may be applied to both the class and the interface. Class polymorphism allows a variable that is declared as one type to contain types it inherits. To illustrate, if we declare myBaton of type Baton,
Baton myBaton;
then it will be valid to assign an object of type Baton to that variable, which is what we have been doing all along. However, it is also permissible to assign a
LeadBaton object to myBaton, and in fact it is permissible to assign any other class that it inherits from the Baton class to that variable:
Polymorphism applies to the arguments of methods as well. If we declare an argument as type Baton, we are saying that the class must be a Baton or else some class that is a child class of Baton. This is possible because the child classes will have the same methods as the original Baton class (a child class may override a method or leave it alone, but it may not eliminate it).
4.10 Supplementary Exercises
Use a Java interface to introduce another object corresponding to the polar representation of complex numbers:
![]()
1. Define a constructor Complex (r, theta, 1) that constructs the polar representation of a complex number from r and θ. (The 1 is there just to add a third argument and thereby to make the constructor unique.)
2. Define a method (static or nonstatic) that permits conversion from the Cartesian to the polar representation of complex numbers.
3. Define a method (static or nonstatic) that permits conversion from the polar to the Cartesian representation of complex numbers.
4. Define methods (static or nonstatic) for addition, subtraction, multiplication, and division of complex numbers in polar representation. (Hint: Multiplication and division are a snap for complex numbers in polar representation, while addition and subtraction are easier for complex numbers in Cartesian representation.)
![]()
4.11 OOP Example: Superposition of Motions
The isotropy of space implies that motion in one direction is independent of motion in other directions. So, when a soccer ball is kicked, we have acceleration in the vertical direction and simultaneous, yet independent, uniform motion in the horizontal direction.In addition, Galilean invariance (velocity independence of Newton’s laws of motion) tells us that when an acceleration is added to uniform motion, the distance covered due to the acceleration adds to the distance covered due to uniform velocity.
Your problem is to describe motion in such a way that velocities and accelerations in each direction are treated as separate entities or objects independent of motion in other directions. In this way the problem is viewed consistently from both the programming philosophy and the basic physics.
4.12 Newton’s Laws of Motion (Theory)
Newton’s second law of motion relates the force vector F acting on a mass m to the acceleration vector a of the mass:
If the force in the x direction vanishes, Fx = 0, the equation of motion (4.34) has a solution corresponding to uniform motion in the x direction with a constant velocity v0x:
![]()
Equation (4.35) is the base or parent object in our example. If the force in the y direction also vanishes, then there will also be uniform y motion:
![]()
We consider uniform x motion as a parent and view uniform y motion as a child.
Equation (4.34) tells us that a constant force in the x direction causes a constant acceleration ax in that direction. The solution of the x equation of motion with uniform acceleration is
![]()
For projectile motion without air resistance, we usually have ax = 0 and ay = -g = -9.8 m/s2:
![]()
This y motion is a child of the parent x motion.
4.13 OOP Class Structure (Method)
The class structure we use to solve our problem contains the objects
Parent class Um1D: 1-D uniform motion for given initial conditions,
Child class Um2D: uniform 2-D motion; child class of Um1D,
Child class Am2d: 2-D accelerated motion; child class of Um2D.
The member functions include
x: position after time t,
archive: creator of a file of position versus time.
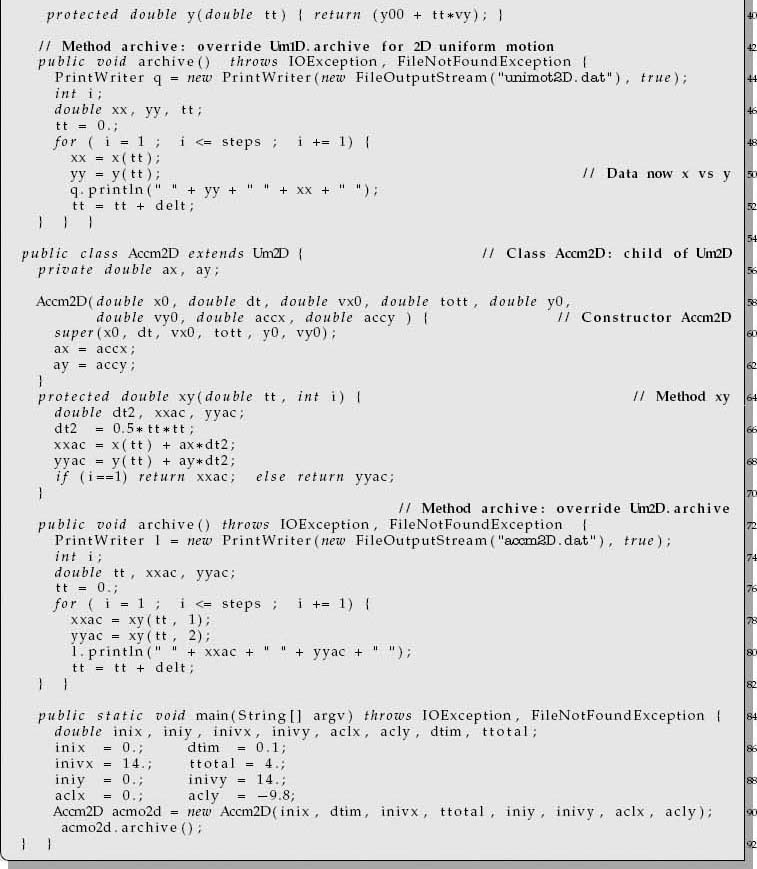
For our projectile motion, encapsulation is a combination of the initial conditions (x0,vx0) with the member functions used to compute x(t). Our member functions are the creator of the class of uniform 1-D motion Um1D and the creator x(t) of a file of x as a function of time t. Inheritance is the child class Um2D for uniform motion in both the x and y directions, it being created from the parent class Um1D of 1-D uniform motion. Abstraction is present (although not used powerfully) by the simple addition of motion in the x and y directions. Polymorphism is present by having the member function that creates the output file different for 1-D and 2-D motions. In this implementation of OOP, the class Accm2D for accelerated motion in two dimensions inherits uniform motion in two dimensions (which in turn inherits uniform 1-D motion) and adds to it the attribute of acceleration.
4.14 Java Implementation
Listing 4.13 Accm2D.java is an OOP program for accelerated motion in two dimensions.
1 These two nonstatic methods are special as they permit the parameters characterizing the object that they construct to be passed via a new statement.
2 Actually, the Java compiler looks through all the directories in your classpath and imports the first instance of the needed class that it finds.