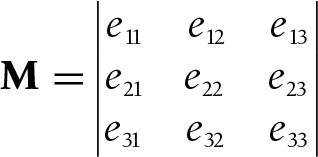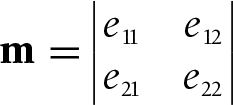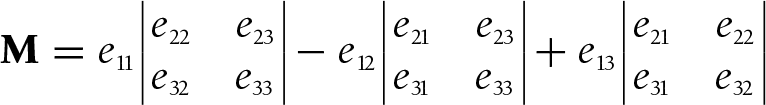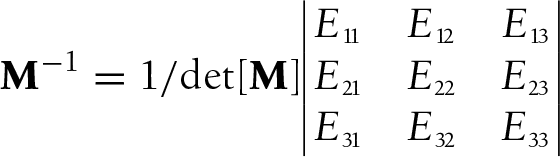Appendix B. Matrix Operations
This appendix implements a class called Matrix3x3 that encapsulates all of the operations
you need to handle 3×3 (nine-element) matrices when writing 3D rigid-body
simulations.
Matrix3×3 Class
The Matrix3x3 class is defined with nine elements, eij,
where i represents the ith row
and j the jth column. For
example, e21 refers to the
element on the second row in the first column. Here’s how all of the
elements are arranged:
The class has two constructors, one of which initializes the matrix elements to zero, and the other of which initializes the elements to those passed to the constructor:
class Matrix3x3 {
public:
// elements eij: i -> row, j -> column
float e11, e12, e13, e21, e22, e23, e31, e32, e33;
Matrix3x3(void);
Matrix3x3(float r1c1, float r1c2, float r1c3,
float r2c1, float r2c2, float r2c3,
float r3c1, float r3c2, float r3c3 );
float det(void);
Matrix3x3 Transpose(void);
Matrix3x3 Inverse(void);
Matrix3x3& operator+=(Matrix3x3 m);
Matrix3x3& operator-=(Matrix3x3 m);
Matrix3x3& operator*=(float s);
Matrix3x3& operator/=(float s);
};
// Constructor
inline Matrix3x3::Matrix3x3(void)
{
e11 = 0;
e12 = 0;
e13 = 0;
e21 = 0;
e22 = 0;
e23 = 0;
e31 = 0;
e32 = 0;
e33 = 0;
}
// Constructor
inline Matrix3x3::Matrix3x3(float r1c1, float r1c2, float r1c3,
float r2c1, float r2c2, float r2c3,
float r3c1, float r3c2, float r3c3 )
{
e11 = r1c1;
e12 = r1c2;
e13 = r1c3;
e21 = r2c1;
e22 = r2c2;
e23 = r2c3;
e31 = r3c1;
e32 = r3c2;
e33 = r3c3;
}Determinant
The method, det, returns the
determinant of the matrix. The determinant of a 2×2
matrix:
is as follows:
| det [m] = e11 e22 − e21 e12 |
We find the determinant of a 3×3 matrix by first expanding the matrix by minors, and then resolving the determinants of the 2×2 minors. Here’s how you expand a 3×3 matrix by minors:
Here’s how this all looks in code:
inline float Matrix3x3::det(void)
{
return e11*e22*e33 -
e11*e32*e23 +
e21*e32*e13 -
e21*e12*e33 +
e31*e12*e23 -
e31*e22*e13;
}Transpose
The method Transpose transposes
the matrix by swapping rows with columns—that is, the
elements in the first row become the elements in the first column and so
on for the second and third rows and columns. The following relations
are true for transpose operations:
| (Mt)t = M |
| (s M)t = s (Mt) |
| (M N)t = Nt Mt |
| (M + N)t = Mt + Nt |
| det[Mt] = det[M] |
Here M and N are matrices, t is the transpose operator, and s is a scalar.
Here’s the Transpose method for
our Matrix3x3 class:
inline Matrix3x3 Matrix3x3::Transpose(void)
{
return Matrix3x3(e11,e21,e31,e12,e22,e32,e13,e23,e33);
}Inverse
The method Inverse computes
the inverse matrix such that the following relation is
satisfied:
M M−1 = M−1 M = I
Here M−1 is the inverse of matrix M, and I is the identity matrix. For a 3×3 matrix, we find the inverse as follows:
Here Eij represents the cofactor of element eij, which we can find by taking the determinant of the minor of each element. Only square matrices, those with the same number of rows as columns, can be inverted. Note, however, that not all square matrices can be inverted. A matrix can be inverted only if its determinant is nonzero.
The follow relation applies to matrix inversion:
| (M N)−1 = N−1 M−1 |
Here’s how matrix inversion looks in code for our Matrix3x3 class:
inline Matrix3x3 Matrix3x3::Inverse(void)
{
float d = e11*e22*e33 -
e11*e32*e23 +
e21*e32*e13 -
e21*e12*e33 +
e31*e12*e23 -
e31*e22*e13;
if (d == 0) d = 1;
return Matrix3x3( (e22*e33-e23*e32)/d,
-(e12*e33-e13*e32)/d,
(e12*e23-e13*e22)/d,
-(e21*e33-e23*e31)/d,
(e11*e33-e13*e31)/d,
-(e11*e23-e13*e21)/d,
(e21*e32-e22*e31)/d,
-(e11*e32-e12*e31)/d,
(e11*e22-e12*e21)/d );
}Matrix Addition: The += Operator
This operator simply adds the passed matrix to the current one on an element-by-element basis. For two matrices to be added, they must be of the same order—that is, they must have the same number of rows and columns:
inline Matrix3x3& Matrix3x3::operator+=(Matrix3x3 m)
{
e11 += m.e11;
e12 += m.e12;
e13 += m.e13;
e21 += m.e21;
e22 += m.e22;
e23 += m.e23;
e31 += m.e31;
e32 += m.e32;
e33 += m.e33;
return *this;
}Matrix addition (and subtraction) is commutative, associative, and distributive; thus:
| M + N = N + M |
| M + (N + P) = (M + N) + P |
| M (N + P) = M N + M P |
| (N + P) M = N M + P M |
Matrix Subtraction: The −= Operator
This operator simply subtracts the passed matrix from the current one on an element-by-element basis. For two matrices to be subtracted, they must be of the same order—that is, they must have the same number of rows and columns:
inline Matrix3x3& Matrix3x3::operator-=(Matrix3x3 m)
{
e11 -= m.e11;
e12 -= m.e12;
e13 -= m.e13;
e21 -= m.e21;
e22 -= m.e22;
e23 -= m.e23;
e31 -= m.e31;
e32 -= m.e32;
e33 -= m.e33;
return *this;
}Scalar Multiplication: The *= Operator
This operator simply multiplies each element by the scalar s:
inline Matrix3x3& Matrix3x3::operator*=(float s)
{
e11 *= s;
e12 *= s;
e13 *= s;
e21 *= s;
e22 *= s;
e23 *= s;
e31 *= s;
e32 *= s;
e33 *= s;
return *this;
}The following relation applies for scalar multiplication (and division):
| s(M N) = (sM) N = M (s N) |
Matrix Functions and Operators
The functions and overloaded operators that follow are useful when you are
performing operations with two matrices, or with a matrix and a scalar, or
a matrix and a vector. Here, the matrices are assumed to be of the type
Matrix3x3, and vectors of the type
Vector, as discussed in Appendix A.
Matrix Addition: The + Operator
This operator adds the two matrices together on an element-by-element basis:
inline Matrix3x3 operator+(Matrix3x3 m1, Matrix3x3 m2)
{
return Matrix3x3( m1.e11+m2.e11,
m1.e12+m2.e12,
m1.e13+m2.e13,
m1.e21+m2.e21,
m1.e22+m2.e22,
m1.e23+m2.e23,
m1.e31+m2.e31,
m1.e32+m2.e32,
m1.e33+m2.e33);
}Matrix Subtraction: The − Operator
This operator subtracts matrix m2 from m1 on an element-by-element basis:
inline Matrix3x3 operator-(Matrix3x3 m1, Matrix3x3 m2)
{
return Matrix3x3( m1.e11-m2.e11,
m1.e12-m2.e12,
m1.e13-m2.e13,
m1.e21-m2.e21,
m1.e22-m2.e22,
m1.e23-m2.e23,
m1.e31-m2.e31,
m1.e32-m2.e32,
m1.e33-m2.e33);
}Scalar Divide: The / Operator
This operator divides every element in the matrix m by the scalar
s:
inline Matrix3x3 operator/(Matrix3x3 m, float s)
{
return Matrix3x3( m.e11/s,
m.e12/s,
m.e13/s,
m.e21/s,
m.e22/s,
m.e23/s,
m.e31/s,
m.e32/s,
m.e33/s);
}Matrix Multiplication: The * Operator
This operator, when applied between two matrices, performs a matrix multiplication. In matrix multiplication, each element, eij, is determined by the product of the ith row in the first matrix and the jth column of the second matrix:
inline Matrix3x3 operator*(Matrix3x3 m1, Matrix3x3 m2)
{
return Matrix3x3(m1.e11*m2.e11 + m1.e12*m2.e21 + m1.e13*m2.e31,
m1.e11*m2.e12 + m1.e12*m2.e22 + m1.e13*m2.e32,
m1.e11*m2.e13 + m1.e12*m2.e23 + m1.e13*m2.e33,
m1.e21*m2.e11 + m1.e22*m2.e21 + m1.e23*m2.e31,
m1.e21*m2.e12 + m1.e22*m2.e22 + m1.e23*m2.e32,
m1.e21*m2.e13 + m1.e22*m2.e23 + m1.e23*m2.e33,
m1.e31*m2.e11 + m1.e32*m2.e21 + m1.e33*m2.e31,
m1.e31*m2.e12 + m1.e32*m2.e22 + m1.e33*m2.e32,
m1.e31*m2.e13 + m1.e32*m2.e23 + m1.e33*m2.e33 );
}Two matrices can be multiplied only if one has the same number of columns as the other has rows. Matrix multiplication is not commutative, but it is associative; thus:
| M N ≠ N M |
| (M N) P = M (N P) |
Scalar Multiplication: The * Operator
This operator, when applied between a matrix and a scalar, multiplies each element in the matrix
m by the scalar s. Two forms are
given here, depending on the order in which the matrix and scalar are encountered:
inline Matrix3x3 operator*(Matrix3x3 m, float s)
{
return Matrix3x3( m.e11*s,
m.e12*s,
m.e13*s,
m.e21*s,
m.e22*s,
m.e23*s,
m.e31*s,
m.e32*s,
m.e33*s);
}
inline Matrix3x3 operator*(float s, Matrix3x3 m)
{
return Matrix3x3( m.e11*s,
m.e12*s,
m.e13*s,
m.e21*s,
m.e22*s,
m.e23*s,
m.e31*s,
m.e32*s,
m.e33*s);
}Vector Multiplication: The * Operator
This operator, when applied between a vector and a matrix, performs a vector multiplication where the ith column in the matrix is multiplied by the ith component in the vector. Two forms are given here, depending on the order in which the matrix and vector are encountered:
inline Vector operator*(Matrix3x3 m, Vector u)
{
return Vector( m.e11*u.x + m.e12*u.y + m.e13*u.z,
m.e21*u.x + m.e22*u.y + m.e23*u.z,
m.e31*u.x + m.e32*u.y + m.e33*u.z);
}
inline Vector operator*(Vector u, Matrix3x3 m)
{
return Vector( u.x*m.e11 + u.y*m.e21 + u.z*m.e31,
u.x*m.e12 + u.y*m.e22 + u.z*m.e32,
u.x*m.e13 + u.y*m.e23 + u.z*m.e33);
}