Appendix A. Vector Operations
This appendix implements a class called Vector that encapsulates all of the vector
operations that you need when writing 2D or 3D rigid-body simulations.
Although Vector represents 3D vectors,
you can easily reduce it to handle 2D vectors by eliminating all of the
z terms or simply constraining the
z terms to 0 where appropriate in your
implementation.
Vector Class
The Vector class is defined with three components—x, y, and
z—along with several methods and operators that implement basic vector
operations. The class has two constructors, one of which initializes the vector components to
0, and the other of which initializes the vector components to those passed to the
constructor:
//------------------------------------------------------------------------
// Vector Class and vector functions
//------------------------------------------------------------------------
class Vector {
public:
float x;
float y;
float z;
Vector(void);
Vector(float xi, float yi, float zi);
float Magnitude(void);
void Normalize(void);
void Reverse(void);
Vector& operator+=(Vector u);
Vector& operator-=(Vector u);
Vector& operator*=(float s);
Vector& operator/=(float s);
Vector operator-(void);
};
// Constructor
inline Vector::Vector(void)
{
x = 0;
y = 0;
z = 0;
}
// Constructor
inline Vector::Vector(float xi, float yi, float zi)
{
x = xi;
y = yi;
z = zi;
}Magnitude
The Magnitude method simply calculates the scalar magnitude of the vector
according to the formula:
| |v| =
|
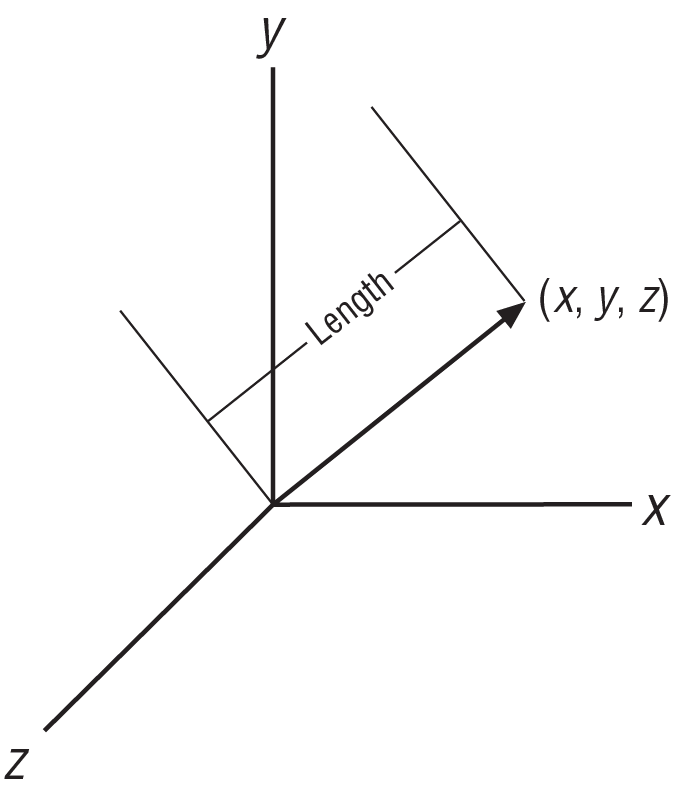
This is for a zero-based vector where the components are specified relative to the origin. The magnitude of a vector is equal to its length, as illustrated in Figure A-1.
Here’s the code that calculates the vector magnitude for our
Vector class:
inline float Vector::Magnitude(void)
{
return (float) sqrt(x*x + y*y + z*z);
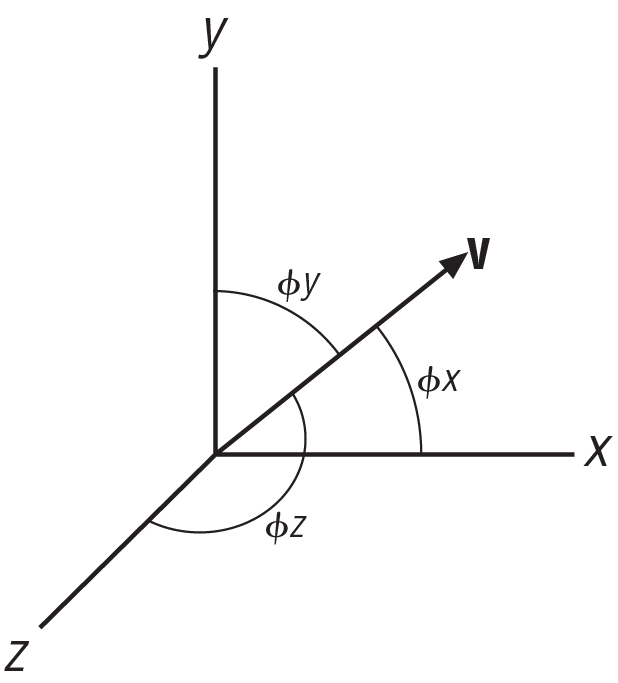
}Note, you can calculate the components of a vector if you know its length and direction angles. Direction angles are the angles between each coordinate axis and the vector, as shown in Figure A-2.
The components of the vector shown in this figure are:
| vx = |v| cos φx |
| vy = |v| cos φy |
| vz = |v| cos φz |
The cosines of the direction angles seen in these equations are known as direction cosines. The sum of the squares of the direction cosines is always equal to 1:
| cos2 φx + cos2 φy + cos2 φz = 1 |
Normalize
The Normalize method
normalizes, or converts, the vector to a unit vector satisfying the
following equation:
| |v| =
|
In other words, the length of the normalized vector is 1 unit. If v is a non-unit vector with components x, y, and z, then we can calculate the unit vector u from v as follows:
| u = v / |v| = (x / |v|) I + (y / |v|) j + (z / |v|) k |
Here |v| is simply the magnitude, or length, of vector v as described earlier.
Here’s the code that converts our Vector class vector to a unit vector:
inline void Vector::Normalize(void)
{
float m = (float) sqrt(x*x + y*y + z*z);
if(m <= tol) m = 1;
x /= m;
y /= m;
z /= m;
if (fabs(x) < tol) x = 0.0f;
if (fabs(y) < tol) y = 0.0f;
if (fabs(z) < tol) z = 0.0f;
}In this function, tol is a
float type tolerance; for example:
float const tol = 0.0001f;
Reverse
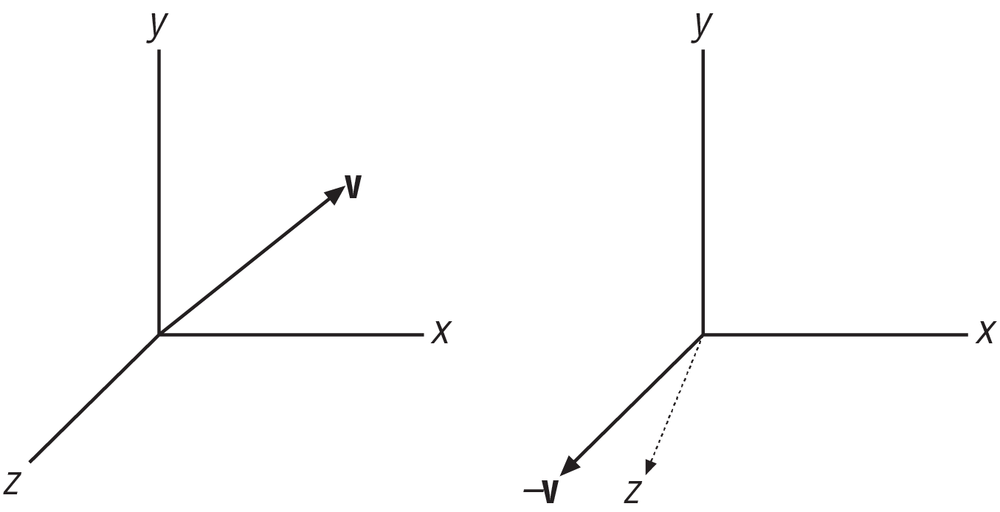
The Reverse method reverses the direction of the vector, which is accomplished by simply taking the negative of
each component. After calling Reverse, the vector will
point in a direction opposite to the direction it was pointing before Reverse was called:
inline void Vector::Reverse(void)
{
x = -x;
y = -y;
z = -z;
}This operation is illustrated in Figure A-3.
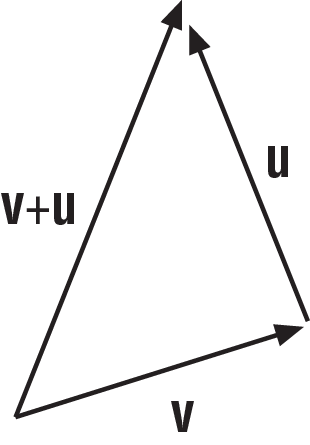
Vector Addition: The += Operator
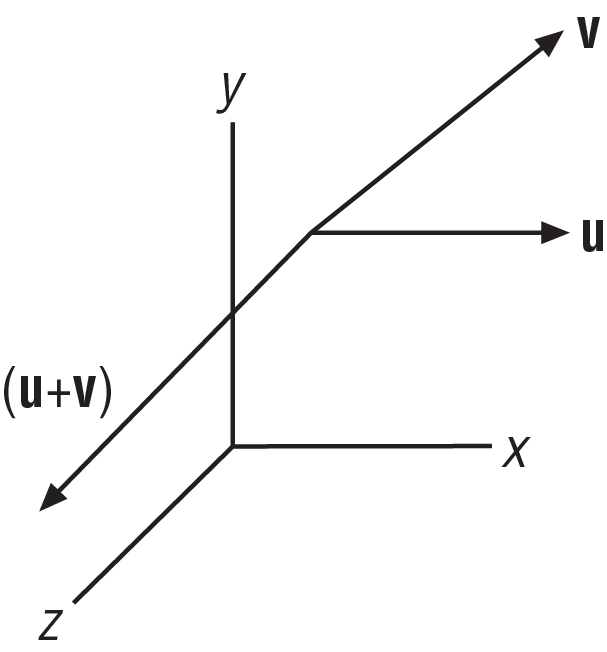
This summation operator is used for vector addition, whereby the passed vector is added to the current vector, component by component. Graphically, vectors are added in tip-to-tail fashion, as illustrated in Figure A-4.
Here’s the code that adds the vector u to our Vector class vector:
inline Vector& Vector::operator+=(Vector u)
{
x += u.x;
y += u.y;
z += u.z;
return *this;
}Vector Subtraction: The −= Operator
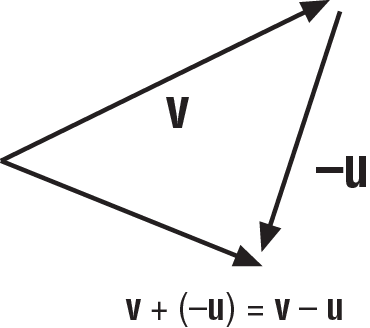
This subtraction operator is used to subtract the passed vector from the current one, which is performed on a component-by-component basis. Vector subtraction is very similar to vector addition except that you take the reverse of the second vector and add it to the first, as illustrated in Figure A-5.
Here’s the code that subtracts vector u from our Vector class vector:
inline Vector& Vector::operator-=(Vector u)
{
x -= u.x;
y -= u.y;
z -= u.z;
return *this;
}Scalar Multiplication: The *= Operator
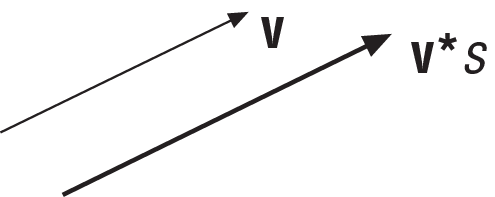
This is the scalar multiplication operator that’s used to multiply a vector by a scalar, effectively scaling the vector’s length. When you multiply a vector by a scalar, you simply multiply each vector component by the scalar quantity to obtain the new vector. The new vector points in the same direction as the unscaled one, but its length will be different (unless the scale factor is 1). This is illustrated in Figure A-6.
Here’s the code that scales our Vector class vector:
inline Vector& Vector::operator*=(float s)
{
x *= s;
y *= s;
z *= s;
return *this;
}Scalar Division: The /= Operator
This scalar division operator is similar to the scalar multiplication operator except each vector component is divided by the passed scalar quantity:
inline Vector& Vector::operator/=(float s)
{
x /= s;
y /= s;
z /= s;
return *this;
}Conjugate: The − Operator
The conjugate operator simply takes the negative of each vector component and can be used when you are subtracting one vector from another or for reversing the direction of the vector. Applying the conjugate operator is the same as reversing a vector, as discussed earlier:
inline Vector Vector::operator-(void)
{
return Vector(-x, -y, -z);
}Vector Functions and Operators
The following functions and overloaded operators are useful when you are
performing operations with two vectors, or with a vector and a scalar,
where the vector is based on the Vector
class.
Vector Addition: The + Operator
This addition operator adds vector v to vector u according to the formula:
| u + v = (ux + vx) i + (uy + vy) j + (uz + vz) k |
Here’s the code:
inline Vector operator+(Vector u, Vector v)
{
return Vector(u.x + v.x, u.y + v.y, u.z + v.z);
}Vector Subtraction: The − Operator
This subtraction operator subtracts vector v from vector u according to the formula:
| u − v = (ux − vx) i + (uy − vy) j + (uz − vz) k |
Here’s the code:
inline Vector operator-(Vector u, Vector v)
{
return Vector(u.x - v.x, u.y - v.y, u.z - v.z);
}Vector Cross Product: The ^ Operator
This cross-product operator takes the vector cross product between vectors u and v (u × v) and returns a vector perpendicular to both u and v according to the formula:
| u × v = (uy * vz − uz * vy) i + (−ux * vz + uz * vx) j + (ux * vy − uy * vx) k |
The resulting vector is perpendicular to the plane that contains vectors u and v. The direction in which this resulting vector points can be determined by the right hand rule. If you place the two vectors u and v tail to tail, as shown in Figure A-7, and curl your fingers (of your right hand) in the direction from u to v, then your thumb will point in the direction of the resulting vector.
In this case, the resulting vector points out of the page along the z-axis since the vectors u and v lie in the plane formed by the x- and y-axes.
If two vectors are parallel, then their cross product will be 0. This is useful when you need to determine whether or not two vectors are indeed parallel.
The cross-product operation is distributive; however, it is not commutative:
| u × v ≠ v × u |
| u × v = −(v × u) |
| s (u × v) = (s)(u) × v = u × (s)(v) |
| u × ( v + p) = (u × v) + (u × p) |
Here’s the code that takes the cross product of vectors u and v:
inline Vector operator^(Vector u, Vector v)
{
return Vector( u.y*v.z - u.z*v.y,
-u.x*v.z + u.z*v.x,
u.x*v.y - u.y*v.x );
}Vector cross products are handy when you need to find normal (perpendicular) vectors. For example, when performing collision detection you often need to find the vector normal to the face of a polygon. You can construct two vectors in the plane of the polygon using the polygon’s vertices and then take the cross product of these two vectors to get normal vector.
Vector Dot Product: The * Operator
This operator takes the vector dot product between the vectors u and v, according to the formula:
| u • v = (ux * vx) + (uy * vy) + (uz * vz) |
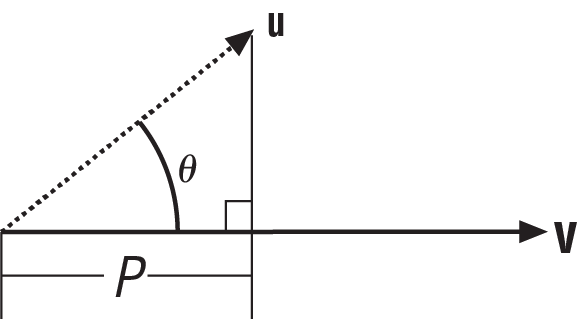
The dot product represents the projection of the vector u onto the vector v, as illustrated in Figure A-8.
In this figure, P is the result of the dot product, and it is a scalar. You can also calculate the dot product if you the know the angle between the vectors:
| P = u • v = |u| |v| cos θ |
Here’s the code that takes the dot product of u and v:
// Vector dot product
inline float operator*(Vector u, Vector v)
{
return (u.x*v.x + u.y*v.y + u.z*v.z);
}Vector dot products are handy when you need to find the magnitude of a vector projected onto another one. Going back to collision detection as an example, you often have to determine the closest distance from a point, which may be a polygon vertex on one body (body 1) to a polygon face on another body (body 2). If you construct a vector from the face under consideration on body 2, using any of its vertices, to the point under consideration from body 1, then you can find the closest distance of that point from the plane of body 2’s face by taking the dot product of that point with the normal vector to the plane. (If the normal vector is not of unit length, then you’ll have to divide the result by the magnitude of the normal vector.)
Scalar Multiplication: The * Operator
This operator multiplies the vector u by the scalar s on a component-by-component basis. There are two versions of this overloaded operator depending on the order in which the vector and scalar are encountered:
inline Vector operator*(float s, Vector u)
{
return Vector(u.x*s, u.y*s, u.z*s);
}
inline Vector operator*(Vector u, float s)
{
return Vector(u.x*s, u.y*s, u.z*s);
}Scalar Division: The / Operator
This operator divides the vector u by the scalar s on a component-by-component basis:
inline Vector operator/(Vector u, float s)
{
return Vector(u.x/s, u.y/s, u.z/s);
}Triple Scalar Product
This function takes the triple scalar product of the vectors u, v, and w according to the formula:
| s = u • (v × w) |
Here, the result, s, is a scalar. The code is as follows:
inline float TripleScalarProduct(Vector u, Vector v, Vector w)
{
return float( (u.x * (v.y*w.z - v.z*w.y)) +
(u.y * (-v.x*w.z + v.z*w.x)) +
(u.z * (v.x*w.y - v.y*w.x)) );
}