Phase-field modeling of thin film growth
Abstract:
Step-flow models are an efficient multiscale approach to model film growth, as they allow kinetic effects due to atomic interactions to be incorporated in continuum models. We consider phase-field approximations of such models and demonstrate their applicability through various examples, including trench formation on W(110), spiral and mound growth on Pt(111) and anomalous spiral growth on Si(001).
3.1 Introduction
We think of the crystal film as an atomic landscape of terraces, separated by steps of one atomic height and build our modeling description of crystal thin film growth on it. Microscopic processes in crystal thin film growth include the deposition of atoms or molecules on the terraces of the film, adatom (adsorbed atoms) desorption from the terraces, adatom diffusion on terraces, and the attachment and detachment of adatoms to and from the steps, respectively. Through the net attachment, the position of the steps changes, which means that the upper terrace expands by overgrowing the terrace below. This induces vertical growth of the film. If a finite number of adatoms meet, they coalesce and form a new terrace, which induces vertical growth by nucleation. When a screw dislocation intersects a crystal surface, a step emerges from the intersection point. This step cannot be removed by growth or evaporation. The attachment of adatoms to such steps results in spiral growth with the step turning around the intersection point, which also leads to vertical growth.
We use a phase-field approximation of the moving boundary value problem first formulated by Burton, Cabrera, and Frank (1951) and today known as BCF-type models. Key parameters are the surface diffusion coefficient D for adatom diffusion on terraces and the deposition flux F, as well as the kinetic coefficients k governing the attachment of adatoms to a step from the lower and upper terrace, respectively. Step thermodynamics enter through the step stiffness and the equilibrium adatom concentration. In the phase-field approximation the crystal surface is represented by a continuous field which couples to the adatom concentration and is subjected to a multiwell potential that pins the phase-field variable to the prefered integer value representing the height of the discrete terraces. From a numerical point of view, it is desirable to have such a diffuse interface approximation. It smears out the discrete height function (which counts the atomic monolayers) on a length scale ε. The smeared-out height function (phase-field variable) ϕ thus (approximately) describes the position of the steps. The advantage is that both ϕ and the adatom density ρ can be discretized with respect to the same grid. Moreover, the vanishing of islands and the coalescence of steps are automatically handled. Diffuse interface approximations for BCF-type models have been introduced in Liu and Metiu (1997) and Karma and Plapp (1998). In Liu and Metiu (1997) the motion of a one-dimensional step train is analysed, whereas in Karma and Plapp (1999) the growth of a spiral is simulated. In Yeon et al. (2003) the effect of a lattice mismatch between substrate and film is incorporated into the phase-field approximation. The Ehrlich–Schwoebel barrier, an additional barrier an adatom at a ‘ step down’ has to overcome in order to attach at the step, has been incorporated into these phase-field approximations by Otto et al. (2004). With these modifications it was possible to analyse growth instabilities using phase-field approximations. Among them are step bunching instabilities as a result of elastic interactions (Yeon et al. 2007), step meandering as a result of an Ehrlich–Schwoebel barrier (Hausser and Voigt 2008, Hu et al. 2011), mounding resulting from an Ehrlich–Schwoebel barrier and strong anisotropic step edge barriers (Yu et al. 2008) as well as spiral growth (Redinger et al. 2008, Yu et al. 2009).
We will review these phase-field approximations and apply them to simulate trench formation on W(110), a competition between spiral and mound growth on Pt(111) as well as anomalous spiral growth on Si(001).
3.2 Modeling
We recall the classical BCF model. The adatom density on the terraces obeys the following diffusion equation
where D is the diffusion constant and F is the deposition flux rate. Desorption of adatoms has been neglected. The fluxes of the adatoms to a step are given by
where subscripts +, − denote quantities at the upper and lower terrace respectively, n denotes the normal pointing from upper to lower terrace and v is the normal velocity of the step. Assuming first-order kinetics for the attachment and detachment of adatoms at the steps, the adatom densities satisfy the following kinetic boundary conditions at the step:
With this notation, asymmetric attachment rates 0 < k+ < k− model the Ehrlich-Schwoebel effect. The equilibrium density ρeq is given by the linearized Gibbs–Thomson relation
where Ω = a*a is the atomic area, ‘a’ being the lattice spacing, ‘γ’ the step free energy density, and γ + γ″ the step stiffness. Finally, the normal velocity of a step is given by
where ∇s denotes the tangential derivative along the step and Dstep is the diffusion constant at atoms along the step. The second term in the velocity law 3.5 represents edge diffusion of edge atoms along the step, whereas the first term ensures mass conservation. Other effects such as step permeability or downward funneling will be neglected.
A phase-field formulation for Eqs 3.1-3.5 has been given and justified by matched asymptotic expansions by Hu et al. (2011). We will here consider a simpler form in which the edge diffusion term is neglected and a quasi-stationary approximation is assumed. The phase-field model then reads in the isotropic case in non-dimensional form:
with an appropriate normalized multiwell potential G(φ), being a periodic function of j with period 1, which vanishes for φ = …, –1, 0, 1, …, appropriate coefficients ζ1(φ) and ζ2(φ), which are again periodic functions of φ with period 1. They can be interpreted as friction coefficients for step and adatom movement, respectively. An appropriate choice of ζ1(φ) and ζ2(φ) allows the approximation of any kinetic coefficients k+ and k−, which can be shown using matched asymptotic analysis. The model can be extended to include anisotropic effects in the same way as done in classical phase-field models (see, e.g., Torabi et al. 2009).
3.3 Numerical results
We will demonstrate various simulation results of practical interest, which are validated by experiments on mound and spiral growth. We thereby highlight the influence of the Ehrlich–Schwoebel barrier, anisotropic kinetics and stress effects.
3.3.1 Trench formation
Using the phase-field model we simulate formation and growth of stripe arrays, which result from anisotropic growth of islands under the Ehrlich–Schwoebel barrier. Due to the Ehrlich-Schwoebel barrier, mounds form and coarsen during growth. Due to the anisotropy, the coarsening is slow in one direction and fast in the other direction, which causes formation of trench arrays. The anisotropy is incorporated in terms of attachment kinetics and is locally limited at the island edge aligned to the < 100 > orientation and instantaneous at the island edge aligned to the < 110 > orientation. This anisotropy suppresses coarsening in the < 110 > direction in the early stages. After a period of time the stripe arrays develop a quasi-periodic uniaxial structure with a selected transversal slope and a decreasing longitudinal slope as a consequence of the competition between coarsening and rougening. A detailed discussion can be found in Yu et al. (2008). Figure 3.1 shows a typical configuration for W(110) which is in qualitative agreement with the experimental results in Borca et al. (2007).
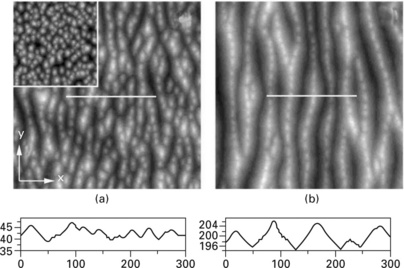
3.1 Simulated trench morphology on W(110) after deposition of (a) 40 ML and (b) 200 ML, and cross-section profile along the white line at the bottom. Inset: morphology of nucleated islands after deposition of 2 ML in cut image of the same scale as the main image. The simulations were performed by Y.-M. Yu.
The formed arrays have the potential to be used as templates for the growth of one-dimensional nanostructures. A key feature to produce nanowires using this approach is the perfect ordering of the trenched templates. The final ordering of the trenches depends sensitively on the nucleation of islands in the submonolayer regime. By influencing the nucleation, e.g. through a periodic strain field of a buried misfit dislocation network or a compliant substrate, ordered arrays can be formed. In Yu and Voigt (2009) such a strain field is used to nucleate islands in an ordered array which leads to perfectly ordered trenches with tunable size in the phase-field simulation.
3.3.2 Spiral and mound growth
The large-scale shape of spirals and mounds are similar. However, it is clear that the growth mechanism near the top of the structure is completely different for spiral mounds and so-called wedding cakes. The growth of wedding cakes is governed by the rate of two-dimensional nucleation of islands on the top terrace, which is enhanced by the confinement of adatoms due to the Ehrlich–Schwoebel barrier. In contrast, atoms landing near the top of the spiral mound can avoid the Ehrlich–Schwoebel barrier by moving around the core which should reduce the local adatom concentration and hence the growth rate. On the other hand the indelible presence of the step emanating from the screw dislocation obviates the need for two-dimensional nucleation, which should increase the rate of vertical growth. We use a setup in which both growth modes are possible and are interested in their competition. Two-dimensional nucleation is thereby modeled as an intrinsic feature of the phase-field approximation. If the adatom density becomes sufficiently large a new terrace nucleates as a result of the changing barrier in the multiwell potential. Figure 3.2 shows a typical surface configuration after deposition of 200 monolayers. Under these conditions in which the adatom concentration is allowed to become sufficiently large so that islands nucleate deterministically, spiral mounds were generally seen to grow higher than regular wedding cakes. The results nicely coincide with the experiments on Pt(111) surfaces in Redinger et al. (2008).

3.2 Growth spirals and mounds obtained from phase-field simulation with D = 10, F = 0.2 ML/s, γ = 1, ρ* = 0.1, k+ = 10 and k− = 1. The surface is shown after deposition of 200 ML showing spiral mounds and wedding cakes and demonstrating the faster growth of the spiral mounds. The simulations were performed by A. Rätz.
3.3.3 Anomalous spiral growth
The approach discussed in the previous section neglects the influence of the strain field resulting from the screw dislocation. Taking this effect into account might lead to anomalous spiral step motion as found on a Si(001) surface by Hannon et al. (2006) and Voorhees (2006). The anomalous behavior is attributed to interaction between the surface structure and the strain field of the screw dislocation. The screw dislocation thereby breaks two single atomic height steps. At each step, the surface phase switches between (1 × 2) and (2 × 1). The strain field of the screw dislocation causes an asymmetry between the two phases, with one phase more energetically favored than the other. The step growth is coupled with the asymmetric phase switching between (1 × 2) and (2 × 1), causing the anomalous spiral profile. The related dynamics for this growth mode is analysed by Yu et al. (2009). In order to account for the elastic effects we use alternating surface phases of (1 × 2) and (2 × 1) with different surface energies. We define Δγ = γ2 × 1 − γ1 × 2 corresponding to the strain field of the screw dislocation, which enters the definition of the multiwell potential. Figure 3.3 shows typical configurations under the influence of Δγ.

3.3 Images of the spiral growth at the steady-state regime simulated using F = 0.005 ML/s (left), 0.02 ML/s (middle) and 0.04 ML/s (right) for non-zero in (a)–(c) and zero in (d)–(f). The lightest gray color corresponds to the highest surface height, being around 109, 193, 231, 111, 200 and 233 atomic layers in (a)–(f), respectively. The sharp change in gray indicates the position of the step. Inset (enlarged): the corresponding simulated image of the surface termination, where the (2 × 1) and (1 × 2) phases are denoted by bright and dark, respectively, and the position of the step is indicated by switching between bright and dark. The simulations were performed by Y.-M. Yu.
3.4 Conclusion
Phase-field models have been used to approximate BCF-type models for step flow growth. The phase-field variable thereby models the discrete height of the film. The novelty of such models is the ability to approximate not only the jump in the fluxes across the step edges but also the jump in the density field which results from the kinetic boundary conditions. This is realized through a degenerate mobility function in the phase-field equation, which can be interpreted as a degenerate Cahn-Hilliard-type equation. The phase-field approach allows the nucleation of new islands, it allows for coalescence and also for vanishing of islands, without special treatment. The derived set of equations can be solved with standard tools; however, an adaptive mesh refinement along the step edges is desirable. Using matched asymptotic analysis the connection between these phase-field models and the BCF model can be shown.
The approach is applied to understand various interesting phenomena in thin film growth. Among them are the formation of trenches as a result of the Ehrlich–Schwoebel barrier and anisotropic kinetic coefficients, the competition between mound and spiral growth, which for typical material parameters will always be dominated by spirals, and an anomalous spiral growth mode, which results from the interaction of the strain field associated with the screw dislocation and the surface structure.
3.5 References
Borca, B., Fruchart, O., David, P., Rousseau, A., Meyer, C. Kinetic self-organization of trenched templates for the fabrication of versatile ferromagnetic nanowires. Appl. Phys. Lett.. 2007; 90:142507.
Burton, W.K., Cabrera, N., Frank, F.C. The growth of crystals and the equilibrium of their surfaces. Phil. Trans. R Soc. 1951; 243:299–358.
Hannon, J.B., Shenoy, V.B., Schwarz, K.W. Anomalous spiral motion of steps near dislocations on silicon surfaces. Science. 2006; 313:1266–1269.
Hausser, F., Voigt, A. Step meandering in epitaxial growth. J. Cryst. Growth. 2008; 303:80–84.
Hu, Z.Z., Lowengrub, J.S., Wise, S.M., Voigt, A., Phase-field modeling of epitaxial growth: applications to step trains and island dynamics, 2011. [Physica D (to appear)].
Karma, A., Plapp, M. Spiral surface growth without desorption. Phys. Rev. Lett.. 1998; 81:4444–4447.
Liu, F., Metiu, H. Stability and kinetics of step motion on crystal surfaces. Phys. Rev. 1997; 49:2601–2616.
Otto, F., Penzler, P., Ratz, A., Rump, T., Voigt, A. A diffuse interface approximation for step flow in epitaxial growth. Nonlin.. 2004; 17:477–491.
Redinger, A., Ricken, O., Kuhn, P., Rätz, A., Voigt, A., Krug, J., Michely, T. Spiral growth and step edge barriers. Phys. Rev. Lett. 100, 2008. [035506].
Torabi, S., Lowengrub, J., Voigt, A., Wise, S. A new phase-field model for strongly anisotropic systems. Proc. Roy. Soc. 2009; 465:1337–1359.
Voorhees, P.W. Materials science – step dances on surfaces. Science. 2006; 313:1247–1248.
Yeon, D.H., Cha, P.R., Chung, S.I., Yonn, J.K. Phase-field model for the dynamics of steps and islands on crystal surfaces. Metals Mater. Int.. 2003; 9:67–76.
Yeon, D.H., Cha, P.R., Lowengrub, J.S., Voigt, A., Thornton, K. Linear stability analysis for step meandering instabilities with elastic interactions and Ehrlich-Schwoebel barriers. Phys. Rev. 76, 2007. [011601].
Yu, Y.-M., Voigt, A. Directed self-organization of trenched templates for nanowire growth. Appl. Phys. Lett. 94, 2009. [043108].
Yu, Y.-M., Backofen, R., Voigt, A. Phase-field simulation of stripe arrays on metal bcc(110) surfaces. Phys. Rev. 77, 2008. [051605].
Yu, Y.-M., Liu, B.G., Voigt, A. Phase-field modeling of anomalous spiral step growth on Si(001) surfaces. Phys. Rev. 79, 2009. [235317].
