
78 3. LIMITS, DERIVATIVES, RULES, AND THE MEANING OF THE DERIVATIVE
Example 3.3 Compute:
lim
x!1
x e
x
e
x
x 1
Solution:
is function is like our original example in the sense that
x e
x
e
x
x 1
D
e
x
.x 1/
x 1
D
e
x
.x 1/
x 1
D e
x
;
which tells us that
lim
x!1
x e
x
e
x
x 1
D e
1
D e:
˙
Example 3.4 Compute:
lim
x!2
x
3
6x
2
C 11x 6
x 2
Solution:
If we plug in x D 2 to the top of the fraction on a trial basis we get 8 24 C 22 6 D 0. So, at
x D 2 we have the forbidden configuration
0
0
. e root-factor theorem for polynomials tells us
that .x 2/ is a factor of x
3
6x
2
C 11x 6. So, a little work gives us that
x
3
6x
2
C 11x 6
x 2
D
.x 3/.x 2/.x 1/
x 2
D
.x 3/
.x 2/.x 1/
x 2
D .x 3/.x 1/
So we have that:
lim
x!2
x
3
6x
2
C 11x 6
x 2
D .2 3/.2 1/ D 1
˙
3.1.1 SPLIT-RULE FUNCTIONS
It is sometimes desirable to have functions that obey different rules for different values of x.
Retailers often offer bulk pricing discounts, for example, with different costs per unit purchased
for larger and smaller numbers of units. ere is a notation for this kind of function, called split
rule notation. Suppose that s.x/ is a function that squares negative numbers but adds one to
positive numbers and zero. en we would say:
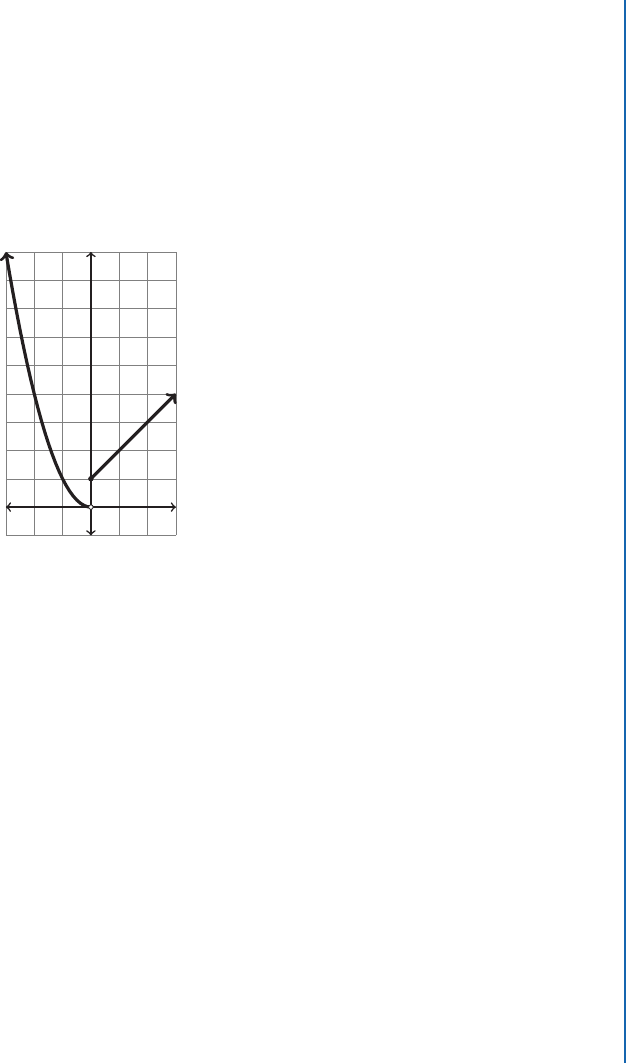
3.1. LIMITS 79
f .x/ D
x
2
x < 0
x C 1 x 0
If we look at the graph of this function in Figure 3.1, we see that split-rule functions give us
a lot of scope for creating functions that lack a limit at a point. Notice that the inequality at
the change point is denoted in the graph by using a filled circle for the point that is part of the
function and an empty circle for the point that is not part of the function.
f .x/ D
x
2
x < 0
x C 1 x 0
9
-1
3-3
Figure 3.1: A split-rule function.
Example 3.5 Examine the following function:
f .x/ D
x
2
C 1 x < 1
3x 1 x 1
What is the value of lim
x!1
f .x/?
Solution:
As we approach from below 1, the limit will be determined by the rule x
2
C 1, and so
the limit at 1 is 2, from below. As we approach from above 1, the limit will be determined by
the rule 3x 1, which will make the limit 2. Since the upper and lower limits both agree, the
limit of the function at x D 1 is 2.
˙

80 3. LIMITS, DERIVATIVES, RULES, AND THE MEANING OF THE DERIVATIVE
Example 3.6 Examine the following function: g.x/ D
1
x 2
What is the value of lim
x!2
f .x/?
Solution:
For this function we need to look at the graph, at least until we learn more:
g.x/ D
1
x 2
5
-5
-1
5
As we approach 2 from below, the
value of g.x/ is negative. But, since
we are dividing by numbers that are
approaching more and more closely
to zero, those numbers get bigger in
absolute value, and the function shoots
off toward 1. is means the limit
doesn’t exist. Similarly, the limit from
above shoots off toward C1 and also
fails to exist. is means the desired
limit also does not exist.
˙
PROBLEMS
Problem 3.7 For each of the following limits, give a reason the limit does not exist or compute
its value.
1. lim
x!3
x
2
9
x 3
2. lim
x!1
x
2
16
x C 4
3. lim
x!3
x
3
C 6x
2
C 11x C 6
x C 3
4. lim
x!0
e
x
1
e
x
C 1
5. lim
x!0
e
x
C
1
e
x
1
6. lim
x!1
2
x
3
6x
2
C 11x 6
7. lim
x!2
p
x 2
8. lim
x!0
ln.x/
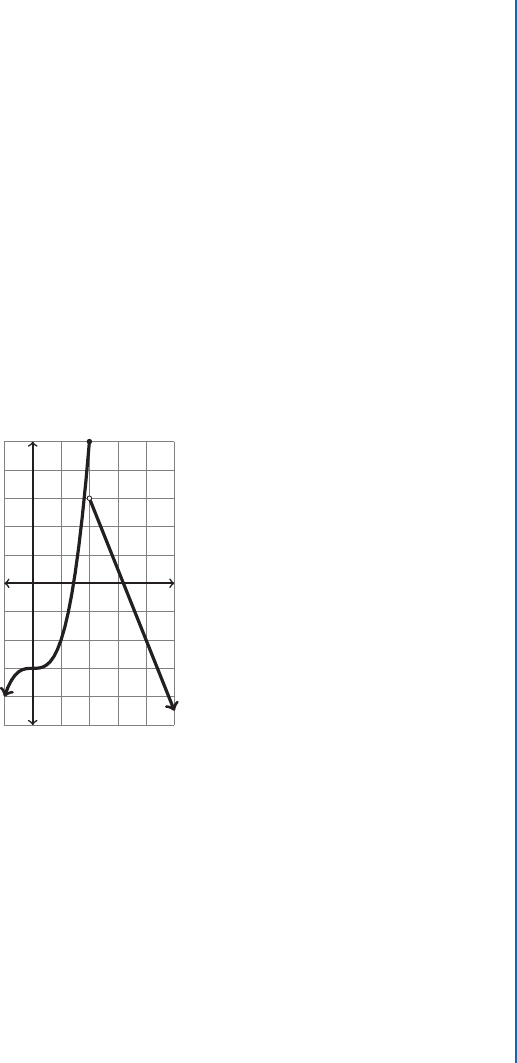
3.1. LIMITS 81
Problem 3.8 For each of the following limits, give a reason the limit does not exist or compute
its value. Use the functions f .x/, g.x/, and h.x/ that follow.
f .x/ D
x
3
x 1
4x C 5 x >D 1
g.x/ D
x
2
C 2 x < 1
3 x
2
x >D 1
h.x/ D
2x C 5 x 2
9 2x x >D 2
1. lim
x!1
f .x/ 2. lim
x!1
f .x/ 3. lim
x!1
g.x/
4. lim
x!1
g.x/ 5. lim
x!2
h.x/ 6. lim
x!2
h.x/
5
-5
-1
5
f(x)
Problem 3.9 Using f .x/ shown in the graph above answer the following questions.
1. What is the value of the point x D c where the rules change over?
2. What is lim
x!c
f .x/?
3. What is lim
x!c
C
f .x/?
4. Does the limit of f .x/ at c exist?
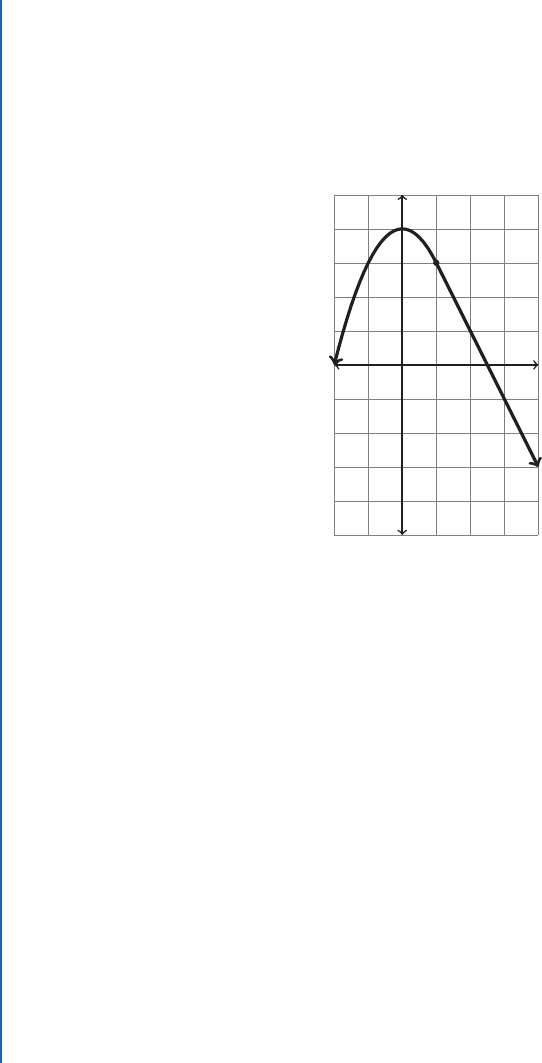
82 3. LIMITS, DERIVATIVES, RULES, AND THE MEANING OF THE DERIVATIVE
Problem 3.10 For which values of c does the function
f .x/ D
x
2
1 x < c
2x C 5 x c
have a limit at x D c?
5
-5
-2
4
g(x)
Problem 3.11 Using g.x/ in the graph above answer the following questions.
1. What is the value of the point x D c where the rules change over?
2. What is lim
x!c
g.x/?
3. What is lim
x!c
C
g.x/?
4. Does the limit of g.x/ at c exist?
5. What evidence is there that the function changes rules?
Problem 3.12 For which values of c does the function
g.x/ D
x
2
C 7x C 1 x < c
x 8 x c
have a limit at x D c?
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
