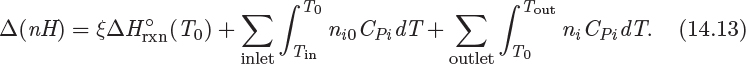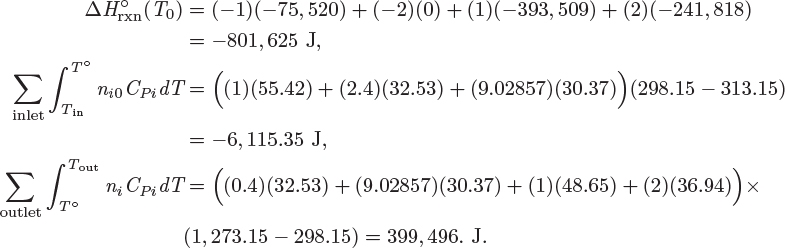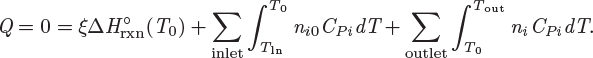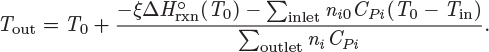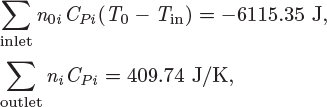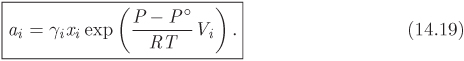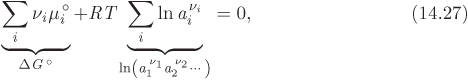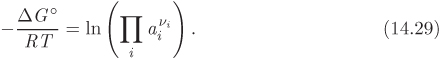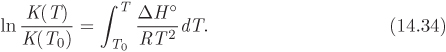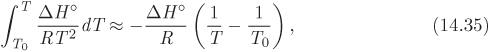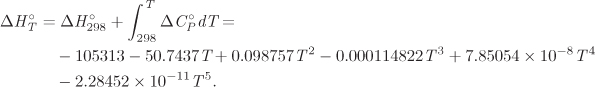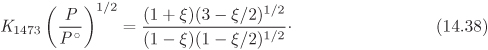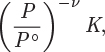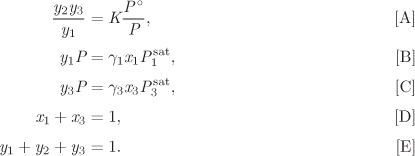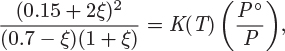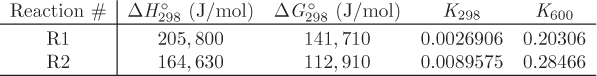Chapter 14. Reactions
Up to this point we have concentrated exclusively on nonreacting systems, namely, systems in which the molecular identity of all species is preserved. In reactions, chemical identity is not preserved, as a reactant species is converted into a product species. Even so, the atomic identity of the constituent elements is preserved. In fact, a chemical reaction is simply a rearrangement of atoms into new molecules, and in this respect, is very similar to the passages of molecules from one phase into another. There are more analogies between chemical reactions and mixing of two liquids, for example. In both cases we observe the transition from an initial state to a final one that is accompanied by heat effects. A chemical reaction may not go to completion, just as two liquids may only be partially miscible. Chemical equilibrium refers to a state where no net interconversion is observed between products and reactants. The situation is again analogous to phases at equilibrium with no net mass transfer between them. In this qualitative picture, products and reactants can be viewed as analogous to phases, with matter being transferred from the reactant side to the product side until equilibrium is achieved. With this analogy in mind, it should not be surprising that the general concepts developed in phase equilibrium apply to reacting species as well. Thus, we will be talking about fugacity, chemical potential, and the Gibbs energy.
In this chapter, you will learn to:
1. Calculate the standard enthalpy and Gibbs free energy of reaction from tabulated values.
2. Calculate the equilibrium constant of a reaction.
3. Perform energy and material balances in reacting systems.
14.1 Stoichiometry
For the purposes of thermodynamic calculations, a chemical reaction represents a process in which, reactants, on the left-hand side of the reaction equation, are converted into products on the right-hand side. For example, for the formation of ammonia by reaction between nitrogen and hydrogen we write,
The stoichiometric coefficients that appear in the above equation ensure that the reaction is balanced. We will represent the stoichiometric coefficients of species i by νi and will adopt the convention by which, the stoichiometric coefficients of the reactants are negative, and of the products positive. For the ammonia reaction,
Stoichiometric coefficients represent the ratios by which reactant and product species participate in the chemical reaction, and may be fractional, as in the above example. Since ratios are preserved if all stoichiometric coefficients are multiplied by the same number, the stoichiometry of a chemical reaction can be represented in many equivalent ways. It is, important, therefore, to clearly specify the stoichiometry that is adopted in a particular calculation and use it consistently throughout. The sum of the stoichiometric coefficients,
is the change in the total number of moles when the reaction proceeds from left to right according to the indicated stoichiometry. For the ammonia example, ν = − 3/2 − 1/2+1 = −1, i.e., for each mole of ammonia produced there is a net decrease in the total number of moles by 1 mole.
When reactants are converted into products the moles of all species change but these changes are not independent of each other because they are interrelated through stoichiometry. For each 3/2 moles of hydrogen reacted, we have 1/2 moles of nitrogen consumed, and 1 mole of ammonia produced. If δnH2 moles of hydrogen are consumed, then
These results can be combined into a simpler relationship,1
1. Keep in mind that δnH2 and δnN2 are negative (consumed) while δnNH3 is positive.
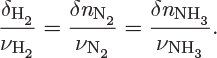
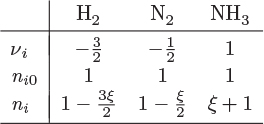
The common value of the ratio δni/νi is called extent of reaction. For a general reaction with any number of species, the reaction extent ξ is defined as
where ni − ni0 = δni is the change in the moles of species i by reaction from its initial number ni0. Solving for ni, the moles of species i after reaction is
The total number of moles is calculated by summing this equation over all species:
where n0 and n are the total moles before and after the reaction, and ν is the sum of the stoichiometric coefficients, defined in eq. (14.2). Finally, the mole fraction of species i after the reaction is
These equations demonstrate the usefulness of the extent of reaction. While the number of moles of all species changes during reaction, these changes are interrelated through a common variable, the extent of reaction. If the extent of reaction is known, all compositions can be calculated. The extent of reaction is a measure of how far the reaction has proceeded. If it is positive, it indicates that the reaction has advanced from left to right; if negative, it indicates that the reaction has advanced from right to left. Although we will be referring to the species on the left as “reactants” and those on the right as “products,” these terms should be understood to be by convention. The actual direction of the chemical reaction would be indicated by the sign of the reaction extent.
14.2 Standard Enthalpy of Reaction
A chemical reaction that proceeds to completion is a process whose initial state consists of all reactants and its final state of all products. This process is accompanied by a change in enthalpy, which is given by the difference between products and reactants:
ΔHrxn = Hproducts − Hreactants.
The precise value of this difference depends on various process details such as the temperature of reactants, whether reactants are mixed before entering the reactor or fed as pure components, whether the reaction product is delivered as a mixture or is separated into its pure components, etc. To avoid such ambiguities and to facilitate tabulations of reaction properties, we adopt a standard state for each component in the reaction and report all reaction properties based on these states. The following standard states are in use:
Standard state for gases (g): It is defined as the pure substance in the ideal-gas state at 1 bar.
Standard state for liquids (l): It is defined as the pure substance in the liquid phase at 1 bar.
Standard state for solids (s): It is defined as the pure substance in the solid phase at 1 bar.2
2. This standard state is sometimes denoted by (c) for crystalline.
Standard state for aqueous solutes (aq): The standard state of a dissolved solute is defined as a solution at 1 bar that obeys Henry’s law at concentration of unit molality, that is, 1 mol of solute per kg of solvent.
The standard state specifies the pressure (always 1 bar) and purity of component. With the exception of the standard state for aqueous solutes, components are taken to be pure. Temperature is not specified but is fixed by the user according to the problem at hand. Since pressure and composition (purity) are fixed, all properties of the standard state are functions of temperature only.
Standard enthalpies of reaction are tabulated for the formation reaction of a species. The formation reaction is a balanced chemical equation that produces one mole of the species in its standard state from the pure constituent elements, also at their standard states.3 By convention, the standard enthalpy of pure elements is zero. Tabulated values of the standard enthalpy of formation at 25 °C are available for a large number of components in various handbooks (selected values are given in Appendix C.) These values are accompanied by an indication of the standard state to which the reported value refers.
3. The stoichiometry of the formation reaction is fixed by the requirement that the reaction produces one mole of the species. Accordingly, the species appears on the product side with stoichiometric coefficient νi = +1.
The enthalpy of formation allows the calculation of the standard enthalpy of any reaction. For the reaction
ν1A + ν2B + ... → νiC + νi+1D + ...
it is calculated as the algebraic sum of the standard enthalpies of formation of all species:
where ΔH° is the standard enthalpy of the reaction, and ![]() is the standard formation enthalpy of species i. Since the coefficients of the reactants are negative, this is the difference between the formation enthalpies of reactants and products. The reaction is exothermic if ΔH° < 0; in this case the enthalpy of the products is lower than that of the reactants and the difference is released as heat. If ΔH° > 0, the reaction is endothermic and requires heat to proceed as written.
is the standard formation enthalpy of species i. Since the coefficients of the reactants are negative, this is the difference between the formation enthalpies of reactants and products. The reaction is exothermic if ΔH° < 0; in this case the enthalpy of the products is lower than that of the reactants and the difference is released as heat. If ΔH° > 0, the reaction is endothermic and requires heat to proceed as written.
Note
Standard Enthalpy of Reaction
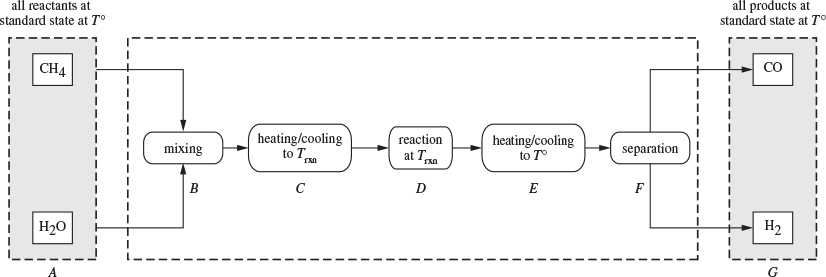
The standard enthalpy of reaction should be understood as a calculation between two very specific states, that of the pure reactants before reactions, and the pure products after reaction. The calculation can be visualized as a process, as shown schematically in Figure 14-1 for the methane reforming reaction. The pure reactants, methane and water in the ideal-gas state at 25 °C and 1 bar, are mixed, possibly compressed, and heated to reaction temperature. The products are cooled and separated to be delivered as pure gases at 25 °C, 1 bar. The standard enthalpy corresponds to the difference between states A and G. Since we are dealing with a state function, the enthalpy of reaction depends only on the end states but is independent of the internal details of the process.
Figure 14-1: Path for the calculation of standard enthalpy of reaction.
Effect of Temperature on Enthalpy of Reaction
As we have seen, the standard enthalpy of any reaction at 25 °C may be calculated from tabulated values of the enthalpy of formation. If the enthalpy is needed at a different temperature, it can be easily calculated from its value at 25 °C. The calculation is done according to the following path:
1. Begin with all reactants at their standard state at T and calculate the enthalpy change to bring each reactant to its standard state at 25 °C (ΔH1).
2. Calculate the standard enthalpy of reaction at 25 °C (![]() ). This calculation delivers the products in their standard state at 25 °C.
). This calculation delivers the products in their standard state at 25 °C.
3. Calculate the enthalpy change to bring the products from their standard state at 25 °C to their standard state at temperature T (ΔH3).
The total change is
The enthalpy change for step 1 is4
4. To obtain the result in the far right, change the order of the limits in ΔH1. This brings a minus sign out which we use to write −|νi| = νi, since νi for the reactants is negative.

where ![]() is the heat capacity of species i in its standard state, |νi| is the absolute value of its stoichiometric coefficient, and the summation runs only through the reactants. The enthalpy change for the third step is given by a similar expression,
is the heat capacity of species i in its standard state, |νi| is the absolute value of its stoichiometric coefficient, and the summation runs only through the reactants. The enthalpy change for the third step is given by a similar expression,
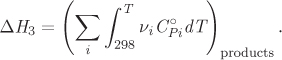
Combining these expressions the standard enthalpy of reaction at temperature T is
where we exchanged the order of the integral and the summation. To write the result in simpler form, we define the heat capacity difference between reactants and products,
Using this definition, we obtain the final result in the form
In summary, the only additional step in the calculation of the standard heat of reaction at temperature T is the integration of ![]() from 298 K (the temperature of tabulated formation standard enthalpies) to T. The superscript ° indicates that all heat capacities are those of the standard state. For example, if the standard state is notated as (g), the ideal-gas heat capacity must be used, regardless of whether the real state under the conditions of the reaction is indeed an ideal gas or not.
from 298 K (the temperature of tabulated formation standard enthalpies) to T. The superscript ° indicates that all heat capacities are those of the standard state. For example, if the standard state is notated as (g), the ideal-gas heat capacity must be used, regardless of whether the real state under the conditions of the reaction is indeed an ideal gas or not.
14.3 Energy Balances in Reacting Systems
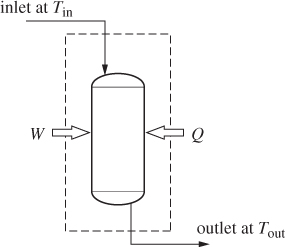
A chemical reactor is a vessel in which a reaction takes place. Industrial reactors come in a variety of designs, shapes and sizes. Liquid-phase reactors are usually stirred tanks whereas gas-phase reactions often take place inside tubular reactors. In general, chemical reactions operate at elevated temperatures to achieve practical rates of conversion. Additional heating/cooling is supplied to account for endothermic or exothermic effects. Chemical reactors may operate in batch mode (all chemicals loaded and the reaction is allowed to proceed for a certain time), semi-batch (some chemicals are loaded initially, others are continuously added), or continuous. As with other unit operations considered in previous chapters, the internal details of chemical reactors are not important when performing overall material and energy balances, as long as the inlet and outlet states are specified. For the purposes of illustration we will consider a flow reactor, as in Figure 14-2.
Figure 14-2: Setup for energy balance of reactor.
The steady-state energy balance around the reactor is
Unless pumps, stirrers, or other mechanical devices are part of the reactor, the shaft work is zero. Typically, a reactor will exchange heat with the surroundings but it is also possible that operation may be adiabatic. The inlet stream contains the reactants, not necessarily in stoichiometric form, and possibly other species that do not participate in the reaction.5 The outlet contains the products plus any leftover reactants. The energy balance under these conditions is
5. The feed may also contain some product species, usually in small amounts that are left in the stream after a separation process.
or,
The last result expresses the energy balance over a period of time δt. For the calculation of the enthalpy change we adopt the following path:
1. Inlet stream is separated to its pure components and each component is brought to its standard state at T0 = 25 °C.
2. Reaction progresses to extent ξ at T0 to produce all species at their standard state at the same temperature.
3. The species after the reaction are mixed and brought to the pressure and temperature of the outlet.
This procedure can be applied to any reacting system to obtain the enthalpy change. A general expression cannot be written for all cases because the details of the process (phase of streams, enthalpy of mixing) can vary between cases. A simple result will be given here under the following simplifying assumptions: (i) neglect all mixing effects on enthalpy during mixing and separation of components, and (ii) assume that no phase transitions take place during the heating/cooling steps between T0 and the temperature of the inlet and outlet streams. With these assumptions the enthalpy change is
Here, ![]() (T0) is the standard heat of reaction at T0, ni are the moles of species i in the outlet stream, ni0 are the moles of species i in the inlet, and CPi is its heat capacity. Notice that the moles in the inlet, the moles in the outlet, and the extent of reaction are interrelated by stoichiometry:
(T0) is the standard heat of reaction at T0, ni are the moles of species i in the outlet stream, ni0 are the moles of species i in the inlet, and CPi is its heat capacity. Notice that the moles in the inlet, the moles in the outlet, and the extent of reaction are interrelated by stoichiometry:
The general procedure for the calculation is to first obtain the mole balance through stoichiometry, and then to calculate the energy balance via eqs. (14.12) and (14.13). If the simplifying assumptions are not valid, the enthalpy must be calculated by applying steps 1 to 3 of the calculation path to the inlet and outlet streams.
14.4 Activity
Calculations of chemical equilibrium, which will be the topic of the next section, are facilitated through the introduction of the activity, a property closely related to fugacity and chemical potential. The activity of a component i in mixture is defined as the ratio of its fugacity over the fugacity of the same component at its standard state:
Activity is dimensionless fugacity, normalized by the fugacity at the standard state. An immediate consequence of the definition of activity is its relationship to the chemical potential. First, recall that the standard state, which was introduced in Section 14.2, is at the same temperature as the state of interest. We now return to eq. (10.18), which relates fugacities and chemical potentials between two states at the same temperature:

We apply this equation with B referring to the state of interest and A the standard state. The result is
Solving for the chemical potential we obtain the desired relationship:
If the activity is known, the chemical potential can be immediately calculated, and vice versa. As we will see with examples, the definition of the standard states provides all the necessary information for the calculation of the activity.
Note
Activity and Chemical Potential
Equation (14.16) is very similar in form to eq. (10.12) for the chemical potential of component in ideal-gas mixture,
and eq. (12.15) for the chemical potential in ideal solution,
In both equations the dependence of the chemical potential on the mol fraction of component i is contained in the term RT ln xi. Compare this with eq. 14.16, which contains the term RT ln ai. In light of this observation, we view activity as the effective concentration of a component in a mixture, in the sense that when it is used in eq. (10.12) or (12.15) in place of xi it returns the chemical potential of the component. In nonideal systems, the activity of a component depends not only on the mol fraction of the component of interest, but also on the composition of the entire mixture. This dependence will become more clear in the following section where we develop expressions for the activity for different standard states.
Activity of Gas
The standard state for gases, denoted by (g), is specified as the pure gas in the ideal-gas state, at the temperature of the system and at P° = 1 bar. Accordingly, the fugacity is calculated using the ideal-gas relation ![]() . The fugacities at the actual and at the standard state are
. The fugacities at the actual and at the standard state are
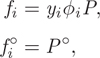
and the corresponding activity is
In general, the activity of gas components will require the calculation of the fugacity coefficient using the methods discussed in Chapter 10. If the ideal-gas approximation is applicable, then we may set ϕi = 1, and in this case the activity reduces to ai = yiP/P°.
Working with P°
It may be tempting to set P° = 1 in the above equation and write ai = yiϕiP. Don’t do it! This substitution produces an equation that is marginally simpler, but dimensionally incorrect, as the left-hand side is dimensionless whereas the right-hand side has units of pressure. Such equation is valid only if special units are used (bar, in this case) and this can lead to confusion and errors in the calculation. To avoid these problems, retain P° in your formulas until final numerical substitution. This recommendation applies to all formulas that involve P° or other constants of the reference state.
Activity of Liquid
To obtain an equation for the activity based on the liquid standard state, we use eq. (12.16) for the fugacity of component in solution,
to write
where fi,pure = fi,pure(P, T) is the fugacity of the pure species i and ![]() is the fugacity of the pure liquid at the standard state. The actual and the standard state are both at the same temperature but different pressures. Accordingly, the ratio of the corresponding fugacities is given by the Poynting factor,
is the fugacity of the pure liquid at the standard state. The actual and the standard state are both at the same temperature but different pressures. Accordingly, the ratio of the corresponding fugacities is given by the Poynting factor,
where Vi is the liquid molar volume of pure component i. Combining these results the activity takes the form
This general equation can be put into simpler form in some special cases: Low pressure: At pressures not much higher than P°, the Poynting correction is negligible and the activity simplifies to
Low pressure, ideal solution. With the additional assumption of ideal solution (γi = 1), the previous result gives
Low pressure, pure liquid. For a pure liquid, γi = 1 and xi = 1, and the activity becomes
Activity of Solute
The fugacity of solute with molality ci is given by eq. (13.19),
where k′H is Henry’s law constant in terms of molality. In this expression we assume that the concentration of solute is low enough that the activity coefficient is unity. The standard state is defined as a solution of molality c° = 1 mol/kg “that obeys Henry’s law.” This specification means that the fugacity in the standard state is
Combining these results we obtain the activity as
where ci is the molality in the solution and c° = 1 mol/kg is the standard molality. In other words, the activity is numerically equal to the concentration of the solute expressed in mol per kg of solvent. It is recommended to retain the term c° in the formulas until final substitution in order to avoid potential confusion with units.
Activity of Solid
Solids generally do not mix intimately with other substances and even when they are part of a multicomponent system, they remain essentially pure. This is certainly true in the case of mechanical mixtures of bulk or powdered solids, for example, sugar and sodium chloride mixed together. There are instances in which solid components intermix to form a solid solution, as in alloys. In most cases of interest, however, solid components may be treated as fully immiscible, and therefore pure. Under these conditions the fugacity of solid in a mixture is equal to the fugacity of the pure solid at the same temperature and pressure:
fi (xi, T, P) = fipure (T, P).
The fugacity at the standard state is
The two fugacities are related through the Poynting factor,6
6. Solids are incompressible; therefore, the Poynting factor can be used to relate the fugacity at different pressures on the same isotherm.
where Vi is the molar volume of the solid. Using the above results, the activity of the solid is
Unless pressure is substantially higher than 1 bar, the Poynting factor can be neglected and the activity simplifies to
This result suffices for most practical situations.
Note
Activity and Standard State
The standard state should be viewed as a set of precise and unambiguous instructions on how to calculate the absolute properties of a species. For the activity, these instructions are summarized below:
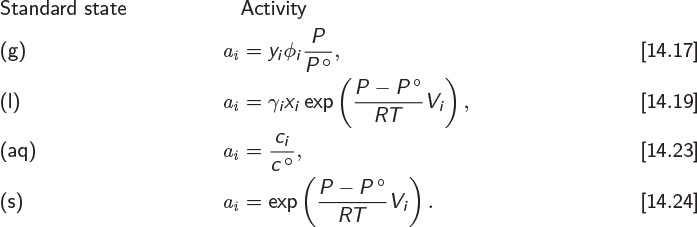
When these instructions are put into words, they often involve states that are not real but hypothetical. This is of no consequence because the sole purpose of the standard state is to specify the mathematical formulas for the calculation of absolute properties. For example, eq. (14.17) reads: “The activity of a component in a gas mixture is equal to its fugacity in the mixture, divided by the standard pressure.” This is more conventionally expressed by saying that the denominator is “the activity of pure component in the ideal-gas state at pressure P°”. This wordier expression, which makes reference to the standard state, has the advantage that it provides instructions for the calculation of any property, not just activity.
14.5 Equilibrium Constant
In principle all reactions are reversible: just as reactants have a tendency to combine and form products, products have the tendency to recombine and form the initial reactants. At equilibrium, the forward rate is balanced by the reverse rate, all net conversion ceases, and the composition of the system becomes constant in time. Suppose we load a closed reactor with a mixture that contains arbitrary amounts of the reactant and product species, and initiate the reaction while maintaining constant temperature and pressure. If we monitor the progress to equilibrium through the extent of reaction, we will observe it to increase in the positive or negative direction, indicating that the reaction progresses in the forward or reverse direction, until equilibrium is reached. Since temperature and pressure are held constant, the equilibrium state corresponds to conditions that minimize the Gibbs free energy. This condition allows us to obtain precise mathematical relationships for the equilibrium constant of the reaction. As an example, consider the ammonia synthesis reaction,
and suppose that it has reached equilibrium. We perturb the reaction by causing it to proceed by a small δξ to right. This results to the consumption of 3δξ/2 moles of hydrogen, δξ/2 moles of nitrogen, and the production of δξ moles of ammonia. The corresponding change in the Gibbs energy of the mixture is
Before the perturbation the reaction was at equilibrium, that is, the state was located at the bottom of the Gibbs free energy, as shown in Figure 14-3. The small perturbation moves the system along the tangent line at the minimum, leaving the Gibbs free energy unchanged, meaning ΔG = 0, or
Figure 14-3: Determination of reaction equilibrium.
For a reaction with general stoichiometric coefficients νi the corresponding result is
The chemical potentials in this expression are given by eq. (14.16). With this substitution, the result is
where ![]() is the chemical potential of species i in its standard state and ai is its activity based on that standard state. The first term on the right-hand side is the standard Gibbs energy of the reaction at temperature T:
is the chemical potential of species i in its standard state and ai is its activity based on that standard state. The first term on the right-hand side is the standard Gibbs energy of the reaction at temperature T:
By the properties of logarithms, the summation of the logarithms in eq. (14.27) is the log of the product of the activities, each raised to the corresponding stoichiometric coefficient:
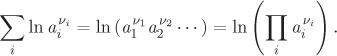
Using these results we rewrite eq. (14.27) in the form
We now define the equilibrium constant of chemical reaction as
Combining this definition with eq. (14.29) we obtain a second expression for the equilibrium constant:
Equation (14.30) gives the equilibrium constant in terms of the standard Gibbs energy of the reaction at temperature T. As we will see, this equation allows us to obtain the value of the equilibrium constant from tabulated thermodynamic properties. Equation (14.31) relates the equilibrium constant to the activities of the participating species and ultimately to the equilibrium composition, since activity depends on the composition of the reacting mixture. This equation allows us to obtain the equilibrium from experimental measurements of the equilibrium composition, or to predict that composition, if the equilibrium constant is known.
The product of activities is in fact a ratio, with the reaction products appearing in the numerator (their stoichiometric coefficients are positive), and the reactants in the denominator. For example, for the ammonia reaction this term takes the form

Since activity is related to concentration, eq. (14.31) can be viewed as a relationship between composition at equilibrium, and standard Gibbs free energy of reaction.
Tip
Equilibrium Constant and Stoichiometry
According to eq. (14.31), the numerical value of the equilibrium constant depends on the stoichiometric coefficients. A simple relationship exists between the values of the equilibrium constant obtained with different stoichiometric coefficients. If the stoichiometric coefficients νi are multiplied by a factor λ, then the new equilibrium constant is
where K is the equilibrium constant with stoichiometric coefficients νi and K′ is the constant for stoichiometric coefficients ν′i = λνi. This follows easily from eq. (14.31).
Equilibrium Constant and Temperature
The equilibrium constant at 25 °C is calculated directly from tabulations of the Gibbs free energy of formation. Once this value is known, the equilibrium constant can be calculated at any other temperature. To obtain the equation that governs the variation of the equilibrium constant with temperature, the starting point is eq. (10.5), which provides the relationship between the Gibbs free energy, temperature, pressure, and composition:

To apply this equation to ΔG°, we replace enthalpy on the right-hand side with ΔH°. Noting that the standard Gibbs free energy is a function of temperature only, the right-hand side reduces to the temperature term alone:
Using ΔG°/RT = − ln K, we obtain
This is known as the van’t Hoff equation and gives the variation of the equilibrium constant with temperature. If K is known at a temperature T0, it is obtained at any other temperature by integration:
The integration is simplified if the standard enthalpy is assumed constant:
and the equilibrium constant at temperature T from eq. (14.34) becomes
Since small errors in ΔH° are amplified inside the exponential term, the proper procedure is to use eq. (14.8) to express ΔH° in terms of T, then integrate the resulting expression in terms of temperature.
Other Forms of the Equilibrium Constant
The fundamental relationship between equilibrium constant and composition is via the product of the activities of species raised to the corresponding stoichiometric coefficients:
If reactants and products are in the gas phase, all activities are given by
where yi is the mole fraction and Pi = yiP is the partial pressure of component i. The equilibrium constant in eq. (14.37) may then be expressed as
where
and ν is the sum of stoichiometric coefficients. Similarly, if all species are aqueous solutes, the equilibrium constant is
K = Kc (c°)−ν
with
The expressions, Ky, KP, Kc, all have the mathematical form of the equilibrium constant in eq. (14.37), with activity replaced by yi, Pi, or ci and are often called “equilibrium constants.” As we see here, they are indeed related to the equilibrium constant. However, the term equilibrium constant should be strictly reserved for the expression that gives the equilibrium constant in terms of activities. This constant is dimensionless and a function of temperature only. The derivative forms, Ky, KP, may have units, and are functions of pressure, if ν is not zero. These expressions may be used in calculations but should not be confused with the thermodynamic quantity that we call equilibrium constant.
14.6 Composition at Equilibrium
A common problem is to calculate the composition of a reacting mixture at equilibrium at a specified temperature. To do this, it is always easier if we start with the stoichiometric table of the reaction. The first step is to express all the concentrations in terms of the extent of reaction, ξ. We then calculate the activity of each species and finally, we equate the product of activities to the equilibrium constant. This produces an equation where the only unknown is ξ. Once the extent of reaction is known, all the mole fractions can be computed from the stoichiometric table. If the temperature of the calculation is at 25 °C, the equilibrium constant is obtained directly from tabulated values of the standard Gibbs free energy of formation. To calculate the equilibrium constant at another temperature, an additional step is neeed to obtain the heat of reaction and the Gibbs energy at the desired temperature. This procedure is demonstrated with examples below.
14.7 Reaction and Phase Equilibrium
The equilibrium constant in eq. (14.31) represents a relationship between the fugacities of the participating species. As such, it is an additional constraint that reduces the degrees of freedom of a thermodynamic system. Specifically, the degrees of freedom are reduced by one for each reaction that takes place. We determine the degrees of freedom by counting unknowns and available equations. In a system with N components distributed among π phases, the unknowns are N − 1 mole fractions per phase7 plus pressure and temperature. This makes for (N − 1)π + 2 unknowns. The available equations are, π − 1 phase equilibrium conditions per component, plus one equilibrium condition per reaction. This makes for N(π − 1) + R equations. The degrees of freedom is the difference between the number of unknowns and the number equations that are available to solve for them:
7. Since the sum of the mol fractions add up to 1, we only have N − 1 unknown fractions in each phase.
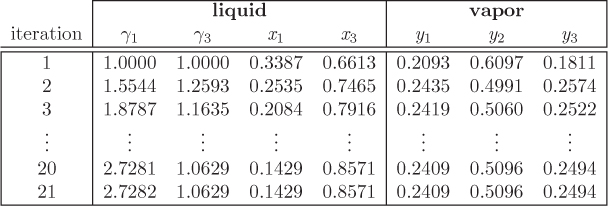
This equation gives the number of variables that we must specify in order to fix the state of the system. In the absence of reactions (R = 0) this reverts to the Gibbs’s phase rule obtained in Chapter 10. The presence of reactions reduces the degrees of freedom. Suppose that nitrogen and hydrogen react to form ammonia in the gas phase. In this case we have three components (N2, H2, and NH3), one phase and one reaction, which leads to three degrees of freedom. To fix the equilibrium state of this system we must specify three intensive variables, for example, pressure, temperature, and mol fraction of one component; or we could specify the mole fraction of two components and temperature or pressure (but not both). If a system of three reactants forms a two-phase system, then the phase equilibrium conditions decrease the degrees of freedom to 2. In this case, fixing the pressure and temperature are sufficient to fully specify the state. The example below demonstrates the calculation of chemical equilibrium in the presence of two phases, in this case a liquid and a vapor.
Note
Phase Equilibrium as a Chemical Reaction
The equilibrium conditions in the previous example (eqs. [A]–[E] in Example 14.16) express relationships between mole fractions. In the case of chemical equilibrium, this is a relationship between the mol fractions of products and reactants. In the case of phase equilibrium, it is a relationship between the mol fraction of the same component in two different phases. The similarity between phase and chemical equilibrium can be made more clear by treating the transfer of a species between phases as a chemical reaction. For example, the evaporation-condensation of water can be represented as
H2O(g) = H2O(l),
with equilibrium constant

where we have used eq. (14.19) for the activity of the liquid and eq. (14.17) for the activity of the vapor and applied the low-pressure approximations to obtain the result on the far right. For the equilibrium constant of this process we also have K = exp(−ΔG° /RT), with ΔG° given in eq. (14.26), which leads to
Combining these results we obtain the following relationship between the mol fractions in the two phases:
We recognize this result as the standard condition for phase equilibrium (to see this more clearly write it as ywP = xw γwPsat) but we may also view it as the equilibrium constant for the equilibrium between phases. That is, whether we treat the problem as a phase equilibrium process, or a reaction equilibrium process, we obtain the same answer. The “reaction” here involves not a change in the chemical nature of the species but a change of the state of “aggregation,” from a vapor into a liquid. This relationship between phase and chemical equilibrium should not come as a surprise. In both cases we are applying the same principle, namely that the equilibrium state at fixed temperature and pressure is the state that minimizes the Gibbs free energy of the entire system. This principle leads to the equality of fugacities in phase equilibrium, and in the introduction of the equilibrium constant in reaction equilibrium.
14.8 Reaction Equilibrium Involving Solids
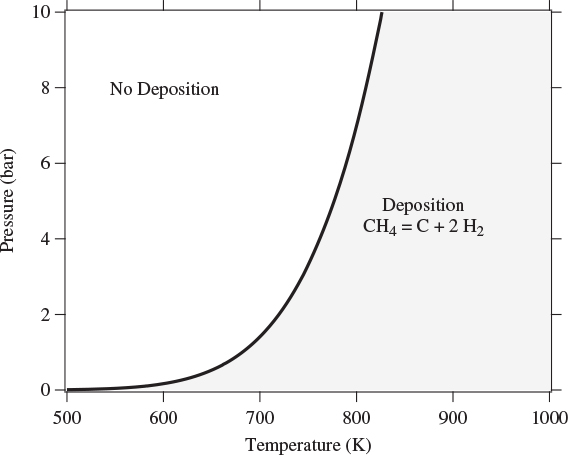
When a gas-phase or liquid-phase system involves a solid as a reactant or product, we have a multi-phase system but this calculation is simplified enormously by the fact that solid phases can be treated as pure. If the reaction involves a gas or liquid phase, only the moles of those species that are present in the gas or liquid participate in the equation that determines the equilibrium of the system. The fact that the activity of solids does not depend on the amount of the solid also implies that it is possible for equilibrium to fully consume a solid reactant. This is not possible with reactions that do not involve solids unless the equilibrium is shifted very strongly towards the products. The calculation of chemical equilibrium is demonstrated with the example below.
14.9 Multiple Reactions
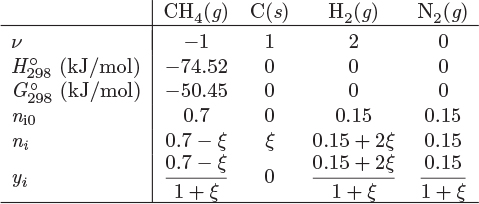
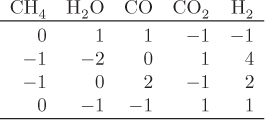
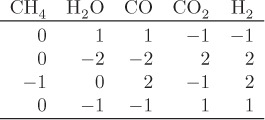
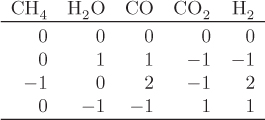
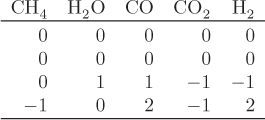
When multiple reactions take place, each reaction provides an equilibrium condition that may be used in the calculation of the final composition. However, it is not always obvious how many independent reactions are present. For example, in the reforming of methane by steam we may write the following four reactions that produce a mixture of carbon monoxide, carbon dioxide and hydrogen:

Notice that reaction R4 can be obtained by subtracting reaction R1 from R2. This means that at least one reaction in this system is not independent. A systematic method to determine the number of independent reactions is to begin with the matrix of stoichiometric coefficients of all components that appear in these reactions. We then proceed to combine rows by linear transformations with the goal of eliminating stoichiometric coefficients by turning them into zeros, one coefficient at a time. When no more eliminations are possible, we count the number of rows that contain nonzero coefficients. This gives the number of independent reactions. The process is demonstrated in the example that follows.
14.10 Summary
As with all equilibrium, the final state in a reacting mixture is such that the Gibbs free energy is at a minimum. In this respect, chemical equilibrium requires no new theories beyond those developed in Chapter 10. However, the fact that the chemical nature of species changes during the reaction requires the introduction of consistent reference states. This is done by the adoption of the standard states for gases (g), liquids (l), solids (s) and aqueous solutes (aq). The specification of the standard state must be understood as a set of rules for the unambiguous calculation of three main properties of a reacting system: the activity of components, the enthalpy of reaction, and the Gibbs free energy of the reaction. Although activity was introduced in the context of reactions, its usefulness is general and can be traced to eq. (14.16)
which shows that activity allows us to obtain the chemical potential of a component in any mixture, reacting or not. In this textbook we did not introduce activity until the discussion of reactions, mainly because we have chosen fugacity, rather than chemical potential, as the primary property in phase equilibrium.
Most problems in chemical equilibrium are solved using the two fundamental equations for the equilibrium constant:
and
The first equation expresses the equilibrium constant in terms of quantities that can be obtained from tabulated values (formation enthalpy and Gibbs free energy, heat capacities). The second equation expresses the equilibrium constant in terms of the activity of species, and ultimately, in terms of mol fractions. We must remember that activities and formation properties of each species must refer to the same standard state.
If multiple equilibria take place, all equilibrium conditions must be satisfied. This is true whether we are dealing with multiple reactions, or with simultaneous reaction and phase equilibrium. The most important consideration in these types of problems is the determination of the number of independent equilibrium conditions that can be written. Specifically, we must write one equilibrium condition for each independent chemical reaction in addition to any phase equilibria that may be present.
Some attention must be paid if one of the reactants is in the solid phase. Equilibrium calculations are simplified in this case because the activity of the solid does not appear in the equilibrium constant (recall from eq. [14.24] that activity of the solid is practically 1 unless pressure is high). This creates the interesting situation that a reversible reaction involving a solid may proceed to completion. This is very similar to the familiar dissolution of solids in water and other solvents. If an amount of a soluble solid (e.g., salt or sugar) is mixed with a liquid, some of the solid dissolves until the solubility limit is reached, at which point we have equilibrium between the undissolved and dissolved fractions of the solid. If, however, the amount of solid is below the solubility limit, the entire amount dissolves. This is an example of a reversible reaction that goes to completion. Such process is possible only if it involves a solid, because the concentration of the solid does not appear in the equilibrium constant. With components in any other phase, the mol fraction of a reactant appears in the denominator of the equilibrium constant, and this prevents a reversible reaction from reaching completion unless the equilibrium constant is a very large number.
14.11 Problems
Problem 14.1: Hydrogen peroxide reacts with sodium thiosulfate according to the reaction,
Na2S2O3 + αH2O2 → βNa2S3O6 + γNa2SO4 + δH2O.
a) Determine the stoichiometric coefficients.
b) A reactor is initially loaded with an aqueous solution that contains 10% hydrogen peroxide (by mole), 10% sodium thiosulfate, and the rest is water. Assuming the reaction goes to completion, what is the composition (mole fractions) of the final solution? The reaction takes place at 25 °C.
c) Determine the amount of heat that is exchanged with the surroundings.
Problem 14.2: A reactor is loaded with equal amounts of hydrogen, nitrogen, ammonia, and helium. If the reaction is
3H2 + N2 = 2NH3,
do the following:
a) Calculate the minimum and maximum values of ξ.
b) Calculate all mole fractions when the mole fraction of helium is 0.3. What is the conversion of hydrogen?
c) Calculate all mole fractions when the mole fraction of helium is 0.215. What is the conversion of hydrogen?
Problem 14.3: Calculate the adiabatic flame temperature of methane in 20% excess air at 1 bar. Both methane and air are initially at 25 °C, 1 bar.
Additional data. Assume that the reaction is complete and that products are carbon dioxide and water.
The ideal-gas CP’s (in J/mol K) of the reactants and products as a function of temperature are given below (T must be in K):

Note: First calculate the temperature assuming the Cp’s to be constant and equal to their value at 25 °C; then repeat using the temperature-dependent heat capacities given above.
Problem 14.4: a) Calculate the standard heat of reaction for the complete combustion of methane at 800 °C.
b) Calculate the amount of heat that is released in a furnace that burns methane in 20% excess air, if the furnace temperature is 800 °C and the pressure is 2 bar. Assume that the inlet gases are already at 800 °C as they enter the furnace.
c) Repeat part b, but this time the inlet gases are at 40 °C, 2 bar.
Additional data. Assume that the reaction is complete and that products are carbon dioxide and water.
The heat capacities of the gases are given in Problem 14.3.
Problem 14.5: a) Determine the heat of vaporization of benzene at 25 °C using tabulated heats of formation.
b) Determine Henry’s law constant of ammonia in water at 25 °C from the tabulated (g) and (aq) Gibbs energies of formation.
c) Generate an entry for the Gibbs energy of formation of CO based on the standard state for aqueous solutes (aq).
d) N2O gas is bubbled through water at 12 bar, 10 °C. Calculate the activity of N2O (aq) and of water (l) in the liquid based on the indicated standard states.
Problem 14.6: The standard enthalpy of formation of water in the gas standard state is ![]() , 818 J/mol. Use this value and information from the steam tables to obtain the enthalpy of formation in the liquid standard state and compare with the tabulated value
, 818 J/mol. Use this value and information from the steam tables to obtain the enthalpy of formation in the liquid standard state and compare with the tabulated value ![]() , 830 J/mol.
, 830 J/mol.
Problem 14.7: The equilibrium constant of the gas-phase reaction 2A(g) + 3B(g) = 2C(g) is experimentally found to be
K = aeb/T,
with b = 1200 K, a = 10−5.
a) Calculate ΔG°, ΔH°, and ΔS°, at 25 °C. Is the reaction exothermic, or endothermic?
b) A constant-volume reactor is loaded with an equimolar mixture of A, B, and C at 12 bar. The reaction is allowed to take place at constant temperature and when equilibrium is reached, the pressure in the reactor is 15 bar. Unfortunately, due to a malfunction in the thermometer, the actual temperature is not known. What is the temperature of the reactor?
Additional data. All three gases may be assumed ideal.
Problem 14.8: Ammonia is produced by the gas-phase synthesis
3H2 + N2 = 2NH3.
The reactor in your plant can operate from 1 to 20 bar, and from 25 to 1000 °C. What conditions would you choose for maximum yield?
Problem 14.9: a) Calculate the equilibrium constant at 1000 °C for ammonia synthesis in the stoichiometry written below:
3H2 + N2 = 2NH3.
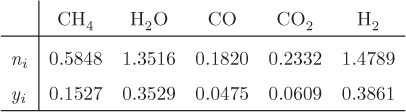
b) An equimolar mixture of the three species enters a reactor at 1000 °C, 10 bar. Determine the composition at equilibrium, if temperature and pressure remain constant.
c) Determine the amount of heat that must be added to, or removed from the reactor to maintain the temperature at 1000 °C. Report the result in J per mol of hydrogen in the feed.
Additional data. The ideal-gas CP (in J/mol K) of hydrogen, nitrogen, and ammonia are 29.52, 30.58, and 45.4, respectively.
Problem 14.10: You are asked to carry out the gas-phase hydrogenation of benzene to cyclohexane.
a) What conditions of pressure and temperature (high/low) would result in maximum conversion?
b) Determine the equilibrium composition of a mixture that contains 30% benzene (by mole) and 70% hydrogen at 200 °C, 5 bar.
Problem 14.11: Benzene is formed from the gas-phase dehydrogenation of cyclohexane according to the reaction:
C6H12(g) = C6H6(g) + 3H2(g).
a) Calculate the standard heat of reaction and the equilibrium constant at 25 °C.
b) A stream that contains 50% by mole cyclohexane in nitrogen is fed to a reactor that operates a constant pressure and temperature. The reactor pressure is 5 bar and the desired conversion of cyclohexane is 85%. Determine the amount of heat per mol in the feed that must be added or removed from the reactor in order to maintain the temperature constant.
c) Determine the composition of all species at the exit of the reactor.
d) Assuming the reaction reaches equilibrium, determine the reactor temperature.
e) It has been suggested that conversion could be increased by operating at different pressure. You may vary the reactor pressure between 1 and 10 bar. If temperature and inlet conditions remain the same, at what pressure would you operate the reactor? Explain your answer.
f) List all of your assumptions and explain where each assumption was used.
Problem 14.12: Isopropyl alcohol (IPA) is dehydrogenated to produce propionaldehylde (PA) according to the reaction
C3H8O(g) = C3H6O(g) + H2(g).
The equilibrium constant for this reaction is
K(T) = e−29.5+6673K/T,
with T in K.
a) Is the reaction endothermic, or exothermic?
b) A reactor is fed with a mixture of IPA and nitrogen that contains 70% IPA by mol. The reaction takes place at T = 500 K, and P = 3 bar. Determine the conversion of IPA if the reaction reaches equilibrium.
Problem 14.13: Acetaldehyde can be produced from the dehydrogenenation of ethanol according to the following reaction:
CH3CH2OH(g) = CH3CHO(g) + H2(g).
Additional data. The ideal-gas heat capacities of the pure species in this reaction are: ethanol: 118 J/mole K; acetaldehyde: 90 J/mole K; hydrogen: 30 J/mole K.
a) Calculate the equilibrium constant at 25 °C.
b) Calculate the heat of reaction at 25 °C. Is the reaction exothermic or endothermic?
c) Assuming that the heat of reaction does not change much with temperature, calculate the equilibrium constant at 550 °C.
d) Is it an acceptable assumption that the heat of reaction does not change much with temperature? (Answers without justification do not count.)
e) The reactor initially contains one mole of ethanol and nothing else. The reaction is run at 550 °C and 2 bar until equilibrium is reached. What is the mole fraction of species at equilibrium?
f) It is desirable to react 98% of the initial amount of ethanol. If the temperature is to remain at 550 °C, at what pressure should you run the reaction?
Problem 14.14: The gas-phase dehydrogenation of propane is carried out according to the reaction
C3H8 (g) = C3H6 (g) + H2 (g).
The reaction takes place in the presence of a catalyst in an isothermal reactor that is maintained at 5 bar.
a) Calculate the equilibrium constant at 25 °C.
b) Calculate the standard enthalpy of reaction at 25 °C. Is the reaction exothermic or endothermic?
c) The reactor feed contains pure propane. If the desired conversion of propane is 95%, at what temperature should you run the reaction? Assume the reaction reaches equilibrium.
d) Due to upstream process modifications, the reactor feed has now changed from pure propane into a mixture that contains 50% nitrogen (by mol). If the reactor pressure remains at 5 bar, how should you adjust the temperature to achieve 95% conversion?
e) Just as you finished adjusting the temperature to handle the propane/nitrogen feed of the previous part, the compressor malfunctions and the reactor pressure drops to 1 bar. How should you adjust the temperature to achieve 95% conversion?
f) Clearly state all the assumptions.
Problem 14.15: The standard Gibbs energy of formation of a substance based on one standard state (s1) may be related to any other standard state (s2) according to the following equation:
ΔG°(s2) − ΔG°(s1) = μ(s2) − μ(s1)
where μ(si) is the chemical potential of the substance at the standard state si (si could be g, l, etc.)
a) Show that
where f(si) is the fugacity of the substance at the standard state si.
b) For CO2, ΔG(g) = 394.6 kJ/mol and ΔG(aq) = 386.5 kJ/mol. Use these data to calculate Henry’s constant for CO2 in water at 25 °C.
c) Calculate the equilibrium constant at 25 °C for the reaction
CO(aq) + H2O(l) = CO2(aq) + H2(aq).
Henry’s constants for CO and H2 in water at 25 °C are 57089 bar and 71673 bar, respectively.
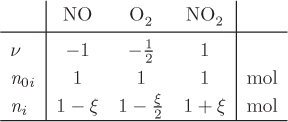
Problem 14.16: A major air pollution problem in combustion is the formation of NO from the reaction between O2 and N2:
N2 + O2 = 2NO.
a) Calculate the equilibrium constant and the heat of reaction at 25 °C for this reaction. Is the reaction exothermic, or endothermic?
b) Determine the effect of pressure and temperature on the amount of NO formed from this reaction. Explain your answer.
c) A high-temperature furnace operates at 5 bar with temperatures in the range 1,000 to 2,000 K by burning methane in 20% excess air. You are concerned that the air in the furnace may produce unacceptable amounts NO. By regulation, the concentration of NO in the gases leaving the furnace may not exceed 500 ppm by mole. At what temperatures can you operate the furnace without violating the regulation?
Note: A concentration of 1 ppm (parts per million) corresponds to mole fraction of 10−6. You may assume that the heat of reaction is independent of temperature.
Problem 14.17: The gas phase reaction oxidation of SO2 to SO3 is carried out at a pressure of 1 bar with 20% excess air in an adiabatic reactor. The reactants enter at 25 °C and equilibrium is obtained at the exit of the reactor.
a) Write the balanced equation for the formation of one mole of sulfur trioxide.
b) What is the heat of reaction of the equation in part (a)?
c) Determine the composition and the temperature of the product stream from the reactor.
The heat capacities of the components are given by the equation
with T in kelvin and with parameters given below:

Problem 14.18: Consider the esterification reaction
CH3COOH(l) + CH3CH2OH(l) = CH3COOCH2CH3(l) + H2O(l).
a) Calculate the equilibrium constant at 25 °C.
b) A reactor is loaded with a solution of acetic acid in ethanol containing 80% acetic acid by mole. The reaction is allowed to proceed to equilibrium at constant temperature of 25 °C. Assuming the components to form an ideal solution, calculate the composition of the equilibrium mixture.
c) Repeat the calculation using activity coefficients calculated from UNIFAC.
Problem 14.19: The water gas shift reaction
CO(g) + H2O(g) = CO2(g) + H2(g),
is used to produce high-purity hydrogen. The reaction is carried out in a 10 m3 reactor that contains a copper catalyst and is operated at 1000 K and 1.5 bar. The equilibrium constant is given by
K(T) = e−5.057+4951.4/T,
where T is in K.
a) Is the reaction exothermic or endothermic?
b) Calculate the value of KP at 1000 K, with P in bar. What are the units of KP?
c) The composition of the reactor feed is 1 mole of CO and 5 moles of steam. Assuming the reaction to reach equilibrium, what is the composition (in terms of mole fraction) of the stream exiting the reactor?
d) After reading your report, your boss points out that for fuel cell applications, the mol fraction of CO must not exceed 5 × 10−3 in order to avoid poisoning of the fuel cell anode. A colleague in your team suggests running the reaction at a different pressure; a young intern suggests running the reaction at a different temperature. Which suggestion do you adopt and why? Determine the new pressure or new temperature (depending on your decision) that meets the CO requirement.
Problem 14.20: Consider the water-gas shift reaction,
CO(g) + H2O(g) = CO2(g) + H2(g).
A reactor initially contains one mole of each of the four species. The temperature is 900 K and the pressure is 1 bar.
a) What is the minimum and maximum possible value of the extent of reaction for this system? What does it mean if the reaction coordinate is negative?
b) Calculate the extent of reaction at equilibrium. What percentage of the initial amount of CO has reacted when equilibrium is achieved?
c) The same reaction now takes place in the presence of 5 moles of nitrogen. (The initial amount of the four reacting species is the same as before). What is the percent conversion of CO at equilibrium? Compare your answer with the result in part (b): is it higher, lower, or the same? Why?
d) Estimate the amount of heat per mole of CO that must be added or removed from the reactor to keep the temperature constant.
e) At what temperature should you run the reaction in order to react 50% of the initial amount of CO?
f) If you don’t want to change the temperature, what else can you do to increase the conversion of CO?
g) State your assumptions.
Problem 14.21: An open bottle in the lab contains crystals of Na2SO4. The temperature is 25 °C, the pressure 1 bar, and the relative humidity 85%. Determine whether the formation of the decahydrate according to the reaction below,
Na2SO4 + 10H2O = Na2SO4 · 10H2O,
can take place under these conditions. What is the minimum relative humidity that will allow the reaction to proceed in the forward direction?
Problem 14.22: A reversible reaction is conducted in a steady-state flow reactor. To improve conversion, a junior member of the design team suggests that you recycle a fraction of the reactor outlet back into the reactor. What is your opinion about this suggestion? Hint: Use the reaction A(g) = B(g) as an example and show that the recycle stream has no effect whatsoever.
Problem 14.23: SO3 is produced by oxidation of SO2 in the presence of air. SO2 is mixed with air so that the molar ratio of SO2 to oxygen is 1:1.2 and is passed through a reactor at 1 bar, 850 K, until equilibrium is established. To improve conversion, SO3 is separated out of the product mixture, while a portion of the other gases (SO2, O2, and N2) is recycled back into the reactor with the rest being used elsewhere in the plant. Assuming that all of the SO3 is obtained at the exit of the separator in pure form (i.e., no oxygen or nitrogen are present), determine the flow rate of the recycle stream (per 100 mol in the feed) that is required to produce an overall conversion of 95% and report the per-pass conversion of the reactor.
Problem 14.24: a) Calculate the solubility of ammonia in water at 25 °C if the partial pressure of ammonia in the gas phase is 2 bar.
b) Calculate Henry’s law constant for ammonia in water at 25 °C.
Additional data:
![]() for NH3(g) = –16450 J/mol,
for NH3(g) = –16450 J/mol,
![]() for NH3(aq) = –26500 J/mol.
for NH3(aq) = –26500 J/mol.