CHAPTER SIX
Cooperative Games
Government and cooperation are in all things the laws of life; anarchy and competition the laws of death.
—John Ruskin, Unto this Last
We must all hang together, or assuredly we will all hang separately.
—Benjamin Franklin, at the signing of the Declaration of Independence
There are two kinds of people: Those who say to God “Thy will be done, ” and those to whom God says, “All right, then, have it your way.”
—C.S. Lewis
6.1 Coalitions and Characteristic Functions
There are n > 1 players numbered 1, 2, …, n. In this chapter, we use the letter n to denote the number of players and N to denote the set of all the players N = {1, 2, …, n}. We consider a game in which the players may choose to cooperate by forming coalitions. A coalition is any subset S ⊂ N, or numbered collection of the players. Since there are 2n possible subsets of N, there are 2n possible coalitions. Coalitions form in order to benefit every member of the coalition so that all members might receive more than they could individually on their own. In this section, we try to determine a fair allocation of the benefits of cooperation among the players to each member of a coalition. A major problem in cooperative game theory is to precisely define what fair means. The definition of fair, of course, determines how the allocations to members of a coalition are made.
First, we need to quantify the benefits of a coalition through the use of a real-valued function, called the characteristic function. The characteristic function of a coalition S ⊂ N is the largest guaranteed payoff to the coalition.
Definition 6.1.1 Let 2N denote the set of all possible coalitions for the players N. If S = {i} is a coalition containing the single member i, we simply denote S by i.
Any function v: 2N → 
satisfying
is a characteristic function (of an n-person cooperative game).
In other words, the only condition placed on a characteristic function is that the benefit of the empty coalition be zero and the benefit of the grand coalition N, consisting of all the players, be at least the sum of the benefits of the individual players if no coalitions form. This means that every one pulling together should do better than each player on his or her own. With that much flexibility, games may have more than one characteristic function. Let’s start with some simple examples.
Example 6.1
) = b|| = 0, and v(N) = b|N| = bn = b ∑i = 1n v(i).}. For simplicity, we are dropping the braces in the notation for any individual coalition.It requires a seller and a buyer to reach a deal. Therefore, we may define the characteristic function as follows:
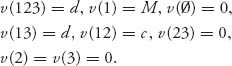
Why? Well, v(123) = d because the car will be sold for d, v(1) = M because the car is worth M to player 1, v(13) = d because player 1 will sell the car to player 3 for d > M, v(12) = c because the car will be sold to player 2 for c > M, and so on. The reader can easily check that v is a characteristic function.
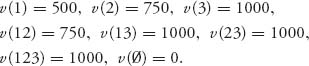
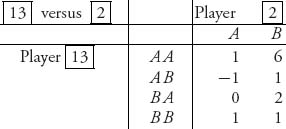
and v(S) = 0 otherwise, we have a simple game that is a model of majority voting. If a coalition contains more than half of the players, it has the majority of votes and is a winning coalition.Example 6.2 In this example, we will construct a characteristic function for a version of the prisoner’s dilemma game in which we assumed that there was no cooperation. Now we will assume that the players may cooperate and negotiate. One form of the prisoner’s dilemma is with the bimatrix
Here, N = {1, 2} and the possible coalitions are 2N = {, 1, 2, 12}. If the players do not form a coalition, they are playing the nonzero sum noncooperative game. Each player can guarantee only that they receive their safety level. For player I that is the value of the zero sum game with matrix 
, which is value(A) = 2. For player II the safety level is the value of the game with matrix 
. Again value(BT) = 2.
Thus, we could define v(1) = v(2) = 2 as the characteristic function for single member coalitions. Now, if the players cooperate and form the coalition S = {12}, can they do better? Figure 6.1 shows what is going on. The parallelogram is the boundary of the set of all possible payoffs to the two players when they use all possible mixed strategies.
The vertices are the pure payoff pairs in the bimatrix. You can see that without cooperation they are each at the lower left vertex point (2, 2). Any point in the parallelogram is attainable with some suitable selection of mixed strategies if the players cooperate. Consequently, the maximum benefit to cooperation for both players results in the payoff pair at vertex point (8, 8), and so we set v(12) = 16 as the maximum sum of the benefits awarded to each player. With v() = 0, the specification is complete.
As an aside, note that (8, 8) is Pareto-optimal as is any point on the two lines connecting (0, 10) and (8, 8) and (10, 0) with (8, 8). This is the Pareto-optimal boundary of the payoff set. This is clear from Figure 6.1 because if you take any point on the lines, you cannot simultaneously move up and right and remain in the set.
Example 6.3 Here is a much more complicated but systematic way to create a characteristic function, given any n-person, noncooperative, nonzero sum game. The idea is to create a two-person zero sum game in which any given coalition is played against a pure opposing coalition consisting of everybody else. The two players are the coalition S versus all the other players, which is also a coalition N − S. The characteristic function will be the value of the game associated with each coalition S. The way to set this up will become clear if we go through an example.
Let’s work out a specific example using a three-player game. Suppose that we have a three-player nonzero sum game with the following matrices:
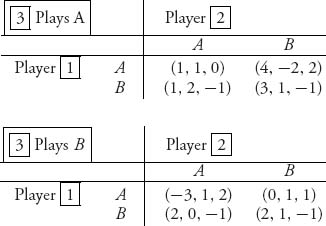
Each player has the two pure strategies A and B. Because there are three players, in matrix form this could be represented in three dimensions. That is a little hard to write down, so instead we have broken this into two 2 × 2 matrices. Each matrix assumes that player 3 plays one of the two strategies that is fixed. Now we want to find the characteristic function of this game.
We need to consider all of the zero sum games that would consist of the two-player coalitions versus each player, and the converse, which will switch the roles from maximizer to minimizer and vice versa. The possible two-player coalitions are {12}, {13}, {23} versus the single-player coalitions, {1, 2, 3}, and conversely. For example, one such possible game is S = {12} versus N − S = 3, in which player S = {12} is the row player and player 3 is the column player. We also have to consider the game 3 versus {12}, in which player 3 is the row player and coalition {12} is the column player. So now we go through the construction.
1. Play S = {12} versus {3}. players 1 and 2 team up against player 3. We first write down the associated matrix game.
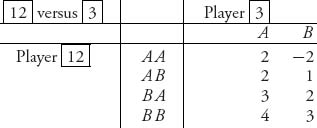
For example, if 1 plays A and 2 plays A and 3 plays B, the payoffs in the nonzero sum game are (−3, 1, 2) and so the payoff to player 12 is −3 + 1 = −2, the sum of the payoff to player 1 and player 2, which is our coalition. Now we calculate the value of the zero sum two-person game with this matrix to get the value(12 vs. 3) = 3 and we write v(12) = 3. This is the maximum possible guaranteed benefit to coalition {12} because it even assumes that player 3 is actively working against the coalition.
In the game {3} versus {12}, we have 
as the row player and players {12} as the column player. We now want to know the maximum possible payoff to player 3 assuming that the coalition {12} is actively working against player 3. The matrix is
The value of this game is −1. Consequently, in the game {3} versus {12} we would get v(3) = −1. Observe that the game matrix for 3 versus 12 is not the transpose of the game matrix for 12 versus 3.
2. Play S = {13} versus {2} . The game matrix is
We see that the value of this game is 1 so that v(13) = 1. In the game {2} versus {13} we have 2 as the row player and the matrix
The value of this game is 
, and so v(2) = .
Continuing in this way, we summarize that the characteristic function for this three–person game is
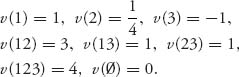
The value v(123) = 4 is obtained by taking the largest sum of the payoffs that they would achieve if they all cooperated. This number is obtained from the pure strategies: 3 plays A, 1 plays A, and 2 plays B with payoffs (4, −2, 2). Summing these payoffs for all the players gives v(123) = 4. This is the most the players can get if they form a grand coalition, and they can get this only if all the players cooperate. The central question in cooperative game theory is how to allocate the reward of 4 to the three players. In this example, player 2 contributes a payoff of −2 to the grand coalition, so should player 2 get an equal share of the 4? On the other hand, the 4 can only be obtained if player 2 agrees to play strategy B, so player 2 does have to be induced to do this. What would be a fair allocation?
One more observation is that player 3 seems to be in a bad position. On her own she can be guaranteed to get only v(3) = −1, but with the assistance of player 1 v(13) = 1. Since v(1) = 1, this gain for S = 13 is solely attributed to 1. Note, however, that v(2) = , while v(23) = 1. Player 3 can definitely add value by joining with player 2.
FIGURE 6.1 Payoff to player I versus payoff to player II.
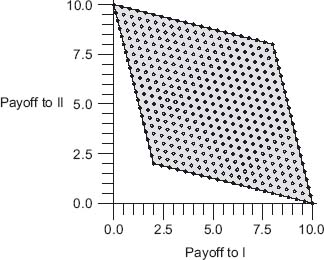
FIGURE 6.2 Core with lots of allocations.
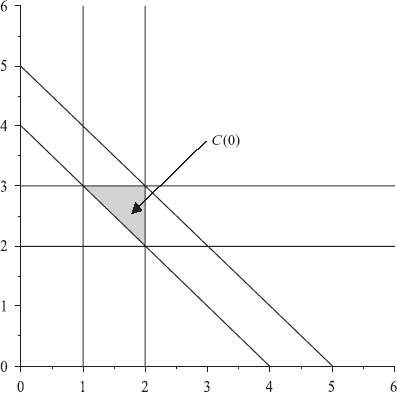
FIGURE 6.3 The set of reasonable imputations.
Remark There is a general formula for the characteristic function obtained by converting an n-person nonzero sum game to a cooperative game. Given any coalition S 
N, the characteristic function is
where XS is the set of mixed strategies for the coalition S, YN − S is the set of mixed strategies for the coalition N − S, Ei(X, Y) is the expected payoff to player i 
S, and ∑i S Ei(X, Y) is the total payoff for each player in i S and represents the payoff to the coalition S. The set of pure strategies for coalition S is the set of all combinations of pure strategies for the members of S. This definition of characteristic function satisfies the requirements to be a characteristic function and the property of superadditivity discussed below.
It is important to not be confused about the definition of characteristic function. A characteristic function is any function that satisfies v() = 0, v(N) ≥ ∑ v(i). It does not have to be defined as we did in the examples with the matrices but that is a convenient way of obtaining one that will work.
Here are some additional observations and definitions.
Remarks on Characteristic Functions.
This is called superadditivity. It says that the benefits of the larger consolidated coalition S 
T of the two separate coalitions S, T must be at least the total benefits of the individual coalitions S and T. Many results on cooperative games do not need superadditivity, but we will take it as an axiom that our characteristic functions in all that follows must be superadditive. With the assumption of superadditivity, the players have the incentive to form and join the grand coalition N.
T) = v(S) + v(T), for all S, T ⊂ N, S ∩ T = , is called an additive game. A game is inessential if and only if it is additive.To see why a characteristic function for an inessential game must be additive, we simply write down the definitions. In fact, let S, T N, S ∩ T = . Then
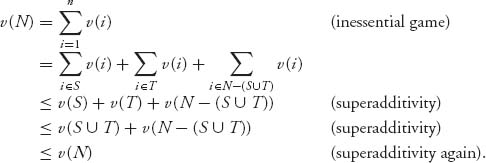
Since we now have equality throughout
and so v(S) + v(T) = v(S T).
We need a basic definition regarding the allocation of rewards to each player. Recall that v(N) represents the reward available if all players cooperate.
Definition 6.1.2 Let xi be a real number for each i = 1, 2, …, n, with ∑i = 1n xi ≤ v(N). A vector 
= (x1, …, xn) is an imputation if
- xi ≥ v(i) (individual rationality);
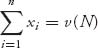(group rationality).
Each xi represents the share of the value of v(N) received by player i. The imputation is also called a payoff vector or an allocation, and we will use these words interchangeably.
Remarks
= (v(1), …, v(n)). The verification is a simple exercise (see the problems). These games are uninteresting because there is no incentive for any of the players to form any sort of coalition and there is no wiggle room in finding a better allocation.The main objective in cooperative game theory is to determine the imputation that results in a fair allocation of the total rewards. Of course, this will depend on the definition of fair, as we mentioned earlier. That word is not at all precise. If you change the meaning of fair you will change the imputation.
We begin by presenting a way to transform a given characteristic function for a cooperative game to one which is frequently easier to work with. It is called the (0, 1) normalization of the original game. This is not strictly necessary, but it does simplify the computations in many problems. The normalized game will result in a characteristic function with v(i) = 0, i = 1, 2 …, n and v(N) = 1. In addition, any two n-person cooperative games may be compared by comparing their normalized characteristic functions. If they are the same, the two games are said to be strategically equivalent.
The lemma will show how to make the conversion to (0, 1) normalized.
Lemma 6.1.3 Any essential game with characteristic function v has a (0, 1) normalization with characteristic function v′. That is, given the characteristic function v(·) set
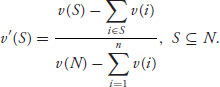
Then v′(·) is a characteristic function that satisfies v′(N) = 1, v′(i) = 0, i = 1, 2, …, n.
It should be obvious from the way v′ is defined that v′ satisfies the conclusions and so is a normalized characteristic function.
Remark How Does Normalizing Affect Imputations? If we have an imputation for an unnormalized game, what does it become for the normalized game? Conversely, if we have an imputation for the normalized game, how do we get the imputation for the original game?
The set of imputations for the original game is
For the normalized game, indeed, for any game with v(i) = 0, v(N) = 1, the set of all possible imputations is given by
That is because any imputation 
= (x′1, …, x′n) must satisfy x′i ≥ v′(i) = 0 and ∑i x′i = v′(N) = 1.
If ′ = (x1′, …, xn′) X′ is an imputation for v′ then the imputation for v becomes for = (x1, …, xn) X,
(6.1)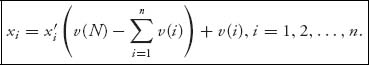
This shows that xi is the amount he could get on his own, v(i), plus the fraction of the left over rewards he is entitled to by his worth to coalitions.
Conversely, if 
= (x1, …, xn) X is an imputation for the original game, then ′ = (x′1, …, x′n) is the imputation for the normalized game, where
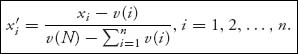
We can make the computations simpler by setting
and then
Example 6.4 In the three-person nonzero sum game considered above we found the (unnormalized) characteristic function to be
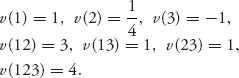
To normalize this game, we compute the normalized characteristic function by v′ as
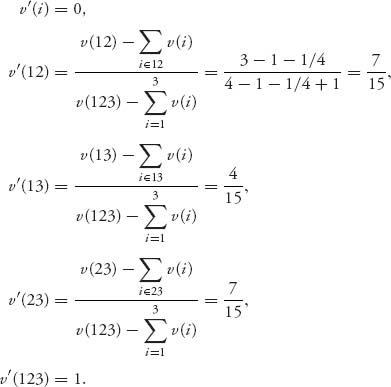
In the rest of this section, we let X denote the set of imputations . We look for an allocation X as a solution to the game. The problem is the definition of the word solution. It is as vague as the word fair. We are seeking an imputation that, in some sense, is fair and allocates a fair share of the payoff to each player. To get a handle on the idea of fair we introduce the following subset of X.
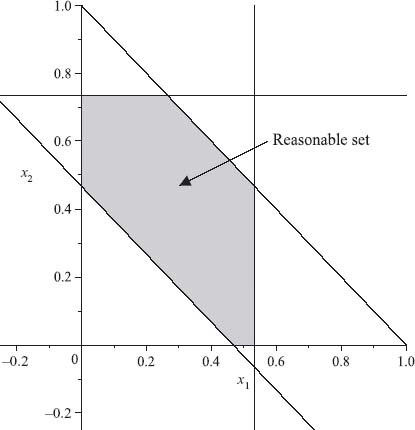
Definition 6.1.4 The reasonable allocation set of a cooperative game is a set of imputations R X given by
where Πi is the set of all coalitions for which player i is a member. If T Πi, then i T N, and T − i denotes the coalition T without the player i.
In other words, the reasonable set is the set of imputations so that the amount allocated to each player is no greater than the maximum benefit that the player brings to any coalition of which the player is a member. The difference v(T) − v(T − i) is the measure of the rewards for coalition T due to player i. The reasonable set gives us a first way to reduce the size of X and try to focus in on a solution.
If the reasonable set has only one element, which is extremely unlikely for most games, then that is our solution. If there are many elements in R, we need to cut it down further. In fact, we need to cut it down to the core imputations, or even further. Here is the definition.
Definition 6.1.5 Let S N be a coalition and let X. The excess of coalition S N for imputation X is defined by
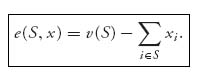
It is the amount by which the rewards allocated to the coalition S differs from the benefits associated with S.
The core of the game is
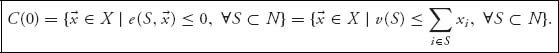
The core is the set of allocations so that each coalition receives at least the rewards associated with that coalition. The core may be empty.
The ε-core, for −∞ < ε < +∞, is
Let ε1 (−∞, ∞) be the first ε for which C(ε) ≠ . The least core, labeled X1, is C(ε1). It is possible for ε1 to be positive, negative, or zero.
Since any allocation must satisfy v(N) = ∑i = 1n xi, the excess function with the grand coalition e(N, ) = v(N) − ∑i = 1n xi = 0. The grand coalition is excluded in the requirements for C(ε) because if N were an eligible coalition, then e(N, ) = 0 ≤ ε, and it would force ε to be nonnegative. That would put too strict a requirement on ε in order for C(ε) to be nonempty. That is why N is excluded. In fact, we could exclude it in the definition of C(0) because any imputation must satisfy e(N, ) = 0 and it automatically satisfies the requirement e(N, ) ≤ 0. Similarly, e(, ) = 0 and we exclude S = .
We will use the notation that for a given imputation = (x1, …, xn) and a given coalition S N
the total amount allocated to coalition S. The excess function then becomes e(S, ) = v(S) − (S).
Remarks
is a member of the core if no matter which coalition S is formed, the total payoff given to the members of S, namely, (S) = ∑i S xi, must be at least as large as v(S), the maximum possible benefit of forming the coalition. If e(S, ) > 0, this would say that the maximum possible benefits of joining the coalition S are greater than the total allocation to the members of S using the imputation . But then the members of S would not be very happy with since the amount available is not actually allocated. In that sense, if C(0), then e(S, ) ≤ 0 for every coalition S, and there would be no a priori incentive for any coalition to try to use a different imputation. An imputation is in the core of a game if it is acceptable to all coalitions. The excess function e(S, ) is a measure of dissatisfaction of a particular coalition S with the allocation . Consequently, is in the core if all coalitions are satisfied with . If the core has only one allocation, that is our solution. C(ε), then the measure of dissatisfaction of a coalition with is limited to ε . The size of ε determines the measure of dissatisfaction because e(S, ) ≤ ε . C(ε′). The idea is that we should shrink (or expand if necessary) C(ε) by adjusting ε until we get one and only one imputation in it, if possible. C(ε). If ε < 0, C(ε) C(0). If the core of the game C(0) is empty, then there will be a positive ε > 0 such that C(0) C(ε) ≠ and the first such ε = ε1 gives us the least core C(ε1). If C(0) is not empty but contains more than one allocation, then the first ε = ε1 which will make C(ε1) nonempty will be negative, ε1 < 0. There will always be some ε (−∞, ∞) so that C(ε) ≠ . The least core uses the first such ε . Make a note that ε1 > 0 means that C(0) = . R, every allocation in the core is always in the reasonable set.Example 6.5 Let’s give an example of a calculation of C(0). Take the three-person game N = {1, 2, 3}, with characteristic function
The excess functions for a given imputation = (x1, x2, x3) C(0) must satisfy
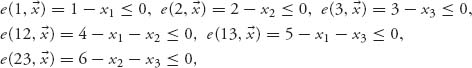
and we must have x1 + x2 + x3 = 8. These inequalities imply that x1 ≥ 1, x2 ≥ 2, x3 ≥ 3, and
If we use some algebra and the substitution x3 = 8 − x1 − x2 to solve these inequalities, we see that
If we plot this region in the (x1, x2) plane, we get the diagram as in Figure 6.2. The problem with the core is that it contains more than one allocation. The problem of allocating the rewards v(N) has many reasonable allocations but not a single well defined allocation. For this we next need to calculate the least core.
We will show that the first ε for which C(ε) ≠ is ε = ε1 = −
. In fact, the least core is the single imputation 
. Indeed, the imputations in C(ε) must satisfy e(S, ) ≤ ε for all nonempty coalitions S 
N. Written out, these inequalities become
where we have eliminated x3 = 8 − x1 − x2. Adding the inequalities involving only x1, x2 we see that 4 − ε ≤ x1 + x2 ≤ 5 + 2ε, which implies that ε ≥ −. You can check that this is the first ε for which C(ε) ≠ . With ε = −, it follows that x1 + x2 = 
and x1 ≤ 
, x2 ≤ 
. Then,
which implies that x1 = , x2 = because two nonnegative terms adding to zero must each be zero. This is one technique for finding ε1 and C(ε1).
We now have determined the single allocation 
and this is our solution to the cooperative game. Of the 8 = v(N) units available for distribution to the members, player 1 should get , player 2 should get , and player 3 should get 
.
Now we will formalize some properties of the core. We begin by showing that the core must be a subset of the reasonable set.
Lemma 6.1.6 C(0) R.
Proof We may assume the game is in normalized form because we can always transform it to one that is and then work with that one. So v(N) = 1, v(i) = 0, i = 1, …, n. Let C(0). If 
R there is some player j such that
This means that for every T N with j T, xj > v(T) − v(T − j), and so the amount allocated to player j is larger than the amount of her benefit to any coalition of which she is a member. Take T = N since she certainly is a member of N. Then
But then, v(N − j) > 1 − xj = ∑i ≠ j xi = (N − j), and so e(N − j, ) = v(N − j) − (N − j) > 0, which means C(0). 
Example 6.6 In this example, we will normalize the given characteristic function, find the reasonable set, and find the core of the game. Finally, we will find the least core, show that it has only one allocation, and then convert back to the unnormalized imputation.
We have the characteristic function in the three–player game from Example 6.3:
This is an essential game that we normalized in Example 6.4 to obtain the characteristic function that we will use:
The normalization constants are 
, and 
, and 
. Since this is now in normalized form, the set of imputations is
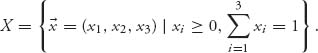
The reasonable set is easy to find and here is the result:
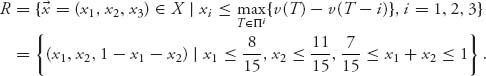
To see how to get this let’s consider
The coalitions containing player 1 are {1, 12, 13, 123}, so we are calculating the maximum of
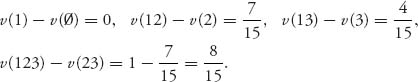
Hence, 0 ≤ x1 ≤ 
. Similarly, 0 ≤ x2 ≤ 
. We could also show 0 ≤ x3 ≤ , but this isn’t good enough because we can’t ignore x1 + x2 + x3 = 1. That is where we use
Another benefit of replacing x3 is that now we can draw the reasonable set in (x1, x2) space. Figure 6.3 is a plot of R.
You can see from Figure 6.2 that there are lots of reasonable imputations. This is a starting point. We would like to find next the point (or points) in the reasonable set which is acceptable to all coalitions. That is the core of the game:
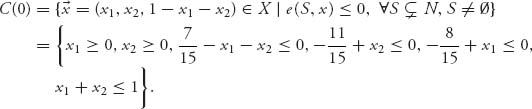
Unfortunately, this gives us exactly the same set as the reasonable set, C(0) = R in this example, and that is too big a set.
Now let’s calculate the ε-core for any ε (−∞, ∞). The ε-core is, by definition
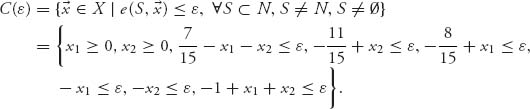
We have used the fact that x1 + x2 + x3 = 1 to substitute x3 = 1 − x1 − x2.
By working with the inequalities in C(ε), we can find the least core X1. We verify that the first ε so that C(ε) ≠ is ε1 = −
. The procedure is to add the inequality for x2 with the one for x1 and then use the first inequality:
but x1 + x2 ≥ 
− ε, so that
which can be satisfied if and only if ε ≥ − = ε1.
If we replace ε by ε1 = −, the least core is the set
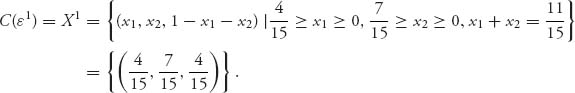
The least core is exactly the single point (x1 = , x2 = , x3 = ) because if x1 + x2 = , then ( − x1) + ( − x2) = 0 and each of the two terms is nonnegative, and therefore, both zero or they couldn’t add to zero. This says that there is one and only one allocation that gives all coalitions the smallest dissatisfaction.
If we want the imputation of the original unnormalized game, we use 
i = (xi − ai)/c and obtain
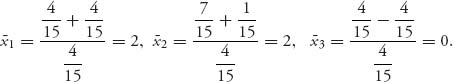
It is an exercise to directly get this imputation for the original game without going through the normalization and solving the inequalities from scratch.
Now here is a surprising (?) conclusion. Remember from Example 6.3 that the payoff of 4 for the grand coalition {123} is obtained only by cooperation of the three players in the game in which the payoffs to each player was (4, −2, 2). But remember also that player 3 was in a very weak position according to the characteristic function we derived. The conclusion of the imputation we derived is that players 1 and 2 will split the 4 units available to the grand coalition and player 3 gets nothing. That is still better than what she could get on her own because 
(3) = −1. So that is our fair allocation.
We have already argued that the core C(0) should consist of the good imputations and so would be considered the solution of our game. If in fact C(0) contained exactly one point, then that would be true. Unfortunately, the core may contain many points, as in the last example, or may even be empty. Here is an example of a game with an empty core.
Example 6.7 Suppose that the characteristic function of a three-player game is given by
Since this is already in normalized form, the set of imputations is
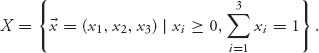
To calculate the reasonable set R, we need to find
Starting with Π1 = {1, 12, 13, 123}, we calculate
so x1 ≤ max{0, 1, 1, 0} = 1. This is true for x2 as well as x3. So all we get from this is R = X, all the imputations are reasonable.
Next we have
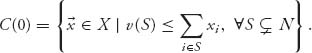
If C(0), we calculate
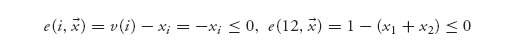
and, in likewise fashion
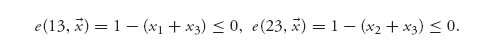
The set of inequalities we have to solve are as follow:
But clearly there is no X that can satisfy these inequalities, because it is impossible to have three positive numbers, any two of which have sum at least 1, which can add up to 1. In fact, adding the three inequalities gives us 2 = 2x1 + 2x2 + 2x3 ≥ 3. Therefore, C(0) = .
As mentioned earlier, when C(0) = , it will be true that the least core C(ε) must have ε > 0.
In the next proposition, we will determine a necessary and sufficient condition for any cooperative game with three players to have a nonempty core.
We take N = {1, 2, 3} and a characteristic function in normalized form
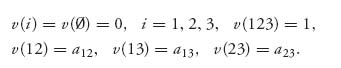
Of course, we have 0 ≤ aij ≤ 1. We can state the proposition.
Proposition 6.1.7 For the three-person cooperative game with normalized characteristic function v we have C(0) ≠ if and only if
Proof We have
So, x1 + x2 ≥ a12, x2 ≤ 1 − a13, and x1 ≤ 1 − a23. Adding the last two inequalities says x1 + x2 ≤ 2 − a23 − a13 so that with the first inequality a12 ≤ 2 − a13 − a23. Consequently, if C(0) ≠ , it must be true that a12 + a13 + a23 ≤ 2.
For the other side, if a12 + a13 + a23 ≤ 2, we define the imputation
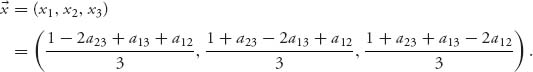
Then x1 + x2 + x3 = 1 = v(123). Furthermore,
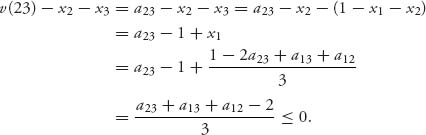
Similarly, v(12) − x1 − x2 ≤ 0 and v(13) − x1 − x3 ≤ 0. Hence, C(0) and so C(0) ≠ .
Remark An Automated Way to Determine Whether C(0) = .
With the use of a computer algebra system there is a simple way of determining whether the core is empty. Consider the linear program:
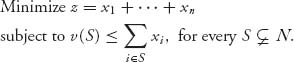
It is not hard to check that C(0) is not empty if and only if the linear program has a minimum, say, z*, and z* ≤ v(N). If the game is normalized, then we need z* ≤ 1. When this condition is not satisfied, C(0) = . For instance, in the last example the Maple commands would be
> with(simplex):
> obj:=x+y+z;
> cnsts:={1-x-z<=0, 1-y-z<=0, 1-x-y<=0};
> minimize(obj, cnsts, NONNEGATIVE);
> assign(%);
> obj;
Maple gives the output {x = 
, y = , z = } as the allocation and obj = 
as the sum of the allocation components. Since this is a game in which the allocation components must sum to 1, because v(N) = 1, we see that the core must be empty.
In Mathematica the commands are even simpler:
> obj=x+y+z
cnsts={1-x-z<=0, 1-y-z<=0, 1-x-y<=0}
Minimize[{obj, cnsts}, {x, y, z}]
It produces {, {x → , y → , z → }} .
Remark Cost Allocation Games. In many games, we are interested in allocating costs rather than rewards to members of a coalition. In this case, the appropriate characteristic function is c: 2N → that is subadditive
This says that it costs less for two coalitions to act together than to operate independently.
Next, a cost allocation is a vector = (x1, …, xn) that satisfies the following:
- xi ≥ 0, i = 1, 2, …, n, ∑i = 1n xi = c(N).
- xi ≤ c(i), i = 1, 2, …, n (individual rationality).
- ∑i S xi ≤ c(S)(collective rationality).
We may either work with c(S) directly, or define the ordinary characteristic function
which represents the savings that the coalition S can achieve. If we obtain a solution of the game with v, say 
= (y1, …, yn), then the cost allocation game has solution = (x1, …, xn), xic(i) = yi, i = 1, 2, …, n. The basic difference is that each player wants to minimize its cost allocation but maximize its savings allocation.
Problems
6.1 A stag-hunt game has characteristic function v(S) = α|S|, S N, v(N) = 1, where 
> α > 0.
6.2 A customer wants to buy a bolt and a nut for the bolt. There are three players but player 1 owns the bolt and players 2 and 3 each own a nut. A bolt together with a nut is worth 5 but is worthless otherwise. Also, a nut without a bolt is worthless. Define a characteristic function for this game and verify that it is superadditive.
6.3 A river has n pollution-producing factories dumping water into the river. Assume that the factory does not have to pay for the water it uses but it may need to expend money to clean the water before it is suitable for use. Assume the cost of a factory to clean polluted water before it can be used is proportional to the number of polluting factories. Let c = cost per factory. Assume also that a factory may choose to clean the water it dumps into the river at a cost of b per factory. We assume the inequalities 0 < c < b < nc.
If a coalition S forms, all of its members could agree to pollute with a payoff of −|S|(nc). The other possibility is all of its members could agree to clean the water and the factories not in the coalition pollute the river, which results in a total payoff to coalition S of −|S|(n − |S|)c − |S|b. Hence, the characteristic function is
Show that = (−b, −b, …, −b) C(0), which means C(0) ≠ . The allocation in which every factory cleans the water before it is dumped in the river is in the core.
6.4 A small research drug company, labeled 1, has developed a drug. It does not have the resources to get FDA (Food and Drug Administration) approval or to market the drug, so it considers selling the rights to the drug to a big drug company. Drug companies 2 and 3 are interested in buying the rights but only if both companies are involved in order to spread the risks. Suppose that the research drug company wants $1 billion, but will take $100 million if only one of the two big drug companies are involved. The profit to a participating drug company 2 or 3 is $5 billion, which they split. Here is a possible characteristic function with units in billions:
because any coalition that doesn’t include player 1 will be worth nothing.
) = {(, , )}. Find the least core in unnormalized allocations.6.5 Look back at Example 6.5. Find the normalized characteristic function and the normalized element in the least core.
6.6 Consider the bimatrix game with
6.7 Given the characteristic function v(i) = 0, i = 1, 2, 3, 4 and
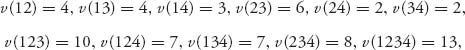
find the normalized characteristic function. Given the fair allocation
for the normalized game find the unnormalized allocation.
6.8 Odd Man Out is a three player coin toss game in which each player chooses H or T. If all three make the same choice, the house pays each player 1; otherwise the odd man out pays the other players 1. Consider this as a three player nonzero sum game.
6.9 Find the characteristic function for the following three-player game. Each player has two strategies, A, B. If player 1 plays A the matrix is
while if player 1 plays B the matrix is
In each matrix, player 2 is the row player and player 3 is the column player. Next, find the normalized characteristic function.
6.10 Derive the least core for the game with
6.11 Given the characteristic function
find the least core without normalizing.
6.12 Larger amounts of money invested in things like CDs (certificates of deposit) get a better rate of return. Suppose the rates of return depend on the amount invested as follows:
| Invested amount | Rate of return |
| 0–1, 000, 000 | 4% |
| 1, 000, 000–3, 000, 000 | 5% |
| >3, 000, 000 | 5.5% |
Three companies are going to form an investment partnership to pool their money. Suppose Company 1 will invest $1, 800, 000, company 2, $900, 000, and company 3, $300, 000. How should the net amount earned on the total investment be split among the three companies? Define an appropriate characteristic function. Find the core.
6.13 A constant sum game is one in which v(S) + v(N − S) = v(N) for all coalitions S N. Show that any essential constant sum game must have empty core C(0) = .
6.14 In this problem, you will see why inessential games are of no interest. Show that an inessential game has one and only one imputation and is given by
that is, each player is allocated exactly the benefit of the one-player coalition.
6.15 A player i is a dummy if v(S) = v(S i), for every S N with i S. It looks like a dummy contributes nothing. Show that if i is a dummy and v(i) = 0, then for any C(0), it must be true that xi = 0.
6.16 Show that a vector = (x1, x2, …, xn) is an imputation if and only if there are nonnegative constants ai ≥ 0, i = 1, 2, …, n, such that ∑i = 1n ai = v(N) − ∑i = 1n v(i), and xi = v(i) + ai for each i = 1, 2, …, n.
6.17 Let δi = v(N) − v(N − i). Show that C(0) = if ∑i = 1n δi < v(N).
6.18 Verify the statement: C(0) ≠ if and only if the linear program
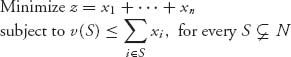
has a finite minimum, say z*, and z* ≤ v(N).
6.19 Show that in any n ≥ 2 player cooperative game, each player belongs to exactly 2n − 1 coalitions.
6.1.1 MORE ON THE CORE AND LEAST CORE
The next theorem formalizes the idea above that when e(S, ) ≤ 0 for all coalitions, then the player should be happy with the imputation and would not want to switch to another one.
One way to describe the fact that one imputation is better than another is the concept of domination.
Definition 6.1.8 If we have two imputations X, X, and a nonempty coalition S N, then dominates (for the coalition S) if xi > yi for all members i S, and (S) = ∑i S xi ≤ v(S). If dominates for the coalition S, we write 
S .
If dominates for the coalition S, then members of S prefer the allocation to the allocation , because they get more xi > yi, for each i S, and the coalition S can actually achieve the allocation because v(S) ≥ ∑i S xi. The next result is another characterization of the core of the game.
Theorem 6.1.9 The core of a game is the set of all undominated imputations for the game; that is,
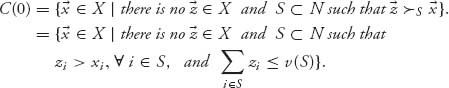
Proof Call the right-hand side the set B. We have to show C(0) B and B C(0).
We may assume that the game is in (0, 1) normalized form.
Let C(0) and suppose B. Since B that means that must be dominated by another imputation for at least one nonempty coalition S N; that is, there is X and S N such that yi > xi for all i S and v(S) ≥ ∑i S yi. Summing on i S, this shows
contradicting the fact that C(0). Therefore, C(0) B.
Now let B. If C(0), there is a nonempty coalition S N so that e(S, ) = v(S) − ∑i S xi > 0. Let
Let s = |S|, the number of players in S, and
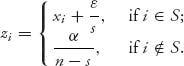
If i S zi is an allocation which is xi plus the (positive) excess equally divided among members of S. If i S, zi allocates the total rewards minus the rewards for S equally among the members not in S.
We will show that 
= (z1, …, zn) is an imputation and dominates for the coalition S; that is, that is a better allocation for the members of S than is .
First, zi ≥ 0 and
Therefore, is an imputation.
Next, we show is a better imputation than is for the coalition S. If i S zi = xi + ε/s > xi and ∑i S zi = ∑i S xi + ε = v(S). Therefore, dominates . But this says B and that is a contradiction. Hence, B C(0).
Example 6.8 This example1 will present a game with an empty core. We will see again that when we calculate the least core X1 = C(ε1), where ε1 is the first value for which C(ε1) ≠ , we will obtain a reasonable fair allocation (and hopefully only one). Recall the fact that C(0) = means that when we calculate ε1 it must be the case that ε1 > 0 because if ε1 < 0, by the definition of ε1 as the first ε making C(ε) ≠ , we know immediately that C(0) ≠ because C(ε) increases as ε gets bigger.
Suppose that Curly has 150 sinks to give away to whomever shows up to take them away. Aggie (1), Maggie (2), and Baggie (3) simultaneously show up with their trucks to take as many of the sinks as their trucks can haul. Aggie can haul 45, Maggie 60, and Baggie 75, for a total of 180, 30 more than the maximum of 150. The wrinkle in this problem is that the sinks are too heavy for any one person to load onto the trucks so they must cooperate in loading the sinks. The question is: How many sinks should be allocated to each person?
Define the characteristic function v(S) as the number of sinks the coalition S N = {1, 2, 3} can load. We have v(i) = 0, i = 1, 2, 3, since they must cooperate to receive any sinks at all, and
The set of imputations will be X = {(x1, x2, x3) | xi ≥ 0, ∑ xi = 150}. First, let’s use Maple to see if the core is nonempty:
> with(simplex):
> obj:=x1+x2+x3:
> cnsts:={105-x1-x2<=0, 120-x1-x3<=0, 135-x2-x3<=0};
> minimize(obj, cnsts, NONNEGATIVE);
> assign(%);
> obj;
Maple gives the output x1 = 45, x2 = 60, x3 = 75, and obj = x1 + x2 + x3 = 180 > v(123) = 150. So the core of this game is empty. A direct way to get this is to note that the inequalities
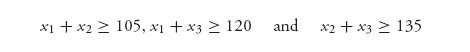
imply that 2(x1 + x2 + x3) = 2(150) = 300 ≥ 360, which is impossible.
A second way to see C(0) = is to use the proposition Proposition 6.1.7. If we do that, we normalize v to get 
. Then, since v′(12) + v′(13) + v′(23) = 
> 2, the proposition tells us that C(0) = .
Finally, a third way to see C(0) = is to use Problem 6.17. We calculate
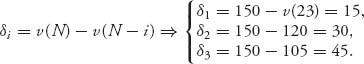
Then δ1 + δ2 + δ3 = 90 < 150, and the core is empty.
Since C(0) = we know that no matter what allocation we use, there will be some coalition S and some allocation so that S . For example, if = (45, 50, 55) we could take S = 23 and = (43, 51, 56). Since z2 > x2, z3 > x3 and z2 + z3 ≤ v(23), clearly S . No matter what allocation you want, it would be dominated by some other allocation for some coalition.
Now that we know the core is empty, the next step is to calculate the least core. We also know that the first ε for which C(ε) ≠ must be positive (since otherwise C(ε) C(0) = ). Begin with the definition:
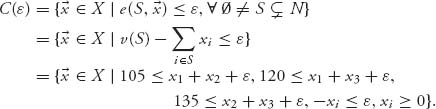
We know that x1 + x2 + x3 = 150 so by replacing x3 = 150 − x1 − x2 we obtain as conditions on ε that
We see that 45 ≥ x1 + x2 − 2ε ≥ 105 − 3ε, implying that ε ≥ 20. This is in fact that the first ε1 = 20, making C(ε) ≠ . Using ε1 = 20, we calculate
Hence, the fair allocation is to let Aggie have 35 sinks, Maggie 50, and Baggie 65 sinks, and they all cooperate.
We conclude that our fair allocation of sinks is as follows:
| Player | Truck capacity | Allocation |
| Aggie | 45 | 35 |
| Maggie | 60 | 50 |
| Baggie | 75 | 65 |
| Total | 180 | 150 |
Observe that each player in the fair allocation gets 10 less than the capacity of her truck. It seems that this is certainly a reasonably fair way to allocate the sinks; that is, there is an undersupply of 30 sinks so each player will receive 
= 10 less than her truck can haul. You might think of other ways in which you would allocate the sinks (e.g., along the percentage of truck capacity to the total), but the solution here minimizes the maximum dissatisfaction over any other allocation for all coalitions.
We have already noted that C(0) = . Therefore, no matter what allocation you might use, there will always be a level of dissatisfaction with that allocation for at least one coalition. The least core allocation provides the lowest level of dissatisfaction for all coalitions.
Naturally, a different characteristic function changes the solution as you will see in the exercises.
The least core plays a critical role in solving the problem when C(0) = or there is more than one allocation in C(0). Here is the precise description of the first ε making the set C(ε) nonempty.
Lemma 6.1.10 Let
Then the least core X1 = C(ε1) ≠ . If ε < ε1 then C(ε) = . If ε > ε1, then C(ε1) C(ε).
Proof Since the set of imputations is compact (=closed and bounded) and ↦ maxS e(S, ) is at least lower semicontinuous, there is an allocation 0 so that the minimum in the definition of ε1 is achieved, namely, ε1 = maxS e(S, 0) ≥ e(S, 0), 
S N. This is the very definition of 0 C(ε1) and so C(ε1) ≠ .
On the other hand, if we have a smaller ε < ε1 = min maxS N, then for every allocation X, we have ε < maxS e(S, ). So, for any allocation there is at least one coalition S N for which ε < e(S, ). This means that for this ε, no matter which allocation is given, C(ε). Thus, C(ε) = . As a result, ε1 is the first ε so that C(ε) ≠ .
Remarks These remarks summarize the ideas behind the use of the least core.
, the coalition S0 that most objects to is the coalition giving the largest excess and so satisfies
For each fixed coalition S, the allocation giving the minimum dissatisfaction for that coalition is
The value of ε giving the least ε-core is
The procedure is to find the coalition giving the largest excess for a given allocation and then find the allocation which minimizes the maximum excess.
maxS N e(S, ) < 0, then there is at least one allocation * that satisfies maxS e(S, *) < 0. That means that e(S, *) < 0 for every coalition S N. Every coalition is satisfied with * because v(S) < *(S), so that every coalition is allocated at least its maximum rewards. Obviously, this says * C(0) and is undominated.If ε1 = min maxS N e(S, ) > 0, then for every allocation X, maxS e(S, ) > 0. Consequently, there is at least one coalition S so that e(S, ) = v(S) − (S) > 0. For any allocation, there is at least one coalition that will not be happy with it.
) is a measure of dissatisfaction of S with the imputation . It makes sense that the best imputation would minimize the largest dissatisfaction over all the coalitions. This leads us to one possible definition of a solution for the n-person cooperative game. An allocation * X is a solution to the cooperative game if
so that * minimizes the maximum excess for any coalition S. When there is only one such allocation *, it is the fair allocation. The problem is that there may be more than one * providing the minimum, then we still have a problem as to how to choose among them.
Remark Maple Calculation of the Least Core. The point of calculating the ε-core is that the core is not a sufficient set to ultimately solve the problem in the case when the core C(0) is (1) empty or (2) consists of more than one point. In case (2) the issue, of course, is which point should be chosen as the fair allocation. The ε-core seeks to address this issue by shrinking the core at the same rate from each side of the boundary until we reach a single point. We can use Maple to do this.
The calculation of the least core is equivalent to the linear programming problem
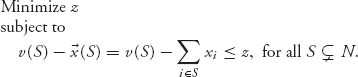
The characteristic function need not be normalized. So all we really need to do is to formulate the game using characteristic functions, write down the constraints, and plug them into Maple. The result will be the first z = ε1 that makes C(ε1) ≠ , as well as an imputation that provides the minimum.
For example, let’s suppose we start with the characteristic function
The constraint set is the ε-core
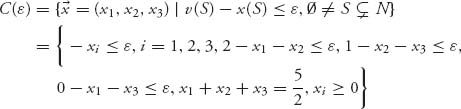
The Maple commands used to solve this are very simple:
> with(simplex):
> cnsts:={-x1<=z, -x2<=z, -x3<=z, 2-x1-x2<=z, 1-x2-x3<=z,
-x1-x3<=z, x1+x2+x3=5/2};
> minimize(z, cnsts);
Maple produces the output
Hence, the first ε1 = z for which the ε-core is nonempty is ε1 = − . Now, Maple also gives us the allocation 
that will be in 
, but we don’t know if that is the only point in C 
−
. With Maple, we can graph the core and the set C − with the following commands:
> cnsts:={-x1<=z, -x2<=z, -(5/2-x1-x2)<=z, 2-x1-x2<=z,
1-x2-(5/2-x1-x2)<=z, -x1-(5/2-x1-x2)<=z};
> Core:=subs(z=0, cnsts);
> with(plots):
> inequal(Core, x1=0..2, x2=0..3, optionsfeasible=(color=red),
> optionsopen=(color=blue, thickness=2),
> optionsclosed=(color=green, thickness=3),
> optionsexcluded=(color=yellow));
> ECore:=subs(z=-1/4, cnsts);
> inequal(ECore, x1=0..2, x2=0..3, optionsfeasible=(color=red),
> optionsopen=(color=blue, thickness=2),
> optionsclosed=(color=green, thickness=3),
> optionsexcluded=(color=yellow));
Figure 6.4 shows the core C(0).
You can even see how the core shrinks to the ε-core using an animation:
> animate(inequal, [cnsts, x1=0..2, x2=0..3, optionsfeasible=(color=red), optionsopen=(color=blue, thickness=2), optionsclosed=(color=green, thickness=3), optionsexcluded=(color=white)], z=-1..0, frames=50);
Figure 6.5 results from the animation at z = −0.18367 with the dark region constituting the core C(−0.18367). You will see that at z = − the dark region becomes the line segment. Hence, C − is certainly not empty, but it is also not just one point.
In summary, we have solved any cooperative game if the least core contains exactly one point. But when C(ε1) = X1 has more than one point, we still have a problem, and that leads us in the next section to the nucleolus.
FIGURE 6.4 Graph of C(0).
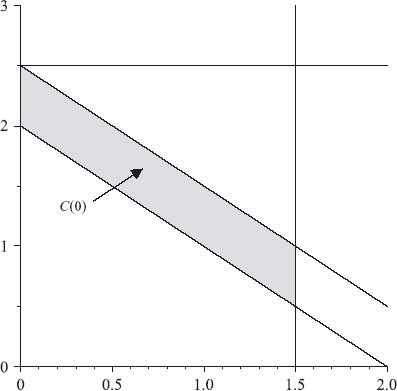
FIGURE 6.5 The shrinking of the core frozen at C(−0.18367).
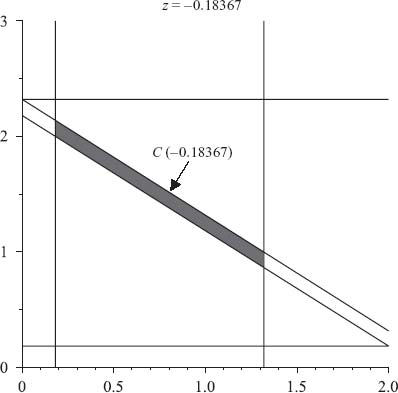
FIGURE 6.6 C(−0.07): shrinking down to a line segment.
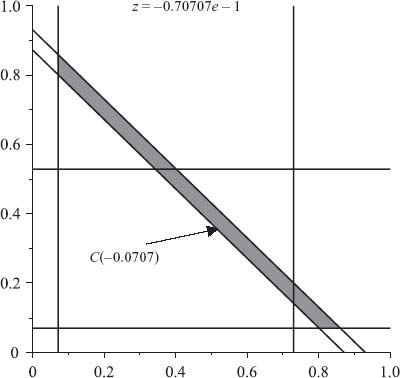
FIGURE 6.7 Three cities and a water tower.
FIGURE 6.8 Shortest path routing.
Problems
6.20 In a three-player game, each player has two strategies A, B. If player 1 plays A, the matrix is
while if player 1 plays B, the matrix is
In each matrix, player 2 is the row player and player 3 is the column player. The characteristic function is v() = 0, v(1) = 
, v(2) = 2, v(3) = 1, v(12) = 5, v(13) = 4, v(23) = 3, v(123) = 16. Verify that and then find the core and the least core.
6.21 In the sink problem (Example 6.8), we took the characteristic function v(i) = 0, v(12) = 105, v(13) = 120, v(23) = 135, and v(123) = 150, which models the fact that the players get the number of sinks each coalition can load and anyone not in the coalition would get nothing. The truck capacity and least core allocation in this case was
| Player | Truck capacity | C(20) Allocation |
| Aggie | 45 | 35 |
| Maggie | 60 | 50 |
| Baggie | 75 | 65 |
| Total | 180 | 150 |
6.22 A weighted majority game has a characteristic function of the form
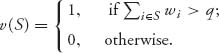
Here, wi ≥ 0 are called weights and q > 0 is called a quota. Take q = ∑i N wi. Suppose that there is one large group with two-fifths of the votes and two equal-sized groups with three-tenths of the vote each.
6.23 A classic game is the garbage game. Suppose that there are n property owners, each with one bag of garbage that needs to be dumped on somebody’s property (one of the n). If n bags of garbage are dumped on a coalition S of property owners, the coalition receives a reward of −n. The characteristic function is taken to be the best that the members of a coalition S can do, which is to dump all their garbage on the property of the owners not in S.
) = 0, where |S| is the number of members in S. dominates an imputation through the coalition S if e(S, ) ≥ 0 and yi > xi for each member i S. Take n = 4 in the garbage game. Find a coalition S so that = (−1.5, −0.5, −1, −1) dominates = (−2, −1, −1, 0).6.24 In the pollution game, we have the characteristic function
Here, 0 < c < b < nc, and b is the cost of cleaning water before dumping while c is the cost of cleaning the water after dumping. We have seen that C(0) ≠ since = (−b, −b, …, −b) C(0). Find the least core if c = 1, b = 2, n = 3.
6.2 The Nucleolus
The core C(0) might be empty, but we can find an ε so that C(ε) is not empty. We can fix the empty problem. Even if C(0) is not empty, it may contain more than one point and again we can use C(ε) to maybe shrink the core down to one point or, if C(0) = , to expand the core until we get it nonempty. The problem is what happens when the least core C(ε) itself has too many points.
In this section, we will address the issue of what to do when the least core C(ε) contains more than one point. Remember that e(S, ) = v(S) − ∑i S xi = v(S) − (S) and the larger the excess, the more unhappy the coalition S is with the allocation . So, no matter what, we want the excess to be as small as possible for all coalitions and we want the imputation which achieves that.
In the previous section, we saw that we should shrink C(0) to C(ε1), so if C(ε1) has more than one allocation, why not shrink that also? No reason at all.
Let’s begin by working through an example to see how to shrink the ε1-core.
Example 6.9 Let us take the normalized characteristic function for the three-player game:
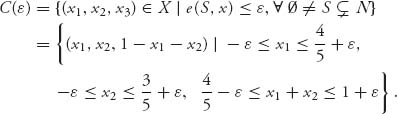
We then calculate that the first ε for which C(ε) ≠ is ε1 = −
, and then
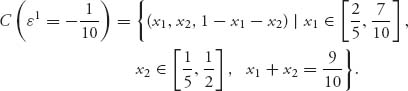
This is a line segment in the (x1, x2) plane as we see in Figure 6.6, which is obtained from the Maple animation shrinking the core down to the line frozen at z = −0.07.
So we have the problem that the least core does not have only one imputation that we would be able to call our solution. What is the fair allocation now? We must shrink the line down somehow. Here is what to do.
= (x1, x2, x3), with 
≤ x1 ≤ 
, 
≤ x2 ≤ , and x1 + x2 = 
. This last equality then requires that x3 = 1 − x1 − x2 = .If we take any allocation C(ε1), we want to calculate the excesses for each coalition:
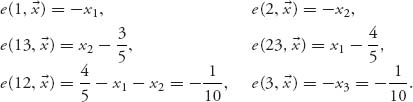
Since C(ε1), we know that these are all ≤ − . Observe that the excesses e(12, ) = e(3, ) = − do not depend on the allocation as long as it is in C(ε1). But then, there is nothing we can do about those coalitions by changing the allocation. Those coalitions will always have an excess of − as long as the imputations are in C(ε1), and they cannot be reduced. Therefore, we may eliminate those coalitions from further consideration.
Now we set
This is a set of coalitions with excesses for some imputation smaller than ε1. These coalitions can use some imputation that gives a better allocation for them, as long as the allocations used are also in C − . For our example, we get
The coalitions {12} and {3} are out because the excesses of those coalitions cannot be dropped below − no matter what allocation we use in C(−). Their level of dissatisfaction cannot be dropped any further.
Now pick any allocation in C(−) and calculate the smallest level of dissatisfaction for the coalitions in Σ1:
The number ε2 is then the first maximum excess over all allocations in C(−). It is defined just as is ε1 except we restrict to the coalitions that can have their dissatisfaction reduced. Finally, set
The set X2 is the subset of allocations from X1 that are preferred by the coalitions in Σ1. It plays exactly the same role as the least core C(ε 1), but now we can only use the coalitions in Σ1. If X2 contains exactly one imputation, then that point is our fair allocation, namely, the solution to our problem.
In our example, we now use allocations X1 so that x1 + x2 = , ≤ x1 ≤ , and ≤ x2 ≤ . The next least core is
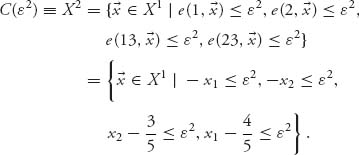
We need to find the first ε2 for which X2 is nonempty. We do this by hand as follows. Since x1 + x2 = , we get rid of x2 = − x1. Then
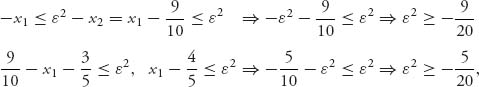
and so on.
The first ε2 satisfying all the requirements is then ε2 = −
= − . Next, we replace ε2 by − in the definition of X2 to get
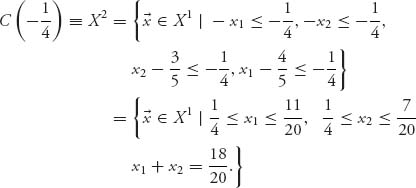
The last equality gives us
since both terms are nonnegative and cannot add up to zero unless they are each zero. We have found 
, and, finally, 
. We have our second least core
and X2 consists of exactly one point. That is our solution to the problem. Note that for this allocation
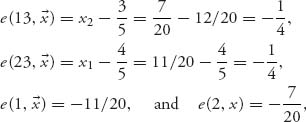
and each of these is a constant smaller than −. Because they are all independent of any specific allocation, we know that they cannot be reduced any further by adjusting the imputation. Since X2 contains only one allocation, no further adjustments are possible in any case. This is the allocation that minimizes the maximum dissatisfaction of all coalitions. In this example, X2 is the nucleolus for our problem.
The most difficult part of this procedure is finding ε1, ε2, and so on. This is where Maple is a great help. For instance, we can find ε2 = − very easily if we use the following commands:
> with(simplex):
> cnsts:={-x1<=z, -x2<=z, x2-3/5<=z, x1-4/5<=z, x1+x2=9/10};
> minimize(z, cnsts);
In Mathematica, the commands are as follows:
cnsts = z, {-x1 <= z, -x2 <= z, x2 - 3/5 <= z,
x1 - 4/5 <= z, x1 + x2 == 9/10}
Minimize[cnsts, {x1, x2}]
We find that z = −1/4, x1 = 11/20, x2 = 7/20, but you have to be careful of the x1 and x2 because these are points providing the minimum but you don’t know whether they are the only such points. That is what you must verify.
In general, we would need to continue this procedure if X2 also contained more than one point. Here are the sequence of steps to take in general until we get down to one point:
:
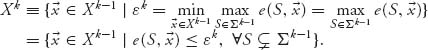
Alternatively, calculate the first εk so that
and then Xk = C(εk).
we are done; otherwise set k = k + 1 and go to step (2) with the new k.When this algorithm stops at, say, k = m, then Xm is the nucleolus of the core and will satisfy the relationships
Also, Σ0 蠵 Σ1 蠵 Σ2 · · · Σm − 1 蠵 Σm = . The allocation sets decrease down to a single point, the nucleolus, and the unhappiest coalitions decrease down to the empty set. The nucleolus is guaranteed to contain only one allocation , and this is the solution of the game. In fact, the following theorem can be proved.2
Theorem 6.2.1 The nucleolus algorithm stops in a finite number of steps m < ∞ and for each k = 1, 2, …, m, we have
are convex, closed, and bounded. for k = 1, 2, …, m − 1.In addition, Xm is a single point, called the nucleolus of the game:
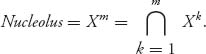
The nucleolus algorithm stops when all coalitions have been eliminated, but when working this out by hand you don’t have to go that far. When you see that Xk is a single point you may stop.
The procedure to find the nucleolus can be formulated as a sequence of linear programs that can be solved using Maple.
To begin, set k = 1 and calculate the constraint set
The first ε that makes this nonempty is ε1, given by
The first linear programming problem that will yield ε1, X1, Σ1 is
The set of values that provide the minimum in this problem is labeled X1 (this is the least core). Now we take
which is the set of coalitions that give excess ε1 for any allocation in X1. Getting rid of those gives us the next set of coalitions that we have to deal with, Σ1 = Σ0 − Σ1.
The next linear programming problem can now be formulated:
The minimum such ε is ε2, and we set X2 to be the set of allocations in X1 at which ε2 = maxS Σ1 e(S, ). Then
Set Σ2 = Σ1 − Σ2 and see if this is empty. If so, we are done; if not, we continue until we get our solution.
Basically, the algorithm says: (1) calculate the least core; (2) eliminate coalitions whose excesses cannot be reduced any further; (2) calculate the next least core using the remaining coalitions, and so on. When you get down to the last least core you have the nucleolus.
Example 6.10 Three hospitals, A, B, C, want to have a proton therapy accelerator (PTA) to provide precise radiological cancer therapy. These are very expensive devices because they are subatomic particle accelarators. The hospitals can choose to build their own or build one, centrally located, PTA to which they may refer their patients. The costs for building their own PTA are estimated at 50, 30, 50 for A, B, C, respectively, in millions of dollars. If A and B cooperate to build a PTA, the total cost will be 60 because of land costs for the location, coordination, and so on. If B and C cooperate, the cost will be 70; if A and C cooperate, the cost will be 110. Because the cost for cooperation between A and C is greater than what it would cost if they built their own, they would decide to build their own, so the cost is still 100 for AC cooperation. Finally, the cost to build one PTA for all three hospitals A, B, C is 105.
In this setup, the players want to minimize their costs, but since our previous theory is based on maximizing benefits instead of minimizing, we reformulate the problem by looking at the amount saved by each player and for each coalition. The characteristic function is then
With A = player 1, B = player 2, C = player 3, we get
For instance, v(123) = 50 + 30 + 50 − 105 = 25. We are looking for the fair allocation of the savings to each hospital that we can then translate back to costs. This game is not in normalized form and need not be.
Once we find the fair allocation of the cost savings game, say = (x1, x2, …, xn), we allocate the costs to each player with the cost allocation vector:
The first linear program finds the least core:
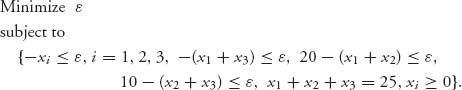
This gives us ε1 = −
. Replacing ε by ε1 = − and simplifying, we see that the least core will be the set
Note that x3 = 25 − 
= . Next, we have to calculate
Calculate the excesses for all the coalitions except N, , assuming that the allocations are in X1:
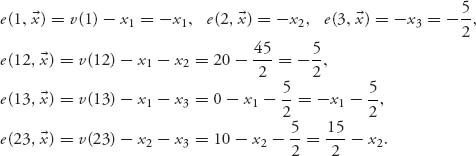
Thus, the coalitions that give ε1 = − (and have no further dependence on any allocation) are Σ1 = {12, 3}, and so these two coalitions are dropped from consideration in the next step. The remaining coalitions are as follows:
This is going to lead to the constraint set for the next linear program:
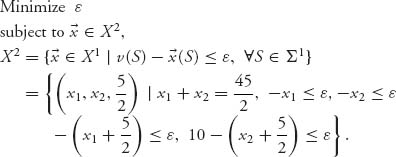
We get the solution of this linear program as
Furthermore, it is the one and only solution, so we should be done, but we will continue with the algorithm until we end up with an empty set of coalitions.
Calculate the excesses for all the coalitions excluding N, , assuming that the allocations are in X2:
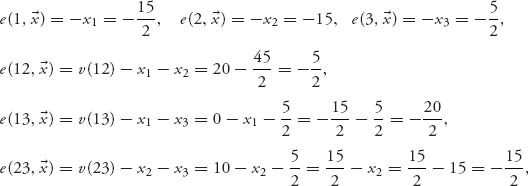
so that e(23, ) = e(1, ) = −
. Now we can get rid of coalitions Σ2 = {1, 3, 12, 13, 23} because none of the excesses for those coalitions can be further reduced by changing the allocations. Then
We are now done, having followed the algorithm all the way through. We conclude that
Therefore, the fair allocation of savings to hospital A is , the savings to B is 15, and the savings to C is . Consequently, the costs allocated to each player if all the hospitals cooperate is as follows: A pays 50 − 7.5 = 42.5, B pays 30 − 15 = 15, and C pays 50 − 2.5 = 47.5. Hospital B saves the most and pays the least.
6.2.1 AN EXACT NUCLEOLUS FOR THREE-PLAYER GAMES
Finding the nucleolus for a game can be a formidable task. It turns out that there is a formula derived by Leng and Parlar (2010) giving the nucleolus for any three-person cooperative game of the type we have been considering. Let’s get to the results. They are split into two cases—the case when C(0) = and the case when C(0) ≠ .
The simplest result is the case when the core of the game is empty. We have seen that and empty core would imply that the least core X1 = C(ε1) must have ε1 > 0 and X1 is nonempty. Of course, it might then have more than one point and might have to be cut down even further as we did earlier. The end result of all that work is the following general formula when C(0) = .
For the characteristic function v(·) the theorems assume that vis superadditive and one player coalitions have v(i) = 0, i = 1, 2, …, n. Further, it is assumed that v(S) ≥ 0 for all two-player coalitions. If these assumptions are not satisfied then we work with the 0 − 1 normalized game instead.
Theorem 6.2.2 Leng and Parlar (2010). Suppose we have the three player cooperative game with players N = {1, 2, 3} and characteristic function v(S), S N with v(i) = 0, i = 1, 2, 3, v(S) ≥ 0. If C(0) = the nucleolus allocation is given by
(6.2)
Proof The core is assumed empty. That is, we have
Claim At least one of e(12, ), e(13, ), e(23, ) must be > 0 for every .
Suppose that this is not true. Then for some allocation 0 these excesses are ≤ 0. Since e(i, ) = v(i) − xi = 0 − xi ≤ 0, i = 1, 2, 3, for any individually rational allocation, it must be the case that 0 C(0), contradicting the fact that C(0) is assumed empty.
From the claim we may conclude that for every allocation
We want to choose in order to minimize f().
Claim The minimum of f() must occur at an allocation 0 where e(12, 0) = e(13, 0) = e(23, 0).
Suppose the coalition S = {12} provides the maximum in (6.3), f() = e(12, ). We seek to minimize
Now in order to decrease f() we need to increase x1 or x2. But if we do that the other two terms in (6.4) increase. The most we can increase either x1 or x2 is until have at least two equal terms in (6.4) and then
Say the larger of the two is v(13) − v(N) + x2. But then we can decrease x2 and increase x1 to keep the left side constant and this can be done until
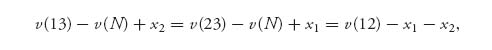
but that is exactly what the claim says.
Using the claim we obtain the two equations for two unknowns:
which are solved to obtain the formulas in the statement of the theorem.
Next, we write down the result in case we begin with a nonempty core. The proof is skipped. The inequlities of the theorem are not easy to check but the implementation is easy using Maple or Mathematica.3
Theorem 6.2.3 Leng and Parlar (2010) Let * = (x1, x2, x3) denote the imputation in the nucleolus of a 3 player cooperative game with nonempty Core. Assume that v(i) = 0, i = 1, 2, 3, v(S) ≥ 0, C(0) ≠ . Then
.
Then 
.
Then 
.
Then
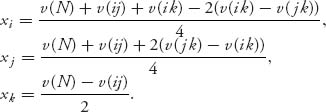
Then
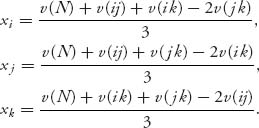
Of course remembering these formulas is more difficult than deriving the nucleolus from scratch, but the formulas are very helpful in writing computer code to find the nucleolus (see the end of this chapter).
Example 6.11 Here’s an application of the formulas.
1. Empty Core. Let v(12) = 5, v(13) = 6, v(23) = 8, v(123) = 9. All the others are zero. First, the core is
which is clearly empty since if there was an allocation in the core we would have 5 ≤ x1 + x2 ≤ 4. So we can use the empty core formulas in Theorem 6.2.2 to get
Similarly, x2 = 
, x3 = 9 − x1 − x2 = .
2. Nonempty Core. Take v(i) = 0, i = 1, 2, 3, and v(12) = 1, v(13) = 4, v(23) = 3, v(123) = 6. Using Proposition 6.1.7, we have for the normalized characteristic function 
,
Next, we have to verify one of the sets of conditions in the Theorem 6.2.3. Since
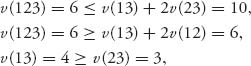
the third case of the theorem (with i = 3, j = 1, k = 2) is satisfied. Using the formulas, there we have
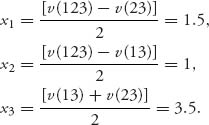
The next example illustrates the application of cost allocation in a municipal water problem.
Example 6.12 Three cities are to be connected to a water tower at a central location. Label the three cities 1, 2, 3 and the water tower as 0. The cost to lay pipe connecting location i with location j is denoted as cij, i ≠ j. Figure 6.7 contains the data for our problem.
Coalitions among cities can form for pipe to be laid to the water tower. For example, it is possible for city 1 and city 3 to join up so that the cost to the coalition {13} would be the sum of the cost of going from 1 to 3 and then 3 to 0. It may be possible to connect from 1 to 3 to 0 but not from 3 to 1 to 0 depending on land conditions. We have the following costs in which we do not treat the water tower as a player:
The single-player coalitions correspond to hooking up that city directly to location 0. Converting this to a savings game, we let c(S) be the total cost for coalition S and
This is a three-player game and we calculate the characteristic function as
We find the nucleolus of this game using the Theorem 6.2.3. First, let’s check to see if the core is empty. Using Proposition 6.1.7, we see that for the normalized characteristic function 
and so we have a nonempty core.
Since we have a nonempty core, we must check the cases in the theorem. We check
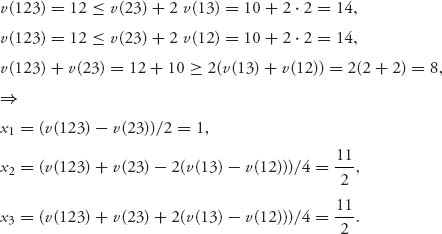
The conclusion is that the nucleolus is = {(1, 
, )} . Our conclusion is that of the 12 units of savings possible for all the cities to cooperate, city 1 only gets 1 unit, while cities 2 and 3 get units each. It makes sense that city 1 would get the least because city 1 brings the least benefit to any coalition compared with 2 and 3.
The next example shows how cooperative game theory can be applied to important transport problems with applications in many areas including computer science.
Example 6.13 Shortest Path Routing (Figure 6.8). Let c(S) denote the total mileage driven in order to inspect the machinery of towns in S.
The home headquarters is Chicago. We have the choice of going to each city in a round trip or combining cities. We have (with Minneapolis = 1, St Louis = 2, Detroit = 3)
and c(123) = 1500. We are ignoring things like hotels and other expenses but these too can be taken into account. The characteristic function for a cost savings game is v(S) = ∑i S ci − c(S), and we get
Using Proposition 6.1.7, we have that v′(12) + v′(13) + v′(23) = 1 ≤ 2, where 
is the normalized characteristic function, and hence, we have a nonempty core. Since
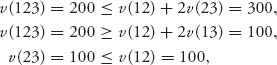
we use the formulas from Theorem 6.2.3 and get the allocation of cost savings:
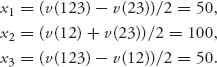
Remark The examples make it look like finding which set of conditions in Theorem 6.2.3 is easy. It is easy but extremely time consuming if you do it by hand. Leng and Parlar (2010) wrote a Maple procedure to do the calculations. A Mathematica translation is provided at the end of this chapter. The Mathematica notebook is available from my web site www.math.luc.edu/∼enb.