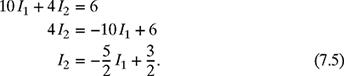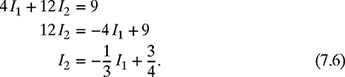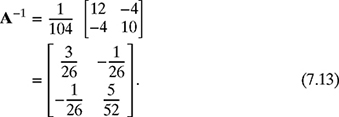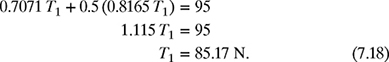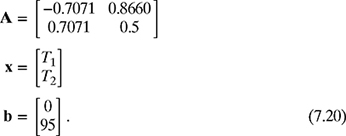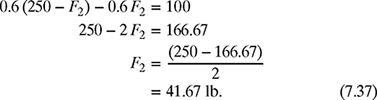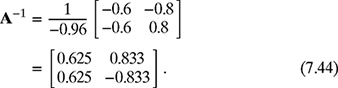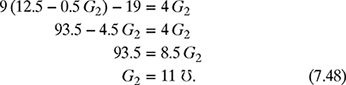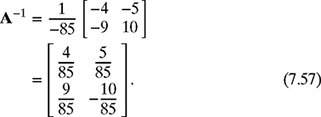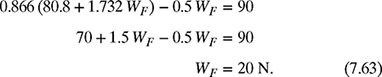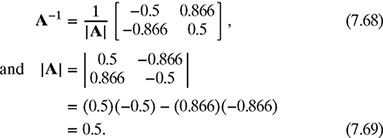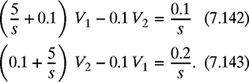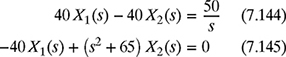Systems of Equations in Engineering

CHAPTER 7

7.1 INTRODUCTION

The solution of a system of linear equations is an important topic for all engineering disciplines. In this chapter, the solution of 2 × 2 systems of equations will be carried out using four different methods: substitution method, graphical method, matrix algebra method, and Cramer's rule. It is assumed that the students are already familiar with the substitution and graphical methods from their high school algebra course, while the matrix algebra method and Cramer's rule are explained in detail. The objective of this chapter is to be able to solve the systems of equations encountered in beginning engineering courses such as physics, statics, dynamics, and DC circuit analysis. While the examples given are limited to 2 × 2 systems of equations, the matrix algebra approach is applicable to linear systems having any number of unknowns and is suitable for immediate implementation in MATLAB.

7.2 SOLUTION OF A TWO-LOOP CIRCUIT

Consider a two-loop resistive circuit with unknown currents I₁ and I₂ as shown in Fig. 7.1. Using a combination of Kirchhoff's voltage law (KVL) and Ohm's law, a system of two equations with two unknowns I₁ and I₂ can be obtained as

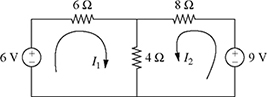
Figure 7.1 A two-loop resistive circuit.

Equations (7.1) and (7.2) represent a system of equations for I₁ and I₂ that can be solved using the four different methods outlined as follows:

1. Substitution Method: Solving equation (7.1) for the first variable I₁ gives

   

   The current I₂ can now be solved by substituting I₁ from equation (7.3) into equation (7.2), which gives

   

   The current I₁ can now be obtained by substituting the value of the second variable I₂ from equation (7.4) into equation (7.3) as

   

   Therefore, the solution of the system of equations (7.1) and (7.2) is given by

   (I₁, I₂) = (0.3462 A, 0.6346 A).

2. Graphical Method: Begin by assuming I₁ as the independent variable and I₂ as the dependent variable. Solving equation (7.1) for the dependent variable I₂ gives

   

   Similarly, solving equation (7.2) for I₂ gives

   

   Equations (7.5) and (7.6) are linear equations of the form y = mx + b. The simultaneous solution of equations (7.5) and (7.6) is the intersection point of the two lines. The plot of the two straight lines along with their intersection point is shown in Fig. 7.2. The intersection point, (I₁, I₂) ≈ (0.35A, 0.63A), is the solution of the 2 × 2 system of equations (7.1) and (7.2).

   

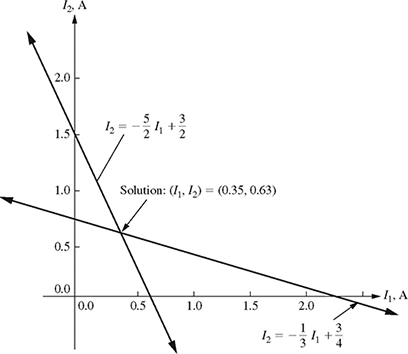
   Figure 7.2 Plot of 2 × 2 system of equations (7.1) and (7.2).

   Note that the graphical method gives only approximate results; therefore, this method is generally not used when an accurate result is needed. Also, if the two lines do not intersect, then one of the following two possibilities exist:

   (i) The two lines are parallel lines (same slope but different y-intercepts) and the system of equations has no solution.

   (ii) The two lines are parallel lines with same slope and y-intercept (the two lines lie on top of each other; they are the same line) and the system of equations has infinitely many solutions. In this case, the two equations are dependent (i.e., one equation can be obtained by performing linear operations on the other equation).

3. Matrix Algebra Method: The matrix algebra method can also be used to solve the system of equations given by equations (7.1) and (7.2). Rewriting the system of equations (7.1) and (7.2) in the form so that the two variables line up gives

   

   

   Now, writing equations (7.7) and (7.8) in matrix form yields

   

   Equation (7.9) is of the form Ax = b, where

   

   is a 2 × 2 coefficient matrix,

   

   is a 2 × 1 matrix (column vector) of unknowns, and

   

   is a 2 × 1 matrix on the right-hand side (RHS) of equation (7.9) For any system of the form Ax = b, the solution is given by

   x = A⁻¹ b

   where A⁻¹ is the inverse of the matrix A. For a 2 × 2 system of equations where

   

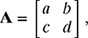
   the inverse of the matrix A is given by

   

   where Δ = ∣A∣ is the determinant of matrix A and is given by

   

   Note that if Δ = ∣A∣ = 0, A⁻¹ does not exist. In other words, the system of equations Ax = b has no solution. Now, for the two-loop circuit problem,

   

   The inverse of matrix A is given by

   

   where Δ = ∣A∣ = ad − cb = (10) (12) − (4) (4) = 104. Therefore, the inverse of matrix A can be calculated as

   

   The solution of the system of equations 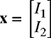can now be found by multiplying A⁻¹ (given by equation (7.13)) with the column matrix b (given by equation (7.12)) as

   

   The solution of the system of equations (7.1) and (7.2) is therefore given by

   (I₁, I₂) = (0.3462A, 0.6346A).

4. Cramer's Rule: For any system Ax = b, the solution of the system of equations is given by

   

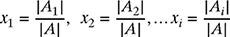
   where ∣A_i∣ is obtained by replacing the ith column of the matrix A with the column vector b. Writing the 2 × 2 system of equations

   a₁₁ x₁ + a₁₂ x₂ = b₁
   a₂₁ x₁ + a₂₂ x₂ = b₂

   in matrix form as

   

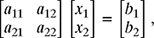
   Cramer's rule gives the solution of the system of equations as

   

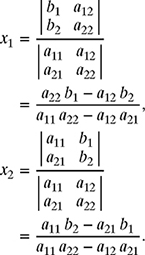
   For the two-loop circuit, the 2 × 2 system of equations is

   

   Using Cramer's rule, the currents I₁ and I₂ can be determined as

   

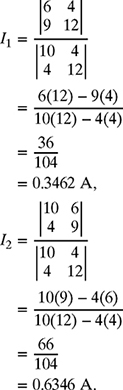
   Therefore, I₁ = 0.3462 A and I₂ = 0.6346 A. Note that Cramer's rule is probably fastest for solving 2 × 2 systems but not faster than MATLAB.

7.3 TENSION IN CABLES

An object weighing 95 N is hanging from a roof with two cables as shown in Fig. 7.3. Determine the tension in each cable using the substitution, matrix algebra, and Cramer's rule methods.

Since the system shown in Fig. 7.3 is in equilibrium, the sum of all the forces shown in the free-body diagram must be equal to zero. This implies that all the forces in the x- and y-directions are equal to zero (see Chapter 4). The components of the tension in the x- and y-directions are given by −T₁ cos(45°) N and T₁ sin(45°) N, respectively. Similarly, the components of the tension in the x- and y-directions are given by T₂ cos(30°) N and T₂ sin(30°) N, respectively. The components of the object weight is 0 N in the x-direction and −95 N in the y-direction. Summing all the forces in the x-direction gives

Figure 7.3 A 95 N object hanging from two cables.

Similarly, summing the forces in the y-direction yields

Equations (7.14) and (7.15) make a 2 × 2 system of equations with two unknowns T₁ and T₂ that can be written in matrix form as

The solution of the system of equations (T₁ and T₂) will now be obtained using three methods: the substitution method, the matrix algebra method, and Cramer's rule.

1. Substitution Method: Using equation (7.14), the second variable T₂ is found in terms of the first variable T₁ as

   

   Substituting T₂ from equation (7.17) into equation (7.15) gives

   

   Now, substituting T₁ obtained in equation (7.18) into equation (7.17) yields

   

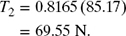
   Therefore, T₁ = 85.2 N and T₂ = 69.6 N.

2. Matrix Algebra Method: The two unknowns (T₁ and T₂) in the 2 × 2 system of equations (7.14) and (7.15) are now determined using the matrix algebra method. Write equations (7.14) and (7.15) in the matrix form as

   

   where matrices A, x, and b are given by

   

   Therefore, the solution of the 2 × 2 system of equations can be found by solving equation (7.19) as

   

   where A⁻¹ is the inverse of matrix A. If A , then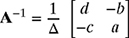

   

   where Δ = ad − bc. Since, for this example, a = −0.7071, b = 0.8660, c = 0.7071, and d = 0.5, therefore,

   

   Substituting matrices A⁻¹ from equation (7.22) and b from equation (7.20) into equation (7.21) gives

   

   Therefore, T₁ = 85.2 N and T₂ = 69.6 N.

3. Cramer's Rule: The two unknowns (T₁ and T₂) in the 2 × 2 system of equations (7.14) and (7.15) are now determined using Cramer's rule. Using matrix equation (7.19), the tensions T₁ and T₂ can be found as

   

   Therefore, T₁ = 85.2 N and T₂ = 69.6 N.

7.4 FURTHER EXAMPLES OF SYSTEMS OF EQUATIONS IN ENGINEERING

Solution

(a) Substitution Method: Using equation (7.23), find R₁ in terms of R₂ as

Substituting R₁ from equation (7.25) into equation (7.24) gives

Now, substituting R₂ from equation (7.26) into equation (7.25) yields

Therefore, R₁ = 1920 lb and R₂ =; 2880 lb.

(b) Writing equations (7.23) and (7.24) in the matrix form gives

(c) Matrix Algebra Method: From the matrix equation (7.27), the matrices A, x, and b are given by

The reaction forces can be found by finding the inverse of matrix A and then multiplying this with column matrix b as

x = A⁻¹ b

where

and

Substituting equation (7.32) in equation (7.31), the inverse of matrix A is given by

The reaction forces can now be found by multiplying A⁻¹ in equation (7.33) with matrix b given in equation (7.29) as

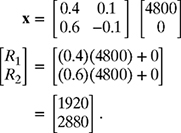
Therefore, R₁ = 1920 lb and R₂ = 2880 lb.

(d) Cramer's Rule: The reaction forces R₁ and R₂ can be found by solving the system of equations (7.23) and (7.24) using Cramer's rule as

Therefore, R₁ = 1920 lb and R₂ = 2880 lb.

Solution

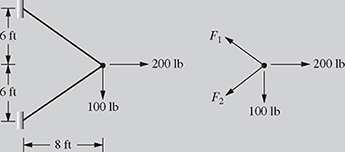
(a) Substitution Method: Using equation (7.34), find force F₁ in terms of F₂ as

Substituting F₁ from equation (7.36) into equation (7.35) gives

Now, substituting F₂ from equation (7.37) into equation (7.36) yields

Therefore, F₁ = 208.33 lb and F₂ = 41.67 lb.

(b) Writing equations (7.34) and (7.35) in the matrix form yields

(c) Matrix Algebra Method: Writing matrix equation in (7.38) in the form Ax = b gives

The forces F₁ and F₂ can be found by finding the inverse of matrix A and then multiplying this with matrix b as

x = A⁻¹ b

where

and

Substituting equation (7.43) in equation (7.42), the inverse of matrix A is given by

The forces F₁ and F₂ can now be found by multiplying A⁻¹ in equation (7.44) by column matrix b given in equation (7.40) as

Therefore, F₁ = 208.33 lb and F₂ = 41.67 lb.

(d) Cramer's Rule: The forces F₁ and F₂ can be found by solving the system of equations (7.34) and (7.35) using Cramer's rule as

Therefore, F₁ = 208.33 lb and R₂ = 41.67 lb.

Solution

(a) Substitution Method: Using equation (7.45), find the admittance G₁ in terms of G₂ as

Substituting G₁ from equation (7.47) into equation (7.46) gives

Now, substituting G₂ from equation (7.48) into equation (7.47) yields

Therefore, G₁ = 7 ℧ and G₂ = 11 ℧.

(b) Rewrite equations (7.45) and (7.46) in the form

Now, write equations (7.49) and (7.50) in matrix form as

(c) Matrix Algebra Method: Writing the matrix equation in (7.64) in the form Ax = b gives

The admittance G₁ and G₂ can be found by finding the inverse of matrix A and then multiplying this with matrix b as

x = A⁻¹ b

where

and

Substituting equation (7.56) in equation (7.55), the inverse of matrix A is given as

The admittance G₁ and G₂ can now be found by multiplying A⁻¹ in equation (7.57) and the column matrix b given in equation (7.53) as

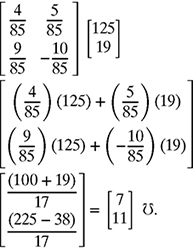
Therefore, G₁ = 7 ℧ and G₂ =11 ℧.

(d) Cramer's Rule: The admittance G₁ and G₂ can be found by solving the system of equations (7.45) and (7.46) using Cramer's rule as

Therefore, G₁ = 7 ℧ and G₂ =11 ℧.

Solution

(a) Rewriting equations (7.58) and (7.59) in terms of given information yields

(b) Substitution Method: Using equation (7.60), find the force F_m in terms of W_F as

Substituting F_m from equation (7.62) into equation (7.61) gives

Now, substituting W_F from equation (7.63) into equation (7.62) yields

Therefore, F_m = 115.4 N and W_F = 20 N.

(c) Writing equations (7.60) and (7.61) in the matrix form Ax = b gives

where

(d) Matrix Algebra Method: The forces F_m and W_F can be found by finding the inverse of the matrix A and then multiplying this by vector b as

x = A⁻¹ b,

where

Substituting equation (7.69) in equation (7.68), the inverse of matrix A is given as

The forces F_m and W_F can now be found by multiplying A⁻¹ in equation (7.70) and the column matrix b given in equation (7.66) as

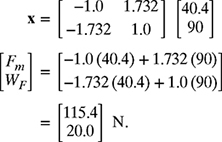
Therefore, F_m = 115.4 N and W_F = 20 N.

(e) Cramer's Rule: The forces F_m and W_F can be found by solving the system of equations (7.60) and (7.61) using Cramer's rule as

Therefore, F_m = 115.4 N and W_F = 20 N.

Solution

(a) Rewriting equations (7.71) and (7.72) in terms of the given information yields

(b) Substitution Method: Using equation (7.73), find the volume v₂ in terms of v₁ as

Substituting v₂ from equation (7.75) into equation (7.74) gives

Now, substituting v₁ from equation (7.76) into equation (7.75) yields

Therefore, v₁ = 400 L and v₂ = 600 L.

(c) Writing equations (7.73) and (7.74) in matrix form Ax = b gives

where

and

(d) Matrix Algebra Method: The volumes v₁ and v₂ can be found by finding the inverse of the matrix A and then multiplying this by column vector b as

x = A⁻¹ b,

where

Substituting equation (7.82) in equation (7.81), the inverse of matrix A is given as

The volumes v₁ and v₂ can now be found by multiplying A⁻¹ in equation (7.83) and the column vector b given in equation (7.79) as

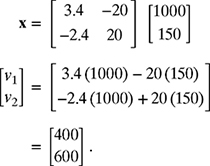
Therefore, v₁= 400 L and v₂ = 600 L.

(e) Cramer's Rule: The volumes v₁ and v₂ can be found by solving the system of equations (7.73) and (7.74) using Cramer's rule as

Therefore, v₁ = 400 L and v₂ = 600 L.

PROBLEMS

1. 7-1. Consider the two-loop circuit shown in Fig. P7.1. The currents I₁ and I₂ (in A) satisfy the following system of equations:

   

   

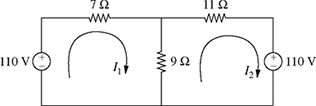
   Figure P7.1 Two-loop circuit for problem P7-1.

   (a) Find I₁ and I₂ using the substitution method.

   (b) Write the system of equations (7.84) and (7.85) in the matrix form AI = b, where I = .

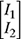   (c) Find I₁ and I₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find I₁ and I₂ using Cramer's rule.

2. 7-2. Consider the two-loop circuit shown in Fig. P7.2. The currents I₁ and I₂ (in A) satisfy the following system of equations:

   

   

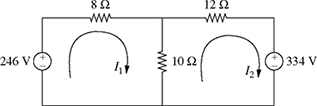
   Figure P7.2 Two-loop circuit for problem P7-2.

   (a) Find I₁ and I₂ using the substitution method.

   (b) Write the system of equations (7.86) and (7.87) in the matrix form AI = b, where .

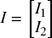   (c) Find I₁ and I₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find I₁ and I₂ using Cramer's rule.

3. 7-3. Consider the two-loop circuit shown in Fig. P7.3. The currents I₁ and I₂ (in A) satisfy the following system of equations:

   

   

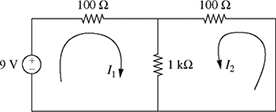
   Figure P7.3 Two-loop circuit for problem P7-3.

   (a) Find I₁ and I₂ using the substitution method.

   (b) Write the system of equations (7.88) and (7.89) in the matrix form AI = b, where .

   (c) Find I₁ and I₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find I₁ and I₂ using Cramer's rule.

4. 7-4. Consider the two-node circuit shown in Fig. P7.4. The voltages V₁ and V₂ (in V) satisfy the following system of equations:

   

   

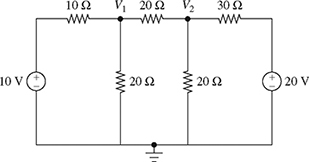
   Figure P7.4 Two-node circuit for problem P7-4.

   (a) Find V₁ and V₂ using the substitution method.

   (b) Write the system of equations (7.90) and (7.91) in the matrix form AV = b, where .

   (c) Find V₁ and V₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find V₁ and V₂ using Cramer's rule.

5. 7-5. Consider the two-node circuit shown in Fig. P7.5. The voltages V₁ and V₂ (in V) satisfy the following system of equations:

   

   

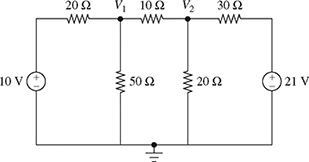
   Figure P7.5 Two-node circuit for problem P7-5.

   (a) Find V₁ and V₂ using the substitution method.

   (b) Write the system of equations (7.92) and (7.93) in the matrix form AV = b, where .

   (c) Find V₁ and V₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find V₁ and V₂ using Cramer's rule.

6. 7-6. Consider the two-node circuit shown in Fig. P7.6. The voltages V₁ and V₂ (in V) satisfy the following system of equations:

   

   

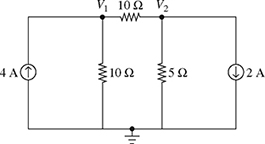
   Figure P7.6 Two-node circuit for problem P7-6.

   (a) Find V₁ and V₂ using the substitution method.

   (b) Write the system of equations (7.94) and (7.95) in the matrix form AV = b, where .

   (c) Find V₁ and V₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find V₁ and V₂ using Cramer's rule.

7. 7-7. An analysis of the circuit shown in Fig. P7.7 yields the following system of equations:

   

   

   Figure P7.7 Two-node circuit for problem P7-7.

   (a) Find V₁ and V₂ using the substitution method.

   (b) Write the system of equations (7.96) and (7.97) in the matrix form AV = b, where .

   (c) Find V₁ and V₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find V₁ and V₂ using Cramer's rule.

8. 7-8. A summing Op-Amp circuit is shown in Fig. 7.6. An analysis of the Op-Amp circuit shows that the admittances G₁ and G₂ in mho (℧) satisfy the following system of equations:

   

   (a) Find G₁ and G₂ using the substitution method.

   (b) Write the system of equations (7.98) and (7.99) in the matrix form AG = b, where .

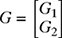   (c) Find G₁ and G₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find G₁ and G₂ using Cramer's rule.

9. 7-9. A summing Op-Amp circuit is shown in Fig. 7.6. An analysis of the Op-Amp circuit shows that the admittances G₁ and G₂ in mho (℧) satisfy the following system of equations:

   

   (a) Find G₁ and G₂ using the substitution method.

   (b) Write the system of equations (7.100) and (7.101) in the matrix form AG = b, where .

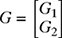   (c) Find G₁ and G₂ using the matrix algebra method. Perform all computations by hand and show all steps.

   (d) Find G₁ and G₂ using Cramer's rule.

10. 7-10. A 20 kg object is suspended by two cables as shown in Fig. P7.10. The tensions T₁ and T₂ satisfy the following system of equations:

    

    

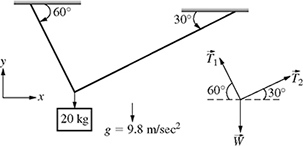
    Figure P7.10 A 20 kg object suspended by two cables for problem P7-10.

    (a) Write the system of equations (7.100) and (7.101) in the matrix form AT = b, where

    

    In other words, find matrices A and b. What are the dimensions of A and b?

    (b) Find T₁ and T₂ using the matrix algebra method. Perform all matrix computation by hand.

    (c) Find T₁ and T₂ using Cramer's rule.

11. 7-11. A 100 lb weight is suspended by two cables as shown in Fig. P7.11. The tensions T₁ and T₂ satisfy the following system of equations:

    

    (a) Write the system of equations (7.104) and (7.105) in the matrix form Ax = b, where

    

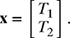
    In other words, find matrices A and b.

    (b) Find T₁ and T₂ using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (c) Find T₁ and T₂ using Cramer's rule.

    

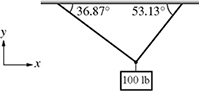
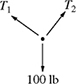
    Figure P7.11 A 100 lb weight suspended by two cables for problem P7-11.

12. 7-12. A two-bar truss supports a weight of W = 750 lb as shown in Fig. P7.12. The forces F₁ and F₂ satisfy the following system of equations:

    

    (a) Write the system of equations (7.106) and (7.107) in the matrix form AF = b, where

    

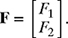
    In other words, find matrices A and b.

    (b) Find F₁ and F₂ using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (c) Find F₁ and F₂ using Cramer's rule.

    

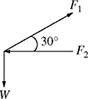
    Figure P7.12 A two-bar truss supporting a weight for problem P7-12.

13. 7-13. A 10 kg object is suspended from a two-bar truss shown in Fig. P7.13. The forces F₁ and F₂ satisfy the following system of equations:

    

    

    Figure P7.13 An object suspended from a two-bar truss for problem P7-13.

    (a) Write the system of equations (7.108) and (7.109) in the matrix form AF = b, where

    

    In other words, find matrices A and b.

    (b) Find F₁ and F₂ using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (c) Find F₁ and F₂ using Cramer's rule.

14. 7-14. A F = 100 N force is applied to a two-bar truss as shown in Fig. P7.14. The forces F₁ and F₂ satisfy the following system of equations:

    

    (a) Write the system of equations (7.110) and (7.111) in the matrix form AF = b, where

    

    In other words, find matrices A and b.

    (b) Find F₁ and F₂ using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (c) Find F₁ and F₂ using Cramer's rule.

    

    Figure P7.14 A 100 N force applied to a two-bar truss for problem P7-14.

15. 7-15. A force F = 200 lb is applied to a two-bar truss as shown in Fig. P7.15. The forces F₁ and F₂ satisfy the following system of equations:

    

    (a) Write the system of equations (7.112) and (7.113) in the matrix form AF = b, where

    

    In other words, find matrices A and b.

    (b) Find F₁ and F₂ using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (c) Find F₁ and F₂ using Cramer's rule.

    

    Figure P7.15 A 200 lb force applied to a two-bar truss for problem P7-15.

16. 7-16. The weight of a vehicle is supported by reaction forces at its front and rear wheels as shown in Fig. P7.16. If the weight of the vehicle is W = 4800 lb, the reaction forces R₁ and R₂ satisfy the following system of equations:

    

    (a) Find R₁ and R₂ using the substitution method.

    (b) Write the system of equations (7.114) and (7.115) in the matrix form Ax = b, where

    

    In other words, find matrices A and b.

    (c) Find R₁ and R₂ using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (d) Find R₁ and R₂ using Cramer's rule.

    

    Figure P7.16 A vehicle supported by reaction forces.

17. 7-17. Solve problem P7-16 if the system of equations are given by equations (7.116) and (7.117).

    

18. 7-18. Solve problem P7-16 if the system of equations are given by (7.118) and (7.119).

    

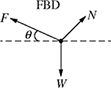
19. 7-19. A vehicle weighing W = 10 kN is parked on an inclined driveway (θ = 21.8°) as shown in Fig. P7.19. The forces F and N satisfy the following system of equations:

    

    where forces F and N are in kN.

    (a) Write the system of equations (7.120) and (7.121). in the matrix form Ax = b, where

    

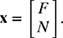
    In other words, find matrices A and b.

    (b) Find F and N using the matrix algebra method. Perform all matrix computations by hand and show all steps.

    (c) Find F and N using Cramer's rule.

    

    Figure P7.19 A truck parked on an inclined driveway.

20. 7-20. A vehicle weighing W = 2000 lb is parked on an inclined driveway (θ = 35°) as shown in Fig. P7.19. The forces F and N satisfy the following system of equations:

    

    where forces F and N are in lb. Solve parts (a)–(c) of problem P7-19 for system of equations given by (7.122) and (7.123).

21. 7-21. A 100 lb crate weighing W = 100 lb is pushed against an incline (θ = 30°) with a force of F_a = 30 lb as shown in Fig. P7.21. The forces F_f and N satisfy the following system of equations:

    

    (a) Write the system of equations (7.124) and (7.125) in the matrix form Ax = b, where

    

    In other words, find matrices A and b.

    (b) Find F_f and N using the matrix algebra method. Perform all matrix computation by hand and show all steps.

    (c) Find F_f and N using Cramer's rule.

    

    Figure P7.21 A crate being pushed by a force.

22. 7-22. A crate weighing W = 500 N is pushed against an incline (θ = 20°) with a force of F_a = 100 N as shown in Fig. P7.21. The forces F_f and N satisfy the following system of equations:

    

    Solve parts (a)–(c) of problem P7-21 for system of equations given by (7.126) and (7.127).

23. 7-23. A 100 kg desk rests on a horizontal plane with a coefficient of friction of μ = 0.4. It is pulled with a force of F = 800 N at an angle of θ = 45° as shown in Fig. P7.23. The normal force N_f and acceleration a in m/s² satisfy the following system of equations:

    

    (a) Find N_f and a using the substitution method.

    (b) Write the system of equations (7.128) and (7.129) in the matrix form Ax = b, where

    

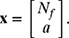
    In other words, find matrices A and b.

    (c) Find N_f and a using the matrix algebra method.

    (d) Find N_f and a using Cramer's rule.

    

    Figure P7.23 Desk being pulled by a force F.

24. 7-24. A 200 kg desk rests on a horizontal plane with a coefficient of friction of μ = 0.3. It is pulled with a force of F = 1000 N at an angle of θ = 20° as shown in Fig. P7.23. The normal force N_f and acceleration a in m/s² satisfy the following system of equations:

    

    Solve parts (a)–(d) of problem P7-23 for system of equations (7.130) and (7.131).

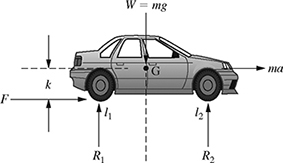
25. 7-25. The weight of a vehicle is supported by reaction forces at its front and rear wheels as shown in Fig. P7.25. The reaction forces R₁ and R₂ satisfy the following system of equations:

    

    (a) Write the system of equations (7.132) and (7.133) if l₁ = 2 m, l₂ = 1.5 m, k = 1.5 m, g = 9.81 m/s², m = 1000 kg, and a = 5 m/s².

    (b) For the system of equations found in part (a), find R₁ and R₂ using the substitution method.

    (c) Write the system of equations in the matrix form Ax = b, where

    

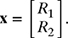
    In other words, find matrices A and b.

    (d) Find R₁ and R₂ using the matrix algebra method.

    (e) Find R₁ and R₂ using Cramer's rule.

    

    Figure P7.25 A vehicle supported by reaction forces.

26. 7-26. Repeat problem P7-25, if l₁ = 2 m, l₂ = 1.5 m, k = 1.5 m, g = 9.81 m/s², m = 1000 kg, and a = −5 m/s².

27. 7-27. Repeat problem P7-25, if l₁ = 2 m, l₂ = 2 m, k = 1.5 m, g = 9.81 m/s², m = 1200 kg, and a = 4.5 m/s².

28. 7-28. Repeat problem P7-25, if l₁ = 2 m, l₂ = 2 m, k = 1.5 m, g = 9.81 m/s², m = 1200 kg, and a = −4.5 m/s^2.

29. 7-29. A driver applies a steady force of F_P = 25 N against a gas pedal, as shown in Fig. P7.29. The free-body diagram of the driver's foot is also shown. Based on the x-y coordinate system shown, the force of the gastrocnemius muscle F_m and the weight of the foot W_F satisfy the following system of equations:

    

    

    Figure P7.29 A driver applying a steady force against the gas pedal.

    (a) Knowing that N and R_y = 105 N, rewrite the system of equations (7.134) and (7.135) in terms of F_m and W_F.

    (b) Find F_m and W_F using the substitution method.

    (c) Write the system of equations obtained in part (a) in the matrix form Ax = b, where .

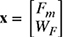    (d) Find F_m and W_F using the matrix algebra method. Perform all computations by hand and show all steps.

    (e) Find F_m and W_F using Cramer's rule.

30. 7-30. An environmental engineer wishes to blend a single mixture of insecticide spray solution of volume V = 500 L with a specified concentration C = 0.2 from two spray solutions of concentration c₁ = 0.15 and c₂ = 0.25. The required volumes of the two spray solutions v₁ and v₂ can be determined from a system of equations describing conditions for volume and concentration, respectively as

    

    (a) Knowing that V = 500 L, c₁ = 0.15, c₂ = 0.25, and C = 0.2, rewrite the system of equations (7.136) and (7.137) in terms of v₁ and v₂.

    (b) Find v₁ and v₂ using the substitution method.

    (c) Write the system of equations obtained in part (a) in the matrix form Ax = b, where .

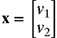    (d) Find v₁ and v₂ using the matrix algebra method. Perform all computations by hand and show all steps.

    (e) Find v₁ and v₂ using Cramer's rule.

31. 7-31. Repeat problem P7-30 if V = 400 L, C = 0.25, c₁ = 0.2, and c₂ = 0.4.

32. 7-32. Consider the two-loop circuit shown in Fig. P7.32. The currents I₁ and I₂ (in A) satisfy the following system of equations:

    

    

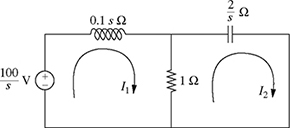
    Figure P7.32 Two-loop circuit for problem P7-32.

    (a) Find I₁ and I₂ using the substitution method.

    (b) Write the system of equations (7.138) and (7.139) in the matrix form AI = b, where .

    (c) Find I₁ and I₂ using the matrix algebra method.

    (d) Find I₁ and I₂ using Cramer's rule.

33. 7-33. Consider the two-loop circuit shown in Fig. P7.33. The currents I₁ and I₂ (in A) satisfy the following system of equations:

    

    

    

    Figure P7.33 Two-loop circuit for problem P7-33.

    (a) Find I₁ and I₂ using the the substitution method.

    (b) Write the system of equations (7.140) and (7.141) in the matrix form AI = b, where .

    (c) Find I₁ and I₂ using the matrix algebra method.

    (d) Find I₁ and I₂ using Cramer's rule.

34. 7-34. Consider the two-node circuit shown in Fig. P7.34. The voltages V₁ and V₂ (in V) satisfy the following system of equations:

    

    

    Figure P7.34 Two-loop circuit for problem P7-34.

    (a) Write the system of equations (7.142) and (7.143) in the matrix form AV = b, where .

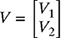    (b) Find V₁ and V₂ using the matrix algebra method.

    (c) Find V₁ and V₂ using Cramer's rule.

35. 7-35. A mechanical system along with its free body diagram is shown in Fig. P7.35, where f = 50 N is the applied force. The linear displacements X₁(s) and X₂(s) of the two springs in the s-domain satisfy the following system of equations:

    

    (a) Write the system of equations (7.144) and (7.145) in the matrix form AX(s) = b, where X(s) = .

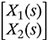    (b) Find the expressions of X₁(s) and X₂(s) using the matrix algebra method.

    (c) Find the expressions of X₁(s) and X₂(s) using Cramer's rule.

    

    Figure P7.35 Mechanical system for problem P7-35.

36. 7-36. Fig. P7.36 shows a system with two-mass elements and two springs. The mass m₁ is pulled with a force f = 100 N, and the displacements X₁(s) and X₂(s) of the two masses in the s-domain satisfy the following system of equations:

    

    

    Figure P7.36 Mechanical system for problem P7-36.

    (a) Write the system of equations (7.146) and (7.146) in the matrix form AX(s) = b, where X(s) = .

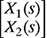    (b) Find the expressions of X₁(s) and X₂(s) using the matrix algebra method.

    (c) Find the expressions of X₁(s) and X₂(s) using Cramer's rule.

37. 7-37. A co-op student at a composite materials manufacturing company is attempting to determine how much of two different composite materials to make from the available quantities of carbon fiber and resin. The student knows that Composite A requires 0.15 pounds of carbon fiber and 1.6 ounces of polymer resin while Composite B requires 3.2 pounds of carbon fiber and 2.0 ounces of polymer resin. If the available quantities of carbon fiber and resin are 15 pounds and 10 ounces, respectively, the amount of each composite to manufacture satisfies the system of equations:

    

    where x_A and x_B are the amounts of Composite A and B (in pounds), respectively.

    (a) Find x_A and x_B using the substitution method.

    (b) Write the system of equations (7.148) and (7.149) in the matrix form Ax = b, where .

    (c) Find x_A and x_B using the matrix algebra method. Perform computation by hand and show all steps.

    (d) Find x_A and x_B using Cramer's rule.

38. 7-38. Repeat parts (a)–(d) of problem P7-37 if Composite A requires 1.6 pounds of carbon fiber and 0.5 ounces of polymer resin while Composite B requires 1.75 pounds of carbon fiber and 0.78 ounces of polymer resin. If the available quantities of carbon fiber and resin are 17 pounds and 12 ounces, respectively, the amount of each composite to manufacture satisfies the system of equations (7.150) and (7.151).

    

39. 7-39. A structural engineer is performing a finite element analysis on an aluminum truss support structure subjected to a load as shown in Fig. P7.39. By the finite element method, the displacements in the horizontal and vertical directions at the node where the load is applied can be determined from the system of equations:

    

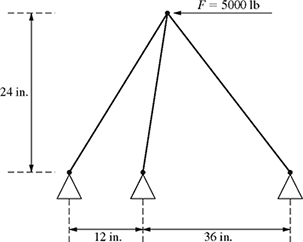
    Figure P7.39 Finite element idealization of truss structure subject to loading.

    

    where u and v are the the displacements in the horizontal and vertical directions, respectively.

    (a) Find u and v using the substitution method.

    (b) Write the system of equations (7.152) and (7.153) in the matrix form Ax = b, where .

    (c) Find u and v using the matrix algebra method. Perform computation by hand and show all steps.

    (d) Find u and v using Cramer's rule.

40. 7-40. A structural engineer is designing a crane that is to be used to unload barges at a dock. She is using a technique called finite element analysis to determine the displacement at the end of the crane. The finite element idealization of the crane structure picking up a 2000 lb load is shown in Fig. P7.40. The displacement in the horizontal and vertical directions at the end of the crane can be determined from the system of equations:

    

    where u and v are the the displacements in the horizontal and vertical directions, respectively.

    (a) Find u and v using the substitution method.

    (b) Write the system of equations (7.154) and (7.155) in the matrix form Ax = b, where .

    (c) Find u and v using the matrix algebra method. Perform computation by hand and show all steps.

    (d) Find u and v using Cramer's rule.

    

    Figure P7.40 Finite element idealization of crane structure subject to loading.