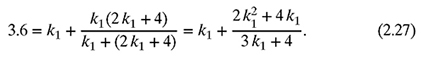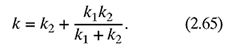Quadratic Equations in Engineering |
CHAPTER 2 |
In this chapter, the applications of quadratic equations in engineering are introduced. It is assumed that students are familiar with this topic from their high school algebra course. A quadratic equation is a second-order polynomial equation in one variable that occurs in many areas of engineering. For example, the height of a ball thrown in the air can be represented by a quadratic equation. In this chapter, the solution of quadratic equations will be obtained by three methods: factoring, the quadratic formula, and completing the square.
2.1 A PROJECTILE IN A VERTICAL PLANE
Suppose a ball thrown upward from the ground with an initial velocity of 96 ft/s reaches a height h(t) after time t s as shown in Fig. 2.1. The height is expressed by the quadratic equation h(t) = 96 t − 16 t2 ft. Find the time t in seconds when h(t) = 80 ft.

Figure 2.1 A ball thrown upward to a height of h(t).
Solution:
h(t) = 96 t − 16 t2 = 80
or
Equation (2.1) is a quadratic equation of the form ax2 + bx + c = 0 and will be solved using three different methods.
Method 1: Factoring Dividing equation (2.1) by 16 yields
Equation (2.2) can be factored as
(t − 1)(t − 5) = 0.
Therefore, t − 1 = 0 or t = 1 s and t − 5 = 0 or t = 5 s. Hence, the ball reaches the height of 80 ft at 1 s and 5 s.
Method 2: Quadratic Formula If ax2 + bx + c = 0, then the quadratic formula to solve for x is given by
Using the quadratic formula in equation (2.3), the quadratic equation (2.2) can be solved as

Therefore, ![]() and
and ![]() . Hence, the ball reaches the height of 80 ft at 1 s and 5 s.
. Hence, the ball reaches the height of 80 ft at 1 s and 5 s.
Method 3: Completing the Square First, rewrite the quadratic equation (2.2) as
Adding the square of ![]() (one-half the coefficient of the first-order term) to both sides of equation (2.4) gives
(one-half the coefficient of the first-order term) to both sides of equation (2.4) gives
![]()
or
Equation (2.5) can now be written as
![]()
or
t − 3 = ±2.
Therefore, t = 3 ± 2 or t = 1, 5 s. To check if the answer is correct, substitute t = 1 and t = 5 into equation (2.1). Substituting t = 1 s gives
16 × 1 − 96 × 1 + 80 = 0,
which gives 0 = 0. Therefore, t = 1 s is the correct time when the ball reaches a height of 80 ft. Now, substitute t = 5 s,
16 × 52 − 96 × 5 + 80 = 0,
which again gives 0 = 0. Therefore, t = 5 s is also the correct time when the ball reaches a height of 80 ft.
It can be seen from Fig. 2.2 that the height of the ball is 80 ft at both 1 s and 5 s. The ball is at 80 ft and going up at 1 s, and it is at 80 ft and going down at 5 s. Hence, the maximum height of ball must be halfway between 1 and 5 s, which is 1 + ((5 − 1)/2) = 3 s. Therefore, the maximum height can be found by substituting t = 3 s in h(t), which is h(3) = 96(3) − 16(3)2 = 144 ft. These three points (height at t = 1, 3, and 5 s) can be used to plot the trajectory of the ball. However, to plot the trajectory accurately, additional data points can be added. The height of the ball at t = 0 is zero since the ball is thrown upward from the ground. To check this, substitute t = 0 in h(t). This gives h(0) = 96(0) − 16(0)2 = 0 ft. The time when the ball hits the ground again can be calculated by equating h(t) = 0. Therefore,

Therefore, t = 0 and 6 − t = 0 or t = 6 s. Since the ball is thrown in the air from the ground (h(t) = 0) at t = 0, it will hit the ground again at t = 6 s. Using these data points, the trajectory of the ball thrown upward with an initial velocity of 96 ft/s is shown in Fig. 2.2.

Figure 2.2 The height of the ball thrown upward with an initial velocity of 96 ft/s.
Suppose now you wish to find the time t in seconds when the height of the ball reaches 144 ft. Setting h(t) = 144 gives
h(t) = 96 t − 16 t2 = 144.
16 t2 − 96 t + 144 = 0
or
The quadratic equation given in equation (2.6) can also be solved using the three methods as

Now suppose you wish to find the time t when the height of the ball reaches h(t) = 160 ft. Setting h(t) = 160 gives
h(t) = 96t − 16t2 = 160.
Therefore,
16t2 − 96t + 160 = 0
or
The quadratic equation given in equation (2.7) can be solved using the three methods as

In the above solution i = j = ![]() is the imaginary number, therefore the roots of the quadratic equation are complex. Hence, the ball never reaches the height of 160 ft. The maximum height achieved is 144 ft at 3 s.
is the imaginary number, therefore the roots of the quadratic equation are complex. Hence, the ball never reaches the height of 160 ft. The maximum height achieved is 144 ft at 3 s.
2.2 CURRENT IN A LAMP
A 100 W lamp and a 20 Ω resistor are connected in series to a 120 V power supply as shown in Fig. 2.3. The current I in amperes satisfies a quadratic equation as follows. Using KVL,
120 = VL + VR.

Figure 2.3 A lamp and a resistor connected to a 120 V supply.
From Ohm's law, VR = 20 I. Also, since the power is the product of voltage and current, PL = VL I = 100 W, which gives ![]() . Therefore,
. Therefore,
Multiplying both sides of equation (2.8) by I yields
Dividing both sides of equation (2.9) by 20 and rearranging gives
The quadratic equation given in equation (2.10) can be solved using the three methods as

Note that the two solutions correspond to two lamp choices.
Case I: For I = 1 A,
![]()
Case II: For I = 5 A,
![]()
Case I corresponds to a lamp rated at 100 V, and Case II corresponds to a lamp rated at 20 V.
2.3 EQUIVALENT RESISTANCE
Suppose two resistors are connected in parallel, as shown in Fig. 2.4. If the equivalent resistance ![]() and R1 = 4R2 + 100 Ω, find R1 and R2.
and R1 = 4R2 + 100 Ω, find R1 and R2.

Figure 2.4 Equivalent resistance of two resistors connected in parallel.
The equivalent resistance of two resistors connected in parallel as shown in Fig. 2.4 is given by
Substituting R1 = 4R2 + 100 Ω in equation (2.11) gives
Multiplying both sides of equation (2.12) by 5R2 + 100 yields
Simplifying equation (2.13) gives
Dividing both sides of equation by (2.14) by 4 gives
Equation (2.15) is a quadratic equation in R2 and cannot be factored with whole numbers. Therefore, R2 is solved using the quadratic formula as
![]()
Therefore,
![]()
Since R2 cannot be negative,
![]()
Substituting the value of R2 in R1 = 4R2 + 100 Ω yields
R1 = 4(120.7) + 100 = 582.8 Ω.
Therefore, R1 = 582.8 Ω and R2 = 120.7 Ω.
2.4 FURTHER EXAMPLES OF QUADRATIC EQUATIONS IN ENGINEERING
Example 2-1
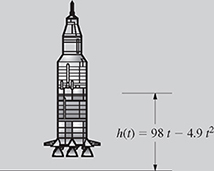
A model rocket is fired into the air from the ground with an initial velocity of 98 m/s as shown in Fig. 2.5. The height h(t) satisfies the quadratic equation
(a) Find the time when h(t) = 245 m.
(b) Find the time it takes the rocket to hit the ground.
(c) Use the results of parts (a) and (b) to sketch h(t) and determine the maximum height.
(a) Substituting h(t) = 245 in equation (2.16), the quadratic equation is given by
Dividing both sides of equation (2.17) by −4.9 gives
The quadratic equation given in equation (2.18) can be solved using the three methods used in Section 2.1 as

(b) Since the rocket hit the ground at h(t) = 0,
![]()
Therefore, t = 0 s and t = 20 s. Since the rocket is fired from the ground at t = 0 s, the rocket hits the ground again at t = 20 s.
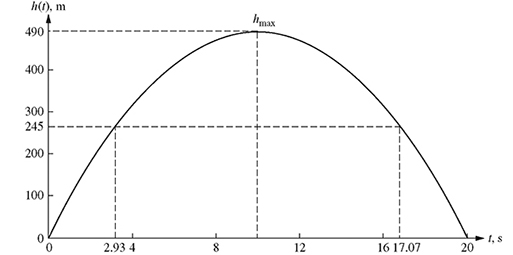
(c) The maximum height should occur halfway between 2.93 and 17.07 s. Therefore,
![]()
Substituting t = 10 s into equation (2.16) yields
hmax = 98(10) − 4.9(10)2 = 490 m.
The plot of the rocket trajectory is shown in Fig. 2.6. It can be seen from this figure that the rocket is fired from the ground at a height of zero at 0 s, crosses a height of 245 m at 2.93 s, and continues moving up and reaches the maximum height of 490 m at 10 s. At 10 seconds, it starts its downward descent and after crossing the height of 245 m again at 17.07 s, it reaches the ground again at 20 s
Figure 2.6 The height of the rocket fired vertically in the air with an initial velocity of 98 m/s.
Example 2-2
The equivalent resistance R of two resistors R1 and R2 connected in parallel as shown in Fig. 2.4 is given by
(a) Suppose R2 = 2R1 + 4 Ω and the equivalent resistance R = 8.0 Ω. Substitute these values in equation (2.19) to obtain the following quadratic equation for R1:
![]()
(b) Solve for R1 by each of the following methods:
(i) Completing the square.
(ii) The quadratic formula. Also, determine the value of R2 corresponding to the only physical solution for R1.
Solution
(a) Substituting R2 = 2R1 + 4 and R = 8.0 in equation (2.19) gives
Multiplying both sides of equation (2.20) by (3R1 + 4) yields
![]()
or
Rearranging terms in equation (2.21) gives
(b) The quadratic equation given in equation (2.22) can be now be solved to find the values of R1.
(i) Method 1: Completing the square:
Dividing both sides of equation (2.22) by 2 gives
Taking 16 on the other side of equation (2.23) and adding ![]() to both sides yields
to both sides yields
Now, writing both sides of equation (2.24) as squares yields
![]()
Therefore,
R1 − 5 = ±6.4,
which gives the values of R1 as 5 + 6.4 = 11.4 Ω and 5 − 6.4 = −1.4 Ω. Since the value of R1 cannot be negative, R1 = 11.4 Ω and R2 = 2R1 + 4 = 2(11.4) + 4 = 26.8 Ω.
(ii) Method 2: Solving equation (2.22) using the quadratic formula:
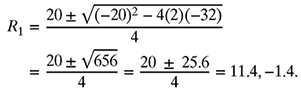
Since R1 cannot be negative, R1 = 11.4 Ω. Substituting R1 = 11.4 Ω in R2 = 2 R1 + 4 gives
R2 = 2(11.4) + 4 = 26.8 Ω.
Example 2-3
An assembly of springs shown in Fig. 2.7 has an equivalent stiffness k, given by
If k2 = 2k1 + 4 lb/in. and the equivalent stiffness is k = 3.6 lb/in., find k1 and k2 as follows:
(a) Substitute the values of k and k2 into equation (2.25) to obtain the following quadratic equation for k1:
(b) Using the method of your choice, solve equation (2.26) and determine the values of both k1 and k2.
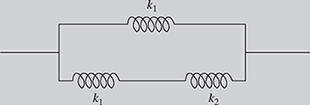
Solution
(a) Substituting k2 = 2k1 + 4 and k = 3.6 in equation (2.25) yields
Multiplying both sides of equation (2.27) by (3k1 + 4) gives
Rearranging terms in equation (2.28) gives
(b) The quadratic equation (2.29) can be solved using the quadratic formula as

Since k1 cannot be negative, k1 = 2.0 lb/in. Now, substituting k1 = 2.0 in k2 = 2k1 + 4 yields
k2 = 2(2) + 4 = 8.0.
Therefore,
k2 = 8.0 lb/in.
A capacitor C and an inductor L are connected in series as shown in Fig. 2.8. The total reactance X in ohms is given by ![]() , where ω is the angular frequency in rad/s.
, where ω is the angular frequency in rad/s.
(a) Suppose L = 1.0 H and C = 0.25 F. If the total reactance is X = 3.0 Ω, show that the angular frequency ω satisfies the quadratic equation ω2 − 3ω − 4 = 0.
(b) Solve the quadratic equation for ω by each of the following methods: factoring, completing the square, and the quadratic formula.
![]()
Solution
(a) The total reactance of the series combination of L and C shown in Fig. 2.8 is given by
Substituting L = 1.0 H, C = 0.25 F, and X = 3.0 Ω in equation (2.30) yields
Multiplying both sides of equation (2.31) by ω gives
Rearranging terms in equation (2.32) yields
(b) The quadratic equation (2.33) can be solved by three different methods: factoring, completing the squares, and the quadratic formula.
(i) Method 1: Factoring:
The quadratic equation (2.33) can be factored as
(ω − 4)(ω + 1) = 0,
which gives ω − 4 = 0 or ω + 1 = 0. Therefore, ω = 4 rad/s or ω = −1 rad/s. Since ω cannot be negative, ω = 4 rad/s.
(ii) Method 2: Completing the squares:
The quadratic equation (2.33) can be written as
Adding ![]() to both sides of equation (2.34) gives
to both sides of equation (2.34) gives

Therefore,
Writing both sides of equation (2.35) as a square gives
Taking the square root of both sides of equation (2.36) yields
![]()
Therefore,
![]()
which gives ![]() rad/s or
rad/s or ![]() rad/s. Since ω cannot be negative, ω = 4 rad/s.
rad/s. Since ω cannot be negative, ω = 4 rad/s.
(iii) Method 3: Quadratic formula:
Solving the quadratic equation (2.33) using the quadratic formula gives
Equation (2.37) can be written as

which gives ω = 4, −1. Since ω cannot be negative, ω = 4 rad/s.
Example 2-5
For the circuit shown in Fig. 2.3, the power P delivered by the voltage source Vs is given by the equation P = I2 R + I VL.
(a) Suppose that P = 96 W, VL = 32 V, and R = 8 Ω. Show that the current I satisfies the quadratic equation I2 + 4 I − 12 = 0.
(b) Solve the quadratic equation for I by each of the following methods: factoring, completing the square, and the quadratic formula.
(a) Substituting P = 96 W, VL = 32 V, and R = 8 Ω into the power delivered P = I2 R + I VL yields
Dividing both sides of equation (2.38) by 8 gives
Rearranging terms in equation (2.39) yields
(b) The quadratic equation given in equation (2.40) can be solved by three different methods: factoring, completing the squares, and the quadratic formula.
(i) Method 1: Factoring:
The quadratic equation (2.40) can be factored as
(I + 6)(I − 2) = 0,
which gives I + 6 = 0 or I − 2 = 0. Therefore, I = −6 A or I = 2 A.
(ii) Method 2: Completing the square:
The quadratic equation (2.40) can be written as
Adding ![]() to both sides of equation (2.41),
to both sides of equation (2.41),
Writing both sides of equation (2.42) as a square yields
Taking the square root of both sides of equation (2.43) gives
I + 2 = ±4.
Therefore,
I = −2 ±4,
which gives I = −2 −4 = −6 A or I = −2 + 4 = 2 A
(iii) Method 3: Quadratic formula:
Solving the quadratic equation (2.40) using the quadratic formula gives
Equation (2.44) can be written as
![]()
which gives I = −2 − 4 = −6 A or I = −2 + 4 = 2 A.
Case I: For I = −6 A, the power absorbed by the lamp is −6 × 32 = −192 W. Since the power absorbed by the lamp cannot be negative, I = −6 A is not one of the solutions of the quadratic equation given by (2.40).
Case II: For I = 2 A, the power absorbed by the lamp is 2 × 32 = 64 W and the power dissipated by the resistor is 96 − 64 = 32 W. The voltage across the resistor VR = 2 × 8 = 16 V and using KVL, Vs = 16 + 32 = 48 V. Therefore, for the applied power of 96 W (source voltage = 48 V), I = 2 A is the solution of the quadratic equation given by (2.40).
Example 2-6
A diver jumps off a diving board 1.5 m above the water with an initial vertical velocity of 0.6 m/s as shown in Fig. 2.9. The diver's height above the water is given by

Figure 2.9 Person jumping off a diving board.
(a) Find the time in seconds when the diver hits the water. Use both the quadratic formula and completing the square.
(b) Find the maximum height of the diver if it is known to occur at t = 0.0612 s.
(c) Use the results of parts (a) and (b) to sketch the height h(t) of the diver as a function of time.
Solution
(a) The time when the diver hits the water is found by setting h(t) = 0 in equation (2.45) as
Dividing both sides of equation (2.46) by −4.905 gives
The quadratic equation given in equation (2.47) can be solved using the quadratic formula and completing the square as outlined below.
(i) Method 1: Quadratic formula:
Solving the quadratic equation (2.47) using the quadratic formula gives
Equation (2.48) can be written as
![]()
which gives t = 0.0612 − 0.5563 = −0.495 s or t = 0.0612 + 0.5564 = 0.617 s. Since the time cannot be negative, it takes 0.617 s for the diver to hit the water.
(ii) Method 2: Completing the square:
The quadratic equation (2.47) can be written as
![]()
Adding ![]() to both sides gives
to both sides gives
Writing both sides of equation (2.50) as a perfect square yields
![]()
Taking the square root of both sides gives
t − 0.0612 = ±0.5563.
Therefore,
t = 0.0612 ±0.5563,
which gives t = 0.0612 − 0.5563 = −0.495 s or t = 0.0612 + 0.5563 = 0.617 s. Since the time cannot be negative, it takes 0.617 s for the diver to hit the water.
(b) The maximum height of the diver is found by substituting t = 0.0612 in equation (2.45) as
hmax = h(0.0612) = −4.905(0.0612)2 + 0.6(0.0612) + 1.5 = 1.518 m.
(c) Using the results of parts (a) and (b), the diver's height after jumping from the diving board is plotted as shown in Fig. 2.10.
Figure 2.10 Height of the diver after jumping from the diving board.
Example 2-7
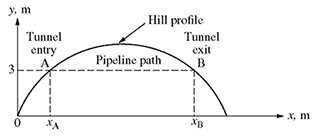
Pipeline Through Parabolic Hill: A level pipeline is required to pass through a hill having the parabolic profile
The origin of the x- and y-coordinates is fixed at elevation zero near the base of the hill, as shown in Fig. 2.11.
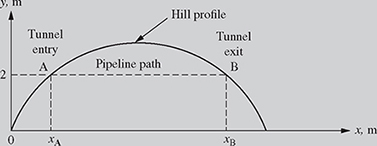
Figure 2.11 Pipeline path through a parabolic hill.
(a) Write the quadratic equation for a pipeline elevation of y = 2 m.
(b) Solve the quadratic equation found in part (a) to determine the positions of the tunnel entry xA and exit xB using both the quadratic formula and completing the square.
(c) Find the length of the tunnel.
(a) Since the height y of the tunnel is 2 m, equation (2.52) can be written as
2 = −0.004x2 + 0.3x
which gives
0.004x2 − 0.3x + 2 = 0
or
(b) The quadratic equation given in equation (2.53) can be solved using the quadratic formula and completing the square as outlined below.
(i) Method 1: Quadratic formula:
Solving the quadratic equation (2.53) using the quadratic formula gives
Equation (2.54) can be written as
![]()
which gives x = 37.5 − 30.1 = 7.4 m or x = 37.5 + 30.1 = 67.6 m. Therefore, the tunnel entry position is 7.4 m and the tunnel exit position is 67.6 m.
(ii) Method 2: Completing the square:
The quadratic equation (2.53) can be written as
Adding  to both sides gives
to both sides gives
Writing both sides of equation (2.56) as a perfect square yields
Taking the square root of both sides gives
x − 37.5 = ±30.1.
Therefore,
x = 37.5 ± 30.1,
which gives x = 37.5 − 30.1 = 7.4 m or x = 37.5 + 30.1 = 67.6 m. To check if the answer is correct, substitute x = 7.4 and x = 67.6 into equation (2.53). Substituting x = 7.4 m gives

Now, substituting x = 67.6 m into equation (2.53) gives

Therefore, xA = 7.4 m and xB = 67.6 m are the correct positions of the tunnel entry and exit, respectively.
(c) The tunnel length can be found by subtracting the position xA from xB as
Tunnel length = xB − xA = 67.6 − 7.4 = 60.2 m
PROBLEMS
-
2-1. An analysis of a circuit shown in Fig. P2.1 yields the quadratic equation for the current I as 3I2 + 6 I = 45, where I is in amps.
(a) Rewrite the above equation in the form I2 + aI + b = 0, where a and b are constants.
(b) Solve the equation in part (a) by each of the following methods: factoring, completing the square, and the quadratic formula.

-
2-2. Repeat problem P2-1 for the circuit shown in Fig. P2.2, which yields the quadratic equation for the current I as 3I2 − 6 I = 45, where I is in amps.

-
2-3. Repeat problem P2-1 for the circuit shown in Fig. P2.3, which yields the quadratic equation for the current I as 210 = 10 I2 + 40 I, where I is in amps.

-
2-4. The current flowing through the inductor shown in Fig. P2.4 is given by the quadratic equation i(t) = t2 − 8t. Find t when
(a) i(t) = 9 A (use the quadratic formula), and
(b) i(t) = 84 A (use completing the square).

-
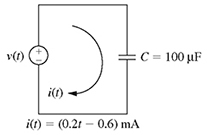
2-5. The voltage across the capacitor shown in Fig. P2.5 is given by the quadratic equation v(t) = t2 − 6t. Find t when
(a) v(t) = 16 V (use the quadratic formula), and
(b) v(t) = 27 V (use completing the square).
-
2-6. In the purely resistive circuit shown in Fig. P2.6, the total resistance R of the circuit is given by
If the total resistance of the circuit is R = 100 Ω and R2 = 2R1 + 100 Ω, find R1 and R2 as follows:
(a) Substitute the values of R and R2 into equation (2.58), and simplify the resulting expression to obtain a single quadratic equation for R1.
(b) Using the method of your choice, solve the quadratic equation for R1 and compute the corresponding value of R2.

-
2-7. Repeat problem P2-6 if R = 1600 Ω and R2 = R1 + 500 Ω.
-
2-8. The energy dissipated by a resistor shown in Fig. P2.8 varies with time t in s according to the quadratic equation W = 3t2 + 6t. Solve for t if
(a) W = 3 joules
(b) W = 9 joules
(c) W = 45 joules

-
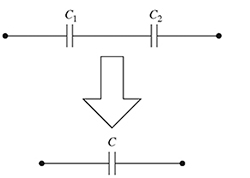
2-9. The equivalent capacitance C of two capacitors connected in series as shown in Fig. P2.9 is given by
If the total capacitance is C = 120 μF and C2 = C1 + 100 μF, find C1 and C2 as follows:
(a) Substitute the values of C and C2 in equation (2.59) and obtain the quadratic equation for C1.
(b) Solve the quadratic equation for C1 obtained in part (a) by each of the following methods: factoring, completing the square, and the quadratic formula. Also, compute the corresponding values of C2.
-
2-10. Repeat problem P2-9 if C = 75 μF and C2 = C1 + 200 μF.
-
2-11. The equivalent capacitance C of three capacitors connected in series-parallel as shown in Fig. P2.11 is given by
If the total capacitance is C = 125 μF and C2 = C1 + 100 μF, find C1 and C2 as follows:
(a) Substitute the values of C and C2 in equation (2.60) and obtain the quadratic equation for C1.
(b) Solve the quadratic equation for C1 obtained in part (a) by completing the square and the quadratic formula. Also, compute the corresponding values of C2.

-
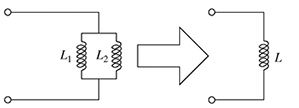
2-12. The equivalent inductance L of two inductors connected in parallel as shown in Fig. P2.12 is given by
If the total inductance L = 80 mH and L1 = L2 + 300 mH, find L1 and L2 as follows:
(a) Substitute the values of L and L1 in equation (2.61) and obtain the quadratic equation for L2.
(b) Solve the quadratic equation for L2 obtained in part (a) by completing the square, and the quadratic formula. Also, compute the corresponding values of L1.
-
2-13. Repeat problem P2-12 if L = 150 mH and L1 = L2 + 400 mH.
-
2-14. The equivalent inductance L of three inductors connected in series-parallel as shown in Fig. P2.14 is given by
(a) Suppose L2 = L1 + 200 mH and that the equivalent inductance is L = 200 mH. Substitute these values in equation (2.62) and obtain the following quadratic equation:
(b) Solve the quadratic equation (2.63) for L1 by each of the following methods: factoring, completing the square, and the quadratic formula.

Figure P2.14 Series-parallel combination of three inductors.
-
2-15. A model rocket is launched in the vertical plane at time t = 0 s as shown in Fig. P2.15. The height of the rocket (in feet) satisfies the quadratic equation h(t) = 64 t − 16 t2.
(a) Find the value(s) of the time t when h(t) = 48 ft.
(b) Find the value(s) of the time t when h(t) = 60 ft.
(c) Find the time required for the rocket to hit the ground.
(d) Based on your solution to parts (a) through (c), determine the maximum height of the rocket and sketch the height h(t).

-
2-16. The ball shown in Fig. P2.16 is dropped from a height of 1000 meters. The ball falls according to the quadratic equation h(t) = 1000 − 4.905t2. Find the time t in seconds for the ball to reach a height h(t) of
(a) 921.52 m
(b) 686.08 m
(c) 509.5 m
(d) 0 m

-
2-17. At time t = 0, a ball is thrown vertically from the top of the building at a speed of 56 ft/s, as shown in Fig. P2.17. The height of the ball at time t is given by
h(t) = 32 + 56t − 16t2 ft.

Figure P2.17 A ball thrown vertically from the top of a building.
(a) Find the value(s) of the time t when h(t) = 32 ft.
(b) Find the time required for the ball to hit the ground.
(c) Use the results to determine the maximum height, and sketch the height h(t) of the ball.
-
2-18. Two springs connected in series shown in Fig. P2.18 can be represented by a single equivalent spring. The stiffness of the equivalent spring is given by
where k1 and k2 are the spring constants of the two springs. If keq = 1.2 N/m and k2 = 2k1 − 1 N/m, find k1 and k2 as follows:
(a) Substitute the values of keq and k2 in equation (2.64) and obtain the quadratic equation for k1.
(b) Solve the quadratic equation for k1 obtained in part (a) by completing the square, and the quadratic formula. Also, compute the corresponding values of k2.

-
2-19. The equivalent stiffness of a series-parallel combination of three springs shown in Fig. P2.19 is given by
If k1 = k2 + 2 lb/in and the equivalent stiffness is k = 1.75 lb/in, find k1 and k2 as follows:
(a) Substitute the values of k and k1 into equation (2.65) and obtain the quadratic equation for k2.
(b) Using the method of your choice, solve the quadratic equation obtained in part (a) and determine the values of k2. Also, find the values of k1.

-
2-20. An assembly of three springs connected in series as shown in Fig. P2.20 has an equivalent stiffness k given by
(a) Suppose k2 = 6 lb/in., k3 = k1 + 8 lb/in., and the equivalent stiffness is k = 2 lb/in. Substitute these values into equation (2.66) to obtain the following quadratic equation:
(b) Solve equation (2.67) for k1 by each of the following methods: (i) factoring, (ii) quadratic formula, and (iii) completing the square. For each case, determine the value of k3 corresponding to the only physical solution for k1.

-
2-21. Consider a capacitor C and an inductor L connected in parallel, as shown in Fig. P2.21. The total reactance X in ohms is given by
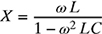 , where ω is the angular frequency in rad/s.
, where ω is the angular frequency in rad/s.(a) Suppose L = 1.0 mH and C = 1 F. If the total reactance is X = 1.0 Ω, show that the angular frequency ω satisfies the quadratic equation ω2 + ω − 1000 = 0.
(b) Solve the quadratic equation for ω by the methods of completing the square and the quadratic formula.
-
2-22. Assume that the total reactance in problem P2-21 is X = −1 Ω. Show that the angular frequency ω satisfies the quadratic equation ω2 − ω − 1000 = 0, and find the value of ω using both the quadratic formula and completing the square.
-
2-23. If L = 0.5 H, C = 0.005 F, and the total reactance in problem P2-21 is X =
 Ω, show that the angular frequency ω satisfies the quadratic equation ω2 − 30ω − 400 = 0. Also, find the value of ω using both the quadratic formula and completing the square.
Ω, show that the angular frequency ω satisfies the quadratic equation ω2 − 30ω − 400 = 0. Also, find the value of ω using both the quadratic formula and completing the square. -
2-24. When converting resistances connected in a Δ formation to a Y formation as shown in Fig. P2.24, the resistance R1 is obtained as
(a) Suppose R1 = 100, Ra = Rb = R, and Rc = 100 + R, all measured in ohms. Substitute these values into equation (2.68) to obtain the following quadratic equation for R.
R2 − 300 R − 10,000 = 0
(b) Solve the quadratic equation for R by the methods of completing the square and the quadratic formula.

-
2-25. When converting resistances connected in a Δ formation to a Y formation as shown in Fig. P2.24, the resistance R1 is given by equation (2.68).
(a) Suppose R1 = 6, Ra = R, Rb = 3 R, and Rc = 100 + R, all measured in ohms. Substitute these values into equation (2.68) to obtain the following quadratic equation for R.
R2 − 10R − 200 = 0
(b) Solve the quadratic equation for R by the methods of completing the square and the quadratic formula.
-
2-26. When converting resistances connected in a Δ formation to a Y formation as shown in Fig. P2.24, the resistance R2 is obtained as
(a) Suppose R2 = 12, Ra = R, Rb = 3 R, and Rc = 100 + R, all measured in ohms. Substitute these values into equation (2.69) to obtain the following quadratic equation for R.
R2 + 40R − 1200 = 0
(b) Solve the quadratic equation for R by the methods of completing the square and the quadratic formula.
-
2-27. When converting resistances connected in a Δ formation to a Y formation as shown in Fig. P2.24, the resistance R3 is obtained as
(a) Suppose R3 = 36, Ra = R, Rb = 3R, and Rc = 100 + R, all measured in ohms. Substitute these values into equation (2.70) to obtain the following quadratic equation for R.
R2 + 40R − 1200 = 0
(b) Solve the quadratic equation for R by the methods of completing the square and the quadratic formula.
-
2-28. The characteristic equation of a series RLC circuit shown in Fig. P2.28 is given as
(a) If R = 7 Ω, L = 1 H, and C = 0.1 F, solve the quadratic equation (2.71) for the values of s (called the eigenvalues of the system) using the methods of completing the square and the quadratic formula.
(b) Repeat part (a) if R = 10 Ω, L = 1 H, and
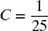 F.
F.
-
2-29. The characteristic equation of a parallel RLC circuit shown in Fig. P2.29 is given as
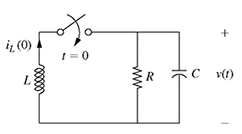
If R = 200 Ω, L = 50 mH, and C = 0.2 μF, solve the quadratic equation (2.72) for the values of s by the methods of completing the square and the quadratic formula.
-
2-30. The characteristic equation of a mass, spring, and damper system shown in Fig. P2.30 is given by
(a) If m = 1 kg, c = 3 Ns/m, and k = 2 N/m, solve the quadratic equation (2.73) for the values of s using the methods of completing the square and the quadratic formula.
(b) Repeat part (a) if m = 1 kg, c = 2 Ns/m, and k = 1 N/m.
Figure P2.30 Mass, spring, and damper system for problem P2-30.
-
2-31. The perimeter of a rectangle shown in Fig. P2.31 is given by

Figure P2.31 A rectangle of length L and width W.
If the perimeter P = 30 m and the area A = W × L = 36 m2, find the length L and width W as follows:
(a) Substitute the values of P and A in equation (2.74) and obtain the quadratic equation for L.
(b) Solve the quadratic equation for L obtained in part (a) by completing the square, and the quadratic formula. Also, compute the corresponding values of W.
-
2-32. A diver jumps off a diving board 2.0 m above the water with an initial vertical velocity of 0.981 m/s as shown in Fig. P2.32. The height h(t) above the water is given by
h(t) = −4.905 t2 + 0.981t + 2.0 m.
(a) Find the time in seconds when the diver hits the water. Use both the quadratic formula and completing the square.
(b) Find the maximum height of the diver if it is known to occur at t = 0.1 s.
(c) Use the results of parts (a) and (b) to sketch the height h(t) of the diver.

Figure P2.32 Diver jumping off a diving board.
-
2-33. A level pipeline is required to pass through a hill having a parabolic profile
The origin of the x- and y-coordinates is fixed at elevation zero near the base of the hill, as shown in Fig. P2.33.
Figure P2.33 Pipeline path through a parabolic hill.
(a) Write the quadratic equation for a pipeline elevation of y = 3 m.
(b) Solve the quadratic equation found in part (a) to determine the positions of the tunnel entry xA and exit xB using both the quadratic formula and completing the square.
(c) Find the length of the tunnel.
-
2-34. A research group is using a drop test to measure the force of attenuation of a helmet liner they designed to reduce the occurance of brain injuries for soldiers and athletes. The helmet attached to a weight is propelled downward with an initial velocity vi of 3 m/s from an initial height of 30 m. The behavior of the falling helmet is characterized by a quadratic equation h(t) = 30 − 3 t − 4.9 t2.
(a) Write the quadratic equation for time t when the helmet and weight hit the ground, i.e., h(t) = 0 m.
(b) Solve the quadratic equation for t obtained in part (a) by completing the square, and the quadratic formula.
-
2-35. The modulus of elasticity (E) is a measure of a material's resistance to deformation; the larger the modulus, the stiffer the material. During fabrication of a ceramic material from a powder form, pores were generated that affect the strength of the material. The magnitude of elasticity is related to volume fraction porosity P by
(a) If a porous sample of silicon nitride has a modulus of elasticity of E = 209 GPa, obtain the quadratic equation for volume fraction porosity P.
(b) Solve the quadratic equation found in part (a) using both the methods of completing the square and the quadratic formula.
(c) Repeat parts (a) and (b) to find the volume fraction porosity of a silicon nitride sample with a modulus of elasticity of 25 GPa.
-
2-36. Consider the following reaction having an equilibrium constant of 4.66 × 10−3 at a certain temperature:
A(g) + B(g) ⇌ C(g)
If 0.300 mol of A and 0.100 mol of B are mixed in a container and allowed to reach equilibrium, the concentrations of A = 0.300 − x and B = 0.100 − x reaction that form the concentration of C = 2x are related to the equilibrium constant by the expression
 .
.(a) Write the quadratic equation for x.
(b) Solve the quadratic equation found in part (a) by completing the square and the quadratic formula.
(c) Find the equilibrium concentration A, B, and C.
-
2-37. Consider the following reaction having an equilibrium constant of 1.00 at 1105°K temperature:
CO(g) + H2O(g) ⇌ CO2(g) + H2(g)
Suppose the feed to a reactor contains 1.000 mol of CO and 2.000 mol of H2O(g), and the reaction mixture comes to equilibrium at 1105 K. The concentrations of CO = 1.000 − x and H2O = 2.000 − x reaction that form the concentration of CO2 = x and H2 = x are related to the equilibrium constant as

(a) Write the quadratic equation for x.
(b) Solve the quadratic equation found in part (a) by completing the square and the quadratic formula.
(c) Find the equilibrium concentration of CO, H2O, CO2, and H2.
-
2-38. An engineering co-op wants to hire an asphalt contractor to widen the truck entrance to the corporate headquarters as shown in Fig. P2.38.

Figure P2.38 New asphalt dimensions of the corporate headquarters driveway.
The height h is required to be 10 ft. more than the width b, and the total area of the new asphalt is given by

(a) If A = 200 sq. ft., obtain the quadratic equation for b.
(b) Solve the quadratic equation found in part (a) by completing the square and the quadratic formula.
(c) Find the dimensions of the width and height.
-
2-39. Repeat problem P2-38 if the total area of the new asphalt needs to be 300 sq. ft.
-
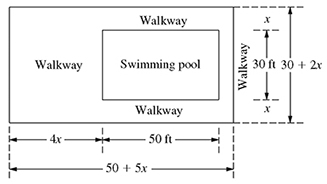
2-40. A city wants to hire a contractor to build a walkway around the swimming pool in one of its parks. The dimensions of the walkway along with the dimensions of the pool are shown in Fig. P2.40. The area of the walkway is given by
A = (50 + 5 x)(30 + 2 x) − 1500
(a) If A = 4500 sq. ft., obtain the quadratic equation for x.
(b) Solve the quadratic equation found in part (a) by completing the square and the quadratic formula.