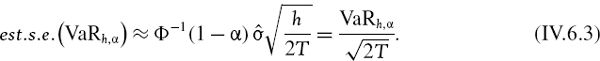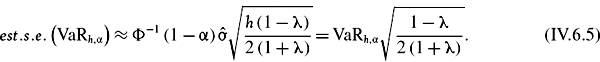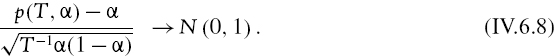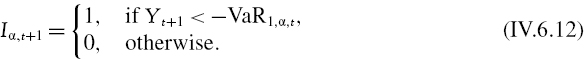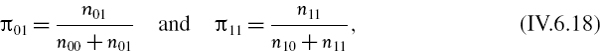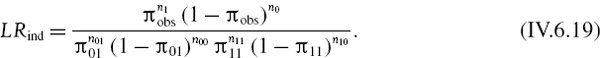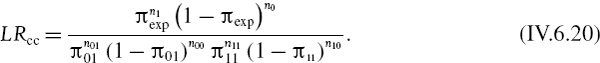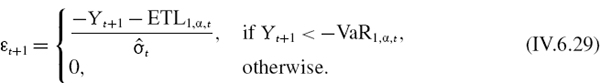IV.6
Risk Model Risk
IV.6.1 INTRODUCTION
Portfolio risk is a measure of the uncertainty in the distribution of portfolio returns, and a risk model is a statistical model for generating such a distribution. A risk model actually contains three types of statistical models, for the
(a)portfolio's risk factor mapping,
(b)multivariate distribution of risk factor returns, and
(c)resolution method.
The choice of resolution method depends on the risk metric that we apply to the risk model. In this chapter we shall be focusing on VaR models, so the choice of resolution method is between using different analytic, historical or Monte Carlo VaR models.
The choices made in each of (i)–(iii) above are interlinked. For instance, if the risk factor mapping is a linear model of risk factor returns and these returns are assumed to be i.i.d. multivariate normal, then the resolution method for estimating VaR is analytic. This is because historical simulation uses an empirical distribution, not an i.i.d. normal one, and under the i.i.d. normal assumption there is no point in using Monte Carlo simulation because it only introduces sampling error into the exact solution, which may be obtained using an analytic formula.
Of course, the distribution of portfolio returns has an expected value, and if the risk model is also used to forecast this expected value then we could call the model a returns model as well. What we call the model depends on the context. For instance, fund managers normally call their model a returns model, or an alpha model, because the primary purpose is to provide a given level of performance. But most clients also require some limit on risk, and fund managers should take care to assess risk in the same statistical model as they assess expected returns, i.e. using their alpha model.
What about banks? Banks accept risks from their clients because they are supposed to know how to hedge them. Since the main business of banks is risk rather than returns, a risk manager in banking will call his model for generating portfolio return distributions a risk model. Banks account for profits and losses in their balance sheets and they use expected returns (or expected P&L) in risk adjusted performance measures. But those figures are only for accounting and capital allocation purposes. Banks often use risk models that are quite different from the models used to compute the expected returns (or P&L) on their balance sheets. More often than not their risk model assumes that all activities earn the risk free rate, even though their balance sheets and their economic capital estimates may use different figures for expected returns.
It is important to specify the expectation in the risk model. For instance, volatility is one, very common, risk metric that represents the extent to which the realized return can deviate from the expectation of the risk model distribution. Of course, it says nothing at all about deviations from any other expected return, and the market risk analyst must be careful to specify the expected return that this volatility relates to. Suppose the expected return is fixed by some external target. Unless the target happens to be the expected value of the risk model distribution, the risk model volatility says nothing at all about whether this target will be outperformed or underperformed. One cannot just assume the expected return is equal to the target without changing the risk model. Unless the model is changed to constrain the expected return to be the target – and this will also change the volatility in the model – the model is not appropriate for measuring risk relative to the target.1 But this chapter is not about expected returns, and it is not until Chapter IV.8 that we shall be concerned with the interplay between risk and expected return. Here we focus on the accuracy of risk models, and we begin by putting the questions we ask about this into two categories:
- Model risk. Which models should we use for the risk factor mapping, for modelling the evolution of the risk factor returns and for the resolution of the model to a single measure of risk? How do the three sub-models' statistical assumptions affect the accuracy of the risk model's risk forecasts?
- Estimation risk. Given the assumptions of the risk model, how should we estimate the model parameters, and how do these estimates affect the accuracy of our risk measures?
Notice that we call the second type of model risk ‘estimation risk’ rather than sampling error. Estimation risk includes sampling error, i.e. the variation in parameter estimates due to differences in sample data. But it may also be that more than one estimation method is consistent with the risk model assumptions, and this is a different source of estimation risk. For instance, if the risk factor returns are assumed to be multivariate normal then we could apply either equally or exponentially weighted moving averages to estimate the risk factor returns covariance matrix.2 Different estimation methods will give different parameter estimates, based on the same assumptions and given the same sample data.
To answer the questions about model risk and estimation risk above we need a methodology for testing the accuracy of a risk model. In the industry we call such a methodology a backtest. In academia we call it an out-of-sample diagnostic (or performance) analysis. Since the term ‘backtest’ is shorter, we shall use that term in this chapter. Several academic studies report the results of backtesting VaR models. Notably, Berkowitz and O'Brien (2002) and Berkowitz et al. (2006) suggest that the VaR models used by banks are not sufficiently risk-sensitive to generate the short-term VaR estimates they need.3 And the results of Alexander and Sheedy (2008) suggest that risk models based on constant parameter assumptions cannot forecast short-term risk accurately, even at the portfolio level. Both volatility clustering in portfolio returns and heavy-tailed conditional return distributions are required for accurate VaR and ETL forecasts at high confidence levels and over short-term horizons.
The outline of this chapter is as follows. Section IV.6.2 clarifies the different sources of risk model risk and estimation risk. Section IV.6.3 derives some simple confidence intervals for VaR. Section IV.6.4 presents the core, technical part of this chapter. We first describe the general methodology for backtesting and then discuss the simple backtests required by regulators. Then we describe a more sophisticated and informative type of backtest based on the Kupiec (1995) test for coverage and the Christoffersen (1998) test for conditional coverage. Thereafter we cover backtests based on regression, which may provide a means of identifying why the VaR model fails the backtest, if it does. We describe a method for backtesting ETL due to McNeil and Frey (2000) and the application of bias statistics in the normal linear VaR framework. We also discuss backtests that examine the accuracy of the entire portfolio return distribution. As usual, Excel examples are provided to illustrate how each test is implemented, and we end the section by describing the results of some extensive backtests performed by Alexander and Sheedy (2008). Section IV.6.5 concludes.
IV.6.2 SOURCES OF RISK MODEL RISK
This section introduces the main sources of model risk and estimation risk in risk models, explaining how the two risks interact. For instance, if the risk factor returns are assumed to be multivariate normal i.i.d., in which case the model parameters are the means and the covariance matrix of these returns, then the estimation of the covariance matrix cannot be based on a GARCH model; it can only be based on a moving average model, because returns are not i.i.d. in GARCH models. So in this case estimation risk depends on the choice between three alternatives: an equally weighted covariance matrix, an exponentially weighted moving average with the same smoothing constant for all risk factors, or an orthogonal EWMA covariance matrix estimate. Further to this choice, the choice of sample data and, in the case of the EWMA matrices the smoothing constant, also influences sampling error, which is a part of estimation risk.
Sampling error in statistical models has been studied for many generations and estimated standard errors of estimators that we commonly use are well known. Almost always, in an unconditional (i.i.d.) framework, the larger the estimation sample size the greater the in-sample accuracy of the estimator. But this does not necessarily imply that we should use as large a sample as possible for VaR and ETL estimation. Apart from the fact that backtests are out-of-sample tests, we might encounter problems if the risk model is an unconditional model, because backtests are usually performed using short-term, time-varying forecasts. So there is no guarantee that larger estimation sample sizes will perform better in backtests. Indeed, the opposite is likely to be the case, because the VaR and ETL would become less risk sensitive.
In this section we shall examine the decisions that must be made at each step of the risk model design, from the models used for risk factor mapping, risk factor returns and VaR resolution to the choice of sample data and estimation methodology. We already know from previous chapters that portfolio risk may be assessed at the portfolio level, the risk factor level or even at the asset level. Each approach has its own advantages and limitations, which are summarized in Table IV.6.1. This section assumes that portfolio risk is assessed at the risk factor level, as it will be whenever the model is used for risk attribution, and we focus on the model risk that is introduced by the use of a risk factor mapping.
Table IV.6.1 Advantages and limitations of different levels of risk assessment
IV.6.2.1 Risk Factor Mapping
The main focus of academic research and industry development has been on the specification of the risk factor returns model, with much less attention paid to the model risk arising from the risk factor mapping itself. However, the type of risk factor mapping that is applied, and the method and data used to compute factor sensitivity estimates, could each have a considerable impact on the VaR and ETL estimates.4
Effect of Vertex Choice on Interest Rate VaR
Suppose a portfolio is represented as a sequence of cash flows.5 Given a set of vertices for the risk factor mapping, we know that we should map the cash flows to these vertices in a present value, PV01 and volatility invariant fashion. Following the method explained in Section III.5.3.4, we can do this by mapping each cash flow to three vertices. We now ask which fixed set of vertices should be chosen for the risk factor mapping. For instance, should we use vertices at monthly or 3-monthly intervals? And does this choice matter – how much does it influence the VaR estimate?
EXAMPLE IV.6.1: MODEL RISK ARISING FROM CASH-FLOW MAP
Estimate the 1% annual VaR of a cash flow with a present value of $1 million in 250 calendar days, when it is mapped in a present value, PV01 and volatility invariant fashion to three vertices, and these vertices are:6
- 8 months, 9 months and 10 months;
- 6 months, 9 months and 12 months.
The correlation matrix of continuously compounded discount rates at monthly maturities, and their volatilities (in basis points per annum), are shown in Table IV.6.2. In each case base your calculations on the assumption that the changes in discount rates are i.i.d. with a multivariate normal distribution.
SOLUTION In each case we map the cash flow to the three vertices using the methodology explained in Section III.5.3.4 and illustrated in Example III.5.3. That is, first we use linear interpolation on variances to estimate the volatility of the 250-day discount rate, and also calculate the covariance matrix corresponding to the volatilities and correlation. Then we apply the Excel Solver to compute the cash-flow mapping, and the result is shown in the columns headed cash-flow PV in Table IV.6.3. Next, we compute the PV01 vector of the mapped cash flow, as described in Section IV.2.3.2, and the results are shown in the columns headed PV01.7Finally, we use the PV01 vector to calculate the 1% annual normal linear VaR, using the usual formula (IV.2.25). The results for the 1% annual VaR are $5856.56 in case (a) and $5871.18 in case (b).
Table IV.6.2 Discount rate volatilities and correlations

Table IV.6.3 Computing the cash-flow map and estimating PV01
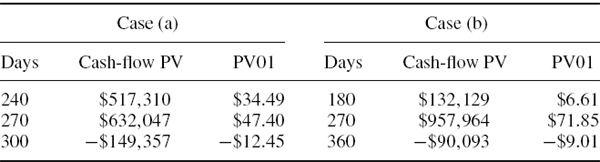
The above example shows that the choice of vertices for the cash-flow map makes little difference to a normal linear VaR estimate, even over an annual horizon. The 1% annual VaR of a cash flow with present value $1 million is 0.5856% of the portfolio value when mapped to monthly vertices, or 0.5871% of the portfolio value when mapped to quarterly vertices. Readers can verify, using the spreadsheet for the above example, that even when interest rates are more volatile and have lower correlation than in the above example, the influence of our choice of vertices in the risk factor mapping on the interest rate VaR is minor.
The reason for this is that if the VaR is proportional to the portfolio volatility, as it is in the normal linear VaR model, the choice of the three vertices to map to should not influence the result because the VaR should be invariant under the mapping.8 However, if we had used a VaR resolution method based on historical simulation then the difference between the two results could have been greater. Typically there are thousands of cash flows, and then the precision of the historical VaR estimate could be significantly affected by the choice of vertices for the cash-flow map. But this choice is far less crucial than other choices that the market risk analyst faces. For example, the choice of multivariate distribution to use for the interest rate changes, and the decision to assume they are i.i.d. or otherwise, would have a much more significant influence on the VaR estimate than the choice of vertices in the cash flow map.
Effect of Sample Size and Beta Estimation Methodology on Equity VaR
Now suppose we have spot exposures in a stock portfolio. There may be little or no flexibility regarding the choice of market risk factors. For instance, a hedge fund market risk analyst may be estimating portfolio risk in the context of a pre-defined returns model with many factors. By contrast, a market risk analyst in a large bank will probably, for the sake of parsimony, be using a single broad market index for each country. Sometimes there is a choice to be made between two or more broad market indices, but usually these indices would be highly correlated and so the choice of index is a relatively minor source of model risk. Thus, in the case of an equity portfolio held by a bank, the main sources of risk factor model risk are the sample data and the methodology that are used to estimate the market betas. The estimation of a market beta in the single index model is the subject of Section II.1.2. There we compare the ordinary least squares (OLS) and exponentially weighted moving average (EWMA) methods, illustrating the huge differences that can arise between the two estimates.9
Whilst fund managers are likely to base capital allocation on a returns model that uses many risk factors, with OLS estimates for risk factor betas, market risk analysts require fewer risk factors but more risk sensitive estimates for their betas. Risk managers may choose between:
- fund manager's OLS beta estimates, which are typically based on weekly or monthly data over a sample period covering several years;
- OLS betas based on daily data over a smaller sample, under the belief that these are more risk sensitive than the fund manager's betas;10 or
- EWMA or GARCH time-varying beta estimates.
We shall now illustrate the effect of this choice on the VaR estimate, in the context of a very simple portfolio.
EXAMPLE IV.6.2: MODEL RISK ARISING FROM EQUITY BETA ESTIMATION
On 30 May 2008, estimate the 1% 10-day systematic VaR of a position currently worth £4 million on Halifax Bank of Scotland (HBOS) PLC, using the FTSE 100 index as the market factor.11 Compare your results when both the beta estimate and the index volatility estimate are based on:
(a)OLS estimation using weekly data since 31 December 2001;
(b)OLS estimation using weekly data since 28 December 2006
(c)OLS estimation using daily data since 31 December 2001;
(d)OLS estimation using daily data since 28 December 2006;
(e)EWMA estimation using weekly data with a smoothing constant of 0.95;
(f)EWMA estimation using weekly data with a smoothing constant of 0.9;
(g)EWMA estimation using daily data with a smoothing constant of 0.95;
(h) EWMA estimation using daily data with a smoothing constant of 0.9.
In each case base your calculations on the assumption that the returns on the stock and the index are i.i.d. with a bivariate normal distribution.
SOLUTION The stock and the index prices since 31 December 2001 are shown in Figure IV.6.1.12 The effects of the credit crunch on the stock price are very evident here: its price tumbled from a high of nearly £12 per share in January 2007 to only £4 per share by the end of May 2008. The stock returns volatility was clearly much higher at the end of the sample than it had been, on average, over the sample period, and this will be particularly reflected in the EWMA volatility estimate (h), which has a low value for the smoothing constant. The stock's index beta will currently also be much lower according this EWMA estimate because the correlation between the stock and index returns, which was fairly high during the years 2002–2006, had become very low indeed by the end of the sample.
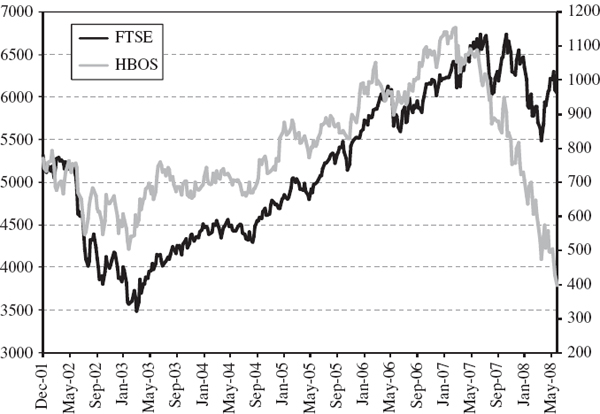
Figure IV.6.1 HBOS stock price and FTSE 100 index
We shall estimate the VaR using the usual normal linear formula, expressing VaR as a percentage of the portfolio value. That is, the 100α% h-day VaR estimate is given by
![]()
where ![]() is the beta estimate for HBOS relative to the FTSE 100 index and
is the beta estimate for HBOS relative to the FTSE 100 index and ![]() is the estimate of the index volatility. In each of the cases (a)–(h) we use a different estimate for
is the estimate of the index volatility. In each of the cases (a)–(h) we use a different estimate for ![]() and for
and for ![]() . These and the resulting 1% 10-day VaR estimates, in percentage and nominal terms, are displayed in Table IV.6.4.13
. These and the resulting 1% 10-day VaR estimates, in percentage and nominal terms, are displayed in Table IV.6.4.13
Table IV.6.4 OLS and EWMA beta, index volatility and VaR for HBOS stock.

Considering the OLS estimates (a)– (d) first, we find that the betas are fairly similar whether they are based on weekly or daily data over either estimation period, but the index volatility estimates are much higher when based on daily data. As a result, the VaR estimates are greater when based on daily data. This is expected because, unless the returns are really i.i.d. as we have assumed, the volatility clustering effects are likely to be more pronounced in daily data. However, when there is volatility clustering it is not correct to scale VaR using the square-root-of-time rule. Instead we should use a GARCH model, which has a mean reversion in volatility, and the square-root-of-time rule does not apply.
For the VaR there is much less variation between the four different OLS estimates (a)– (d) than there is between the four different EWMA estimates (e)– (h). These range from 4.72% to 14.68% of the portfolio value, i.e. from £188,796 to £587,358! In this case the choice between weekly and daily data has a great effect on the VaR estimate, and so does the choice of smoothing constant in the EWMA. It is the product of the volatility and the beta that we use in the VaR so the daily data could lead to either a higher or a lower value for VaR than the weekly data.14 In this case, it turns out that the daily data give the lower VaR estimates.
The above example illustrates some important points:
- When short-term VaR estimates are scaled to longer risk horizons using the square-root-of-time rule, a large model risk is introduced.15 Although we should base daily VaR estimates on daily data, weekly data may provide more accurate VaR estimates over a 5-day or longer risk horizon.
- When the EWMA methodology is applied the choice of smoothing constant has a very significant effect on the VaR estimate. The problem with EWMA is that this choice is ad hoc.16
- Calculating equity VaR by mapping to major indices is fraught with difficulties. The mapping methodology (e.g. the OLS or EWMA) and the choice of parameters (e.g. estimation period, or smoothing constant) may have an enormous influence on the result. Completely counterintuitive results could be obtained, such as the result shown in column (h) above. More generally, a high risk portfolio could be uncorrelated with the market, in which case it would have a very small beta. Thus its systematic VaR could be very low indeed.
A few months later, during September 2008, HBOS became insolvent. In this light, even the largest VaR estimate in the example above would seem too conservative. However, market risk capital is not for holding against this type of loss. It is only for covering everyday losses, usually in a balanced portfolio of shares. To quantify losses that arise from stress events such as the insolvency of a major bank, stress VaR analysis should be used.
IV.6.2.2 Risk Factor or Asset Returns Model
Much of our discussion in previous chapters has concerned the specification of the risk factor or asset returns model, i.e. the way that we model the evolution of the risk factors (or assets) over the risk horizon. The analyst faces several choices here and the most important of these are now reviewed.
1. Should we assume the returns are i.i.d. or should we capture volatility clustering and/or autocorrelation in returns?
This choice influences both the VaR estimate itself and the way that we scale VaR over different risk horizons, if this is done. Numerous examples and case studies in the previous four chapters have discussed the impact of volatility clustering and autocorrelated returns on VaR.17 In each case the importance of including volatility clustering effects in VaR estimates over risk horizons longer than a few days was clear. And, for a linear portfolio, we showed that even a small degree of autocorrelation in returns can have a significant impact on the scaling of short-term VaR to long-term risk horizons.
2. Should the distribution be parametric or historical?
At the daily frequency the historical distribution captures all the features of returns that we know to be important such as volatility clustering, skewness and leptokurtosis. It does this entirely naturally, i.e. without the complexity of fitting a parametric form. But to estimate VaR over a horizon longer than 1 day we need an h-day distribution for portfolio returns, and for reasons explained in previous chapters it is difficult to obtain an h-day historical distribution using overlapping data in the estimation sample. The exception is when we use filtered historical simulation (FHS), where the volatility adjusted historical distribution is augmented with a parametric dynamic model such as GARCH. An alternative to historical simulation is to find a suitable parameterization of the conditional distributions of the risk factor returns and to model these in a dynamic framework.
The advantages and limitations of both the parametric and the empirical (historical) approaches to building a statistical model for risk factor returns have been discussed earlier in this text. In Chapter IV.3 we described the influence of this choice on VaR estimates for a linear portfolio and in Chapter IV.5 we examined option portfolios, comparing Monte Carlo with historical VaR estimates.18 It is unlikely that the h-day risk factor return distributions based on historical data without filtering will provide VaR estimates that are as accurate as those based on appropriate parametric representations of the conditional risk factor return distributions. FHS may be more or less accurate than Student t EWMA VaR, but we cannot draw any conclusion without backtesting the performance of different models, as described later in this chapter.
3. If parametric, should the risk factor return distribution be normal, Student t, mixture or some other form (e.g. based on a copula)?
Our empirical exercises and studies have demonstrated, convincingly, that daily returns are usually neither i.i.d. nor normally distributed.19 Typically, both daily and weekly returns exhibit skewed and leptokurtic features. When volatility clustering is included and the model has a conditional framework, as in GARCH, it is possible for unconditional distributions to be skewed and leptokurtic even when conditional distributions are normal. But when skewness and leptokurtosis in portfolio returns are very pronounced even conditional distributions should be non-normal. Hence, for a daily VaR estimate to be truly representative of the stylized empirical features mentioned above, non-normal conditional distributions should be incorporated in the risk model at this stage.
What about VaR estimates over a horizon of a month or more? If daily log returns are i.i.d. then their aggregate, monthly log return has an almost normal distribution, by the central limit theorem. And if daily log returns exhibit volatility clustering their aggregates still (eventually) converge to a normal variable, even though the central limit theorem does not apply.20 Thus the decision about parametric form for the risk factor return distributions depends on the risk horizon. For example, whilst non-normal conditional models for risk factor return distributions are important for short-term VaR estimates, they are not especially useful for long-term VaR estimates. For long-term risk factor return distributions we may be fine using the multivariate normal i.i.d. assumption. Again, a complete answer can only be given after backtesting the models that are being considered.
4. How should the parameters of the risk factor returns model be estimated?
Even once we have fixed the distributional assumptions in parametric VaR estimates, the method used to estimate parameters can have a large impact on the VaR estimates. For instance, the RiskMetrics™ VaR estimates given in Example IV.2.26 are all based on the same i.i.d. normal assumption for risk factor returns, with an ad hoc value chosen for the smoothing constant. But the estimated VaR can differ enormously, depending on the sample data and the methodology used to estimate the risk factor returns model parameters. On changing the assumptions made here, a VaR or ETL estimate could very easily be doubled or halved! And we have seen that if the estimates are based on historical data, the sample size used to estimate the model parameters has a very significant impact on the VaR estimate. So, as well as backtesting the risk factor returns model, we also have to backtest the sample size, and/or anything else which determines the values that are chosen for the model parameters.
In summary, the four previous chapters have informed readers about the consequences of their decisions about the choices outlined above. Using numerous empirical examples and case studies to illustrate each choice, it has been possible to draw some general conclusions. For convenience, these conclusions are summarized below.
- If returns are autocorrelated, this affects the way that we scale the VaR estimate to longer horizons. Positive autocorrelation increases the VaR, and negative autocorrelation decreases the VaR.
- Incorporating volatility clustering makes the VaR estimate more risk sensitive. It will increase the VaR estimate if the market is currently more volatile than usual, and decrease the VaR estimate if the market is currently less volatile than usual.
- Parametric models for returns may produce VaR estimates that are less than or greater than the VaR estimates based on empirical return distributions. Often the empirical VaR estimates are greater than normal VaR estimates based on the same historical data, but this depends on the estimation sample and on the confidence level at which VaR is estimated.
- When the functional form of parametric distribution has leptokurtosis and negative skewness, the VaR at high confidence levels will be greater than the normal VaR. However, the opposite is the case at lower confidence levels.
- The data and methodology that are applied to estimate the parameters of the risk factor mapping and the returns model parameters can have a huge effect on the VaR estimate. However, it is not easy to know a priori how this choice will affect a particular VaR estimate.
When building a VaR model a market risk analyst enters a labyrinth where the path resulting from each choice leads to further choices, and each path branches into several paths. The outcome from each path is difficult to predict and outcomes resulting from quite different paths could be similar, or very different indeed. Given the myriad decisions facing the market risk analyst about the risk factor or asset return distributional assumptions, and given that the choices made play such an important role in the estimation of VaR and ETL, it is helpful to offer some guidance.
First, an analyst should choose distributional assumptions, including the assumptions about parameter values, that reflect his beliefs about the evolution of risk factor returns over the risk horizon. These assumptions need not be unique; indeed, the analyst may hold a distribution of beliefs over several different scenarios. In particular, these assumptions need not be based on the empirical distributions observed in the past, unless historical simulation is used to resolve the model. But it is sensible to base assumptions for short-term VaR estimates on current market conditions. For instance, at the time of writing, in the wake of the credit crisis, it is hardly feasible that equity markets and credit spreads will return to their previous levels of volatility within a short risk horizon. So the parameter estimates for short-term VaR estimation should take the current market conditions into account, even when subjective values are used rather than estimating model parameters from historical data.
Secondly, the analyst should build his model on sound principles, based on all the information that he believes is relevant to the evolution of the risk factors over the risk horizon. Nevertheless, building a model that – in the analyst's view – properly represents the returns process is not necessarily the same thing as building an accurate model. So the third point of guidance is to recognize that by far the most important aspect of building a risk model is the backtesting of this model.
The main purpose of this chapter is to explain how to perform backtests. Backtests need to be run using several alternative model assumptions. These assumptions concern the evolution of risk factor return distributions and the estimation of factor model parameters. The backtest results will tell the analyst how accurate the VaR and ETL estimates are for each of the models he is considering, using out-of-sample performance analysis that embodies the way that the model is actually used.
The model construction is based on many decisions, as we have explained above. And each choice facing the analyst should be backtested. Thus an analyst must invest much thought, time and effort into comparing how different model specifications perform in out-of-sample diagnostic tests. Backtests should be based on an estimation sample that is rolled over a long historical period. Additionally, the backtest data may include hypothetical scenarios that are designed to evaluate model performance during stressful markets.
IV.6.2.3 VaR Resolution Method
If historical VaR estimates at extreme quantiles are required there are several ways in which semi-parametric or parametric methods can be applied to fit the lower tails of the empirical portfolio returns or P&L distribution.21 Or, if we require historical VaR estimates over a risk horizon longer than a few days, then filtering the evolution of returns over the risk horizon has a very significant impact on the VaR estimates. And if Monte Carlo VaR estimation is used, there are several advanced sampling and variance reduction techniques that could be applied to reduce the sampling error.22
The only way to decide which VaR resolution method best suits the positions that the analyst must consider is to invest considerable time and effort in backtesting different approaches. Such research is likely to take months or years, but it is one of the most interesting parts of the analyst's job. Given the turmoil that has hit many markets during the year preceding the publication of this book, senior managers may be predisposed to allocate resources in this direction. Distributions that are approximated using Cornish–Fisher expansion may offer significant improvement on backtesting results for a standard historical VaR model. Adding filtering to simulate 3-day risk factor returns may have little impact on the quality of the 3-day backtest results. We do not know how much value is added by refining the VaR resolution method unless we do the backtests. However, sophisticated resolution methods may be less important to senior management than applying other types of refinements to enterprise-wide risk models. The implementation of an enterprise-wide VaR model that is capable of netting the risks of a large corporation is a huge undertaking, and aggregation risk in enterprise-wide risk estimates is by far the most important aspect of enterprise-wide risk model risk.23 Indeed, a market risk analyst may be well advised to accept a simple kernel fit and a simple EWMA filtering if he is using historical VaR, so that he can focus resources on the major challenge of aggregating different market risks across the firm.
IV.6.2.4 Scaling
Market risk analysts are also faced with a decision regarding the holding period of the VaR and ETL estimates. Should we estimate VaR and ETL directly over every risk horizon that is applied? The alternative is to estimate them over a short risk horizon and then scale them up, somehow, to obtain the VaR and ETL over a longer risk horizon. But how should this scaling be done? The answer depends on the type of portfolio (whether linear, or containing options) and the resolution method.
In the normal linear VaR model it is straightforward to implement either of these alternatives. In fact, if the risk factor returns are multivariate normal and i.i.d. and the expected excess return is zero, scaling will produce identical results to estimation directly over an h-day horizon. This is because we can scale either the covariance matrix or the final VaR estimate using the square-root-of-time rule. The exception is when the portfolio is not assumed to return the risk free rate. In that case, VaR does not scale with the square root of time, even when returns are i.i.d., and we should estimate the normal linear VaR directly over the risk horizon. And when the portfolio is assumed to return the risk free rate, as is usually the case in banks, but the portfolio returns are positively (negatively) autocorrelated, we should scale up short-term VaR to be greater than (less then) the VaR that is implied by a square-root scaling rule.
In the historical VaR model without filtering, the use of overlapping data truncates the tail of the portfolio return distribution, so that ETL (and VaR at extreme quantiles) can be seriously underestimated. So unless we add some parametric filtering for modelling dynamic portfolio returns over the h-day horizon we are initially forced to estimate VaR and ETL at the daily level. As explained in Section IV.3.2, it may be possible to uncover a power law scaling rule, to extend the daily VaR to longer horizons, but this can only be applied to linear portfolios, or to estimate the dynamic VaR of option portfolios.24 If there is no power law or if it is not the square root of time, using a square-root-of-time rule can lead to a very serious error in long-term VaR estimates.
In the Monte Carlo VaR model we can either estimate VaR directly over the risk horizon or, under certain assumptions, scale up a short-term VaR estimate to a longer horizon. If the risk factor returns are multivariate normal i.i.d. the two approaches only give the same result for a linear portfolio.25 For option portfolios the two approaches to estimating long-term VaR yield different results. The approach that is used will depend on the portfolio's valuation (i.e. Taylor approximation versus full valuation) and the rebalancing assumption for the portfolio over the risk horizon.26
IV.6.3 ESTIMATION RISK
Even in the context of a single risk factor returns model and a single VaR resolution method, VaR estimates can vary enormously according to our choice of sample data and our choice of estimation methodology. For example, the resolution method may be a standard historical simulation, in which case the risk factor return distribution will be a simulated empirical distribution, but VaR estimates can be very sensitive to the sample size, i.e. the number of historical simulations used. In fact, the case study in Section IV.3.3.1 showed that the sample size is a much more important determinant of the VaR estimate than the resolution method.
For another example, under the normal i.i.d. assumption for returns, a risk factor covariance matrix might be estimated using an equally weighted average of the previous T daily returns, the estimation sample size T being chosen fairly arbitrarily. Or we may use an exponentially weighted moving average with some ad hoc value for the smoothing constant λ. In both these cases we can estimate the standard error of the estimator.27 It is useful to extend these standard errors to an approximate standard error for a VaR estimate. These standard errors could indicate, for example, whether there is a statistically significant difference between two different VaR estimates. Alternatively, they can be used to obtain an approximate confidence interval for a VaR estimate. That is what we do in this section: we derive approximate confidence intervals for VaR estimates, based on both analytic and simulation VaR resolution methods.
IV.6.3.1 Distribution of VaR Estimators in Parametric Linear Models
If the portfolio is expected to return the risk free rate, the VaR estimate in the normal or Student t linear model behaves like volatility. For a fixed significance level α and a fixed risk horizon of h days, the 100α% h-day VaR estimate is a constant times the portfolio volatility. If this volatility is estimated using an equally weighted average of squared returns based on a sample of size T, or if it is estimated using EWMA with a given λ, we can derive the confidence interval for VaR from the known confidence interval for volatility, as described below.
Normally Distributed Portfolio Returns
The assumption that portfolio returns are i.i.d. normal leads to the formula
where ![]() is the estimated standard deviation of the portfolio's daily returns. For simplicity, we assume the portfolio is expected to return the risk free rate.
is the estimated standard deviation of the portfolio's daily returns. For simplicity, we assume the portfolio is expected to return the risk free rate.
Since the quantile Φ−1(1 − α) of the standard normal distribution and the square root of the holding period ![]() are both constant, we may use the standard error of the standard deviation estimator to derive a standard error for the VaR estimate. In Section II.3.5.3 it is proved that the standard error of the equally weighted standard deviation estimator
are both constant, we may use the standard error of the standard deviation estimator to derive a standard error for the VaR estimate. In Section II.3.5.3 it is proved that the standard error of the equally weighted standard deviation estimator ![]() , when it is based on a sample of size T, is approximated by
, when it is based on a sample of size T, is approximated by
Hence, in this case the standard error of the VaR estimator at the portfolio level is approximately equal to
In Section II.3.8.5 it is proved that the standard error of the EWMA standard deviation estimator ![]() , when it is based on a smoothing constant λ, is approximated by
, when it is based on a smoothing constant λ, is approximated by
Hence, the standard error of the VaR estimator at the portfolio level is approximately equal to
EXAMPLE IV.6.3: CONFIDENCE INTERVALS FOR NORMAL LINEAR VAR
Portfolio returns are assumed to be i.i.d. and normally distributed. When the portfolio volatility is estimated as 20%, estimate the 100α% h-day normal linear VaR and its approximate standard error for different values of α and h,
(a) an equally weighted model with a sample size 100, and
(b) EWMA with a smoothing constant of 0.94.
How do your results change for different sample sizes in (a) and for different smoothing constants in (b)?
SOLUTION The VaR estimates based on (IV.6.1) and their standard errors based first on (IV.6.3) with T = 100, and then on (IV.6.5) with λ = 0.94, are calculated in the spreadsheet for different values of α and h, and the results are displayed in Table IV.6.5. The VaR estimates and their standard errors increase with both the risk horizon and the confidence level. For our choice of parameters, i.e. T = 100 and λ = 0.94, the EWMA VaR estimates are less precise than the equally weighted estimates, since their standard errors are always greater.
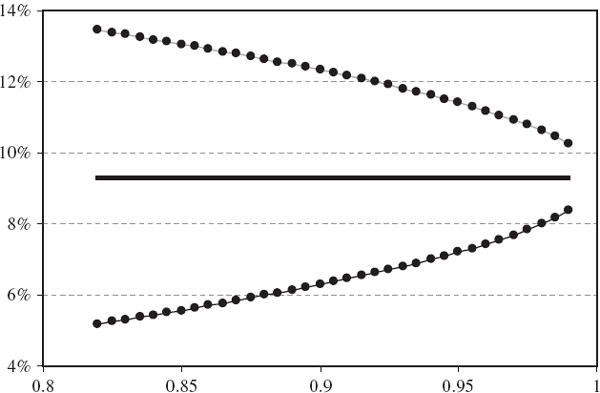
How do these standard errors behave as the sample size changes in the equally weighted model, or as the smoothing constant changes in the EWMA model? Figure IV.6.2 depicts the 1% 10-day normal linear VaR estimate (by the horizontal black line at 9.31%) and two-standard-error bounds, based on the equally weighted estimate (IV.6.3) for different values of T. Figure IV.6.3 depicts the same VaR estimate of 9.31% and two-standard-error bounds based on the EWMA estimate (IV.6.5) for different values of λ. Both graphs are based on the assumption that returns are i.i.d. and the portfolio volatility is 20%. The standard errors decrease as the sample size increases in the equally weighted model, and decrease as the smoothing constant increases in the EWMA model.
The equally weighted variance estimate is a sum of i.i.d. variables,28 so by the central limit theorem its distribution converges to a normal distribution. But the VaR estimate behaves like the square root of the variance.29 In fact, the standard errors shown in these figures are approximated using Taylor expansion, as in Section II.3.5.3, without knowing the functional form of the volatility estimator.
Table IV.6.5 Normal linear VaR estimates and approximate standard errors
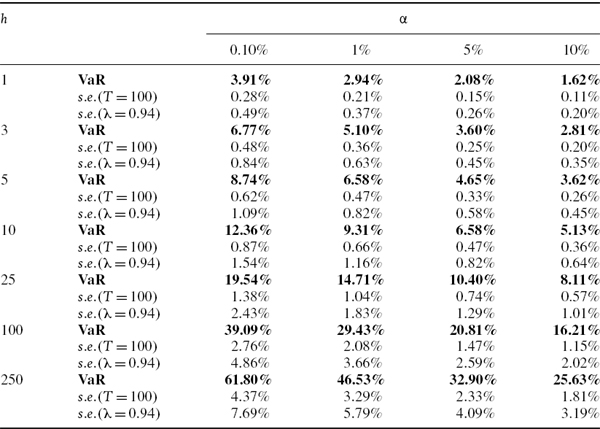
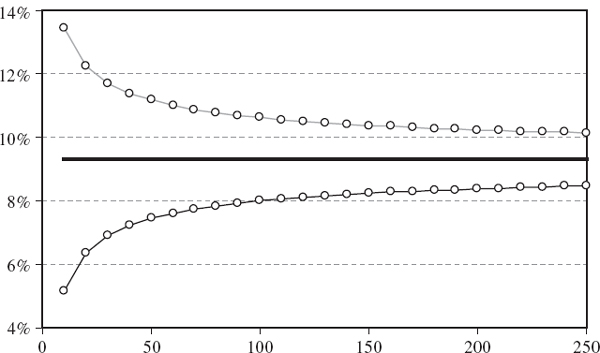
Figure IV.6.2 1% 10-day VaR with two-standard-error bounds versus sample size
Figure IV.6.3 1% 10-day VaR with two-standard-error bounds versus EWMA λ
Student t Distributed Portfolio Returns
From our discussion in Section IV.2.8.2 we know that the one-period VaR estimate based on an assumed i.i.d. Student t distribution for portfolio returns, with ν degrees of freedom, is
where σ is the standard deviation of the portfolio's daily returns and the portfolio is expected to return the risk free rate. When h is relatively small the errors from square-root scaling on a Student t distribution are not too large, so a very approximate formula for the 100α% h-day VaR,30 as a proportion of the portfolio value, is
When h is more than about 10 days (or more, if ν is relatively small) the normal linear VaR formula should be applied, because the sum of h i.i.d. Student t distributed returns will have an approximately normal distribution, by the central limit theorem.
In the linear VaR model the leptokurtosis of a Student t distribution usually increases the 1% VaR estimate and its estimated standard errors, relative to a normal distribution assumption. Figure IV.6.4 compares the 1% 10-day VaR estimate, and the two-standard-error bounds, based on normal returns and based on Student t returns with 6 degrees of freedom.31 As in the previous figures the sample size is shown on the horizontal axis, and we suppose that the portfolio volatility is 20%, but this – and the degrees of freedom and other parameters – can be changed in the spreadsheet. As expected, the confidence intervals become wider under the Student t assumption, but the main effect of the leptokurtosis that is introduced by the Student t distribution is to increase the 1% VaR estimate itself, from 9.31% 10.26%. This is depicted by the horizontal grey line in the figure, and the two-standard-error bounds on the student t VaR are depicted by the lines with circle markers.
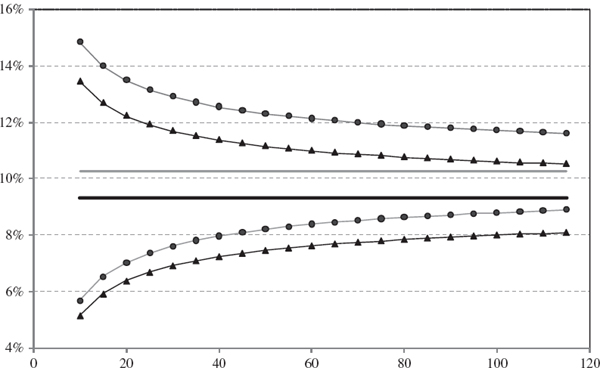
Figure IV.6.4 1% 10-day VaR with two-standard-error bounds – Student t versus normal
When linear VaR estimates are based on a multivariate elliptical (i.e. normal or Student t) i.i.d. model for risk factor returns, estimation risk arises from the covariance matrix estimator which, as we know from Chapter II.3, can be equally weighted or exponentially weighted. In the case of equities, another important source of estimation risk arises from the model used to estimate the factor betas. The risk factor return distribution parameters, and the factor betas are not necessarily based on the same model, or even on the same sample. And even when they are, it is quite complex to estimate the standard error of a quadratic form: the VaR estimator is a non-linear estimator and so its variance does not obey simple rules.
IV.6.3.2 Distribution of VaR Estimators in Simulation Models
Rather than derive an approximate formula for the multivariate elliptical linear VaR estimates, we might consider using an approximate standard error for a quantile estimator directly, as explained below. But these standard errors are much less precise than those considered in the previous subsection. That is because those derived from the variance estimator, whilst still approximate, utilize the normality (or Student t) assumption for the portfolio returns, whilst the standard errors for quantile estimators use no information about the return distribution (other than that it be continuous) and – so that we can derive a relatively simple form for the standard error of a quantile estimator – they employ a very crude assumption that the density is constant in the relevant region of the tail.
When VaR estimation is based on historical or Monte Carlo simulation, sampling error can be a major cause of estimation risk. Even in the standard historical model (i.e. the model with no parametric or semi-parametric volatility adjustment or filtering of returns) sampling error can introduce considerable uncertainty into the VaR estimate. Sampling error is usually much easier to control in the Monte Carlo VaR model but, unlike standard historical simulation, the Monte Carlo approach is also prone to estimation risk stemming from inaccuracy in parameter estimates.
For instance, using a normal i.i.d. model for portfolio returns in Monte Carlo VaR, we have a sampling variation which depends on the number of Monte Carlo simulations, and we also have a standard error of the VaR estimate arising from the volatility estimator, as described in the previous subsection. Variance reduction techniques – and using a very large number of simulations – can reduce sampling variation substantially, so the parameter estimation risk and the more general model risk arising from the choice of parametric form tend to dominate the standard error of the Monte Carlo VaR estimate. Quite the opposite is the case for the standard historical simulation VaR model. Here there are no parameters to estimate so the historical sample size has everything to do with the efficiency of the quantile estimator.
As a proportion of the portfolio value, VaRh,α is −1 times the α quantile of an h-day portfolio return distribution. So standard errors for historical VaR may be derived from an approximate distribution for the estimator of an α quantile, based on a random sample size T.
Let us denote the α quantile estimator based on a random sample size T by q(T, α). First we derive the distribution of the number of observations less than the α quantile, denoted X(T, α). Then we translate this into a distribution for p(T, α) = T−1X(T, α), the proportion of returns less than the α quantile. Finally. we derive the distribution of q(T, α) = F−1(p(T, α), where F denotes the distribution function of the portfolio returns, using an approximation.
Since the sample is random, X(T, α) has a binomial distribution with parameters T and α. Hence, its expectation and variance are Tα and Tα (1 − α), respectively.32 But as T → ∞ and when α is fixed, a special case of the central limit theorem tells us that the binomial distribution converges to a normal distribution,
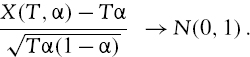
Dividing both the numerator and the denominator of this statistic by T, we have
We have already used this result to derive approximate confidence intervals for quantiles, and a numerical example to demonstrate this is given in Section II.8.4.1. But here we want to derive an approximate standard error for the quantile in large samples. So, on noting that p(T, α) = F(q(T, α), we first write (IV.6.8) as
Following Kendall (1940), we now assume that F is approximately linear ‘in the material range of the sampling distribution’. That is, we use the local approximation
![]()
where f(q(T, α) is the density function at q(T, α). In other words, the density function is assumed to be flat in the region of the tail that we are considering. Substituting this in (IV.6.9) gives an approximate distribution for q(T, α) as
In particular, an approximate standard error for the quantile estimator q (T, α) is given by
Since the 100α%VaR is − q(T, α), it has the same standard error as q(T, α).
The formula just derived requires knowledge of the portfolio return distribution, and in particular of its density function f. Then it may be applied to estimate approximate standard errors for historical VaR estimates. However, these standard errors are based on a very strong assumption about the shape of the tail of the distribution, i.e. that it is locally flat. So the standard errors (IV.6.11) are very approximate indeed. To demonstrate this, the following example compares standard errors that are estimated using (IV.6.11) with those based on (IV.6.3) in the case where the density function in (IV.6.11) is known to be normal.
EXAMPLE IV.6.4: CONFIDENCE INTERVALS FOR QUANTILES
Given a random sample of size 1000 from a normal distribution with known mean zero and volatility 20%, derive the approximate standard errors (IV.6.11) for 100α% h-day VaR, for different values of α and h. How does the result change with the random sample size? Compare these standard errors with the estimated standard errors (IV.6.3) that are based on sampling error in equally weighted volatility estimators.
SOLUTION When the distribution is known to be normal with mean zero and volatility σ, the quantile estimate q(T, α) is given by the Excel function NORMINV (α, 0, σ), and this is independent of the sample size T. The first factor on the right-hand side of (IV.6.11), i.e. f(q(T, α)−1, is given by the Excel function
![]()
and the dependence of the estimated standard error on sample size only enters through the second factor ![]() in (IV.6.11).
in (IV.6.11).
In the spreadsheet we compute (IV.6.11) for different values of α and h and with a sample size of 1000. Results are summarized in Table IV.6.6, which is similar to Table IV.6.5 except that, for comparison with the quantile-based standard errors, the sample size for the equally weighted volatility-based standard errors is 1000 rather than 100. As a result, the estimated standard errors based on σ are much smaller than those in Table IV.6.5.
Figure IV.6.5 depicts the estimated standard error of the 1% 10-day VaR estimate based on (a) the equally weighted volatility estimator for σ and (b) the quantile estimator. As in the example above, we assume the population is normal with mean zero and volatility 20%, so the VaR estimate is 9.31% of the portfolio value. The figure shows the effect that sample size has on the standard error of the VaR estimate. For small samples, the precision of the quantile estimates is very low. For every sample size, the quantile-based standard error is approximately twice the size of the volatility-based standard errors.33
Table IV.6.6 VaR standard errors based on volatility and based on quantile
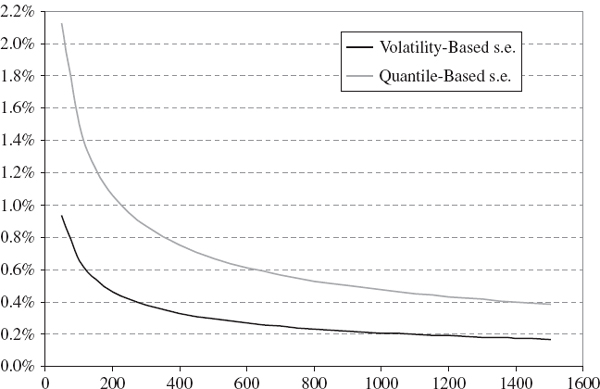
Figure IV.6.5 Standard errors of 1% 10-day VaR estimate Note: This graph assumes portfolio returns are normal with volatility of 20%.
IV.6.4 MODEL VALIDATION
This section presents a series of increasingly complex approaches to VaR model validation through out-of-sample forecast evaluation techniques that are commonly termed backtests. Failure of a backtest indicates VaR model misspecification and/or large estimation errors, and regression-based backtests may also help diagnose the cause of a model failure.
IV.6.4.1 Backtesting Methodology
A backtest takes a fixed portfolio, which we shall call the candidate portfolio, and uses this portfolio to assess the accuracy of a VaR model. The term ‘candidate portfolio’ is used to denote a portfolio that represents a typical exposure to the underlying risk factors. If the portfolio is expressed in terms of holdings in certain assets or instruments, we assume the weights or the holdings are fixed for the entire backtest.34 More usual is to express the portfolio in terms of a risk factor mapping, in which case – for a dynamic VaR estimate – we assume the risk factor sensitivities are constant throughout the backtest.
The result of a backtest depends on the portfolio composition, as well as on the evolution of the risk factors and the assumptions made about risk factor return distributions when building the model. Thus, it is possible for the same VaR model to pass a backtest for portfolio A, but fail a backtest for portfolio B, even when the portfolios have identical underlying risk factors.
We should perform a backtest using a very long period of historical data on the asset or risk factor values. Otherwise the test will lack the power to reject inaccurate VaR models. And because we need to base the test on a very large non-overlapping sample, backtests are usually performed at the daily frequency. So in the following we shall assume we have a large sample of daily returns on all the relevant risk factors. The entire data period will often encompass many years. For instance, more than 10 years of daily data are needed to backtest ETL, as described later in this section. The longer the backtest period, the more powerful the results will be.
First, assuming the VaR estimate will be based on historical data,?35 we fix an estimation period which defines the sample used to estimate the VaR model parameters. We tend to use much shorter estimation periods for parametric linear VaR models and Monte Carlo VaR models than we do for historical simulation VaR models. And in the parametric models, the estimation period also tends to increase with the risk horizon. This is because smaller samples yield VaR estimates that are more risk sensitive, i.e. that respond more to changes in the current market conditions.
Then we employ a rolling window approach as follows. The estimation sample is rolled over almost the entire data period, keeping the estimation period constant, starting at the beginning of the data period. We fix the length of the risk horizon, and the test sample starts at the end of the estimation sample. If the risk horizon is h days, we roll the estimation and test periods forward h days, and we keep rolling the estimation and test samples over the entire data period until the test sample ends on the last day of our data period. In this way, we do not use overlapping data in the test sample.
Figure IV.6.6 illustrates the rolling window approach: the bold line at the bottom indicates the whole sample covering the entire historical data period. The estimation and test samples are shown in black and grey, respectively; during the backtest these are rolled progressively, h days at a time, until the entire sample is exhausted.
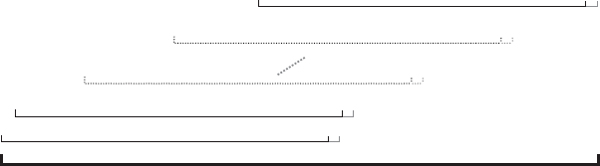
Figure IV.6.6 Rolling windows with estimation and test samples
For example, consider a sample with 10,000 daily observations where the estimation sample size is 1000 days and the risk horizon is 10 days. The backtest proceeds as follows. Use the estimation sample to estimate the 10-day VaR on the 1000th day, at the required confidence level. This is the VaR for the 10-day return from the 1000th to the 1010th observation. Then, assuming the VaR is expressed as a percentage of the portfolio value, we observe the realized return over this 10-day test period, and record both the VaR and the realized return.36 Then we roll the window forward 10 days and repeat the above, until the end of the entire sample. The result of this procedure will be two time series covering the sample from the 1010th until the 10,000th observation, i.e. covering all the consecutive rolling test periods. One series is the 10-day VaR and the other is (what econometricians call) the 10-day ‘realized’ return or P&L on the portfolio. The backtest is based on these two series.
Figure IV.6.7 depicts two such series that will form the basis of most of the backtests that are illustrated in this section.37 The backtest sample, which is constructed from all the consecutive test periods, is from January 2000 until December 2007. For simplicity there will be 2000 observations in many of the backtests, and we shall base the tests on the 1% daily VaR. So we expect the VaR to be exceeded 20 times (in other words, the expected number of exceedances is 20). Exceedances occur when the portfolio loses more than the VaR that was predicted at the start of the risk horizon.38 We have depicted the series −1 times the VaR prediction in the figure so that the exceedances are obvious when the grey P&L line crosses the black VaR line; for instance, an exceedance already occurs on the very first day of the backtest sample. In total the VaR is exceed 33 times, not 20 times, in this figure. By changing the parameters in the spreadsheet readers will see that the 5% daily VaR is exceeded 105 times instead of 100 times.39 It appears that our VaR estimates may be too low because a higher VaR would give fewer exceedances. How can we use this information to construct a statistical test of the hypothesis that the VaR estimates provide accurate forecasts?
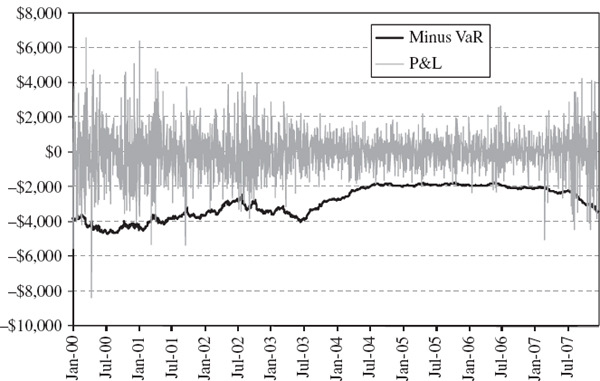
Figure IV.6.7 1% daily VaR and daily P&L
Most backtests on daily VaR are based on the assumption that the daily returns or P&L are generated by an i.i.d. Bernoulli process. A Bernoulli variable may take only two values, which could be labelled 1 and 0, or ‘success’ and ‘failure’. In our context, we would call ‘success’ an exceedance of the VaR by the return or P&L, and further assign this the value 1. Thus we may define an indicator function Iα,t on the time series of daily returns or P&L relative to the 100α% daily VaR by
Here Yt+1 is the ‘realized’ daily return or P&L on the portfolio from time t, when the VaR estimate is made, to time t + 1.40
If the VaR model is accurate and {Iα, t} follows an i.i.d. Bernoulli process, the probability of ‘success’ at any time t is α. Thus the expected number of successes in a test sample with n observations is nα. Denote the number of successes by the random variable Xn, α. From Section I.3.3.1 we know that our assumptions imply that Xn, α has a binomial distribution with parameters n and α. Thus
The standard error of the estimate, ![]() , provides a measure of uncertainty around the expected value. Due to sampling error we are unlikely to obtain exactly the expected number of exceedances in a backtest; instead we should consider a confidence interval around the expected value within which it is very likely that the observed number of exceedances will fall. When n is very large the distribution of Xn, α is approximately normal, so a two-sided 95% confidence interval for Xn, α under the null hypothesis that the VaR model is accurate is approximately
, provides a measure of uncertainty around the expected value. Due to sampling error we are unlikely to obtain exactly the expected number of exceedances in a backtest; instead we should consider a confidence interval around the expected value within which it is very likely that the observed number of exceedances will fall. When n is very large the distribution of Xn, α is approximately normal, so a two-sided 95% confidence interval for Xn, α under the null hypothesis that the VaR model is accurate is approximately
For instance, if n = 2000 and α = 1% the standard error is ![]() . So, based on (IV.6.15), a 95% confidence interval for the number of exceedances is approximately (11.28, 28.72). The observed value of 33 exceedances for the 1% daily VaR in Figure IV.6.7 lies outside this interval, so obtaining such a value is likely to lead to a rejection of the null hypothesis, but this depends on the particular backtest that we employ. The rest of this section describes different backtest statistics, most of which are based on the exceedances that have been described above.
. So, based on (IV.6.15), a 95% confidence interval for the number of exceedances is approximately (11.28, 28.72). The observed value of 33 exceedances for the 1% daily VaR in Figure IV.6.7 lies outside this interval, so obtaining such a value is likely to lead to a rejection of the null hypothesis, but this depends on the particular backtest that we employ. The rest of this section describes different backtest statistics, most of which are based on the exceedances that have been described above.
IV.6.4.2 Guidelines for Backtesting from Banking Regulators
Section IV.8.2.4 describes the use of VaR models for estimating regulatory market risk capital and, in particular, the use of a multiplier to convert VaR estimates into the minimum market risk capital requirement. Banking supervisors will only allow internal models to be used for regulatory capital calculation if they provide satisfactory results in backtests. The 1996 Amendment to the 1988 Basel Accord contains a detailed description of the backtests that supervisors will review and models that fail them will either be disallowed for use in regulatory capital calculations, or be subject to the highest multiplier value of 4.
Regulators recommend a very simple type of backtest, which is based on a 1% daily VaR estimate and which covers a period of only 250 days. Hence, the expected number of exceedances is 2.5 and the standard error of the number of exceedances, i.e. the square root of (IV.6.14), is ![]() . Regulators wish to guard against VaR models whose estimates are too low. Since they are very conservative they will only consider that models having 4 exceptions or less as sufficiently accurate. These so-called green zone models have a multiplier of 3. If there are between 5 and 9 exceptions, the model is yellow zone, which means it is admissible for regulatory capital calculations but the multiplier is increased as shown in Table IV.6.7. A red zone model means there are 10 or more exceptions. Then the multiplier takes its maximum of value 4, or the VaR model is disallowed.
. Regulators wish to guard against VaR models whose estimates are too low. Since they are very conservative they will only consider that models having 4 exceptions or less as sufficiently accurate. These so-called green zone models have a multiplier of 3. If there are between 5 and 9 exceptions, the model is yellow zone, which means it is admissible for regulatory capital calculations but the multiplier is increased as shown in Table IV.6.7. A red zone model means there are 10 or more exceptions. Then the multiplier takes its maximum of value 4, or the VaR model is disallowed.
When regulatory capital is calculated using an internal VaR model it is based on 1% 10-day VaR. So why do regulators ask for backtests of daily VaR? It would be difficult to perform a backtest on 250 non-overlapping 10-day returns, since the data would need to span at least 10 years for the backtest to have sufficient accuracy. Is it possible to derive a simple table such as Table IV.6.7 using overlapping data in certain backtests, i.e. to roll the estimation and test periods forward by only one day even when the risk horizon is longer than one day? Then we could not use our standard assumption that exceedances follow an i.i.d. Bernoulli process. Exceedances would be positively autocorrelated (for instance, one extremely large daily loss would impact on ten consecutive 10-day returns) and so, whilst the expected number of exceedances would remain unchanged from (IV.6.13), the variance would no longer be equal to (IV.6.14). In fact, it would be much greater than (IV.6.14) because the exceedances are positively autocorrelated, so the confidence interval (IV.6.15) would become considerably wider and the backtest would have even lower power that it does already.
Table IV.6.7 Basel zones for VaR models
| Number of exceedances | Multiplier for capital calculation |
| 4 or less | 3 |
| 5 | 3.4 |
| 6 | 3.5 |
| 7 | 3.65 |
| 8 | 3.75 |
| 9 | 3.85 |
| 10 or more | 4 |
Nevertheless, in practice 10-day VaR estimates are based on overlapping samples, since we estimate 1% 10-day VaR every day. So we have allowed readers to use most of the spreadsheets for this chapter to examine the pattern of exceedances based on overlapping data. Daily clustering of exceptional losses that exceed the VaR is much more likely when both the VaR estimate and the P&L are based on a 10-day risk horizon. By examining series such as these 10-day returns based on overlapping samples, banks could gauge the likelihood that their minimum regulatory capital may be exceeded on every day during one week, for instance. Formal backtests are difficult to derive theoretically for overlapping estimation samples, but at least banks would be examining the 10-day VaR estimates that they actually use for their risk capital calculations.
Most regulators allow banks to base regulatory capital on daily VaR estimates and then scale these estimates up using a square-root-of-time rule. But this rule is only valid for linear portfolios with i.i.d. normally distributed returns, and since most portfolios have non-normally distributed returns that are not i.i.d., the use of square-root scaling is a very common source of model risk. If regulators changed the number exceedances in green, yellow and red zones to correspond to autocorrelated 10-day VaR estimates, resulting from overlapping estimation samples, then banks would have the incentive to increase the accuracy of 10-day VaR estimates by scaling their daily VaR appropriately, or by estimating 10-day VaR directly without scaling up the daily VaR at all. Another feature of regulatory backtests that is not easy to understand is why they require only 250 days in the backtest. With such a small sample the power of the test to reject a false hypothesis is very low indeed. So, all in all, it is highly likely that an inaccurate VaR model will pass the regulatory backtest.
VaR estimates are based on one of two theoretical assumptions about trading on the portfolio. Either the portfolio is assumed to be rebalanced over the risk horizon to keep its asset weights or risk factor sensitivities constant, or it is assumed that the portfolio is held static so that no trading takes place and the holdings are constant. The assumption made here influences the VaR estimate for option portfolios over risk horizons longer than 1 day. But both assumptions lack realism. In practice, portfolios are actively managed at the trader's discretion, and the actual or realized P&L on the portfolio is not equal to the hypothetical, unrealized P&L, i.e. the P&L on which the VaR estimate is based. In accountancy terminology the unrealized P&L is the mark-to-market P&L, whereas the realized P&L includes all the P&L from intraday trading and is based on prices that are actually traded. Realized P&L may also include fee income, any use of the bank's reserves and funding costs. With these additional items we call it actual P&L and without these it is called cleaned P&L. To avoid confusion, we shall call the hypothetical, unrealized P&L the theoretical P&L.
Many banking regulators (for instance, in the UK) require two types of backtests, both of which are based on the simple methodology described above. Their tests must be based on both realized (actual or cleaned) P&L and on theoretical P&L. Backtests based on theoretical P&L are testing the VaR model assumptions. However, those based on realized 1-day P&L are not testing how the model will perform in practice, as a means of estimating regulatory capital, unless the scaling of 1-day VaR to 10-day VaR is accurate.
IV.6.4.3 Coverage Tests
Unconditional coverage tests, introduced by Kupiec (1995), are also based on the number of exceedances, i.e. the number of times the portfolio loses more than the previous day's VaR estimate in the backtest. They may be regarded as a more sophisticated and flexible version of the banking regulators' backtesting rules described above. The idea was both formalized and generalized by Christoffersen (1998) to include tests on the independence of exceedances (i.e. whether exceedances come in clusters) and conditional coverage tests (which combine unconditional coverage and independence into one test). Section II.8.4.2 described these tests in the context of any model for forecasting either or both tails, or indeed any interval of a distribution. In this subsection we discuss their application to VaR models, which specifically forecast the lower tail of a portfolio returns or P&L distribution.
An unconditional coverage test is a test of the null hypothesis that the indicator function (IV.6.12), which is assumed to follow an i.i.d. Bernoulli process, has a constant ‘success’ probability equal to the significance level of the VaR, α. The test statistic is a likelihood ratio statistic given by (II.8.17) and repeated here for convenience. It is
where πexp is the expected proportion of exceedances, πobs is the observed proportion of exceedances, n1 is the observed number of exceedances and n0 = n − n1 where n is the sample size of the backtest. So n0 is the number of returns with indicator 0 (we can call these returns the ‘good’ returns). Note that πexp = α and πobs = n1/n. The asymptotic distribution of −2ln LRuc is chi-squared with one degree of freedom.
EXAMPLE IV.6.5: UNCONDITIONAL COVERAGE TEST
Perform an unconditional coverage test on the 1% daily VaR for a $100 per point position on the S&P 500 index, where the backtest is based on 2000 observations from January 2000 to December 2007, as in Figure IV.6.7.
SOLUTION We have 33 exceedances based on sample of size 2000. Hence
It is better to compute the log of the likelihood ratio statistic directly, rather than computing (IV.6.16) and afterwards taking the log, because in this way the rounding errors are reduced. Hence, we use the parameter values (IV.6.17) to calculate
![]()
obtaining the value −3.5684. Hence −2ln LRuc = 7.1367. The 1% critical value of a chi-squared distribution with one degree of freedom is 6.6349. So we reject, at the 1% significance level, the null hypothesis that the VaR model is accurate in the sense that the total number of exceedances is close to the expected number.
Using the spreadsheet for Example IV.6.5 we can plot the indicator function (IV.6.12) for the case α = 1% and h = 1. This is shown in Figure IV.6.8. It is clear from this figure that the exceedances come in clusters. There are no exceedances at all in 2003 and 2004, but plenty during 2007. In fact, during the last six months of the backtest there are 12 exceedances, shown in the inset to the figure, although the expected number is less than 2.
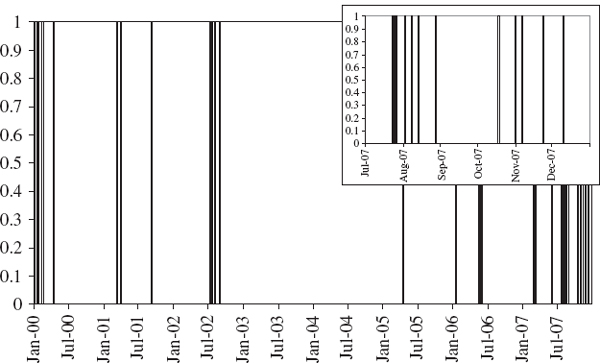
Figure IV.6.8 Indicator of exceedances
Clustering of exceedances indicates that the VaR model is not sufficiently responsive to changing market circumstances. In the case in point, the last six months of the backtest marked the beginning of the credit crisis. But the normal linear VaR estimates here were based on an equally weighted average of the last 250 squared log returns, so this model does not account for the volatility clustering that we know is prevalent in many markets. Even if the model passes the unconditional coverage test, i.e. when the observed number of exceedances is near the expected number, we could still reject the VaR model if the exceedances are not independent.
A test for independence of exceedances is based on the formalization of the notion that when exceedances are not independent the probability of an exceedance tomorrow, given there has been an exceedance today, is no longer equal to α. As before, let n1 be the observed number of exceedances and n0 = n − n1 be the number of ‘good’ returns. Further, define nij to be the number of returns with indicator value i followed by indicator value j, i.e. n00 is the number of times a good return is followed by another good return, n01 the number of times a good return is followed by an exceedance, n10 the number of times an exceedance is followed by a good return, and n11 the number of times an exceedance is followed by another exceedance. So n1 = n11 +n01 and n0 = n10 +n00. Also let
i.e. π01 is the proportion of exceedances, given that the last return was a ‘good’ return, and π11is the proportion of exceedances, given that the last return was an exceedance. Now we can state the independence test statistic, derived by Christoffersen (1998), as
The asymptotic distribution of −2ln LRind is chi-squared with one degree of freedom.
EXAMPLE IV.6.6: INDEPENDENCE TEST
Perform the independence test for the data of the previous example.
SOLUTION In addition to the results in (IV.6.17) we have only two sets of two consecutive exceedances. The rest are isolated, if only separated by a few days in many cases, as is evident from Figure IV.6.8. Hence,
![]()
Using these values in (IV.6.18) and in (IV.6.19) gives ln (LRind) = −1.2134, so −2ln LRuc = 2.4268. The 10% critical value of a chi-squared distribution with one degree of freedom is 2.7055. Hence, we cannot even reject the null hypothesis that the exceedances are independent at 10%.
Why is the independence test unable to detect the clustering in exceedances that is clearly evident from Figure IV.6.8? The problem is that in the above example we often have a day (or two or three) with no exceedance coming between two exceedances, and the Christoffersen independence test only works if exceedances are actually consecutive. That is because the test is based on a first order Markov chain only, and to detect the type of clustering we have in this example it would have to be extended to a higher order Markov chain, to allow more than first order dependence.
A combined test, for both unconditional coverage and independence, is the conditional coverage statistic given by
The asymptotic distribution of −2ln LRcc is chi-squared with two degrees of freedom. On comparing the three test statistics it is clear that LRcc = LRuc × LRind, i.e.
![]()
For instance, in the above examples we have
![]()
The 5% critical value of the chi-squared distribution with 2 degrees of freedom is 5.9915 and the 1% critical value is 9.2103. Hence we reject the null hypothesis at 5% but not (quite) at 1%.
IV.6.4.4 Backtests Based on Regression
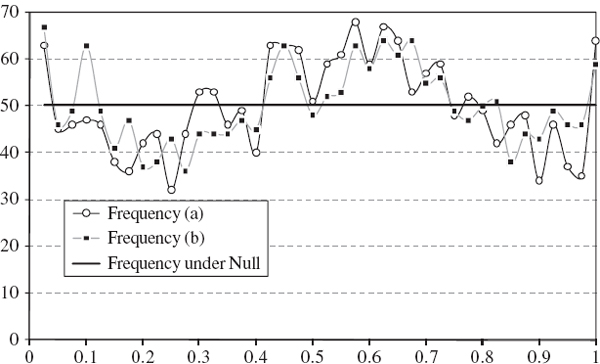
In our empirical examples of the previous subsection, where we were backtesting a normal linear VaR model for a simple position on the S&P 500 index, the results suggested that the clustering of exceedances could be linked to market volatility. This would be the case when a VaR model is not accounting adequately for the volatility clustering in a portfolio's returns. Indeed, such a link is clear from Figure IV.6.9, which shows the indicator of exceedances alongside the Vix (the S&P 500 implied volatility index) over the same period as the backtest. Exceedances are more common when there is a large daily change in the implied volatility, especially when volatility jumps upward after a long period of low volatility. This observation explains why we have so many exceedances during the recent credit crisis, and provides an understanding of how to improve the VaR model. This observation also suggests a backtest based on a regression model that takes the indicator function as the dependent variable and, in this case, the daily change in the Vix as the explanatory variable.
If past information can be used to predict exceedances, the VaR model is not utilizing all the information available in the market. More generally, if we believe that the VaR model is misspecified because it is not utilizing information linked to lagged values of one or more variables, which we summarize in the vector x = (X1,…, Xk), then a backtest could be based on a regression model of the form
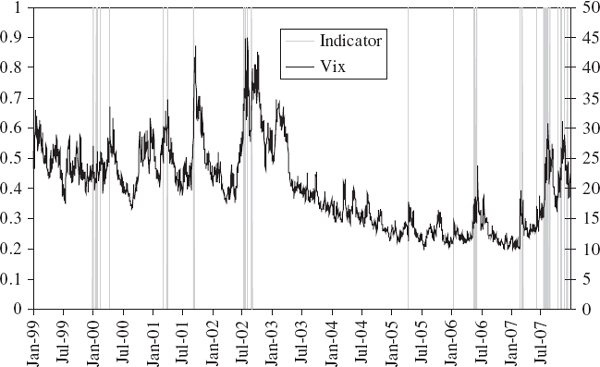
Figure IV.6.9 Relation between exceedances and implied volatility
Taking the conditional expectation of this yields
since
But if the model is well specified, then P(It = 1|xt−1) = α. Hence, the backtest is based on the null hypothesis
This can be tested by estimating the parameters using OLS, and then using one of the hypothesis tests described in Section I.4.4.8.
We now illustrate this approach to backtesting using a standard F test of the composite hypothesis (IV.6.24), based on the statistic (I.4.48), repeated here for convenience:
where p is the number of restrictions and ν is the sample size less the number of variables in the regression including the constant. The regression model is estimated twice, first with no restrictions, giving the unrestricted residual sum of squares RSSU, and then after imposing the restrictions in the null hypothesis, to obtain the restricted residual sum of squares RSSR.
EXAMPLE IV.6.7: REGRESSION-BASED BACKTEST
For our S&P 500 normal linear model for 1% daily VaR, implement a backtest using the statistic (IV.6.25) and based on a model of the form
SOLUTION In the spreadsheet for this example we first estimate (IV.6.26) using OLS, giving RSSU = 32.4317. Then we take the sum of the squared deviations of the indicator function from α, where α is set to 1% in this case, giving RSSR = 32.5409. We have p = 2 and ν = 1998, and substituting these values into (IV.6.25) gives a value for the F statistic of 3.3637. The 5% critical value for the F distribution is 3.0002 and the 1% critical value is 4.6158. So we reject the null hypothesis
at 5%, but only just.
However, the rejection of the null in this case is because β0 ≠ α and not because β1 ≠ 0. We can verify this using a simple t test for the two hypotheses H0: β0 = α and H0: β1 = 0 separately.41 For H0: β0 = α versus H1: β0 ≠ α we obtain a t ratio of 2.2817, whereas the 5% critical value is 1.9612 and the 1% critical value is 2.5783. So we can reject the null hypothesis at 5% but not at 1%. But for H0: β1 = 0 versus the two-sided alternative, we obtain a t ratio of only 1.2109, so we cannot even reject this hypothesis at 10%.42
Given the features observed in Figure IV.6.9, why does the regression model indicate no significant relationship between the exceedances and the lagged changes in the Vix? Because the large increases in the Vix index are recorded on the actual day that the VaR is exceeded, not on the day before. In fact, the contemporaneous correlation between the indicator variable and daily changes in the Vix is approximately 0.4, and a regression model (IV.6.26) with current changes in the Vix instead of lagged changes indicates a very strong relationship between the two variables. The t statistic for H0: β1 = 0 versus the two-sided alternative gives a t ratio of 19.2358, so we can reject this hypothesis at the very highest significance level.
Note that the regression-based backtest must be based on lagged values of explanatory variables, because the test is derived by taking the conditional expectation of the indicator assuming the values of the explanatory variables are known. So the fact that current changes in Vix can explain the exceedances is of no value for the backtest in the above example. However, this observation does help to identify the cause of the failure of the backtest, and it helps to determine ways in which the model could be improved. In our example above it may well be that accounting for volatility clustering will improve the model's VaR forecasts. The next example investigates this possibility.
EXAMPLE IV.6.8: COVERAGE TESTS WITH VOLATILITY CLUSTERING
Repeat the coverage tests on the 1% daily VaR for the $100 per point position on the S&P 500 index, this time replacing the equally weighted volatility estimate by the RiskMetrics™ daily volatility estimate.
SOLUTION The RiskMetrics™ daily volatility estimate is an EWMA estimate with a smoothing constant of 0.94.43 For the S&P 500 index and for the period of the backtest, this is shown in Figure IV.6.10. The spreadsheet for this example repeats the unconditional coverage test, the independence test and the conditional coverage test as before, but now using 1% daily VaR estimates based on the normal linear model with the RiskMetrics™ EWMA volatility. The VaR estimates in the earlier examples used an equally weighted volatility based on the past 250 daily returns, and there were 33 exceedances of the VaR, with two consecutive pairs. The unconditional coverage statistic was 7.1367 and we rejected the null hypothesis of a well-specified model at 1%. With the RiskMetrics™ EWMA volatility there are now only 30 exceedances, so the unconditional coverage statistic takes a lower value of 4.3785; as a result we can only reject the null at 5%.
Moreover, the independence test is irrelevant because there are no consecutive exceedances. However, the exceedances are still clustered. Readers will be able to see from the spreadsheet that there are no exceedances at all between April 2002 and April 2004 and that, again, exceedances are clustered around periods of high volatility. We conclude that the RiskMetrics™ daily VaR estimates can improve the forecasting properties of basic VaR models, but the methodology may still be too simple to properly capture volatility clustering.44 In fact, there is a considerable academic literature that examines coverage tests and other backtests on different types of VaR models and the consensus of this applied research is that non-normal GARCH models are much better than other parametric models (such as EWMA) for forecasting volatility and VaR.45
Figure IV.6.10 RiskMetrics™ daily volatility of S&P 500 index
Table IV.6.8 sets out the coverage test results for backtesting the RiskMetrics™ daily VaR for our position on the S&P 500, for different values of the VaR significance level α. Below the table we display the relevant critical values for the test statistics shown in the last three rows of the main table. The results indicate that the model becomes less accurate as α decreases, i.e. as we try to forecast VaR at higher confidence levels. The failure of the unconditional coverage tests for high confidence levels indicates that a normal distribution does not capture the tail behaviour of the S&P 500 returns adequately. A possible improvement, which is left to the reader to investigate, is the use of a leptokurtic (and possibly also skewed) conditional distribution to generate the VaR estimates.
Table IV.6.8 Coverage tests on RiskMetrics™ VaR of S&P 500 index
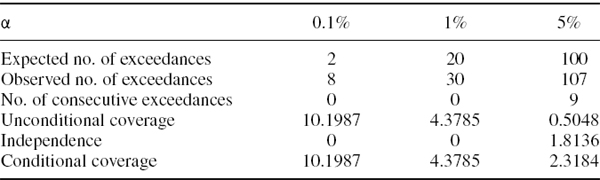
Chi-squared critical values:
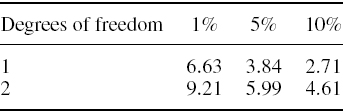
Another feature of the RiskMetrics™ daily VaR estimates is that they never fail the independence test, even though visual examination of the exceedances shows that they are clustered, and related to the index volatility. In general, there are too few exceedances during tranquil markets when volatility is low, and too many when volatility is high. Also, we find that although two exceedances are not consecutive they are often separated by only one or two days.46
IV.6.4.5 Backtesting ETL Forecasts
Section IV.1.8.2 defines the expected tail loss as the expected loss given that the loss exceeds the VaR. There, and in Section IV.2.11 where we derived some analytic formulae for ETL in the context of an i.i.d. risk model, the notation we used expressed the expectation as conditional on the loss exceeding the VaR, but it was not conditional on time. However, we need to use a slightly more elaborate notation now that we are concerned with backtesting. We must consider the VaR and ETL that are estimated at time t and are used to forecast the tail of the distribution of the return from time t to time t + 1. So in this subsection we use the following notation for the 100α% daily ETL, measured at time t, and used to forecast returns 1 day ahead:
where VaR1, α, t is the 100α% daily VaR that is estimated at time t. If Yt+1 denotes the realized daily return on the portfolio from time t to time t + 1, both the VaR and the ETL are expressed as a proportion of the portfolio's value; if Yt+1 denotes the theoretical daily P&L on the portfolio from time t to time t + 1, both the VaR and the ETL are expressed in value terms.
McNeil and Frey (2000) develop a methodology for backtesting ETL that is based on a time series of standardized exceedance residuals, defined as
Here, as in the next subsection, ![]() t is the forecast of the standard deviation of the daily return (or P&L) from time t to time t + 1, so
t is the forecast of the standard deviation of the daily return (or P&L) from time t to time t + 1, so ![]() t is the 1-day forecast that is made at time t.
t is the 1-day forecast that is made at time t.
The test is based on the observation that, if the process dynamics are correct and ETL is an unbiased estimate of the expectation in the tail below the VaR, the standardized exceedance residuals should behave as a sample from an i.i.d. zero mean process. The null hypothesis is that ∈t has zero mean, against the alternative that the mean is positive, since it is a positive mean that suggests that the ETL is too low, and underestimation of the ETL is what we want to guard against. So the test statistic is
here denoted t because it looks like a standard t ratio, where ![]() denotes the sample mean of the standardized exceedance residuals. But (IV.6.30) does not have a standard distribution. Instead, we must estimate its distribution using a bootstrap simulation such as that described in Section II.8.2.3.
denotes the sample mean of the standardized exceedance residuals. But (IV.6.30) does not have a standard distribution. Instead, we must estimate its distribution using a bootstrap simulation such as that described in Section II.8.2.3.
A sample size problem arises, because we only use the observations corresponding to exceedances in the test, simply throwing away the rest of the original sample. For instance, if we are backtesting a 1% 1-day ETL using an original sample size for the backtest of 5000 daily observations, we expect to have only 50 data points on which to calculate (IV.6.30). To alleviate this problem, at least somewhat, in the following example we use daily data on the S&P 500 from 3 January 1950 until 31 December 2007. So the original sample has 14,470 observations and our backtest sample has 14,220 observations. Thus the ETL backtest should be based on approximately 150 observations.47
EXAMPLE IV.6.9: BACKTESTING ETL
Find the standardized exceedance residuals (SER) for the normal linear VaR models of the S&P 500 position considered in this section, using (a) the RiskMetrics™ regulatory model, which is based on an equally weighted variance estimate based on 250 days, and (b) the RiskMetrics™ daily model, which is based on the EWMA variance with a smoothing constant of 0.94. Hence, calculate the statistic (IV.6.30) and comment on the results.
SOLUTION The ETL is calculated using the formula derived in Section IV.2.11.1. Note that in the time series for ∈t we only use those dates for which the VaR is exceeded, and the other observations are simply excluded. The expected number of exceedances is 142.2 in both cases. However, there are 248 exceedances in case (a) and 270 exceedances in case (b). Clearly the models are underestimating VaR.
Table IV.6.9 summarizes the results, including the values of the ETL backtest t statistic (IV.6.30). Do not be fooled by the low values of the test statistic in this table, because although (IV.6.30) looks like a t statistic its critical values are much lower than the usual critical values of the Student t distribution. Indeed, if we had used the bootstrap to simulate the critical values (which we do not in this example, since it is too onerous in Excel without using VBA) we would almost certainly find that the null hypothesis would be rejected at a very high significance level in both cases.
Examination of the exceedance residuals shows that there are many small positive and negative residuals and a few very large positive ones. That is, the observed loss is usually a little more or less than the ETL, but occasionally very much larger. This is evident from Figures IV.6.11 and IV.6.12, which plot the standardized exceedance residuals for each case.
IV.6.4.6 Bias Statistics for Normal Linear VaR
In the normal linear VaR model the VaR is proportional to the standard deviation of the portfolio return. Hence, we can assess the accuracy of the VaR model by assessing the accuracy of the standard deviation or variance forecast. Let Yt+1 denote the daily return on the portfolio that is realized from time t to time t + 1. Denote by ![]() t the forecast, made at time t, of the standard deviation of the daily return from time t to time t + 1. Then the standardized return at time t + 1 is defined as
t the forecast, made at time t, of the standard deviation of the daily return from time t to time t + 1. Then the standardized return at time t + 1 is defined as
Table IV.6.9 Exceedances and t ratio on standardized exceedance residuals
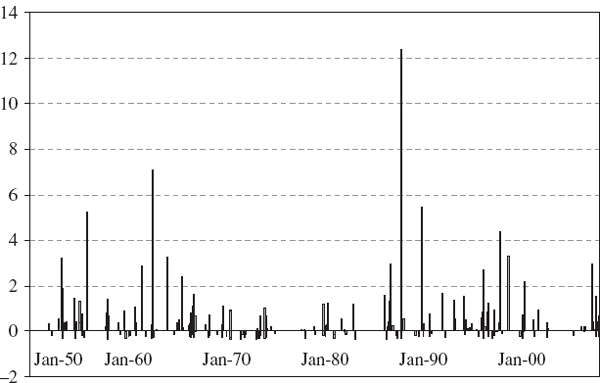
Figure IV.6.11 Standardized exceedance residuals from RiskMetrics™ regulatory VaR
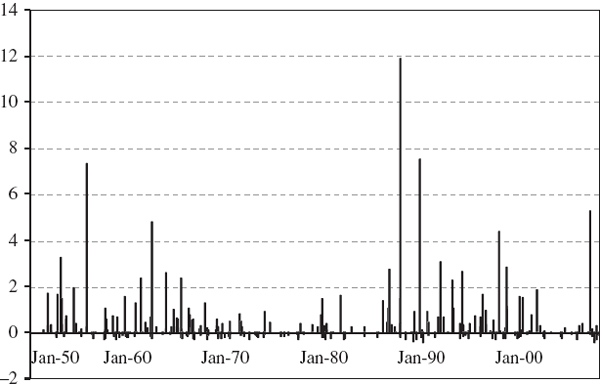
Figure IV.6.12 Standardized exceedance residuals from RiskMetrics™ daily VaR
Thus, if the returns are i.i.d. with standard deviation σ and the risk model forecasts σ accurately, then the standard deviation of the time series {Zt} should be unity.
Following Connor (2000), we define the bias statistic, b, to be the standard deviation of {Zt}. So the null hypothesis that the risk model forecasts σ (and hence also the normal linear VaR) accurately is
The alternative can be two-sided or one-sided. For instance, the alternative hypothesis
corresponds to the case where the model is under-predicting the normal linear VaR, which is usually the hypothesis of interest.
Returns are assumed to be i.i.d. and normally distributed in the normal linear VaR model. So in this case we can base the test statistic for (IV.6.32) on the assumption that {Zt} is an i.i.d. standard normal series. Then, when the backtest is based on a sample of size T, the estimated standard error of b is approximately equal to (2T)−1/2, as shown in Section II.3.5.3. However, b is not normally distributed so we cannot base the test on a sort of t ratio such as ![]() , where
, where ![]() denotes the estimated standard deviation of {Zt} over the backtest sample. This is because this ratio does not have a standard distribution such as the Student t.
denotes the estimated standard deviation of {Zt} over the backtest sample. This is because this ratio does not have a standard distribution such as the Student t.
In fact, we only know that if we assume the portfolio returns series is an i.i.d. normal process then ![]() . The mean and variance of a chi-squared distribution with T degrees of freedom are T and 2T, respectively. Hence, by the central limit theorem,
. The mean and variance of a chi-squared distribution with T degrees of freedom are T and 2T, respectively. Hence, by the central limit theorem,
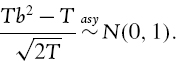
In other words, when the backtest sample size is very large,
From this, using the same type of Taylor expansion argument that was used in Section II.3.5.3 to derive the standard error of a volatility estimator from the standard error of a variance estimator, we can derive a normal approximation for the distribution of the bias statistic that is valid only for large backtest sample sizes, and on i.i.d. normal portfolio returns:
Very approximate confidence intervals for the bias statistic can therefore be based on normal standard error bounds. For instance, an approximate 95% confidence interval for b when T is large is
If we obtain a value ![]() that lies above this interval the model may be under-predicting VaR, and if
that lies above this interval the model may be under-predicting VaR, and if ![]() lies below this interval it could indicate that the model over-predicts VaR.
lies below this interval it could indicate that the model over-predicts VaR.
EXAMPLE IV.6.10: BIAS TEST ON NORMAL LINEAR VAR
Find an approximate 95% confidence interval for the bias of each of the two volatility estimators that have been used in this section. That is, using (a) the RiskMetrics™ regulatory VaR model and (b) the RiskMetrics™ daily VaR model. Use a 1-day risk horizon and base your results on the sample of S&P 500 prices from 4 January 1999 to 31 December 2007.
SOLUTION Rather than restricting the backtest sample size to 2000, which was convenient when discussing coverage statistics, now we shall use the maximum number of observations in the backtest, i.e. 2011. With T = 2011 we have ![]() . Hence the approximate 95% confidence interval (IV.6.36) is
. Hence the approximate 95% confidence interval (IV.6.36) is
![]()
For each case, the spreadsheet computes the standardized returns and their standard deviation, which is the bias statistic ![]() . We obtain a value of 1.0364 for the equally weighted estimator (a) and a value of 1.0515 for the EWMA estimator (b). Thus our conclusion should be that, if the assumptions of the test are valid, then both of the RiskMetrics™ volatility estimators underestimate S&P 500 volatility and hence will also underestimate the VaR, for every value of the significance level α. Moreover, it appears from this result that the EWMA VaR estimator is the more biased of the two.
. We obtain a value of 1.0364 for the equally weighted estimator (a) and a value of 1.0515 for the EWMA estimator (b). Thus our conclusion should be that, if the assumptions of the test are valid, then both of the RiskMetrics™ volatility estimators underestimate S&P 500 volatility and hence will also underestimate the VaR, for every value of the significance level α. Moreover, it appears from this result that the EWMA VaR estimator is the more biased of the two.
These conclusions agree with those drawn from the coverage tests, where there were too many exceedances, indicating that the VaR was underestimated rather than overestimated. However, readers are urged to exercise extreme caution when using bias statistics. If returns are not generated by a normal i.i.d. process, as assumed for the bias statistics, the results are not valid. In fact, it makes no sense at all to use the bias statistic in this setting. Therefore, before considering the use of a bias statistic, analysts should test their sample of portfolio returns for normality and for i.i.d. behaviour, as explained in Chapter I.4.48
IV.6.4.7 Distribution Forecasts
A VaR estimate is just one quantile of an entire distribution that is forecast over an h-day risk horizon. Hence, an assessment of the accuracy of the entire distribution, instead of just one of its quantiles, is a more extensive test of the risk model. In this subsection we ask: what is the probability of obtaining any of the out-of-sample returns resulting from the backtest, according to our risk model? In other words, we assess the quality of the entire distribution forecast, rather than focusing exclusively on the tails.
Let us denote the forecasted distribution function by Ft. The subscript t is there to remind us that the forecast of the forward-looking h-day return or P&L is made at time t. Set
where Yt+h denotes the realized return or P&L on the portfolio between time t and time t +h in the backtest. Assuming that the backtest is based on non-overlapping data, our null hypothesis is
where U[0, 1] denotes the standard uniform distribution.49 In other words, our null hypothesis is that the probabilities pht should be a sequence of random numbers. Put another way, our risk model should not be able to predict the probability of the realized return.
Why does testing the hypothesis (IV.6.38) constitute a backtest? Suppose our risk model systematically underestimates the tail risk. Then there will be more realized returns in the tail than are predicted by the model. As a result, the backtest will generate too many values for pht that are near 0 or near 1. Likewise too many values will lie near the centre also, due to the higher peak of a leptokurtic density. In other words, the empirical density of the return probabilities would have a ‘W’ shape instead of being flat, as it should be according to the standard uniform distribution.
A test of (IV.6.38) is therefore a test on the proximity of our empirical distribution to a theoretical distribution, which in our case is standard uniform. However, tests on the standard uniform distribution are not as straightforward as tests on the standard normal distribution, so we transform pht to a variable that has a standard normal distribution under the null hypothesis. To do this, we set
where Φ denotes the standard normal distribution function. The null hypothesis may now be written
and a very simple alternative is
A parametric test statistic may now be based on a likelihood ratio statistic of the form
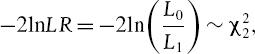
where the likelihood function under the null hypothesis, L0 is the product of the standard normal density functions based on the realized returns, and the likelihood function under the alternative hypothesis, L1 is the product of the normal density functions with mean μh and standard deviation σh based on the realized returns. If the backtest sample size is T then, using the log likelihood of the normal distribution,50 it can be shown that
where ![]() h and
h and ![]() h denote the sample mean and standard deviation of Zht.
h denote the sample mean and standard deviation of Zht.
EXAMPLE IV.6.11: LIKELIHOOD RATIO BACKTEST OF NORMAL RISK MODELS
Perform a likelihood ratio test on the normal linear risk model using each of the two volatility estimators that have been used in this section, i.e. (a) the RiskMetrics™ regulatory VaR model and using (b) the RiskMetrics™ daily VaR model. Use a daily risk horizon and base your results on the sample of S&P 500 prices from 4 January 1999 to 31 December 2007.
SOLUTION For each risk model we first compute the time series Z1t, in this example denoted just Zt for convenience, using (IV.6.37) and (IV.6.39). The backtest sample size is T = 2011 and the sample means and standard deviations of these series are given in the spreadsheet. They are summarized in the first two rows of Table IV.6.10. The third row shows the value of the test statistic (IV.6.42) in each case, which should be compared with the critical value of a chi-squared variable with 2 degrees of freedom. The 5% critical value is 5.9915 and the 1% critical value is 9.2103. Hence, we do not reject the null hypothesis at 5% in case (a) but we reject the null hypothesis at 1% in case (b).
This leads to the conclusion that the RiskMetrics™ regulatory model provides better 1-day-ahead distributions for portfolio returns than the RiskMetrics™ EWMA daily model, which is again rather counterintuitive. However, the inadequacy of both risk models for the S&P 500 is clearly evident from a histogram of the probabilities p1t, which is shown in Figure IV.6.13 for each of the models. We see that, rather than being flat, both histograms have the ‘W’ shape one would expect if the normal risk model were systematically underestimating the tails and the centre.
We can conclude that the use of an i.i.d. alternative, as in this example, is too simple. Instead we could consider a more complex, non-i.i.d. alternative. In the next example we consider an alternative where the variance in the alternative hypothesis (IV.6.41) is time-varying.51
Table IV.6.10 Results of likelihood ratio test

Figure IV.6.13 Empirical frequencies of the return probabilities
EXAMPLE IV.6.12: A DYNAMIC DISTRIBUTION BACKTEST
Repeat the likelihood ratio test for the two risk models of the previous example, but in this case use an alternative hypothesis of the form
Base the time-varying variance in the alternative hypothesis on a simple EWMA model with smoothing constant 0.94 in both case (a) and case (b).
SOLUTION With this alternative the value of the test statistic (IV.6.42) changes considerably. In fact we now obtain values for −2lnLR that far exceed the critical values. They are 480.37 in case (a) and 248.87 in case (b). With the time-varying volatility alternative we always reject the null at the very highest confidence level, for any reasonable choice of the EWMA smoothing constant. As the smoothing constant increases from 0.94 to 1 we converge to the result for the i.i.d. alternative that was obtained in the previous example.
Figure IV.6.14 shows the EWMA standard deviation of the realized return probabilities under each of the risk models, when the smoothing constant is 0.94.52 It is clear from this figure that neither VaR model is accurate, because the realized return probabilities show signs of non-i.i.d. behaviour.
IV.6.4.8 Some Backtesting Results
Alexander and Sheedy (2008) provide extensive backtests of simple linear exposures to different currency pairs, using eight risk models that are popular in the industry. Our backtesting methodology is designed for VaR models that are used for stress testing, so the paper assesses the accuracy of extreme quantile forecasts over short risk horizons. The results provide strong support for VaR models with both volatility clustering and non-normal conditional distributions for portfolio returns.
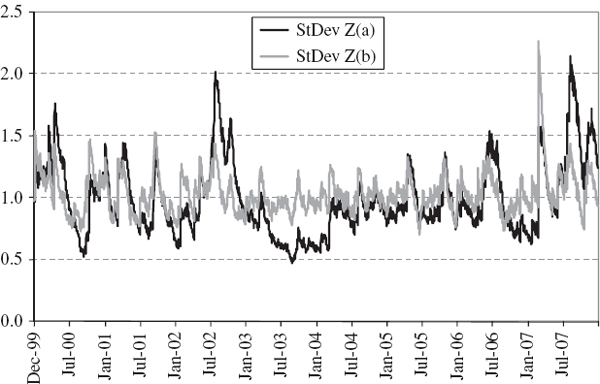
Figure IV.6.14 EWMA standard deviation of the realized return probabilities
The models that are tested specify the following distributions for the portfolio returns:
(a) unconditional normal;
(b) unconditional Student t;
(c) historical, using the Epanechnikov kernel for smoothing the distribution;53
(d) unconditional mixture of two normal distributions;54
(e) symmetric normal GARCH;
(f) symmetric Student t GARCH;
(g) filtered historical simulation, with symmetric GARCH;
(h) normal mixture with volatility clustering.
Models (e)–(h) are the extension of the first four models to include volatility clustering. To extend models (a) and (b) we use a symmetric GARCH process with innovations drawn from the specified distribution in each case. To extend the standard historical simulation (c) to its filtered counterpart (g) we standardize the returns with a filtering based on the symmetric GARCH process and simulate using the methodology described in Section IV.3.3.4. For the normal mixture with volatility clustering the historical returns are standardized, as in case (g), but a mixture of two normal distributions is fitted to the standardized returns.
The eight risk models were applied to long and short positions on three currency pairs: the British pound in terms of US dollars (GBP/USD), the US dollar in terms of Japanese yen (USD/JPY) and the Australian dollar in terms of US dollars (AUD/USD). A range of possible estimation sample sizes of between 250 and 2000 daily log returns were used for each model. Approximately 6000 estimates of VaR and ETL were obtained for a 1-day horizon, and around 2000 non-overlapping estimates of VaR and ETL for a 3-day horizon. We considered confidence levels of 99%, 99.5% and 99.9%. Each time the VaR and ETL were estimated they were based on revised estimates using the most recent estimation window.
Then the coverage tests that are described in Section IV.6.4.3, and the ETL tests described in Section IV.6.4.5, were applied. Our results confirmed that large estimation sample sizes (say, 2000 days) performed better than small estimation sample sizes (say, 250 days), especially for historical simulation and also for all four of the volatility clustering models. Our results for the normal and normal GARCH models showed that the assumption of normality cannot be justified, particularly when estimating ETL. Including volatility clustering using the GARCH process improved the performance of the normal linear VaR model, but even then the ETL consistently understated the true potential for losses beyond the VaR. Our ETL results for the normal mixture model were also disappointing, even with volatility clustering. However, the Student t GARCH model produced ETL test results that were the best of all the risk models considered in our study. In fact, our results indicated that the Student t GARCH model may even be too conservative, since no exceedances were recorded at all for two of the portfolios.
For each portfolio and at each significance level the two top performing models were the Student t GARCH model and the historical simulation with GARCH filtering. This suggested that the distribution of major currency returns could be adequately described by a single heavy-tailed distribution, in combination with a GARCH model. In other words, occasional large shocks are observed from time to time, which are then followed by further large price movements, which is consistent with volatility clustering. Very often we found that if we did not adjust for volatility clustering the model failed the independence test, i.e. the P&L would exceed the VaR on several days in succession. We also concluded that it is important to capture non-normality in the conditional return distributions, at least for portfolios of these major currencies.
IV.6.5 SUMMARY AND CONCLUSIONS
This chapter deals with the accuracy of risk models: the sources of risk model risk and the methods for testing risk model accuracy. Building a risk model, and specifically a VaR model, actually involves three distinct types of statistical analysis: firstly, we need the specification and estimation of a factor model for mapping the portfolio to its risk factors; secondly, we need a design for modelling the evolution of the risk factors, including the methods for estimating parameters if the risk factor returns model contains parametric elements; and thirdly, we need a method for resolving the model, either analytically or using some type of historical or Monte Carlo simulation.
The market risk analyst faces numerous decisions concerning the theoretical specifications of the factor model for portfolio mapping and the risk factor returns model. These decisions focus on the choice of sample data and statistical methods used to estimate the model parameters. The choices made about the theoretical model specification affect the model risk, and the parameter estimation data and methods affect the estimation risk.
We have shown that the factor model risk, i.e. the model risk associated with the portfolio mapping, is relatively small for interest rate sensitive portfolios that are mapped as cash flows, but it is relatively large for stock portfolios. And, for any type of portfolio, the model risk arising from the specification of the risk factor returns model is huge. The analyst needs to make many choices here: the returns might be assumed to be i.i.d. or otherwise; the distribution could be parametric or empirical; and if parametric, the analyst must choose between several possible functional forms. It is not very realistic to assume risk factor returns are i.i.d., and this assumption can induce very large errors in VaR estimates. For instance, the VaR could be seriously underestimated if the risk factor returns were positively correlated, especially over a long risk horizon.
For short-term risk horizons the most important effect to include in the risk factor returns model is volatility clustering. This makes the VaR estimate more risk sensitive, increasing the VaR if the market is currently more volatile than usual, and decreasing the VaR estimate if the market is currently less volatile than usual. There is a considerable body of empirical research which demonstrates that volatility clustering also makes short-term VaR and ETL estimates more accurate.
Next the analyst must choose between an empirical and a parametric model for the evolution of risk factor returns – or a combination of the two. There is little doubt that using the empirical distribution without any adjustment for volatility clustering, as in standard historical simulation, produces VaR estimates that are quite inaccurate. Accuracy is increased considerably if one augments the empirical distribution with parametric volatility clustering behaviour – as in the filtered historical simulation model. Empirical studies have shown that it is also important to allow for non-normal conditional distributions in a parametric risk factor model specification. Otherwise both VaR and ETL can be underestimated, especially at high confidence levels and over short-term risk horizons.
As the risk horizon increases to several months or more, it becomes less important to include volatility clustering and non-normal effects. Over long horizons an important source of model risk stems from the inappropriate scaling of short-term VaR estimates to represent VaR over long horizons. Often analysts simply measure market VaR at the daily horizon and scale up this estimate to longer risk horizons using a square-root scaling law. But this law is only applicable if all exposures are linear and all risk factors are i.i.d. and normally distributed. Since these conditions are rarely met in practice, the model risk for long-term VaR and ETL estimates that are scaled up in this fashion is huge. Moreover, it is very difficult to test the accuracy of these estimates, since most backtesting methodologies are designed for use with daily or weekly historical data and can therefore only test the accuracy of short-term VaR and ETL.
Estimation risk stems from two decisions: about the sample data and about the methodology applied to estimate the model parameters. There is some evidence that – assuming the model accounts properly for volatility clustering – larger samples lead to more accurate short-term VaR and ETL estimates. This is because a large part of estimation risk is sampling error. By considering the sampling error of a volatility estimator, and then of a quantile estimator, we have derived confidence intervals for VaR. Those based on the standard error of the volatility estimator are much tighter than those for quantile estimators, but they are only valid in the parametric linear VaR model with elliptical i.i.d. risk factor returns.
By far the most important aspect of building a risk model is the backtesting of this model. So the main, technical focus of this chapter was to present a variety of statistical tests that can be used to backtest VaR or ETL. After explaining the general backtesting methodology underpinning these tests, we presented a critical discussion of the Basel recommendations for backtesting. Then we presented empirical examples of the various backtests that we have described, on a normal linear VaR model applied to a simple position on the S&P 500 index. The index volatility was estimated using two different methods: one in which variance is set to an equally weighted average of the past 250 squared returns (the RiskMetrics™ regulatory model); and another with a exponentially weighted moving average variance based on a smoothing constant of 0.94 (the RiskMetrics™ daily EWMA model). These two models were backtested using unconditional coverage, independence and conditional coverage criteria, using regression-based backtests and using backtests for ETL. We also examined the bias statistics for these VaR models, and discussed various means of evaluating the entire distribution that is forecast by the risk model, rather than merely focusing on the lower tail.
All the empirical examples on backtesting in this chapter were performed at the portfolio level. So we have not illustrated one of the most important sources of model risk, i.e. aggregation risk. This is the risk arising from the inappropriate aggregation of component risks into a total risk. Aggregation risk affects the accuracy of VaR and ETL at every level of the organization. It stems from the use of an inaccurate correlation matrix (or, indeed, the inappropriate use of correlation as a dependency metric) and from the application of simple rules to aggregate VaR and ETL estimates from different lines of business to a total risk estimate for the entire firm. The implementation of an enterprise-wide risk model that is capable of netting the risks of a large organization accurately is a huge undertaking, and aggregation risk in enterprise-wide risk management is much the most important aspect of enterprise-wide risk model risk. The plethora of parametric and non-parametric models for the evolution of risk factor returns may seem confusing but, in the final analysis, a market risk analyst would be well advised to accept a simple but ‘good enough’ fit for the VaR models applied to different types of portfolios so that he can focus resources on the major challenge of aggregating different market risks across the entire firm. We shall discuss this is more detail in Section IV.8.3.3.
1 See Chapter II.1 for a thorough discussion of expected returns models, and their relationship with the risk metric.
2 Or, if an asymmetric GARCH model is assumed, we could choose an E-GARCH or an A-GARCH parameterization in an asymmetric conditional multivariate normal framework.
3 Typically, the horizons are 1 day for regulatory backtests, up to about 3 days for stress testing (or more, in illiquid markets), and 10 days for regulatory capital calculations.
4 For instance, in an equity factor model we could use one broad market risk factor, or several fundamental factors, or statistical factors etc. Different factor models will give different VaR estimates.
5 This includes any interest rate sensitive portfolio, and any portfolio with forward exposures to currencies, equities or commodities. But currency, equity and commodity portfolio also have a spot price as a risk factor. See Section III.5.2 if any clarification is required.
6 Using a 30/360 day-count convention.
7 Since the mapped cash flow is already in present value terms, we simply multiply the cash-flow present value by its maturity in years and then by 10−4. This gives an accurate approximation to the PV01, using (IV.2.29).
8 The small difference between the VaR estimates in this example was due to rounding errors.
9 We could also estimate betas using a bivariate GARCH model, as described in Section II.4.8.4. Typically, there is less difference between the GARCH and the EWMA beta estimates than between these and the OLS estimates.
10 But when OLS beta estimates are rolled over time they exhibit ‘ghost features’ which introduce a serious bias to the estimate. The reason is that OLS assumes the returns on a financial asset are i.i.d. when they are not. So when a volatility cluster appears, the effect of this cluster does not diminish over time. Instead it persists for exactly T periods after the cluster, where T is the sample size. This is explained in detail in Section II.3.7.
11 The price of HBOS stock on that day was £4, so 1 million shares are held. Data were downloaded from Yahoo! Finance, symbols HBOS and ^FTSE.
12 Note that the stock price, shown on the right-hand scale, is given in pence.
13 The VaR in nominal terms is the percentage VaR estimate multiplied by the portfolio value of £4 million.
14 Again the index volatilities are higher when based on daily data but the beta estimates are much lower. Because of the crash in the stock price just before the VaR is estimated, the lower value of 0.9 used in (h) produces the highest volatility estimate. But because of the higher index volatility and also because the daily stock returns have a lower correlation with the index returns, the daily beta estimates are much lower than those based on weekly data.
15 See also Table IV.3.4 in Section IV.3.2.6, which shows the errors of square-root scaling under different scale exponents and over different risk horizons.
16 And this is the reason why it is better to use a GARCH model, at least when the model is based on daily data, because the GARCH parameters may be estimated using maximum likelihood estimation. See Section II.4.2.2 for further details.
17 In particular, for the effect of autocorrelation on scaling parametric linear VaR, see Examples IV.2.1, IV.2.23 and the case study on credit spread VaR in Section IV.2.12. And, for the influence of volatility clustering effects on historical VaR estimates, see Example IV.3.1 and all five case studies in Section IV.3.5. These case studies deal with cash flows, a small stock portfolio, a large international stock portfolio, an international fixed income portfolio and a portfolio of crack spreads. Finally, for the effect of volatility clustering in Monte Carlo VaR estimates, see Example IV.4.6 and, for the comparison of i.i.d. versus GARCH returns on a forex portfolio, see Example IV.4.14.
18 Comparisons of parametric and historical VaR estimates for linear portfolios are discussed in Section IV.3.1 and empirical results are presented in the case studies of Sections IV.3.5.1 (for cash flows) and IV.3.5.2 (for a stock portfolio). For the comparison of historical VaR and parametric (Monte Carlo) VaR for option portfolios, see Example IV.5.18 for S&P 500 options, Example IV.5.20 for an international equity index option portfolio, and the case studies in Sections IV.5.4.5 and IV.5.5.8 for an energy option portfolio.
19 Numerous exercises and case studies in Chapter IV.2 have addressed this question, by examining the VaR for a linear portfolio under different parametric assumptions. We also asked a similar question in the context of Monte Carlo VaR models in Chapter IV.4. Normal, Student t, and normal or Student t mixture i.i.d. VaR estimates for a linear portfolio are compared in Examples IV.2.19, IV.2.21 and IV.2.22. The case study of Section IV.2.12 also compares the effect of different parametric assumptions on credit spread VaR. Finally, the comparison of i.i.d. normal, Student t and copula-based Monte Carlo VaR estimates is presented in Examples IV.4.8–IV.4.11.
20 See Alexander et al. (2008) for the proof.
21 These are described in Section IV.3.4.
22 See Section IV.4.2.2 and IV.4.2.3 for further details.
23 See Section IV.8.3.3 for further details.
24 Dynamic VaR is based on the assumption that the portfolio is rebalanced daily to keep its risk factor sensitivities constant.
25 But in this case it is more accurate to use an analytic formula, if available.
26 If Taylor approximation is used, do not overlook the huge model risk that is introduced by using h-day changes in risk factors, when even daily changes can be too large for low-order Taylor approximations to be accurate. See Section IV.5.2.4 for further details.
27 This is described in Section II.3.5.3 and II.3.8.5.
28 Since the returns are assumed to be i.i.d., so are their squares.
29 The distribution of the volatility estimator is not the square root of the distribution of the variance estimator, so we cannot just use the square root of the standard errors of the variance estimator as the standard errors of the volatility estimator.
30 Approximate because the Student t distribution is not stable.
31 Here if we assume that the degrees of freedom parameter is imposed rather than estimated from the portfolio returns. When the degrees of freedom parameter is estimated from the portfolio returns, another sampling error is introduced, so the confidence interval become seven wider.
32 See Section I.3.3.1.
33 This depends on the significance level of the VaR but not on the sample size. For a 1% VaR estimate, the quantile-based standard error is 2.28 times as large as the volatility-based standard error; but for a 0.1% VaR, this multiple increases to 4.3.
34 If it is a long-only (or short-only) portfolio, we could keep either the portfolio weights or the portfolio holdings constant; otherwise we keep the holdings constant. Note that keeping the weights constant assumes dynamic rebalancing over the risk horizon (i.e. dynamic VaR) whereas keeping the holdings constant produces a static VaR estimate.
35 This is always the case for the historical simulation model. It may also be the case for parametric linear and Monte Carlo VaR models, where historical data are used to estimate the parameters of the risk factor returns distribution.
36 Here we are using the term ‘realized return’ in the econometric rather than the accountancy sense. However, if the VaR is expressed in value terms, so we need to observe the P&L over this 10-day test period, to say we record the ‘realized P&L’ is rather confusing. For clarification, see Section IV.6.4.2, where we emphasize the distinction between realized P&L and unrealized P&L. An econometrician does not make this distinction, and in fact realized return or P&L for an econometrician is hypothetical, un realized return or P&L for an accountant!
37 In the spreadsheet for this figure readers will see that the VaR is for a $100 per point position on the S&P 500 index, and the estimate is based on the normal linear model using 250 daily log returns to estimate the standard deviation.
38 Other terms used instead of ‘exceedance’ are ‘violation’ and ‘hit’.
39 We keep the number of observations in the backtests constant at 2000, whatever the risk horizon, so for a 1% VaR the expected number of exceedances is always 20, but for a 5% VaR we expect 100 exceedances.
40 If VaR is expressed in value terms our series {Yt} is a series of P&L, and if VaR is expressed as a percentage of portfolio value our series {Yt} is a series of portfolio returns.
41 See Section I.4.2.5 for further details.
42 The 10% critical value is 1.6456.
43 See Section II.3.8 for an introduction to EWMA and Section II.3.8.3 for a description of RiskMetrics.
44 Also, the EWMA methodology may be disallowed by regulators, for reasons that will be explained in Section IV.8.2.3.
45 For instance, see Berkowitz and O'Brien (2002), Berkowitz et al. (2006) and Alexander and Sheedy (2008)
46 Readers can see from the indicator function in the spreadsheet that runs of 5 or more exceedances of 10-day VaR estimates are found around the time of the September 2001 terrorist attack on the World Trade Center, in May 2006 and again February 2007. During these periods the minimum regulatory capital based on the RiskMetrics VaR model would have been exceeded on every day during one week. Recall that whilst readers will see coverage test results for risk horizons longer than 1 day in these spreadsheets, the coverage tests are not valid because the assumption that exceedances are i.i.d. cannot be justified.
47 The spreadsheet is so large that this example has its own workbook.
48 A simple way to test for independence is to test for autocorrelation in the returns, and also for autocorrelation in the squared returns and higher powers of returns. These tests are described in Section I.4.5.3. If one of these tests is rejected (and often squared returns are found to be autocorrelated, due to volatility clustering) then the returns cannot be independent. However, acceptance of these tests does not imply independence. Similarly, rejecting a test for heteroscedasticity (see Section I.4.5.4) does not imply the distributions are identical. Finally, see Section I.4.3.5 for the Jarque – Bera normality test.
49 See Section I.3.3.3.
50 See Example I.3.16.
51 An alternative with a time-varying mean is considered by Christoffersen (2003, pp. 192–193).
52 This is still rather simplistic, because of course the test results will depend on this ad hoc choice. In fact, the reader can change the smoothing constant value in cell R2 and see the effect on the test statistic. A better alternative would use a GARCH model. Then the GARCH model parameters would be estimated optimally in the usual way (see Section II.4.2.2) and the degrees of freedom for the test statistic would increase by the number of parameters in the GARCH model.
53 See Section IV.3.4.1.
54 This is fitted using the EM algorithm – see Section I.5.4.3.