Description of Minimum Spanning Trees
Picture a number of pegs on a board connected by pieces of string. Assuming that every peg is reachable from any other by traveling along one or more strings, imagine a game in which the object is to remove some of the strings until all of the pegs remain connected using the least amount of string. This is the idea behind a minimum spanning tree. Formally stated, given an undirected, weighted graph G = (V, E ), a minimum spanning tree is the set T of edges in E that connect all vertices in V at a minimum cost. The edges in T form a tree because each vertex ends up with exactly one parent that precedes it in the span, with the exception of the first vertex, which is the root of the tree.
Prim’s Algorithm
One approach to computing a minimum spanning tree is Prim’s algorithm. Prim’s algorithm grows a minimum spanning tree by adding edges one at a time based on which looks best at the moment. The fact that Prim’s algorithm adds edges using this approach makes it greedy (see Chapter 1). Although greedy algorithms often yield approximations rather than optimal solutions, Prim’s algorithm actually provides an optimal result.
Fundamentally, the algorithm works by repeatedly selecting a vertex and exploring the edges incident on it to determine if there is a more effective way to span the vertices explored thus far. The algorithm resembles breadth-first search because it explores all edges incident on a vertex before moving deeper in the graph. To determine the vertex to select at each stage, we maintain a color and a key value with every vertex.
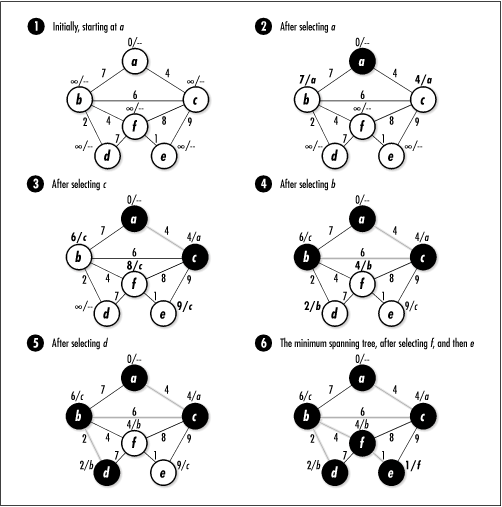
Initially, we set all colors to white and we set all key values to ∞, which represents an arbitrarily large value greater than the weight of any edge in the graph. We set the key value of the vertex at which to start the span to 0. As the algorithm progresses, we assign to all vertices except the start vertex a parent in the minimum spanning tree. A vertex is part of the minimum spanning tree only after it is colored black. Before this time, its parent can fluctuate.
Prim’s algorithm proceeds as follows. First, from among all white vertices in the graph, we select the vertex u with the smallest key value. Initially, this will be the start vertex since its key value is 0. After we select the vertex, we color it black. Next, for each white vertex v adjacent to u, if the weight of the edge (u, v) is less than the key value of v, we set the key value of v to the weight of (u, v) and we set the parent of v to u. We then repeat this process until all vertices have been colored black. As the minimum spanning tree grows, it consists of all edges in the graph that have a black vertex on either end.
Figure 16.1 illustrates the computation of a minimum spanning tree using Prim’s algorithm. In the figure, the key value and parent of each vertex are displayed beside the vertex. The key value is to the left of the slash, and the parent is to the right. The edges shaded in light gray are the edges in the minimum spanning tree as it grows. The minimum spanning tree computed in the figure has a total weight of 17.