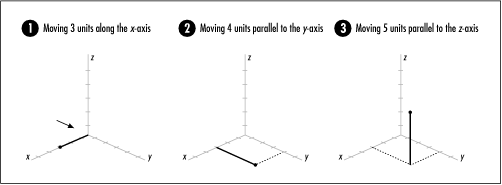
The rectilinear coordinate system is the coordinate system that is most familiar to us. In rectilinear coordinates, a point’s location is specified using three values, x, y, z, which are its positions along the x-axis, y-axis, and z-axis. Referring to Figure 17.5, the z-axis is positive going upward. Standing at the arrow looking forward, the x-axis is positive to the right, and the y-axis is positive straight ahead. From this vantage point, the positive directions for x and y look the same as in two dimensions. Thus, to locate (3, 4, 5), for example, we move three units to the right along the x-axis, four units ahead parallel to the y-axis, and five units up parallel to the z-axis (see Figure 17.5).

Figure 17.5. Locating the point (3, 4, 5) in a rectilinear coordinate system

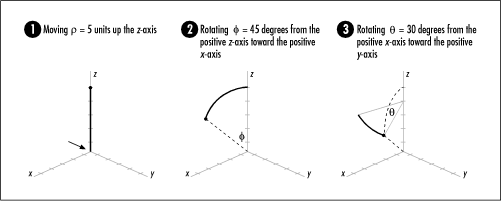
In spherical coordinates, a point’s location is specified in terms of a distance ρ (rho) and two angles, θ (theta) and φ (phi): ρ is the distance along an imaginary line from the origin to the point (a radius), θ is the angle the point forms from the positive x-axis toward the positive y-axis, and φ is the angle the point forms from the positive z-axis heading toward the positive x-axis. To locate (5, 30, 45), for example, we move five units up the z-axis, sweep 45 degrees from the positive z-axis toward the positive x-axis, and spin 30 degrees from the positive x-axis toward the positive y-axis (see Figure 17.6). (Notice that it is easier to visualize φ before θ even though θ precedes φ in the triple.)

Figure 17.6. Locating the point (5, 30, 45) in a spherical coordinate system

When speaking about an arc on a spherical surface, it is often convenient to have its endpoints specified in spherical coordinates. Therefore, the algorithm presented here assumes this representation to begin with. However, to compute an arc’s length, we will need its endpoints in rectilinear coordinates. Consequently, the first step is to convert the points p ₁ = ( ρ , θ ₁, φ ₁) and p ₂ = ( ρ , θ ₂, φ ₂) to the rectilinear equivalents p ₁ = (x ₁, y ₁, z ₁) and p ₂ = (x ₂, y ₂, z ₂). To do this, we start with the following equations. Of course, the locations of the points do not change, only their representations.

Another relationship between ρ and the rectilinear coordinates x, y, and z is:

This formula calculates the distance from a point to the origin in three dimensions.

Now we are ready to compute the length of the arc between p ₁ and p ₂ on the sphere. First, we picture two imaginary lines extending from the center of the sphere to each of the points (see Figure 17.7a) and calculate α , the angle between them. To do this, we use the formula:

where cos ^-1 is the inverse cosine of the argument in parentheses. Think of an inverse cosine this way: the cosine of what angle gives us the value of the argument in parentheses? The expression in the numerator of the argument comes from treating the imaginary line segments from the center of the sphere to p ₁ and p ₂ as vectors U and V (see the related topics at the end of the chapter) and computing the dot product U ⋅ V.

Figure 17.7. The length of an arc as viewed (a) on a sphere and (b) in the plane containing the lines from the center of the sphere to each point

The lines that form α lie in a plane that slices across the sphere. The importance of α is that where the sphere and this plane intersect, a circle is projected onto the plane with the same radius as the sphere (see Figure 17.7b). Since the arc between points p ₁ and p ₂ lies along a section of this circle, α helps to determine how much of the circle’s perimeter the arc covers. This is determined from the percentage α/2π, since there are 2π radians in a circle. Using this and the circumference of the circle, 2πρ, we see that the length s of the arc between p ₁ and p ₂ is (α/2π)(2πρ), which simplifies to the equation that follows. This is the equation that is used in the implementation presented later: