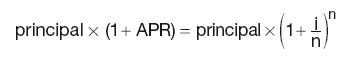3
Money market products
Overview of money market products
INTRODUCTION
The essence of a successful investment is profit enhancement and risk reduction. Whilst risks associated with unforeseeable events always remain, it is crucial to understand the products underlying a chosen investment strategy and be able to make comparisons with the alternatives. The concepts of compounding, reinvestment rates and future vs. present value of money are necessary tools for such comparisons. By using the virtually riskless loans and deposits as a benchmark, we can assess the suitability of more risky securities. This chapter introduces the fundamental concepts of financial investments and the simplest products – short-term lending and borrowing instruments. Their understanding will greatly enhance progress through the more complex topics that follow. Readers familiar with the pricing fundamentals can simply skip to the next section.
TIME VALUE OF MONEY
The reasoning behind even the most complex financial markets products can be reduced to two concepts:
‘There is no such thing as a free lunch’ – in an efficient market it is generally not possible to achieve risk-free profit
It should not be possible to purchase an asset and immediately sell it for profit. If that were the case, the supply and demand for such an instrument would soon eliminate this opportunity. If we expect more profit, we have to accept a greater risk.
The time value of money – in a positive interest rate environment any amount of money is worth more today than in the future
If we have money now, we can put it on deposit in a bank and earn interest, we can invest it in a business venture, purchase assets that would appreciate in value and much more. If have to wait for it, we expect to be compensated. That is why we expect to receive higher interest on longer term deposits than on our current bank account.
To help us understand these concepts and compare different investment strategies, the following sections will introduce interest and cashflow comparison methods.
Simple interest
The interest on short-term (less than one year) instruments is usually ‘simple’. If we place £100 on a deposit at 6 per cent for 80 days, as the interest rate is usually quoted annually, we expect to receive the correct proportion, i.e.:
£0.06 × 80/365
which would bring our total to:
£100 (1 + 0.06 × 80/365)
In general:
Calculation Summary
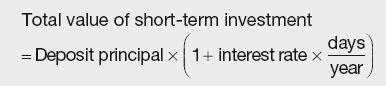
Where the interest rate is quoted annually, the deposit principal is usually abbreviated only to ‘principal’ and days/year implies ‘number of days in the period divided by number of days in the year’. The reason for the abbreviation is twofold: firstly it is, of course, easier to write in equations and secondly, and more importantly, it applies to all countries and markets where year conventions vary (365, 366 or 360).
Compound interest
If the above investment period is extended to two years, we would expect to receive £6 at the end of the first year and another £6 at the end of the second. Hence the total proceeds would be £112. But it is quite possible that the first £6 would be reinvested for the second period of one year together with the original £100. Thus, in the second year the interest would not only apply to the principal, but to the interest as well, bringing the total amount after two years to:
£100 (1 + 0.06) × (1 + 0.06) = £112.36
In general, for any principal amount invested for N years, the total proceeds are:
Calculation Summary
Total long-term investment proceeds after N years
= Principal × (1 + interest rate)N
NOMINAL AND EFFECTIVE RATES
If we, as above, deposit £100 at 6 per cent for one year, but with interest payments made quarterly, payments of 1.5 per cent would be made every three months. Hence, instead of £6 at the end of the year, we would have on deposit (assuming that the quarterly interest payments were reinvested for the remainder of the deposit period):
After the first period: £100 × (1 + 0.015) After the second period: £100 × (1 + 0.015)2 After the third period: £100 × (1 + 0.015)3 After the fourth period: £100 × (1 + 0.015)4
Therefore our total investment proceeds would be £106.14.
This concept can be extended to any payment frequency, monthly, weekly or daily, so that in general:
Calculation Summary
Investment proceeds at rate i with n payments per year
= Principal × (1 + i/n)n
Banks often quote rates for different tenors (monthly, daily etc.) and with various frequencies of compounding (how often the interest is credited to the account). Therefore it is essential to be able to convert the rate from one quote to another. The most useful quotation is the annual percentage rate (APR).
Let’s assume that we invest £100 for one year at 10 per cent annual rate. With the interest paid at the end (annual compounding) we would receive:
£100 × (1 + 0.1) = £110
However, if the interest was compounded semi-annually we would receive:
£100 × (1 + 0.05) × (1 + 0.05) = £110.25
Compounding quarterly, we would get:
£100 × (1 + 0.025)4 = £110.38
and so on. Clearly the amount increases with the frequency of compounding. The general formula is:
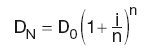
where D is the deposit amount, i is the quoted annual rate and n is the compounding frequency.
Therefore to calculate the effective rate, we would calculate the equivalent annualised rate that would give us the same proceeds, i.e. we would equate:
yielding:
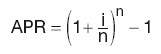
Generally the quoted (nominal) rate and the effective (APR) rate are linked by the following expressions:
Calculation Summary
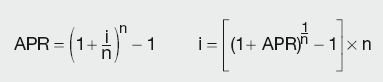
Continuous compounding
If the above ideas are extended to ever increasing interest payment frequency down to a second, millisecond etc. we would reach the limit, called the continuously compounded interest rate. This, of course, has no bearing on real-life investments as no bank would credit an account continuously, but it is an important concept in financial instrument pricing.
It can be shown that the equivalent rate in the case of continuous compounding is ln(1+ nominal annual rate), where ln is the natural logarithm loge (e ≈ 2.7183).
The continuously compounded rate is:
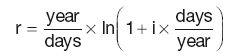
where i is the nominal interest rate.
For the annual effective rate (APR) the expression above simplifies to:
r = ln(1 + APR)
Reinvestment rates
The above ideas of reinvestment can be further extended to encompass the more realistic scenario where reinvestment rates for different periods are not the same. If we place £100 on deposit for a period of three years, it is likely that the interest rate will be reset at the prevailing market rate at the end of each year (or other pre-agreed period). Therefore the situation can be that for the first year we would receive 4 per cent, for the second 5 per cent and for the third 3 per cent, giving our total proceeds at maturity:
£100 × (1 + 0.04) × (1 + 0.05) × (1 + 0.03)
In general, investment proceeds at maturity at different rates ik for N years are:
Calculation Summary
![]()
Future value vs. present value of money
As could be seen above, it is essential that we can compare different investment scenarios that differ in investment periods, the absolute period to which the quoted interest rate applies and the frequency of interest payments. In order to do that, we introduce the concept of present value (PV), the key concept to pricing financial instruments.
Key Point
Present value (PV) is the value of future cashflows today
Short-term investments
If we put £100 on deposit for 90 days at 6 per cent annual rate we will receive at the end of investment period:
£100 × (1 + 0.06 × 90/365) = £101.48
It can be said that the present value (PV) of our investment is £100 and the future value (FV) is £101.48.
In other words, at the prevailing annual interest rate of 6 per cent, we should be indifferent whether we accept £100 now, or £101.48 in 90 days’ time.
Now another important question could be asked: if somebody offered us £104 in 120 days in exchange for £100 now, what rate of return (yield) did we achieve?
The above equation can be turned around to give:
Yield = (£104/£100 − 1) × 365/120 = 0.1216 or 12.16%
In general, for short-term investments:
Calculation Summary

Long-term investments
For investment periods over one year, compounding has to be taken into account. As we have seen earlier, £100 now invested at 6 per cent for two yeas would give:
![]()
Again, this means that the PV of £100 results in FV of £112.36 at 6 per cent annual rate. Or the yield on investment can be calculated as:
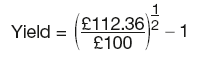
Generally, for long-term investments we have:
Calculation Summary
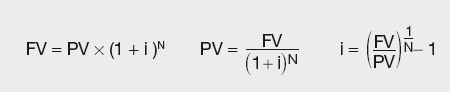
Discount factors
As in financial calculations PVs and FVs are often calculated, the division by 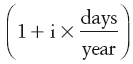 is so common that it is standard practice to introduce a new term, discount factor (DF), equivalent to its reciprocal value. Hence we have:
is so common that it is standard practice to introduce a new term, discount factor (DF), equivalent to its reciprocal value. Hence we have:
Calculation Summary

CASHFLOW ANALYSIS
Net present value (NPV)
In the examples above we assumed that all our cashflows were positive, i.e. we simply put the money on deposit and didn’t have any expenses. However, in reality, our cashflows would be both positive and negative. To calculate their present value, we simply discount them back to today at the prevailing interest rate to get net present value (NPV).
Internal rate of return (IRR)
When a client is deciding between several choices of investment, they are discounting future cashflows to today, and whichever one gives them greater PV would be the most beneficial choice. So from the previous example of APR, we could see that they would be indifferent between £100 now and £110 in one year’s time providing that prevailing market rates are at 10 per cent compounding annually. However, if they could get the interest to compound more frequently, e.g. semi-annually, they would be better off (£110.25/1.1 = £100.23, which is more than £100 today). What the investor would like to know is the margin of error in their calculation, i.e. how far the interest rates can move before their choice of investment becomes unfavourable. The interest rate that allows the investor to break even is the internal rate of return (IRR).
Example
We have £100 and the choice of three investments:
- Put the money in the bank at 10% for 3 years
- Get £40 at the end of each year
- Get £135 at the end of 3 years
We have to decide which one is the best under the prevailing interest rates of 10%.
- Money in the bank will grow to £100(1 + 0.1)3 = £133.10, which discounted back to today at 10% will give us £100 as expected
- £40 each year will have the PV of:
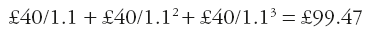
This is clearly less than investment A by £0.53 - £135 discounted back to today gives us £135/1.13 = £101.43
which is better than both A and B
Hence we decide to go with the investment choice C.
All the above assumptions are based on 10 per cent rates. What would happen if the rates changed?
Below is the NPV of the investments B and C (compared to the bank deposit) based on different interest rates:
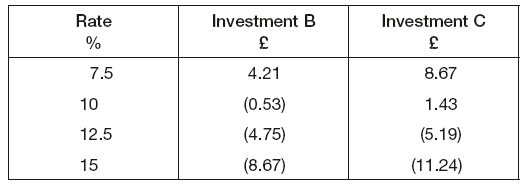
In other words, in lower interest rate environments the investment C would actually be a better choice than B. But with an increasing interest rate, both investments become unfavourable compared to option A. From the table above it is clear that the rate that would make the NPV = 0 (IRR) is somewhere between 10 per cent and 12.5 per cent, as that is the point where NPV changes sign.
To calculate IRR we could simply interpolate between 10 per cent and 12.5 per cent, but that would be too crude. Ideally we would take an iterative approach, whereby we keep repeating linear interpolations and changing the boundaries until we have reached IRR.
| Rate | NPV |
|---|---|
| 10 | 1 |
| 12 | –0.5 |
Linear interpolation will give us:
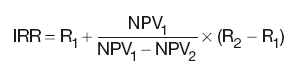
IRR = 10 + 1 × (12 − 10)/(1 − (–0.5)) = 10 + 2/1.5 = 11.33
Let’s assume that the NPV for the rate of 11.33 per cent is –0.1. As it is of the same sign as for 12 per cent, we will replace 12 per cent with 11.33 per cent and proceed with the linear interpolation:
IRR = 10 + 1 × (11.33 − 10)/(1 − (–0.1)) = 11.21
We will then calculate the NPV for 11.21 per cent and proceed as above until we reach NPV ≈ 0.
Key Point
Internal rate of return (IRR) is the rate that discounts all the cashflows, including any cashflow now, to zero.
IRR discounts all the future cashflows to a given NPV.
OVERVIEW OF MONEY MARKET PRODUCTS
Money market products is the term that describes all short-term financial instruments based on the current interest rate. It is often called ‘cash market’, as there is virtually no risk involved. If we are investing today for a period under one year, there is no uncertainty in the interest rate, it is publicly known. One may wonder why banks and other institutions trade them. The answer is that the rate the investor can achieve depends on many factors, creditworthiness being the main one. Banks can borrow their funds more cheaply than individuals, hence they make profit by offering loans at a higher rate than they have achieved. There are also several types of money market products where their features affect the interest rate.
Time deposit – loan
This is the simplest form of financial instrument, familiar to all. It refers to a deposit placed in the bank, which typically cannot be withdrawn until maturity. It cannot be transferred to another party, i.e. it is not ‘negotiable’. Typically the investment term is less than one year, with all interest paid at maturity. For longer periods, the interest payment frequency is agreed at the outset.
Certificate of deposit (CD)
A CD is similar to a time deposit, in that the funds are deposited at the bank, but the certificate (CD) is issued to the depositor, and can then be traded in a secondary market. It is typically not registered, i.e. any holder (‘bearer’) of a CD can withdraw the funds at maturity. It can be quoted in any currency.
Commercial paper (CP)
A CP is issued in the same way as a CD, but instead of banks, the issuers are companies with high credit rating (although some banks do issue CPs). It typically pays no interest, hence it is issued at a discount. From the difference between the FV and PV, the yield on investment can be calculated. It is in ‘bearer’ form, allowing it to be traded in secondary markets. As companies typically have lower credit rating than banks, the yield on CP is expected to be higher, accounting for the credit risk that the investor is accepting. It can be quoted in any currency.
Treasury bill (T-bill)
Again, a T-bill is similar to the above instruments, but the issuer is the government. It is typically issued at a discount and can be traded in the secondary market. Unlike, CDs and CPs, in most countries T-bills are issued only in domestic currency.
Bill of exchange
All the instruments described above were deposits. If a client needs funds, instead of simply borrowing at the prevailing rates (higher than deposits, to allow for the bank’s profit) they can enter into a contact called a bill of exchange. The client becomes the drawer of the bill and the bank the acceptor and the client is issued a banker’s acceptance (BA). In this way the bank becomes the guarantor for the repayment at maturity. The BA is very valuable to the client as it passes the credit risk to the bank. It is used for trade purposes, where the client’s creditworthiness may make their position unfavourable. Bills of exchange are typically issued at discount, i.e. the client receives less than he/she is required to repay instead of having to pay interest on the loan. The term is typically under six months.
Repurchase agreement (Repo)
Repo is another instrument used for borrowing funds. It is essentially a collateralised loan, as one party agrees to sell a security now to another party and repurchase it later at higher price. The collateral is usually a government bond, or another asset of high credit quality. Hence the interest rate implied by the repurchase price is generally lower than for an unsecured loan. A repo can also be used by an investor who accepts the collateral in exchange for funds now and receives repayment at maturity. From the investor’s point of view, this is a reverse repo. The term is usually very short. A repo can be issued in any currency, but is not negotiable.
MONEY MARKET CALCULATIONS
As money market instruments are basically short-term loans and deposits, there is no complex maths involved in pricing them and analysing cashflows. As all variables are known at the time of entering into an agreement, pricing money market instruments comes down to the fact that an investor is prepared to pay for an instrument today no more than the present value of all future cashflows, i.e. Price = PV.
Pricing a CD
A CD is issued at face value and pays interest (coupon) at maturity together with the principal amount. Hence, the price the investor is prepared to pay for it in the secondary market at any time until maturity depends on the prevailing interest rates in the market and the size of the coupon (which can be higher or lower).
Calculation Summary
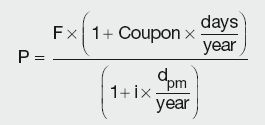
where F is the face value of CD and dpm is the number of days from purchase to maturity.
If the CD is bought in the secondary market after the issue and sold before maturity, and hence no coupon was received, the yield achieved can be calculated as:
Calculation Summary
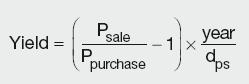
where dps is the number of days between the purchase and the sale.
Pricing discount instruments
Coupon bearing (interest paying) instruments repay more in the future compared to the face value today. In contrast, discount instruments repay face value in the future, compared to less now, to account for the lack of a coupon. But pricing formulae are essentially the same, as the price in the secondary market will always be the PV of the future cashflows (in this case, the face value of security).
Calculation Summary
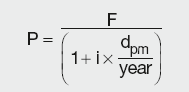
where F is the face value of the instrument and dpm is the number of days from purchase to maturity.