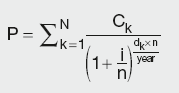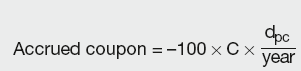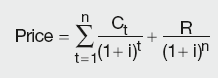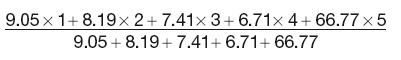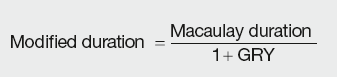Overview of capital markets instruments

Bond pricing fundamentals

Other bond markets

OVERVIEW OF CAPITAL MARKETS INSTRUMENTS

To raise capital for periods longer than one year, companies turn to capital markets. The lenders and borrowers tend to transact without the bank acting as an intermediary. The medium- and long-term securities that pay fixed coupon at regular intervals and repay the principal at maturity (redemption) are typically called bonds. There are many variations of this basic concept, some are discussed below.

Domestic, foreign and Eurobonds

The first distinction is made by the country of bond issue. A domestic bond is issued in the currency of the country of origin, whilst a foreign bond is issued in a different currency. Eurobond is somewhat confusing term that applies to an internationally issued bond, regardless of currency. Some bonds are registered, and if sold, the new owner has to be registered, in order to receive coupon payments and principal at maturity; whilst ‘bearer’ bonds pay to whoever is holding the certificate and can be transacted anonymously.

Bonds can be issued by companies or governments. Government-issued bonds (in the UK called Gilts) tend to dominate domestic capital markets as they offer good liquidity and are considered risk-free. They tend to offer a lower yield than corporate-issued bonds on account of the absence of risk to the investors.

Fixed-coupon bonds

Fixed-coupon bonds offer a long-term investment with known cashflows until maturity. The principal amount is invested at the outset, and in return regular coupon payments are received until maturity when the bond is redeemed (principal returned). However, the risk associated with interest rates still remains. If the rates rise, the coupon may seem unfavourable, but it can be reinvested at the prevailing rates at the time, thus yielding more income and vice versa. Thus bond pricing calculations tend to be very complex.

Floating rate notes (FRNs)

FRNs are a variation of bond whereby the coupon is not fixed at the inception, but is reset at regular intervals to a level linked to (and typically above) a pre-agreed benchmark. In Eurobond markets, the benchmark rate is typically the six-month Libor (London Interbank Offered Rate – the interest rate at which a London bank of high creditworthiness offers funds to another London bank of the same credit standing). For an investor who believes the rates are on the rise, this can be a better choice of investment than a fixed-rate bond, as it provides potentially higher returns.

Index-linked bonds

Index-linked bonds pay a coupon (and sometimes redemption amount) that is linked to a particular index. Bonds issued by governments are typically linked to the domestic inflation rate, whilst corporation tend to issue stock index-linked or commodity price-linked bonds.

Zero-coupon bonds

A zero-coupon bond is a capital market instrument akin to the shorter-term T-bill, whereby there are no coupon payments during the lifetime of the bond. Instead it is issued at discount to its face value. As the only cashflows are the principal and the redemption amount, there is no interest rate risk associated with fixed-coupon bonds. This is reflected in the yield, which is typically lower for zero-coupon bonds.

Strips

Stripping is the term used for separating all bond cashflows – coupons and redemption amount – and trading them as separate securities. It is a process previously done only by investment banks, but now some governments trade strippable bonds. Investors who cannot afford the principal amount to purchase a bond in the usual manner find strips attractive, as they offer similar market exposure to a standard bond with added flexibility in the choice of strip tenors (payment timings).

Perpetual bonds

Perpetual bonds have no redemption date. They pay coupons indefinitely. As such, they can be very useful tools for pension funds, as the pensioners require regular payments over an unknown period without the need for a lump sum.

Amortising bonds

The concept behind amortising bonds is opposite to the above. This type of bond pays the principal in stages over the lifetime of the bond, i.e. the principal is amortised. This affects the coupon payments, which are also gradually reduced, as they are based on the principal amount.

Asset-backed securities

An asset-backed security is a bond collateralised (guaranteed) by an asset or a group of assets, such as properties. As in standard bonds, the creditworthiness of the issuer is the primary determinant of the coupon payments (riskier bonds would pay higher coupons). Asset-backed securities provide counterparty credit default protection as the underlying assets create the necessary funds (mortgage payments or rental income). However, they are heavily dependent on the property market and its fluctuations. As mortgages are repaid, so is the bond amortised and the cashflows are not easy to predict. There is also an inherent risk of mortgage repayment default or property market downturn. Investors tend to rely on historical data as the best estimate of the bond’s likely performance.

BOND PRICING FUNDAMENTALS

Bond price at inception

The basic concept behind bond pricing is much the same as for money market instruments. The investor is prepared to pay today the present value (PV) of all future cashflows (coupon and redemption amount). As bonds issued by governments and large corporates tend to be for very large amounts, the investors typically buy units, hence the pricing is based on the unit of 100 (£ or other currency). There is a large secondary market for bonds, thus they do not have to be purchased at the time of issue. At any point during the lifetime of the bond, it can be purchased/sold in the open market. This makes the bond valuation quite complex. Nevertheless, the simple concept of time value of money still applies, i.e. the purchaser is only willing to pay for the asset the present value of all the future cashflows.

Hence the simple pricing formula is:

It is clear from the above that for the same redemption amount:

The above formula makes a crucial assumption that the bond yield is known at the outset. However, in practice, the investors are quoted bond prices and from the future cashflows they calculate the implied bond yield by iteration. By trial and error, they calculate the rate that would discount all outstanding cashflows back to the bond price. In that way they can compare different bonds in the market to see which one provides the greatest yield.

Bond pricing calculations also incorporate several important simplifications:

1. As bonds are typically issued for very long periods, even up to 50 years, and coupon payments (if there are any) are usually paid semi-annually, the coupon payments are assumed to be paid at exact intervals, without taking into account the actual number of days in those periods. For example, a bond with a 10 per cent annual coupon would be paying 5 per cent twice a year, even if the time periods do not match exactly.
2. When coupon payment are discounted back to present value, they are assumed to be paid at regular and equal intervals, not taking into account weekends, public holidays, leap years etc.
3. As bonds can be transacted at any time, the purchaser may acquire the security with the first outstanding coupon period shorter than the standard one. Even though technically this first coupon should be priced (discounted to the present time) using the money market convention of simple interest, compound interest is used instead. The reason for this discrepancy is to make bond pricing techniques more uniform.

Accrued coupon

When the bond is purchased/sold in the secondary market (at some point after the issue) it is likely that the time of transaction would not exactly match the coupon payment date. As neither party is willing to give up their rightful profit, the seller of the bond should be compensated for the loss of the portion of the coupon accumulated from the last payment date to the time of the sale. This is called accrued interest or accrued coupon. The original investor has earned it by holding the bond until the transaction date, but in fact when the next coupon is due the new owner will receive the full amount even though his/her holding period will be shorter than the standard coupon period. Accrued coupon is calculated using the expression below:

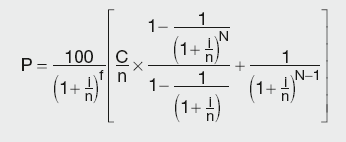
In market terminology the bond calculation formula provides a so-called ‘dirty price’. Once it is adjusted for the accrued coupon, it is called the ‘clean price’, which is typically quoted in the market. To take into account the accrued coupon payments, the bond valuation formula (based on units of 100) expands to:

Coupon dates

As mentioned previously, when calculating bond price, the coupon periods are assumed to be equal, depending on the payment frequency. The market conventions vary regarding when the payments are actually made. For example, for a bond with a 10 per cent coupon paid semi-annually that is issued on 15 March 2000, the assumed coupon dates would be 15 September 2000, 15 March 2001 and so on. Should any of those dates fall on a non-working day, the payments would be made either the day before or the day after, depending on market conventions. Also some markets make payments at the end of the month, regardless of the fact that it can be 28 February, 30 April or 31 August, whilst some pay on the exact day. The pricing formulae do not take account these discrepancies and the valuation is virtually unaffected.

Ex-dividend

Another issue related to the secondary bond market valuation is the change of bond ownership. If a bond is a bearer bond, i.e. not registered, this does not apply, but in the majority of cases the administrative procedure may take some time to complete. If the bond is sold before the coupon date but the ownership is transferred some days after, the bond becomes ex-dividend or ex-coupon. The original owner receives the full coupon, whilst he/she has only earned a portion of it, i.e. the rightful new owner did not receive his/her fraction. The ex-dividend coupon is calculated similarly to the accrued interest, but the payment is due to the buyer, rather than seller.

Bond yield

As mentioned earlier, the bond pricing calculations are based on the assumption that the bond yield is known. In reality, the reverse is true and the yield is calculated from other known parameters. There are many yield measures, each with their own advantages and disadvantages. The simplest yield measure is the flat yield or current yield. It ignores the time value of money, as it does not take into account the timing of coupon payments and gain/loss on the redemption amount compared to the purchase price. It simply gives the value of the coupon as a fraction of the price paid. It is a crude measure of the bond yield and only provides a ‘quick glance’ idea of its value.

A better measure of bond yield is the simple yield to maturity, also known as Japanese gross redemption yield (JGRY). It does take into account capital gain/loss arising from the difference between the price and the redemption amount, but not the timing of the payments.

In practice, the bond yield is calculated by iteration, using more complex formulae, where timing of payments, capital gain/loss and time value of money is taken into account. Market practitioners would typically use the formulae below, entering various yields i into the valuation formula until the market price is reached. This measure of yield is known as redemption yield, yield to maturity or gross redemption yield (GRY).

Assuming the yield applies to the coupon period and that all the periods are equal:

Taking into account the irregular first coupon payment period:

Whilst the flat yield underestimates the actual bond yield, as it takes no account of the capital gains, the JGRY overestimates it (it spreads the capital gains evenly until redemption). Hence the correct yield is somewhere in between. It is useful to calculate the flat yield and the JGRY, as they will bound the true yield from either side, and proceed with iteration using those boundaries.

Portfolio duration

Convexity

The relationship between bond prices and their yields is non-linear. Let’s assume that we have three bonds B₁, B₂ and B₃ with the prices equally spaced out, i.e. B₂ – B₁ = B₃ – B₂. We can calculate their respective yields to be Y₁, Y₂ and Y₃. Even though the bond prices are equidistant, the same cannot be said about their yields, i.e. Y₂ ≠ (Y₁ + Y₃)/2. The expected yield will exceed the actual bond yield. This difference is known as convexity adjustment. The calculation of convexity adjustment is not a simple process and is the subject of extensive research, but is not within the scope of this book.

Duration

Most financial products (particularly exchange-traded ones) are easy to compare when it comes to the income they provide. That is normally not the case with bonds, as there are so many different varieties (different coupons, payment frequencies, maturities etc.).

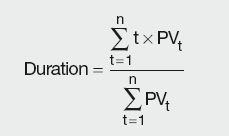
One useful measure of risk/return often used for bond comparison is duration or Macauley’s duration. Duration is a composite measure of bond risk/return expressed in years. It is a weighted average length of time to the receipt of half of the bond benefits (both the notional and the coupons) where the weights are the PVs of the cashflows.

Mathematically the above can be expressed by the following formula:

Properties of duration

• Lower coupon bonds will have longer durations. This intuitively makes sense, as the biggest proportion of cashflows (redemption amount) will be received at the end of a bond’s lifetime. Ultimately, the zero-coupon bond will have duration = maturity, since there are no cashflows until redemption.
• Longer dated bonds will have longer duration. Again, we will have to wait longer for the largest proportion of the cashflows.
• Lower yield bonds will have longer duration. This is because the PV of the cashflows far in the future (which are weighted the most) will rise and will tip the balance.

Modified duration

Modified duration is developed as a means of measuring the impact of yield change on price. The basic proposition is that the product of yield and its sensitivity will give the proportionate change in price:

Modified duration is linked to Macaulay duration by:

The properties of modified duration are the same as for duration, i.e. modified duration is higher for:

• Longer dated bonds
• Lower coupon bonds
• Lower yield bonds.

PV01

We have seen from the above that modified duration (MD) relates the bond price sensitivity to the change in yield. For example, a bond with MD = 6.5 will change price by 0.065 per cent for every basis point (bp – 100^th of 1 per cent) change in yield. The change in the market price is then simply the product of this sensitivity and the current market price. It is useful to calculate a present value of the basis point (PVBP) or PV01, which is a measure of the absolute change in price of £100 nominal bond for a 1bp (0.01 per cent).

This is done using the following calculation:

Due to the curvature of the yield curve, the change in yield will not correspond to the linear change in price due to convexity (see above). Moreover, as we move in time, the change in yield is the result of both passage of time (horizontal shift) and actual upward/downward shift in rates (vertical shift).

The two can be separated out by moving one day at a time without changing the rates (for horizontal shift) and shifting the rate up/down on the same day (vertical shift).

OTHER BOND MARKETS

So far we have discussed bonds as capital markets instruments. This market is very large and active, but bonds play a crucial role in other, more speculative markets, the most prominent being the derivatives market. Here, the most common instruments are bond futures (an agreement to purchase/sell a bond at some future date at the price agreed today) and Repos (repurchase agreements, whereby the bond is bought/sold today and sold/bought back at an agreed price at some future date), which will be covered in Chapter 10. Furthermore, many structured financial products incorporate bonds (e.g. convertible, callable or puttable bonds), with the examples given in Chapter 12. They are of further interest in the wide range of credit derivatives, whereby protection against a bond downgrade or default can be bought or sold. Some examples of credit derivative products are covered in Chapter 11.