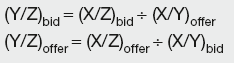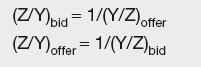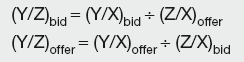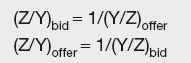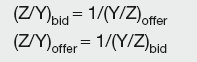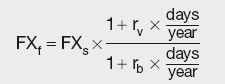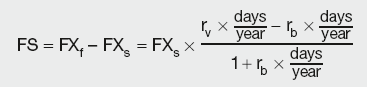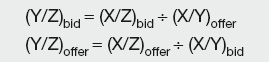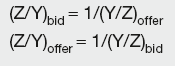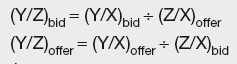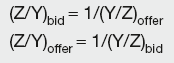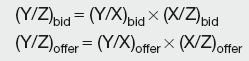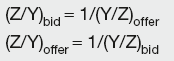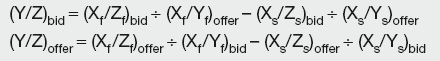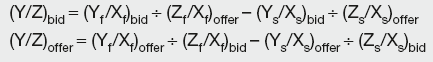Spot exchange rates

Direct and cross-rates

Forward exchange rates

INTRODUCTION

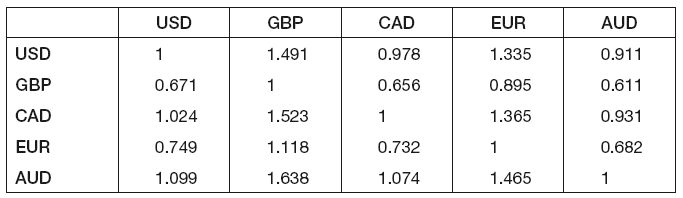
Foreign exchange refers to the exchange of one currency for another. It is written in the form CCY₁/CCY₂. The two currencies are referred to as ‘base currency’ on the left and ‘variable currency’ on the right. Its value refers to how much variable currency is paid/received for one unit of base currency. In domestic markets the base currency is the domestic currency, whilst in international markets it is typically USD. More and more frequently, various currencies are quoted against EUR. In financial markets trades involving virtually any combination of currencies are executed and the exchange rate tables (FX tables) are used. Table 8.1 gives an example.

Table 8.1 Example of foreign exchange tables

The currencies in the column headings are ‘base currencies’, i.e. on the left of the CCY₁/CCY₂, whilst the currencies in the row headings are ‘variable currencies’ on the right.

SPOT EXCHANGE RATES

Spot exchange rates apply to trades executed now. In financial markets the delivery is typically two working days from the trade date to allow for necessary bank transfers and paperwork. The adjustments for holidays in both countries have to be made. As stated above, any currency pairs can be traded. However, most currencies are quoted either against EUR (interbank spot market), or USD (futures market), referred to as the direct rate.

Other currency combinations have to be calculated from two rates against USD or EUR and are called cross-rates. For example, to obtain the CHF/CAD exchange rate, the amount of USD received on sale of CHF would be calculated first, and then the amount of CAD purchased by USD would imply the CHF/CAD rate. The important aspect of cross-rates is that they involve both sale and purchase. As traders make profits from buying/bidding ‘low’ and selling/offering ‘high’, each exchange rate has two sides, creating bid/offer spread. Supply and demand influence the width of the spread. Typically for major currencies it is very tight; whilst for currencies quoted as cross-rates it is wider, accounting for lower liquidity and the implied intermediate sale/purchase of base currency.

DIRECT AND CROSS-RATES

Direct rates, regardless of the choice of the ‘base’ and ‘variable’ currency, are two-way bid/offer quotations, where bid indicates how much variable currency is received on the sale of one unit of base currency and offer gives the amount of variable currency needed to purchase one unit of base currency. For example, the USD/GBP rate would be 1.490/1.492.

Cross-rates involve a currency pair that does not have a direct exchange rate quotation in the market. Thus it requires two calculations, each against the base currency. As there is no market convention for non-standard currency pairs, the trader decides which is the ‘base’ currency in the final quotation.

We can see that the spread is wider than for quotations against the base currency, as two transactions are implicit in its calculation. If we accepted NOK as the ‘base’ currency, similar calculations would be performed. The bid side would be worked out as the amount of CHF received on sale for USD and then converted to NOK, i.e. 1.072 ÷ 6.055 = 0.164. The offer would be calculated by working out the rate at which NOK would be exchanged for USD and then converted to CHF, i.e. 1.069 ÷ 6.061 = 0.176. This creates the NOK/CHF exchange rate 0.164/0.176.

The above could have been done more simply, by taking reciprocals of the CHF/NOK and reversing the sides. To avoid confusion, it is important to remember the following:

• Traders always ‘buy low and sell high’, hence the lower number is always on the left.
• Cross-currency spreads are always wider, and thus combine quotations from the opposite sides of direct rates.

The above scenarios can be summarised as:

• The exchange rates are always calculated to create the worst possible outcome, i.e. the lowest number for the bid, and the highest for the offer.
• From two rates with the same base currency, opposite sides are divided. In the cross-currency quotation the numerator in the division becomes the variable currency, whilst the denominator is the base currency.
• From two rates with the same variable currency, opposite sides are also divided. But in the cross-currency quotation the numerator in the division becomes the base currency, whilst the denominator is the variable currency.
• From two rates where the common currency is the base currency in one quotation, but the variable in another, multiply the same sides. This creates a cross-currency quotation where the base currency in the original quotation remains the base currency, and vice versa.

This can be expressed more simply using mathematical notation:

FORWARD EXCHANGE RATES

The spot rates from the previous sections refer to transactions settled two working days from today. Even though the settlement is in the future, these transactions are not considered to be ‘futures’ or ‘forwards’, as the additional two working days have to be added to all cross-currency trades regardless of the security involved. The ‘true’ forward trades settle at some future date different from the spot settlement date.

Forward outrights

Forward outright contracts involve the outright purchase or sale of one currency in exchange for another currency for settlement in the future. The same rules of exchange rate calculations apply, i.e. there is a two-way price where the sale is made using a bid quotation and the purchase uses an offer quotation. In major currency pairs the two cashflows are exchanged at maturity, whilst in some less liquid contracts only the difference between the agreed rate and the prevailing market exchange rate is settled. The pricing of the forward outright is the same in both cases. Whilst the motivation behind trading forward outrights is the same as for FRAs, i.e fixing the rate for a time period in the future, the contracts are influenced by different underlying variables. FRAs are only exposed to the interest rate risk in the currency they are denominated in, whilst forward outrights are affected not only by the fluctuations in the exchange rate between the two currencies, but also by the interest rates in their domicile countries. This is reflected in their pricing. The forward outright is calculated as the ratio of variable and base currencies that would be available on the future date if they were both placed on deposit at their respective interest rates.

Forward swaps

From the formula above it can be seen that by entering into a forward outright transaction the counterparties are essentially taking a view on interest rates in the two currencies involved in the exchange, without actually participating in the interest rate market. An alternative is to actually buy/sell one currency now (at spot rate) and reverse the transaction by selling/buying back the same currency at a forward rate. This is known as a forward swap (briefly described in the previous chapter). As this involves selling low and buying high, if actual bid/offer spreads were taken into account, the swap would become prohibitively expensive. Thus mid quotes are typically used. As the initial swap is transacted at spot and reversed at maturity at the forward exchange rate, to avoid arbitrage the swap must be valued as the difference between the two rates:

From the equation above it is clear that the forward swap enables traders to exploit interest rate differentials between the two currencies. If they expect the gap to narrow (either the base currency interest rate rises or the variable currency interest rate falls) they will speculate by buying the base currency now and selling it forward. The net effect of this transaction is borrowing in the base currency and depositing in the variable currency.

Discounts and premiums

From the equation above it follows that if the variable currency interest rates are higher than for the base currency, the forward exchange rate will be higher than the spot, and vice versa. The logic behind this pricing is that if we exchange higher-interest variable currency into lower-interest base currency at spot and place the amount on deposit, we would earn lower interest. However, if we buy the base currency forward, we are left with the original variable currency that can be invested at the higher interest rate until settlement. To make the investor indifferent as to which path to take, the forward rates have to be higher to compensate for the low interest rate. In this case the base currency is said to be ‘at premium’. If the variable currency interest rates are lower than the base currency rates, the opposite is true. The base currency is then ‘at discount’ and the forward rate is lower than the spot.

Cross-rate forwards

Calculation of cross-rate forward follows the same rules as for spot cross-rate quotations:

Cross-rate forward swaps

The forward swap price is the difference between the forward outright and the spot exchange rate. When the currencies involved in the swap do not have a direct market exchange rate quotation, the cross-currency spot rate, as well as forward outright rates, have to be calculated using a common currency. Thus the cross-rate forward swap price calculation requires five steps:

1. Calculate spot cross-rate as previously described.
2. Calculate forward outright for one currency against the common currency.
3. Calculate forward outright for second currency against the common currency.
4. Calculate forward outright cross-rate.
5. Calculate cross-rate forward swap price as the difference between the forward outright rate and the spot rate.