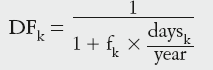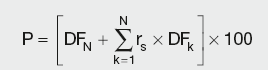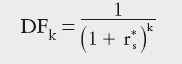7
Basic swap concepts and applications
INTRODUCTION
As mentioned in the introduction, derivatives products can be split into single settlement and multiple settlement products. FRAs, covered in the previous chapter, are single settlement securities that provide protection against fluctuations in an underlying interest rate for a short period of time. If a longer period needs to be covered, a FRA strip can be purchased, but liquidity of far-dated contracts might make this strategy impractical. An alternative is an interest rate swap.
BASIC SWAP CONCEPTS AND APPLICATIONS
Swaps are OTC products, specifically tailored to customer needs, but typical periods they cover range from 2 to 30 years. They are effectively a series of cashflow (coupon) exchanges over a period of time. The principal amount may be exchanged at inception and maturity, or alternatively only coupons based on a notional amount are exchanged at regular intervals (typically every six months). The two sides of the swap are commonly referred to as ‘legs’. In practice, swaps where both legs are in the same currency do not involve principal exchange, as the net effect would be zero. The exchange of coupons is also ‘netted’, i.e. only the difference between the two legs is paid/received to minimise credit risk exposure. The market is liquid, particularly for shorter contracts. As in other derivatives products, the market participants can be split into three main categories: speculators, hedgers and arbitrageurs.
Speculators take risky swap positions independent of any underlying instruments, hence they can take a view on any type of swap. However, if a coupon swap (fixed vs. floating) is used, the receiver of the fixed leg takes the position with the view that interest rates are on the decline, thus benefiting by locking in the higher rate, whereas the receiver of the floating leg takes the opposite view. Since there is no principal exchange and no payments at the outset in terms of fees and premiums, it is very cost-effective to speculate in either a short- or a long-term interest rate derivatives market.
Hedgers enter into swaps to fix their borrowing cost. If they believe that the interest rates will rise, they can protect their floating rate borrowing (typically spread over Libor) by entering into a swap, whereby they pay fixed rate and receive Libor. The net cost of their borrowing thus becomes fixed rate + spread, as the Libor payment under the swap and the loan repayment cancel out. In this respect swap hedge works in a similar way to hedging futures and FRAs, as they aim to establish an equal and opposite position.
Example
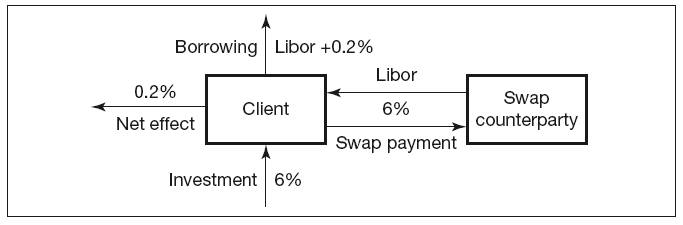
A client has invested in a fixed rate bond, thus receiving a fixed coupon semi-annually. However, his liabilities arise from floating rate borrowing, whereby he is exposed the risk of floating rate fluctuations. To mitigate the position unfavourably affected by the interest rate rise, a coupon swap can be used as a hedge. The arrangement is illustrated in Figure 7.1.
Figure 7.1 Matching asset and liability exposure using coupon swap
Arbitrageurs use swaps to exploit the discrepancies in the different funding methods. If two counterparties have access to both fixed and floating markets, but one counterparty has a relative advantage in one market over the other, they can enter into a swap and both achieve borrowing at reduced cost. This is best shown in an example.
Example
A company X requires floating rate borrowing and has access to funds at either 6% fixed rate, or Libor + 0.2%.
A company Y requires fixed rate borrowing and has access to funds at either 7% fixed rate, or Libor + 0.8%.
They can both transact in their preferred markets, or enter into a mutually beneficial swap. Company X clearly has better credit rating, reflected in more favourable rates in both markets. Hence, to understand the motivation for such a transaction the rates are summarised in Table 7.1.
Table 7.1 Comparative borrowing rate advantage in fixed and floating markets
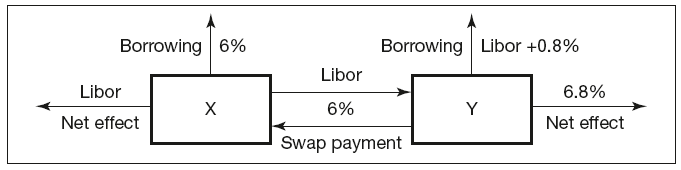
Clearly company X has a bigger advantage in the fixed market than in the floating market. The absolute advantage is the difference between comparative values in both markets, i.e. 1% – 0.6% = 0.4%. This is the rate difference available for sharing between the two counterparties.
Even though company X requires floating rate funding, it will borrow in the market where it has most advantage, i.e. at 6% fixed rate, while company Y will borrow at Libor + 0.8%. If the absolute advantage is to be split equally, they enter into a swap, whereby company X pays Libor and receives 6%, whilst company Y pays 6% and receives Libor. The net effect, as shown in Figure 7.2, is:
- Company X pays Libor (0.2% improvement on the original rate)
- Company Y pays 6.8% (0.2% improvement on the original rate).
Figure 7.2 Exploiting comparative borrowing rate advantage using coupon swap
In practice the rate advantage may not be split equally due to the difference in credit rating. Furthermore, an investment bank would typically act as an intermediary, taking a cut of the profit and then passing on the difference to the counterparties.
The above swap involving the exchange of fixed coupon vs. floating rate is the simplest and the most common one. Other varieties are discussed below.
TYPES OF SWAPS
Asset swap
The swap in the example above was initiated due to the discrepancy between the funding costs in different markets. However, clients often wish to be net payers of fixed rate (to protect the borrowing costs) and would enter into a swap whereby they pay a fixed rate and receive a floating rate. This type of swap is also known as a ‘vanilla’ swap, as it is the most basic type of this security. The two legs typically have the same payment frequency (e.g. six months) and the underlying floating rate is equal to the payment period (e.g. the floating swap leg is fixed semi-annually against spot six-month Libor). This may not always be the case, as swaps are tailored to meet clients’ needs, but any modifications need to be priced into the swap. Alternatively, if the rates are on the rise, a client receiving a fixed rate income could enter into a swap to benefit from this increase, without changing the investment strategy, as shown in Figure 7.3.
Figure 7.3 Graphical representation of asset swap
Basis swap
Counterparties with payment obligations based on one floating interest rate but receiving funds in the same currency based on another rate may enter into a basis swap to neutralise their basis exposure. For example, a high-street bank that receives mortgage payments on a monthly basis, but has outstanding debts incurring payments based on the three-month Libor, would benefit from bringing its assets and liabilities under the same denominator (basis). Just as in the earlier asset swap example, there is potential comparative advantage between floating rate funding costs that can be exploited by two counterparties. For example, if a company has a mortgage payment income based on the one-month Libor + 0.5 per cent and an outstanding loan based on the three-month Libor, it may be possible (subject to credit rating) to enter into a swap under which the client receives the three-month Libor and pays the one-month Libor + 0.3 per cent, thus not only converting assets and liabilities into the same rate, but achieving an improvement of 0.2 per cent. In practice, the opposite is more likely to be true. Basis swaps are highly sought after by the clients, thus the bank would charge spread over the leg that the client pays, as shown in Figure 7.4.
Figure 7.4 Graphical representation of basis swap
Currency swap
A currency swap, much like an interest rate swap, refers to an exchange of payments between two counterparties at regular intervals over a period of time. However, these cashflows are in different currencies and are subject to interest rate fluctuations in different countries. There is also the exchange rate exposure. Hence currency swaps typically involve exchange of principals where the initial amounts are fixed at the spot FX rate and the amounts at maturity are fixed to the forward FX rate, whilst the actual rate at delivery may be substantially different. The different types of currency swaps are:
- Fixed-fixed, where both interest rates are fixed
- Fixed-floating, where one leg is based on a fixed rate and another on a floating rate
- Floating-floating, where both interest rates are floating.
Amortising swap
An amortising swap attracts clients whose borrowing principal amount is repaid over time (amortised), such as mortgage obligations. Hence the required amount of interest rate protection reduces over time. If they entered into a ‘vanilla’ swap, receiving a floating rate and paying a fixed rate, their obligations under the swap would become increasingly mismatched to the underlying borrowing amount. Alternatively, if they estimate amortisation (e.g. at 25 per cent every six months) and enter into a ‘stack’ of four swaps, each based on 25 per cent of principal but with decreasing maturities, they would not only achieve an uneven payment schedule but also enter into too many transactions. The amortising swap is then the ‘all-in’ solution. The above example assumed fixed-floating swap, but basis or currency swaps can also be amortising in order to meet client requirements.
Forward-start swap
A forward starting swap is akin to a strip of FRAs, as the contract starts at some point in the future. Any type of swap described above can be tailored to start forward.
SWAP PRICING FUNDAMENTALS
Short-term interest rate swaps
Valuation at contract inception
Swap pricing is based on FRA rates, as the fundamental idea behind both these products is to fix the cost of funds. Since it is possible to purchase a series of FRAs to cover periods of 3v6 months, 6v9 months, 9v12 months and so on, it is possible to calculate an equivalent rate for an entire period that would achieve the same net result, the swap rate. A client should be indifferent to whether they borrow on a rolling quarterly basis at a three-month Libor and simultaneously entering into a swap (quarterly paying fixed and receiving a three-month Libor) or they borrow on a rolling quarterly basis at the three-month Libor and fix the cost of that borrowing by purchasing corresponding FRA contracts. Since the Libor transactions in both scenarios are the same, it is implicit that the swap and the FRA strip must be of equal value. This concept is the basis for swap pricing. The all-in swap rate calculated using discount factors (DFs) based on FRAs can be calculated from the equation below:
Calculation Summary: Short-term swap valuation at inception
where:
rS is the annual swap rate, or coupon
daysk is the number of days covered by the kth FRA contract
DFk is the discount factor derived from the kth FRA rate fk using:
Swap valuation in the secondary market
Clearly at the inception it is implicit that both swap legs are of equal value. However, at any point in the future, as interest rates change, they move away from the equilibrium resulting in the payment from one counterparty to another. The later valuation follows the same principle of discounting future cashflows of both legs. Two approaches can be taken:
1. Valuation of the original swap using prevailing swap rates
In this scenario, the two legs are valued separately. Regardless of the change in the interest rates, the floating leg is still valued at par, as the rates used for discounting are the same as those for projecting the cashflows, i.e. any changes cancel out.
The fixed leg, however is affected by the change, as the discount factors used for the valuation have moved away from the original calculation. Hence, its valuation can be summarised as:
Calculation Summary: Later valuation of short-term swap fixed leg
where:
P is the value of the fixed leg at a later date
rS is the swap rate, fixed at inception
daysk is the number of days covered by the kth FRA contract
DFk is the discount factor derived from the kth FRA rate fk using:
As the swap valuation at inception was based on a notional amount of 100, clearly the difference between the calculated fixed leg and the 100 is paid/received, depending on the prevailing interest rates. The receiver of the fixed benefits from rising interest rates, and vice versa.
An alternative approach to swap valuation follows.
2. Valuation of fixed swap leg using new swap rate
An alternative is to calculate a new swap rate that would price the swap at par. This is done using the original swap valuation formula, resulting in a new swap rate rS*.
This new swap rate is used to discount all future fixed leg cashflows, as follows:
Calculation Summary: Later valuation of short-term swap fixed leg using new equilibrium swap rate
where:
P is the value of the fixed leg at a later date
rS is the swap rate, fixed at inception
daysk is the number of days covered by the kth FRA contract
DFk is the discount factor derived from the newly calculated equilibrium swap rate applicable to the kth period:
It is worth noting that even though they are practically interchangeable, the two methods may produce slight discrepancies between the two values, due to the fact that the first method uses exact daycounts, whilst the second applies fixed periods for all future swap legs.
Long-term interest rate swaps
The above valuation is possible for swaps of relatively short maturity, so that their entire period is covered by futures and FRA contracts. If that is not the case, there isn’t sufficient market information for arbitrage-free valuation. The long-term swap prices are normally linked to capital markets products, such as bonds. As with any other product, the supply and demand will ultimately dictate their price. Liquidity of long-term swaps is also an issue, as there are fewer market prices that can be used as references.
The typical approach to pricing long-term swaps is to evaluate each leg separately, using bond valuation principles. As the floating leg is directly liked to the long-term interest rate forward market, its value is always at par, whether it is priced at inception or at some future date. However, the fixed leg at inception also has to be valued at par; hence its rate needs to be iteratively adjusted until the convergence criteria are reached.
At any future date the two legs are simply valued separately and the net sum is paid/received depending on the prevailing interest rates.
PRICING CURRENCY SWAPS
Even though this chapter has so far dealt with interest rate swaps – by far the most popular type of swap – currency swaps are also included, as they are closely linked to the interest rate market. Foreign exchange (FX) and related financial instruments are covered in the following chapter. For more details on FX terminology and products see Chapter 8.
Currency swap is a contract between two counterparties to exchange cashflows in different currencies, thus exposing them to both the exchange rate risk and the interest rates linked to the currencies in question. Even though there are many ‘flavours’ of currency swaps (as there are for any other type), the main distinction is in the swap type:
Short-term swaps are typically structured so that only the principal is exchanged at inception and reversed at maturity, thus incorporating the interest rate and FX exposure through the uncertainty of the final cashflow market value.
Long-term swaps are structured similarly to other swap types, i.e. the contract commits the two parties to the exchange of regular payments (in their respective currencies), with the final exchange of principals at the exchange rate agreed at inception. The initial principal exchange may or may not be a part of the contract.
Short-term currency swap valuation
As in all other foreign exchange contracts, one of the two currencies is defined as a primary currency and most deals are structured so that the nominal value of the primary currency leg is equal at both inception and maturity. The secondary currency in the swap deal determines the notional amount of the second leg, as a function of the spot and forward exchange rates. In other words, at inception the notional amount of secondary currency is calculated as the product of the primary currency notional and the spot exchange rate. The principal amounts to be exchanged at maturity are fixed at the inception and calculated as the product of the primary currency notional and the forward exchange rate. Clearly, just like interest rate swaps, currency swaps are used for speculation, hedging and arbitrage.
Their valuation conforms to the same principles as described above, i.e. at inception the two swap legs are of equal value (based on the spot FX rate). The valuation at any point in the future, including maturity, is done in relation to the secondary currency (the primary leg being fixed); whereby the profit/loss on the secondary leg is calculated in relation to the prevailing FX rates for the corresponding tenor.
Long-term currency swap valuation
As explained above, the long-term currency swap involves both the regular cashflow exchanges throughout the contract and the exchange of principals at maturity (and sometimes at inception). Akin to other swap types, several variations may exist, the most common ones being:
- Cross-currency coupon swaps in which fixed rate in one currency is exchanged for a floating rate in another, or
- Cross-currency basis swaps, where floating legs in both currencies are exchanged.
Graphically, the structure can be represented as shown in Figure 7.5.
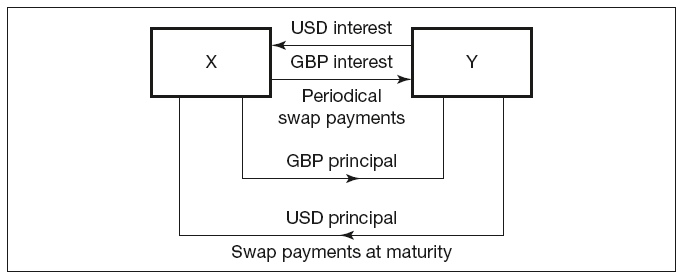
Figure 7.5 Graphical representation of cross-currency swap
Valuation of the long-term currency swap, once again, conforms to the standard calculation of present value of cashflows implicit in the two legs. At inception this value is equal. At any other time the valuation implies the calculation of the present value of the the two legs, using (as in interest rate swaps) bond calculation principles. As here the two legs (i.e. bonds) are denominated in different currencies, the following steps are taken:
- Each leg (bond) is valued in its own currency, based on the outstanding cashflows and relevant spot rates.
- The two legs are converted to the same currency (base currency) using the prevailing spot rate for the tenor equal to the outstanding contract period.
- The swap value is calculated as the difference between the two legs.
EQUITY SWAP VALUATION
Equity derivatives are covered in more detail in Chapter 10, whilst equity swaps are covered here as they are closely related to interest swaps and their valuation.
Akin to interest rate swaps, equity swaps are contracts between two counterparties to exchange a series of cashflows (typically semi-annually), without the exchange of principals at either inception or maturity. However, whilst one swap leg is typically linked to an interest rate corresponding to the payment frequency (e.g. six-month Libor), the other leg is linked to the performance of an equity investment (capital gains and dividends). Most commonly, the equity leg is based on the performance of an equity index (further discussed in Chapter 10). An important difference between the interest rate swaps and equity swaps is that the payments under different legs cannot be netted, as they are linked to different underlying variables. Thus, one counterparty always pays Libor, whilst the other pays total return on the equity investment. The important implication is that should the equity market fall, the payer of the Libor leg is responsible for both the floating leg payments and the equity capital depreciation.
As with all other swaps, the value of the two legs at inception is equal. It might seem improbable that the two legs are equal at inception, as in all previous cases one leg was adjusted in order to price the swap at zero. In contrast, in this case one leg is linked to Libor, and the other to an equity index performance, thus no adjustments can be made. However, using the principles of fair value, it is clear that the Libor leg will always be equal to par, as the rates used for discounting the cashflows are also used for projecting them. On the other hand, the equity performance is linked to the interest rate market, such that if there are any discrepancies between the returns in the two markets, an arbitrage opportunity would arise, quickly eliminating the discrepancy. Hence at inception an investor should be indifferent to which market he/she invests in, providing that all the products are priced fairly and disregarding transaction costs, market accessibility and volume limits.
At any other time the two legs are valued separately and the net value is paid/received depending on the equity performance. Three calculations are required:
- Capital performance of the equity index.
- Dividend income under the equity contract.
- Floating rate payment.
Capital performance is calculated as the product of the notional amount and the ratio of the initial index value to its value at the time of valuation. It is important to note that, as stated earlier, in the event of a decline in the equity market, the receiver of the equity return is responsible for both the floating payment and the equity depreciation compensation.
Dividend income is calculated as the percentage of the notional amount, having clearly specified in the swap contract to which period the dividend payment relates.
Finally, the floating leg is calculated in the same way as for all other swaps, i.e. as a percentage of the notional amount accounting for the number of days in the relevant period. Thus, the value of the equity swap is equal to:
Calculation Summary: Valuation of the equity index swap
![]()
For more information on equities and equity derivatives, please refer to Chapter 10.