Chapter 4
Living a Life without Limits
In This Chapter
Seeing what people choose when unconstrained
Understanding the concept of marginal utility
Sometimes you just can’t seem to choose what you want — limits are everywhere: speed limits, calorie limits, age limits, height limits on rollercoasters that drive the child who’s just an inch short of the restriction wild with frustration. Well, no limits in this chapter. Here we look at unconstrained consumer choice. This situation may not be very realistic, but it allows economists to examine consumer behavior with no nasty intrusions to get in the way of what people want, such as lack of time or money (don’t worry, Chapter 5 covers constraints).
Chapter 2 looks at the consumer choice model that economists use to investigate people’s preferences and introduces some of the key tools of analysis — for example, indifference curves and the concept of utility (the value a representative consumer gets from consuming something). This chapter looks at utility in a more mathematical way, in particular in terms of something called the utility function. This tool occurs frequently in economics and is helpful for understanding what lies behind demand and supply in a given market, and so it’s a tool with much utility (groan).
We build up a mathematical picture of the way in which utility motivates the choices of a representative consumer, and for that we need to build up a picture of how people choose when they don’t have constraints (see Chapter 5 for more on constraints and Chapter 6 for how the picture in this chapter changes when you introduce them). We look at how to evaluate the amount of utility consumers get from their choices, including marginal utility, which is the amount of utility gained by consuming an extra unit of something. To keep things straightforward, we suppose that these choices aren’t constrained.
Eating Until You’re Sick: Assuming that More Is Always Better
In general, economists assume that, given the choice, people prefer more goods to less. This assumption holds, up to a limit, because at some point people get satiated by their consumption of a good and don’t want to consume any more of it.
If you’ve ever been unable to consume a tenth bar of chocolate, you’ve experienced this phenomenon. Economists call it diminishing marginal utility, meaning that as you consume increasing amounts of the same thing, the utility gained from each additional amount is smaller, as you add more and more. At some point, the marginal utility can fall to zero and you desire no more of the good — it can even turn negative afterwards (yes, it’s true, you can eat so much chocolate that eating any more causes displeasure rather than pleasure).
However — and this is quite a big however — up to that point, the more-over-less assumption operates. The later section “Deciding How Low You’ll Go: Marginal Utility” looks more closely at this issue. But here we begin from the assumption that more is better and define some terms that economists commonly use “in the field.” The key starting point is the concept of a consumption bundle, something touched on in Chapter 2 but examined in more detail in this section.
Once you get the idea of what utility is to the economist, you can start putting together the building blocks that economists use for modelling. In this section, we go through the terminology, showing you how economists represent preferences in a special shorthand that you can then use to ensure that models are consistent.
Making your choice: The consumption bundle
A consumption bundle is a set of goods that a consumer may choose to consume. Suppose the only goods available in the world are tea and coffee. Then a consumption bundle is any combination of cups of tea and coffee that the person could choose, and you can write
For the bundle containing one cup of tea and one cup of coffee, the bundle would be written as
Now imagine that the items in the brackets can represent any goods whatsoever. We call them xi, where i is an index identifying the good in which you’re interested. You can then rewrite the bundle as follows:
Here n denotes the number of all goods possible to consume.
Although this bundle of n goods is realistic (in that at some level, every good competes for your wallet with every other good), it’s also cumbersome. Instead, for simplicity economists often use two goods: the one they’re interested in and everything else, which you can think of as money. We follow this two-good layout for now, but if you’re interested in doing so, you can eventually generalize the simple model to all goods.
The two-good layout leaves the consumption bundle as being the following:
Here x1 is usually plotted on the horizontal axis of any graph or space, and x2 on the vertical axis.
Consumption bundles have to follow the normal rules of preference (discussed in Chapter 2), which means that, for instance, with three bundles, A, B, and C, and where A is preferred to B, and B to C, A must be preferred to C.
Provided that your tastes satisfy the rules for well-behaved preferences (completeness, reflexivity, and transitivity — see Chapter 2), any consumption bundle can be associated with an indifference curve, and an indifference curve describes all the consumption bundles that yield an identical level of utility. If you were to take any bundles on the curve (call them P and Q for the moment), you’d be indifferent between them and can write, as Chapter 2 does, the following:
Thinking about utility in another way: Possible sets
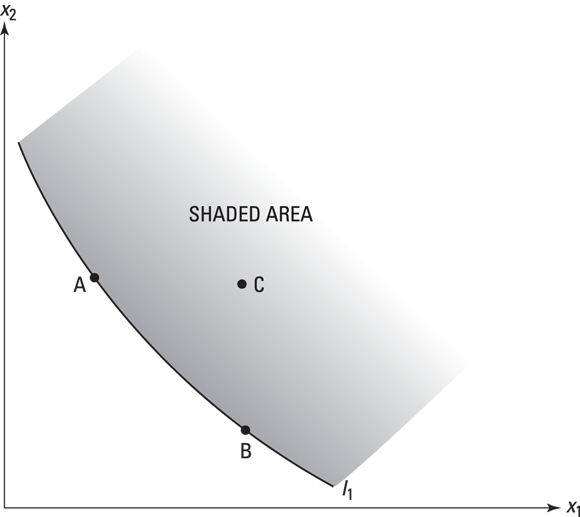
Another way to think about consumption bundles and preferences is to think about all the possible choices. If we describe the set of possible choices in a diagram, we can see pretty easily which choices the consumer would prefer. For instance, Figure 4-1 draws an indifference curve for all the consumption bundles for which Bob gets the same amount of utility. We mark on it two equivalent bundles, A and B. The shaded area shows the set of all possible points yielding higher utility than bundles A and B. He’s now offered a bundle that offers more utility than these two — call it bundle C — and we translate this into microeconomist speak as follows:
© John Wiley & Sons, Inc.
Figure 4-1: Bob’s preferred consumption bundle: Bundle C yields higher utility than A and B and would therefore be Bob’s preferred consumption.
This expression confirms that C is strictly preferred to B and A. In Figure 4-1 we picture C as being a member of the set of points that are strictly preferred to A and B, and we shade the area covered by that set. Because we specify that that relationship is strict preference (see Chapter 2), it can’t include the indifference curve itself, because that would mean Bob gets at least as much utility from something we’ve already said yields more utility.
Drawing a utility function
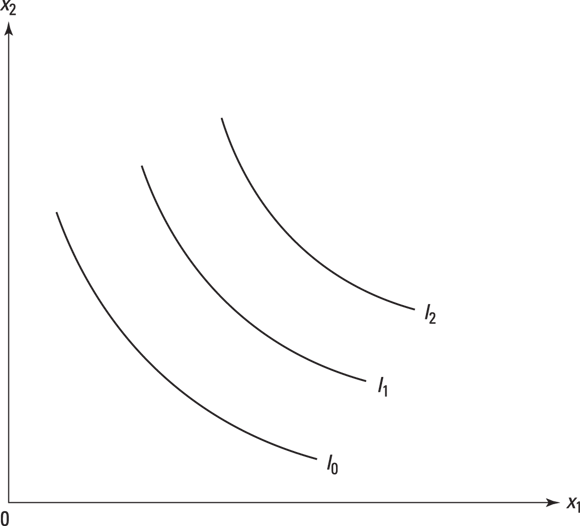
In the preceding section, we draw indifference curves corresponding to different levels of utility, and that level of utility is the same along all the points of the curve. But suppose you want to compare bundles that are on different levels of utility. Easy! You draw a set of indifference curves moving away from the origin. Each individual curve has the same level of utility along the curves, and each curve expresses a higher level of utility the further away from the origin it is! Check out Figure 4-2.
© John Wiley & Sons, Inc.
Figure 4-2: Indifference curves farther away from the origin yield higher utility for Bob.
The great thing about this depiction is that if you connect a line going through the indifference curves, and the indifference curves are derived from well-behaved preferences, any point on the new line is part of a nice, well-behaved utility function. Figure 4-3 shows this, where the new line goes from the origin through the indifference curves.
© John Wiley & Sons, Inc.
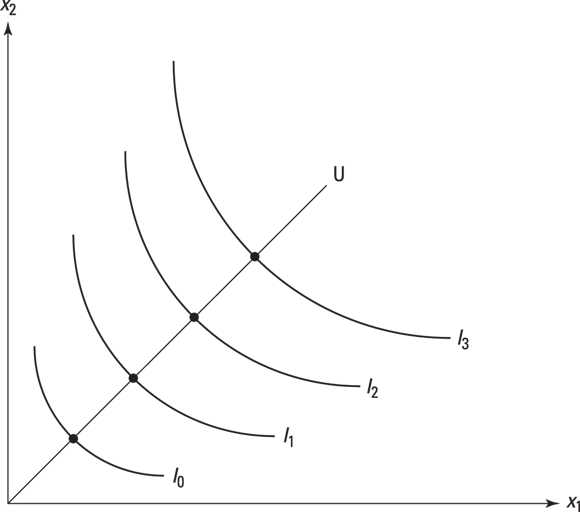
Figure 4-3: Bob gets more utility each time he moves to a higher indifference curve.
But, you may ask, what if all those points are different combinations of goods? After all, imagine that you’ve shown that for indifference curve 1, Bob will be indifferent between the bundle of three cups of tea and four cups of coffee and the bundle of five cups of tea and two cups of coffee, but prefers the bundle on indifference curve 2 of six cups of tea and two cups of coffee. What is this telling you?
The answer is something very important about utility functions, which is that if preferences are well-behaved, almost anything that satisfies those rules could be part of a utility function! (In fact, a near infinite number of possible, consistent, utility functions could satisfy those rules. You just wouldn’t know which particular one any individual consumer is on until his behavior reveals it in some way.)
The absolutely crucial point to take away is that well-behaved preferences make well-behaved utility functions.
Deciding How Low You’ll Go: Marginal Utility
One really big thing to get clear is the difference between total and marginal utility. Total utility (the amount of utility gained in total from consuming something) is a useful concept, but economists far more commonly look at how utility changes as consumption at the margin changes. For that, they use the concept of marginal utility: the utility that is gained from consuming one extra unit of a good.
Considering the last in line: The marginal unit
The concept of the marginal unit is one of the most important concepts in the economics toolkit. Economists use it to analyze pretty much all production and consumption decisions. For instance, as Chapter 7 shows, firms optimize their production based on the relationship between marginal revenue and marginal cost. For a consumer, the concept of marginal utility is key in looking at consumption decisions. But what is this mysterious marginal unit of which we speak? We’re glad you asked.
The marginal unit is defined as only the last, incremental unit of something, whether that be cost, benefit, utility, or revenue.
Suppose that chocoholic Ray is looking at six bundles of chocolate bars, each containing one more chocolate bar than the preceding bundle. Table 4-1 describes the utility gained by Ray from consuming the different bundles. As in the preceding section, Ray’s preferences can be described by the points on this utility function, and we now add an extra column, which tells only the gain (or loss!) in utility from consuming an extra bar of chocolate. This is the marginal utility obtained from only the incremental last extra unit of chocolate, which does not include the utility from the consumption of the other bars in favor of looking just at what happens to Ray’s utility as he consumes that last extra unit.
Table 4-1 Ray’s Total and Marginal Utility from Consuming Chocolate Bars
|
Bar of Chocolate |
Total Utility |
Marginal Utility |
|
1 |
5 |
5 |
|
2 |
11 |
6 |
|
3 |
16 |
5 |
|
4 |
19 |
3 |
|
5 |
19 |
0 |
|
6 |
17 |
–2 |
Table 4-1 uses cardinal measures of utility (flip to Chapter 2 for an explanation), so you can see what happens with some simple numbers. Suppose Ray gets 5 units of utility from his first bar. The second bar is even more enjoyable than the first and he gets 6 units of utility from it. The third, however, is starting to cause icky chocolate tummy and he gets less utility from that, and the fourth is really not giving all that much more utility. By the time he’s on to the fifth he’s feeling queasy and not so much enjoying it as suffering it.
Quantifying all the utility, we draw up a table for Ray in Table 4-1.
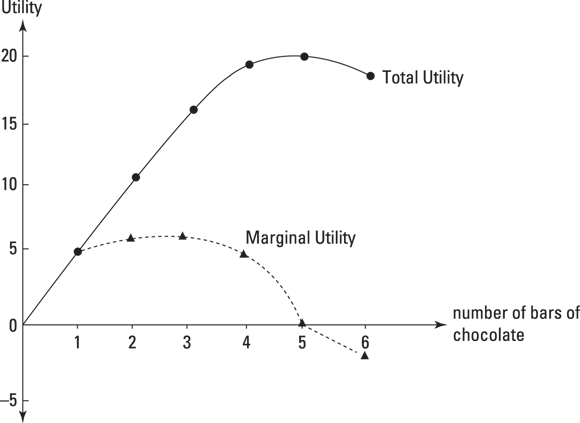
Figure 4-4 plots the table, and, as you can see, utility rises to a peak level — what economists call satiation — and then becomes disutility. Peak utility is found somewhere between the fourth and fifth bars (and we hope that these are fun-sized rather than full-sized bars). Assuming Ray is economically rational (and doesn’t have any other constraints), he stops eating there.
© John Wiley & Sons, Inc.
Figure 4-4: Ray’s total and marginal utility functions for chocolate.
Don’t confuse marginal utility with the marginal rate of substitution (MRS is the slope of the indifference curve — see Chapter 2). Marginal utility is the gain in utility associated with an extra unit of something, whereas MRS tells you how much of one thing you have to give up in order to get an extra unit of something else.
Creating a formula to model utility
Chapter 2 says that utility gets revealed from behavior rather than measured up front. Well, if you know how a person exchanges one good for another along the indifference curve (which you can infer from behavior), you can use the formula we present in this section to learn something about the marginal utility gained from consumption of an extra unit.
You can write the formula for the marginal utility of a good when the quantity of the good changes. Start by writing a utility function (U) for the utility gained from consuming quantities of two goods, x1 and x2:
Note that if you write U(x1, x2) equals a constant — that is, U(x1, x2) = K — you’ve written a mathematical description of an individual indifference curve, that is, you’ve described all the consumption bundles (x1,x2) that yield the same level of satisfaction or utility, which we denote by K. In other words you’ve gone through the earlier section “Making your choice: The consumption bundle,” but in reverse, generating an indifference curve from a utility function.
Now, you take the changes in the utility achieved when only x1 changes. To do so, you first write that marginal utility (MU) is the change in total utility when x1 changes. Using a formula, that makes it like this:
Okay, now you expand the top of the equation using the formula for a utility function. Replace U with the original expression for utility (x1, x2) and then the new utility when x changes becomes the following:
This means that MU equals all the right-hand side of the equation, all over Δx1!
Here’s something interesting. The preceding section warns you not to confuse marginal rates of substitution and marginal utility, but the two concepts do have a special relationship. Recall that the marginal rate of substitution is the slope of the indifference curve and that points on the same indifference curve yield the same level of utility. Now think about a change in the consumption of both goods that leads to utility staying the same, so that both the before and after consumption bundles are on the same indifference curve. The change in the consumption bundles means that whatever utility you gained by adding more of one good, say x1, you lost by taking away some of the other good, x2. Overall the marginal utility gained from the change equals zero, or alternatively:
This doesn’t seem all that Earth-shattering. Now, solving for the slope of the indifference curve, which you can write as Δ x1/Δ x2, we find that Δ x2/Δ x1= MU1/MU2. And because MRS is the slope of the indifference curve, we can see that MRS = MU1/MU2:
So here, using a little bit of simple but clever math, you can reconstruct information about what you’d like to know (utility) from something you do know (MRS). Now that’s microeconomics!
Ray is in conformity with the rules of choice, which makes his preferences well-behaved and therefore workable. If he isn’t, inferring anything about his behavior becomes a far more challenging task. Compare Ray, for example, to Cookie Monster. As a monster, Cookie Monster “eat cookie” irrespective of how much utility he gets from cookie. Cookie Monster, therefore, doesn’t behave as if he has well-behaved preferences, and you can make no inferences whatsoever about marginal substitution or utility.