Chapter 16
Playing Games with Economic Theory
In This Chapter
![]() Seeing how games are designed
Seeing how games are designed
![]() Exploring three games useful to economists
Exploring three games useful to economists
![]() Finding out how repeating a game affects what happens
Finding out how repeating a game affects what happens
Game theory provides a powerful set of tools for probing into and modeling situations from an economist’s perspective. It’s a way to think about strategic behavior and help clarify how outcomes affect behavior, and vice versa. Economists have used game theory to look at problems as diverse as nuclear deterrence, how animals display dominance, and even the best way for a striker and a goalkeeper to act in a penalty shootout in soccer. You can approach these problems using an underlying model that takes into account the behavior of more than one decision-maker at a time and considers what they may do in a situation where the benefits — and of course the costs — depend on everyone’s actions.
Game theory is one of the most popular areas of microeconomics. When you know some of the models, you begin to recognize that game-theoretic situations feature in many films and TV shows, from The Godfather and The Wire to Dr. Strangelove. The famous Prisoner’s Dilemma game (discussed later in this chapter) is a staple of cop and detective dramas.
In this chapter, we walk you through some of the basic concepts of game theory. We show you three cornerstone one-shot models and how dealing with these situations has led to — for good and for ill — some of the institutions people live with today. We also describe some of the ways in which you can apply game theory, sometimes all too practically, to real-world situations, and how things change when a game is repeated. We explore strategy through game theory, describe how cooperation and competition shape outcomes, and see what “the best you can do” means when someone else is doing his or her best as well. Let the games begin!
Setting Up the Game: Mechanism Design
To show you what we mean, consider this example: You’ve been left with the demanding job of ensuring that two hyped-up five-year-olds cut a cake fairly between the two of them. You can frame their decision, but you can’t make the decision itself for either child (that has to be up to them). How do you do it?
The government would like to implement the best allocation of the resource, in this case the spectrum, but not know the value of the resource to the players of the game. Therefore, the government wants to design its auction in such a way that players with the highest valuation will self-select a bidding strategy that allocates them the resource. In this way, the government makes consistent individual optimal choices with its own objectives.
- Hawk: The party acting strictly in his own interests.
- Dove: The party acting in the collective interest of the group. It’s important to recognize though, that the Dove is doing so because its own individual interests lead it to do so.
- Payoff: The outcome to a player of following any particular strategy.
Locking Horns with the Prisoner’s Dilemma
The setup of the Prisoner’s Dilemma is designed to give a police investigator the best chance of getting a confession from a suspect. As a result, the structure of the payoffs or the incentives of the game are designed so that police have to do the least work in getting a suspect to play the Hawk. In other words, the police engineer a situation, by offering penalties and rewards, to extract a confession. During questioning, the police offers one suspect a lighter sentence or even freedom if he confesses. The police can use the confession as evidence to nail the other suspect. Each suspect is interrogated separately and made the offer. When you find yourself being made an offer in a Prisoner’s Dilemma game, you’re likely already in a precarious situation.
The Prisoner’s Dilemma allows economists to think about the behavior that goes on when there is a conflict between cooperation (Dove) and self-interest (Hawk). For example, another way of looking at oligopoly (see Chapter 11) is to see it as a type of Prisoner’s Dilemma where firms have to decide whether to play hawks and produce more, or play doves and produce less.
Reading the plot of the Prisoner’s Dilemma
The story goes like this. A bookmaker is robbed, and the police apprehend two suspects for the crime. The detective investigating the robbery puts the two suspects in separate rooms — so that they can’t communicate — and makes each of them a one-time offer of a deal:
- If neither participant confesses: Both get six months in the slammer.
- If one participant confesses and the other doesn’t: The participant who confesses is released, while the one who doesn’t confess gets a five-year sentence.
- If both participants confess: They both go to jail for two years.
The question is: When the suspects are presented individually and separately with the same deal, what happens?
On the face of it, you may think this is a no-brainer for the suspects. Obviously, the best outcome is that neither of them confess and they each end up serving six months. After all, this means that the total time served by the two suspects is the least. Obviously, they’d be crazy to take any other action. So neither suspect should confess, right?
If you are thinking like that (and many do before they investigate the scenario), alas, you’d be wrong. To see this, suppose the first suspect, whom we’ll call Mr. Pink, thinks like you did and decides he doesn’t want to confess. He doesn’t know what Mr. Blue (his partner in crime) has decided. Mr. Pink would like to think that Mr. Blue hasn’t already taken a deal that puts Pink in prison for five years. However, on second thought, Mr. Pink realizes that Mr. Blue has a big incentive to rat on him if Mr. Blue thinks for a moment that Mr. Pink won’t confess. And of course, if Mr. Pink does confess, Mr. Blue is better off confessing too. Similarly, locked away from Mr. Pink, Mr. Blue doesn’t know whether or not Mr. Pink has decided to rat him out too, sending Mr. Blue to prison for five years. Because neither suspect can take the chance that the other person isn’t a stool pigeon cooperating with the police to cut himself a better deal, neither can rely on the other not confessing. So both confess and get a two-year sentence each — game over.
Solving the Prisoner’s Dilemma with a payoff matrix
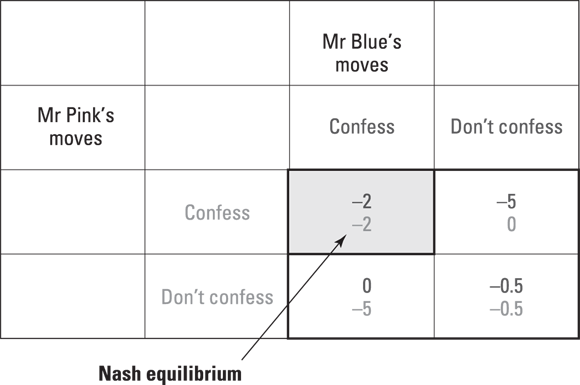
Economists look at the Prisoner’s Dilemma through some of the tools of game theory. The first and perhaps clearest way to do so is with a payoff matrix — a simple chart that shows what the payoffs are to both participants given their choices in the game. In Figure 16-1, we label the two participants as Mr. Pink and Mr. Blue, and the two actions they can perform in this setting as “Confess” and “Don’t confess.”

© John Wiley & Sons, Inc.
Bolded payoffs go to Blue, and shaded go to Pink.
Figure 16-1: Payoff matrix for the Prisoner’s Dilemma.
When you read down the columns, the payoffs to Mr. Blue’s actions (or moves, in game terminology) are shown against the payoffs to Mr. Pink’s moves. For example, in the situation where Mr. Blue doesn’t confess but Mr. Pink does, the payoffs are no loss of time in jail for Mr. Pink and a loss of five hard years for Mr. Blue. Similarly, when you read along the rows, the same pair of moves gives the payoffs a loss of nothing for Mr. Pink and a loss of five years for Mr. Blue.
Finding the best outcome: The Nash equilibrium
In the Prisoner’s Dilemma, the Nash equilibrium is a pair of strategies — in this case, one for Blue and one for Pink — such that playing that strategy makes the player as well off as he or she can be given the other player’s strategy. The outcomes for the Nash equilibrium are in the top left corner of Figure 16-2. This pair of strategies make each player as well off as he or she can be, given each other’s options.
© John Wiley & Sons, Inc.
Bolded payoffs go to Blue, and shaded go to Pink.
Figure 16-2: Nash equilibrium in the Prisoner’s Dilemma.
Applying the Prisoner’s Dilemma: The problem of cartels
Let’s think of the cartel’s dilemma as a Prisoner’s Dilemma and look at it using the strategic form of the game. We begin by walking through the payoff matrix in Figure 16-3 as representing an agreement between two companies, (Blue PLC and Pink, Ltd.). Either company has a choice of playing Hawk or Dove (refer back to the section “Setting the Game: Mechanism Design” for a definition of these terms).
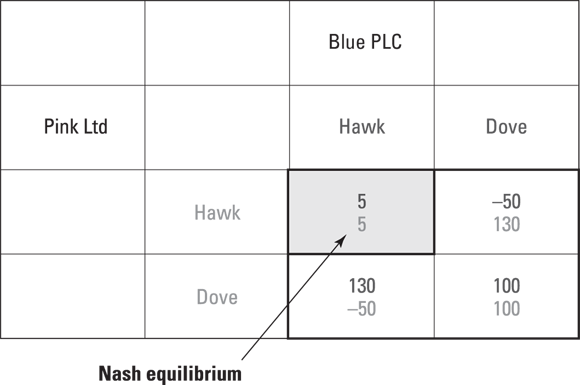
© John Wiley & Sons, Inc.
Bolded payoffs go to Blue, and shaded go to Pink.
Figure 16-3: Applying the Prisoner’s Dilemma to a cartel.
Looking at the payoffs in Figure 16-3 (which are all in millions of dollars), you can see that the collective best, which the cartel or collusive agreement wants to achieve, is in the bottom right corner, where both Blue and Pink are playing Dove. But if one plays Hawk while the other plays Dove, the Hawk (which means cutting prices and selling more) gets a higher return ($130 million in this case) by stealing market share from the other, who in this case takes a loss being the high price seller (top right corner).
This is one reason why cartels don’t tend to be long-lasting, irrespective of whether a regulator is able to use legal action to keep them in line. As the saying goes, there’s no honor among thieves, and the logic of the Prisoner’s Dilemma bears that out to some extent.
Of course, regulators also help cartels break down and get to the Nash equilibrium — as the police do in the earlier section “Reading the plot of the Prisoner’s Dilemma” by giving the parties an extra incentive, such as shorter prison terms, to give in evidence. In the case of competition law, the practice is to give a free pass to the first party who talks to the authorities. That way, any party that thinks it may get caught has an incentive to come forward and tell tales on its former cartel partners.
Escaping the Prisoner’s Dilemma
An alternative heading for this section could be “How to form an organized crime syndicate without really trying.” Game theory has investigated one particularly interesting example of cartel behavior: that of organized crime syndicates, when they operate a cartel that tends to work for the benefit of those under its influence, although not generally for society as a whole.
In Figure 16-4, we summarize the strategic form of the Prisoner’s Dilemma when a crime syndicate can change the payoffs. As you can see, the payoff to any actions involving confessing are now “Dead” (which you can interpret as infinitely large and negative). Thus the Nash equilibrium is now not to confess.

© John Wiley & Sons, Inc.
Bolded payoffs go to Blue, and shaded go to Pink.
Figure 16-4: Payoffs for an organized crime syndicate enforcing the cartel.
Looking at Collective Action: The Stag Hunt
Game theorists have turned their attention to many different situations, ranging far and wide and covering many issues. One of these is the problem of collective action, where a bigger prize is available only to those who can coordinate their actions.
Designing the Stag Hunt
The Stag Hunt is set somewhere around the dawn of time. Littlenose and Bigfoot set out from their village one morning to go hunting. They can choose from two possible locations: One field contains a population of hares, and the other field has stags. Any hunter on his own can capture a hare, but to capture a stag, both hunters must work together. The model assumes that they must both make their decisions with no idea of whether the other is going to make the same choice or a different one.
- Hawk: They strike out individually looking for hares.
- Dove: They turn up independently at the same field as the stags, hoping to coordinate their actions so that they can bring home a bigger meal for the village.
Next we assign values to the potential meals:
- Hare: As the smaller creature, the hare gets a smaller value. Call that a value of 1.
- Stag: To the larger stag, we assign a larger value of 4. Any number larger than 1 will do, but we’ll use 4 to keep things clear.
We want to compare possibilities and solve for a Nash equilibrium, so we put up the payoffs in strategic form, as in Figure 16-5. Now look at the possible strategies and outcomes to see where the Nash equilibrium lies. Can you spot it?

© John Wiley & Sons, Inc.
Figure 16-5: The Stag hunt payoffs.
Sorry, that was a sly question, because in fact two Nash equilibria exist: one that maximizes payoffs (top left) and one that minimizes risk (bottom right). To see why, we think through Littlenose’s decisions:
- Littlenose plays Dove: He goes to the field where the stags reside and hopes that Bigfoot makes the same decision to play Dove. If Bigfoot doesn’t, Littlenose will have an incentive to change. But if Bigfoot does, they successfully get a stag and the higher payoff, and neither has an incentive to change.
- Littlenose plays Hawk: He goes to the hare field and whatever happens, he gets something to eat. If Bigfoot also plays Hawk, they bring home a nice hare each and are in equilibrium. If not, and Bigfoot plays Dove, it has no effect on Littlenose, although he could’ve brought home a far bigger meal if he had also played Dove and visited the stag field.
Examining the Stag Hunt in action
To our great delight, a Stag Hunt came to light in an economics class at an American university, where a poor choice of mechanism design led to students being able to exploit the system.
The key to this problem lies in two points:
- Analyzing this situation, an economist would use the Stag Hunt model to see where the benefit of collective action is.
- The corollary of a ranking system is that if everyone is equally terrible, then everyone is equally good. Another way of looking at it is that if everyone gets last place, they all tie for first.
Suppose that the exact marking scheme gives the first-place student 90 percent, the second 89, the third 88, and so on. Call that scheme the “teacher’s offer” and denote it M:
- If all students play Hawk: They play by the test scheme and their mark at the end is Mi.
-
If all students play Dove, don’t play by the test rules, and instead submit blank papers: They all receive the payoff for first place: a mark of 90.
 Hawk and Dove refer to the strategies of players in cooperating with each other and not the teacher.
Hawk and Dove refer to the strategies of players in cooperating with each other and not the teacher. - If some of the players play Hawk and some play Dove: The Hawks take the test and get the teacher’s offer based on their place in class, M. The Doves don’t take the test and get a mark that reflects their worse performance; call it W (for this to work the offer, W, must be worse than any given possible mark M).
- Hawk, Hawk equilibrium: Every student goes along and takes the exam as normal and is placed on the curve.
- Dove, Dove equilibrium: Every student submits a blank paper and guarantees themselves 90 per cent.
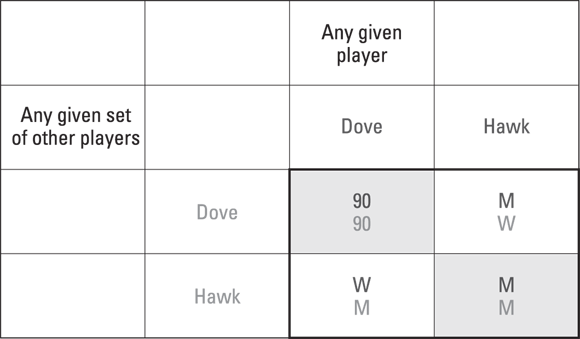
© John Wiley & Sons, Inc.
Figure 16-6: Strategic form of the Stag Hunt for the class economics exam.
The coordination problem is how to coordinate students’ decisions so that they all end up playing Dove. This particular class solved it by waiting outside the exam room so that they were able to monitor anyone going in to the room. If they saw someone go in, they rushed after the person eager to get started on the exam with the hope that they’d get M (rather than W) at least. In fact, no one walked into the room and all students got 90!
Annoying People with the Ultimatum Game
Sometimes the value of a game is in illustrating the difference between people who act according to the microeconomic model of rationality and those who don’t. A classic example of a game that can be used to test rationality is the ultimatum game. Many forms of this game exist, but we show you a simple version that characterizes the problem.
In this version Polly starts with $100. She makes an offer to Quentin that she’ll split some of the $100 with him, and if Quentin accepts the offer, they’ll both take home their respective shares of the $100. If, however, Quentin doesn’t accept the offer, they both get zero. How much do you think Polly should offer? (To make it easy, the offer has to be in whole numbers of dollars.)
The answer is for Polly to offer Quentin $1. After all, if Quentin is economically rational, he’ll realize that $1 is better than nothing, which is what he would get if he doesn’t accept the offer. However, this is not what is observed when the game is played. In fact, more often than not, people reject any offer that doesn’t give them a fair — their definition of fair, of course — share of the sum of money.
Getting out of the Dilemma by Repeating a Game
In all the models discussed so far, the game is one shot — that is, it’s played only once. Think of this as being tantamount to a forced deadline (often used in negotiations to get a deal, especially when one party is holding out for a better deal). The key thing is that the Nash equilibria we’ve found are all based on the fact that both parties participate only once (check out the earlier section “Finding the best outcome: The Nash equilibrium”).
But what happens if the players are in a game that’s repeated over many rounds, such as in the Prisoner’s Dilemma, where neither party can be sure whether the other’s going to cooperate?
But you may say, hang on a sec: what about where you said that the Nash equilibrium for the Prisoner’s Dilemma is Hawk, Hawk? Yes, but the difference between the two situations is whether the parties get to play the game again. If you play a Prisoner’s Dilemma repeatedly, it turns out many behaviors can lead to a Nash equilibrium — a result that in fact can help game design and play.
To distill this point into a bit of folk wisdom, that great economist Marx — Groucho, not Karl — said that the key to success in life is honesty and fair play: “If you can fake that, you got it made.” In the case of a repeated game, signaling honesty may confer the advantage of making it more likely that you’ll move to the Dove, Dove outcome and avoid being stuck in Hawk, Hawk.
Investigating a repeated game using the extensive form

© John Wiley & Sons, Inc.
Figure 16-7: Extensive form of a one-shot Prisoner’s Dilemma game.
The extensive form and the strategic form are equivalent ways of depicting a game, in the sense that the final payoffs have to be the same. The key advantage of the extensive form is that it can make the sequence of moves clearer where that’s something that matters in the game. In these one-shot games where players move at the same time, we don’t really need the extensive form all that much to tell you about the equilibrium. As games get more fiendish, however, the extensive form yields more information about the underlying structures of the game.
Mixing signals: Looking at pure and mixed strategies
In many games — especially sporting matches — a player gains by being unpredictable. To understand why a tennis player or a quarterback wants to keep their opponent guessing, game theorists make a distinction between a pure and a mixed strategy for a player:
- Pure strategy: Describes what the player will do, with probability 1 at each point in the game in the game. In the Prisoner’s Dilemma, both Hawk and Dove strategies are pure strategies.
- Mixed strategy: Describes what the player will do, with some probability at each point. Imagine that the two players from the Prisoner’s Dilemma example toss a coin in order to decide whether to play Hawk or Dove. In this case, each plays Hawk with 50 percent probability and Dove with 50 percent probability.
Game theory can help us look at the best strategy for a penalty taker in a soccer match, as mentioned at the beginning of this chapter.

 One of the key uses of game theory in the real world is called mechanism design — setting up games so that a particular or desired behavior becomes the best strategy for a player to choose.
One of the key uses of game theory in the real world is called mechanism design — setting up games so that a particular or desired behavior becomes the best strategy for a player to choose. In Chicago during the reign of Al Capone, for instance, the local mafia had a monopoly on the supply of pasta-making machines, which were an essential piece of physical capital for any Italian restaurant in the city. However, the restaurants benefitted from Capone’s patronage. Sure, they had to pay him fees, but they could rely on him to take care of any competition that threatened to undercut them. Thus, the mob ended up as a way of enforcing a cartel agreement and guaranteeing higher profits for its favored establishments.
In Chicago during the reign of Al Capone, for instance, the local mafia had a monopoly on the supply of pasta-making machines, which were an essential piece of physical capital for any Italian restaurant in the city. However, the restaurants benefitted from Capone’s patronage. Sure, they had to pay him fees, but they could rely on him to take care of any competition that threatened to undercut them. Thus, the mob ended up as a way of enforcing a cartel agreement and guaranteeing higher profits for its favored establishments. This change in the Nash equilibrium provides the rationale for the formation of syndicates. If you can’t get criminals to cooperate with each other, change the payoffs so that it’s in their interests at least not to confess. Capone, Corleone, and several others took that lesson to heart.
This change in the Nash equilibrium provides the rationale for the formation of syndicates. If you can’t get criminals to cooperate with each other, change the payoffs so that it’s in their interests at least not to confess. Capone, Corleone, and several others took that lesson to heart. The madman strategy isn’t very good for getting cooperation. There is an important difference in economics between the type of game in which one party can make a gain over the other player and a more cooperative game where both parties gain from achieving cooperation. In a competitive market setting, holding an advantage over the other party in a repeated game can be desirable. But if cooperation is the desired goal, building trust is often the first stage, and you will have difficulty trusting someone who keeps changing his moves on a seeming whim.
The madman strategy isn’t very good for getting cooperation. There is an important difference in economics between the type of game in which one party can make a gain over the other player and a more cooperative game where both parties gain from achieving cooperation. In a competitive market setting, holding an advantage over the other party in a repeated game can be desirable. But if cooperation is the desired goal, building trust is often the first stage, and you will have difficulty trusting someone who keeps changing his moves on a seeming whim.