Chapter 12
Appreciating the Fundamental Theorems of Welfare Economics
In This Chapter
![]() Checking out how to think about social welfare
Checking out how to think about social welfare
![]() Creating a framework for a general equilibrium model of the economy
Creating a framework for a general equilibrium model of the economy
![]() Moving towards efficiency
Moving towards efficiency
Some things just seem wrong, don’t they? Hooters serving champagne, Adam Sandler starring in a serious film, Vladimir Putin singing “Blueberry Hill” … . Well, microeconomics has its own “just doesn’t feel right” moment, too.
When studying any particular market, you want to identify where supply and demand are equal for that particular good. This is called a partial equilibrium. But what happens when you ask the question about all markets rather than just one? Can economists find a general result that holds so that all markets are in equilibrium together? Although it seems to jar with everyday experience and often just doesn’t seem right, surprisingly such a result does exist — given special circumstances. Economists call it a general equilibrium and it’s one of the most startling and least understood parts of microeconomics.
Along the way to building a general equilibrium model, you arrive at two other results, which are quite startling and profound. These are called the fundamental theorems of welfare economics. Now, welfare economics is the part of microeconomics that looks at how people can be made better off and it is ultimately tied to the idea of productive efficiency or making things for the lowest possible cost. But how much of a good should be produced and who should get it? We also need a way of understanding how much of the various goods that people want should be produced and how to distribute these goods in a way to make people better off.
Economists in general believe that people in a society as a whole gain more utility and are therefore better off when some people gain utility and none lose, what economists call a Pareto improvement. Economists say that welfare is increased when a Pareto improvement happens. (The following section explains welfare and its multiple meanings.)
The two fundamental theorems developed in this chapter are important stages in learning about welfare. Without them, most modern economic modeling would be impossible. The mysteries are how to get to those results and how to interpret them. If you enjoy mysteries, join us as we show you what’s really going on!
Getting the Welfare Back into Welfare Economics
Welfare is a difficult thing to define in general. Often people ask about other people’s welfare, talk about a “welfare state,” or discuss different types of “welfare benefit.” This vagueness is unfortunate because welfare needs to be tied down a little more closely in order for us to put it to use in economics.
Economics is concerned with things that you can ultimately measure, so the meaning of welfare has to be related to measurable entities such as prices and quantities. These, in turn, are things that economists hope capture the concept of well-being or utility (see Chapters 2 and 4–6 for a fuller discussion of utility). When economists talk about maximizing welfare, they’re relating the concept of utility to groups of economic decision-makers — whether producers, consumers, or society as a whole.
- Partial equilibrium model: In this context, welfare is the sum of the areas bounded by the supply and demand curves in the market for that particular good — the consumer surplus and the producer surplus.
- General equilibrium model: In this context, welfare means social welfare, the aggregate level of utility across all individuals in the economy. Therefore, seeking the highest level of welfare means making the aggregate level of utility as high as possible.
Meeting two social welfare functions
- Utilitarian function: Sums the level of utility for each individual, so for two individuals, Ted and Bill, it’s entirely indifferent between Bill having 100 percent of the utility and Ted having 100 percent.
- Rawlsian function: Seeks to maximize the welfare of the least well-off individual, so it has only one unique sweet spot, at the corner of the L shape.
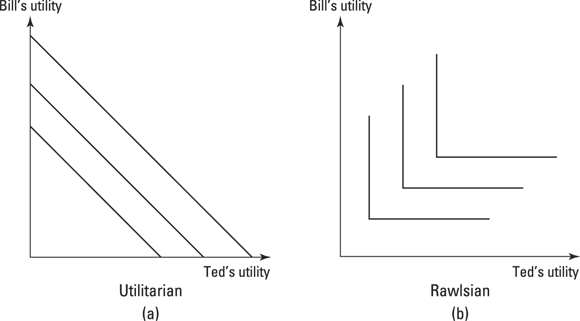
© John Wiley & Sons, Inc.
Figure 12-1: Two social welfare functions.
Understanding Why Partial Equilibrium Isn’t Enough
To describe an economy in all its complexity, you need to have a way of describing a general equilibrium where the interrelationships among all the markets are considered. The problem, of course, is that doing this for a complex economy could be a nightmare task. Imagine the effort necessary to describe every partial equilibrium and extend that analysis to every market in an economy.
Instead, economists use a framework to simplify the process of getting to a general equilibrium. The framework outlined in this chapter is about as simple a version as anyone can use — but don’t worry, you can extend it later as you get more confident in using your knowledge of microeconomics.
- An Edgeworth box: A tool for depicting exchange between individuals
- Pareto efficiency: A concept for categorizing which equilibrium results are efficient
Modeling exchange with an Edgeworth box
In the constrained optimization model (see Chapter 6), we depict levels of utility based on the preferences of one person for two goods. But now our task is to look at exchange, so we need two people making choices (including whether to exchange with each other) based on their preferences.
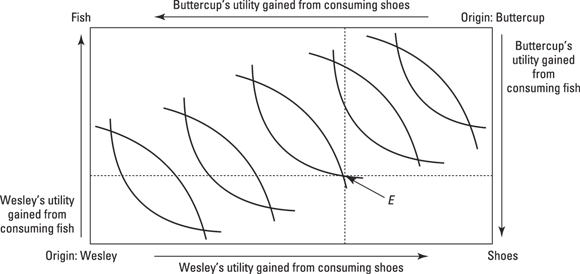
© John Wiley & Sons, Inc.
Figure 12-2: Setting up the Edgeworth box for Wesley and Buttercup.
Each participant has well-behaved preferences, so you can depict their preferences with indifference curves (as described in Chapters 4–6). You get a series of indifference curves going away from the origin in both directions. Point E in Figure 12-2 is special: It specifies an initial endowment of fish and shoes for both Wesley and Buttercup so that:
- EWF is Wesley’s endowment of fish.
- EBF is Buttercup’s endowment of fish.
- EWS is Wesley’s endowment of shoes.
- EBS is Buttercup’s endowment of shoes.
Investigating Pareto efficiency
Having set up the initial endowment in the preceding section, you now want to know whether everyone is happy with it, which means using the concept of Pareto efficiency.
- You can’t make all people better off.
- You can only make one person better off if you make at least one other person worse off.
- No potential gains can be made from trading.
So, to return to the question, is point E Pareto efficient? The answer is a resounding no. At point E Wesley can trade shoes for fish, and Buttercup can trade fish for shoes, and both be made better off. Therefore, points in the “lens” above E are all Pareto superior to E (although they’re not all Pareto efficient — some of the points are closer to Pareto efficiency, without themselves being efficient points). For the points to be Pareto efficient, they must be points where there are no potential gains from trading. This occurs where the two indifference curves are tangent to each other.
Connecting up all the points where Buttercup and Wesley’s indifference curves are tangent gives you a line that goes through every Pareto optimal point in the box. This is called a contract curve (see Figure 12-3). You know by looking at the contract curve whether an allocation of the goods between the two individuals is efficient. If the point is not on the curve, you could make both parties better off by moving to an allocation on the curve.
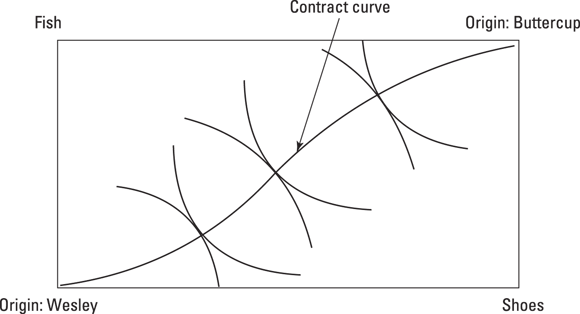
© John Wiley & Sons, Inc.
Figure 12-3: Contract curve for Buttercup and Wesley.
Trading Your Way to Efficiency with Two Fundamental Theorems
Given the setup in the preceding section, we now need to investigate how you go from a Pareto inferior allocation of endowments to a final efficient distribution. At the moment you have an initial endowment, E, which isn’t on the contract curve, so the potential exists to get to a better — Pareto optimal — distribution on the contract curve. This section describes how.
Bidding for the general equilibrium
The 19th century French economist Léon Walras examined this situation with a thought experiment, in which an auctioneer is calling out prices for every possible good in an economy. Walras wants two things to happen: prices are quoted in each market, and there is no excess supply or excess demand in any market. The trades that take place at the prices that satisfy that condition will get you to an allocation on the contract curve for that economy.
The auctioneer can, in theory, keep calling out prices until these two conditions are met. Seeing how this works isn’t always obvious. Let’s look at an example.
You need two earlier results:
- At any point on a contract curve, Wesley and Buttercup’s indifference curves are tangent. That means that the marginal rate of substitution (MRS — check out Chapter 2 for details) of fishes for shoes must be the same for both.
- At any optimum position for any one consumer, the MRS must equal the price ratio between the two goods (check out Chapter 6 for details).
Calling out successive prices for fish and shoes, a process economists call tâttonement (after all, Walras was French — it means “groping” or “trial and error”), the auctioneer eventually finds an equilibrium that satisfies Wesley and Buttercup. At this price, they trade some of their endowments of fish for shoes, or vice versa, until they arrive at the point where their MRS for fish and shoes are equal to the price ratio. This point is the general equilibrium for this — very simple — economy.
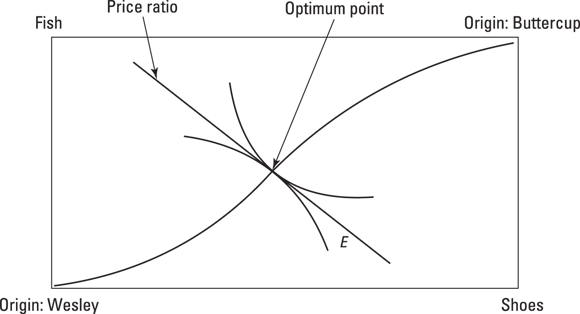
© John Wiley & Sons, Inc.
Figure 12-4: The optimum arrived at by the Walrasian auction.
Grasping for efficiency: How markets set prices through tattonment
The auctioneer is a nice imaginary device, but he doesn’t exist in reality, so Walras went further with his analysis.
Nobody “knows” what that equilibrium might be, but markets find it by continually adjusting. That’s tâttonement, folks.
The first fundamental theorem: A free market is efficient
- No externalities: No costs fall on parties other than those engaged in exchanging. This is probably not true in reality where many trades involve an external cost falling on another party. For example, when paper mills produce and trade paper, there are pollution costs, which are borne by those who live near the mill.
- Perfect competition in each market: Very few markets meet this condition in reality. For perfect competition to hold, each producer must be small in terms of its market share and not able through its trading decisions to influence price. Consumers must be perfectly informed about all products and their prices.
- No transactions costs: There are often costs associated with market transactions, such as the time it takes to find a seller or buyer to trade with. Transactions costs can be significant enough to spur the development of whole industries — for instance, comparison search engines on the Internet can reduce the transactions costs associated with buying insurance or finding a hotel room.
- Full information: Consumers must be perfectly informed about all products — their qualities and their prices. Firms must be able to know and observe the productivity of their workers. Chapter 15 is devoted to dealing with cases where people don’t have full information, so you can probably guess that assuming that they do is not a defensible assumption about reality.
But what the first theorem of welfare economics does do is very interesting. It says that a market is continually trying to get the best outcome — trying in reality, succeeding in textbooks — and is driven by the following three conditions defining equilibrium:
- No one can be worse off than her initial endowment (otherwise she’d simply refuse to trade).
- No one can be made better off without someone else being worse off — otherwise gains could be made by trading their way to equilibrium, which they can’t.
- No overall excess demand or supply can exist.
If you make these three things hold and solve for the allocation you would, given the four assumptions mentioned earlier, achieve a Pareto efficient outcome through the market alone. That’s enough to ask the question of whether someone planning could necessarily do any better. The answer is quite probably not, because the market will continually be processing more information about people’s desires, wants, and needs than someone trying to centrally plan an economy, even given that you may not have a perfect economy that satisfies our four assumptions.
The second fundamental theorem: Any efficient outcome will do
To see why, start with the first theorem from the preceding section: remembering that a Pareto efficient outcome doesn’t mean an equal one; Buttercup getting all of both goods is still Pareto efficient. Now, all outcomes that are market equilibria must be on the contract curve, because in a market equilibrium, each person’s MRS is equal to the same price ratio and hence their indifference curves are tangent to each other. But does that mean that all points on the contract curve could be market equilibria? The answer is that they must be. Here’s why:
- Along the contract curve, every point is a tangent between two indifference curves:
- The tangency point corresponds to the price ratio.
- The price ratio can exist and coordinate trades as long as preferences are well behaved, which means that indifference curves are bow shaped and do not cross.
- That price ratio is therefore the ratio of prices that must support a Pareto efficient equilibrium.
Putting the two theorems together: Equity and efficiency trade-offs
Put simply, the first fundamental theorem says that a free market will lead to an outcome that is efficient and the overall size of the pie to be traded will be as big as possible — if it weren’t, it couldn’t be Pareto efficient because by making the pie bigger you could make both parties better off without making one party worse off. The second theorem says that if you have a Pareto efficient outcome, it can be sustained by a market equilibrium. The two theorems separate out the question of efficiency (the first) from the question of distribution (the second).
Instead, if a government wants to make some people better off, it would be better taxing or taking from the endowment of one person and giving it to the other. That at least would be Pareto optimal and leave the important allocative role of prices alone.
Understanding why markets tend toward one price
Economists talk about the implications of a general equilibrium framework in terms of welfare. And you don’t need to go very far before you can see some interesting real-world applications. One is the observation that the price of a good in any one market tends to be the same across all markets for that good. You can use the general equilibrium framework to get into the logic of why this must be the case.
This is known as the law of one price, and interestingly (unlike much of the general equilibrium framework), you can test it in practice. Suppose you grow apples in Massachusetts and sell them in Massachusetts and New York. If the law of one price is true, the price of an apple in New York can be no higher than the price in Massachusetts plus the cost of transporting those delicious apples to New York. If the prices in New York were higher, someone could make money by buying apples in Massachusetts and driving them up to Albany to sell them.

 A general equilibrium is needed so that many of the models that macroeconomists and policy makers use to describe an economy make sense. It can also, if used carefully, inform policy decisions about the best way to shape an economy.
A general equilibrium is needed so that many of the models that macroeconomists and policy makers use to describe an economy make sense. It can also, if used carefully, inform policy decisions about the best way to shape an economy. Economics uses more than one type of definition of welfare — depending on whether we’re talking about a partial or a general equilibrium model:
Economics uses more than one type of definition of welfare — depending on whether we’re talking about a partial or a general equilibrium model: Pareto efficiency doesn’t mean that everyone has the same amount of goods or income. A distribution where Buttercup has all the fish and all the shoes can be Pareto efficient, if you can’t make Wesley better off without making Buttercup worse off.
Pareto efficiency doesn’t mean that everyone has the same amount of goods or income. A distribution where Buttercup has all the fish and all the shoes can be Pareto efficient, if you can’t make Wesley better off without making Buttercup worse off. The result comes with some pretty big caveats, though. The most important is that you’re better off trying to achieve an equitable distribution — in our example, the distribution is in terms of fish and shoes — by lump sum redistribution than by doing anything that distorts or interferes with the market-determined ratio of prices. The reason is that if prices are competitively set, every buyer consumes up to the point where the price ratio is a measure of the marginal benefit to that consumer. If you change the ratio of prices, you change the decisions of the consumer, and you may not get to a Pareto efficient outcome at all.
The result comes with some pretty big caveats, though. The most important is that you’re better off trying to achieve an equitable distribution — in our example, the distribution is in terms of fish and shoes — by lump sum redistribution than by doing anything that distorts or interferes with the market-determined ratio of prices. The reason is that if prices are competitively set, every buyer consumes up to the point where the price ratio is a measure of the marginal benefit to that consumer. If you change the ratio of prices, you change the decisions of the consumer, and you may not get to a Pareto efficient outcome at all. In practice, of course, things are rarely as simple as this intuition supposes. Take a tax on someone’s labor, for example. A person’s endowment of labor is actually the total amount of labor that she might have provided, not the total amount that she does provide. You can know the latter — it’s how income taxes work — but can never know the former.
In practice, of course, things are rarely as simple as this intuition supposes. Take a tax on someone’s labor, for example. A person’s endowment of labor is actually the total amount of labor that she might have provided, not the total amount that she does provide. You can know the latter — it’s how income taxes work — but can never know the former.