Chapter 17
Keeping Things Stable: The Nash Equilibrium
In This Chapter
![]() Digging deeper into the Nash equilibrium
Digging deeper into the Nash equilibrium
![]() Discovering when a Nash equilibrium has to exist
Discovering when a Nash equilibrium has to exist
![]() Applying the Nash equilibrium
Applying the Nash equilibrium
As we explain in Chapter 16 on game theory, the Nash equilibrium is a combination of strategies whereby each player is doing the best she possibly can given the strategies of the other players. Read the nearby sidebar “A Nash equilibrium aids human survival” for a somewhat chilling example.
Knowing about a Nash equilibrium and how you find one are important for understanding how economists go about looking at issues of competition and cooperation. As we describe in this chapter, economists use the concept of a Nash equilibrium to go beyond exchanges in markets and into wider questions of organizational behavior, bargaining, and even international negotiations, without giving up economic rationality.
A Nash equilibrium is a situation where no one has an incentive to change behavior. In that sense, Nash equilibria tend to be stable as long as the conditions around them stay stable. For instance, in the sidebar example, the peace between the nuclear powers was maintained for as long as nuclear weapons stayed out of the hands of rogue nations — ones that might not act “rationally.” If, for example, North Korea suddenly got the bomb, then the stability of the arrangement would have changed, perhaps catastrophically.
You might find the same thing looking at an oligopoly, as in Chapter 11. The equilibrium described between the two firms in Cournot’s model is a Nash equilibrium. However, if a third, more innovative firm enters the market, things will change. It would change the decisions of the firms in the market and eventually lead to a new Nash equilibrium.
So, finding the Nash equilibrium can be a useful tool for understanding market dynamics and market stability.
If you’re unfamiliar with game theoretical reasoning, we suggest that you read Chapter 16 before proceeding with this one.
Defining the Nash Equilibrium Informally
The Nash equilibrium does have a formal definition (and proof) but it requires some highly advanced math. Mercifully, this section only provides three informal definitions that amount to the same thing without having to dip into the really hard stuff:
-
 A Nash equilibrium is a set of strategies, one for each player, such that when these strategies are played, no one player has an incentive to change strategy. The Cournot, Bertrand, and Stackelberg equilibria in Chapter 11 are Nash equilibria.
A Nash equilibrium is a set of strategies, one for each player, such that when these strategies are played, no one player has an incentive to change strategy. The Cournot, Bertrand, and Stackelberg equilibria in Chapter 11 are Nash equilibria. - A Nash equilibrium exists when each player is maximizing her payoff in response to what she anticipates the other players will do given that the other players are also choosing strategies that maximize their payoffs. Again, this applies very clearly to Oligopoly models, and situations such as a when a monopoly buyer is negotiating with a monopoly seller — the Department of Defense, for example, negotiating with Boeing.
- A Nash equilibrium is an outcome in which adopting a strategy or making a move that makes a player better off is impossible without making other players worse off.
Looking for Balance: Where a Nash Equilibrium Must Apply
If you like, you can think of a Nash equilibrium as being a point of balance. At a Nash equilibrium, no participants have any incentive to change their behavior. You might imagine it as being like balancing on a seesaw — both people at either end could move the seesaw down, but they’d rather stay exactly as they are.
To see where a Nash equilibrium has to exist, we start by pointing out that not every game has one. In many games, if a player is restricted to choose a pure strategy (that is, choose a strategy with a probability of 1 — see Chapter 16 for more on that), it may not be possible to find a Nash equilibrium.
Consider, for example, the game Rock, Paper, Scissors as played by many a child in the playground. Each choice of rock, paper, or scissors is defeated by exactly one opponent’s move — rock smashes scissors, paper wraps rock, scissors cut paper — and also defeats exactly one opponent’s move. Thus the payoff matrix or strategic form of the game (flip to Chapter 16 for a definition) looks like Figure 17-1. (You’ll have to work out the matrix for Sheldon Cooper’s far more complicated version of Rock, Paper, Scissors, Lizard, Spock for yourself.)
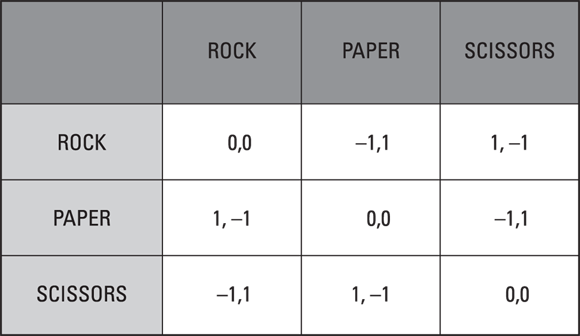
© John Wiley & Sons, Inc.
Figure 17-1: Payoff matrix for pure form of Rock, Paper, Scissors.
- If Kevin also plays rock, Karen would’ve been better off playing paper.
- If Kevin plays paper, he wins that round and Karen would be better off switching.
- If Kevin plays scissors, he loses and would’ve been better off changing his choice.
So, no point exists where both players are going to stay happy with their moves. Irrespective of where you start with Rock, Paper, Scissors, you always end up in a situation where at least one player can be made better off by doing something different. Hence, no Nash equilibrium.
Recognizing that a Nash equilibrium must exist in mixed-strategy games
The pure strategy version of Rock, Paper, Scissors has no Nash equilibrium. But if the strategies were used with a given probability — for example, Karen played rock with probability 1/3 — then you’d see a very different outcome. What does it mean to play a strategy with probability 1/3? It’s as if Karen had a pie chart divided into thirds: one third for rock, one third for scissors, and one third for paper. Before choosing, she spins a pointer on the pie chart, and where it lands is the move or action that she makes. When players mix their strategies, we can show that at least one Nash equilibrium must exist in any finite game. The equilibrium strategies in this case are probability mixes that no player has an incentive to change.
Finding a Nash equilibrium by elimination
The typical way of finding a Nash equilibrium in the strategic form of a game is by eliminating any strategies that can’t be optimal to play. This method relies on the concept of a dominant strategy.
- Weakly dominant: If it’s always at least as good as any other given strategy in terms of payoff the player gets
- Strongly dominant: If it always gives a higher payoff than any other possible strategy the player could choose
Figure 17-2 shows an example of a strategic form of game. The method just described is called the iterated elimination of dominated strategies. It means, very simply, that you go eliminate one by one any strategy that wouldn’t be chosen by a player, because playing another strategy would lead to higher payoffs no matter what the other player does. If you arrive to a point where no player has any incentive to change strategy, then you’ve “solved” the game. You found the Nash equilibrium. In the game in Figure 17-2, start by eliminating Right for the Colm player (she always does better playing Middle than Right). Once Right is eliminated for Colm, then we can eliminate Down for Rowe. Once Down is eliminated, then we can eliminate Left for Colm, and voila we have found the Nash Equilibrium (Up, Middle) and you can award yourself a gold star.
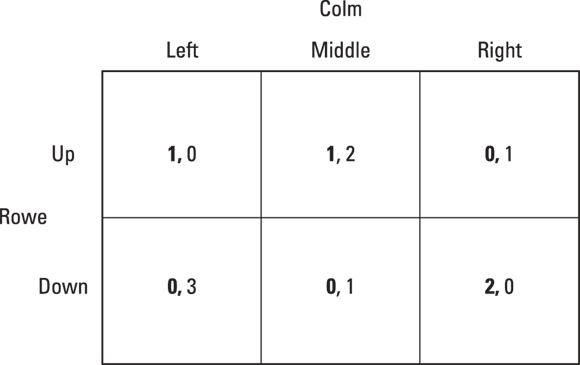
© John Wiley & Sons, Inc.
Figure 17-2: Finding a Nash equilibrium by elimination of dominated strategies.
Solving a repeated game by backward induction
A repeated game, such as a repeated version of the Prisoner’s Dilemma (described in detail in Chapter 16) takes place over many rounds, and the overall payoffs are computed at the end of the game. The matrix you get by looking at the payoffs for one round is the strategic form of the game from the last chapter.
As an example, consider the trust game, which has been applied to the relationship between managers and workers or to the “trust but verify” strategies in disarmament. In the trust game, two participants have to decide whether or not to trust each other. In the first round, the first player, Yvonne, has to decide between trusting the second player, Zak, or not trusting him. After Yvonne makes her choice, Zak has to choose in the second round between honoring Yvonne’s trust or betraying it. We set up the game and see how to solve it.
Start with Yvonne:
- If Yvonne decides not to trust Zak, the relationship is over, and both parties gain zero.
- If Yvonne does trust Zak, he makes the next choice:
- If Zak chooses to honor this trust, he gets 1 and Yvonne gets 1.
- If Zak cheats, he gets 2 and Yvonne gets –1.
- If Yvonne knows this, what should she do?
To solve the game using backward induction, you start by writing the game down in extensive form as a tree. (Or take a look at Figure 17-3, which does this for you.)
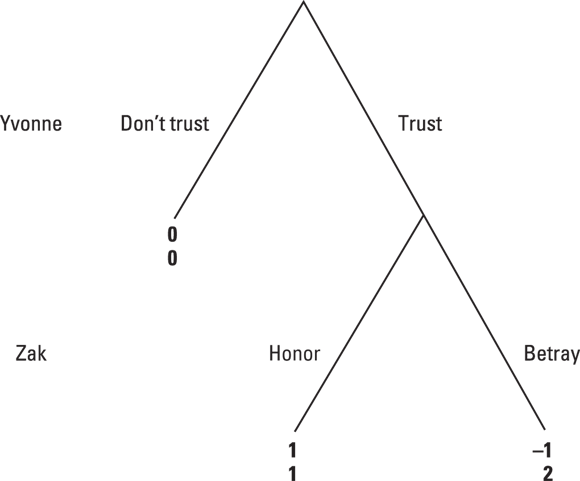
© John Wiley & Sons, Inc.
Figure 17-3: Extensive form of the trust game.
Working backwards from the very end, Zak’s round, note that Zak has a dominant strategy: Starting from this part of the tree, Zak does better, getting 2 (as opposed to 1) when he betrays Yvonne. Thus Zak will betray Yvonne.
Now go roll back to Yvonne’s move. If she knows what Zak’s payoffs to cheating are, then she can anticipate that he’s going to cheat, and so she chooses not to trust. Thus, the business relationship terminates before it has a chance to be poisoned.
You can say that solving this game for a Nash equilibrium finds that Yvonne and Zak do their best given each other’s payoffs by staying well away from each other.
Check out the nearby sidebar “Scoundrels don’t profit in the long run” for a timely financial example.
Applying the Nash Equilibrium in Economics
Microeconomists use game theory to investigate many issues in economics — ranging from bargaining to imperfect competition to choice of political affiliation. Here are two classic examples of how economists use game theory — first to look at what a monopoly might do to defend its dominant share of a market, and then to look at what happens to societies over the long run when members of that society have different strategies for dealing with people who would do them wrong.
Deterring entry: A monopolist’s last resort
If a company has been successful enough to gain a dominant share of a market, it often wants to prevent a rival from coming in and stealing that market away.
In Figure 17-4 we set up the situation as a game between a monopolist and an entrant. The entrant chooses to enter or not, and the monopolist chooses to retaliate (fight the entrant) or not. The monopolist wants to make the payoffs turn out so that the Nash equilibrium has the entrant choosing “Don’t enter.” When you analyze the game, you will see that it is a variant of the trust game in the earlier section “Solving a repeated game by backward induction.”

© John Wiley & Sons, Inc.
Figure 17-4: Entry deterrence game.
Analyzing society with economic reasoning
Economists have come a long way from merely studying markets and often look for ways of applying economic reasoning to difficult problems in other areas. One of these is the evolution of social institutions. Economists are able to use the insights of game theory to consider how cooperation and competition shape the strategies people use to punish those who cross them.
In society people have two ways of dealing with those who act against others: forgiving them or punishing them. If you think of society as a set of repeated Prisoner’s Dilemma games (see Chapter 16), you can develop a model that looks at punishing and forgiving as two different strategies. If the repeated games have different Nash equilibria, you can then think about how to characterize the different ways of behaving and compare the equilibria, telling you over the long run which strategy would be preferred from society’s point of view.
- Tit for Tat: Players start by playing the Dove. When one plays a Hawk, the other players default to Hawk too until the first player to play Hawk returns to playing Dove. Then, everyone else reverts to Dove.
- Grim Trigger: After a player has defaulted, the other players punish her by playing Hawk and never return to playing Dove, whatever the original defaulter’s subsequent moves.
- Firm but Fair: A bit like tit for tat, but the first default to Hawk is forgiven, and only the second one punished.
The evidence is that strategies like Firm but Fair tend to do better in simulations than Grim Triggers — providing evidence that though nice guys may finish last, nice societies tend to be better in the long run.

 The last definition ties the Nash equilibrium to the concept of Pareto efficiency, often used when looking at how people can be made better off. Economists describe an allocation of resources as Pareto efficient when no party can be made better off without making another party worse off. If those conditions hold at the Nash equilibrium, the payoffs are a Pareto efficient distribution. (
The last definition ties the Nash equilibrium to the concept of Pareto efficiency, often used when looking at how people can be made better off. Economists describe an allocation of resources as Pareto efficient when no party can be made better off without making another party worse off. If those conditions hold at the Nash equilibrium, the payoffs are a Pareto efficient distribution. ( Entry deterrence is a key concept in antitrust policy. The main antitrust statute in the United States, the Sherman Act, makes it clear that exploiting monopoly power to impede competition is illegal. So, for example, it is illegal to temporarily price below cost to prevent a competing firm from surviving in the market. If the competing firm is a would-be entrant, it would not be able to afford to enter the industry.
Entry deterrence is a key concept in antitrust policy. The main antitrust statute in the United States, the Sherman Act, makes it clear that exploiting monopoly power to impede competition is illegal. So, for example, it is illegal to temporarily price below cost to prevent a competing firm from surviving in the market. If the competing firm is a would-be entrant, it would not be able to afford to enter the industry.